2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
拓扑优化是结构优化分析中最为复杂的优化,可在优化区域范围内寻找到传力路径最优的子域,使结构在满足约束条件的情况下,达到优化目标。
拓扑优化在结构优化设计中具有重要作用,是结构优化设计的重要手段。夏天翔等[1]对均匀化方法、变密度法连续体结构的拓扑优化方法进行总结和比较。左孔天[2]对连续体结构拓扑优化的理论体系结构、相关算法和应用进行了系统分析。严卫祥[3]研究了基于应力约束的油船货舱区结构拓扑优化,基于优化结果获得了横剖面的优化设计。张会新[4]使用拓扑优化变密度法对上层建筑板架结构进行优化,并对船体板架结构进行形状和尺寸优化。朱俊侠等[5]以VLCC货舱区域内横向强框为优化对象,提出一套适用于复杂工况下横向强框结构的拓扑优化设计流程。
目前,对散货船的结构优化主要集中在结构布置、尺寸优化等方面,唐明非等[6]对某85000 t散货船的布置、总纵强度计算等角度进行了优化;王从晶[7]对散货船规范计算的设计要点进行总结并给出优化建议;阚甜甜等[8]对散货船船体梁静水弯矩、典型横剖面和局部结构进行了优化研究;孙宇[9]对大型散货船舱口围板的局部强度、疲劳强度进行研究并对结构进行了优化设计。研究人员对散货船结构的拓扑优化研究较少,也少有对顶边舱横隔板进行优化研究。本文以某散货船实船为例,对其风暴压载货舱的顶边舱横隔板进行了拓扑优化,建立了拓扑优化的方法和流程,基于优化结果给出了新的横隔板型式,并基于散货船油船协调共同规范(HCSR)计算要求对优化型式进行了常规网格和细化网格的分析校核以满足规范要求。优化后的构型相对原始设计能获得更轻便的重量和更小的应力结果。
1 基于变密度法的散货船顶边舱横隔板拓扑优化模型 1.1 基于变密度法的拓扑优化数学模型拓扑优化的主要目的是通过找到传力效果最好的结构布置型式,提高材料的利用效率,减小结构的重量。拓扑优化中常用的拓扑表达形式和材料差值模型有:均匀化方法、密度法、变厚度法和拓扑函数描述方法[10]。
变密度法基于均匀化方法,以材料的密度为拓扑变量,一般以最小重量、柔度等为优化目标,考虑位移约束和结构平衡条件,最终的方案通过选定密度的阈值,去除密度小于阈值的单元以获得优化构型。通过建立起假想材料单元密度
| $ \varphi\left(\rho_{i}\right)=\rho_{i}^{p} 。$ | (1) |
则可建立单元密度和材料弹性模量的关系,如下式:
| $ E\left(\rho_{i}\right)={E}_{\min }+\phi\left(\rho_{i}\right)\left(E-{E}_{\min }\right)={E}_{\min }+\Delta E \rho_{i}^{p} 。$ | (2) |
式中:
基于变密度法的优化区域内单元的刚度矩阵可表示为:
| $ {\boldsymbol{K}}\left(\rho_{i}\right)=\sum_{i=1}^{m}\left({E}_{\min }+\Delta E \rho_{t}^{{p}}\right) k_{i} 。$ | (3) |
变密度法进行拓扑优化通过迭代设计域内单元密度以获取满足优化约束条件下的优化目标。
本文对散货船顶边舱横隔板的拓扑优化以结构重量为目标,基于舱段计算的多工况对横隔板的应力进行约束,结构拓扑优化的数学模型如下式:
| $ \begin{array}{l} \min \quad {weight}=\int_{\alpha} \rho_{i} {\mathrm{d}} \Omega ,\\ \text { s.t. } \rho_{i} \in[0,1] ,\\ {\boldsymbol{K}}(\rho) \vec{u}_{j}=\vec{F}_{j} ,\\ {{stress}}_{j} \leqslant \left[\sigma_{v m}\right]_{j} ,\\ i=1,2, \cdots, m ; j=1,2, \cdots, n。\end{array} $ | (4) |
式中:weight为优化区域板材的总重量,t;
散货船顶边舱横隔板主要起到支撑甲板、外壳和顶边舱斜板的作用,在描述性设计阶段无特殊要求,通常设计为规范要求的最小板厚,后续进行有限元加强。设计中,散货船顶边舱横隔板一般设计为大开口,开孔通常以面板或偏筋加强,在横隔板上还设置了防倾肘板和屈曲筋。本文以某满足散货船油船协调共同规范要求的散货船实船顶边舱横隔板为研究对象进行拓扑优化,其风暴压载舱的顶边舱横隔板原始设计如图1所示。
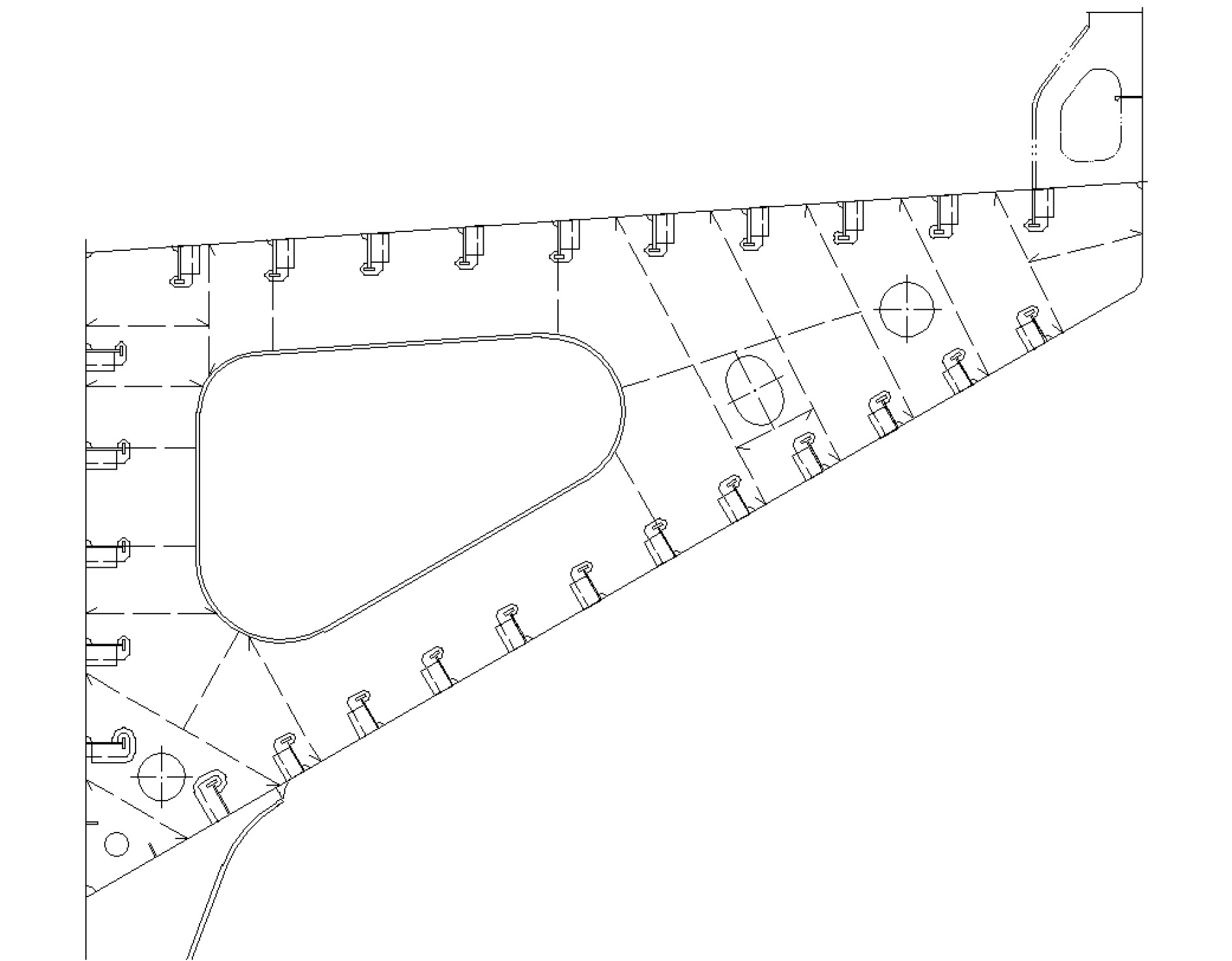
|
图 1 某散货船顶边舱横隔板结构型式 Fig. 1 Topside web frame of bulk carrier |
在拓扑优化设计中,如果要考虑开孔面板、防倾肘板和屈曲筋这3种构件对横隔板的作用,则拓扑模型的优化区域很难选择。另一方面,由于横隔板主要对甲板、外壳和顶边舱斜板起支撑作用,不承受面外压力,在优化时可先不考虑屈曲加强筋和防倾肘板的影响。本文在进行拓扑优化时,去除横隔板模型中上述3种构件,建立横隔板优化有限元模型。
本文以横隔板最小重量为优化目标,在去除上述3种构件后,如何定义约束条件成为优化的关键。顶边舱隔板的设计主要关注开孔边缘和面板的应力,优化分析中将原始设计模型中开孔面板、防倾肘板和屈曲筋等3种构件删除进行强度计算后横隔板上每个工况的应力最大值为应力约束。为获取优化能获得较好的结构构型,将横隔板上网格尺寸细化为100 mm×100 mm。横隔板上应力较大的区域为开孔边缘,假定当优化构型满足上述约束时,可以通过类似原始设计的面板加强以使优化设计满足规范要求。
由于横隔板需对纵骨起支撑作用,按经验横隔板高度至少大于1.5倍纵骨高度,取离边界400 mm外的区域为优化区域。
为提高优化效率,优化使用的舱段子模型进行,如图2(a)所示。拓扑优化区域如图2(b)所示。拓扑优化计算基于HyperWorks/ Optistruct完成。
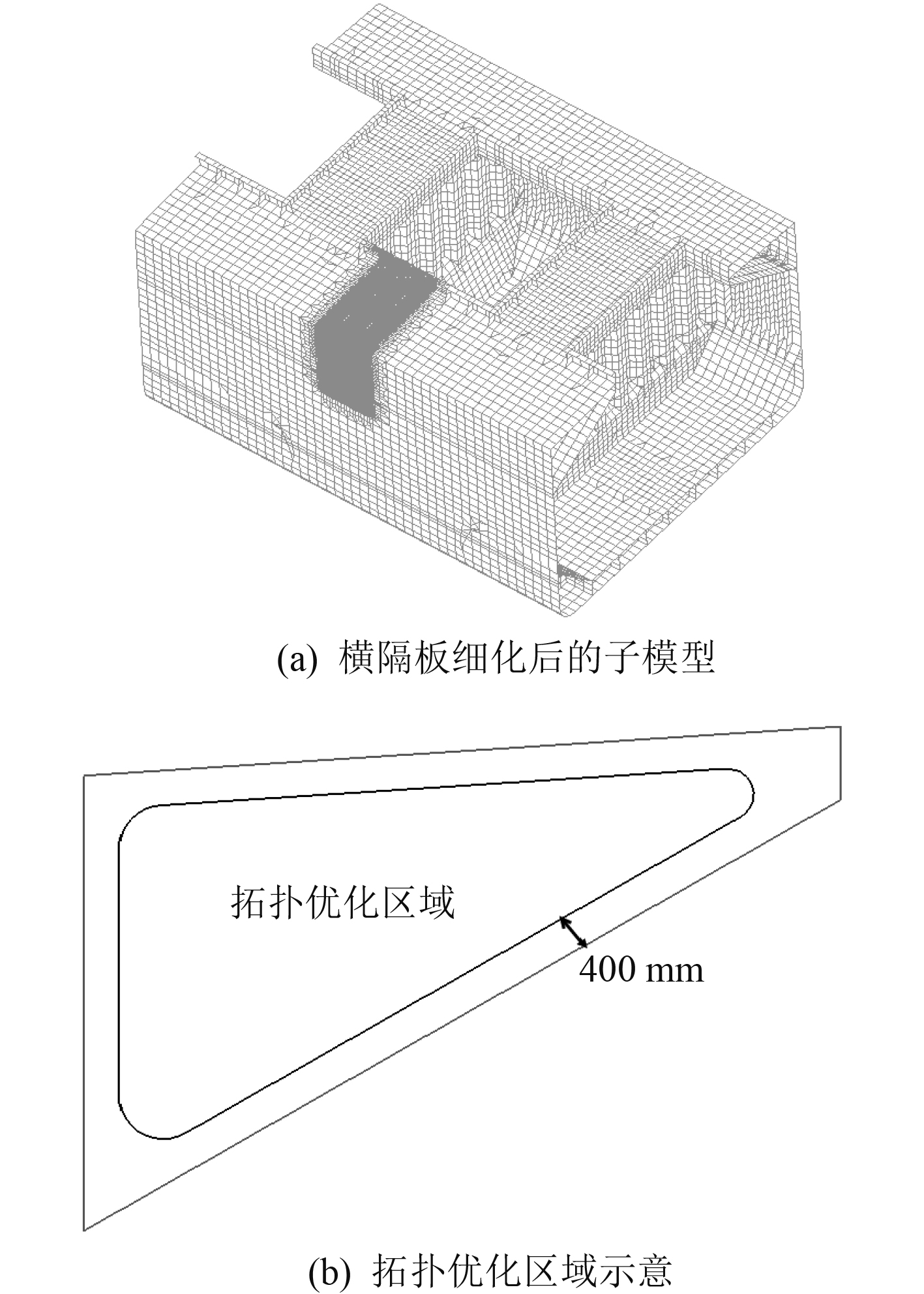
|
图 2 优化分析的有限元子模型和优化区域示意 Fig. 2 Finite element sub model for optimization and the optimization zone |
散货船一个货舱内会设置几档顶边舱横隔板,且为设计和施工方便,各个横隔板的型式会统一。横隔板进行优化设计有2种方法,一是选取原始设计中应力较大的强框进行优化设计,二是同时对货舱内所有横隔板进行拓扑优化,并通过模式重复方法使各个横隔板的优化构型保持一致。
2.1 单个顶边舱横隔板的拓扑优化以原始设计中应力最大的横向强框为优化对象,优化计算的子模型如图2(a)所示。经过优化之后,对拓扑优化结果的单元密度分别按阈值0.3、0.5和0.8获得拓扑构型,所得的拓扑构型分别如图3所示。

|
图 3 单个横隔板优化后不同阈值下的拓扑构型 Fig. 3 Topology shape of different thresholds after optimization with one topside web frame |
以货舱内所有横隔板为优化对象,以原始设计中去除开孔面板、防倾肘板和屈曲筋这3类构件的100 mm×100 mm细化网格的最大应力为应力约束条件,以所有横隔板的重量最轻为优化目标进行拓扑优化。采用模式重复方法设定其中一块横隔板为主设计区,将其余横隔板设置为从设计区,由此可保证各个横隔板上的优化构型保持一致。经过优化之后,对拓扑优化结果的单元密度分别按阈值0.3、0.5和0.8获得拓扑构型,所得的拓扑构型分别如图4所示。

|
图 4 货舱内所有横隔板优化后不同阈值下的拓扑构型 Fig. 4 Topology shape of different thresholds after optimization with all topside web frames in cargo hold |
基于拓扑优化结果可以发现,在相同阈值下,针对单个横隔板进行拓扑优化与同时对所有横隔板进行拓扑优化所得形状基本一致,对所有横隔板进行拓扑优化保留的单元相对更多。
基于拓扑优化结果设计横隔板结构型式,取阈值0.3的拓扑构型,如图5所示。
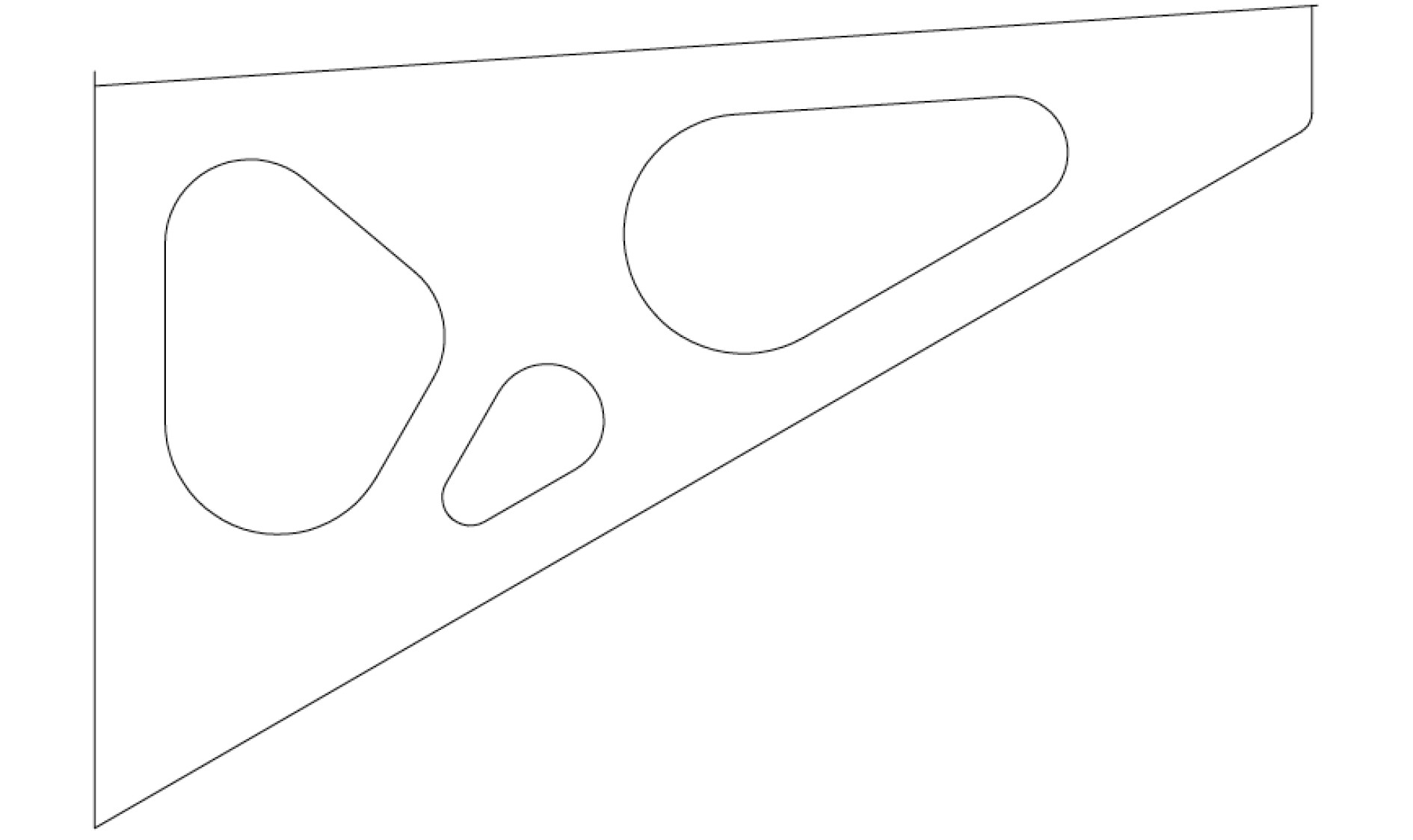
|
图 5 优化后横隔板的开孔型式 Fig. 5 Design of topside web frame after optimization |
按照优化的型式建立100 mm×100 mm的横隔板细化模型,不考虑开孔面板、防倾肘板和屈曲筋与原始方案的细化模型在所有计算工况中应力最大的几个工况下的应力进行比较,所得结果如表1所示。
|
|
表 1 所有优化工况下不同设计方案的横隔板细化模型Von Mises应力 Tab.1 Von mises stress of topside web frame in all load cases of optimization |
基于计算结果可以发现,优化方案的整体Von Mises应力相比原始设计要小很多。
3 散货船顶边舱横隔板优化方案的校核基于优化方案的构型,完成横隔板的详细设计,开孔面板规格选取与原始设计中初始尺寸一致,并代入三舱段有限元模型中完成有限元强度校核和开孔细化分析。将优化方案代入三舱段模型中建立的横隔板有限元模型如图6所示。
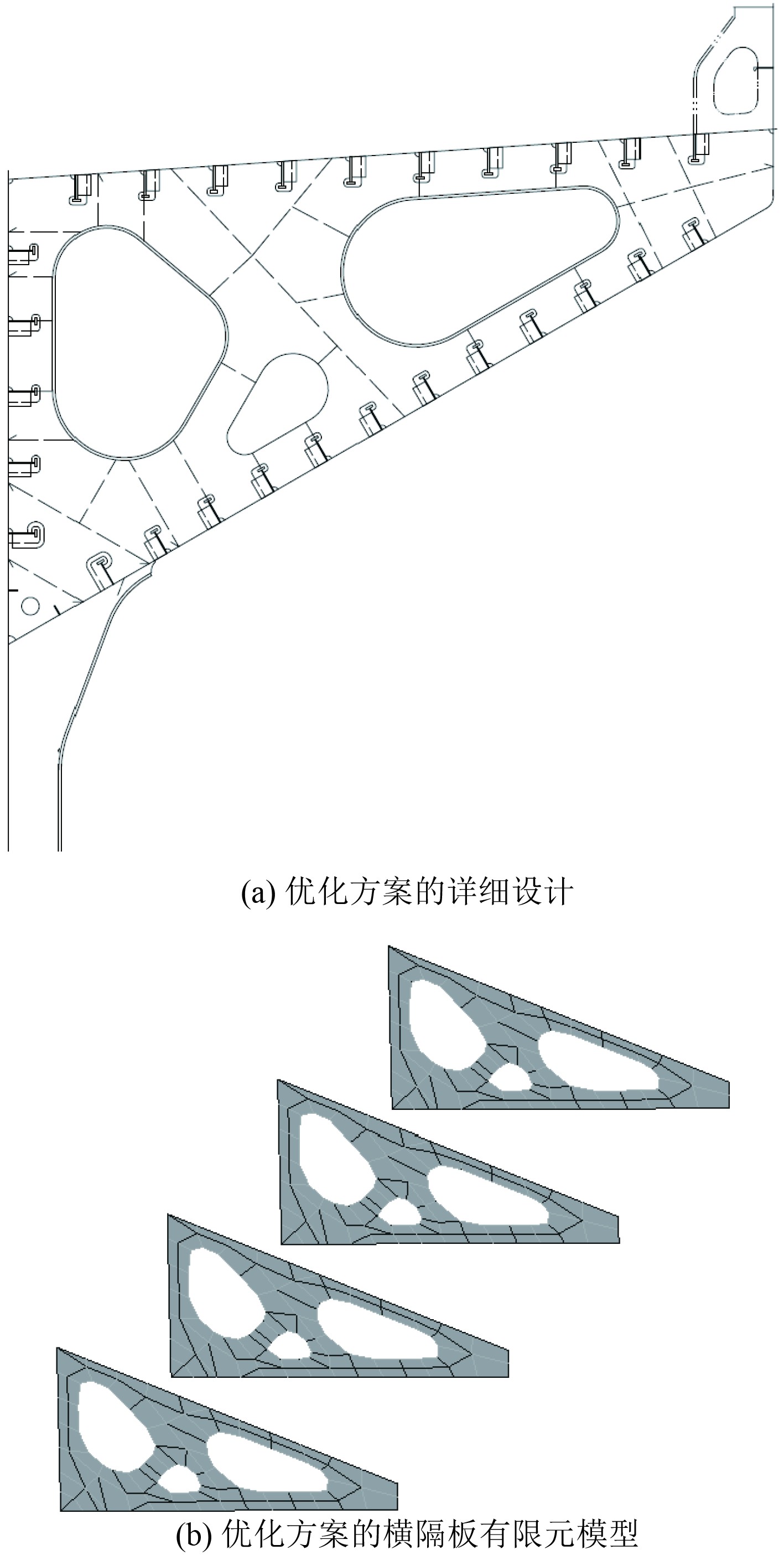
|
图 6 横隔板优化的详细设计和有限元模型 Fig. 6 Detailed design and finite element model of topside web frame after optimization |
基于横隔板优化的详细设计建立有限元模型,代入三舱段模型中进行,原始设计和优化设计在所有计算工况下横隔板的Von Mises应力和开孔面板梁单元轴向应力如表2所示。
|
|
表 2 舱段计算所有工况下横隔板和开孔面板最大应力 Tab.2 Max von mises stress of topside web frame in all load cases |
原始设计中的开孔面板应力超过了规范许用值(326 MPa),需加大面板尺寸。优化方案的横隔板应力和开孔面板应力相对原始设计均较小,且满足规范要求。
3.2 优化方案的细化分析校核基于优化方案选取应力最大的横隔板进行细化分析,并将开孔边缘面板用板单元模拟,细化网格为50 mm×50 mm,计算所有工况下的横隔板、面板应力,为分析不同型式顶边舱斜板对舷侧肋骨的影响,将肋骨端部也进行细化分析,为准确模拟肋骨端部形状,局部区域网格大小为15 mm×15 mm。横隔板优化方案的细化模型如图7所示。

|
图 7 横隔板优化设计的细化模型 Fig. 7 Fine mesh model of topside web frame |
所得应力结果与原始设计进行比较分析,如表3所示。
|
|
表 3 舱段计算所有工况细化分析的横隔板和开孔面板应力 Tab.3 Fine mesh stress of topside web frame and side frame end bracket in all load cases |
优化后的横隔板面板、腹板和舷侧肋骨根部的细化应力均比原始设计要小,且均能满足规范要求,不需进一步加强。
优化后单个横隔板重量为1.972 t,且设计满足规范计算要求。横隔板原始方案初始重量为2.128 t,加强满足规范要求后的重量为2.154 t。在均满足规范要求的情况下,横隔板优化后的重量比原始设计轻8.5%。
4 结 语拓扑优化能提高结构材料的利用效率,获得最佳的传力路径。本文以某散货船顶边舱横隔板为优化对象,建立了横隔板拓扑优化的有限元模型处理简化处理、细化以及对照原始设计进行应力约束的优化流程,得到如下主要结论:
1)本文提出的横隔板拓扑优化的有限元模型处理、应力约束的设置方法能获得较合适的拓扑构型。
2)对散货船顶边舱横隔板进行拓扑优化时,相同阈值下选取原始设计应力最大的横隔板单独优化与对货舱内所有横隔板同时优化相比拓扑形状基本一致,但保留的单元相对更少。
3)本文基于阈值0.3时的拓扑构型对某散货船横隔板进行了重新设计,经舱段粗网格和细化网格分析后所有工况下的最大应力结果均比原始设计要小,且均满足规范要求,无需额外加强。优化后的单个横隔板重量比原始设计轻8.5%。
散货船结构设计时主要关注结构强度,在对相关结构进行拓扑优化时如何简化有限元模型、设置应力约束是优化设计的难点。本文在对散货船顶边舱隔板进行拓扑优化时,去除了横隔板上的加强筋和面板,对有限元模型进行了局部细化处理并参照原始设计进行了这些处理后相关工况的应力作为约束对横隔板进行了拓扑优化,基于优化构型给出了新的设计并进行了验证。本文的研究可以为散货船的拓扑优化、顶边舱横隔板的设计提供一定的参考。
| [1] |
夏天翔, 姚卫星. 连续体结构拓扑优化方法评述[J]. 航空工程进展, 2011, 2(1): 1-11+55. XIA T X, Yao W X. A survey of topology optimization of continuum structure[J]. Advances in Aeronautical Science and Engineering, 2011, 2(1): 1-11+55. DOI:10.3969/j.issn.1674-8190.2011.01.001 |
| [2] |
左孔天. 连续体结构拓扑优化理论与应用研究[D]. 武汉: 华中科技大学, 2004.
|
| [3] |
严卫祥. 基于共同规范的油船货舱区结构优化设计[D]. 上海: 上海交通大学, 2015.
|
| [4] |
张会新, 杨德庆. 典型船舶板架拓扑与形状优化设计[J]. 中国舰船研究, 2015, 10(6): 27-33,59. ZHANG H X, YANG D Q. Typical shape and topology optimization design of the ship grillage structure[J]. Chinese Journal of Ship Research, 2015, 10(6): 27-33,59. DOI:10.3969/j.issn.1673-3185.2015.06.005 |
| [5] |
朱俊侠, 吴嘉蒙. 基于变密度法的VLCC货舱内横向强框架拓扑优化研究[J]. 船舶, 2019, 30(6): 123-132. ZHU J X, WU J M. Topology optimization of transverse web frame in cargo hold of VLCC based on variable density method[J]. Ship, 2019, 30(6): 123-132. |
| [6] |
唐明非, 匡岩, 许汀. 85 000 DWT散货船结构设计及优化[J]. 船舶工程, 2020, 42(12): 43-47. TANG M F, KUANG Y, XU T. Structural design and optimization of 85 000 DWT bulk carrier[J]. Ship Engineering, 2020, 42(12): 43-47. |
| [7] |
王从晶. 76000t CSR散货船结构优化技术浅析[J]. 造船技术, 2015(1): 13-19. WANG C J. Research on structural optimization of 76 000 DWT CSR bulk carrier[J]. Marine Technology, 2015(1): 13-19. DOI:10.3969/j.issn.1000-3878.2015.01.004 |
| [8] |
阚甜甜, 侯家怡, 郦羽, 等. 基于共同协调规范的散货船结构质量优化设计[J]. 船舶工程, 2022, 44(S1): 231-237+255. KAN T T, HOU J Y, LI Y, et al. Structure design and optimization of bulk carrier based on CSR-H[J]. Ship Engineering, 2022, 44(S1): 231-237+255. |
| [9] |
孙宇, 盛利贤, 叶杰. 大型散货船舱口围板优化设计[J]. 舰船科学技术, 2022, 44(8): 30-34. SUN Y, SHENG L X, YE J. Study on the optimization design of hatch coaming of large bulk carrier[J]. Ship Science and Technology, 2022, 44(8): 30-34. DOI:10.3404/j.issn.1672-7649.2022.08.006 |
| [10] |
洪清泉, 赵康, 张攀. Optistruct&HyperStudy理论基础与工程应用[M]. 北京: 机械工业出版社, 2012.
|
 2024, Vol. 46
2024, Vol. 46
