0 引　言

大型水面舰船是最主要的海上作战平台和掌握制海权的关键，以此为中心的攻防对抗是现代海战最主要的样式之一。反舰导弹侵彻舰船外层舱壁进入舱室后，通过延时引信的适时作用引爆战斗部装药，舰船舱壁结构在爆炸冲击载荷作用下产生变形挠度甚至撕裂破口，对舰船的生命力造成重大威胁，结构在爆炸冲击波载荷作用下，动态响应是抗爆设计中的关键性问题，一直受到工程界的广泛关注^{[1 − 3]}。

许多军事目标如舰船、车辆、雷达等多为平板形结构，在目标易损性研究中，采用一定厚度的平板替代真实舱壁进行毁伤效应分析^[4]。薄板在爆炸冲击波载荷作用下，表现出大的变形挠度及破口，其动态响应是典型的爆炸力学问题，很多学者对此类问题进行了相关研究。Zhao等 ^[5]在对固支方形板在爆炸载荷作用的变形挠度求解中，提出了饱和冲量的概念，利用模态分析法给出了靶板变形挠度的解析。Zhu等^[6]在材料的刚塑性模型和弹塑性模型上，将计算机程序应用于处理爆炸载荷作用下，靶板的动态响应问题中。Jones^[7]对均布冲击载荷作用下，简支圆板的动态响应进行了理论分析，所建立的理论模型考虑了板的弯曲效应和中面膜力的影响，并与试验数据进行了验证。Baker等^[8]在能量守恒定律的基础上，以固支方形靶板为研究对象，建立了正方形板中心处的挠度计算公式。Langdon等^[9]结合能量法对爆炸冲击波作用下，固支板的动态响应进行分析，建立了板的塑性变形方程，针对理论模型进行了试验验证。Lee等^[10]利用数值仿真软件，通过改变局部载荷的强度分析固支金属板的变形挠度，结合靶板的极限应变判断是否发生撕裂毁伤。Nurick等^[11]对靶板在近距离爆炸的情况下，毁伤效应进行了大量的试验研究，从试验现象中发现，随着爆炸载荷强度的提高靶板毁伤模式由挠度变形逐渐发展为中心破口。Micallef等 ^[12]以弹塑性理论为基础，考虑了弯曲与中面膜力效应的影响，推导出了近距离局部爆炸载荷作用下，固支靶板的塑性变形计算公式。王芳等^[13]对固支方板在爆炸载荷作用下的挠度求解问题进行了大量的试验研究，基于能量守恒原理推导了固支板在爆炸冲击波作用下，靶板挠度的理论计算模型。何建等^[14]从力学角度对靶板的动态响应特性进行分析，建立了固支方形靶板中心点的挠度计算模型，并与试验结果进行了验证。张舵等^[15]以固支方板为研究对象，基于靶板的内力平衡控制方程，建立了方板在爆炸载荷下的运动微分方程，可对靶板的塑性变形挠度进行理论求解。朱锡等^[6]以金属板的弹塑性理论为基础，根据极限应变准则确定了靶板的临界毁伤挠度值。吴有生等^[16]在考虑应变关系和中面拉伸膜力的情况下，采用能量法考虑大变形时，应变关系及中面膜力的影响，求解了船体板结构塑性大变形。陈长海等^[17]基于能量守恒定律，对近距空爆冲击波作用下，固支靶板的毁伤机理展开研究，给出了靶板中心点最大挠度的求解模型，并进行了试验验证。

本文以动量定理和能量守恒定理为基础，研究固支金属方形板在爆炸冲击波作用下的塑性变形及破损，建立了可应用于计算固支方板在爆炸冲击波作用下发生的塑性变形挠度理论模型。以极限塑性应变为准则得到了破口半径的计算公式，并开展了近距离空中爆炸试验对所建立的理论模型进行了验证，实验结果与理论求解吻合度较好，验证了本文建立的理论模型具有一定准确性，研究成果可应用于固支靶板在爆炸冲击波作用下的毁伤效应工程预测。

1 理论分析 1.1 初始动能

炸药爆炸后产生大量的高温高压的爆炸产物急剧膨胀压缩空气，当入射波在刚性壁面上发生正反射后，壁面处的气体介质瞬间压缩并形成沿远离壁面方向传播的反射冲击波，冲击波作用下，方形金属板结构的反射比冲量$ {I}_{r} $可表示为^[17]：

$ I_{r}=2 A_{i} \sqrt[3]{G} /\bar r 。$

(1)

式中：G为装药量；$ \bar r$为比例距离；A_i为系数，$ A_{i} $≈300~370。其中，比例距离$ \bar r$可通过爆距与药量表示，即：

$ \bar r=R / \sqrt[3]{G} ，$

(2)

根据动量定理有：

$ v= \frac{I_r}{\rho H} ，$

(3)

由动能定理，方形金属板的动能为：

$ T=\frac{8a^{2}A_i^2 \sqrt[3] {G^4}}{R^{2}H\rho}。$

(4)

1.2 方形金属板的塑性变形能

方形金属板为正方形板，长宽为L，板厚为H，材料为Q235钢，密度为ρ，屈服强度为$ \sigma_0$，爆距为R。为了便于理论计算，以方形金属板几何中心为坐标原点建立坐标系，水平方向为x轴，向右为正；竖直方向为y轴，向上为正；截面水平方向设为z轴，向上为正，方形金属板在冲击波载荷作用下，出现如图1所示的塑性绞线。

由理论分析可知，舱壁的塑性变形能$ { E } $主要由塑性绞线弯曲变形能$ {E}_{1} $和舱壁板面内的拉伸变形能$ {E}_{2} $组成^[14]。OO₁为挠度$ W_{(t)} $大小，如图2所示。舱壁上塑性绞线弯曲变形能与舱壁板面内拉伸变形能可分别用下式表示：

$ \left\{\begin{aligned} & E_{1}=\frac{2}{\sqrt{3}} \times 4 \int M_{0}(2 \beta+\theta) {\rm{d}} l_{i}，\\ & E_{2}=4 H \int\int \sigma_{x} \varepsilon_{x}+\sigma_{y} \varepsilon_{y}+\tau_{s} \gamma_{xy} {\rm{d}} x {\rm{d}} y。\end{aligned}\right. $

(5)

式中：$ {M}_{0} $为舱壁上所受弯矩，$ {M}_{0}=\sigma_{0} {H}^{2} / 4 $；$ \beta $、$ \theta$均为塑性铰线的旋转角度；I_i为塑性绞线的长度，分别为AB、BC、OB的3条塑性铰线；$ \varepsilon_x$、$ \varepsilon_y $、$ \varepsilon_{xy}$分别为舱壁沿x和y方向的应变分量。

塑性铰线AB、BC处的旋转角度可用$ \beta$表示：

$ \beta=\arctan \frac{W _{(t)}}{a}，$

(6)

同理塑性铰线OB处的旋转角度可用$ \theta $表示：

$ \theta=\arctan \frac{W_{(t)} }{\sqrt{2}a} ，$

(7)

由于材料为刚塑性材料，所以当材料屈服时有：

$ \sigma_{x}=\sigma_{y}=\sigma_{0}，$

(8)

根据V.Mises屈服准则有：

$ \tau_{s}=\sigma_{0} / \sqrt{3}，$

(9)

$ \varepsilon_x$、$ \varepsilon_y$、$ \gamma_{xy} $为舱壁沿x和y方向的应变分量，可分别用下式进行表示：

$ \left\{ \begin{aligned} & {\varepsilon _x} = \frac{{\partial u}}{{\partial x}} + \frac{1}{2}{\left( {\frac{{\partial w}}{{\partial x}}} \right)^2}，\\ & {\varepsilon _y} = \frac{{\partial v}}{{\partial y}} + \frac{1}{2}{\left( {\frac{{\partial w}}{{\partial y}}} \right)^2}，\\ & {\gamma _{{x}y}} = \frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial y}} + \left( {\frac{{\partial w}}{{\partial x}}} \right)\left( {\frac{{\partial w}}{{\partial y}}} \right)。\end{aligned} \right. $

(10)

式中：u、v、w分别为舱壁中任一点在x、y、z方向上的位移，可用挠曲面函数进行表示：

$ \left\{ \begin{aligned} & u = {u_0}\sin \frac{{{\text π} x}}{a}\cos \frac{{{\text π} y}}{a}，\\ & v = {v_0}\cos \frac{{{\text π} x}}{{2a}}\sin \frac{{{\text π} y}}{a}，\\ & w = {w_0}\cos \frac{{{\text π} x}}{{2a}}\cos \frac{{{\text π} y}}{{2a}}。\end{aligned} \right. $

(11)

式中：$ u_{0} $、$ v_{0} $分别为舱壁在x和y方向上的最大位移；$ w_{0} $为舱壁中心在z方向上的最大位移$ W_{(t)} $；a为舱壁边长的一半。

通过式（5）～式（11）求得舱壁的塑性变形能近似为：

$ E=2 \sqrt{3} \sigma_{0} H^{2} W_{(t)}+\frac{1}{4} {\text{π}}^{2} \sigma_{0} H W_{(t)}^{2}，$

(12)

根据能量守恒定理有：

$ \frac{1}{4}{{\text π} ^2}{\sigma _0}H{W^2}(t) + 2\sqrt 3 {\sigma _0}{H^2}{W_{(t)}} - \frac{{8{a^2}A_i^2\sqrt[3]{{{G^4}}}}}{{{R^2}H\rho }} =0，$

(13)

整理得：

$ A W_{(t)}^{2}+B W_{(t)}+C=0 ，$

(14)

式中：$ A=\dfrac{1}{4}{\text π}^{2} \sigma_{0} H $；$ B=2 \sqrt{3} \sigma_{0} H^{2} $；$ C= - \dfrac{{8{a^2}A_i^2\sqrt[3]{{{G^4}}}}}{{{R^2}H\rho }}$。

经计算可知：

$ B^{2}-4 A C>0 ，$

(15)

所以该方程解为:

$W_{(t)}=\frac{-B+\sqrt{B^{2}-4AC}}{2A}。$

(16)

通过上述理论分析，当已知方形金属板的结构尺寸、材料参数、药量与爆距的情况下，可求出方形金属板的塑性变形挠度。

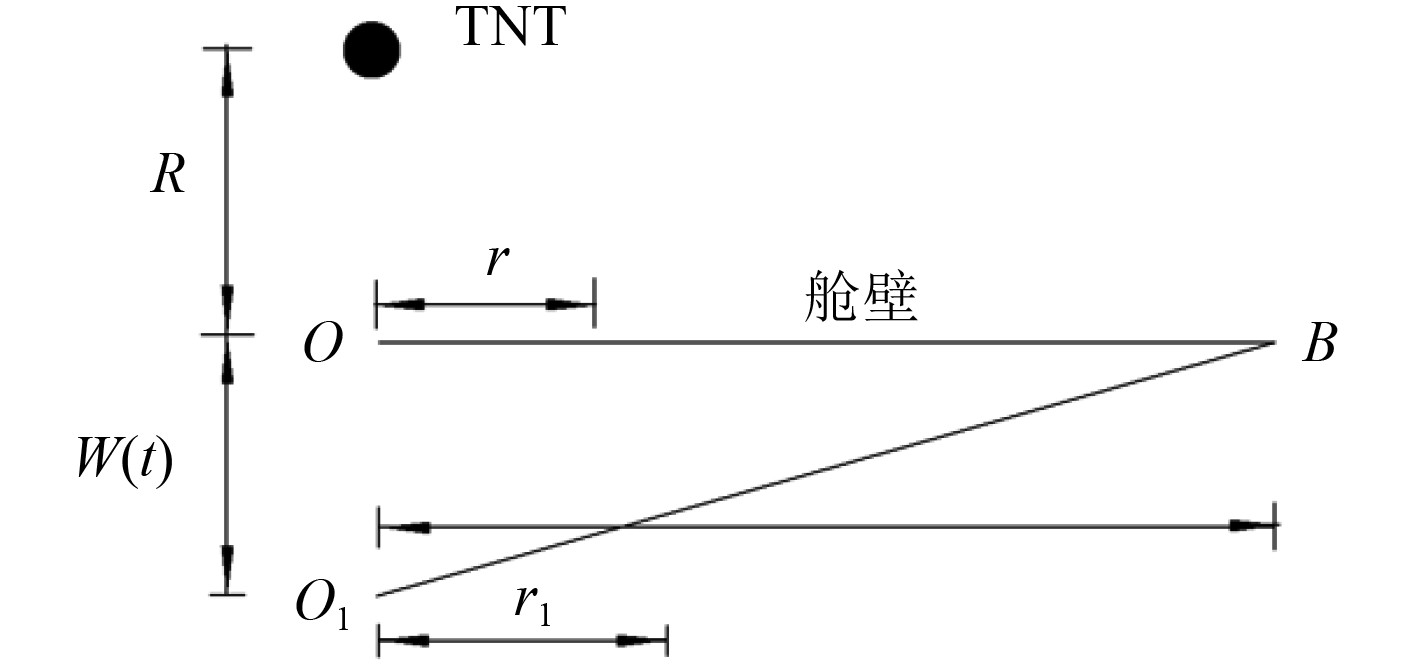
1.3 破口半径计算模型

近距空爆载荷作用下，靶板结构的局部效应非常明显，载荷作用区以外结构的变形很小，随着载荷强度的增大，其挠度并不会持续增大。当挠度增大到一定数值时，结构将首先在离装药最近的点处失效发生撕裂破坏，进而产生破口^[18]。为了便于计算，假设破坏开始发生在塑性铰线上，此时以塑性绞线上某点应变大于失效应变为准则，即当最大应变等于失效应变时，破口不再增大，达到最大尺寸r，此时将破口简化为圆形破口，如图3所示。

在爆炸载荷的作用下，塑性绞线上距中心r 某一点经变形后达到r₁的位置，由几何关系知：

$ r_{1}=\sqrt{2} a-(\sqrt{2} a-r) \cos \theta，$

(17)

则塑性铰线上该点处的拉伸应变为：

$ \varepsilon_{\theta}=\frac{r_1-r}{r}=\left(\frac{\sqrt{2} a}{r}-1\right)(1-\cos \theta)，$

(18)

式中：$ \theta$为冲击波载荷作用于舱壁时，塑性铰线的最大旋转角度，$ \theta=\arctan \dfrac{W_{(t)}}{\sqrt{2} a} $。

塑性绞线上弯曲应变为：

$ \varepsilon_{\theta b}=\frac{H}{2} K_{\theta}。$

(19)

式中：$ K_{\theta}$为塑性铰线上的弯曲曲率，$ K_\theta=\dfrac{\phi}{c}$；$ \phi$为舱壁在塑性铰线处的弯曲角度，用弧度制进行表示，取$ \phi = \arccos \displaystyle\frac{{{a^2}}}{{{a^2} + W_{(t)}^2}} $，c为塑性绞线上弯曲变形范围宽度，取$ {\mathrm{c}}=2 H $。

确定塑性绞线上弯曲应变为：

$ {\varepsilon _{\theta {{b}}}} = \frac{1}{4}\arccos \frac{{{a^2}}}{{{a^2} + {W_{(t)}}^2}} ，$

(20)

即塑性铰线上r 位置处最大塑性应变可表示为：

$ \varepsilon_{\theta} = \varepsilon_{\theta t} + \varepsilon_{\theta b} = \left( \frac{\sqrt{2}a}{r}-1 \right)( 1-\cos \theta) + \frac{1}{4} \arccos \frac{\alpha^{2}}{\alpha^{2} + W_{(t)}} 。$

(21)

当塑性铰线上r位置处塑性应变$ {\varepsilon _\theta }$等于舱壁的失效应变$ \varepsilon_f$时，舱壁破口不再增大，此时破口尺寸达到最大，即：

$ \left(\frac{\sqrt{2}a}{r}-1\right)(1-\cos \theta)+\frac{1}{4} \arccos \frac{\alpha^{2}}{a^{4}+1 W_{(t)}^{2}}=\varepsilon_{f}，$

(22)

则破口半径可表示为：

$ r = \frac{{\sqrt 2 a\left( 1-\cos\theta \right)}}{{1 + {\varepsilon _f} - \cos \theta - \dfrac{1}{4}\arccos \dfrac{{{a^2}}}{{{a^2} + {W_{(t)}}^2}}}} 。$

(23)

2 实验验证

本文开展了近距空爆试验，对爆炸冲击波载荷作用下固支方板破口尺寸进行研究，试验加工的箱体装置材料选用强度较高的 45#钢，舱体壁厚10 mm，为保证内爆试验过程中舱体结构不发生变形，在舱体四周焊有加强筋，舱室模型结构尺寸为900 mm×600 mm×600 mm。靶板试件与舱室模型之间通过螺栓紧固，金属板试件受夹持约束的边界区域布置了 32 个直径为18 mm 的螺栓孔，以保证模型边界不会出现较大的面内移动。根据试验设计的需要，为防止试验金属板试件在内爆作用下发生滑移，从螺栓孔位置撕裂，从而影响试验效果，故利用强度较高的法兰盘将金属板试件夹持约束在舱体上，舱室模型及靶板固定实物，如图4所示。

试验靶板试件为2 mm 厚的 Q235钢板，钢板受载面积尺寸为600 mm×600 mm。试验时，将钢板夹于法兰夹板和舱室模型之间，炸药采用柱形装药，等效TNT当量80 g，将炸药置于薄纸壳上摆放在靶板中心，雷管垂直于炸药上表面，柱形装药的中心距靶板的高度为90 mm，试验装置摆设如图5所示。

近距空爆冲击波载荷对固支靶板的破坏情况试验效果如图6所示，可看到钢板在爆炸冲击波的作用下中心部位产生了一个近似圆形的破口，并呈现出花瓣开裂的破坏形式，靶板中心区域的花瓣破口断开处有明显的拉伸变薄现象，并且在裂瓣尖端存在较严重的拉伸断裂，这说明在发生花瓣开裂之前，板的中心区域已产生了局部拉伸撕裂。破裂的花瓣数为4瓣，各裂瓣之间存在不同程度的翻转，花瓣破口的各裂瓣大小存在一定差异，出现这一现象的原因可能是由于试验过程中，炸药的摆放位置偏离了靶板的正中心。试验结束后，通过测量得到靶板试件的最大破口半径为59 mm，而破口最小处半径为51 mm，破口平均半径约为55 mm。将试验相同工况代入理论公式中进行计算，得到的舱壁靶板破口半径为62.8 mm，将理论计算得到的结果与模型试验得到的结果进行对比分析，相对误差为14.2%，可说明理论计算方法具有一定准确性。

为了进一步验证本文建立的破口尺寸计算模型的适用性，选取陈长海等^[17]近距空爆试验结果进行验证，试验靶板为4 mm 厚的 Q235钢板，靶板尺寸为700 mm×700 mm，炸药为圆柱形状，TNT等效当量为600 g，炸药中心距靶板的距离为108 mm，试验测得破口尺寸的平均半径为137 mm，试验装置示意图及靶板破坏形貌，如图7所示。

按照本文建立的破口尺寸计算方法，将试验工况代入理论公式中，得出计算结果为122.5 mm，与试验结果对比相对误差为10.9%，符合工程计算的要求，进一步证明了本模型的适用性。

3 结　语

本文以战斗部近距爆炸冲击波载荷作用下，舱壁的毁伤效应为研究对象，根据动量定理和能量守恒定理，建立了固支方板在爆炸冲击波作用下的塑性动力响应模型，可较方便地求解爆炸冲击波载荷作用下的板架挠度，以极限塑性应变为准则得到了破口半径的计算公式，并与实验结果进行了验证。结果表明，本文提出的模型可作为冲击波，对平板目标的毁伤量化评估方法，为爆炸冲击波对靶板的毁伤效应等相关工程领域的快速计算提供参考。