2. 上海交通大学 机械与动力工程学院,上海 200240
2. School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China
传统的舰载设备一般安装在刚性基座上,其载荷可直接传到舰艇龙骨。鱼雷、水雷等反舰武器在水下爆炸产生的巨大冲击载荷可由船体直接传递到舰载设备的基座上,因而对舰载设备存在很大威胁。当舰艇在海上航行时,船体结构同时承受着浮力和重力载荷,当在波浪中行进时,会发生“中拱”和“中垂”,同时还存在使舰艇产生扭转的附加扭力载荷。这些对于舰载设备来说都可看作基础或支撑的运动作用,然而在工程上,往往无法通过传感器获取由基础传递给舰载设备的冲击力载荷,而基础的位移、速度以及加速度却很容易测量。在结构的动力响应计算中,根据对基础运动激励所采取的不同等效转换策略,产生了惯性载荷法、大质量法、大刚度法和直接激励法等多种算法[1 − 5]。
由于舰载设备的组成和结构都很复杂,选用不同的算法会对舰载设备动力响应的计算结果以及计算精度都有所影响。因此,本文从结构动力学方程出发,将惯性载荷法、大质量法、大刚度法和直接激励法进行对比,并对这4种算法的特征和应用限制条件进分析。最后给出利用惯性载荷法、大质量法和直接激励法计算的算例结果,并对其正确性进行验证。
1 惯性载荷法、大质量法、大刚度法、直接激励法对比分析 1.1 惯性载荷法原理惯性载荷法的基本思想是通过坐标系转换将基础的加速度载荷转换成作用在结构上的惯性力,具体做法是将空间绝对坐标系转换为固结在结构上的活动坐标系。设
| $ \left\{\boldsymbol{U}\right\}=\left\{\boldsymbol{\delta }\boldsymbol{U}\right\}+\left[{\boldsymbol{D}}_{\boldsymbol{R}}\right]\left\{{\boldsymbol{U}}_{0}\right\} ,$ | (1) |
| $ \left[\boldsymbol{K}\right]\left[{\boldsymbol{D}}_{\boldsymbol{R}}\right]=0 \text{,} \left[\boldsymbol{C}\right]\left[{\boldsymbol{D}}_{\boldsymbol{R}}\right]=0。$ | (2) |
设结构相对于绝对坐标系的动力学方程为:
| $ \left[\boldsymbol{M}\right]\left\{\ddot{\boldsymbol{U}}\right\}+\left[\boldsymbol{C}\right]\left\{\dot{\boldsymbol{U}}\right\}+\left[\boldsymbol{K}\right]\left\{\boldsymbol{U}\right\}=\boldsymbol{P}\left(\boldsymbol{t}\right) 。$ | (3) |
式中,[M]、[C]、[K]分别为结构的质量矩阵、阻尼矩阵和刚度矩阵。
将式(1)代入式(3)同时考虑式(2)可知:
| $ [{\boldsymbol{M}}]\{ \delta {\boldsymbol{\ddot U}}\} + [{\boldsymbol{C}}]\{ \delta {\boldsymbol{\dot U}}\} + [{\boldsymbol{K}}]\{ \delta {\boldsymbol{U}}\} = {\boldsymbol{P}}({\boldsymbol{t}}) - [{\boldsymbol{M}}][{{\boldsymbol{D}}_{\boldsymbol{R}}}]\{ {{\boldsymbol{\ddot U}}_0}\} 。$ | (4) |
式(4)与式(3)相比,可看出其质量、阻尼及刚度矩阵均未发生变化,因此其结构模态也未改变,只是在方程的右端增加了
由上述分析可知惯性载荷法有以下特征:
1)由于释放了结构的刚体运动,在求解时可避免积分过程中因刚体漂移造成的计算误差;
2)获取的结构位移、速度及加速度
3)因结构的弹性变形与刚体运动无关,由位移推导的应力场也未变化;
4)从等效转换过程可知,仅适用于基础载荷为加速度的工况。
1.2 大质量法原理大质量法的等效转换策略是将结构的基础假设为一个大质量点(通常为整个结构质量的103~108倍),这个大质量点在结构与基础的连接处同结构刚性固联,同时在计算时释放基础激励方向的自由度,可知考虑平动与转动的结构动力学方程[2]为:
| $ \begin{split} & \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{M }}+ {\boldsymbol{\tilde M}}}&0 \\ 0&{{\boldsymbol{J}} + {\boldsymbol{\tilde J}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\ddot \delta (t)} \\ {\ddot \theta (t)} \end{array}} \right\} + C\left\{ {\begin{array}{*{20}{c}} {\dot \delta (t)} \\ {\dot \theta (t)} \end{array}} \right\}+ \\ & \left[ {\begin{array}{*{20}{c}} {[{{\boldsymbol{K}}_{xx}}]}&{[{{\boldsymbol{K}}_{x\theta }}]} \\ {[{{\boldsymbol{K}}_{\theta x}}]}&{[{{\boldsymbol{K}}_{\theta \theta }}]} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\delta (t)} \\ {\theta (t)} \end{array}} \right\} = {\boldsymbol{P}}({\boldsymbol{t}})。\end{split} $ | (5) |
式中:M和J为结构的质量和转动惯量矩阵;
| $ \begin{split} &\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{M}} + {\boldsymbol{\tilde M}}} &0 \\ 0&{{\boldsymbol{J}} + {\boldsymbol{\tilde J}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\ddot \delta}} ({\boldsymbol{t}})} \\ {{\boldsymbol{\ddot \theta}} ({\boldsymbol{t}})} \end{array}} \right\} + C\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\dot \delta}} ({\boldsymbol{t}})} \\ {{\boldsymbol{\dot \theta}} ({\boldsymbol{t}})} \end{array}} \right\} +\\ & \left[ {\begin{array}{*{20}{c}} {[{{\boldsymbol{K}}_{xx}}]}&{[{{\boldsymbol{K}}_{x\theta }}]} \\ {[{\boldsymbol{K}}_{\theta x}]}&{[{{\boldsymbol{K}}_{\theta \theta }}]} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\delta}} ({\boldsymbol{t}})} \\ {{\boldsymbol{\theta}} ({\boldsymbol{t}})} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\tilde M}} {{{\boldsymbol{\ddot \delta}} }_0}({\boldsymbol{t}})} \\ {{\boldsymbol{\tilde J}} {{{\boldsymbol{\ddot \theta}} }_0}({\boldsymbol{t}})} \end{array}} \right\} 。\end{split} $ | (6) |
当解决基础激励为位移或速度的结构动力响应问题时,由其产生的激励力可表示为:
| $ {\boldsymbol{P}}({\boldsymbol{t}}) = {\boldsymbol{M}}{{\boldsymbol{\ddot \delta}} _0} = j\omega {\boldsymbol{M}}{\dot \delta _0} = - {\omega ^2}{\boldsymbol{M}}{{\boldsymbol{\delta}} _0}。$ | (7) |
可知,当基础激励为线位移或线速度时,需要在前面分别乘
由上述可知,大质量法有如下特征:
1)其本质是将基础加速度载荷转化为力和力矩,增加了基础的大质量和大转动惯量,其载荷输入误差为
2)因去除了激励方向的自由度,所以增加了激励方向上的刚体模态,但其弹性模态未发生变化;
3)由大质量法求解获得的位移可以是相对位移也可以是绝对位移,只要将基础位移去除即可获得相对位移;
4)大质量法可用于基础激励为位移、速度、加速度的工况。
1.3 大刚度法原理大刚度法的转换策略与大质量法基本相同,只是将对应于基础激励方向自由度的刚度设为大刚度
| $ \begin{split} & \left[ {\begin{array}{*{20}{c}} {\boldsymbol{M}} &0 \\ 0 &{\boldsymbol{J}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\ddot \delta}} ({\boldsymbol{t}})} \\ {{\boldsymbol{\ddot \theta}} ({\boldsymbol{t}})} \end{array}} \right\} + {\boldsymbol{C}}\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\dot \delta}} ({\boldsymbol{t}})} \\ {{\boldsymbol{\dot \theta}} ({\boldsymbol{t}})} \end{array}} \right\} + \\ & \left[ {\begin{array}{*{20}{c}} {[{{\boldsymbol{K}}_{\delta \delta }} + {{{\boldsymbol{\tilde K}}}_{{\delta _0}{\delta _0}}}]}&{[{{\boldsymbol{K}}_{\delta \theta }} + {{{\boldsymbol{\tilde K}}}_{{{\boldsymbol{\delta}} _0}{{{\boldsymbol\delta}} _0}}}]} \\ {[{\boldsymbol{K}}_{\theta \delta } + {{{\boldsymbol{\tilde K}}}_{{\delta _0}{\delta _0}}}]}&{[{{\boldsymbol{K}}_{\theta \theta }} + {{{\boldsymbol{\tilde K}}}_{{\delta _0}{\delta _0}}}]} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\delta}} (t)} \\ {{\boldsymbol{\theta}} (t)} \end{array}} \right\}= \\ & \left[ {\begin{array}{*{20}{c}} {[{{{\boldsymbol{\tilde K}}}_{{\delta _0}{\delta _0}}}]}&{[{{{\boldsymbol{\tilde K}}}_{{\delta _0}{\theta _0}}}]} \\ {[{\boldsymbol{\tilde K}}{}_{{\theta _0}{\delta _0}}]}&{[{{{\boldsymbol{\tilde K}}}_{{\theta _0}{\theta _0}}}]} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{\delta}} _0}({\boldsymbol{t}})} \\ {{{\boldsymbol{\theta}} _0}({\boldsymbol{t}})} \end{array}} \right\}。\end{split} $ | (8) |
由其动力学方程可知大刚度法有以下特征:
1)大刚度法会造成结构的高阶模态,而采用模态叠加法求解时往往忽略高阶模态,所以大刚度法不适宜用模态叠加法进行动力响应的求解;
2)大刚度法适用于基础激励为位移的工况,载荷施加方便,无需进行其他转换,避免了两次微分造成的舍入误差,也可避免刚体漂移问题;
3)大刚度法与大质量法相比,其求解精度和求解效率比大质量法要差,因此除基础激励为位移以外,建议用大质量法求解。
1.4 直接激励法原理直接激励法的基本思路是将基础对结构的运动激励,看作结构与基础连接处的边界条件,与一般形式的动力学方程相同[2]:
| $ \begin{split} & \left[ {\begin{array}{*{20}{c}} {\boldsymbol{M}} &0 \\ 0&{\boldsymbol{J}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\ddot \delta}} ({\boldsymbol{t}})} \\ {{\boldsymbol{\ddot \theta}} ({\boldsymbol{t}})} \end{array}} \right\} + {\boldsymbol{C}}\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\dot \delta}} ({\boldsymbol{t}})} \\ {{\boldsymbol{\dot \theta}} ({\boldsymbol{t}})} \end{array}} \right\} + \\ & \left[ {\begin{array}{*{20}{c}} {[{{\boldsymbol{K}}_{xx}}]}&{[{{\boldsymbol{K}}_{x\theta }}]} \\ {[{\boldsymbol{K}}_{\theta x}]}&{[{{\boldsymbol{K}}_{\theta \theta }}]} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{\delta}} ({\boldsymbol{t}})} \\ {{\boldsymbol{\theta}} ({\boldsymbol{t}})} \end{array}} \right\} = {\boldsymbol{P}}({\boldsymbol{t}})。\end{split} $ | (9) |
可以看出直接激励法有以下特征:
1)未进行等效变换,只将运动激励作为动力学方程的边界条件施加到结构与基础的连接处;
2)适用范围广,能解决结构在任意位置受到激励时的结构动力响应问题;
3)当结构组成较复杂时,由于计算所需最小时间步长与划分单元的最小尺度有关,当单元网格划分较密时,计算花费时间较长,受计算机硬件影响较大。
1.5 工程应用在实际工程应用中,惯性载荷法常用来求解地震或爆炸载荷作用下建筑结构的动力响应问题,可以给出所关心部位相对于基础的响应结果;大质量法、大刚度法和直接激励法则常用于求解绝对响应问题,但直接激励法对于大型复杂结构的计算有时难以实现,所以工程上不得不用大质量法和大刚度法来做等效转换。
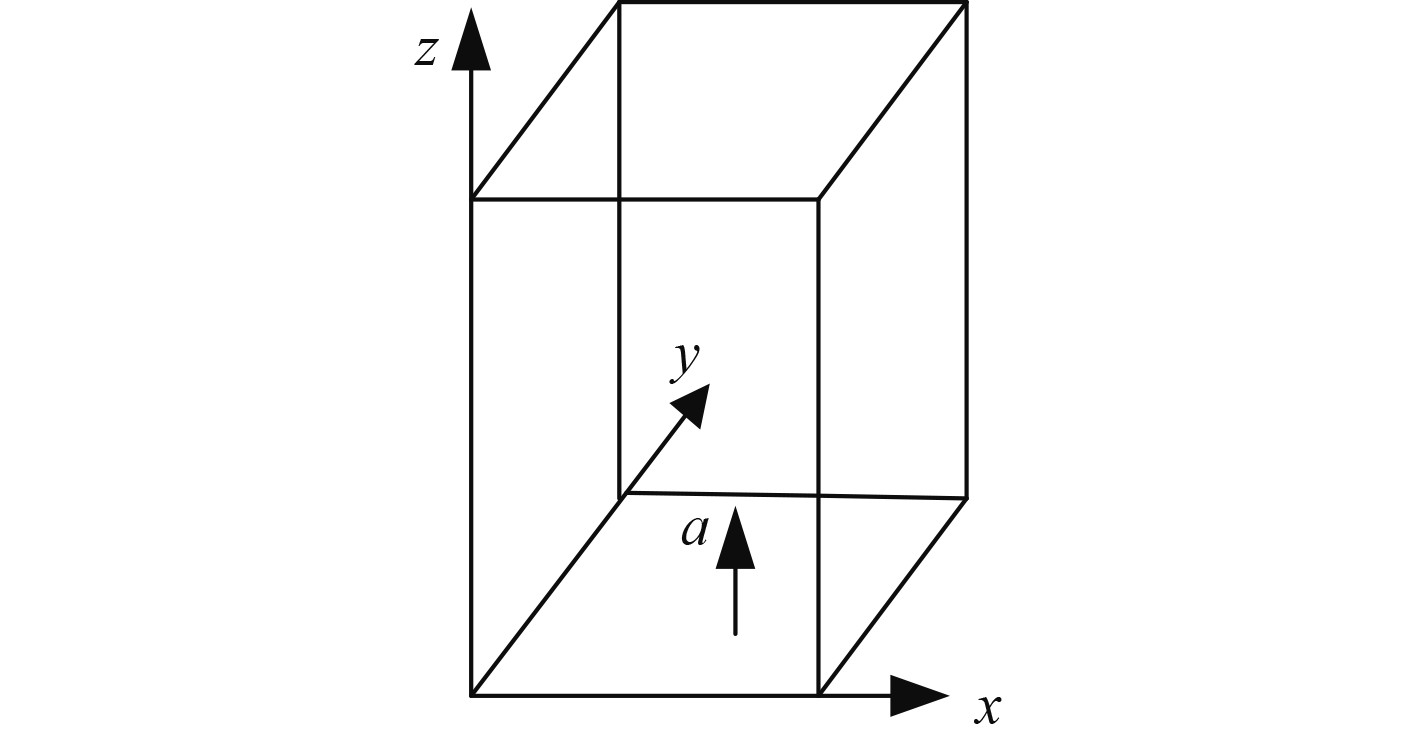
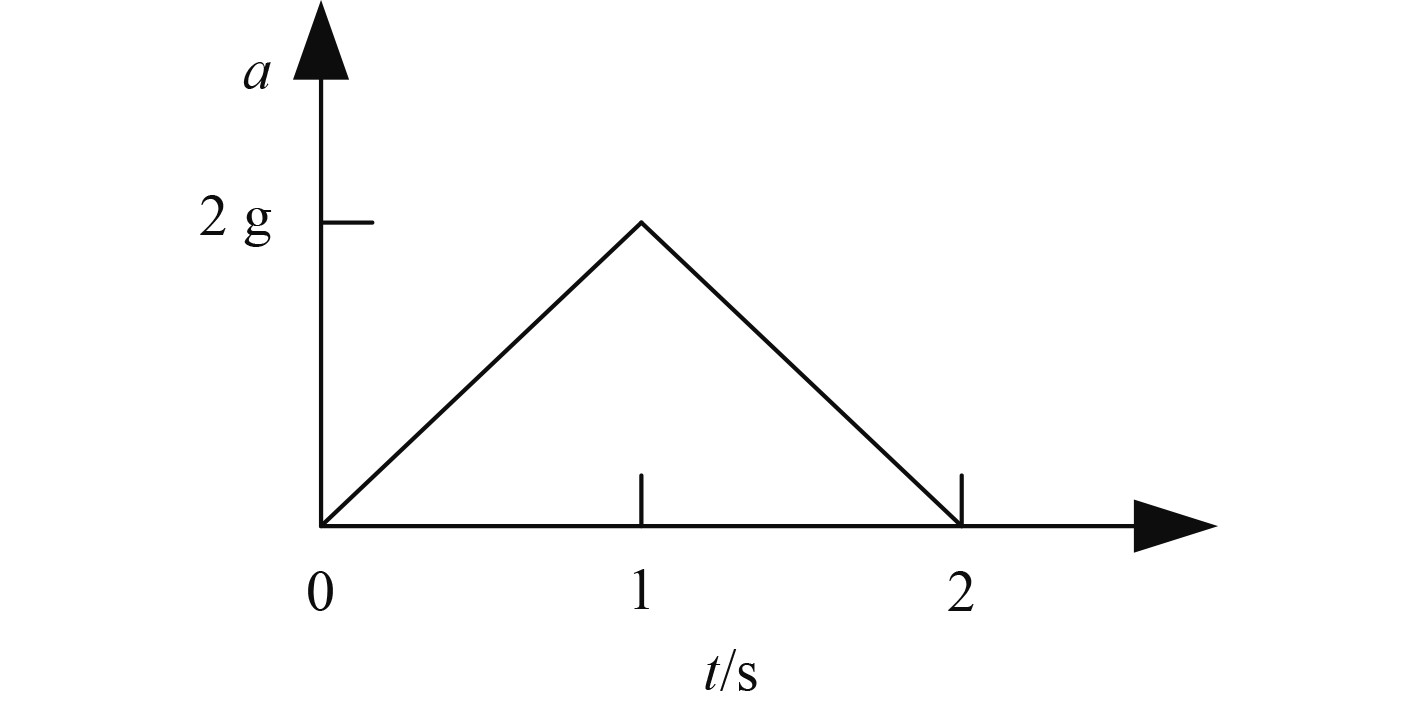
2 算例与结果分析由板形成的箱体结构如图1所示,底部无板材且四边固定于基础上,箱体尺寸为10 m3×10 m3×20 m3,板厚0.02 m。材料特性:弹性模量E=2.1×1011 Pa,泊松比μ=0.3,密度ρ=7800 kg/m3。作用于基础上的Z向加速度a如图2所示,峰值2 g,持续时间为2 s,计算中取时间步长0.02 s。
|
图 1 箱体结构示意图 Fig. 1 Schematic diagram of box structure |
|
图 2 基础加速度曲线 Fig. 2 Foundation acceleration curve |
基于有限元软件Ansys,分别用大质量法、惯性载荷法和直接激励法对算例进行仿真,图3~图5分别为用大质量法、惯性载荷法和直接激励法分析时的有限元模型。大质量法中的大质量为M=1.5×1010 kg,约为结构质量的105倍,在大质量法中节点1000与箱体底部各边上的节点刚性连接,边界条件是结构处于自由状态,不进行约束,所加载荷通过F=Ma求得,然后加于大质量上;在惯性载荷法中用一个质量很小的点质量单元与箱体底部各边节点刚性连接,将点质量所在节点的自由度全约束,所加惯性载荷如图2所示;在用直接激励法时采用了Ansys的Ls-dyna模块,划分的网格较多,结构为自由状态,不作约束,所施加的节点加速度加在箱体底部各边的节点上。

|
图 3 大质量法的有限元模型 Fig. 3 Finite element model of large mass method |

|
图 4 惯性载荷法有限元模型 Fig. 4 Finite element model of inertial load method |

|
图 5 直接激励法有限元模型 Fig. 5 Finite element model of direct excitation method |
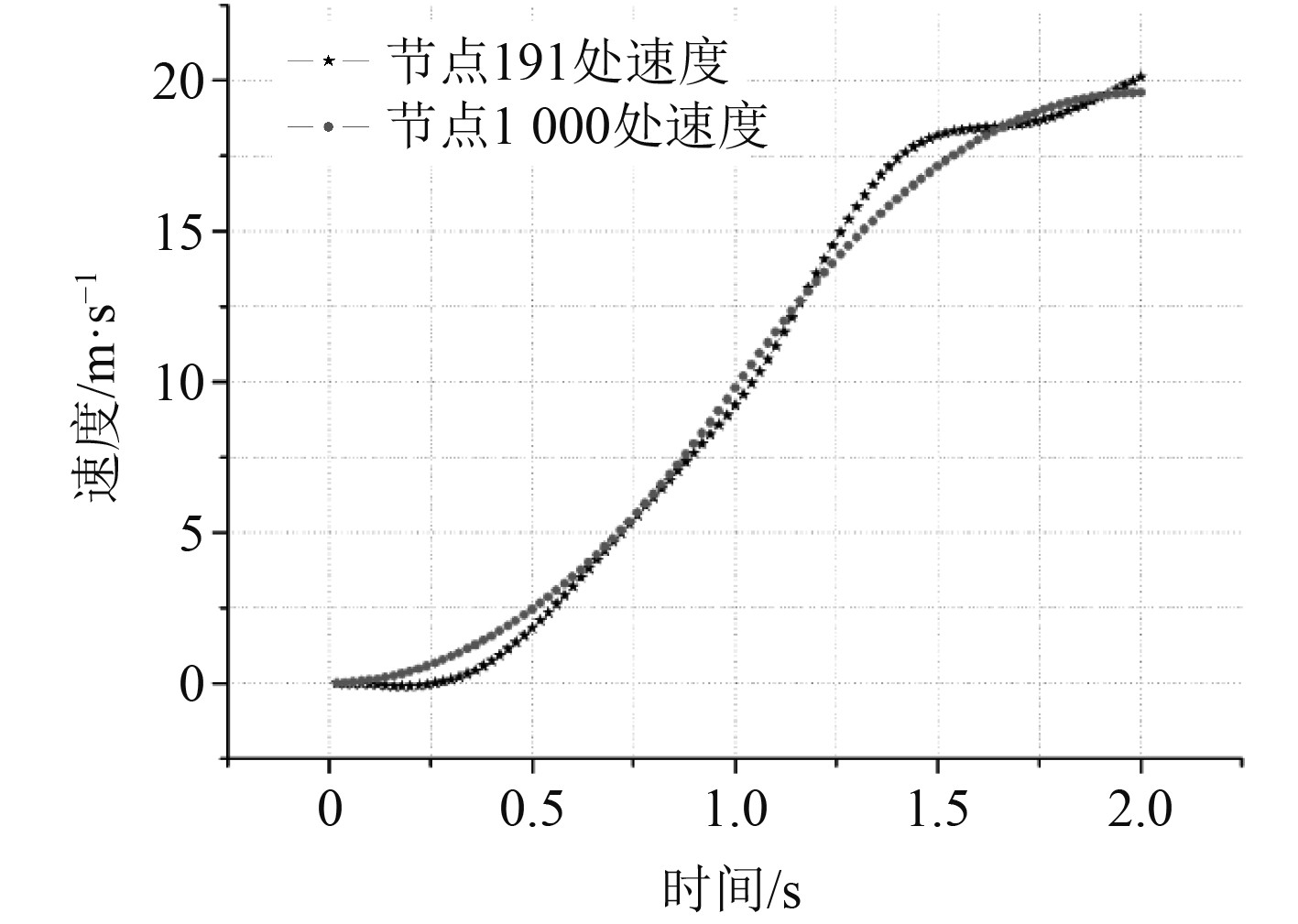
|
图 7 大质量法节点191与节点1000速度比较 Fig. 7 Comparison of speed between node 191 and node 1000 in the large mass method |

|
图 8 大质量法中加速度比较 Fig. 8 Comparison of the acceleration of the large mass method |
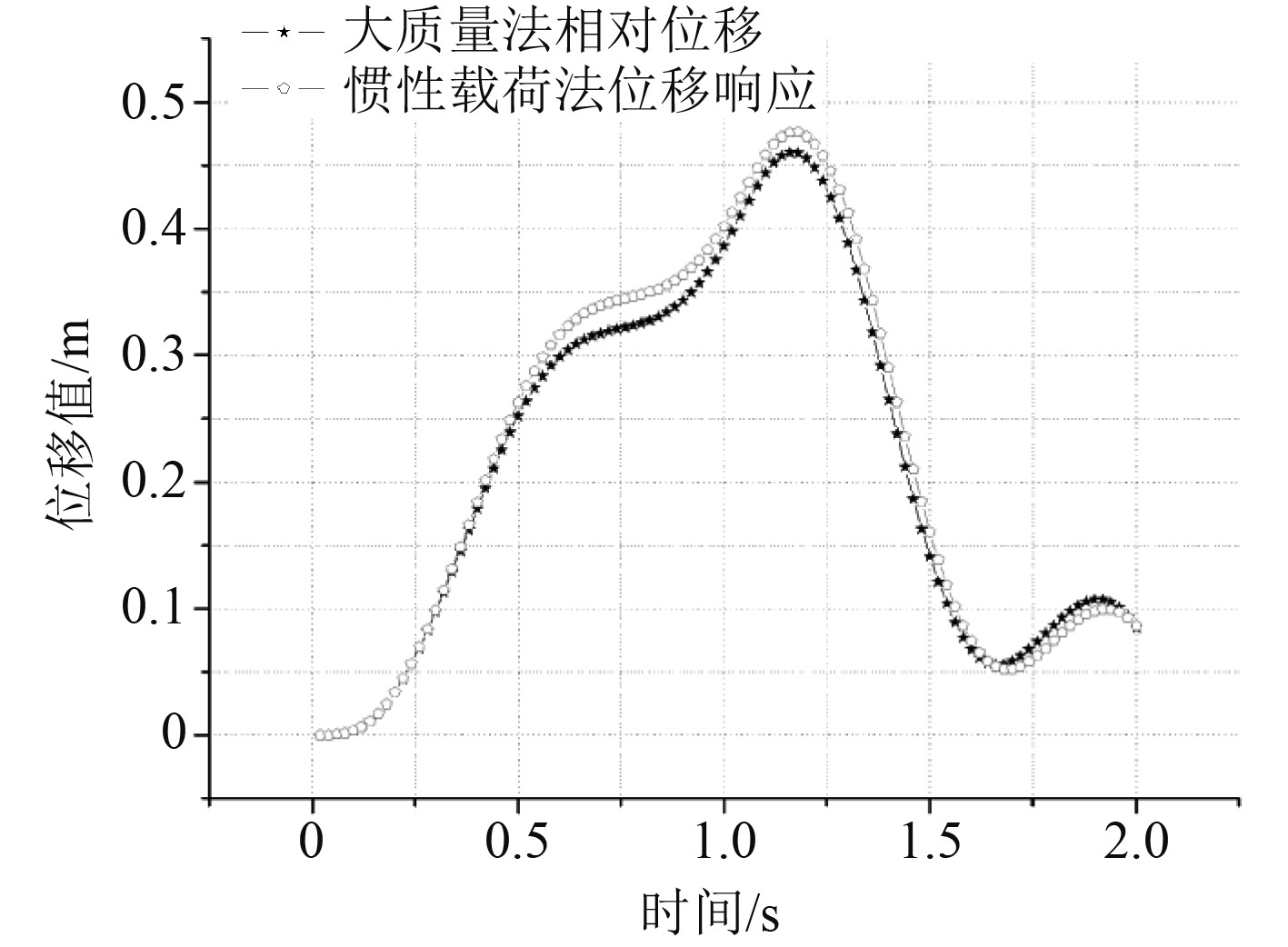
|
图 9 大质量法相对位移与惯性载荷法位移 Fig. 9 Large mass method relative displacement and inertial load method displacement |
|
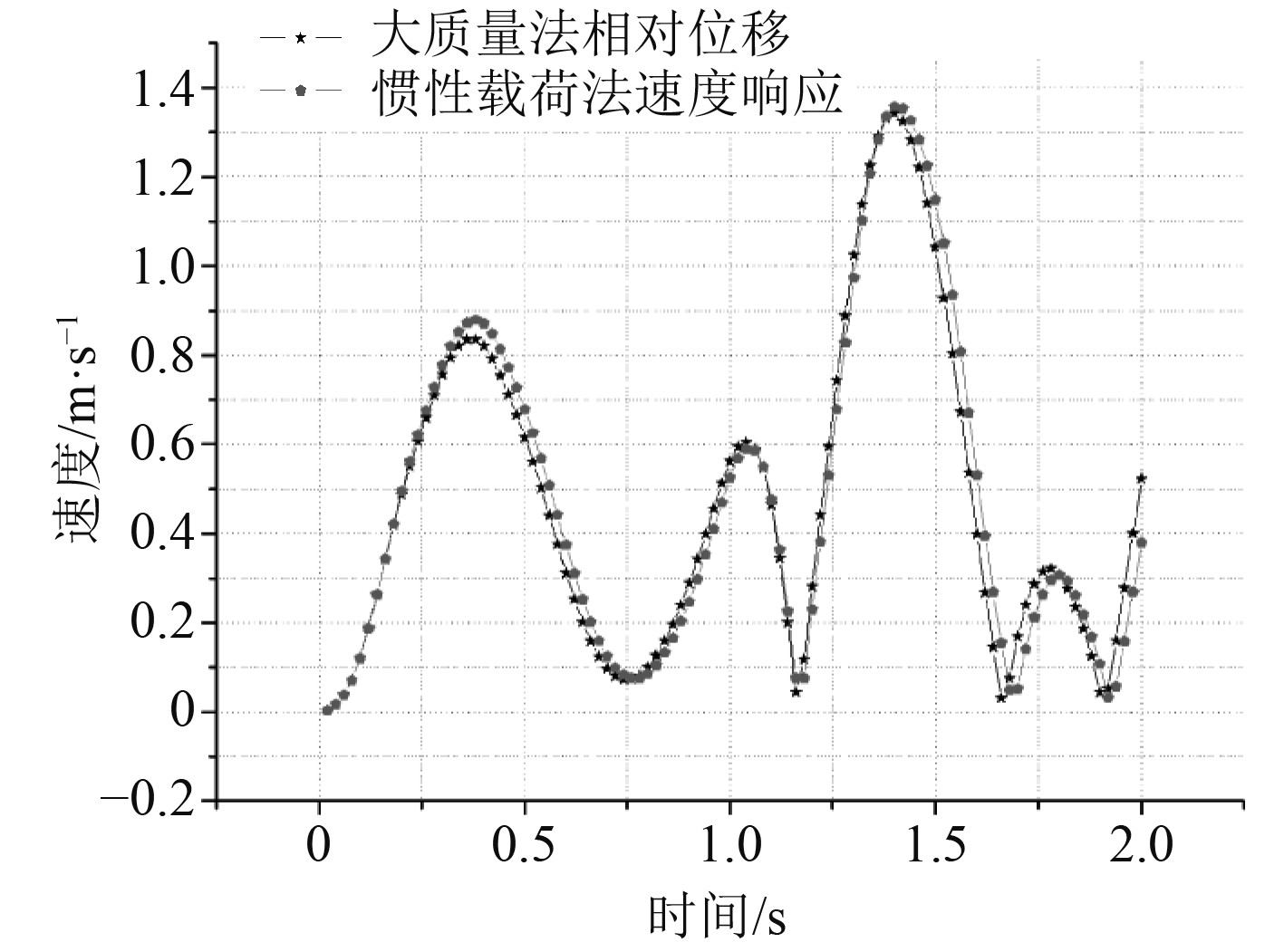
图 10 大质量法相对速度与惯性载荷法速度 Fig. 10 The relative velocity of the large mass method and the inertial load method |

|
图 11 大质量法相对加速度与惯性载荷法加速度 Fig. 11 The relative acceleration of the large mass method and the inertial load method |
|
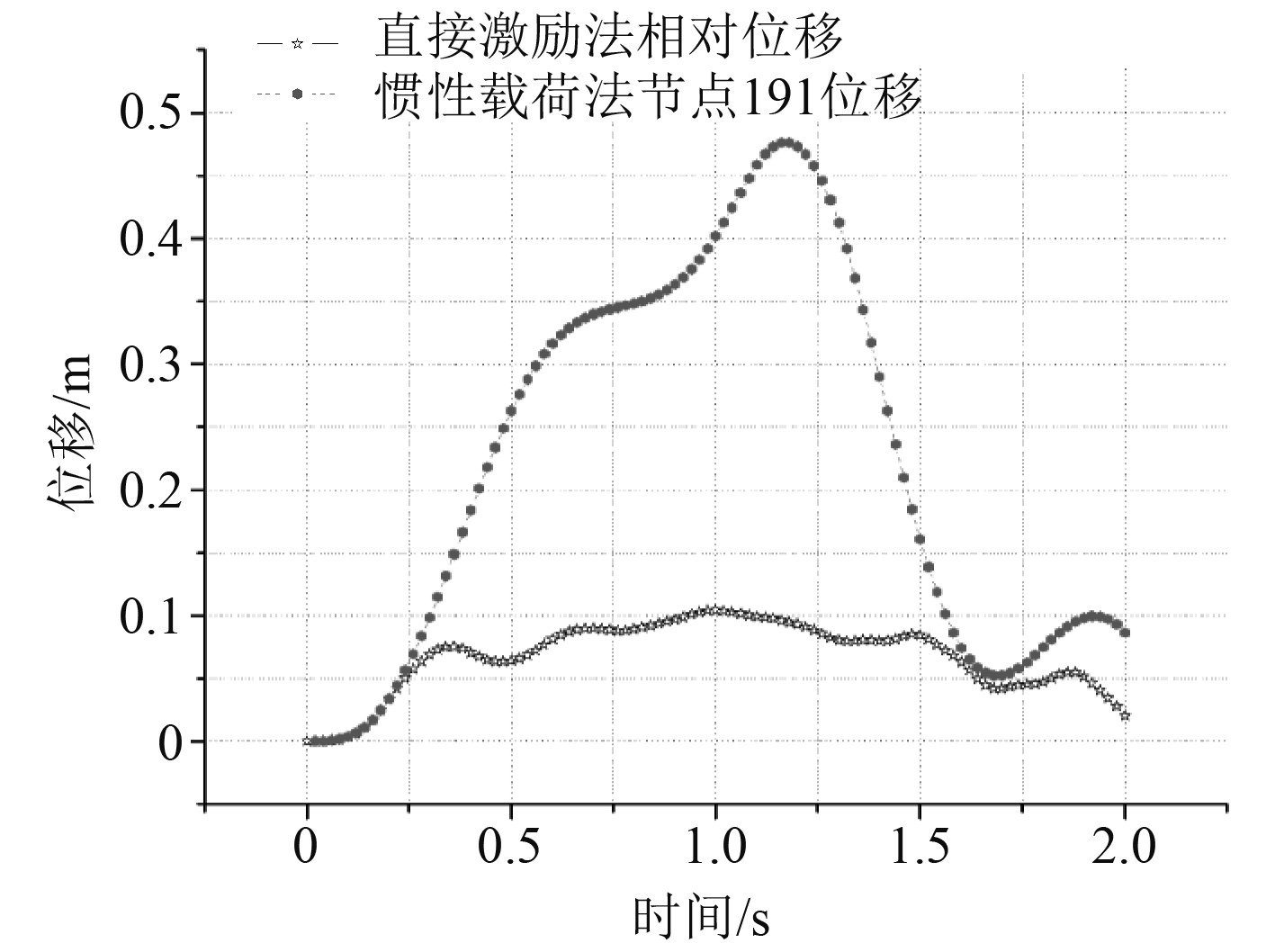
图 12 直接激励法相对位移与惯性载荷法比较 Fig. 12 Comparison of relative displacement between direct excitation method and inertial load method |
|
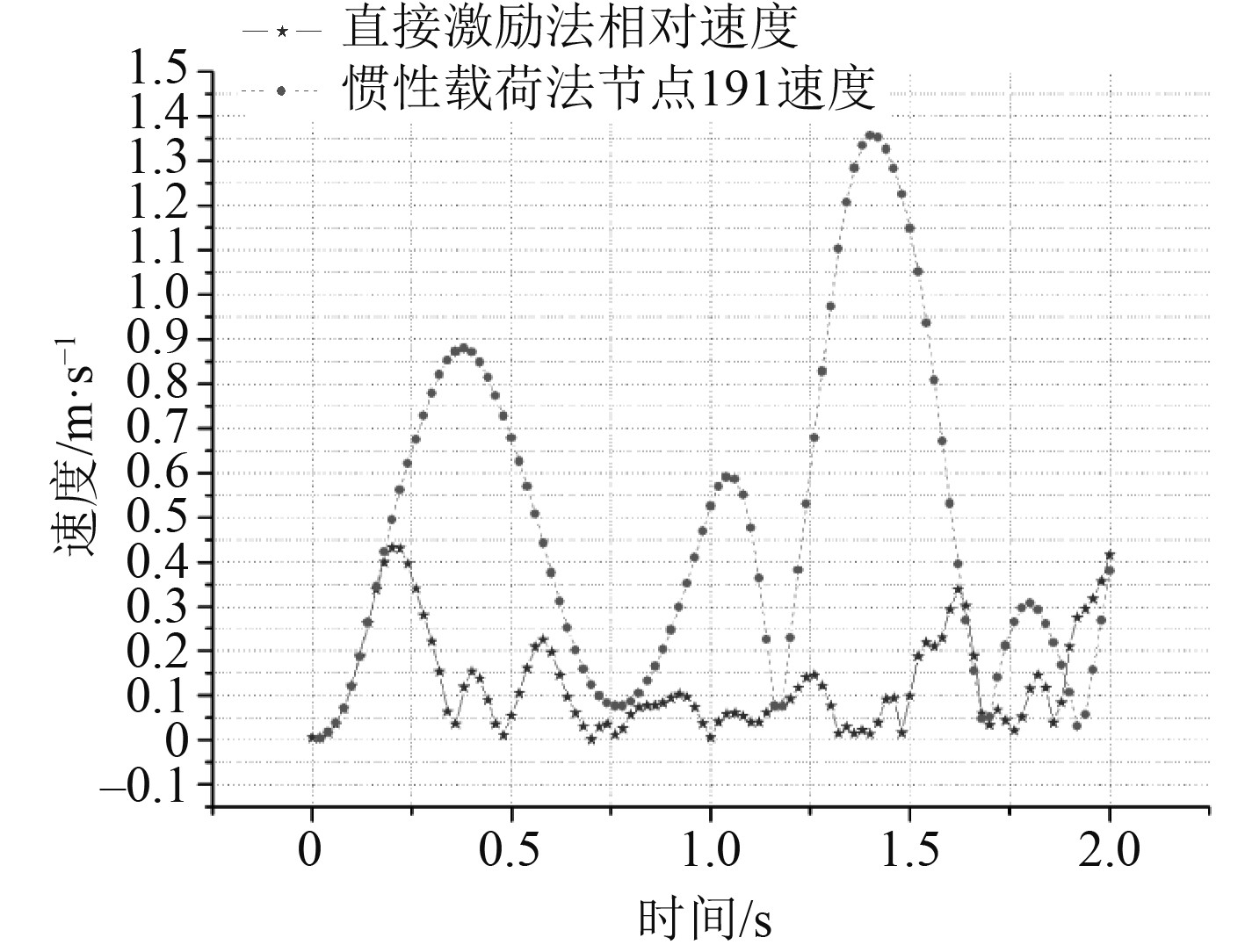
图 13 直接激励法相对速度与惯性载荷法比较 Fig. 13 Comparison of the relative velocity of direct excitation method and inertial load method |
|
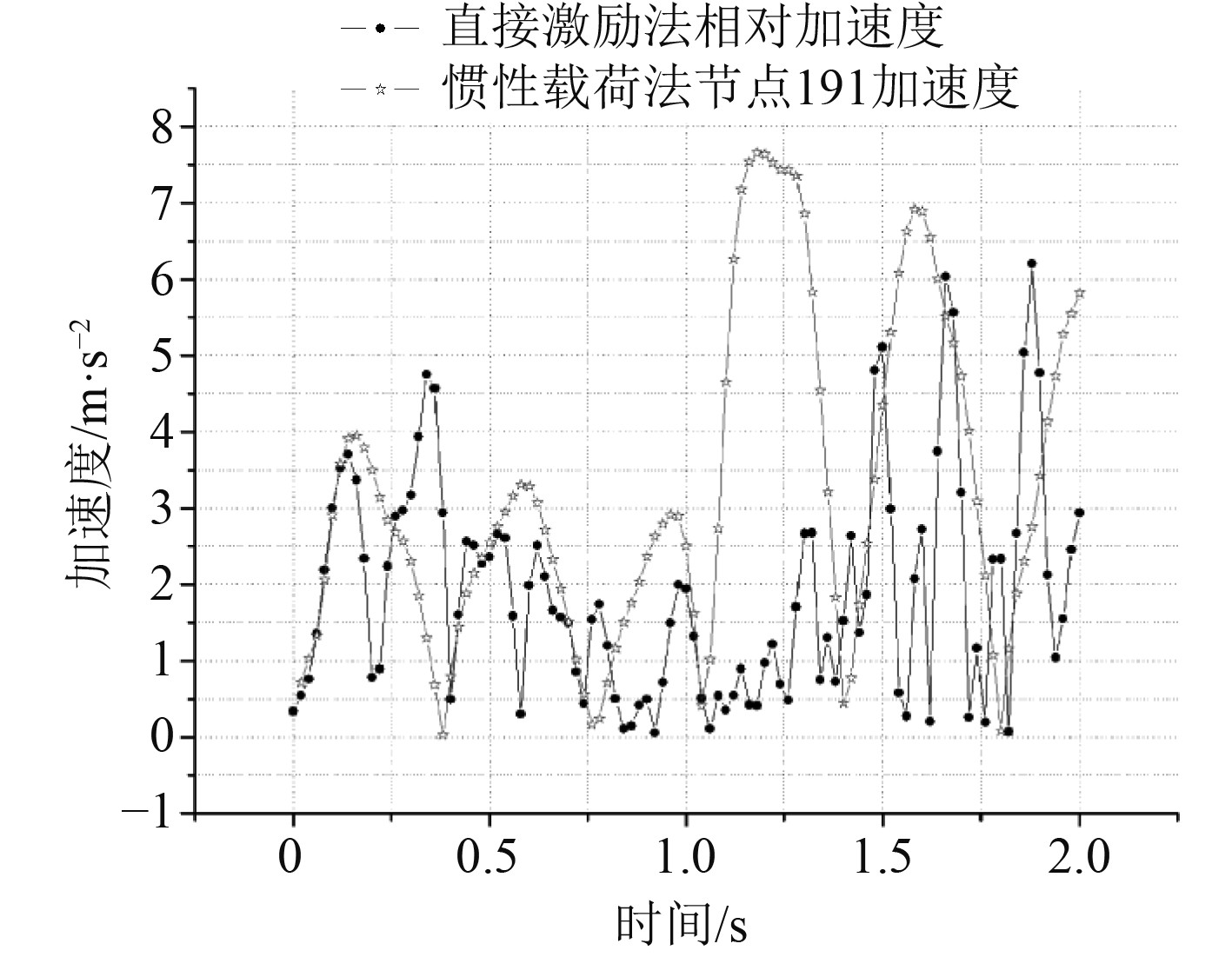
图 14 直接激励法相对加速度与惯性载荷法比较 Fig. 14 Comparison of relative acceleration between direct excitation method and inertial load method |

|
图 15 大质量法、惯性载荷法与直接激励法应力值比较 Fig. 15 Comparison of stress values of large mass method, inertial load method and direct excitation method |

|
图 16 大质量法与直接激励法位移 Fig. 16 Displacement by large mass method and direct excitation method |
|
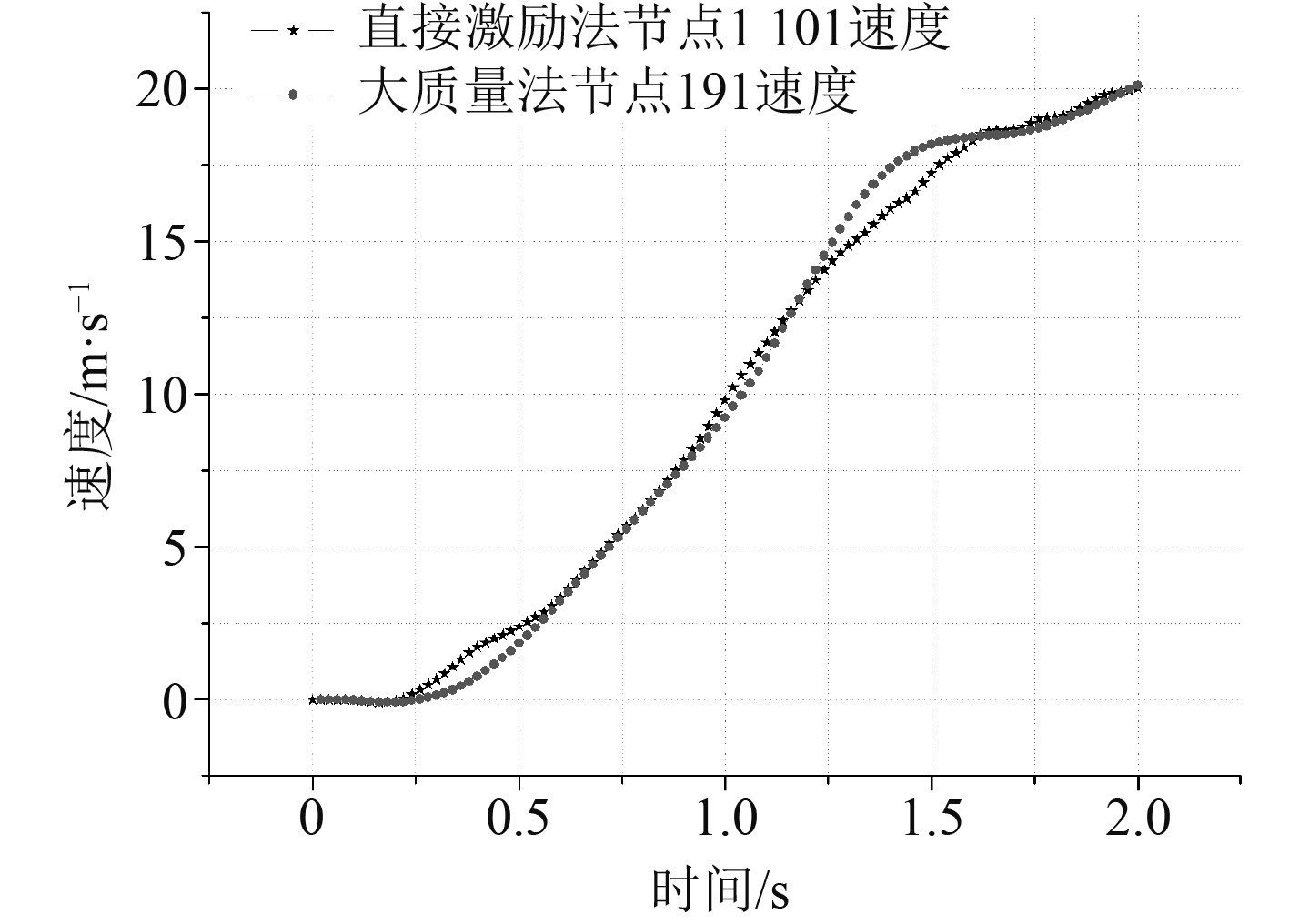
图 17 大质量法与直接激励法速度 Fig. 17 Velocity of large mass method and direct excitation method |
其中在大质量法与惯性载荷法中节点191在结构上部坐标为(5,5,20)处,大质量法中节点1000坐标为(5,5,0),直接激励法中节点72坐标为(10,10,0),节点1101坐标为(5,5,20),由图6~图18中各曲线的比较可知,对大质量法计算的结果进行处理,扣除基础的位移、速度和加速度得出的结果基本上和用惯性载荷法计算的结果相同;但直接激励法扣除基础的位移、速度与加速度后,只有加速度在幅值上与惯性载荷法基本符合,位移与速度仅在0.25 s以前与惯性载荷法相同,其他时间内曲线在形状上基本上相同,但幅值较惯性载荷法小;大质量法与惯性载荷法同一节点处的应力值基本上相同,但数值都比直接激励法要大;大质量法与直接激励法在绝对位移上差别较小,速度与加速度稍有差别。

|
图 6 大质量法节点191与节点1000位移比较 Fig. 6 Comparison of displacement between node 191 and node 1000 in the large mass method |
|
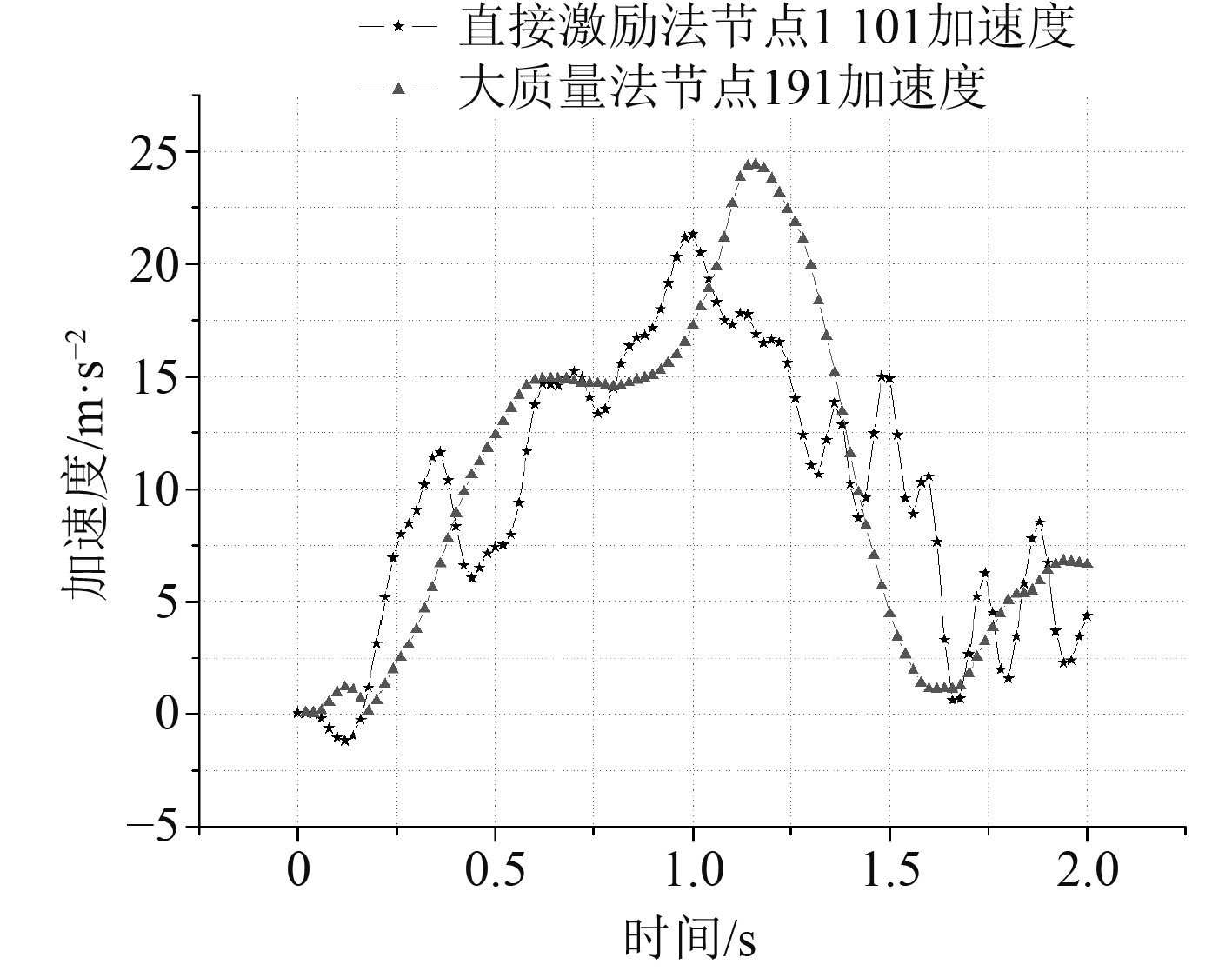
图 18 大质量法与直接激励法加速度 Fig. 18 Acceleration by large mass method and direct excitation method |
从结果可以看出,用大质量法与惯性载荷法计算的结果基本上相同,但直接激励法的结果与大质量法和惯性载荷法相比,相对于基础的位移与速度数值及应力值偏小,因大质量法与惯性载荷法对基础运动都进行了等效处理,其值会偏大,但从其加速度响应来看与直接激励法基本上是相同的。就计算所费时间而言,大质量法与惯性载荷法基本上差不多,直接激励法花费时间最长。
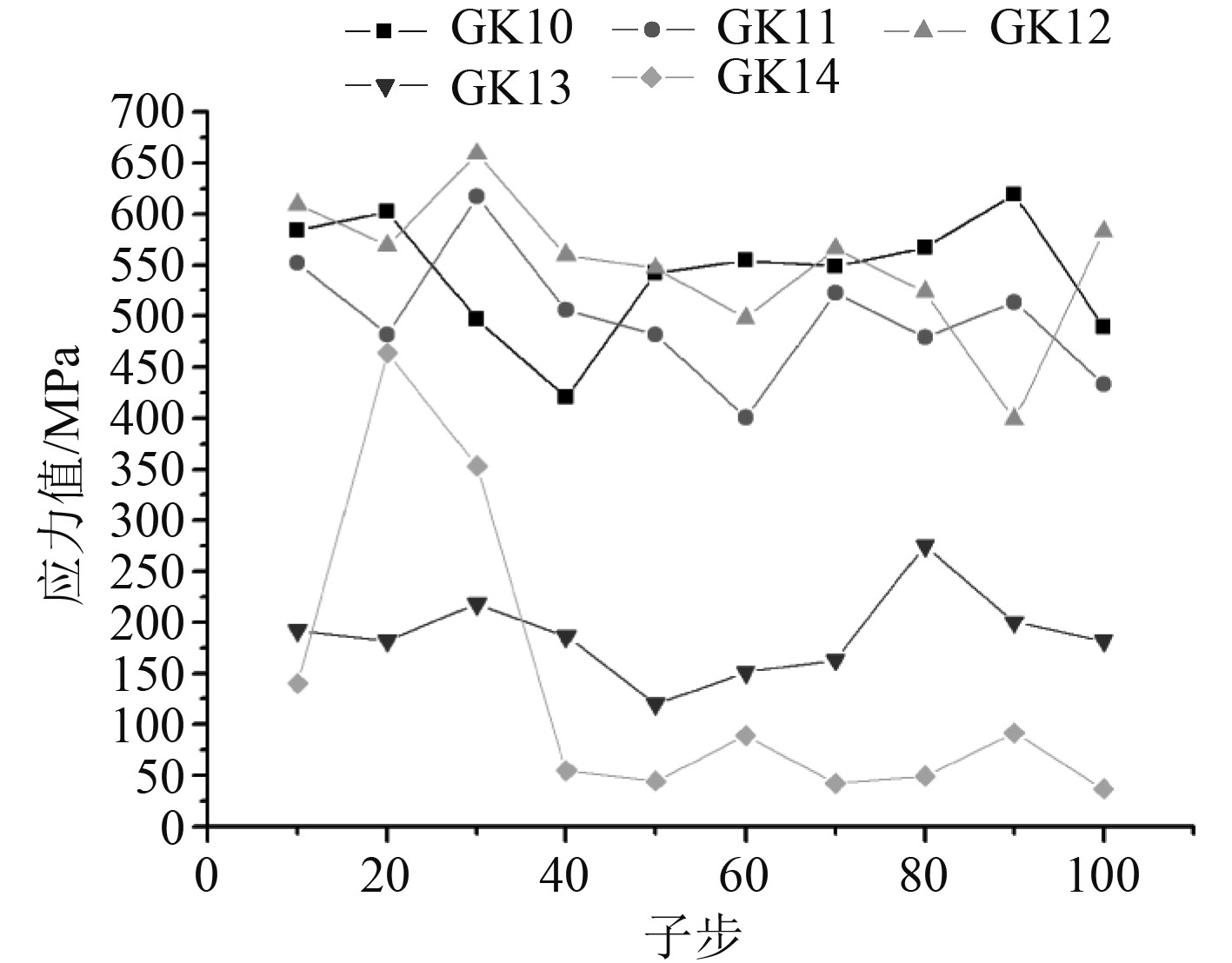
3 某舰载设备在基础运动激励下的动力响应分析某舰载设备由多个模块组成且构造复杂,通过有限元软件Ansys的Ls-dyna模块,采用直接激励法,对基础在加速度激励时的结构动力学响应进行了多工况仿真,得出每隔10个子步下的最大综合应力曲线,如图19所示。从其结果看出,局部的应力值偏大。由于结构复杂,用Ls-dyna计算相当费时,计算一种工况就需5 d的时间,可见为了在较短的时间内进行动力响应分析,只有采用大质量法或惯性载荷法。从上面分析可知无论是大质量法、大刚度法还是惯性载荷法,对由位移向量得出的应变、应力场影响较小,只要大质量或大刚度取值合适,结果都可以满足工程精度要求。
|
图 19 某舰载设备在5种工况下冯·米赛斯最大应力值比较 Fig. 19 Comparison of von Mises maximum stress values of a shipborne equipment under five working conditions |
通过对比结构的惯性载荷法、大质量法、大刚度法、直接激励法的动力学方程,对4种方法的特征和应用条件进行深入分析,并利用算例进行验证,计算结果表明用大质量法与惯性载荷法计算结果是相同的,但用直接激励法计算的位移、速度及应力响应值偏小。因此在选用算法时应权衡时间与精度问题,对于舰载设备在基础运动激励下的动力响应分析而言,用大质量法和惯性载荷法是可以满足工程精度要求的(若取大质量为结构质量的105倍,计算载荷输入误差小于10−5数量级),其计算所消耗时间比直接激励法要少几倍甚至几十倍,但应注意到大质量法与惯性载荷法是近似的方法,其相对位移、速度及应力响应值比直接激励法要大。
| [1] |
王波, 张海龙, 武修雄, 等. 基于大质量的高墩大跨连续刚构桥地震时程反应分析[J]. 桥梁建设, 2006, 36(5): 17-20. WANG B, ZHANG H L, WU X X, et al. Analysis of seismic time-history response of high-rise pier and long span continuous rigid-frame bridge based on great mass method[J]. Bridge Construction, 2006, 36(5): 17-20. DOI:10.3969/j.issn.1003-4722.2006.05.005 |
| [2] |
杨德庆, 王德禹, 汪庠宝. 考虑星-箭动力耦合作用结构瞬态响应分析[J]. 宇航学报, 2003(2): 213-216. YANG D, WANG D Y, WANG X B. Structural transient response analysis considering satellite-rocket dynamic coupling effect[J]. Journal of Astronautics, 2003(2): 213-216. |
| [3] |
周国良, 李小军, 刘必灯, 等. 大质量法在多点激励分析中的应用、误差分析与改进[J]. 工程力学, 2011, 28(1): 48-54. ZHOU G L, LI X J, LIU B D, et al. Error analysis and improvements of large mass method used in multi-support seismic excitation analysis[J]. Engineering Mechanics, 2011, 28(1): 48-54. |
| [4] |
楼梦麟, 田仲业. 基于大质量法的结构零频率振型的动力特性[J]. 力学季刊, 2020, 41(2): 240-248. LOU M L, TIAN Z Y. Dynamic characteristics of structural modes with zero frequency based on large mass method[J]. Chinese Quarterly of Mechanics, 2020, 41(2): 240-248. DOI:10.15959/j.cnki.0254-0053.2020.02.004 |
| [5] |
雷虎军, 李小珍. 车-轨-桥耦合系统中的非一致地震输入方法研究[J]. 铁道科学与工程学报, 2015, 12(4): 769−777. LEI H J, LI X Z. Input methods of non-uniform seismic excitation in coupling system of vehicle- track- bridge[J]Journal of Railway Science and Engineering, 2015, 12(4): 769−777. |
 2024, Vol. 46
2024, Vol. 46
