柴油机法规的升级侧重瞬态和低温工况排放的考核,SCR装置的闭环控制成为必然[1 − 3]。人们尝试将PID控制策略应用于SCR控制,虽然经典PID控制策略在柴油机稳定工况具有较好的控制效果,但柴油机实际运行时工况多变。在瞬态条件下为达到低NOx控制目标,需加大控制力度提高快速性,但此操作易出现控制超调,使尿素量喷射过多,造成氨气泄漏[4 − 5]。此外,运行过程中将不断受到外界与机内干扰,增大了控制难度[6 − 7]。因此经典PID控制策略在柴油机实际运行过程中的控制效果不太理想。
要提高对NOx排放的准确控制仍需采用闭环控制。近年来,自抗扰算法继承了经典PID基于误差来消除误差的控制思想,并进行了改进。自抗扰算法核心思想为将简单的积分串联型作为标准型,并将与标准型不同的部分视为扰动,通过扩张状态观测器进行总扰动估计,然后施加补偿力抵消扰动,以此将被控对象改造成积分串联型,采用跟踪微分器与非线性组合能有效解决PID控制在时滞系统中,控制目标快速性与超调间的矛盾,提高动态响应能力[8]。
采用非线性自抗扰控制器进行了仿真与试验研究,本文中部分相关参数设置来自前期研究结果[9]。前期研究中,非线性反馈增益取值为通过Simulink工具箱中信号约束模块粗略整定得出,本文采用改进粒子群算法对反馈增益进行寻优整定,探究其对SCR自抗扰控制器的控制品质改善情况。
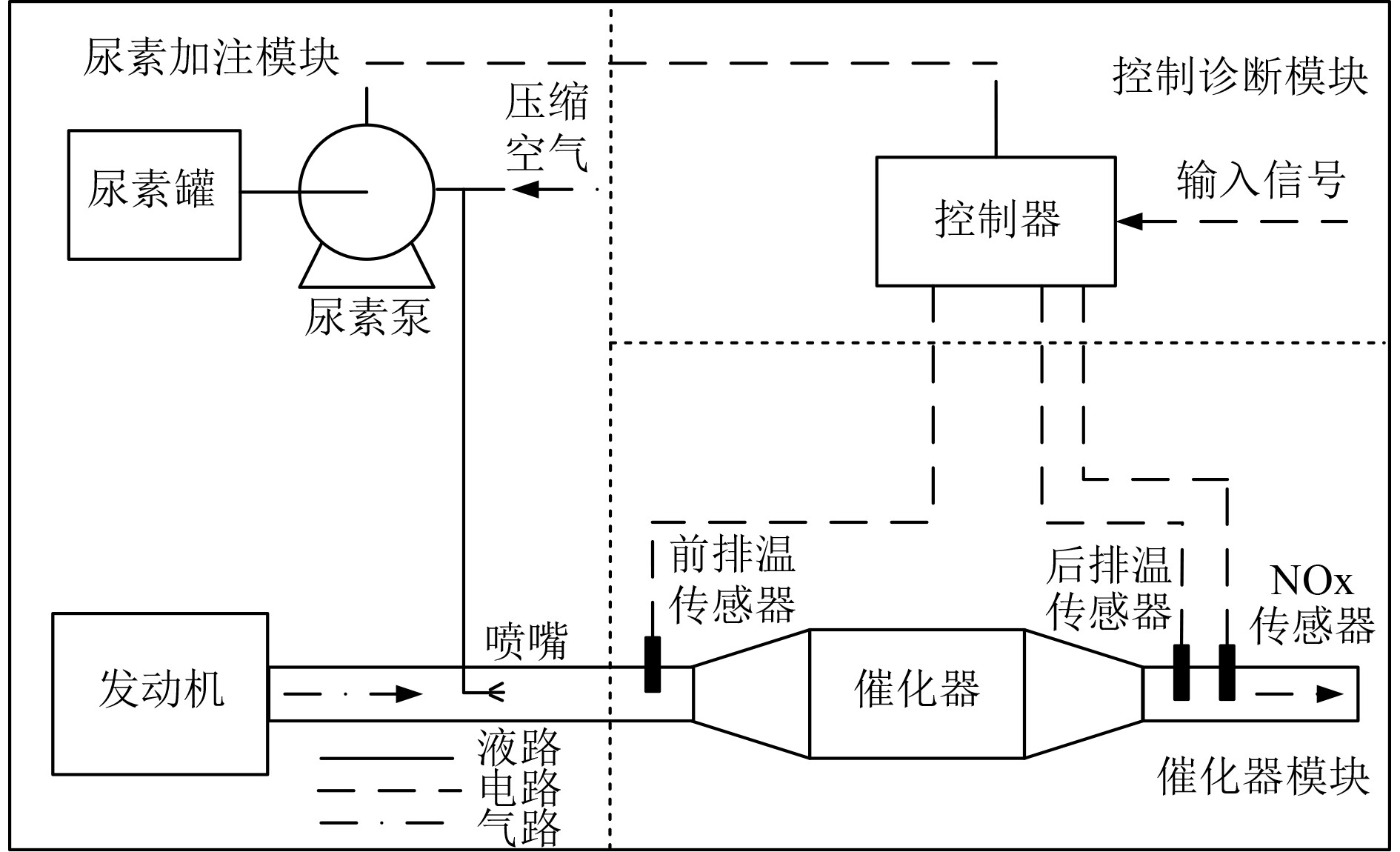
1 SCR装置数学模型的建立 1.1 SCR装置结构SCR装置作为柴油机达到排放国标的主要技术平台,其主要由尿素加注模块、催化器模块和控制诊断模块构成,具体结构见图1。
|
图 1 SCR装置结构示意图 Fig. 1 SCR device structure diagram |
SCR后处理装置中,降低内燃机NOx排放物的化学反应,分为两大过程即尿素的分解过程和氨气与氮氧化合物进行的催化还原反应过程,上述2个过程在排气管与催化器上反应[9]。
1)尿素的分解过程
尿素的分解细分为3步,即尿素晶体的析出、尿素晶体分解为氨气与异氢酸、异氢酸水解。假设尿素和异氢酸完全反应,则一摩尔的尿素生成两摩尔的氨气与一摩尔的二氧化碳,其化学方程式为:
| $ {\left( {{\rm{N}}{{\rm{H}}_2}} \right)_2}{\rm{CO}} + {{\rm{H}}_2}{\rm{O}} \to 2{\rm{N}}{{\rm{H}}_3} + 2{\rm{C}}{{\rm{O}}_2} $ | (1) |
2)氨气还原氮氧化物过程
在催化剂的作用下,尿素分解产生的氨气与内燃机排气管中的氮氧化物发生催化还原反应生成氮气与水。根据化学反应速率的不同,氧化还原反应可分为快速SCR反应,标准SCR反应,反应方程式依此如下:
| $ {\rm{2N{H_3}\left( S \right) + NO + N{O_2} \to 2{N_2} + 3{H_2}O}} $ | (2) |
| $ {\rm{4N{H_3}\left( S \right) + 4NO + {O_2} \to 4{N_2} + 6{H_2}O}}$ | (3) |
可知,在氧化还原反应中,氨气与氮氧化物之间保持等摩尔的关系,即还原一摩尔的氮氧化物需一摩尔的氨气。
由于柴油机在稳定工况时,所生成氮氧化物速率变化较小,因此本文选用稳定工况进行数学建模,经研究发现催化器后端NOx浓度与尿素喷射量间的关系呈现出类似阻容特性曲线的特征[10],且NOx浓度的变化时刻与尿素喷射量的改变时刻有相对滞后现象。因此SCR控制数学模型可看作为一阶惯性加纯时滞的模型,即
| $ G\left( S \right) = {e^{ - \tau s}}\frac{k}{{TS + 1}}。$ | (4) |
式中:
在自抗扰控制器中,对于时滞系统有4种处理方式,分别为无视时滞法、提高阶次法、输出预估法和输入预估法[11]。
为实现简单的控制策略,同时又不至于降低控制品质,针对SCR系统,本研究采用提高阶次法,将SCR系统的一阶惯性加纯时滞数学模型转化为二阶惯性无时滞模型,并设计二阶非线性自抗扰控制器,经处理后,SCR装置传递函数为:
| $ w\left( s \right) = \frac{{{e^{ - \tau s}}}}{{Ts + 1}} = \frac{1}{{Ts + 1}}\frac{1}{{\tau s + 1}} = \frac{1}{{T\tau {s^2} + \left( {T + \tau } \right)s + 1}} 。$ | (5) |
式中:
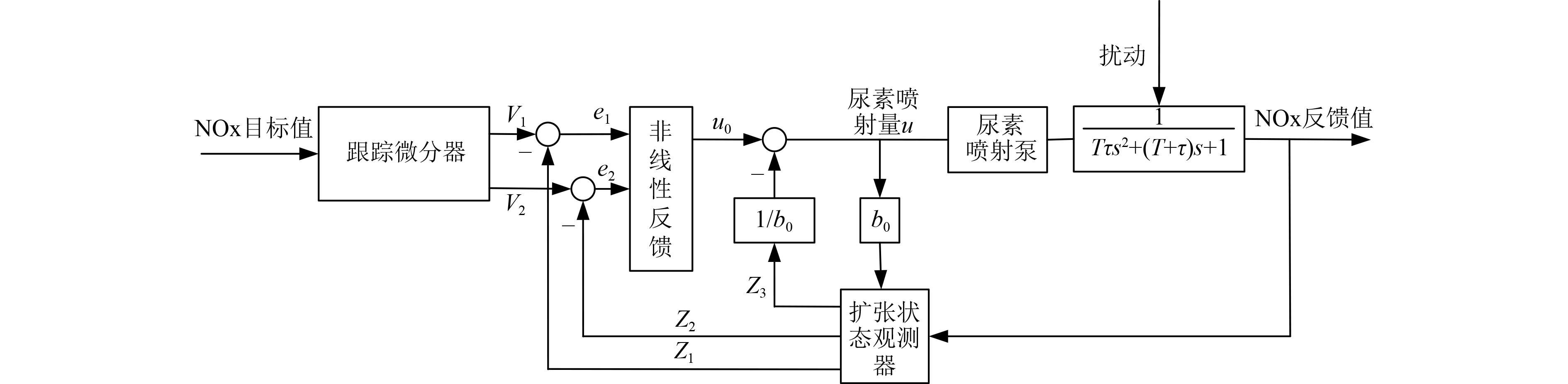
现实中对SCR装置的扰动来自诸多方面,如装置生产一致性、环境条件改变、运行工况改变等时刻影响着SCR装置模型参数的改变,SCR系统未建模部分也将视为扰动,尿素泵喷射与NOx传感器响应的时滞时间也随着工况不同而发生改变。因此,SCR装置可看做受到多种干扰的系统,增加自抗扰控制器后的控制系统反应过程如图2所示。
|
图 2 SCR自抗扰装置反应过程示意图 Fig. 2 Schematic diagram of the reaction process of SCR active disturbance rejection device |
图2中自抗扰控制中的跟踪微分器、扩张状态观测器、非线性组合的离散算法均通过Matlab中S函数实现。对于跟踪微分器选用了非线性最速控制综合函数
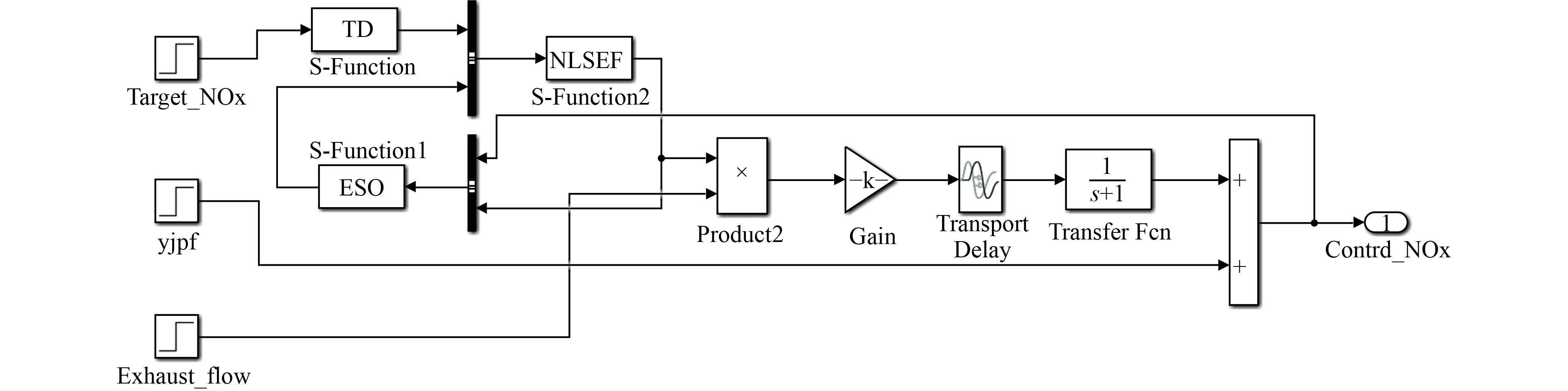
以Matlab/Simulink软件作为仿真平台,搭建SCR非线性自抗扰控制器仿真模型。为体现SCR装置的真实反应过程,在控制器模型搭建时以二阶惯性无时滞模型进行搭建,而对于仿真对象仍采用一阶惯性加纯时滞的模型,根据前期研究[10]将时滞时间设置为6 s,时间常数
|
图 3 SCR非线性自抗扰控制器仿真模型 Fig. 3 Simulation model of SCR nonlinear active disturbance rejection controller |
仿真模型的参数需根据实际装置的采样频率与控制力来进行协调设置,鉴于本研究所采用的NOx传感器采样频率为20 Hz,因此非线性SCR控制器的采样步长
由于粒子群算法(Particle swarm optimization, PSO)在参数寻优方面呈现出的良好效果,本文采用粒子群算法对
| $ \left\{\begin{aligned} & {v}_{id}\left(t+1\right)=\omega \cdot {v}_{id}\left(t\right)+\\ & {c}_{1}{r}_{1}\left({p}_{id}-{x}_{id}\left(t\right)\right)+{c}_{2}{r}_{2}\left(t\right)\left({p}_{gd}-{x}_{gs}\left(t\right)\right),\\ & {x}_{id}\left(t+1\right)={x}_{id}\left(t\right)+{v}_{id}\left(t+1\right)。\end{aligned}\right. $ | (6) |
式中:
权重因子
| $ \omega \left(t\right)=rand \cdot {\omega }_{\mathrm{min}}\cdot \left(1-\mathrm{cos}f\right)+{\omega }_{\mathrm{max}}\cdot \mathrm{cos}f。$ | (7) |
式中:
选用误差绝对值时间积分性能指标和加入控制输入平方项作为目标适应度函数
| $ F = \int_0^\infty {\left( {{\omega _1}\left| {e\left( t \right)} \right| + {\omega _2}{u^2}\left( t \right)} \right)} {\rm{d}}t。$ | (8) |
式中:
使用改进粒子群算法对SCR自抗扰控制器中
步骤1 初始化粒子群规模、粒子的位置及速度、适应度函数。
步骤2 将改进粒子群算法与自抗扰控制器Simulink模型进行链接,根据适应度函数,计算出各粒子每次迭代的适应度值。
步骤3 根据适应度值寻找当时迭代次数下的个体最优解与全局最优解,并对个体最优解与全局最优解进行更新。
步骤4 进行粒子群的速度及位置更新。
步骤5 根据改进权重公式进行权重因子非线性更新。
步骤6 判断是否满足改进粒子群算法终止条件,若满足则停止迭代输出最优解,若不满足则返回步骤2执行。
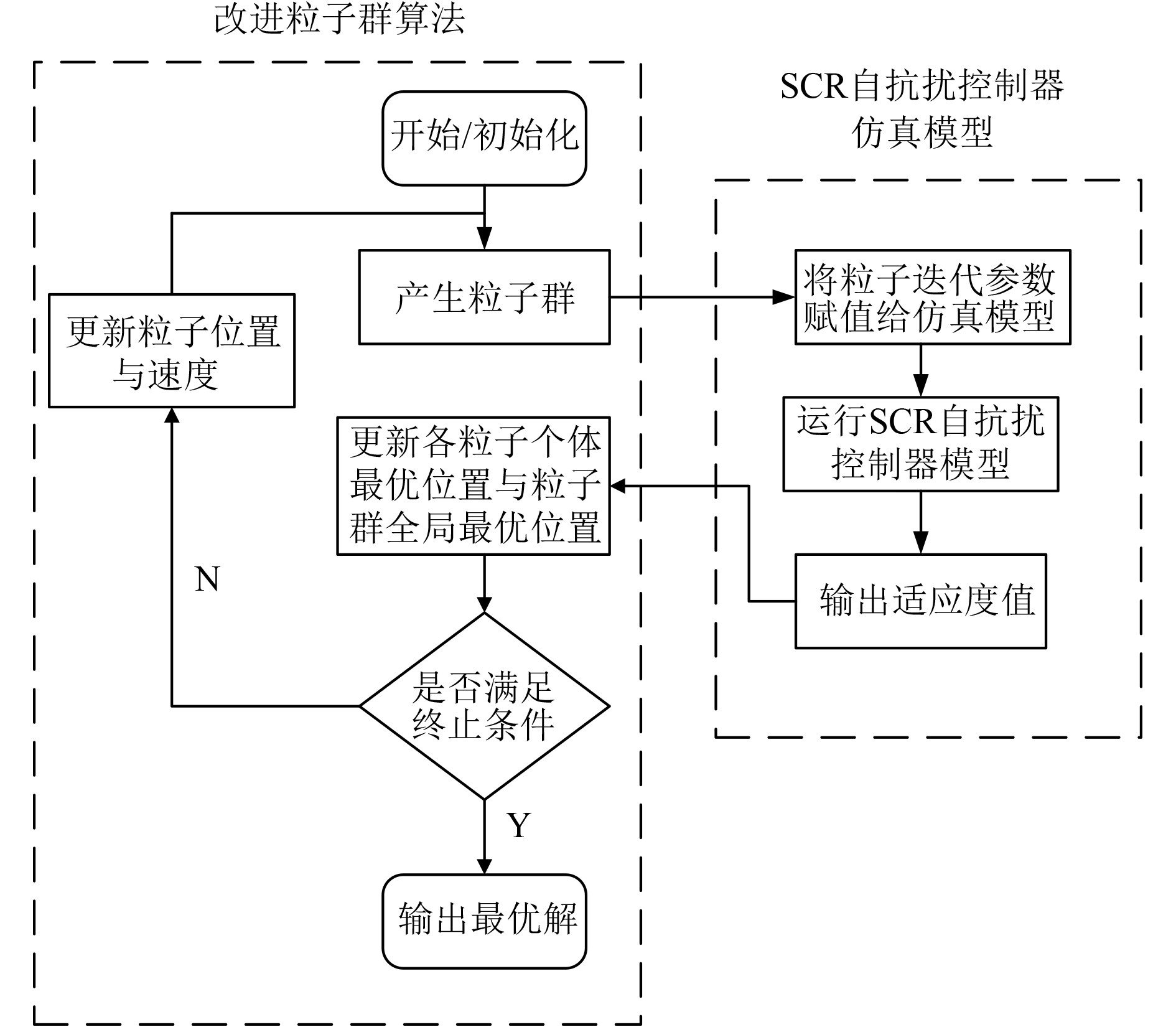
改进粒子群算法整定优化SCR自抗扰控制器过程如图4所示。
|
图 4 算法优化流程 Fig. 4 Algorithm optimization process |
为验证本文基于改进PSO优化的SCR自抗扰控制器的控制品质改善效果,以1台4.7 L柴油机发动机为试验对象,额定功率为132 kW,额定转速为2500 r/min。根据其排放参数,选用原机排放为1150 ppm,目标NOx排放值为200 ppm的工况点进行SCR自抗扰控制器仿真试验。
改进PSO的参数取值,
由图5可知,改进PSO在15次迭代后就开始收敛到最优值,而传统PSO需迭代到40次才开始收敛,并且改进后算法获得的适应值更小,表明改进后PSO在寻优速度与准确度上好于传统PSO。
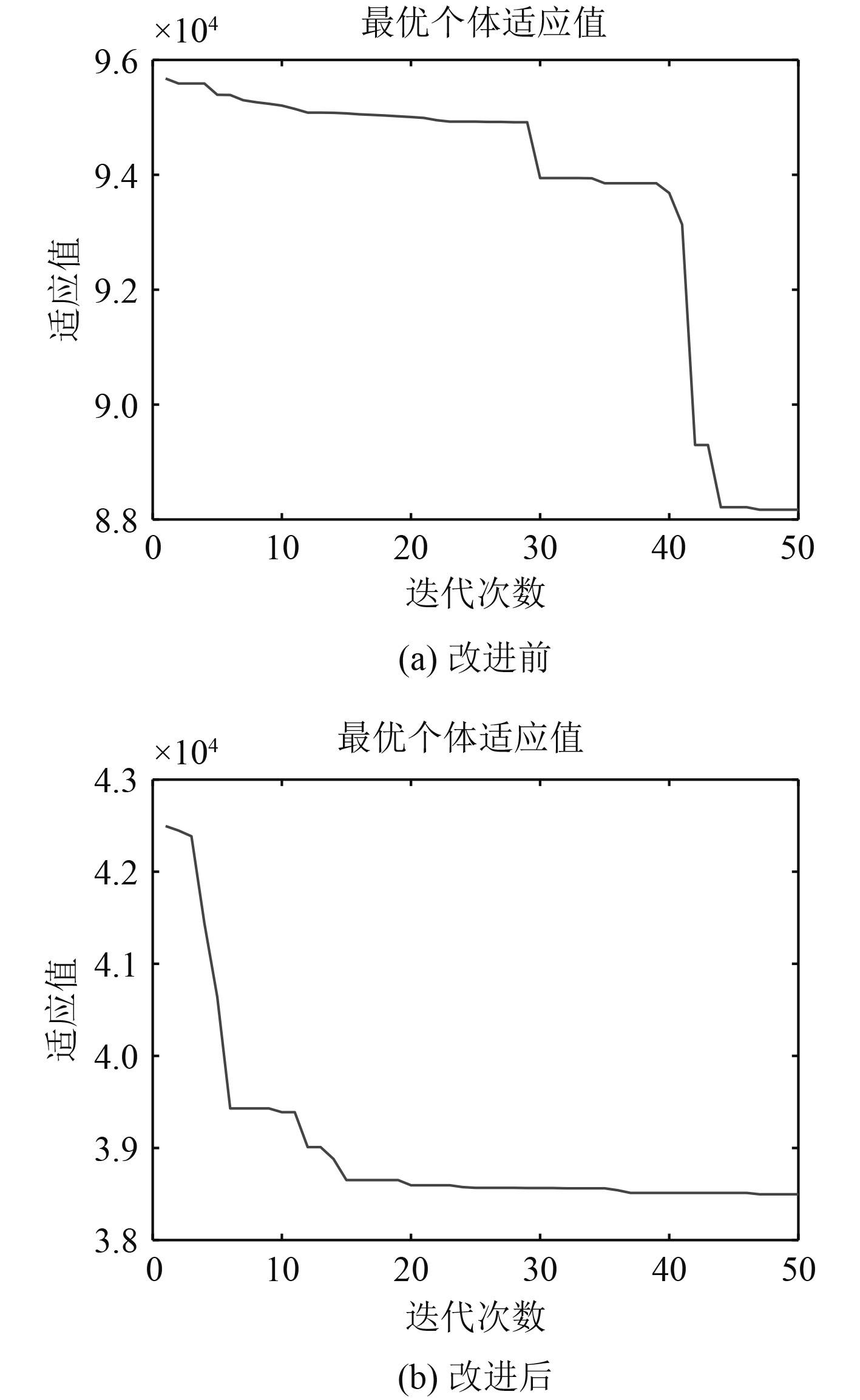
|
图 5 PSO改进前后迭代次数对比 Fig. 5 Comparison of iterations before and after PSO improvement |
在自抗扰控制器参数与目标排放NOx值不变的情况下,为探究经改进算法整定后的非线性反馈增益对补偿因子的可适应性范围,将补偿因子同时扩大和缩小30%,进行仿真分析。
图6仿真结果显示,经改进PSO整定后的非线性反馈增益控制器的控制曲线在约47 s处逼近目标值,最大超调量接近3%,在约55 s处稳定在目标值附近,稳态误差在1.5%左右,对比前期研究中控制输出过渡时间约为63 s,时间缩短11%,稳态误差在3%左右,准确度提升1.5%;在非线性反馈增益不变的情况下,缩小30%的补偿因子控制曲线在27 s时逼近控制目标,经25%最大超调后在80 s处稳定;扩大30%的补偿因子控制曲线在85 s处稳定。在改变补偿因子后,控制曲线最后都能稳定在控制目标附近。
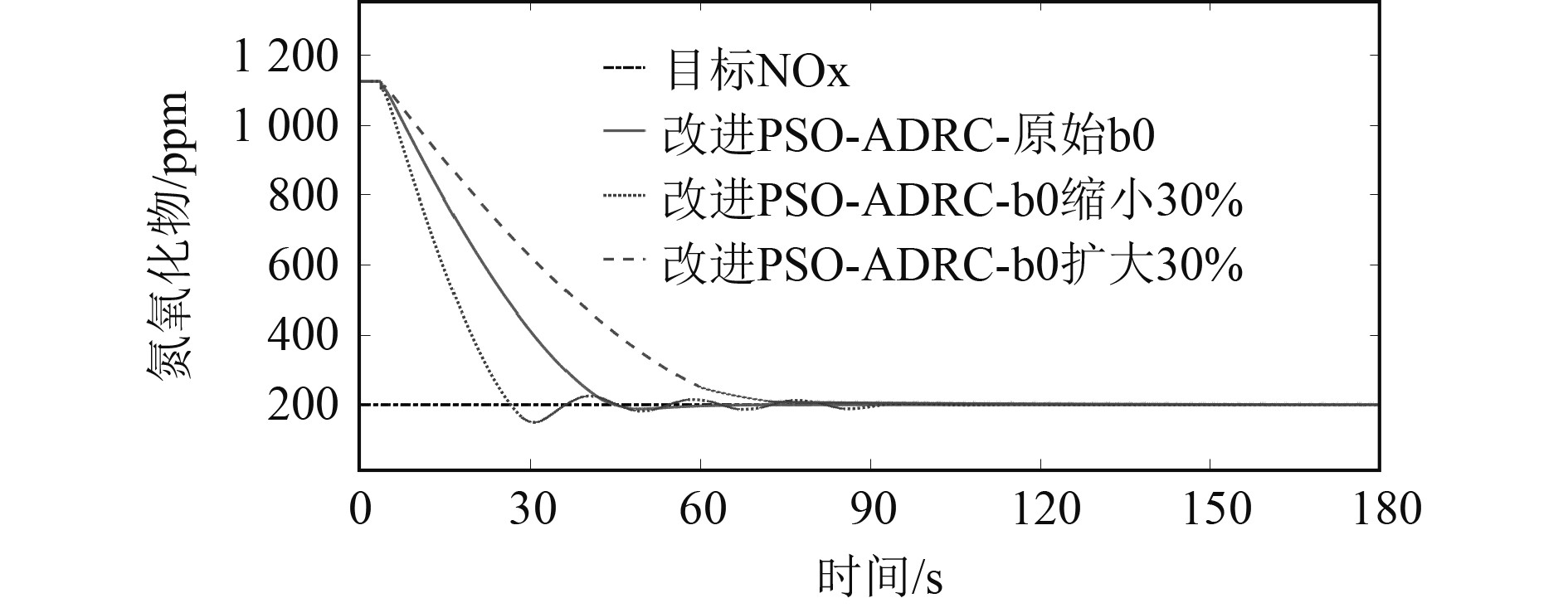
|
图 6 补偿因子改变时仿真结果 Fig. 6 Simulation results when compensation factor changes |
在自抗扰控制器参数与目标排放NOx值不变的情况下,研究原机排放在90 s时,升高100 ppm的控制过程,模拟柴油机变工况运行。
图7仿真结果显示,改进后的控制曲线在约55 s处稳定在目标值附近,传统PSO的自抗扰控制器,最大超调量在20%,在约72 s时稳定在目标值附近,在90 s时使原机排放升高100 ppm,改进PSO与传统PSO自抗扰控制器分别在约18 s后、55 s后稳定在目标值。
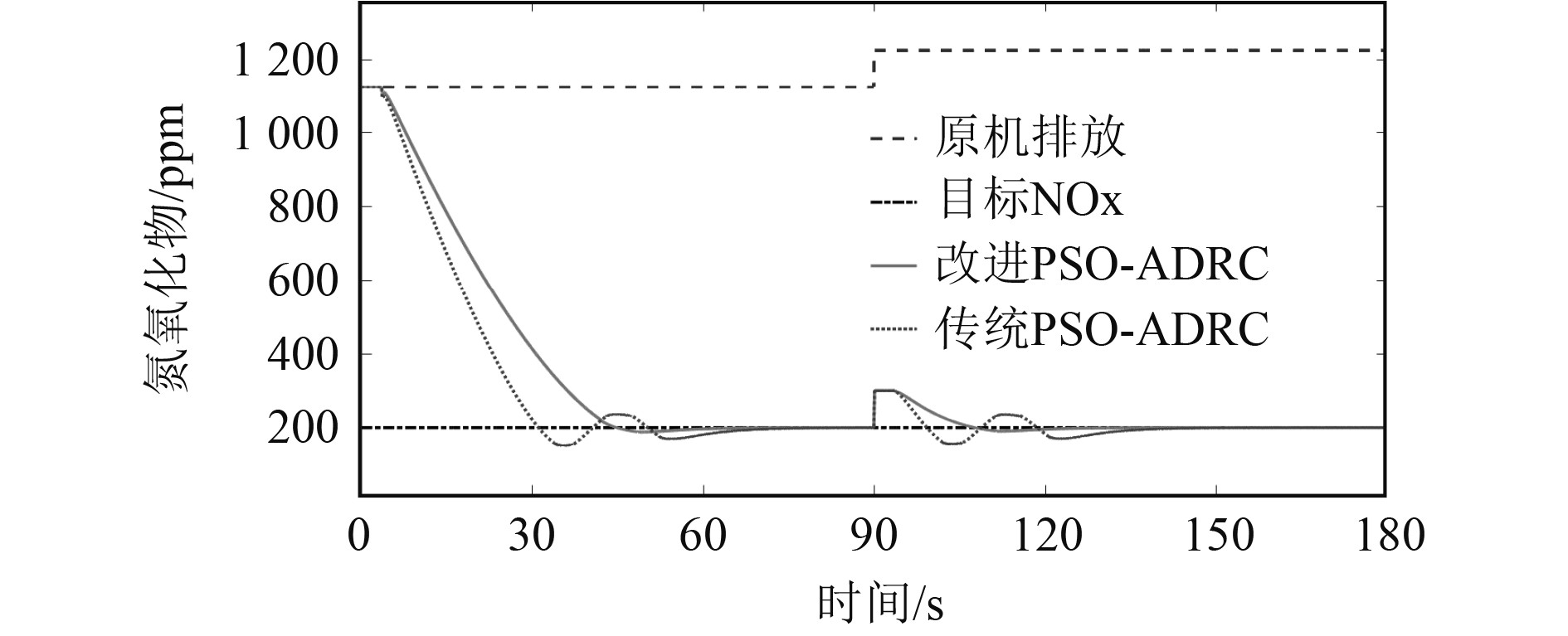
|
图 7 氮氧化物浓度改变时仿真结果 Fig. 7 Simulation results when nitrogen oxide concentration changes |
柴油机SCR系统的反应时滞时间受到催化器温度及工况改变等因素影响,因此在自抗扰控制器参数与目标排放NOx值不变的情况下,将模型时滞时间由6 s变为8 s,研究其控制效果。
图8仿真结果显示,将2种算法的自抗扰控制器时滞时间由6 s调整至8 s,最后都能趋于稳定。对于时滞时间为8 s的控制器,改进算法控制曲线最大超调量在8%左右,最后在约75 s处稳定,稳态误差在2%,传统PSO算法控制曲线最大超调量在29%左右,最后在约155 s处稳定,改进算法的控制器能够较好抵御时滞时间的改变,在超调量与调节时间方面都好于传统PSO算法整定的自抗扰控制器。
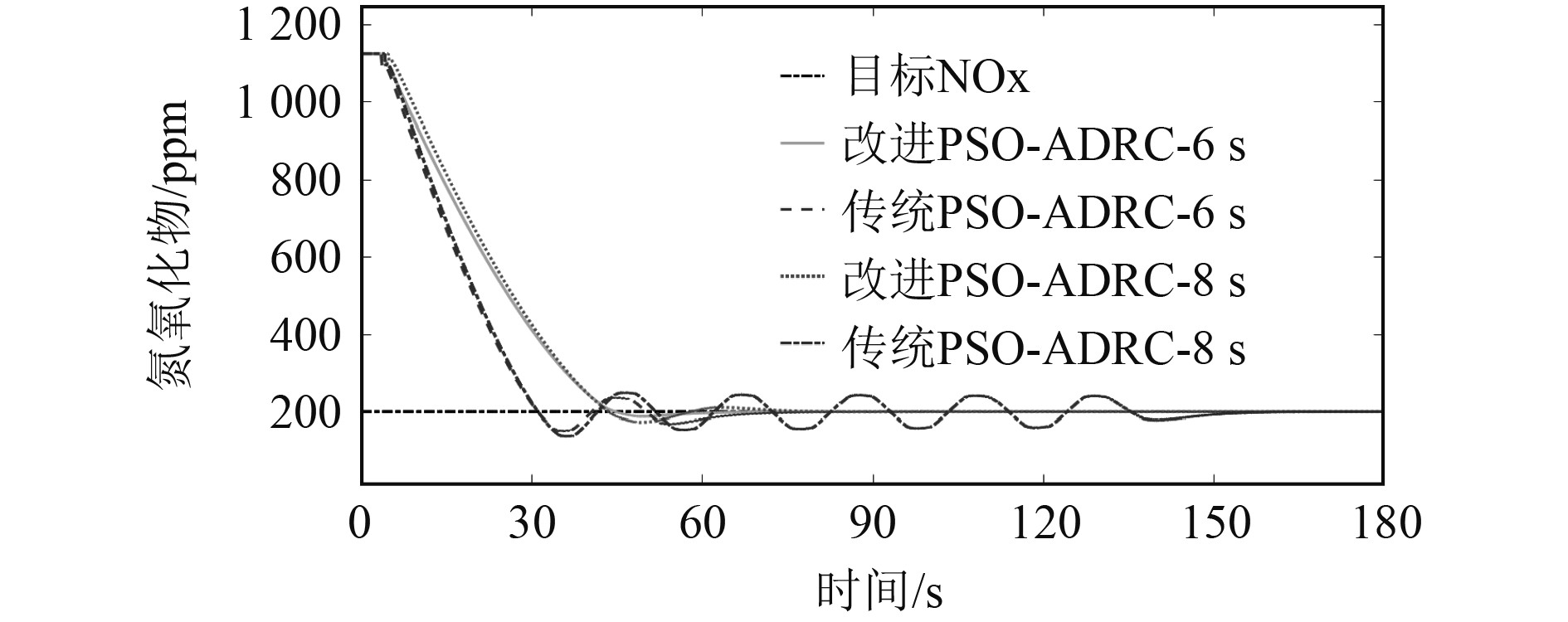
|
图 8 时滞时间改变时仿真结果 Fig. 8 Simulation results when delay time changes |
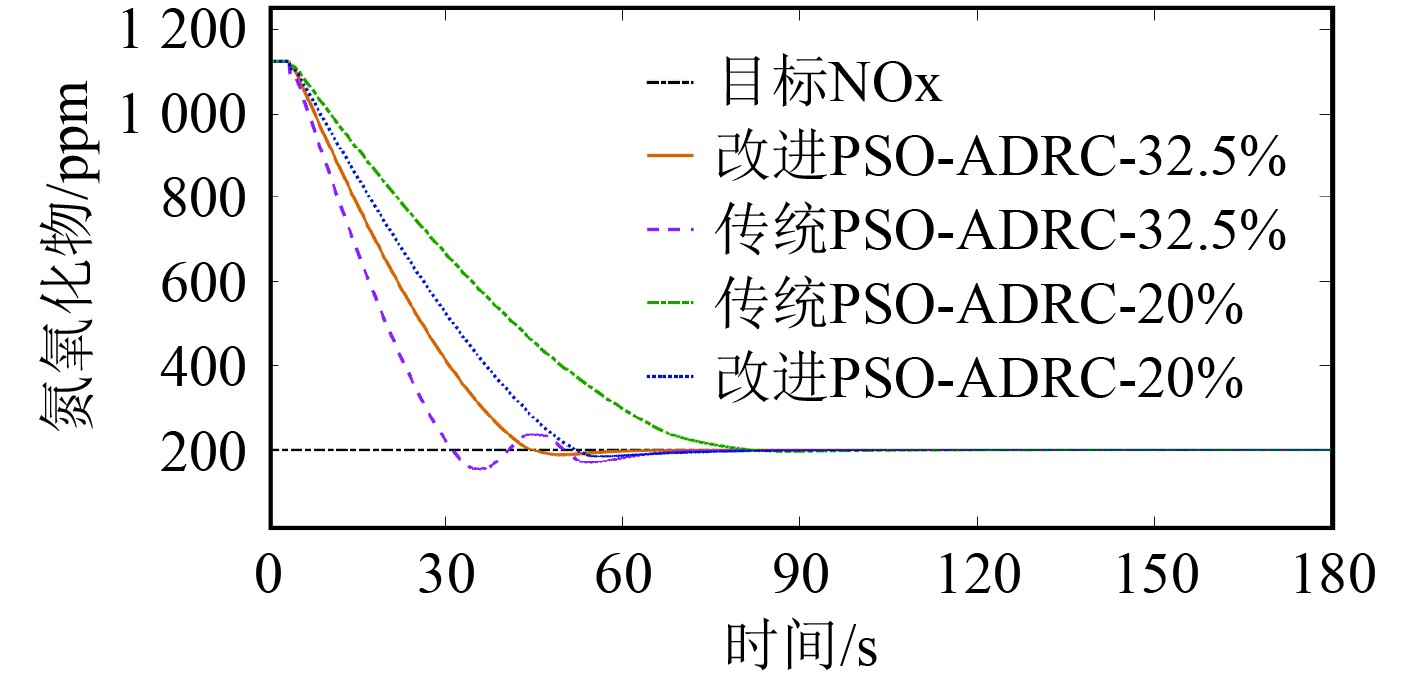
在柴油机实际运行中,会出现尿素浓度降低,质量劣化的情况。现研究在自抗扰控制器参数与目标排放NOx值不变的情况下,将尿素水溶液的浓度由32.5%变为20%后,自抗扰控制器的控制效果。
图9仿真结果显示,对于改进后自抗扰控制器,当尿素水溶液浓度由32.5%转变为20%时,稳定目标值的时间由55 s延长至了73 s,而对于传统PSO自抗扰控制器,稳定时间由72 s延长至了87 s。尿素水溶液浓度改变后,上述2种控制器最后都能趋于稳定,但改进后自抗扰控制器调节时间较短。
|
图 9 尿素浓度改变时仿真结果 Fig. 9 Simulation results when urea concentration changes |
本文针对柴油机SCR后处理系统设计了一种自抗扰控制器,为解决控制系统快速性与超调间的矛盾,采用改进粒子群算法对自抗扰控制器非线性反馈增益进行研究整定。仿真结果表明:优化后SCR控制器对补偿因子取值有较大适应性范围,并能在柴油机排放值突变、SCR装置时滞时间改变、尿素水溶液浓度降低的扰动下,仍快速低超调量地跟踪控制目标,稳态误差均约为1.5%。
综上,非线性反馈增益经过PSO优化后,使控制器能有效地提高控制系统的动态响应和鲁棒性,可为后续开发SCR控制系统提供参考。
| [1] |
覃军. 降低柴油机NO_X排放的SCR系统控制策略研究[D]. 武汉: 武汉理工大学, 2007.
|
| [2] |
SCHÄR C M, ONDER C H, GEERING H P, et al. Control of a urea SCR catalytic converter system for a mobile heavy duty diesel engine[J]. SAE Transactions, 2003, 112: 1180−1188
|
| [3] |
Improvement of low-temperature performance of the NOx reduction efficiency on the Urea-SCR catalysts[C]//SAE 2013 World Congress and Exhibition, 2013.
|
| [4] |
石秀勇, 罗亨波, 倪计民, 等. 基于模型的柴油机Urea-SCR系统闭环控制策略仿真[J]. 内燃机学报, 2017, 35(4): 346-353. SHI Xiuyong, LUO Hengbo, NI Jimin, et al. Simulation of closed-loop control strategy for urea-SCR system of diesel engine based on model[J]. Transactions of CSICE, 2017, 35(4): 346-353. DOI:10.16236/j.cnki.nrjxb.201704049 |
| [5] |
张仁敏. 基于线性自抗扰技术的添蓝喷射控制策略研究[D]. 武汉: 武汉理工大学, 2016.
|
| [6] |
SONG Q, ZHU G. Model-based closed-loop control of urea SCR exhaust aftertreatment system for diesel engine[C]// SAE World Congress & Exhibition, 2002.
|
| [7] |
JOHN N. C. Control challenges for optimal NOx conversion efficiency from SCR aftertreatment systems[C]//SAE 2009 World Congress, 2009.
|
| [8] |
FRANK W, ROBERT C, EDWIN V D E. Is closed-loop SCR control required to meet future emission targets?[C]//2007.
|
| [9] |
刘丙善. 基于自抗扰控制技术的车用选择性催化还原系统控制策略研究[D]. 武汉: 武汉理工大学, 2015.
|
| [10] |
刘丙善, 吕林, 张仁敏. 柴油机Urea-SCR装置非线性自抗扰控制系统研究[J]. 哈尔滨工程大学学报, 2017, 38(3): 385-391. LIU Bingshan, LV Lin, ZHANG Renmin. Study on nonlinear active disturbance rejection control system for urea-SCR device of diesel engine[J]. Journal of Harbin Engineering University, 2017, 38(3): 385-391. |
| [11] |
韩京清. 自抗扰控制技术—估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
|
| [12] |
张继荣, 张天. 基于改进粒子群算法的PID控制参数优化[J]. 计算机工程与设计, 2020, 41(4): 1035−1040. ZHANG Jirong, ZHANG Tian. Optimization of PID control parameters based on improved particle swarm optimization [J]. Computer Engineering and Design, 20, 41(4): 1035−1040. |
| [13] |
康新宇, 刘惠康, 柴琳, 等. 基于改进型粒子群算法优化的塔式吊车自抗扰控制[J]. 制造业自动化, 2022, 44(9): 106-111. KANG Xinyu, LIU Huikang, CHAI Lin, et al. Active disturbance rejection control of tower crane based on improved particle swarm optimization[J]. Manufacturing Automation, 2022, 44(9): 106-111. |
| [14] |
余胜威. Matlab优化算法案例分析与应用[M]. 北京: 清华大学出版社, 2014.
|
 2024, Vol. 46
2024, Vol. 46

