2. 中国人民解放军95778部队,云南 昆明,650000
2. No.95778 Unit of PLA, Kunming 650000, China
某型燃气轮机燃油泵组件是燃油系统中的重要组件,其作用是向发动机燃烧室提供合适的压力与流量的燃油,燃油泵组件内部结构复杂,既有高速旋转的柱塞泵,又有精密动作的步进电机、阀组等部件。该部件故障率较高,严重影响燃机的使用。为了给燃油泵组件的使用和维护工作提供有效的指导意见,迫切需要对燃油泵组件的可靠性进行深入分析[1-2]。
近年来,威布尔分布[3]因其能包括常见的几种分布,适应各种类型实验数据,因此在可靠性工程中得到广泛应用,在可靠性研究中具有很强的生命力[4-5]。三参数威布尔模型在两参数威布尔分布的基础上引入位置参数更能够逼近实际,充分描述失效机理,因此在可靠性研究中大量采用三参数威布尔分布进行故障模型建模分析[6-7],刘宇等[8]对高压开关产品可靠性进行分析,并与统计直方图进行对比,证明了参数估计结果的有效性。由于威布尔分布在分析现场数据具有较好的适应性,因而从舰船维修的角度来看,利用现场数据进行可靠性评估时可重点研究威布尔分布[9]。
虽然威布尔分布可包含多种失效模型,但在3个参数确定的情况下,也只能代表一种分布,而燃油泵组件是机电一体化的产品,其在使用中获得的数据存在不同失效机理的情况,因此单一的分布无法准确描述产品失效机理,而混合分布能够将多种失效分布进行耦合,充分描述产品失效机理[10]。本文通过对某型燃气轮机燃油泵组件故障数据进行分析获得积累频率、失效频率直方图,根据直方图特点推断故障模型,粗估模型参数,然后采用Matlab非线性曲线拟合方法来估计二重三参数威布尔混合分布函数的参数,得出失效分布函数,根据失效分布函数分析燃油泵组件的故障机理及预防维护措施。研究方法及成果能够为燃油泵组件可靠性分析及优化改进提供一定的借鉴。
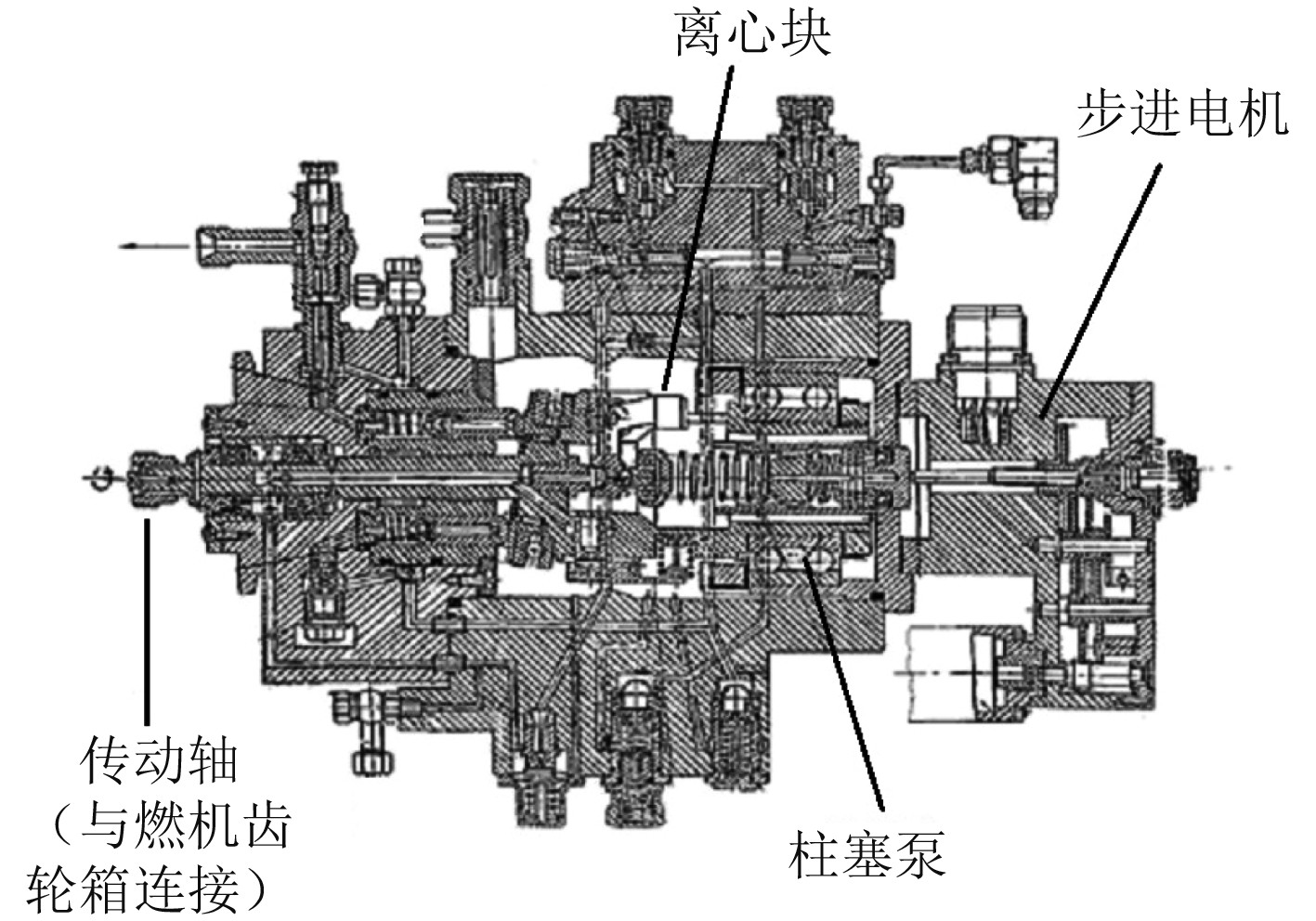
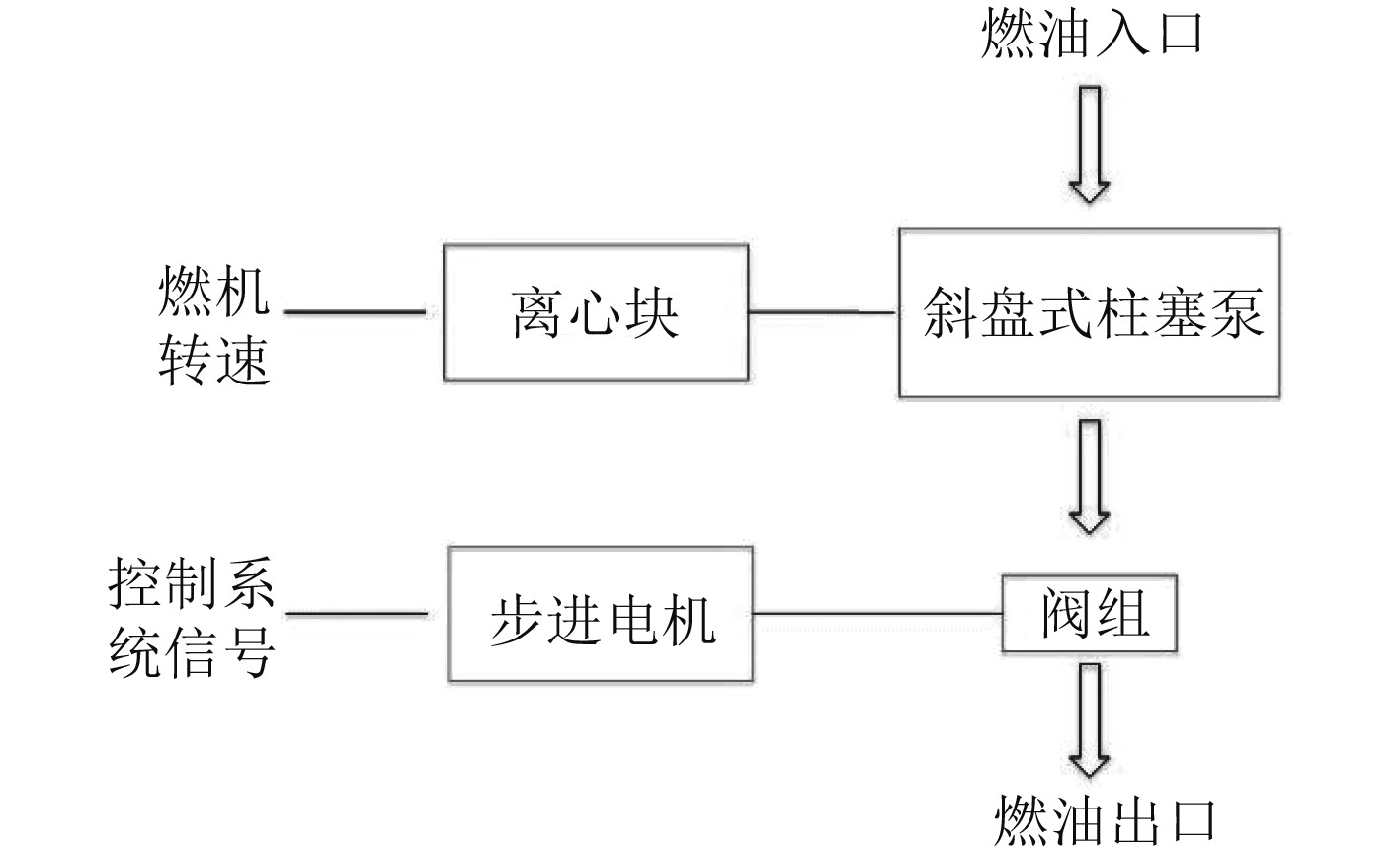
1 燃油泵组件工作原理某型燃机燃油泵组件主要由斜盘式柱塞泵、离心块、步进电机、阀组及密封组件构成(见图1),主要功能是根据控制系统信号为燃油系统提供压力与流量都符合要求的燃油。工作原理是控制系统根据负载情况控制步进电机动作,步进电机调节阀组开阀压力从而改变供油压力,离心块根据燃机转速调节柱塞泵斜盘角度从而改变燃油供应量(见图2)。
|
图 1 燃油泵组件结构剖面图 Fig. 1 Sectional view of fuel pump component |
|
图 2 燃油泵组件工作原理图 Fig. 2 Working diagram of fuel pump component |
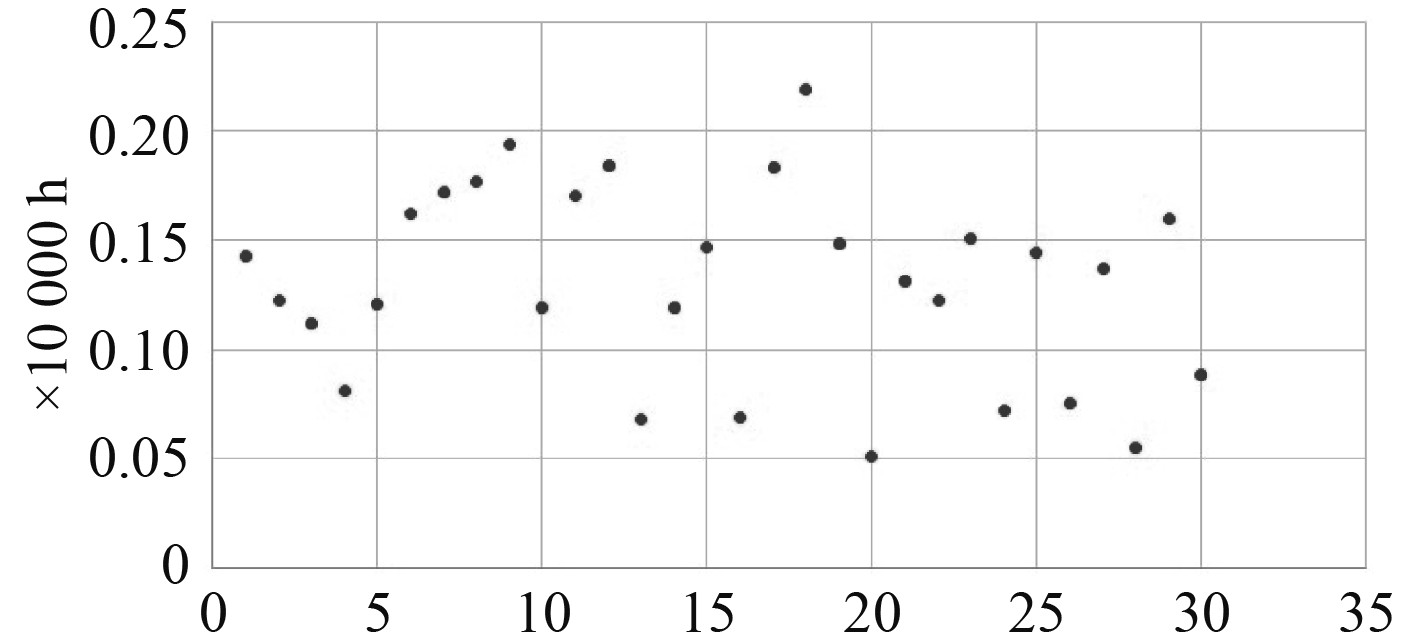
根据某型燃机燃油泵组件故障统计数据(见图3),利用直方图来分析整理数据,判断燃油泵组件故障分布规律以及各项可靠性指标。
|
图 3 故障数据 Fig. 3 Fault data |
根据图3数据,提取无故障工作时间最大值L和最小值S,计算分组数K:
| ${K}=1+3.3{\rm{l}}_{{\rm{g}}}{{n}} 。$ | (1) |
计算组距
| $ \Delta {t}=({L}-{S})/{K} 。$ | (2) |
确定各组分上限值、下限值,按左闭右开区间来分配数据,计算各组中心值:
| $ {t}_{i}=\frac{\mathrm{某}\mathrm{组}\mathrm{下}\mathrm{限}\mathrm{制}+\mathrm{某}\mathrm{组}\mathrm{上}\mathrm{限}\mathrm{值}}{2}。$ | (3) |
统计落入各组的频数Δri和频率
| $ {w}_{i}=\frac{{\mathrm{\Delta }{r}}_{i}}{n} 。$ | (4) |
计算样本均值
| $ \stackrel-{t}=\sum _{i=1}^{k}{w}_{i}\times{t}_{i} 。$ | (5) |
计算样本标准差S:
| $ {S}=\sqrt{\frac{1}{n-1}\sum _{i=1}^{k}\Delta {r}_{i}({t}_{i}-\stackrel-{t}{)}^{2}} 。$ | (6) |
根据故障统计数据,通过式(1)~式(6)获得该部件寿命分组数据累积频率计算结果(见表1)。
|
|
表 1 计算结果 Tab.1 Calculation results |
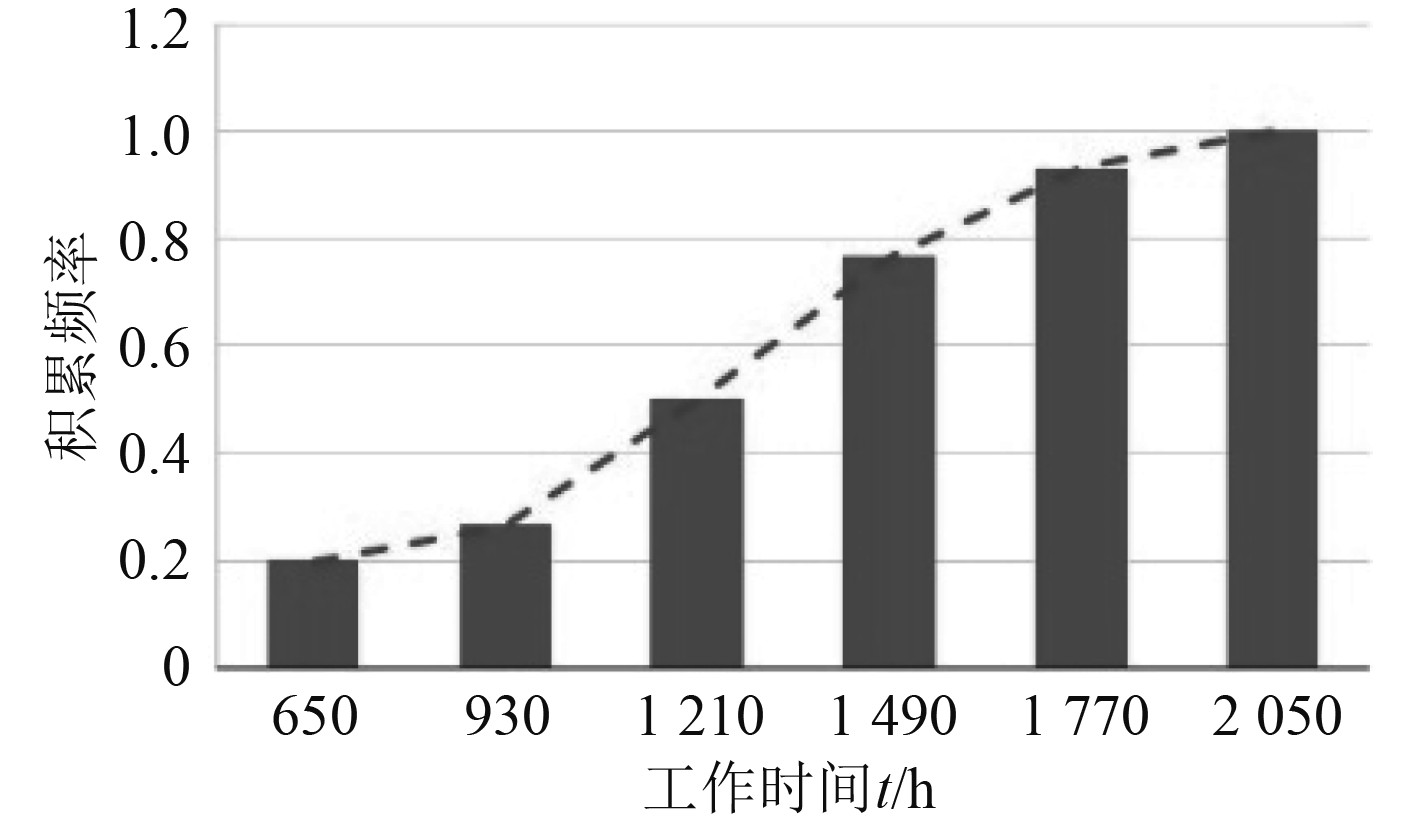
根据分析计算数据绘制直方图,积累频率分布如图4所示,失效频率如图5所示。
|
图 4 累积频率分布图 Fig. 4 Cumulative frequency distribution |
|
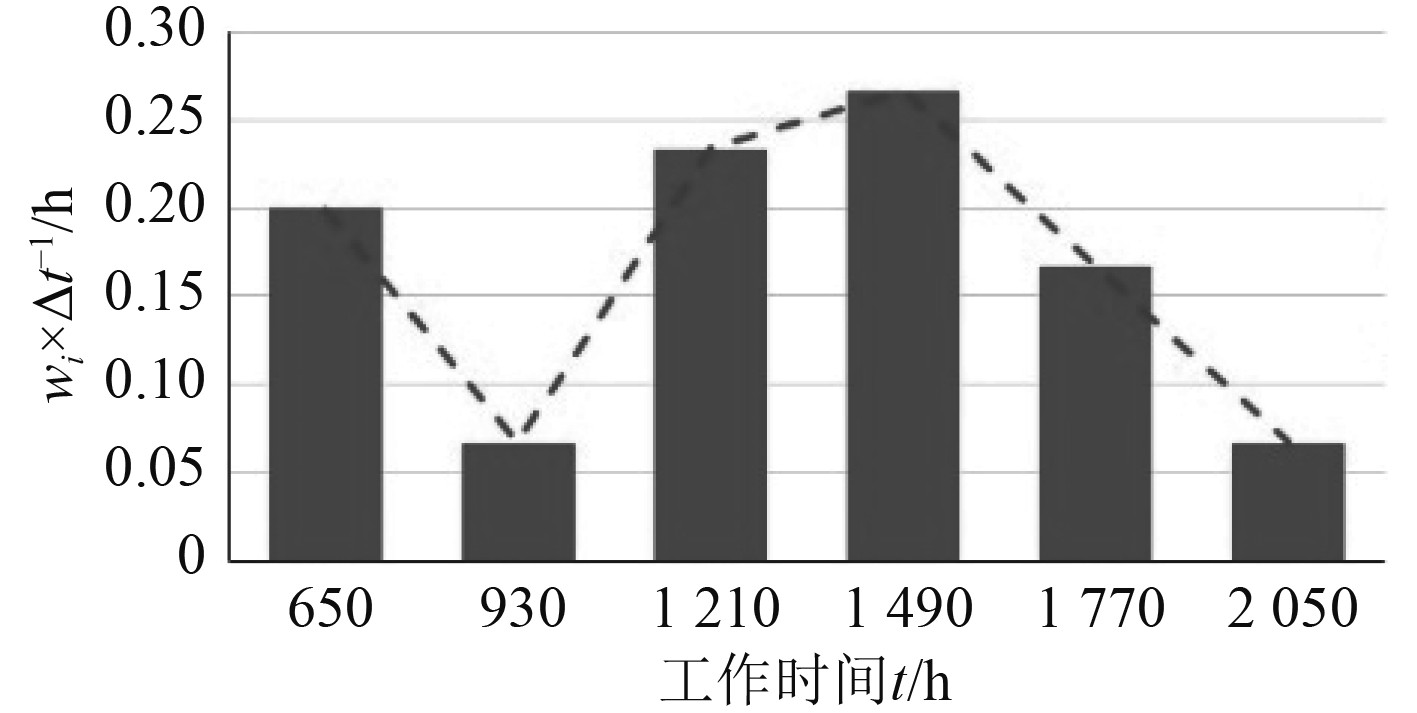
图 5 失效频率直方图 Fig. 5 Failure frequency histogram |
分析图5中失效频率折线走势,失效频率随时间轴,先减小,后增大,到达顶点后再减小,其特点非常符合二重威布尔分布密度函数,结合燃油泵组件的失效机理主要集中在高速转动部件与电动机,因此可以推断燃油泵组件的故障模型较为符合二重混合威布尔分布。同时根据图5中失效频率折线第1个峰谷的位置,可以推断二重威布尔分布位置参数中至少有1个不为0,至此可以基本确定故障模型为二重三参数威布尔混合分布。
3 基于Matlab对故障分布函数参数求解建立二重三参数威布尔混合分布函数:
| $ {F}\left({t}\right)={P}\left\{{1-e}^{-\frac{{(t-\gamma 1)}^{m1}}{\eta 1}}\right\}+\left(1-P\right)\left\{1-{e}^{-\frac{{(t-\gamma 2)}^{m2}}{\eta 2}}\right\}。$ | (7) |
设:
| $ {F}_{1}\left({t}\right)=1-{e}^{-\frac{{(t-\gamma 1)}^{m1}}{\eta 1}} ,$ | (8) |
| $ {{F}_{2}\left(t\right)=1-e}^{-\frac{{(t-\gamma 2)}^{m2}}{\eta 2}}。$ | (9) |
则:
| ${F}\left({t}\right)=P{F}_{1}\left(\mathrm{t}\right)+\left(1-P\right){F}_{2}\left(t\right)。$ | (10) |
式中:P、γ1、η1、m1、γ2、η2、m2均为未知参数。
Matlab中对于非线性数据进行拟合时,为了能够在最短的时间内获得收敛解,需要对未知参数进行初始化,以未知参数的初值作最小二乘拟合,未知参数初始化值直接影响到能否获得收敛解以及拟合曲线的品质。因此如何拟定合适的初始参数是参数求解的关键。
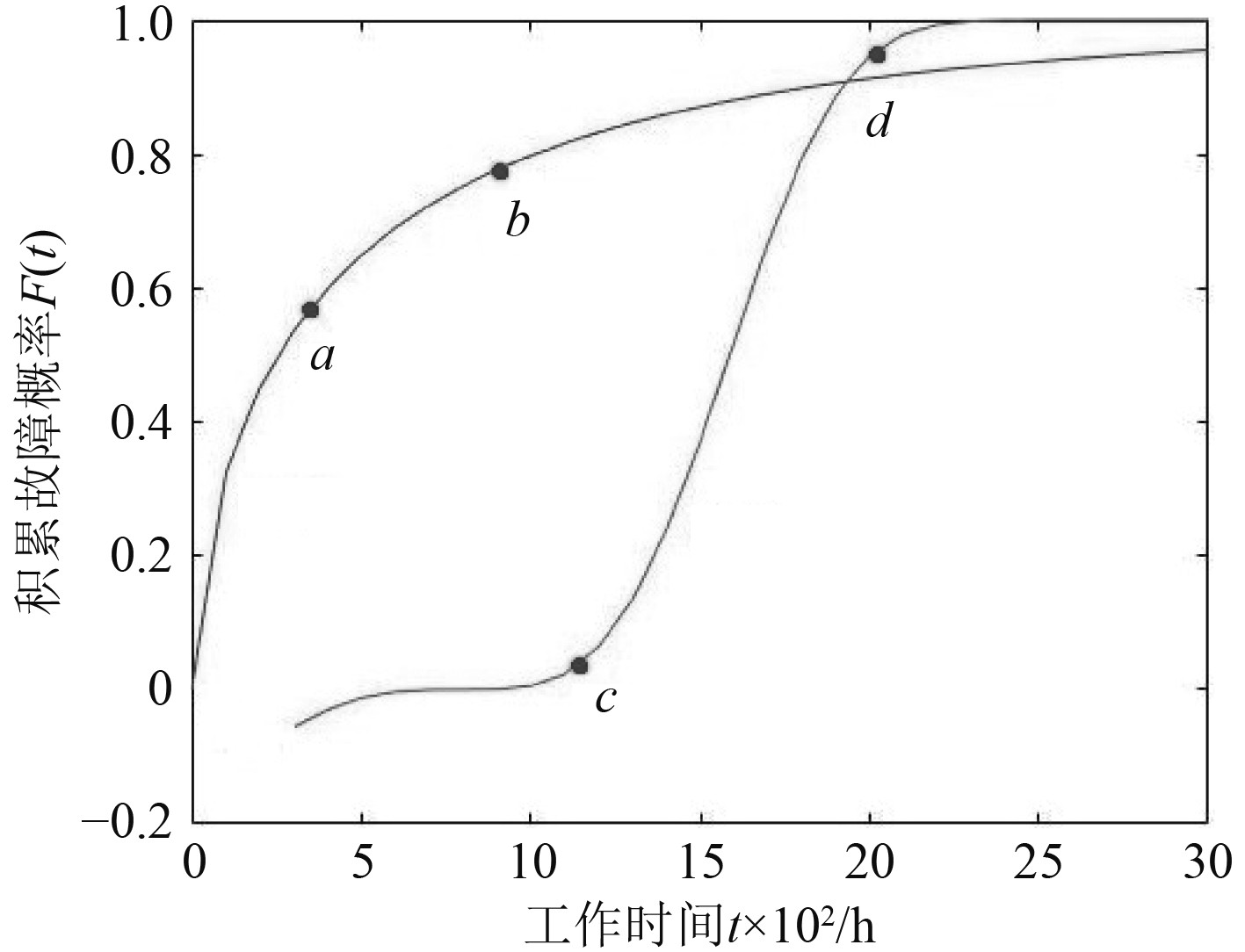
分析图4中积累频率折线走势,折线明显可以在横轴t=930处划分为两段,在折线左段曲线走势平缓,可以推断此时起主导作用的分布函数F1(t)应与图6中曲线1中a、b两点之间相似,此时F1(t)函数的取值范围约为0.6~0.8,而F(t)函数值在0.2~0.27之间,同时考虑到此时F2(t)函数对F(t)函数数值也有一定的影响,因此未知参数P的初始值可取为0.3,而在积累频率折线右段,此时F1(t)函数值变化不大,其主导作用的为F2(t)函数,F2(t)应与图6中曲线2中c、d两点之间相似。
|
图 6 曲线对比分析图 Fig. 6 Similar curve comparison and analysis chart |
根据已确定的初值P,忽略F2(t)函数值的影响,根据F(t)的故障数据分析结果,可以获得粗略的F2(t)函数值,采用以最小二乘法和相关系数法相结合的方法来估计三参数威布尔分布的参数[7,11],最后得出γ1、η1、m1的初始值分别为0、512.2、0.52。同理可根据同样方法估计γ2、η2、m2的初始值,要注意的是此时在计算F2(t)函数值时,不能忽略F1(t)函数值的影响,最后得γ2、η2、m2的初始值分别为910.20、1260.17、3.08。
根据未知参数的初始值,编制故障模型数学模型函数,采用Matlab非线性最小二乘拟合,最后获得失效分布函数参数:
{P γ1 η1 m1 γ2 η2 m2}={0.27 0 463.3 0.61 534.1 861.2 3.375};残差平方=1.3463×10−4,将参数代入式(7)得到失效分布函数:
| $ {F}\left({t}\right)=0.27 \cdot \left({1-e}^{-{\left(\frac{t}{463.3}\right)}^{0.61}}\right)+0.73 \cdot \left(1-{e}^{-({\frac{t-534.1}{861.2})}^{3.375}}\right) 。$ |
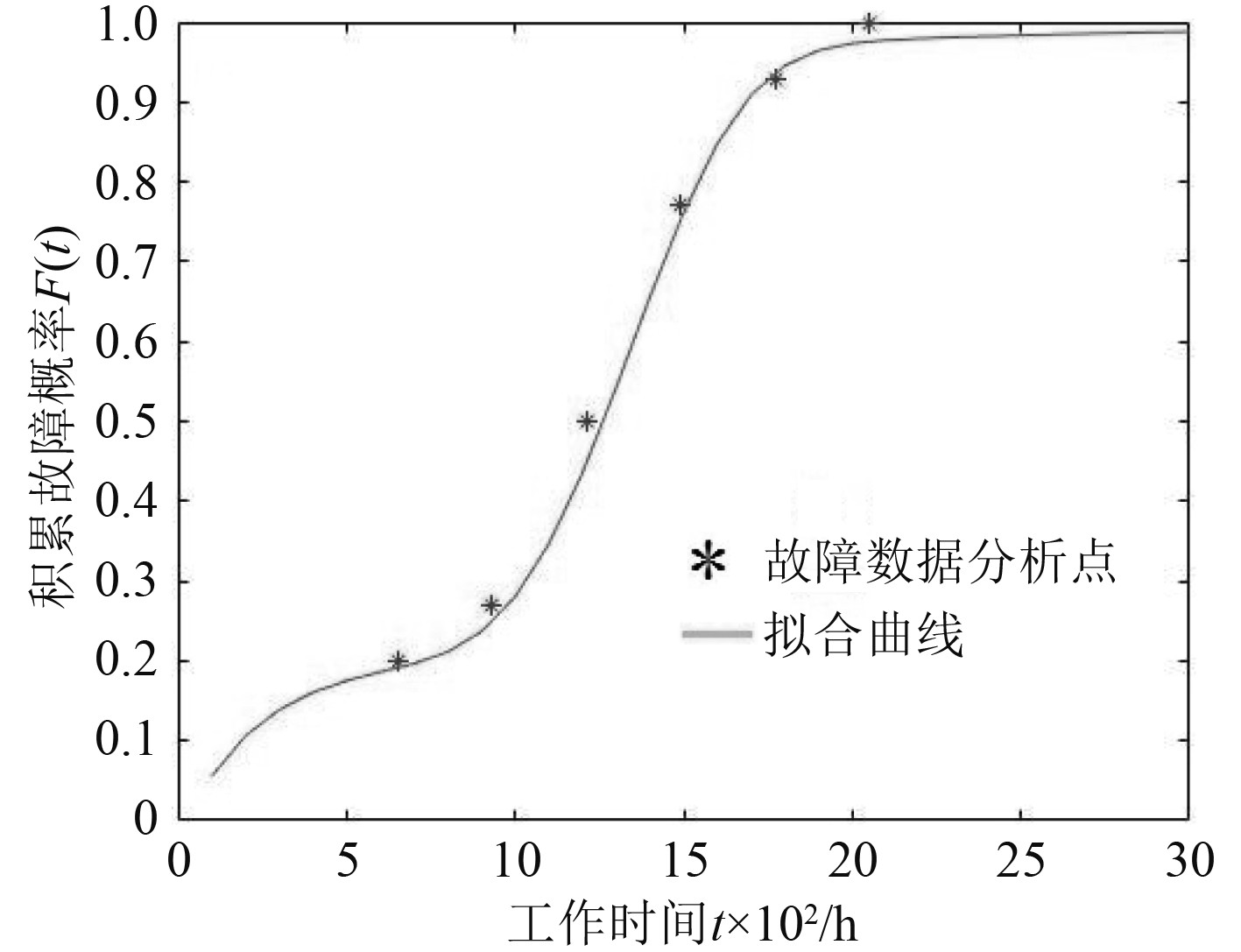
故障数据分析结果与拟合曲线对比如图7所示。根据曲线与点的符合情况以及残差平方值,可以肯定获得的失效分布函数能够准确描述产品失效机理。
|
图 7 拟合曲线与故障数据分析对比图 Fig. 7 Comparison and analysis between fitting curve and fault data chart |
根据失效分布函数求导获得失效率函数:
| $ \begin{split} {f}\left({t}\right) = & 3.6\times{10}^{-4} \times {\left(\frac{t}{463.3}\right)}^{-0.39} \times {e}^{-{\left(\frac{t}{463.3}\right)}^{0.61}} + 2.86 \times {10}^{-3}\times\\ & \left(\frac{t-534.1}{861.2}\right)^{2.375}\times{e}^{-\left(\frac{t-534.1}{861.2}\right)^{3.375}},\\[-10pt] \end{split} $ | (11) |
平均寿命(平均故障间隔时间MTBF):
| $ {{MTBF}}=\theta={{P}}\times\theta_1+(1-{\mathrm{P}})\times\theta_2。$ | (12) |
式中:θ1=γ1+η1×Г(1+1/m1), θ2=γ2+η2×Г(1+1/m2),查Г(·)函数表得到Г(1+1/m1)=1.505、Г(1+1/m2)=0.898,代入平均寿命计算公式:
| $ {{MTBF}} =1\;142.5\;{\mathrm{h}} 。$ |
失效率函数λ(t)为:
| $ \scriptsize\mathrm{\lambda }\left(\mathrm{t}\right) = \frac{3.6 \times {10}^{-4} \times \left( \frac{t}{463.3} \right)^{-0.39} \times {e}^{-\left( \frac{t}{463.3} \right)^{0.61}}+2.86 \times {10}^{-3} \times \left( \frac{t-534.1}{861.2} \right)^{2.375} \times {e}^{-\left(\frac{t-534.1}{861.2}\right)^{3.375}}}{0.27 \times {e}^{-{\left(\frac{t}{463.3}\right)}^{0.61}}+0.73 \times {e}^{-\left(\frac{t-534.1}{861.2}\right)^{3.375}}} 。$ | (13) |
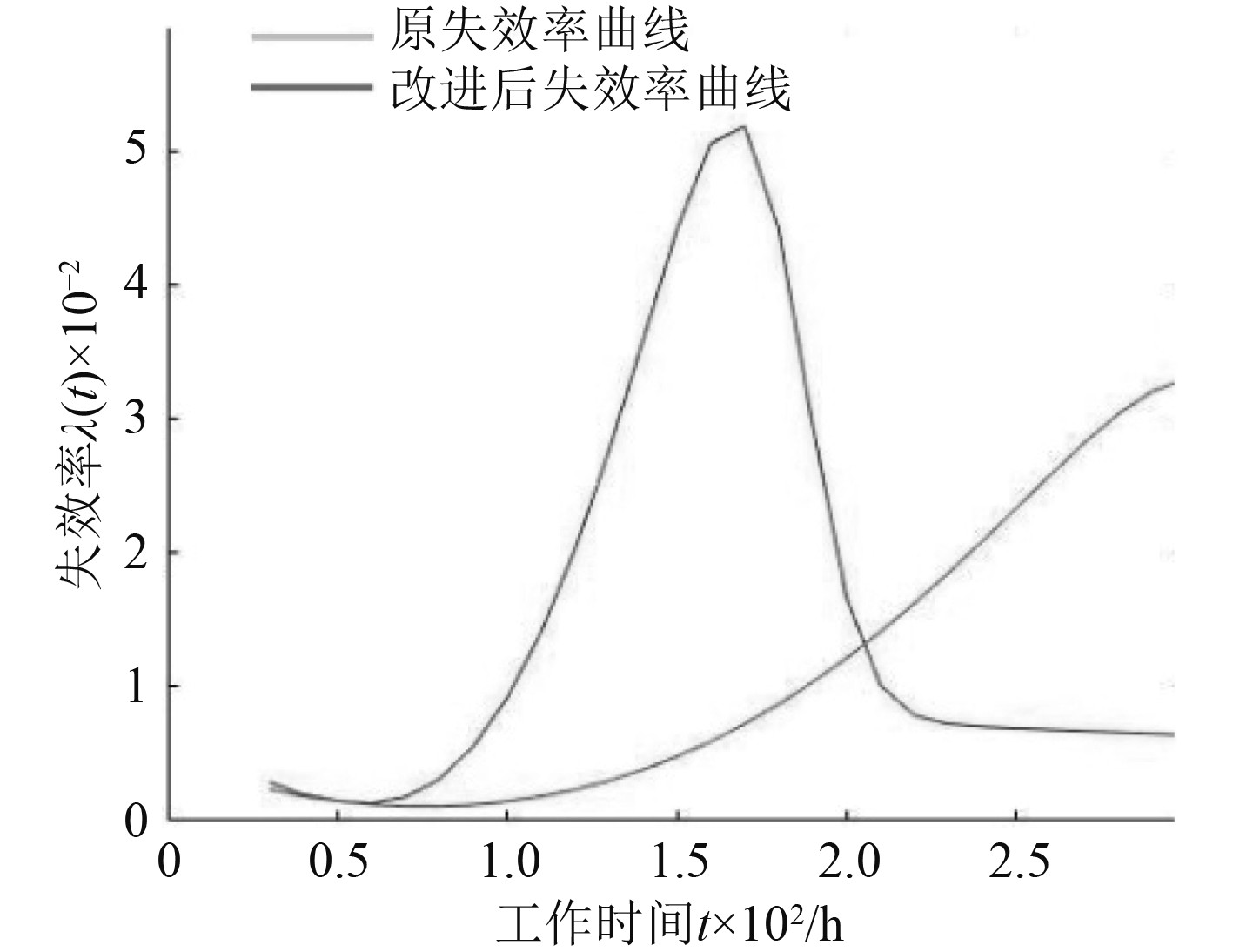
燃油泵组件的原失效率曲线如图8所示。可以看出,失效率在1600 h之前随时间增长呈增长特性,因此燃油泵组件的失效类型为耗损失效,故障原因可能由于老化、疲劳和耗损引起的,而在1600 h后失效率迅速下降,因此可以推断在1600 h之前的失效类型主要是由损耗引起的,并且根据曲线后端失效率迅速下降的特性可以推断损耗是非正常损耗,即燃油泵组件内部磨损异常严重,而通过对故障燃油泵组件的拆解也发现其内部柱塞泵密封件存在异常严重的磨损,是燃油泵组件的薄弱环节,需要采取措施降低失效率,从而提高燃油泵组件的MTBF。
|
图 8 燃油泵组件的失效率曲线 Fig. 8 Failure rate curve of fuel pump component |
通过采取以下措施使燃油泵组件可靠性指标有较大提高,改进优化后失效率曲线见图8,改进后MTBF=1 908.9 h,寿命提高67%。
1)对燃油泵组件中柱塞泵密封环等易损件进行定期拆解更换;
2)改进密封环的材质,在不降低其密封性能的基础上,提高耐磨度;
3)优化燃油泵组件内部润滑结构,提高润滑效果;
4)指导使用人员增加对上游燃油滤清器的清洗频率,减少进入泵燃油组件内部燃油中的杂质。
5 结 语本文通过对某型燃气轮机燃油泵组件故障数据进行分析,根据积累频率、失效频率直方图确定了二重三参数威布尔混合故障模型。采用最小二乘法和相关系数法相结合的方法来粗估威布尔混合分布函数的初始化参数,Matlab非线性曲线拟合方法来估计二重三参数威布尔混合分布函数的参数,得出的失效分布函数精度能充分描述燃油泵组件的失效机理。根据失效分布函数分析燃油泵组件的故障机理及预防维护措施,使燃油泵组件MBTF寿命提高67%。研究方法及成果可为燃油泵组件可靠性分析及优化改进提供一定的借鉴。
| [1] |
张志华. 可靠性理论及工程应用[M]. 北京: 科学出版社, 2012.
|
| [2] |
赵宇. 可靠性数据分析 [M]. 北京: 国防工业出版社, 2011.
|
| [3] |
WEIBULL W. A statistical distribution function of wide applicability[J]. Journal of Applied Mechanics, 1951, 18(3): 293-297. DOI:10.1115/1.4010337 |
| [4] |
徐微, 胡伟明, 孙鹏. 基于两参数威布尔分布的设备可靠性预测研究[J]. 中国工程机械学报, 2013, 11(2): 112-115. XU Wei, HU Wei-ming, SUN Peng. Equipment reliability predietion based on dual-parametric Weibull distribution[J]. Chinese Journal of Construction Machinery, 2013, 11(2): 112-115. DOI:10.3969/j.issn.1672-5581.2013.02.005 |
| [5] |
杨兆军, 李小兵, 许彬彬, 等. 加工中心时间动态可靠性建模[J]. 机械工程学报, 2012, 48(2): 16-21. YANG Zhao-jun, LI Xiao-bing, XU Bin-bin, et al. Time dynamic reliability modelling of machining center[J]. Journal of Mechanical Engineering, 2012, 48(2): 16-21. DOI:10.3901/JME.2012.02.016 |
| [6] |
曹克强, 胡良谋, 熊申辉, 等. 基于三参数威布尔分布的定量泵可靠性分析[J]. 现代制造工程, 2016, 19(12): 99-102. CAO Ke-qiang, HU Liang-mou, XIONG Shen-hui, et al. Reliability analysis of constant displacement pump based on three parameter Weibull distribution[J]. Modern Manufacturing Engineering, 2016, 19(12): 99-102. DOI:10.16731/j.cnki.1671-3133.2016.12.019 |
| [7] |
胡良谋, 曹克强, 熊申辉, 等. 前轮转弯减摆助力器故障分布的三参数威布尔分布模型[J]. 液压与气动, 2016, 13(9): 71-75. HU Liang-mou, CAO Ke-qiang, XIONG Shen-hui, et al. Three parameter weibull distribution model of fault distribution for front-wheel swerve shimmy damper hydraulic booster[J]. Chinese Hydraulics& Pneumatics, 2016, 13(9): 71-75. DOI:10.11832/j.issn.1000-4858.2016.09.013 |
| [8] |
刘宇, 成勇, 李锐鹏, 等. 威布尔分布在高压开关产品运行数据分析中的应用[J]. 高压电器, 2017, 53(12): 151−156. LIU Yu, CHENG Yong , LI Rui-peng , et al. Application of Weibull distribution in service data analysis of high voltage switchgear[J]. High Voltage Apparatus, 2017, 53(12): 151−156. |
| [9] |
梁前超, 彭彪, 等. 柴油机高压泵螺钉断裂的可靠性研究[J]. 武汉理工大学学报, 2005, 29(4): 481-483. LIANG Qian-chao, PENG Biao, et al. On reliability of iimmerging bolt-breaking in diesel pump[J]. Journal of Wuhan University of Technology, 2005, 29(4): 481-483. |
| [10] |
尚永爽, 吴忠德, 王星博. 威布尔分布下竞争性故障装备的可靠性分析[J]. 光电与控制, 2012, 19(8): 90-96. SHANG Yong-shuang, WU Zhong-de, WANG Xing-bo. Reliability analysis for equipment with competing failure in weibull distribution[J]. Electronics Optics & Control, 2012, 19(8): 90-96. |
| [11] |
耿俊豹, 罗梅杰, 谢强, 等. 基于故障统计和材料退化的机械系统可靠性评估[J]. 海军工程大学学报, 2018, 30(1): 13-16. GENG Jun-bao, LUO Mei-jie, XIE Qiang, et al. Reliability assessment of mechanical system based on fault statistics and material degradation[J]. Journal of Navaluniversity of Engineering, 2018, 30(1): 13-16. DOI:10.7495/j.issn.1009-3486.2018.01.003 |
 2024, Vol. 46
2024, Vol. 46
