颗粒碰撞阻尼技术的研究由来已久,起源来自Pagat[1]针对涡轮机叶片振动问题发明的一种冲击减振器。但由于其冲击噪声比较大,慢慢用许多小颗粒替代单一质量块。1969年,Masri[2]提出多单元单颗粒阻尼器,经过数值模拟与试验证明了多单元颗粒阻尼器比单一单元颗粒阻尼器的减振效果更好。颗粒阻尼技术具有减振频带宽、耐高温、结构简单等特点,近年来受到各国学者的关注[3−4]。胡溧等[5]建立了颗粒阻尼的粉体力学模型,并研究了颗粒阻尼容器的截面形状及尺寸关系对其减振特性的影响,首次将颗粒阻尼器运用到局域共振型性周期结构中[6]。Olson[7]提出一种对颗粒阻尼器设计进行分析的数学模型。该模型利用颗粒动力学方法,捕捉了粒子阻尼中涉及的复杂物理现象,并通过实验进行了验证。Lei[8]运用气固流原理和离散单元法,对粒子间碰撞和摩擦引起的阻尼和能量耗散机理进行了研究。现有的研究表明颗粒运动状态与耗能有着密切的关系[9−11],但是更多的侧重于分析颗粒运动与激励条件的对应关系[12−13],而对颗粒的耗能情况研究较少。
随着离散单元法[14]的不断发展,仿真模拟的方法可以较为精确模拟颗粒物质的真实状态,实现对每个颗粒的跟踪,得到实验中无法或者不易测得的数据。本文基于离散单元法研究颗粒的填充比、激振频率、振幅参数对带颗粒阻尼器结构减振效果的影响规律[15−17]。
1 振动参数对颗粒耗能的影响研究基于离散元法建立颗粒阻尼器的仿真模型,数据设定参考段永强等[18]的模型。采用颗粒直径为 1.5 mm的钢质圆球,颗粒填充50%,阻尼容器用密闭的圆柱形有机玻璃,阻尼器的参数为中(D×H=28 mm×40 mm) 。仿真中涉及的相关材料参数如表1所示,恢复系数用实验测得为0.917,其他仿真参数具体设定参考文献[19],并在容器上施加竖直方向的正弦激励。通过调节激励振幅为(1~5 mm)以及激振频率f (30、60、90、120 Hz)可以观察到颗粒的很多运动状态。为保证仿真结果的准确性,设定瑞利时间步长为2.07×10−7 s,仿真时间为2 s,提取0~2 s内的数据作为仿真结果进行分析。
|
|
表 1 DEM仿真材料特性及参数 Tab.1 Physical properties and parameters used in the DEM simulation |
通过分析颗粒在不同激励条件下的运动状态,发现阻尼器中会出现不同的运动状态,不仅会出现蹦床[9]、成拱[19]、小波(小幅表面波)[20],大波(大幅表面波)[21],成块,流化[22]等常见的形态,还会出现莱顿弗罗斯特效应、浮力对流效应,以及双向莱顿弗罗斯特效应。
在振动频率60 Hz、振幅4 mm的正弦激励下,颗粒阻尼器内部出现稳定的颗粒莱顿弗罗斯特现象,如图1所示。可以看出,颗粒受到外界激励达到一定条件并处于稳定状态,在0.486 s时阻尼器从下往上运动,颗粒团下层的颗粒向下运动。在0.488 s时颗粒团最下面一层颗粒盒阻尼器接触,部分颗粒接触阻尼器后颗粒向反方向移动。在0.490 s时颗粒团的底层颗粒与阻尼器有更多的接触,此时的底层颗粒的动能达到最大,底层颗粒支撑颗粒团。在0.492 s时颗粒阻尼器开始往下运动,底层颗粒与阻尼器开始脱离,在此时刻,底层颗粒的矢量图方向还是向上的占大多数,并支撑颗粒团的稳定。在0.494 s颗粒阻尼器继续向下运动,并与阻尼器继续脱离,颗粒底层的运动方向混乱,颗粒最下面的以下部分,开始有往下运动的趋势。在0.496 s时,颗粒底层的大部分颗粒有往下运动的趋势,阻尼器运动到最底处,准备向上运动,并开始下一个周期。

|
图 1 莱登弗罗斯特效应速度云图和矢量图 Fig. 1 Leidenfrost effect velocity cloud and vector |
在颗粒运动期间,会出现一些特别的现象,密集颗粒团被下方一些剧烈运动的稀少颗粒托起,此处的少数颗粒就如同莱顿弗罗斯特效应里的水蒸气,持续托举着上方的颗粒团,在持续的激励下,使下方稀疏的颗粒层不断发生振荡,同时上方密集颗粒区的颗粒层稳定浮动在几乎相同的位置。
再提高一些激励频率,会出现浮力对流现象,颗粒形成浮力对流现象的主要原因是能量在空间不均匀导致,当振动增强时,颗粒莱顿弗罗斯特效应变得不稳定,进入浮力对流状态(见图2和图3)。可以看出,在0.490 s时阻尼盒从下往上运动,颗粒团下层的颗粒向下运动,颗粒的上层成圆弧形,顶层一部分颗粒向两边运动。在0.491 s时颗粒团最下面一层颗粒和阻尼器接触,部分颗粒接触阻尼器后颗粒往反方向移动。在0.492 s时颗粒团的底层颗粒与阻尼器有更多的接触,底层颗粒支撑颗粒团。在0.493 s时颗粒阻尼器开始往下运动,此时的底层颗粒动能达到最大。在0.494 s底层颗粒与阻尼器开始脱离,阻尼盒开始往下运动,由矢量图可以看出,在此时刻,底层颗粒矢量图的方向还是向上的占大多数,并支撑颗粒团的稳定。在0.495 s时颗粒阻尼器继续向下运动,并与阻尼器继续脱离,颗粒底层的运动方向混乱,颗粒底层的部分颗粒开始有往下运动的趋势。在0.496 s时阻尼器继续下落,底层颗粒开始往下运动,在0.497 s时阻尼器继续往下运动,底层颗粒继续往下运动,在0.498 s时阻尼器运动到最底处,底层颗粒继续往下运动,阻尼器开始进入下一个周期。

|
图 2 浮力对流云图 Fig. 2 Buoyancy convection cloud diagram |

|
图 3 浮力对流矢量图 Fig. 3 Buoyancy convection vector diagram |
浮力对流主要表现的现象是颗粒团下方稀薄颗粒层中的高能颗粒会打破颗粒密集区域的六边形密集排结构,产生更多的低密度高能颗粒,可以看到底层高能量的少量颗粒,给与颗粒团持续的撞击,在颗粒团的中心可明显看到颗粒在向上蠕动,颗粒团顶层形成弓形结构,而靠近圆柱壁的颗粒在往下运动。形成典型的浮力对流现象,这也是颗粒的浮力对流效应与莱顿弗罗斯特效应在运动上的本质区别。
在莱登弗罗斯特现象中,颗粒运动会出现一些特别的现象,密集颗粒团被下方一些剧烈运动着的稀少颗粒托起,此处的少数颗粒就如同莱顿弗罗斯特效应里的水蒸气,持续的托举着上方的颗粒团,在持续的激励下,使下方稀疏的颗粒层不断发生着振荡,同时上方密集颗粒区的颗粒层稳定地浮动在几乎相同的位置。
随着振动强度进一步增大,对流状态会演变成为一种新的莱顿弗罗斯特效应,在悬浮的密集颗粒团的上方和下方都存在一层由高能颗粒组成的稀薄层。悬浮密集颗粒团上方的稀薄颗粒层也与振动器的顶部发生碰撞,这与激发强度较低的时候得到的莱顿弗罗斯特效应不同,称之为双向莱顿弗罗斯特效应,如图4所示。可以看出,在0.490 s时阻尼器下落到最低点,颗粒团下层的颗粒向下运动,颗粒团的上层高能颗粒团较多,大部分变成了无序状态,但是能量较高。在0.491 s时颗粒团最下面一层颗粒和阻尼器接触,部分颗粒接触阻尼器后颗粒往反方向移动,颗粒团的上层动能减小,耗能降低。在0.492 s时颗粒团的底层颗粒与阻尼器有更多的接触,大部分矢量图呈现向上的运动状态,且速度较大,上层的颗粒团相比上一时刻再次减小。在0.493 s时颗粒阻尼器继续往上运动,此时的颗粒团底层颗粒的动能达到最大,颗粒团上层的颗粒动能继续减小。在0.494 s时阻尼器达到最高,底层颗粒与阻尼器开始脱离,在此时刻,底层颗粒的矢量图方向是大多数向上,并支撑颗粒团的稳定。在0.495 s阻尼器开始向下运动,颗粒与阻尼器继续脱离,颗粒底层的运动方向混乱,颗粒底层的部分颗粒部分,开始有往下运动的趋势。在0.496 s时阻尼器继续下落,颗粒团的底层颗粒开始往下运动,但是顶层的颗粒与阻尼器接触,顶层的部分颗粒碰撞后改变方向,在0.497 s时阻尼器继续往下运动,底层颗粒继续往下运动,顶层颗粒的大部分高能颗粒与阻尼器碰撞,在0.498 s时阻尼器运动到最底处,底层颗粒继续往下运动,顶层的高能颗粒能量达到最大,阻尼器开始进入下一个周期。
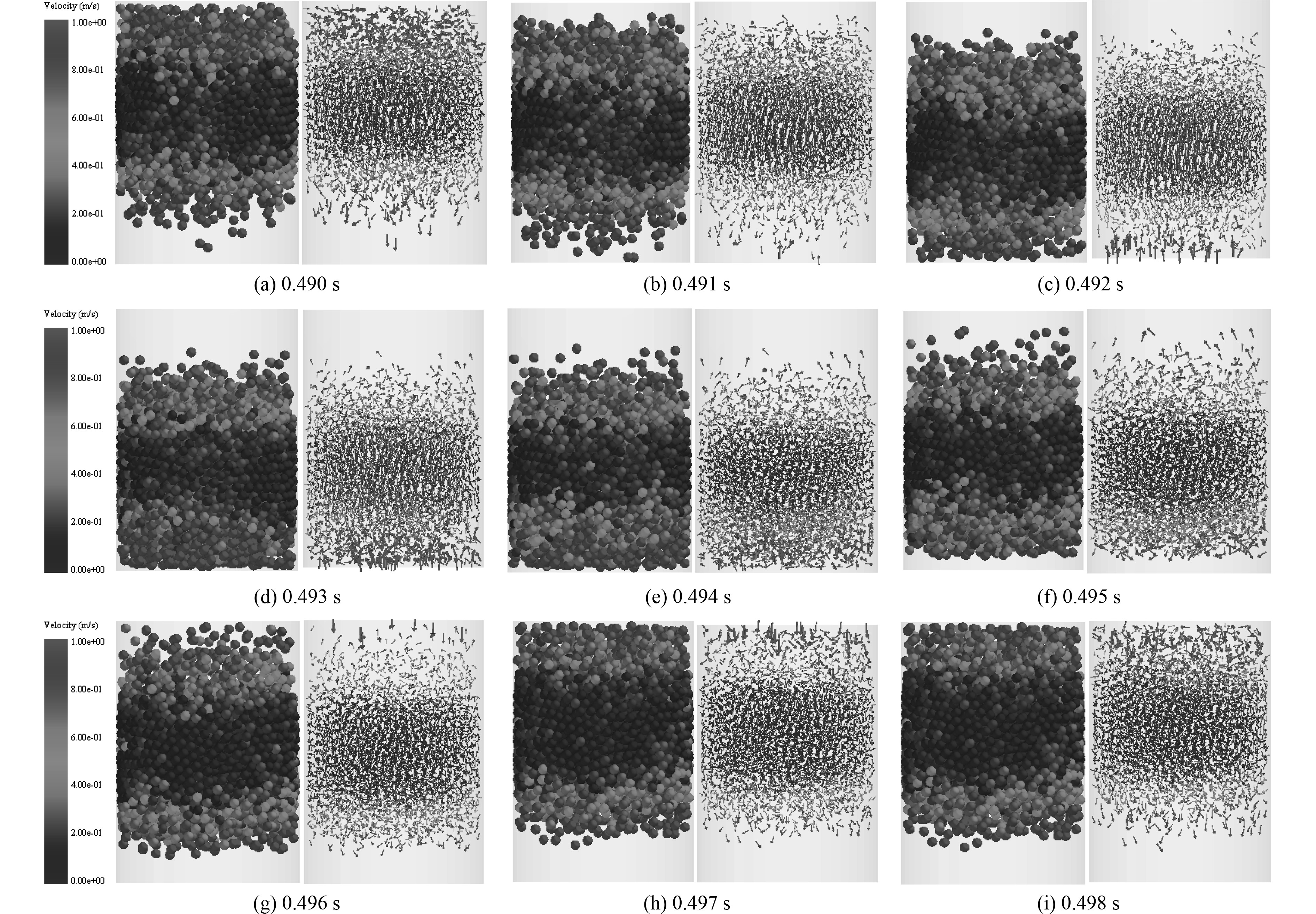
|
图 4 双向莱登弗罗斯特效应速度云图和矢量图 Fig. 4 Two-way Leidenfrost effect velocity cloud map and vector diagram |
为进一步探究阻尼器的耗能机理,对阻尼器的能量损耗随时间的变化情况进行分析。选取出现9种典型运动状态时的激励条件,如表2所示。对9种不同条件下的工况的能耗进行分析,如图5所示。阻尼器能量消耗最大的部分是颗粒与阻尼器之间的冲击碰撞,其他工况下耗能较小,分析颗粒阻尼器在不同频率和不同振幅下的能量消耗。可以看出,阻尼器的能量消耗与运动过程中颗粒的形状密切相关,成块运动的耗能较高,在此填充比下,频率高振幅大,不一定耗能高。
|
|
表 2 激励选取条件 Tab.2 Selection of excitation conditions |

|
图 5 阻尼器损耗能量随时间的变化 Fig. 5 Changes in damper energy loss over time |
结合颗粒运动状态对阻尼器耗能机理进行分析,颗粒在小波、蹦床、大波、成拱的流动状态时耗能较小,颗粒运动有较强的规律性,增强激励时,会出现莱顿弗罗斯特效应。当激励进一步增强时,莱顿弗罗斯特现象转变为浮力对流现象。
当激励更强时,对流状态会演变成为一种新的莱顿弗罗斯特效应,即双向莱顿弗罗斯特效应,在悬浮的密集颗粒团的上方和下方都存在一层由高能颗粒组成的稀薄层。悬浮密集颗粒团上方的稀薄颗粒层也与振动器的顶部发生碰撞,高能颗粒支撑颗粒团使其位置保持稳定,耗能相对来说较小,在运动稳定时没有发生大规模的颗粒冲击碰撞。
2 不同频率对颗粒耗能的影响研究为研究不同的填充比对阻尼器颗粒耗能的影响,对填充比为50%、70%、90%的颗粒耗能工况进行研究,对比其耗能以及损耗因子。图6为50%填充比,不同的振动频率在不同振幅下的耗能图。可以看出,颗粒的耗能情况与振动频率以及振幅有密切的关系。在振动频率为30 Hz时颗粒的损耗能量是随着振动幅度增加逐渐上升,增幅较小,在60 Hz振动频率时,颗粒的损耗能量随着振幅的增加,在1~3 mm颗粒损耗能量增加,在3~4 mm时颗粒的损耗能量下降,在4~5 mm颗粒的损耗能量增加较多,耗能的最高点在振动幅度为5 mm处,在90 Hz振动频率时,颗粒耗能的趋势和振动频率为60 Hz时的趋势是一样的,但是在整个振动区间内,耗能相对60 Hz的振动频率较大,且在3 mm处,耗能达到最大,在120 Hz振动频率时,颗粒的耗能趋势随着振幅的增加耗能持续增加,最高处在振幅为5 mm处。
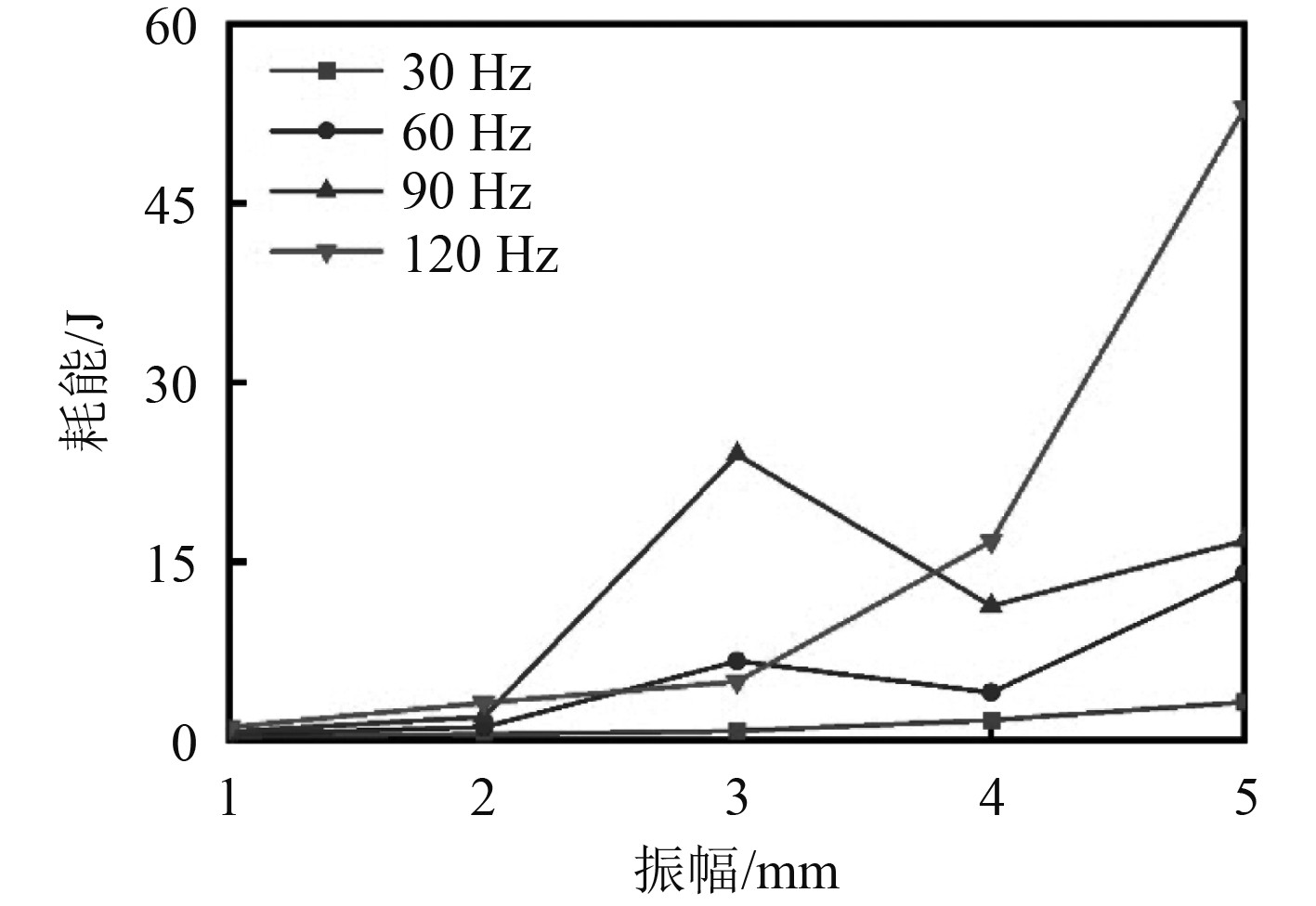
|
图 6 填充比为50%时不同振动频率下的耗能 Fig. 6 Energy consumption at different vibration frequencies when the filling rate is 50% |
图7为填充比为70%时不同振动频率下的耗能情况。可以看出,当振动频率为30 Hz时,随着振幅的增加,耗能也随之增加,但是耗能增加的不是很明显,振动频率为60 Hz时,颗粒的耗能规律也是随着振幅的增加而增加,颗粒的耗能相比30 Hz振动频率有显著的提升,特别是在振幅为5 mm处。当振动频率为90 Hz时,颗粒的耗能规律和振动频率为30、60 Hz的耗能相比出现了一些变化,随着振幅的增加颗粒的耗能是先增加后减少,在4 mm处达到耗能的峰值。当振动频率为120 Hz时,振动消耗得能量随着振幅的增加而增大,从图中还可以看出,在振幅为5 mm时,振动耗能达到最大,这也是填充比为70%的耗能最好的一个工况,具有参考应用价值。
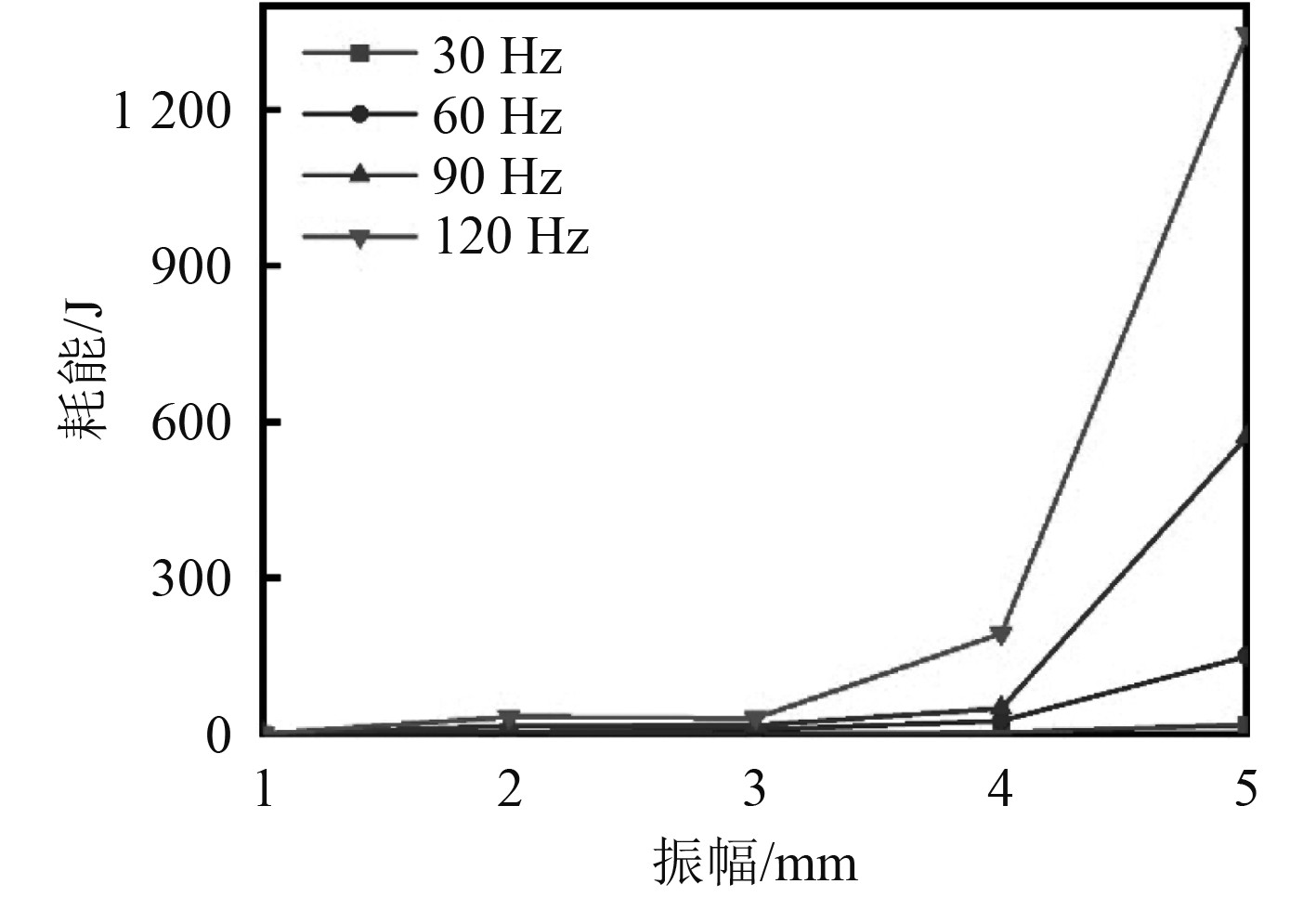
|
图 7 填充比为70%时不同振动频率下的耗能 Fig. 7 Energy consumption at different vibration frequencies when the filling rate is 70% |
图8为填充比为90%时不同振动频率下的耗能情况。可以看出,在不同的振动频率下,随着振幅的增加,颗粒的耗能也随之增加,4种不同振动频率的耗能情况有一定的规律性,高频率的耗能大于低频率的耗能,特别是振动频率为120 Hz时,耗能随着振幅增加明显,不同振动频率的耗能最高点在振幅5 mm处。
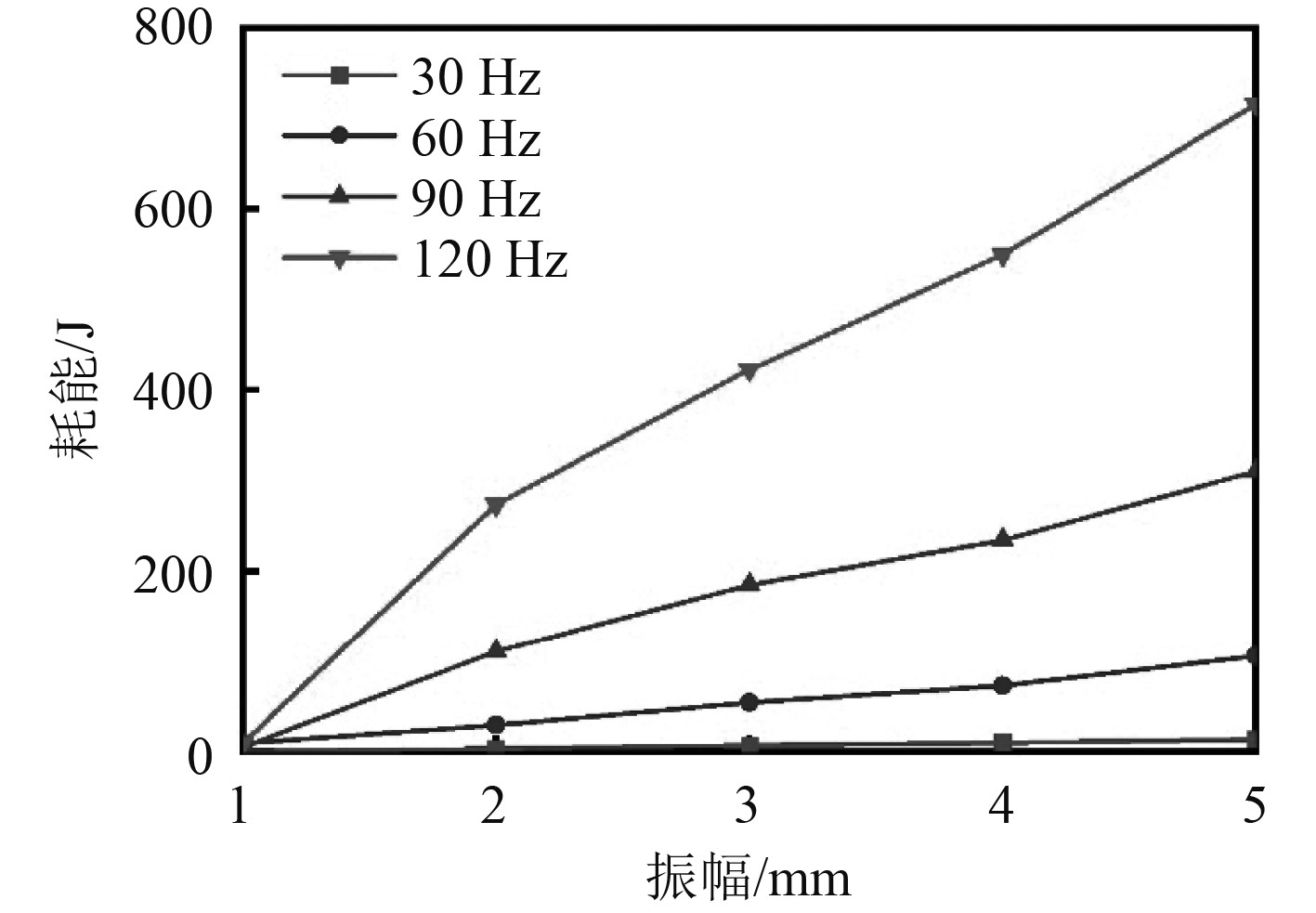
|
图 8 填充比为90%不同振动频率下的耗能 Fig. 8 Energy consumption at different vibration frequencies with a filling rate of 90% |
由图6~图8可知,颗粒的耗能情况不仅与振幅有关也和振动频率有关,振幅和振动频率决定颗粒运动的状态,颗粒在成块时耗能较高,如填充90%时,颗粒的运动状态几乎是成块运动,成块运动的耗能较稳定,因此在30、60、90、120 Hz振动激励时,耗能趋势保持一样,都是随着振幅增大而增加。
3 填充对颗粒耗能的影响研究在填充为70%时,颗粒的运动状态会有些变化。在振幅为5 mm时颗粒的成块情况更为明显,且颗粒的冲击区间变大,和阻尼器壁面的冲撞耗能更为明显。在填充比为50%时,颗粒在不同振幅下运动状态会更多,这是导致其耗能出现不规律性的主要原因。图9为相同振动频率下不同填充比的耗能比较,在填充比为90%的不同振动频率下,颗粒的耗能随着振幅的增加而增加,呈现一定的规律性,这也再次证明90%填充时,块状的运动状态不易随着振动频率的改变而变化,能保持稳定的耗能规律。颗粒填充比为70%时,振动幅度为1~4 mm范围内,耗能随着振幅的增加而缓慢增加;当振幅为5 mm时,颗粒耗能明显增大,这也再次验证了颗粒的冲程增加,成块的撞击耗能大幅上升。
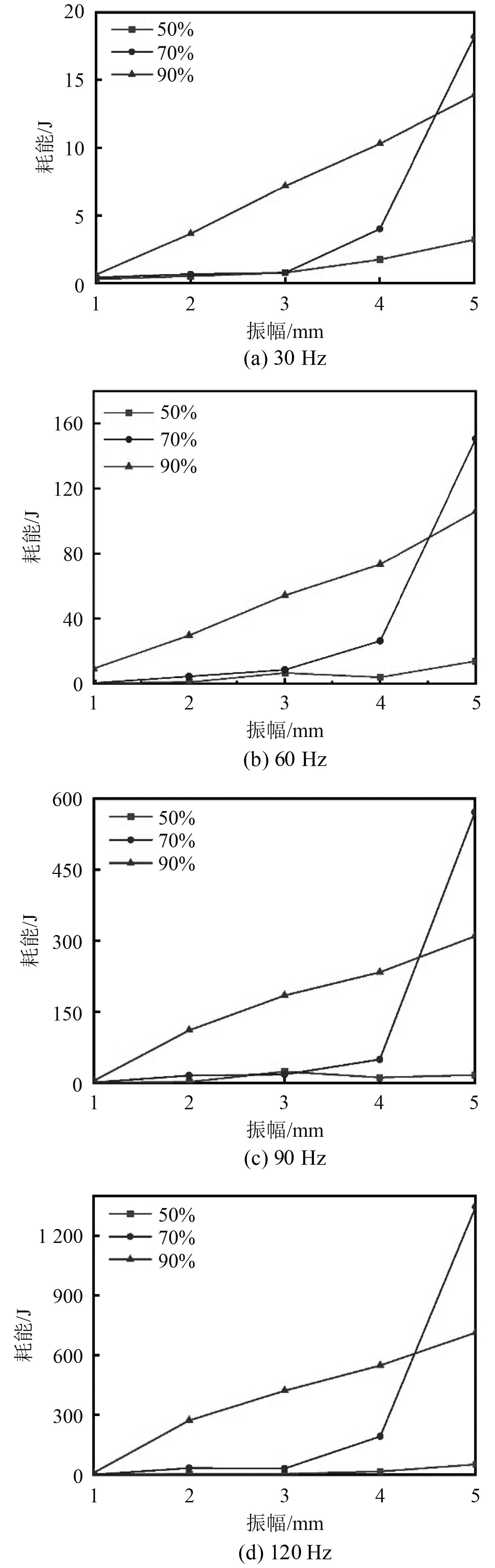
|
图 9 相同振动频率下不同填充比的耗能比较 Fig. 9 Comparison of energy consumption with different filling ratios at the same vibration frequency |
从图10可以看出,在120 Hz的振动频率下不同填充比的耗能因子规律有很大差别,填充比为50%时,颗粒的整体耗能因子较小,随着振幅的增加呈现逐步上升趋势,且其值最高点的振幅为5 mm处。填充比为70%时,耗能因子在1~2 mm振幅时呈上升趋势,在2~3 mm处呈下降趋势,在3~5 mm处为持续上升阶段,增幅较大,最高处为5 mm振幅。填充比为90%时,颗粒的损耗因子随着振幅的增加先增大后减小,且在振幅为2 mm处,损耗因子最大,与其他填充比相比,振幅1~4 mm时90%填充比要明显高于50%、70%填充比。在振幅为5 mm的时候,填充比为90%的损耗因子低于填充比为70%的损耗因子,而高于50%填充比的损耗因子。
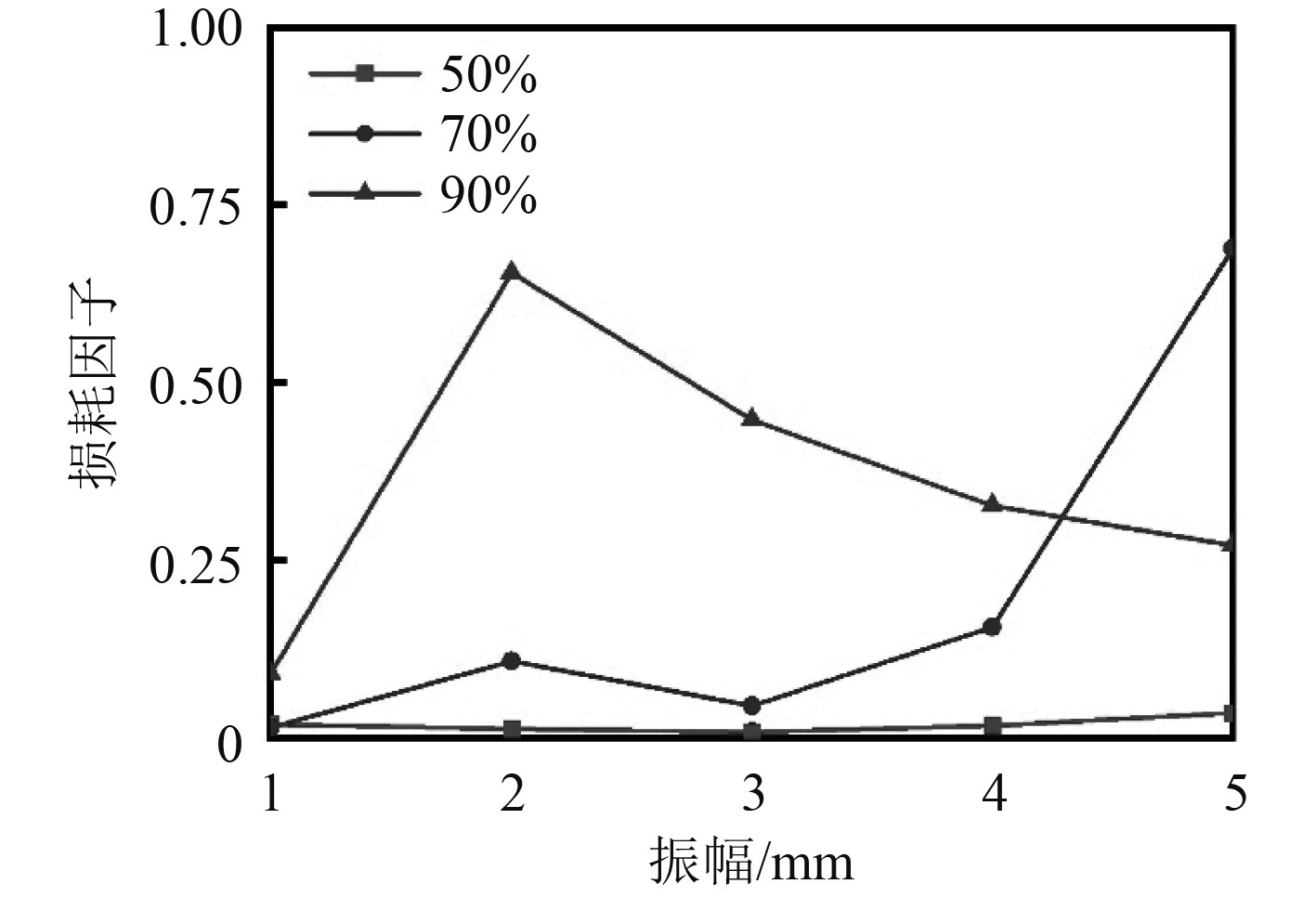
|
图 10 120 Hz振动频率下不同填充比的耗能因子对比 Fig. 10 Comparison of energy dissipation factors for different filling ratios at 120 Hz vibration frequency |
本文研究颗粒的9种运动状态对耗能的影响,并对其中3种特殊的运动状态进行分析,在这9种运动状态中颗粒的成块运动耗能最高,其主要的耗能是碰撞耗能。耗能情况和运动状态有密切关系,也和振幅、振动频率有密切关系。在相同填充比下,不同振动频率的耗能规律受流态的影响。颗粒在50%填充比时在不同振幅和频率下,颗粒的运动比较丰富,出现不规律的耗能现象,颗粒填充比为70%、90%时,由于颗粒较多,运动状态较为单一,颗粒的耗能随着振动幅值和频率的增加而增加,特别是在振动频率为120 Hz、振幅为5 mm的情况下,颗粒的耗能达到了顶峰。在损耗因子方面,振幅1~4 mm时90%填充比要明显高于50%、70%填充比。在振幅为5 mm的时候,填充比为90%的损耗因子低于填充比为70%的损耗因子,而高于50%填充比的损耗因子。
| [1] |
PAGET A L. Vibration in steam turbine buckets and damping by impacts[J]. Engineering, 1937, 143: 305-307. |
| [2] |
MASRI S F. Analytical and experimental studies of multiple-unit impact dampers[J]. Journal of the Acoustical Society of America, 1969, 45(5): 1111-1117. DOI:10.1121/1.1911581 |
| [3] |
DARABI B. Viscoelastic behaviour of element of particle damper: experimental and numerical study[J]. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 2019, 23(4): 1-11. |
| [4] |
ZHSNG K, XI Y, CHEN T, et al. Experimental studies of tuned particle damper: Design and characterization[J]. Mechanical Systems & Signal Processing, 2018, 99: 219-228. |
| [5] |
胡溧, 黄其柏, 许智生. 颗粒阻尼的回归分析研究[J], 中国机械工程, 2008, 19(23): 2834–2837.
|
| [6] |
胡溧, 杨驰杰, 杨啟梁, 等. 周期颗粒阻尼复合板结构的带隙特性研究[J]. 振动与冲击, 2017, 36(3): 77-82. DOI:10.13465/j.cnki.jvs.2017.03.013 |
| [7] |
OLSON S E. An analytical particle damping model[J]. Journal of Sound and Vibration, 2003, 264: 1155-1166. DOI:10.1016/S0022-460X(02)01388-3 |
| [8] |
LEI X F. Non-obstructive particle damping using principles of gas-solid flows[J]. Journal of Mechanical Science and Technology, 2017, 31(3): 1057-1065. DOI:10.1007/s12206-017-0204-3 |
| [9] |
ZHANG K, CHEN T N, WANG X P, et al. Rheology behavior and optimal damping effect of granular particles in a non-obstructive particle damper[J]. Journal of Sound and Vibration, 2016, 364: 30-43. DOI:10.1016/j.jsv.2015.11.006 |
| [10] |
SALUEA C, PSCHEL T, SERGEIE E. Dissipative properties of vibrated granular materials[J]. Physical Review Letters, 1999, 59(4): 4422-4425. |
| [11] |
SACK A, HECKEL M, KOLLMER J E, et al. Energy dissipation in driven granular matter in the absence of gravity[J]. Physical Review Letter, 2013, 111(1): 018001. DOI:10.1103/PhysRevLett.111.018001 |
| [12] |
ESHUIS P, WEELE KVD, MEER DVD, et al. Phase diagram of vertically shaken granular matter[J]. Physics of Fluids, 2007, 19: 123301. DOI:10.1063/1.2815745 |
| [13] |
SANOO. Dilatancy, buckling, and undulations on a vertically vibrating granular layer[J]. Physical Review E, 2005, 72(5): 051302. DOI:10.1103/PhysRevE.72.051302 |
| [14] |
胡国明. 颗粒系统的离散元素法分析仿真[M]. 武汉: 武汉理工大学出版社, 2010.
|
| [15] |
AHMAD N, RANGANATH R, GHOSAL A. Modeling and experimental study of a honeycomb beam filled with damping particles[J]. Journal of Sound and Vibration, 2017, 391(5): 20-34. |
| [16] |
夏兆旺, 茅凯杰, 王雪涛, 等. 海洋平台桁架结构半主动颗粒阻尼减振技术研究[J]. 振动与冲击, 2018, 37(4): 93-98. DOI:10.13465/j.cnki.jvs.2018.04.015 |
| [17] |
姚冰, 陈前, 项红荧, 等. 颗粒阻尼器近似理论模型研究[J]. 机械工程学报, 2015, 51(3): 87-94. DOI:10.3901/JME.2015.03.087 |
| [18] |
段永强, 尹忠俊, 陈兵. 颗粒运动学行为对阻尼器耗能特性影响的研究[J]. 振动与冲击, 2020, 39(4): 7. DOI:10.13465/j.cnki.jvs.2020.04.028 |
| [19] |
ZE HUI J, YUN YING W, JING W. Subharmonic motion of granular particles under vertical vibrations[J]. EPL Europhysics Letters, 2006, 74(3): 417. DOI:10.1209/epl/i2005-10554-7 |
| [20] |
HSIAU S S, WU M H, CHEN C H. Arching phenomena in a vibrated granular bed[J]. Powder technology, 1998, 99(2): 185-193. DOI:10.1016/S0032-5910(98)00103-X |
| [21] |
WASSGREN C R, BRENNEN C E, HUNT M L. Vertical vibration of a deep bed of granular material in a container [J]. Journal of Applied Mechanics, 1996, 63(3): 712-719.
|
| [22] |
李伟. 冲击减振理论的离散单元法研究及应用[D]. 西安: 西安交通大学, 1997.
|
 2024, Vol. 46
2024, Vol. 46
