2. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063;
3. 中国舰船研究设计中心,湖北 武汉 430064
2. School of Naval Architecture, Ocean and Energy Power Engineering, Wuhan University of Technology , Wuhan 430063, China;
3. China Ship Development and Design Center , Wuhan 430064, China
通过提高船舶快速性以节省燃油一直是航运企业关注的重点,同时随着全球变暖以及日渐加剧的能源矛盾凸显了船舶节能减排的重要性。我国提出的“碳达峰”与“碳中和”(双碳)目标[1],也给国内的航运公司提出了更高的要求。船舶纵倾节能技术通过改变重心纵向位置调整船舶浮态来减小船舶阻力,由于不需要对船型、附体进行修改,目前有较广泛的应用[2]。
船舶纵倾节能研究方法始于模型试验[3 − 5],模型试验中通过比较不同纵倾角度的船模阻力来探寻船舶的最佳纵倾角度,是一种可信度较高的方法,但试验周期长、非必要的人力与相关资源消耗大。随着计算机与CFD技术的发展,通过数值模拟与模型试验相结合的方法可以有效地节省研究成本,同时研究结果与结论相对可靠、准确。王伟等[6]采用数值模拟方法预报了KCS船模航行时对应最小阻力的纵倾角度;李振兴等[7]总结了某小型电动船型的最佳纵倾角度;高现娇等[8]采用数值方法确定了某成品油船不同载况下的节能潜力在3.34%~94%之间。研究表明,不同船型及航行载况的船舶均存在对应阻力最低的纵倾角度,船舶纵倾对阻力的影响明显。纵倾节能技术的深入研究与广泛应用,为船舶运输行业带来了一定经济收益。
在利用数值方法研究船舶最佳纵倾方面,相关学者对纵倾节能相关的其他水动力问题进行研究。张元浩等[9]采用数值方法进行了最佳纵倾角浅水效应影响的研究;郭航等[10]研究了波浪条件下纵倾变化对阻力性能的影响等。前述纵倾节能相关的研究对象多为船模尺度,而纵倾节能的实船应用还需完善其尺度效应的研究。
本文通过数值方法研究了纵倾对某双尾鳍内河船型阻力的影响。首先进行数值方法的验证,通过不同缩尺比模型、不同重心纵向位置组合的双尾鳍内河船绕流场数值模拟,总结该船型阻力随纵倾角度的变化规律,探讨了纵倾节能的尺度效应。
1 数值方法与验证通过求解RANS方程的方法对双尾鳍船舶进行绕流场数值模拟及阻力数值预报,进行相关数值方法的验证与不确定度分析。
1.1 数值模拟方法船舶绕流场控制方程RANS的张量形式为:
| $ \frac{\partial u_{i}}{\partial t}+u_{j} \frac{\partial u_{i}}{\partial x_{j}}=F_{i}-\frac{1}{\rho} \frac{\partial p}{\partial x_{i}}+W^{2} u_{i}-\frac{\partial\left(u_{i}^{\prime} u_{f}^{\prime}\right)}{\partial x} 。$ |
式中:ui和uj分别为速度矢量u在xi和xj方向上的分量;
与Navier-Stokes方程相比,RANS方程组多出的雷诺应力项导致了方程组不封闭,为封闭RANS方程组进而进行数值求解[11],需引入湍流模型对雷诺应力项进行求解或模拟,本文采用Realizable
以已有模型试验结果的某双尾鳍内河船为验证船,采用ITTC规程进行阻力数值预报方法的验证。验证船主尺度如表1所示。
|
|
表 1 验证船主要参数(模型) Tab.1 Main parameters of the verification ship (model) |
为体现船舶航态影响,采用重叠网格方法实现船体的纵倾和升沉运动。计算域的背景域与重叠域均采取长方体,船体表面设置为无滑移壁面;入流边界距船首为1倍船长;出口边界(压力出口)距船尾为3倍船长;船侧部边界(速度入口)距船中纵剖面1.8倍船长;自由液面距上边界(速度入口)1倍船长、距下边界(速度入口)2倍船长;由于船体关于中纵剖面对称,为减少计算域网格数量以提升计算效率,船中纵剖面所在的平面设置为对称平面。重叠域中除船中纵剖面所在剖面设置为对称平面以外,其余边界设置为重叠网格边界。典型剖面网格如图1所示。
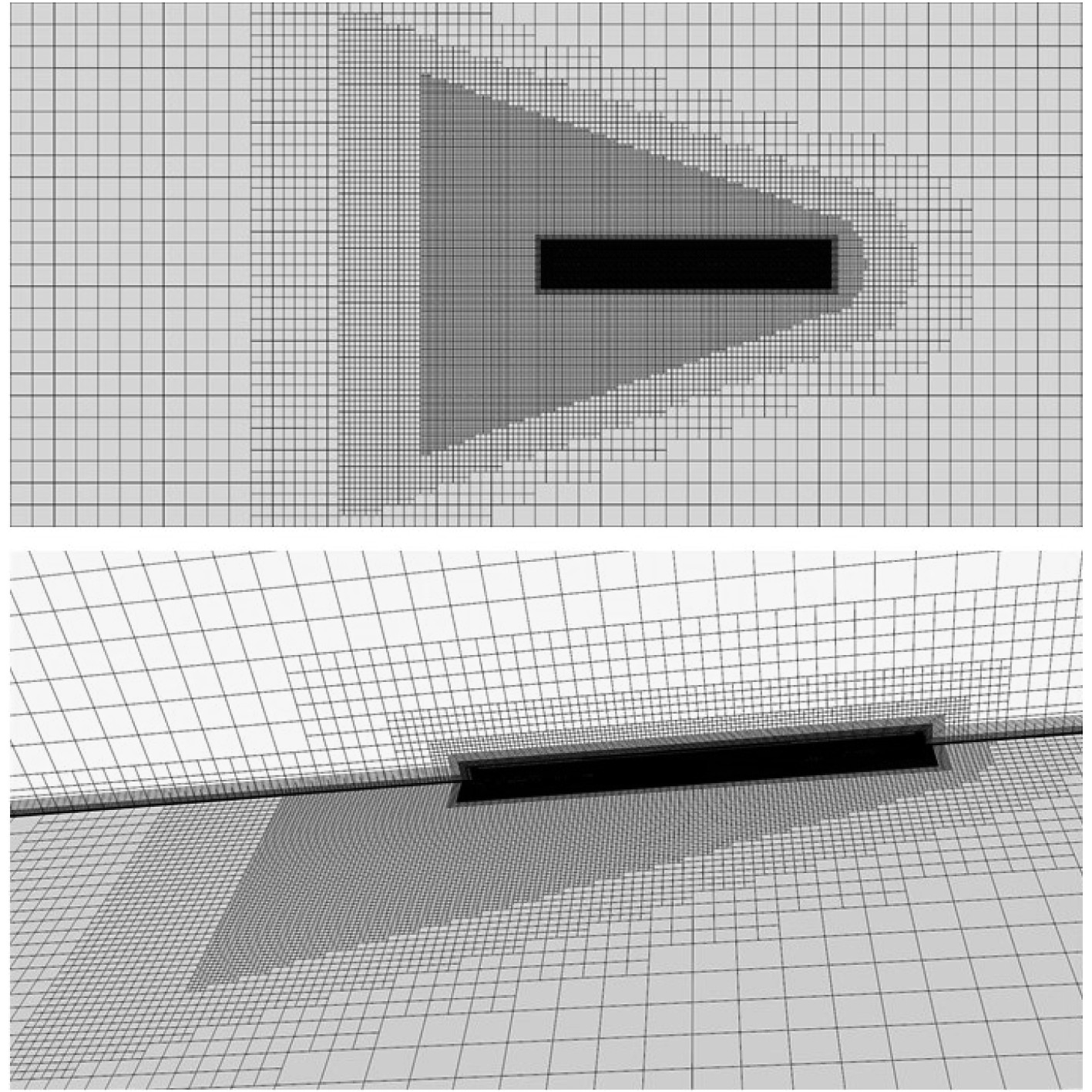
|
图 1 典型剖面网格分布示意图 Fig. 1 Typical profile grid distribution diagram |
计算域采用切割体网格进行离散,在自由液面附近进行垂向加密,水平面方向进行波形区域加密以捕捉自由液面波形;在首、尾部进行了局部加密;近壁流场采用壁面函数模拟,为保证第一层网格法向尺度满足y+=30~300,船体近域采用了棱柱层型式的网格。
数值模拟与模型试验的阻力结果对比如图2所示。两者的相对误差在1% ~ 5%之间。
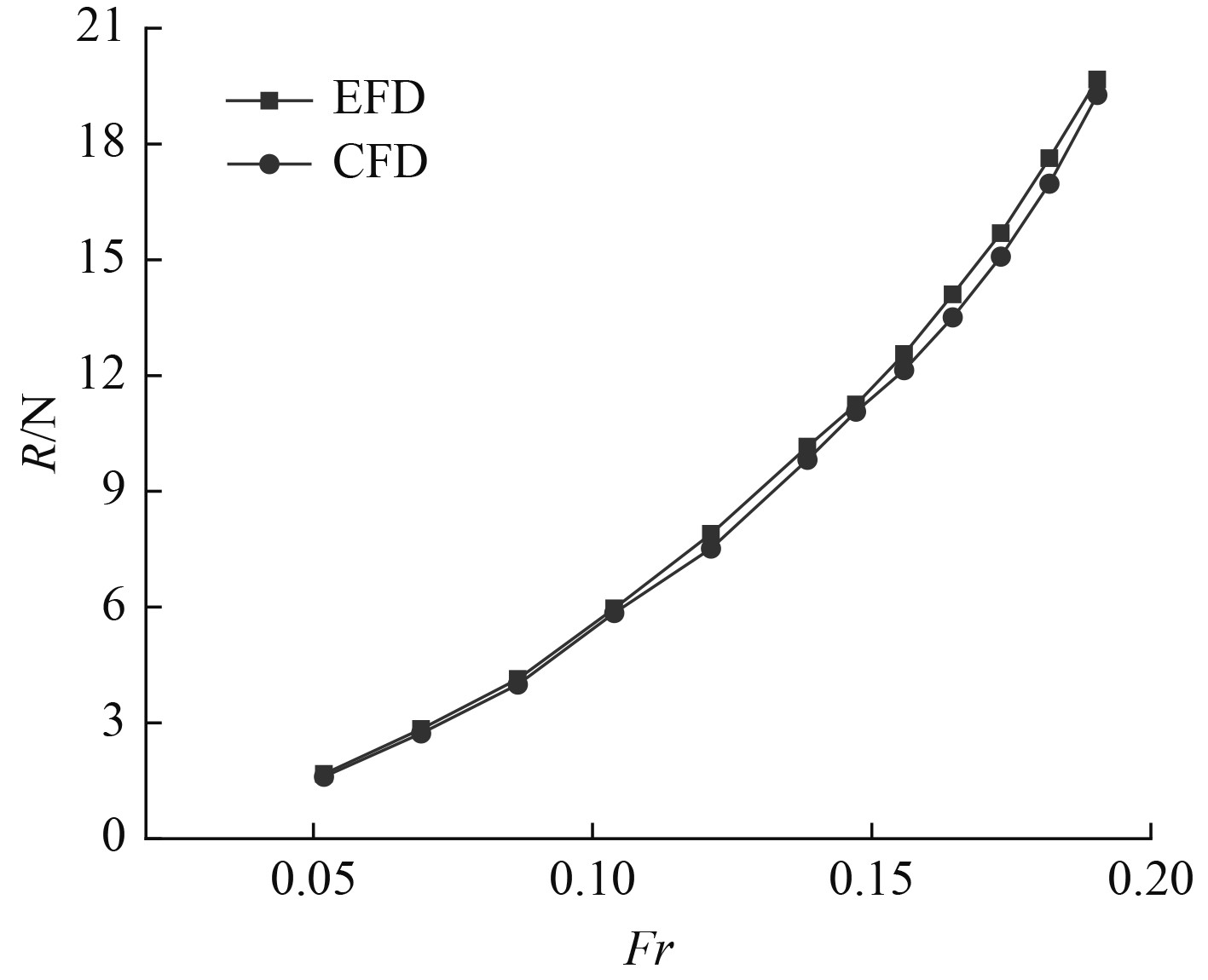
|
图 2 验证船阻力数值结果与试验结果对比 Fig. 2 Comparison of numerical results and experimental results for verification ship resistance |
根据ITTC规程对Fr=0.1904下的阻力数值结果进行了不确定度分析,网格尺度比为
|
|
表 2 三重系列网格数量及数值结果 Tab.2 Number of triple series grids and numerical results |
|
|
表 3 不确定度分析结果 Tab.3 Uncertainty analysis results |
由|E|<Uv、|Evc|<Uvc可知,数值结果及修正后的数值结果均得到确认。
2 双尾鳍内河船纵倾节能数值研究在验证船绕流场数值模拟方法验证实现的基础上,对课题船型(同为低速双尾内河船)进行了不同纵倾角度的流场数值模拟,其中船体纵倾通过给定不同船舶重心纵向位置来实现。
2.1 数值对象与工况

|
图 3 双尾鳍内河船几何模型 Fig. 3 Geometric model of twin skeg inland ship |
|
|
表 4 双尾鳍内河船型主要参数 Tab.4 Main parameters of twin skeg inland ship |
以缩尺比20.8的模型为对象、进行了不同重心纵向位置XG(46%L ~ 56%L)及其对应初始静态纵倾角θ0条件下船模绕流场的数值模拟(初始静态纵倾角θ0为预估值,用以减少船舶航态和绕流场达到稳态的时间,增加计算效率)。其计算域、网格离散、数值方法与验证部分一致。
2.2 数值模拟结果图4为不同重心纵向位置XG下验证船的初始纵倾角即静态纵倾角与以设计航速(Fr=0.1586)航行时船模的纵倾角随重心纵向位置XG的变化曲线。可知,在有航速条件下数值计算稳定后的纵倾角θa与初始静态纵倾角θ0相比有细微的改变。

|
图 4 船模纵倾角随重心纵向位置XG的变化曲线 Fig. 4 Variation curve of trim angle of ship model with longitudinal position of center of gravity XG |
模型阻力数值结果如图5所示。可以看出,随着重心纵向位置向首倾移动,船舶总阻力系数逐渐减小,但当XG超过54%L时趋于稳定,船舶最小阻力对应的最佳纵倾角度约为1.5°左右;最大首倾与最大尾倾的摩擦阻力系数Cf减少约1.49%;剩余阻力系数Cr随重心纵向位置即纵倾的改变相对较为显著,从最大尾倾(XG=46%L)到最大首倾(XG=56%L)数值变化约为42.99%。
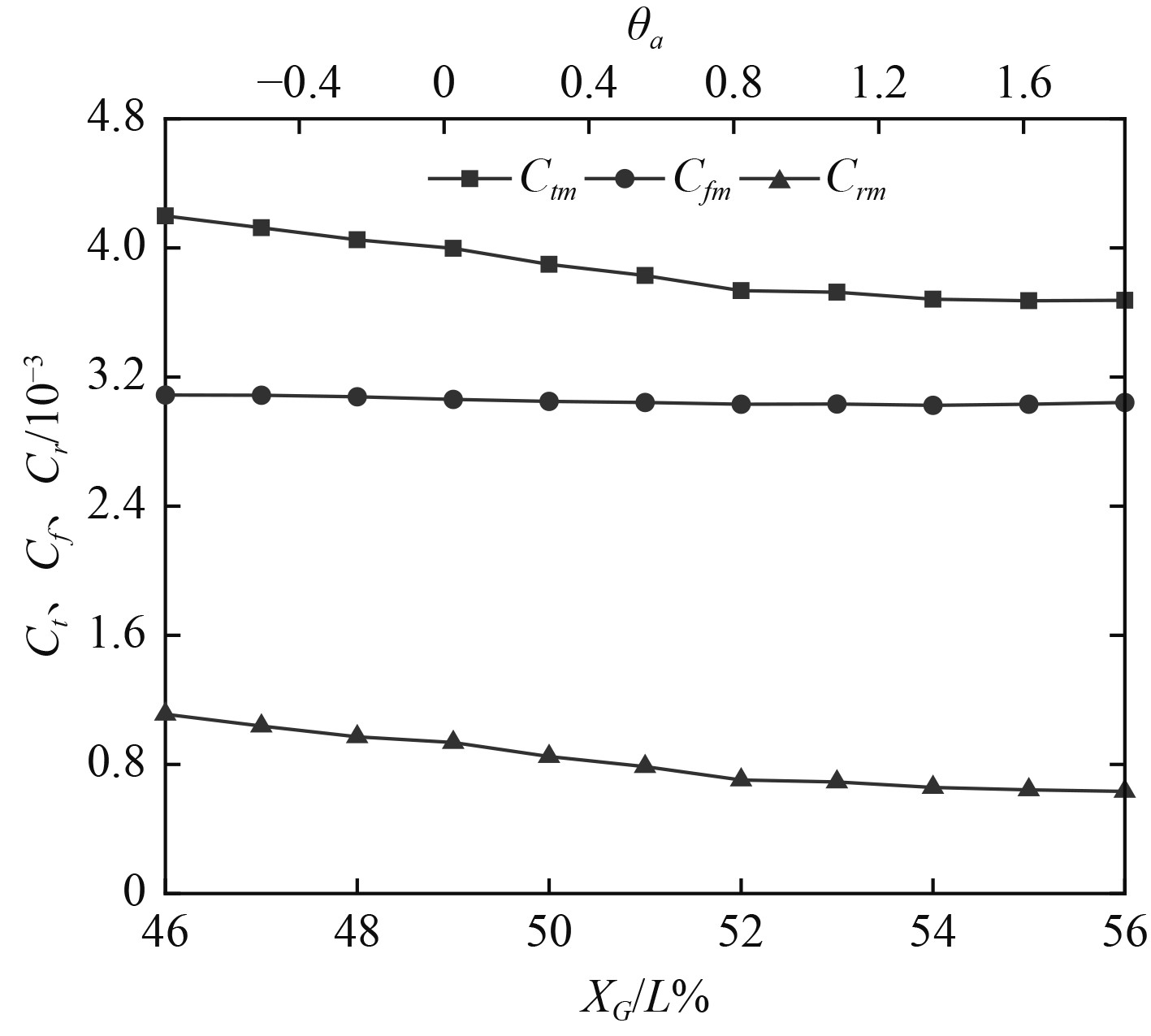
|
图 5 阻力系数随重心纵向位置的变化曲线 Fig. 5 Variation curve of the resistance coefficient with the longitudinal position of the center of gravity |
图6为不同重心纵向位置条件下船模湿表面积的变化曲线,可知,重心纵向位置XG从小到大即船模由尾倾向首倾变化的过程中,船模湿表面积逐渐减少,而船体摩擦阻力受湿表面积影响较大,因而也会呈现一定的下降趋势,但总体来看,湿表面积变化较小,因而摩擦阻力的变化幅度也较小。

|
图 6 湿表面积随重心纵向位置的变化曲线 Fig. 6 Variation curve of wet surface area with the longitudinal position of the center of gravity |
图7为不同纵倾条件下自由液面兴波波形比较图,首倾时首波峰有明显的增加,这是由于首倾时自由面附近的船首形状变得相对丰满,进流角度增大,且船模首倾时船首周围的兴波影响范围明显大于尾倾,2种浮态的船后尾波也有一定差异。
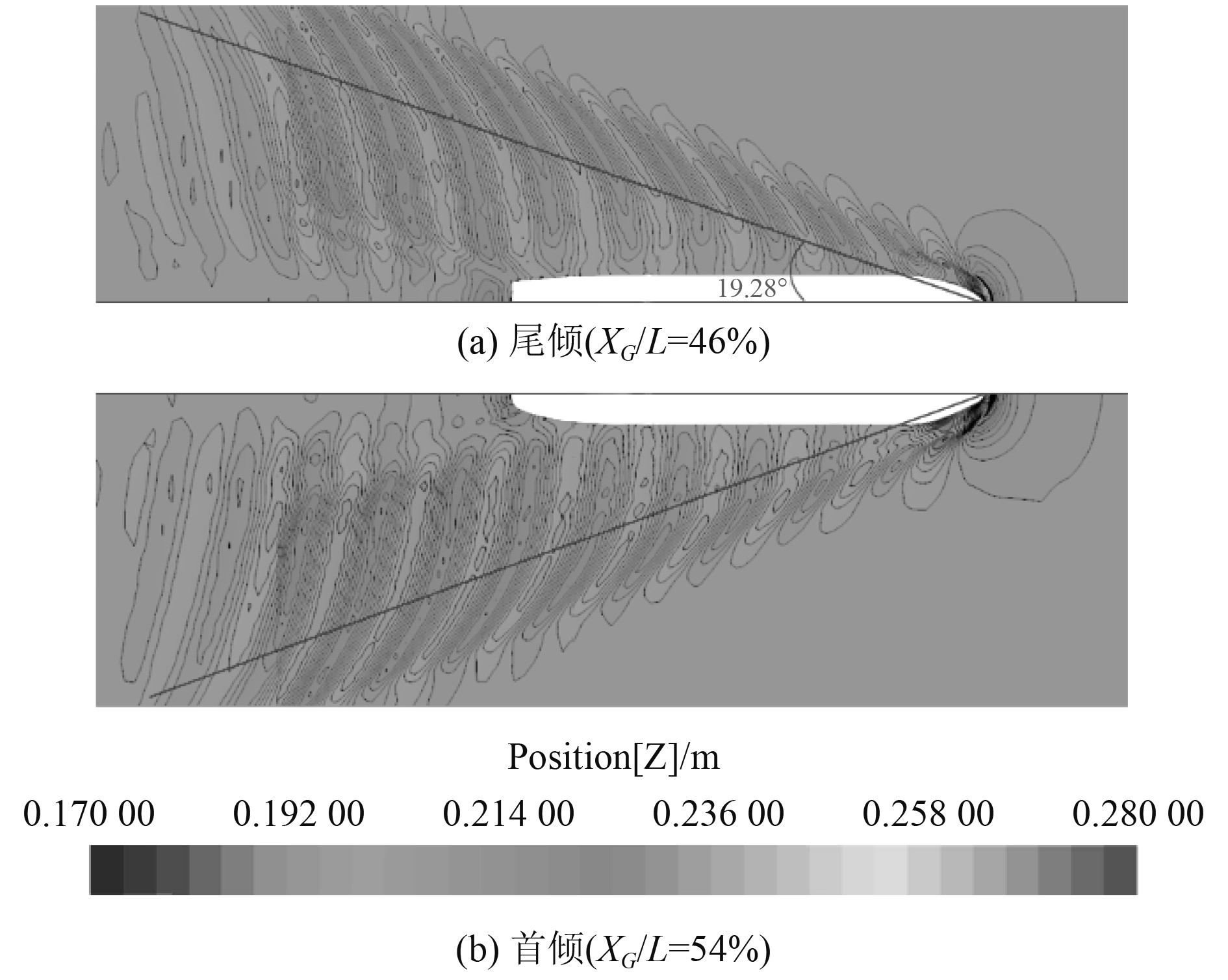
|
图 7 不同纵倾条件下自由液面兴波波形比较图 Fig. 7 Comparison of free surface wave under different trim conditions |
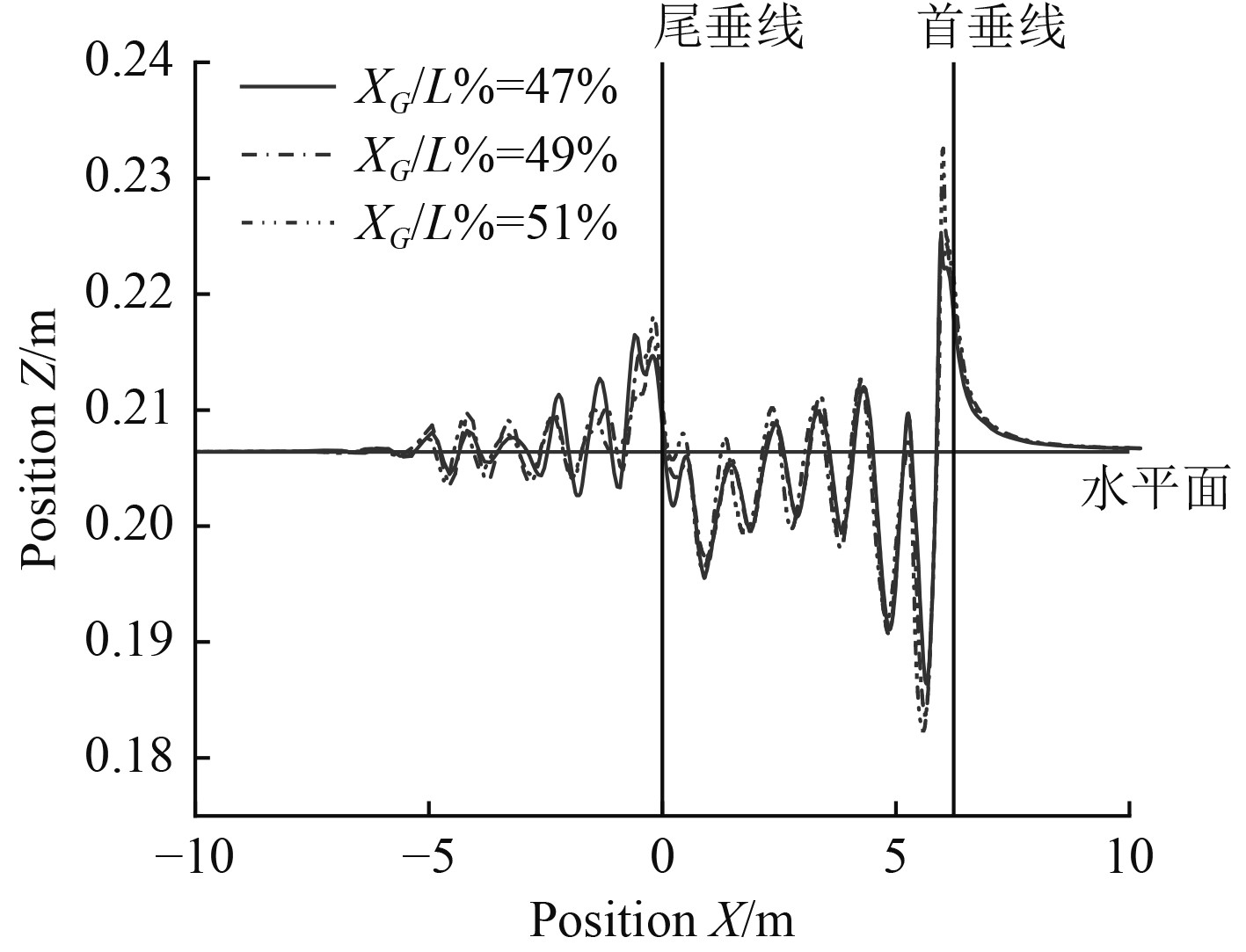
为进一步探寻纵倾对流场兴波波形的影响,XG /L=47%、49%、51%时(分别对应尾倾、正浮以及首倾y/B =0.48位置处(B为船宽,y为兴波纵切波形剖面到中纵剖面的距离)兴波纵切波形剖面对比如图8所示;其中横坐标原点为尾垂线位置,X轴指向船首。
|
图 8 y/B =0.48位置处兴波波形纵切剖面图 Fig. 8 Longitudinal section of the free surface wave at y/B = 0.48 |
由图8可知,除首波峰外船长范围内的波高在3种纵倾下的差异并不明显;船体后方的兴波波幅随不同纵倾变化较为明显,尾倾时兴波波幅最大,首倾时兴波波幅相对较小。
3个重心纵向位置下的船首极限流线如图9所示。可知,3种纵倾状态下的船首极限流线分布差别较小。

|
图 9 船首极限流线分布图 Fig. 9 Limit flow line distribution diagram of bow |
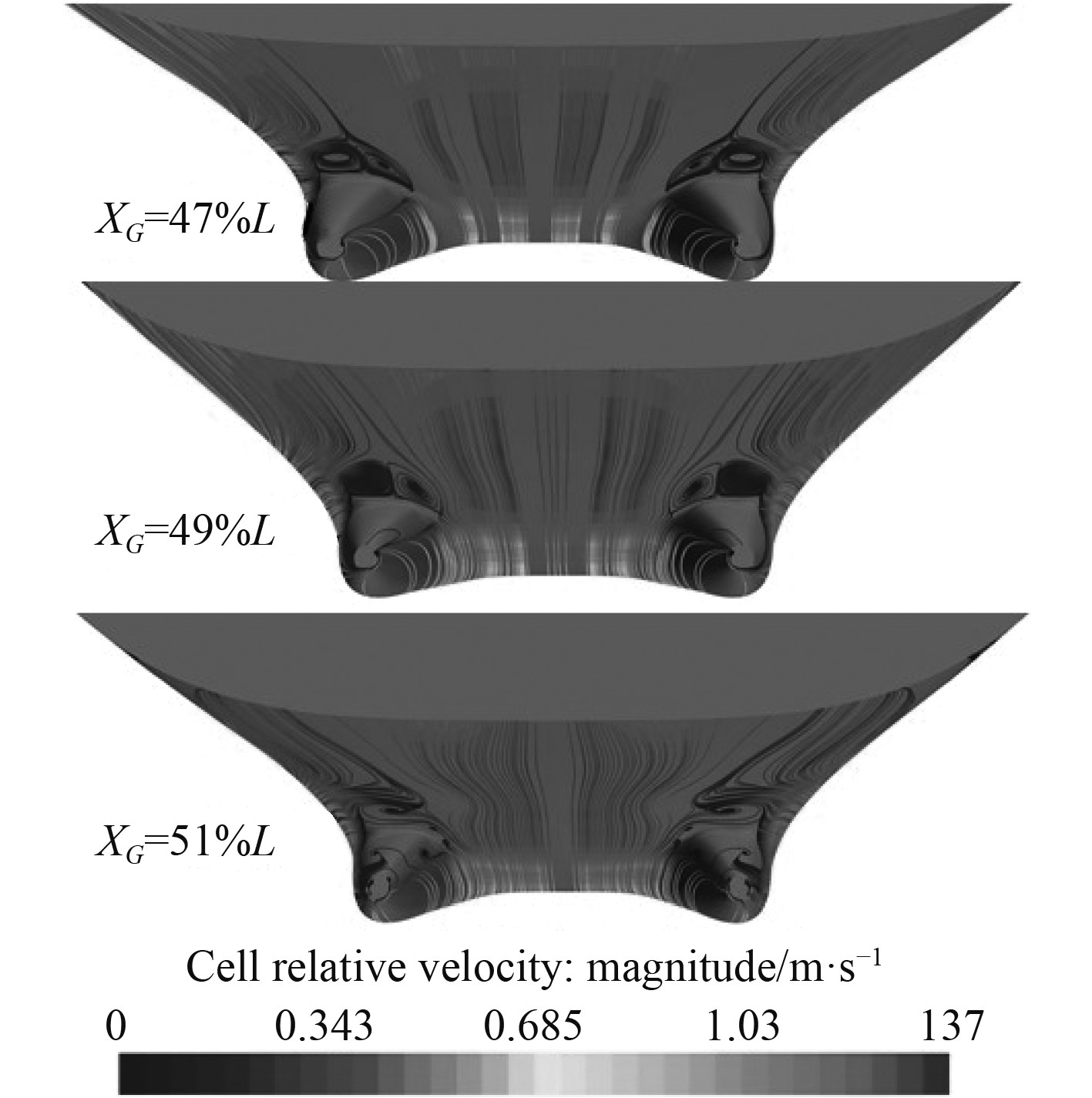
3个重心纵向位置下的船尾极限流线如图10所示。可知,极限流线在船体平行中体与双尾鳍过渡位置发生了分离现象,并产生了明显的舭涡,这是由船体在此位置处曲率变化较大引起。随着船舶纵倾由尾倾向首倾变化,舭涡产生的位置也向船尾方向移动,且云图显示舭涡的形成也有一定的减弱的趋势。
|
图 10 船尾极限流线分布图 Fig. 10 Limit flow line distribution diagram of stern |
图11为不同重心纵向位置对应的船尾压力无量纲系数Cp分布云图。Cp定义为:

|
图 11 不同重心纵向位置下船尾压力系数分布图 Fig. 11 Distribution of stern pressure coefficient under different longitudinal position of center of gravity |
| $ {C_p} = \frac{{p - \rho gh}}{{\frac{1}{2}\rho {v^2}}} 。$ |
式中:p为船体表面总压力;ρgh为任意一点的静压力;v为船速。
随着船舶由尾倾向首倾变化,船尾部高压区位置逐渐向船首移动且集中在双尾鳍中间的低压区域面积逐渐减少,船尾低压程度及分布面积的减小以及舭涡产生趋势的减弱是首倾时船舶阻力降低的原因。
3 双尾鳍内河船纵倾节能的尺度效应从缩尺比λ=20.8的船模数值计算结果的讨论中发现,本文所讨论的双尾鳍内河船总阻力随着重心纵向位置XG的前移而降低,在XG =54%L后基本趋于稳定,此时的船模总阻力与XG =46%L(尾倾)时的船模总阻力相比降低约13.5%。
上述模型尺度绕流场数值模拟得到的纵倾节能相关数据有一定的参考价值,但可否直接将模型尺度的结果应用于实船尚不明确,因此需对纵倾节能的尺度效应进行进一步的研究。
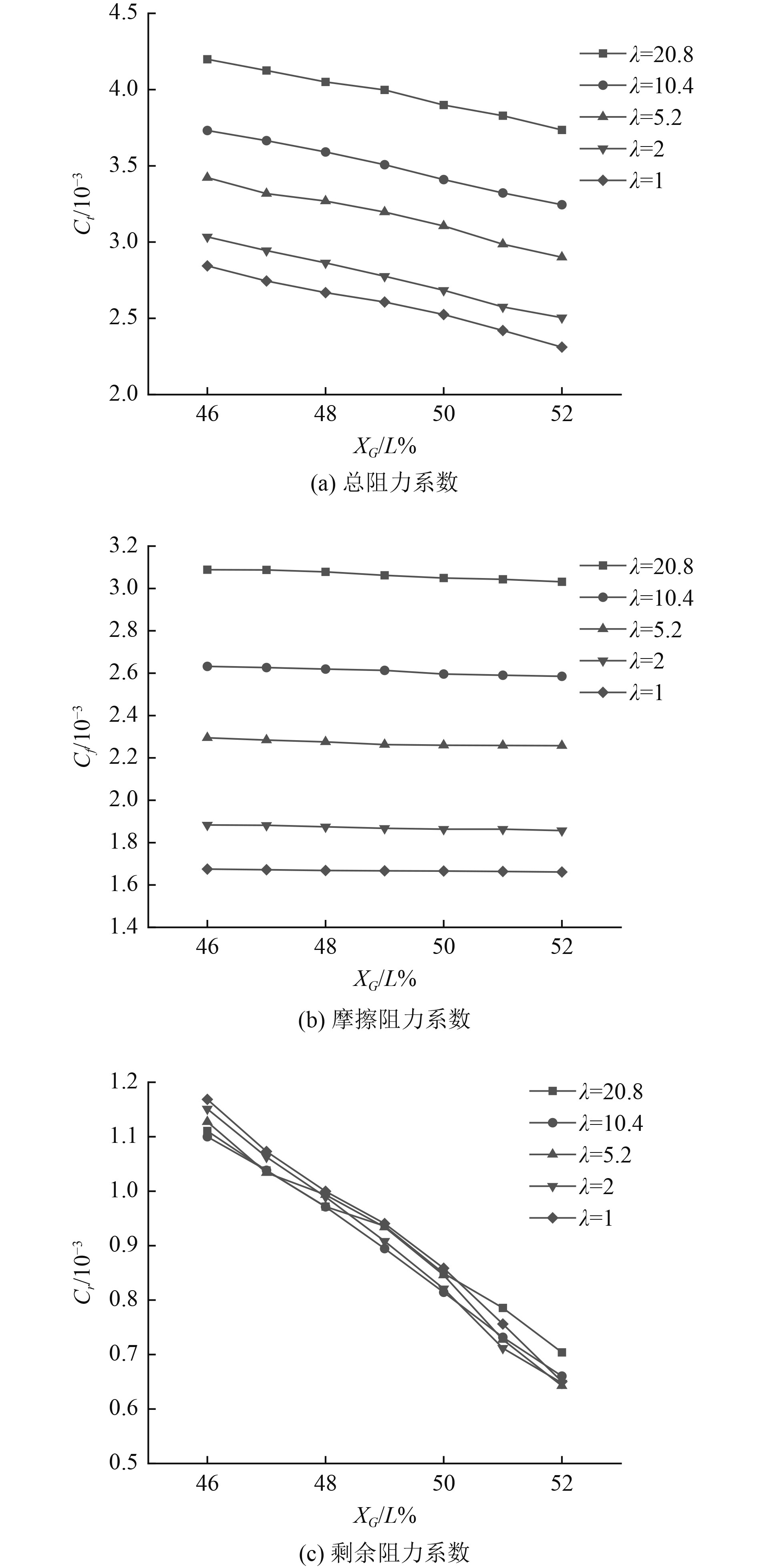
为讨论纵倾节能的尺度效应,对不同尺度(缩尺比为20.8、10.4、5.2、2和实尺度)的双尾鳍内河船舶模型在等Fr下进行不同纵倾角度的数值模拟;由于计算资源的限制,重心纵向位置范围选定为XG /L=46%~52%。不同尺度模型的阻力数值结果对比如图12所示。表5为不同缩尺比船模各阻力系数减少百分比(以XG/L=46%工况为比价基准),其中:
|
图 12 不同缩尺比阻力系数对比图 Fig. 12 Comparison of resistance coefficients for different scale |
|
|
表 5 不同缩尺比模型最大首倾和最大尾倾条件下各阻力系数的差异 Tab.5 Differences in resistance coefficients for different scale models with maximum bow tilt and maximum stern tilt conditions |
| $ \delta = ({C_{\max }} - {C_{\min }})/{C_{\max }}\% 。$ |
由图12(a)可知,随着重心纵向位置XG的前移,不同尺度模型的总阻力曲线均基本呈单调递减的趋势,各尺度模型的总阻力曲线基本平行。由表5可知,随着重心纵向位置XG的前移,不同尺度模型的总阻力系数减少百分比随模型尺度变大逐渐增加,最小尺度(λ=20.8)的总阻力系数减少百分比为11.04%,而实尺度(λ=1)数值模拟的总阻力系数减少百分比为18.71%,即总阻力系数存在一定的尺度效应。
由图12(b)与表5数据可知,摩擦阻力随重心前移略有降低,其减少百分比随模型尺度变大逐渐减少,减少量相对较少(λ=20.8的模型约为1.85%,λ=1时约为0.83%)。
不同缩尺比船模纵倾状态下数值模拟得到的剩余阻力系数差别较大(见图12(c)),缩尺比λ=20.8的模型正浮时(XG /L=49%)剩余阻力系数与实尺度得到的剩余阻力系数相比差距在1%左右,而两者在首倾时的差距最大达到了近8%;同时船舶纵倾从最大尾倾(XG /L=46%)到最大首倾(XG /L=52%),剩余阻力系数减少的百分比在实尺度数值模拟中达到了44.34%,而在缩尺比λ=20.8的数值模拟中减少百分比为36.61%,即纵倾对剩余阻力的影响亦存在较明显的尺度效应。
4 结 语1)本文所讨论的双尾鳍内河船型最佳纵倾角度为首倾1.5°左右;总阻力与剩余阻力随船舶重心纵向位置的前移(船舶由尾倾向首倾变化)而减小,摩擦阻力变化较小。
2)船舶纵倾节能存在明显的尺度效应,在总阻力系数与剩余阻力系数的变化上体现的较为明显。
3)重心纵向位置变化导致船舶纵倾角的改变引起船体周围流场的变化,不同纵倾角下船体表面压力分布也有明显不同,是影响船模阻力变化的重要因素。
| [1] |
魏一鸣, 余碧莹, 唐葆君, 等. 中国碳达峰碳中和时间表与路线图研究[J]. 北京理工大学学报: (社会科学版), 2022, 24(4). |
| [2] |
林安平, 余培文. 几种船舶节能技术性能分析[J]. 武汉船舶职业技术学院学报, 2008, 7(5): 15. |
| [3] |
周熊. 散货船调整压载状态的节能效果[J]. 船舶节能, 1996(4): 41-44. |
| [4] |
王兴权, 赵成壁. “松林”轮最佳纵倾阻力试验[J]. 武汉造船, 1991, 29-35. |
| [5] |
周占群, 宋家瑾, 徐惠民, 等. “门”字型货船的最佳纵倾节能技术研究[J]. 交通部上海船舶运输科学研究所学报, 1986(1): 51-68. |
| [6] |
王伟, 孙守超, 郭春雨, 等. 船舶最佳纵倾及节能[J]. 应用科技, 2017, 44(5): 1. |
| [7] |
李振兴, 徐轶群, 陈皓雯. 小型电动船舶纵倾优化[J]. 舰船科学技术, 2022, 44(13). |
| [8] |
高现娇, 孙江龙, 黄本燊, 等. 基于纵倾优化的油船节能研究[J]. 舰船科学技术, 2017, 39(5): 70−74. GAO X J, SUN J L, HUANG B S, et al. Energy saving research on oil tankers based on trim optimization [J]. Ship Science and Technology, 2017, 39(5): 70−74. |
| [9] |
张元浩, 秦江涛, 李子如, 等. 江海直达船深浅水绕流场数值模拟方法研究[J]. 武汉理工大学学报: (交通科学与工程版), 2019, 43(5). |
| [10] |
郭航. 波浪条件下变纵倾对船舶阻力性能影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2021.
|
| [11] |
LEE J, YOO S, CHOI S, et al. Development and application of trim optimization and parametric study using an evaluation system (solution) based on the RANS for improvement of EEOI[J]. Molecular Plant-Microbe Interactions, 2014, 2(71): 183-204. |
| [12] |
PAPP J, GHIA K. Study of turbulent compressible mixing layers using two-equation turbulence models including an RNG k-epsilon model[C]//36th AIAA Aerospace Sciences Meeting and Exhibit, 1998.
|
 2024, Vol. 46
2024, Vol. 46
