2. 中国船舶集团有限公司第七一五研究所,浙江 杭州 310023
2. The 715 Research Institute of CSSC, Hangzhou 310023, China
在海洋工程领域,拖曳系统目前在深海侦测、海资源勘探等方面受到广泛关注。在拖曳工作中,托曳体因受到拖船航速、波浪和海流等影响,存在探测设备所受载荷过大,导致拖缆断裂,进而导致勘探设备损坏、丢失等海洋事故,因此,对拖曳系统进行动力响应分析至关重要。目前,在拖曳系统动力响应分析方面采用数值模拟的方法已被广泛使用。张大鹏等[1]通过OrcaFlex软件建立了潜艇水下360°回转过程种拖曳系统的动力学仿真模型及拖体自航模式下动力学仿真模型,研究了不同模式下,拖缆对水下拖体的影响。刘铭等[2]基于集中质量法,推出拖曳缆索的动力学方程,模拟了拖船匀速直航、横向正弦运动、升沉运动、回转运动下缆索系统的动力响应,通过与实验对比表明,集中质量模型对缆索在各种边界条件下的运动激励均有较好适应性。LIU等[3]建立了浮体和沉体拖曳系统的数值模型,对被拖曳体的载荷以及位置的变化进行分析,同时对内部阻尼系数与单元数的敏感性进行分析。Yuan等[4]研究了带有VIV的可控硅TDZ之间非线性RSI响应。采用的数值模型分别与一些文献的VIV和RSI实验测量值进行验证,模拟了3种顶部平台升沉运动与涡激振动相结合的情况,分析了TDZ中沟槽的发展以及SCR的响应特性。以上分析方法计算量均较庞大,需要花费较长时间,不能快速获取系统动力响应。为了提高耦合计算效率,有很多学者引入了机器学习的方法。通过已有监测数据或经软件仿真模拟得到的数据,采用机器学习的相关算法,从数据中学习规律,不断改善算法的性能,建立合适的预测模型。机器学习已经渗透到各行各业,在医学[5]、生物学[6]、工程领域[7]等已受到广泛关注,并且已取得重大成就。吕国华等[8]提出一种基于联邦随机森林的船舶AIS轨迹分类算法,实现对渔船、客船、货船和油轮4类典型船舶的联邦分类。罗恒等[9]提出一种预测短期能耗的LightGBM-LSTM模型,与LightGBM、LSTM单项模型、其他常用模型进行对比实验,发现LightGBM-LSTM模型在建筑能耗预测中具有更高准确性。贾子锌等[10]利用BP神经网络对油船系泊运动的运动量即纵移、横移、升沉、横摇、纵摇、回转六分量。韩宇等[11]提出了基于长短期记忆神经网络模型,对软刚臂单点受力进行实时预测。李世锋等[12]研究了一类基于遗传算法和BP网络的系泊船船缆力预测模型。孙晔等[13]提出了基于径向基函数(RBF)神经网络算法在船舶俯仰运动短时预测中的应用。
上述研究均仅限于时域,存在预报误差逐步叠加导致误差大等问题,且均针对的是系泊系统,没有对拖曳系统进行分析研究。本文通过建立拖曳系统数值仿真模型,利用OrcaFlex耦合计算软件提供数据集,提出基于贝叶斯优化的LightGBM算法拖曳系统动力学响应预报方法。在该预报方法中直接将海洋环境条件、拖船航速和拖曳缆下放长度作为输入参数,拖曳缆关键位置处张力值作为输出参数,实现拖曳系统动力响应的即时预报。
1 LightGBMLightGBM(Light Gradient Boosting Machine)是2017年Microsoft提出来的[14],是一个实现GBDT算法的框架,支持高效率的并行训练,并且具有更快的训练速度、更低的内存消耗、更好的准确率、支持分布式可快速处理海量数据等优点。该模型主要是利用决策树迭代训练以获得最优模型。计算公式如下:
| $ F_g(X)=\sum\limits_{k-1}^gf_k(X)\text{。} $ | (1) |
式中:
该模型为了使结果接近真实结果,在每次迭代中寻找目标函数的最小值。其中,目标函数包括损失函数和正则化项2个部分,损失函数的计算公式为:
| $ L({y_q},y_q^{'}) = \frac{1}{A}\sum\limits_{q = 1}^A {\left( {{y_q}\lg {P_q} + (1 - {y_q})\lg (1 - {P_q})} \right)} 。$ | (2) |
式中:
正则化项通过控制叶子节点分裂以降低模型的过拟合,该模型的目标函数为:
| $ O = L({y_q},y_q^{'}) + \gamma Z + \frac{1}{2}\lambda {\sum\limits_{v = 1}^z {({W_v})} ^2}。$ | (3) |
式中:
在处理样本时,LightGBM引入了直方图算法(Histogram-based)、基于梯度的单边采样算法(Gradient-based One-Side Sampling)、互斥特征捆绑算法(Exclusive Feature Bundling),通过这3个算法的引入,LightGBM生成一片叶子需要的复杂度明显降低,极大减少计算时间。
直方图(Histogram)算法对特征值进行装箱处理,把连续的浮点特征值离散化成K个整数,形成一个个箱体,同时构造一个宽度为K的直方图,在遍历数据的时候,根据离散化后的值作为直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,根据直方图的离散值,遍历寻找最优的分割点。将特征由浮点数转换成0~255位的整数进行存储,从而极大节约了内存存储。LightGBM使用的leaf-wise策略,每次在当前叶子节点中,找到分裂增益最大的叶子节点进行分裂,而不是所有节点都进行分裂,提高了计算精度。通过单边梯度采样GOSS算法,对样本进行下采样时保留梯度较大的样本点,随机去掉梯度小的样本,减少计算目标函数增益时候的复杂度。Exclusive Feature Bundling算法将互斥特征绑在一起减少特征维度,有效减少用于构建直方图的特征数量,从而降低计算复杂度。同时LightGBM支持特征并行和数据并行,通过使用分散规约(Reduce scatter),将直方图合并的任务分给不同机器,降低通信和计算开销。
2 贝叶斯优化目前,在机器学习中最困难的部分之一是为模型找到最好超参数。机器学习的性能与超参数直接相关。LightGBM算法中具有较多超参数,如树模型的最大深度、树节点中的最小观察数、一棵树上的节点个数、学习率、每次迭代中随机选择特征的比例等。这些参数很大程度上影响模型的训练精度,因此采取相应的超参数寻优方法选择最优参数。目前调整超参数的方法有网格搜索、随机搜索和贝叶斯优化3种,其中贝叶斯优化方法是当前最为先进的优化框架,已被应用于机器学习各大领域。相比于网格搜索和随机搜索,在计算量和计算时间上有大幅提升。
在数学上,假设有一组超参数组合是
| $ {{x}}^{*} = \arg \min f(x) 。$ | (4) |
式中:
贝叶斯优化迭代得到的数据集为:
高斯过程假设观测点服从高斯分布,其表达式如下:
| $ f({x_{1:n}}) \sim GP\left( {\beta ({{\text{x}}_{1:n}}),\sum {({x_{1:n}},{x_{1:n}})} } \right) ,$ | (5) |
式中,
| $ \sum_{ }^{ }(x_{1:n},x_{1:n})=\left(\begin{array}{*{20}{c}}k(x_1,x_1) & \cdots & k(x_1,x_n) \\ \vdots & \cdots & \vdots \\ k(x_n,x_1) & \cdots & k(x_n,x_n)\end{array}\right)。$ | (6) |
由贝叶斯定理可知:
| $ P\left(f({x}_{n+1})f({x}_{1:n})\right)\infty P\left(f({x}_{1:n})f({x}_{n+1})\right)P\left(x{}_{n+1}\right)。$ | (7) |
将先验概率转化为后验概率,通过不断的迭代更新使得 ,最终得到最优超参数。
3 基于LightGBM的动力响应预报方法拖曳系统灾难性事件,如拖曳缆断裂、拖缆振动剧烈导致拖体声呐信息接收误差较大等,一般是因为拖船航速过快、拖船六自由度数值过大引起的。根据相关经验与理论可知,决定拖曳系统动力响应的主要因素是作用于拖曳系统上的海洋环境条件,如风、浪、流所形成的载荷大小和方向,以及拖船航速、拖缆下放深度等因素。
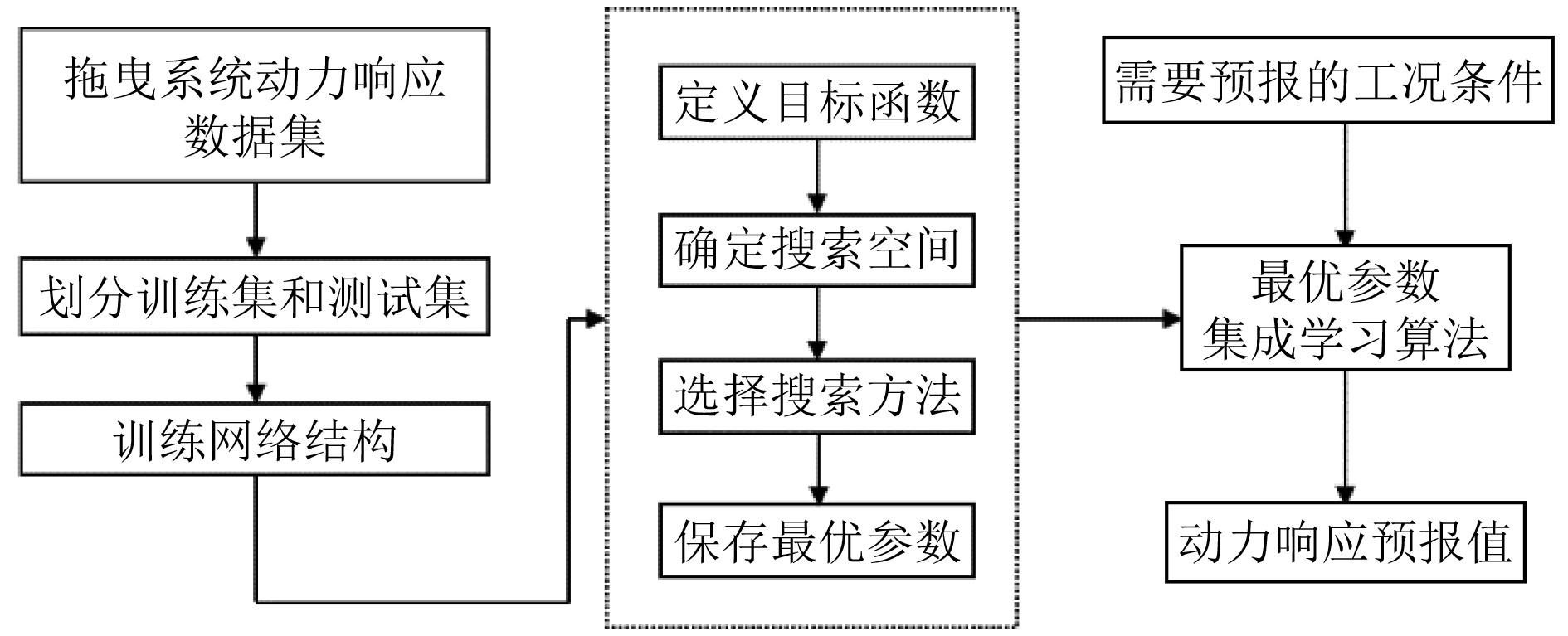
本文提出一种基于LightGBM的拖曳系统动力响应预报方法,基本流程如图1所示。输入参数可根据具体所处环境及拖曳系统条件决定,一般可选择波高、波向、波的周期、波浪作用方向、风速、风向等主要环境条件以及拖船航速、下放缆长等主要拖曳条件作为模型输入;输出参数即为拖曳系统动力响应,可以是拖曳缆张力、拖缆振动位移、拖缆关键节点加速度等。数据集可由现场实测、数值模拟得到。
|
图 1 拖曳系统动力响应预报方法基本流程图 Fig. 1 Basic flow chart of dynamic response prediction method for towing system |
LightGBM是组合多个学习模型得到更好更全面的强学习模型,能够实现以任意精度实现从输入到输出的非线性映射,但模型超参数对精度有明显影响,本文选择贝叶斯优化的超参数搜索方法,选择最优超参数,以保证拖曳系统预报模型结果的准确性。该模型的考核参数采用决定系数(R2)、均方根误差(RMSE),其中R2也称可决指数、可决系数,R2为度量拟合优度的统计量,R2越接近于1,模型拟合效果越好,一般认为超过0.8的模型拟合优度比较高。RMSE为预测值与真实值偏差的平方与观测次数n比值的平方根,其值越小,说明预测精度越高。2种评价衡准分别定义如下:
| $ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{\bar y}_i})}^2}} }} ,$ | (8) |
| $ RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} }。$ | (9) |
式中:
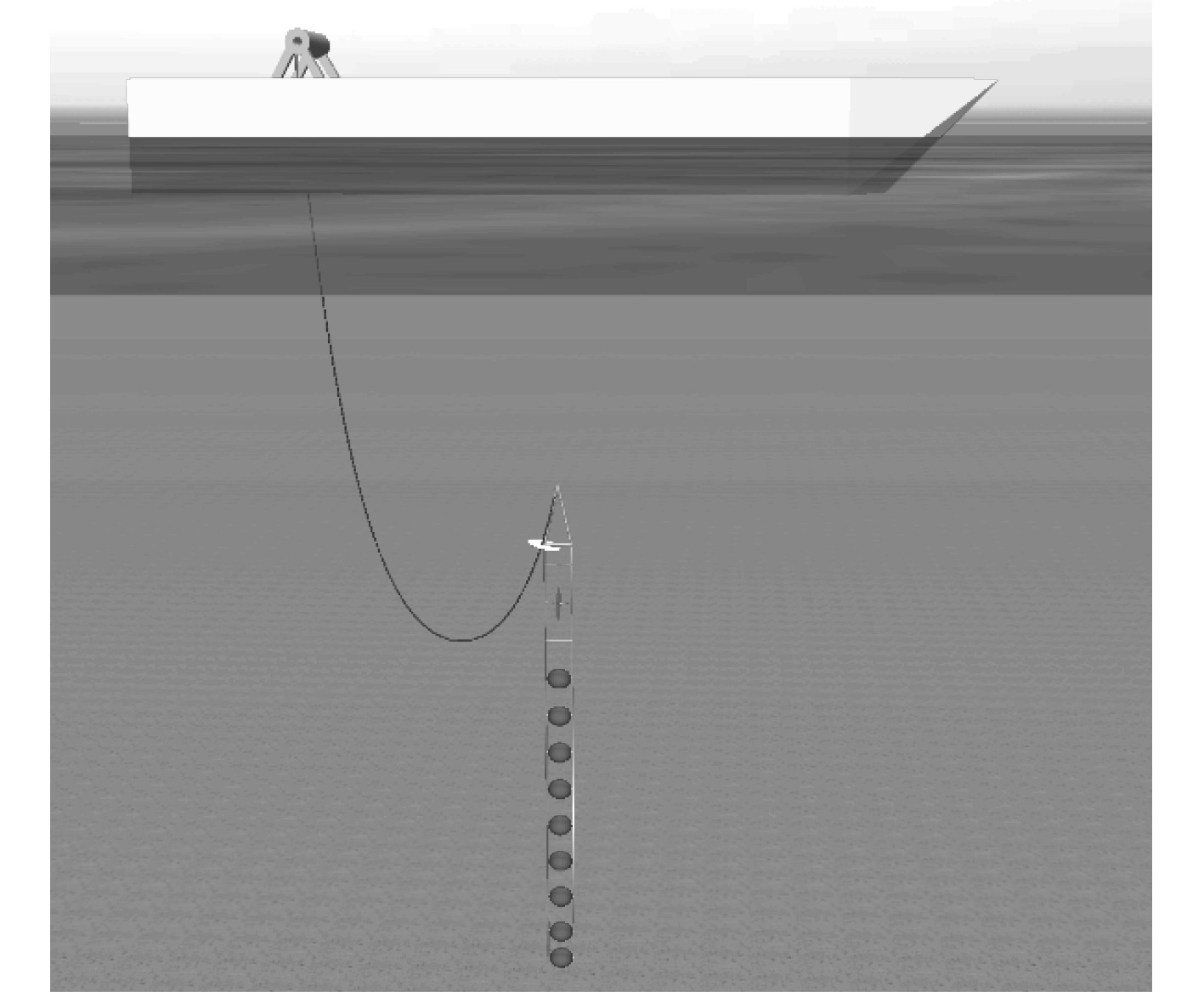
本文的数值模型由OrcaFlex软件建立并进行求解分析。拖船的船体响应幅值算子(RAOs)根据某双体船的运动响应谱得到。拖曳系统的模型如图2所示,拖体为梯形结构,每个阶梯上可搭载不同的探测设备。拖曳系统各构件尺寸参数和水动力参数[15],参数如表1所示。
|
图 2 拖曳系统数值仿真模型 Fig. 2 Numerical simulation model of towing system |
|
|
表 1 构件参数 Tab.1 Component parameter |
搭载在各单元轴上的声呐装备采用Clump单元模拟。声呐装备的相关参数如表2所示。
|
|
表 2 声呐装备参数 Tab.2 Sonar equipment parameters |
整个仿真过程中,波浪采用JONSWAP谱[16],可定义为:
| $ S(w) = \alpha \frac{{{g^2}}}{{{w^5}}}\exp \left[ { - \frac{5}{4}{{\left(\frac{{{w_m}}}{w}\right)}^4}} \right]{\gamma ^{\exp [ - {{(w - {w_m})}^2}/(2{\sigma ^2}w_m^2)]}} 。$ | (10) |
式中:
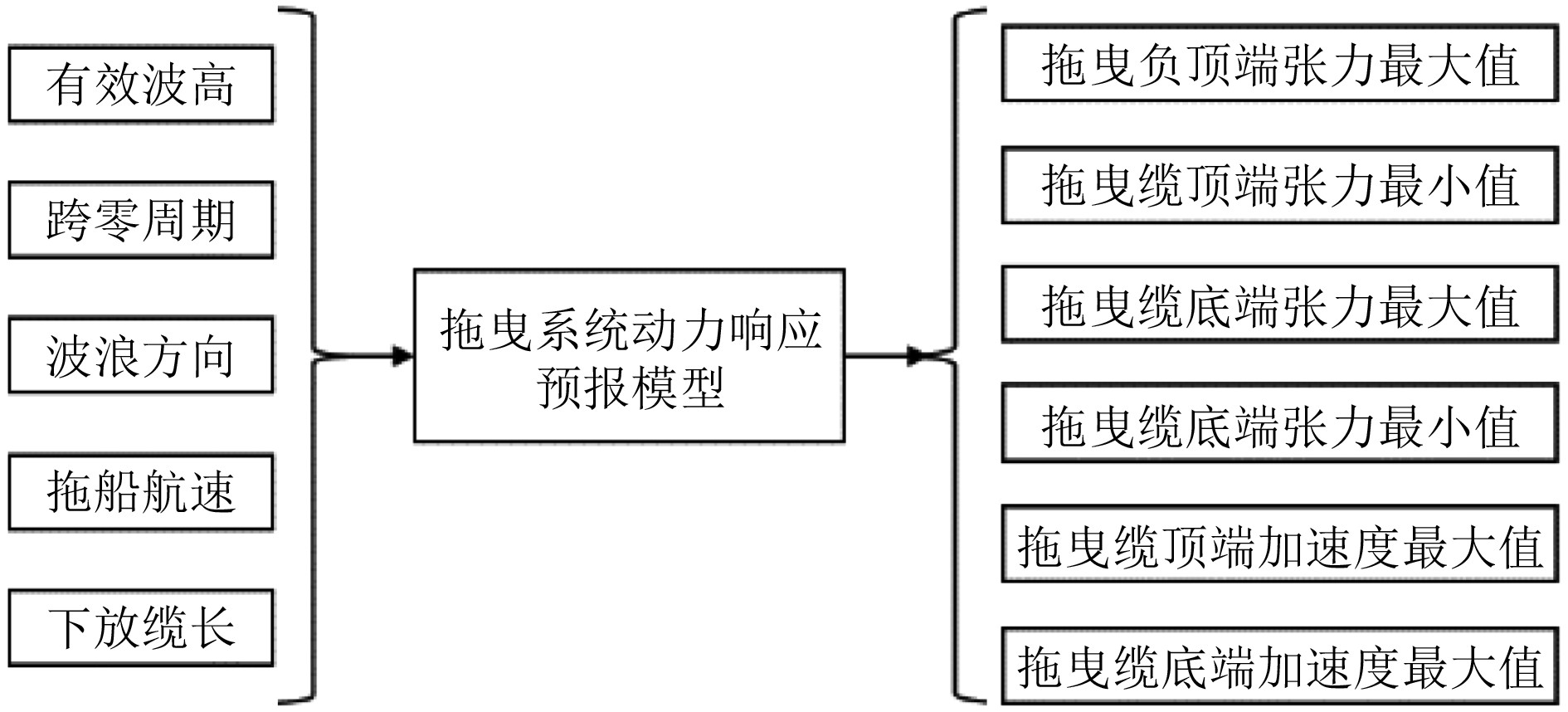
本文将北大西洋[17]作为数值模拟的海况环境,如表3所示。波浪载荷是作用于该浮式系统上的主要海洋环境载荷,因此该拖曳系统仅考虑波浪作为海洋环境条件,同时将拖船航速和拖曳缆下放深度作为工况条件。输入参数为有效波高、跨零周期和作用方向、拖船航速、拖曳缆下放长度5个参数,图3为拖曳系统动力响应预报基本框架。训练数据由OrcaFlex软件仿真得到,共3125组数据。
|
|
表 3 北大西洋海况统计 Tab.3 North Atlantic sea state statistics |
|
图 3 拖曳系统动力响应预报模型 Fig. 3 Dynamic response prediction model of towing system |
本文采用Python及其开源的机器学习框架scikit-learn等实现了集成学习算法。实验环境基于Windows10操作系统,CPU为Intel(R) Core(TM) i7-4770 CPU @ 3.40 GHz,内存共16 GB。为了避免原始数据对模型泛化能力及训练准确性的干扰,将归一化后的数据集种随机抽取70%作为训练集,30%作为测试集,并使用10折交叉验证对回归性能度量。在本算例中,动力响应主要研究拖曳缆顶端张力和底端张力的最大值、最小值,拖曳缆顶端和底端加速度最大值。首先采用集成学习模型即随机森林(RF)、极限梯度提升(XGBOOST)、LightGBM 3种模型,在使用默认参数的情况下,10折交叉验证后的结果如表4所示。
|
|
表 4 3种模型在测试集中的评价指标得分 Tab.4 Evaluation index scores of the three models in the test set |
由表4的评价指标得分可看出,在动力响应预报中,LightGBM对动力响应的预报明显优于随机森林(RF)和极限梯度提升(XGBOOST),而且训练时间也最短,能够起到即时预报的效果。因此,选用LightGBM作为动力响应预报的最优模型。由于集成学习的主要超参数会对网络输出结果的精度具有明显影响。因此需得到LightGBM的最优超参数。根据对算法的使用建议和个人使用经验,需调整的超参数和其最优搜索范围如表5所示。
|
|
表 5 超参数取值范围 Tab.5 Specifies the value range of the hyperparameter |
目前,常见的超参数优化方法有网格搜索、随机搜索、贝叶斯搜索等。研究表明,贝叶斯优化的速度更快,搜索效果更稳健,贝叶斯超参数优化[18]为目前最高效的自动化调参方法之一。贝叶斯优化后得到的最优超参数如表6所示。
|
|
表 6 最优超参数 Tab.6 Optimal hyperparameter |
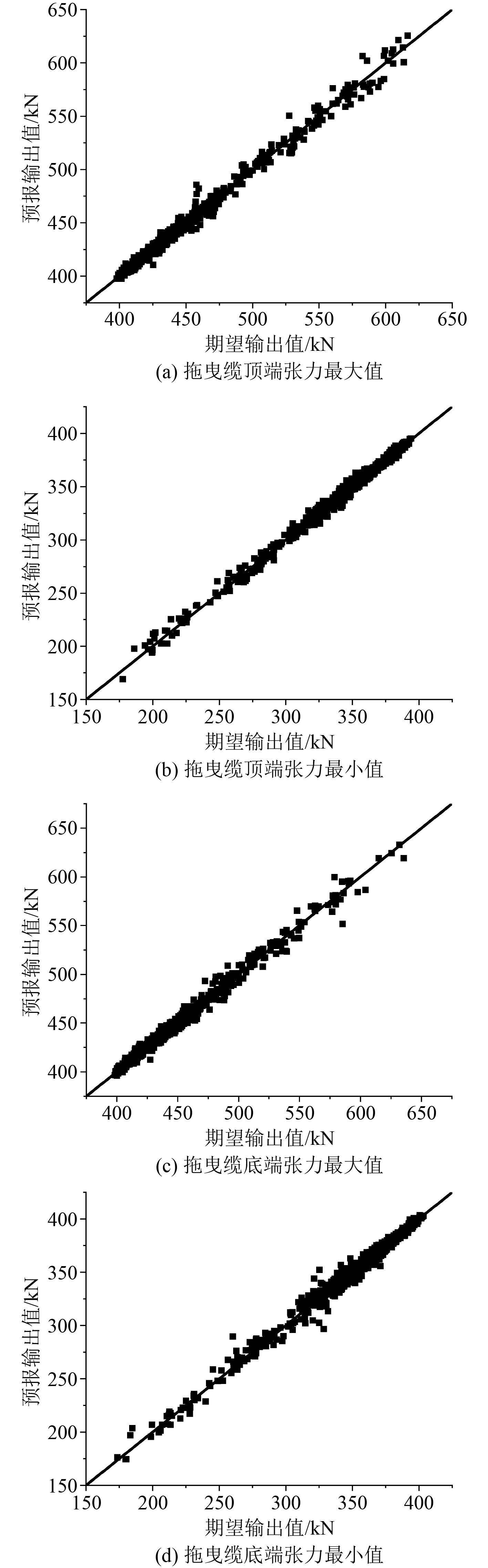
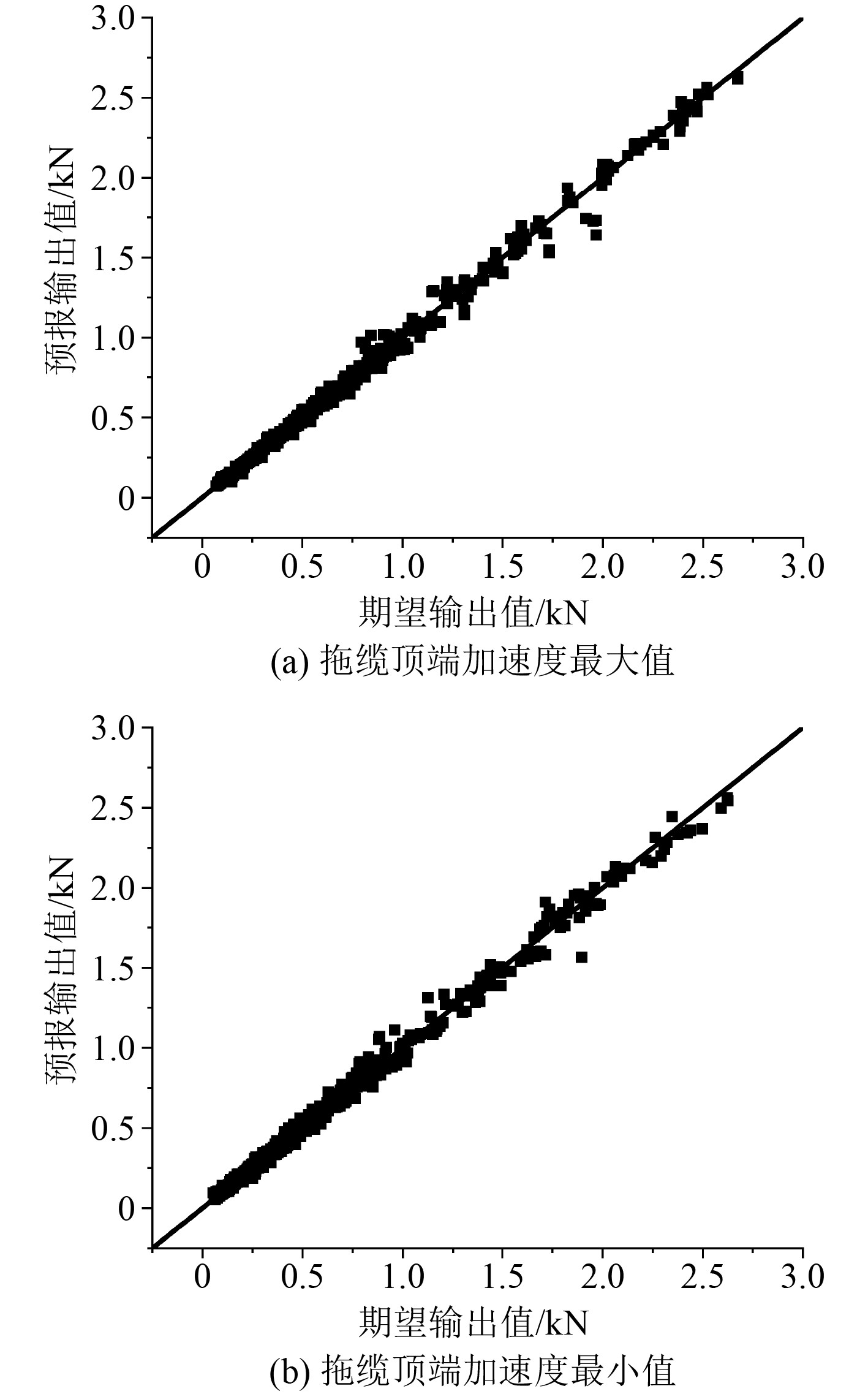
优化后拖曳系统动力响应的真实值与预报值的对比如图4和图5所示。可以看出,每一个数据点越靠近y=x这条直线代表预测效果越好。
|
图 4 拖曳缆关键节点处张力 Fig. 4 Tension at key points of towing cable |
|
图 5 拖曳缆关键节点处加速度 Fig. 5 Acceleration at key point of towing cable |
由表7可知,经过贝叶斯优化后的LightGBM模型在动力响应预报中表现更加精准。LightGBM算法对动力响应目标的R2最小为0.9871,对动力响应目标的RMSE达到3.0525。因此在该动力响应预报模型中,经过贝叶斯参数优化后的LightGBM算法对拖曳系统动力响应的预报更加精准,效率也为最高。
|
|
表 7 3种模型在测试集中的评价指标得分 Tab.7 Evaluation index scores of the three models in the test set |
本文基于集成学习算法开发了一种拖曳系统动力响应预报方法。首先基于OraFlex软件仿真模拟得到的动力响应数据,采用3种集成学习方法对比分析,表明LightGBM算法对拖曳系统动力响应预报精度更好,然后引入贝叶斯优化算法,对其超参数进行优化,优化后的精度进一步提高。结果表明,贝叶斯超参数优化方法在LightGBM预报拖曳系统动力响应问题上对预报精度的提高具有很好效果。能够实现拖曳系统在工作期间的动力响应快速计算和系统危险状态超前预警,防止危险事件的发生。
本文提出的基于LightGBM拖曳系统运动响应预报方法,可为后期建立拖曳系统数字孪生系统提供技术支撑,实现结构的优化疲劳分析,系统延寿指导等,为拖曳系统的设计指标验证和系统安全运维提供直接依据,促进从智能制造到智能健康管理的再度升级。
| [1] |
张大朋, 白勇, 朱克强. 不同模式下拖缆对水下拖体运动姿态的影响研究[J]. 船舶力学, 2018, 22(8): 967-976. ZHANG D M, BAI Y, ZHU K Q, et al. Study on the influence of towing cable on the motion attitude of underwater towing body under different modes[J]. Ship Mechanics, 2018, 22(8): 967-976. DOI:10.3969/j.issn.1007-7294.2018.08.006 |
| [2] |
刘铭, 李家旺, 朱克强. 基于集中质量法的水下拖曳缆索动力响应分析[J]. 水道港口, 2017, 38(4): 405-411. LIU M, LI J W, ZHU K Q. Dynamic response analysis of underwater towing cable based on concentrated mass method[J]. Journal of Waterway and Harbour, 2017, 38(4): 405-411. |
| [3] |
LIU, CHUANG, LI, et al, Dynamic analysis of semi-submersible production platform under the failure of mooring lines[J]. China Ocean Engineering, 2021, 35(1): 84−95.
|
| [4] |
YUAN Y, ZHENG M, XUE H, et al. Nonlinear riser-seabed interaction response among touchdown zone of a steel catenary riser in consideration of vortex-induced vibration[J]. Ocean Engineering, 2021, 227: 108891. DOI:10.1016/j.oceaneng.2021.108891 |
| [5] |
王琰, 胥美美, 童俞嘉, 等. 基于机器学习的环境监测数据对循环系统疾病死亡影响及预测预警模型构建[J]. 数据分析与知识发现, 2022, 6(10): 79-92. WANG Y, XU M M, TONG Y J, et al. The impact of environmental monitoring data on death of circulatory system diseases and the construction of prediction and early warning model based on machine learning[J]. Data Analysis and Knowledge Discovery, 2022, 6(10): 79-92. |
| [6] |
WANG Z, QIAO D, YAN J, et al. A new approach to predict dynamic mooring tension using LSTM neural network based on responses of floating structure[J]. Ocean Engineering, 2022, 249: 110905. DOI:10.1016/j.oceaneng.2022.110905 |
| [7] |
张书旭, 李峰, 谢建平, 等. 基于融合神经网络模型的药物分子性质预测[J]. 计算机科学, 2021, 48(9): 251-256. ZHANG S X, LI F, XIE J P, et al. Prediction of drug molecular properties based on fusion neural network model[J]. Computer Science, 2021, 48(9): 251-256. |
| [8] |
吕国华, 胡学先, 杨明, 等. 基于联邦随机森林的船舶AIS轨迹分类算法[J]. 信息网络安全, 2022, 22(4): 67-76. LV G H, HU X X, YANG M, et al. AIS trajectory classification algorithm for ships based on Federal Random Forest[J]. Netinfo Security, 2022, 22(4): 67-76. |
| [9] |
罗恒, 刘杭. 基于LightGBM-LSTM组合模型的商业建筑能耗预测[J]. 计算机应用与软件, 2022, 39(11): 36-42+65. LUO H, LIU H. Energy consumption forecast of commercial buildings based on LightGBM-LSTM combination model[J]. Computer Applications and Software, 2022, 39(11): 36-42+65. |
| [10] |
贾子锌, 柳淑学, 李金宣, 等. 基于BP神经网络对横浪作用下系泊油船的运动量预测分析[J]. 水道港口, 2022, 43(4): 430-436. JIA Z X, LIU S X. LI J X, et al. Prediction and analysis of motion of mooring tanker under transverse waves based on BP neural network[J]. Journal of Waterway and Harbor, 2022, 43(4): 430-436. |
| [11] |
韩宇, 黄国良, 李鹏. 基于LSTM的软刚臂单点系泊力预测方法研究[J]. 天津科技, 2020, 47(5): 74-80. HAN Y, HUANG G L, LI P, et al. Research on soft rigid arm single point mooring prediction method based on LSTM[J]. Tianjin Science & Technology, 2020, 47(5): 74-80. DOI:10.3969/j.issn.1006-8945.2020.05.025 |
| [12] |
李世峰, 邱占芝. 基于改进GA-BP网络的系泊缆力预测建模与仿真[J]. 系统仿真学报, 2017, 29(7): 1457-1463. LI S F, QIU Z Z. Prediction modeling and simulation of mooring cable force based on improved GA-BP network[J]. Journal of System Simulation, 2017, 29(7): 1457-1463. |
| [13] |
孙晔, 武文华, 樊哲良, 等. 基于RBF神经网络的FPSO系泊力预测方法和原型应用[C]//第十六届中国海洋(岸)工程学术讨论会论文集(上册), 2013: 306−312. SUN Y, WU W H, FAN Z L, et al. Prediction method and prototype application of FPSO mooring based on RBF neural network [C]//Proceedings of the 16th China Ocean (Coastal) Engineering Symposium (Volume 1), 2013: 306−312. |
| [14] |
DIETTERICH T G. Machine learning research: four current directions[J]. AI Magazine, 1997, 18(4): 97-136. |
| [15] |
DNV. GL-RP-C205 Environmental conditions and envirormental loads[S
|
| [16] |
CARTER D J T. Prediction of wave height and period for a constant wind velocity using the JONSWAP results[J]. Ocean Enginerring, 1982, 9(1): 17-33. DOI:10.1016/0029-8018(82)90042-7 |
| [17] |
张雯月. 风浪流联合作用对船舶随机横摇的影响研究[D]. 大连: 大连理工大学, 2019.
|
| [18] |
许亮. 基于贝叶斯优化算法的参数化结构设计[J]. 建筑技术开发, 2022, 49(17): 13-15. XU L. Parametric structure design based on Bayesian optimization algorithm[J]. Building Technology Development, 2022, 49(17): 13-15. |
 2024, Vol. 46
2024, Vol. 46
