2. 中国船舶集团有限公司第七〇五研究所昆明分部,云南 昆明 650106;
3. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074
2. Kunming Branch of the 705 Research Institute of CSSC, Kunming 650106, China;
3. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Techonology, Wuhan 430074, China
浮体自由上浮过程是浮标、潜艇、深潜器等各种潜浮式结构物的一种典型工作工况,尤其是对于潜艇逃生舱而言,从潜艇中释放后会做一个上浮运动,上浮运动的速度、时间以及逃生舱的姿态都与艇员的生命安全息息相关,其研究也显得尤为重要[1]。
针对典型的浮体水下上浮过程,国内外学者开展了相关研究。王世明等 [2]提出一种可以通过内置液压缸顶推和收缩改变排水体积,进而改变浮力的剖面探测浮标,并通过力学分析和数学建模相结合的方法计算出了浮标匀速上浮时的速度,以此为基础对浮标上浮运动开展研究。孙斌和黄祥兵 [3 - 4]以一个外形简单的集体逃生舱为研究对象,使用力学推导和数学建模相结合的方法以及数值模拟方法对逃生舱的上浮速度进行研究,2种研究方法得到的结果具有较好的一致性。黄祥兵和唐鑫[5 - 6]借助流体计算软件Fluent对胶囊形潜艇集体逃生舱在流体中受到的作用力进行研究,通过受力分析计算得到逃生舱的上浮速度,在此基础上通过改变逃生舱的减速翼翼角和减速翼数量研究减速翼对最大上浮速度的影响,带减速翼的逃生舱模型。
众多学者对于不同外形结构物的上浮运动开展了大量研究,对结构物上浮运动的模式,以及导致这些运动的深层原因进行深入研究,但是对满足相似条件的不同尺度结构物上浮运动性能之间相关性的研究却少之又少。即便有学者对不同尺度的结构物上浮运动之间的相似性进行过研究,提出一些通过缩比模型运动参数换算实体运动参数的方法[7],这些方法也是根据结构物在给定速度下的阻力等于剩余浮力得到的一种简单的静态等效方法,难以对上浮过程开展细致描述。本文以圆球状浮体作为对象,研究尺度、密度比对其上浮运动性能的影响,以数值仿真和模型试验相互验证提高研究结果的可靠性,研究结论可拓展至其他浮体,并为缩比模型试验提供支撑。
1 建模与试验验证 1.1 研究对象选取半径为0.1 m的圆球为研究对象,圆球的质量M,重心位置Zg,3个方向的质量惯性矩I如表1所示。坐标系定义原点为圆球释放时球心位置,Z方向为重力加速度反方向,X方向和Y方向满足右手坐标系,如图1所示。
|
|
表 1 研究圆球主要参数 Tab.1 The main parameters of the sphere were studied |

|
图 1 坐标系定义 Fig. 1 Definition of coordinate system |
采用RANS控制方程组,包括连续性方程和动量守恒方程[8 - 9]。
连续性方程:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}}{\text{ = }}0 ,$ | (1) |
动量守恒方程:
| $ \begin{split} & \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial \rho }}{{\partial {x_i}}} + \\ & \left. {\frac{\partial }{{\partial {x_i}}}\left[ {\mu (\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}) - } \right.\frac{2}{3}\mu \frac{{\partial {u_l}}}{{\partial {x_l}}}{\delta _{ij}}} \right] + \frac{\partial }{{\partial {x_j}}}\left( { - p\overline {u_i^{'} u_j^{'}} } \right) + \rho {f_i}。\\[-1pt] \end{split} $ | (2) |
式中:ui为流体时均速度分量;p为流体压强;fi为流体体积力分量;ρ为流体密度;μ为流体的粘性系数;附加应力记为
数值仿真在软件STAR-CCM+中开展,采用有限体积法进行方程离散,通过在每一个控制体积上对控制方程进行积分,从而得出离散的方程组。由于圆球上浮过程中受力和运动特性的不确定性,采用重叠网格来对运动区域进行网格划分,采用动态流固相互作用(Dynamic Fluid Body Interaction,DFBI)来模拟流体和刚体动态相互作用,预报圆球刚体的运动,选用多相流模型—VOF(流体体积)模型完成对自由液面的捕捉[10]。
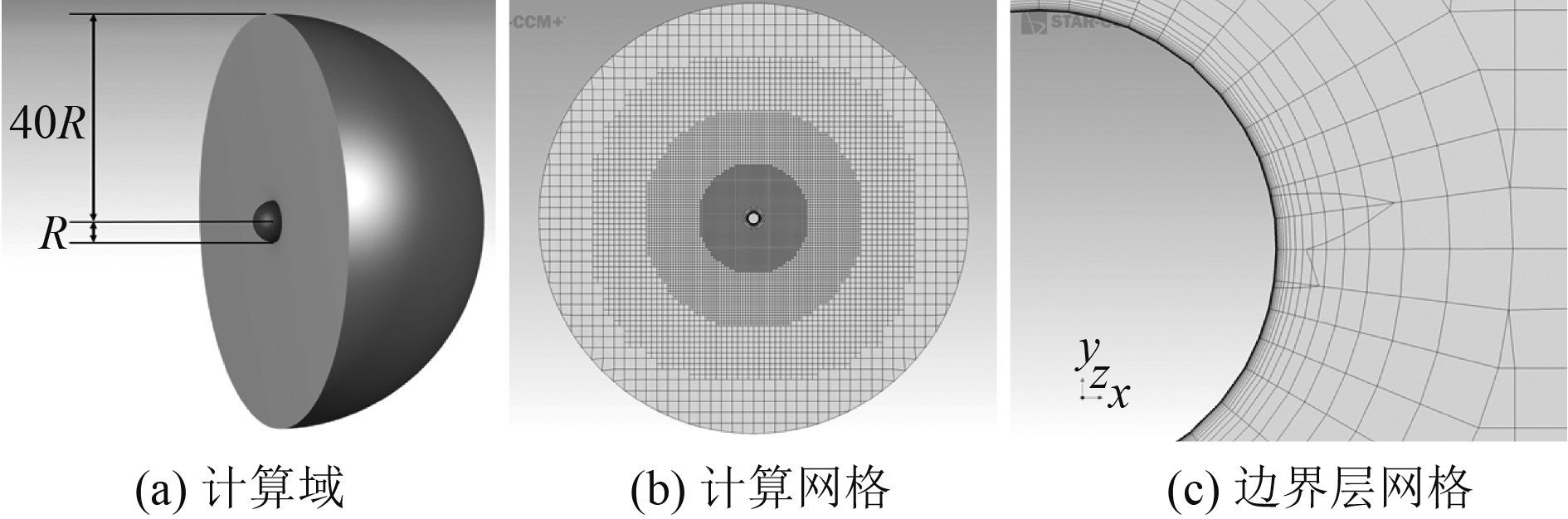
1.3 网格无关性验证选择圆球形区域作为计算域,上浮的圆球位于计算域中心位置,为了有足够区域让尾流充分发展,计算区域的半径选择为上浮圆球半径R的40倍,如图2(a)所示。以圆球为中心的逐层加密方式对计算域进行加密,且靠近壁面的流程变化更加剧烈,需对边界层网格进行加密,网格及边界层加密如图2(b)和图2(c)所示。
|
图 2 计算域及网格 Fig. 2 Computational domain and grid |
通过修改网格生成器中的网格基础尺寸改变流场网格,共生成了4组不同数量的网格(见表2),各组网格数量之比约为1∶2∶3∶4,基于对圆球上浮运动特性的研究,选择稳定上浮速度进行对比分析,根据不同网格数量下稳定上浮速度的差异大小来分析网格无关性。
|
|
表 2 不同网格划分方案下的计算结果 Tab.2 Calculation results of different meshing schemes |
可以看出,随着网格数量的增加,计算域离散更加精细,稳定上浮速度逐渐趋于一个稳定值。计算域网格的精细程度对计算结果存在影响,但是影响很小。为了保证计算精度同时节省计算资源和时间消耗,选择网格划分方案2对圆球的上浮运动开展研究。
2 结果与讨论 2.1 试验验证为验证数值仿真计算结果的有效性,针对计算工况开展模型试验。试验方案如图3(a)所示,在圆球底部固定一细线,细线另一端放置在两块电磁铁之间,电磁铁通电后互相牢牢吸紧,细线也被夹紧。将电磁铁和圆球一起放置池底,圆球同电磁铁一起静止水下,试验时切断电源电磁铁磁性消失,圆球底端细线松开,圆球便开始自由上浮运动。

|
图 3 模型试验方案 Fig. 3 Model test scheme |
试验模型如图3(b)所示,圆球外壳为亚克力,其内部采用3D打印支撑结构,支撑结构主要用于固定传感器和配重,运动传感器放置在球心位置,模型上下均配有压载铅块,调节模型使其重心和质量惯性矩符合要求。
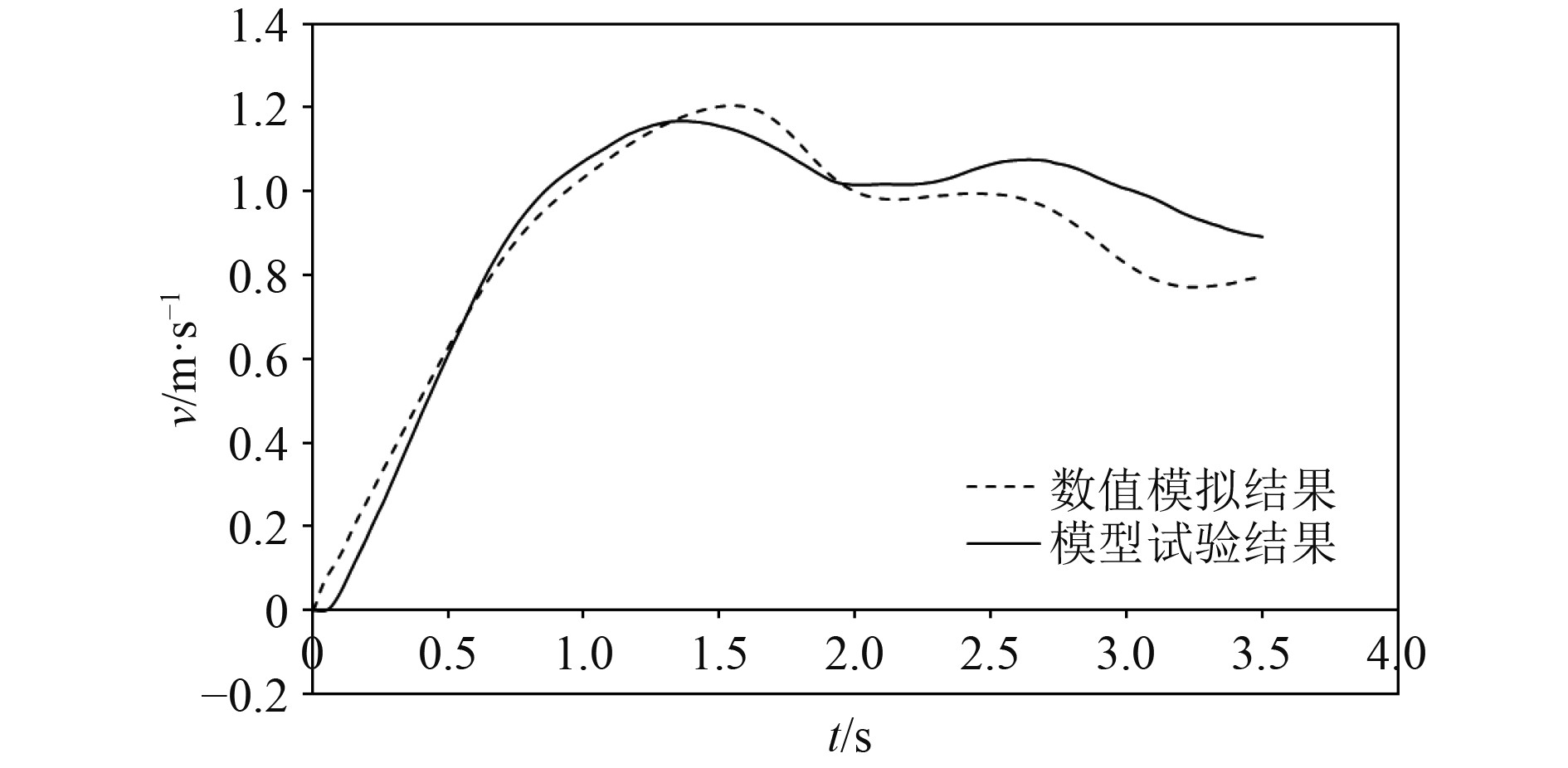
试验时运动传感器直接测量圆球上浮的加速度和速度,将速度对时间积分可得其位移。对比圆球上浮速度、加速度和位移时历曲线,如图4~图6所示。可以看出,数值模拟方法与模型试验得到的结果吻合较好,对比量的总体变化趋势基本一致,且能准确捕捉到上浮过程监测量变化的峰值[11],可以认为使用本文建立的数值模拟方法研究圆球上浮运动具有可靠性。

|
图 4 圆球上浮运动加速度时历对比曲线 Fig. 4 Comparison curve of the acceleration of the floating motion of the sphere |
|
图 5 圆球上浮运动速度时历对比曲线 Fig. 5 Comparison curve of the floating velocity of the sphere |

|
图 6 圆球上浮运动水深时历对比曲线 Fig. 6 Comparison curve of water depth in the floating motion of the sphere |
选取9个具有相同密度比m*,尺寸不同的均质圆球进行仿真计算,9个圆球中最小的半径R=0.004 m,其余8个圆球半径分别最小圆球半径的1.5~5倍。不同球体参数对比如表3所示,其大小直观对比如图7所示。
|
|
表 3 不同直径圆球参数 Tab.3 The parameters of baics with different diameters |

|
图 7 圆球大小对比 Fig. 7 Comparison of sphere sizes |
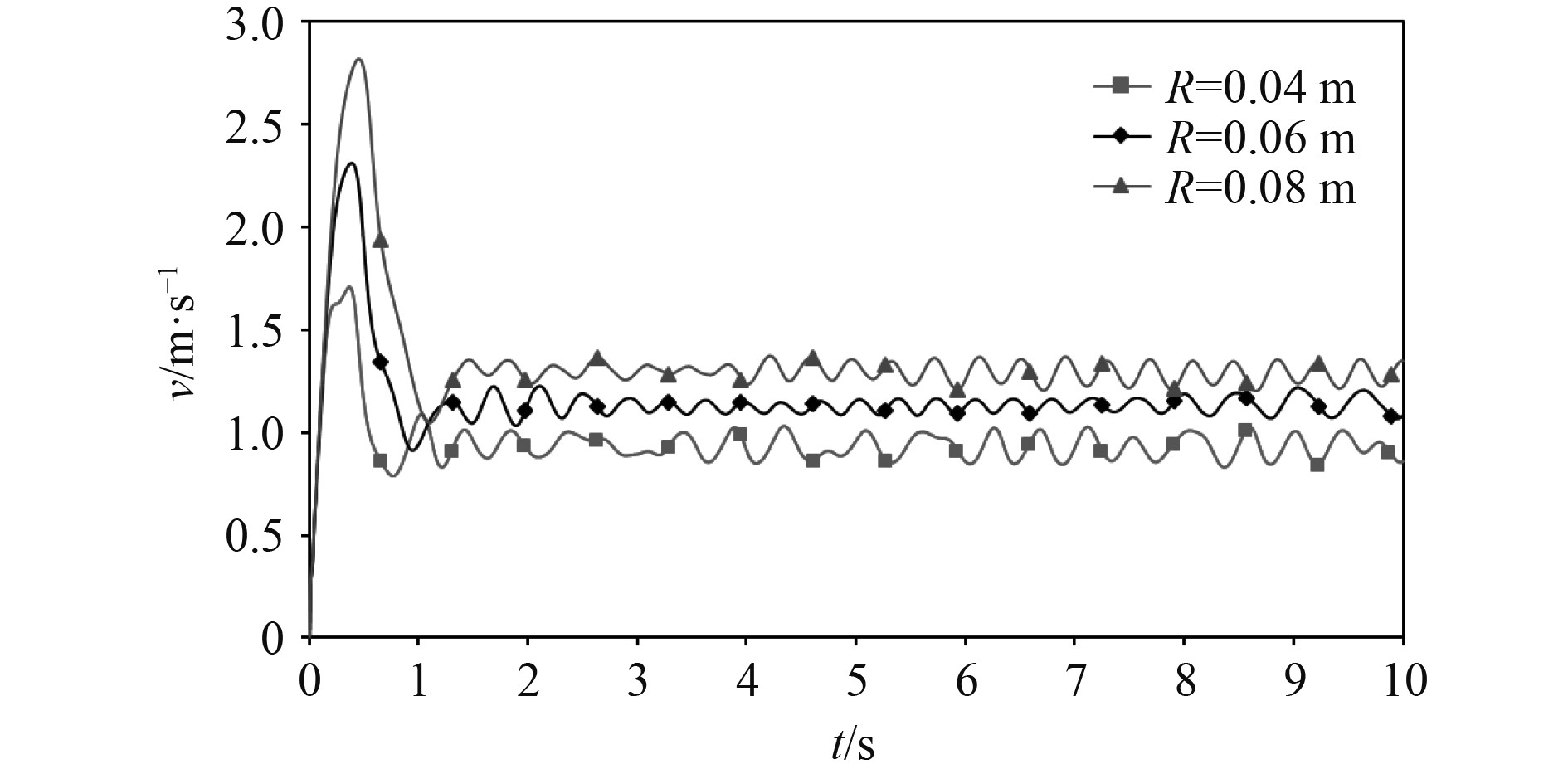
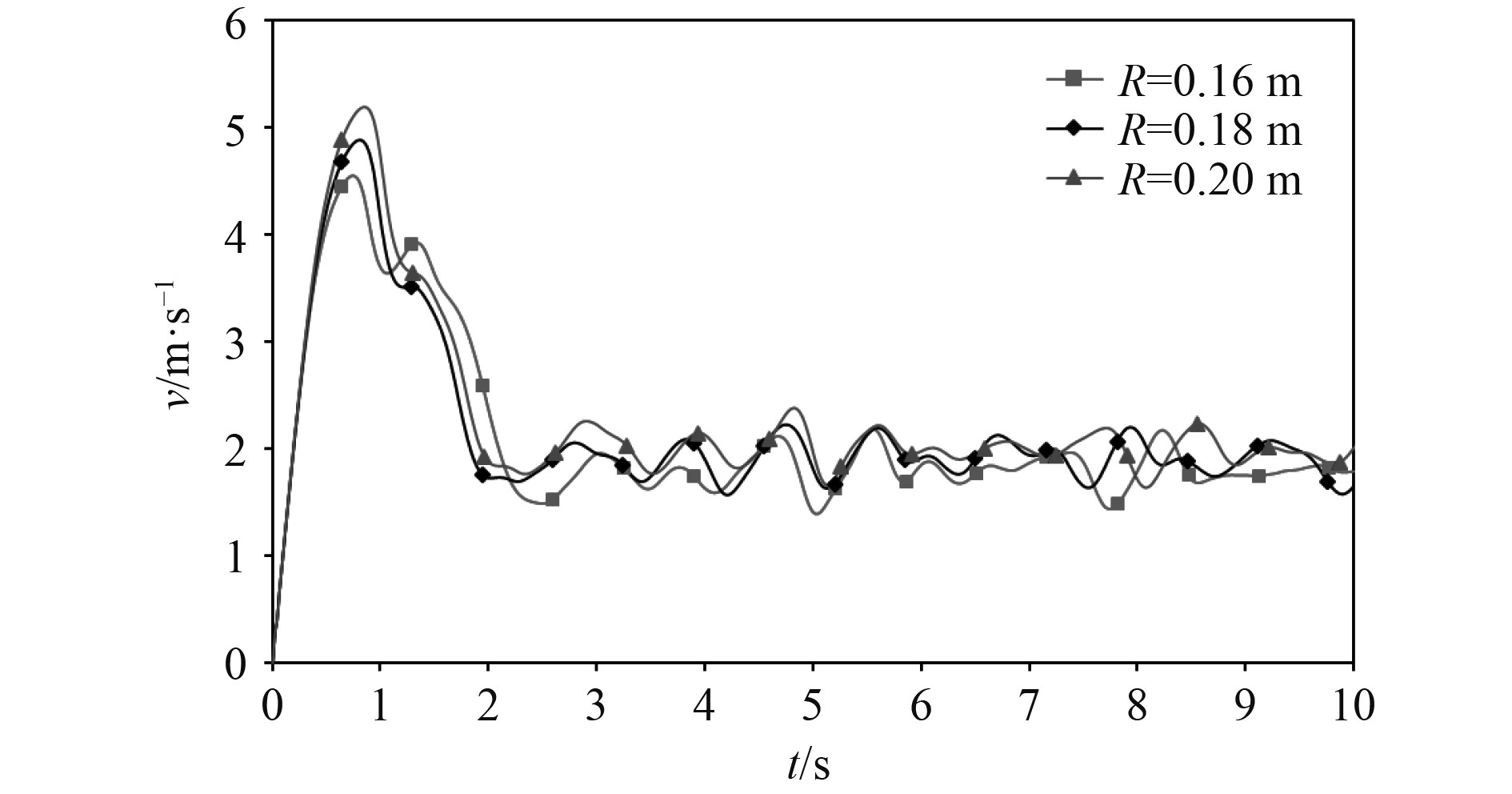
按照同样的数值模拟方法进行求解器设置和网格划分,开展计算与求解。计算过程中监测圆球上浮速度,待圆球上浮速度稳定后停止计算。不同直径的圆球上浮速度时历曲线如图8~图10所示。
|
图 8 R=0.04 m、0.06 m、0.08 m圆球上浮速度时历曲线 Fig. 8 Calendar curves of the floating velocity of R=0.04 m, 0.06 m, and 0.08 m spheres |

|
图 9 R=0. 1m、0.12 m、0.14 m圆球上浮速度时历曲线 Fig. 9 Calendar curves of the floating velocity of R=0.1 m, 0.12 m, and 0.14 m spheres |
|
图 10 R=0.16 m、0.18 m、0.2 m圆球上浮速度时历曲线 Fig. 10 Calendar curves of the floating velocity of the R=0.16 m, 0.18 m, and 0.2 m spheres |
可以看出:圆球在上浮时,上浮速度随着时间变化出现多个峰值;圆球在释放后有一个加速阶段,待上浮速度到达一个最大值后会出现一个减速阶段,速度减小到一定范围后会在某一速度上下波动,不会再发生较大的变化。根据上浮速度时历曲线确定稳定上浮阶段,并求取该阶段圆球上浮速度的平均值,该平均速度便是圆球上浮过程中的稳定速度[12],不同直径圆球稳定速度如图11所示。

|
图 11 不同直径圆球上浮稳定速度 Fig. 11 Stable floating velocity of balls with different diameters |
同时监测其阻力系数如表4所示。
|
|
表 4 不同直径圆球稳定后阻力系数情况 Tab.4 Resistance coefficients of balls with different diameters after stabilization |
可以看出,随着雷诺数增大,圆球的阻力系数都稳定在常数1左右,波动幅值较小,以常数1作为参考值,最大误差仅为4.7%,由此可以近似认为圆球在上浮运动中的阻力系数为常数1。
根据均质圆球的属性和流体的属性可以确定上浮稳定后圆球的阻力F为浮力和重力差值,即
| $ F = \frac{4}{3}{\text{π}} {R^3}\rho (1 - {m^*})g。$ | (3) |
进一步可知:
| $ \dfrac{F}{{\dfrac{1}{2}\rho {v^2}S}} = \frac{{\dfrac{4}{3}{\text{π}} {R^3}\rho (1 - {m^*})g}}{{\dfrac{1}{2}\rho {v^2}{\text{π}} {R^2}}} = {C_d} = 1。$ | (4) |
圆球(密度比0.2时)稳定速度为:
| $ v = \sqrt {\frac{{32g}}{{15}}R}。$ | (5) |
可得当2个满足相似条件的不同尺度圆球作上浮运动时,2个圆球的稳定速度之间存在关系,2个圆球的稳定速度之比应为
以半径为0.2 m的均质圆球作为研究对象,对密度比m*分别为0.3~0.9圆球的上浮运动进行模拟计算,不同密度比小球参数如表5所示。
|
|
表 5 不同密度比圆球的属性参数 Tab.5 Attribute parameters of spheres with different density ratios |
采用建立的数值模拟方法对7个尺寸相同密度比不同圆球的上浮运动进行计算模拟,计算结束后分析其稳定速度和无因次阻力系数如表6所示。
|
|
表 6 不同密度比圆球上浮的计算结果 Tab.6 Calculation results of balls with different density ratios |
可以看出,密度比m*增大后,圆球的上浮稳定速度会变小,其原因是圆球剩余浮力减小。单圆球阻力系数在常数1上下波动,波动幅值较小,最大误差为9.2%,考虑到圆球稳定上浮阶段的运动并非匀速运动,而是在某一速度上下波动,且各圆球上浮时雷诺数相差较大,因此可以认为不同密度比圆球稳定上浮阶段的阻力系数为常数1。
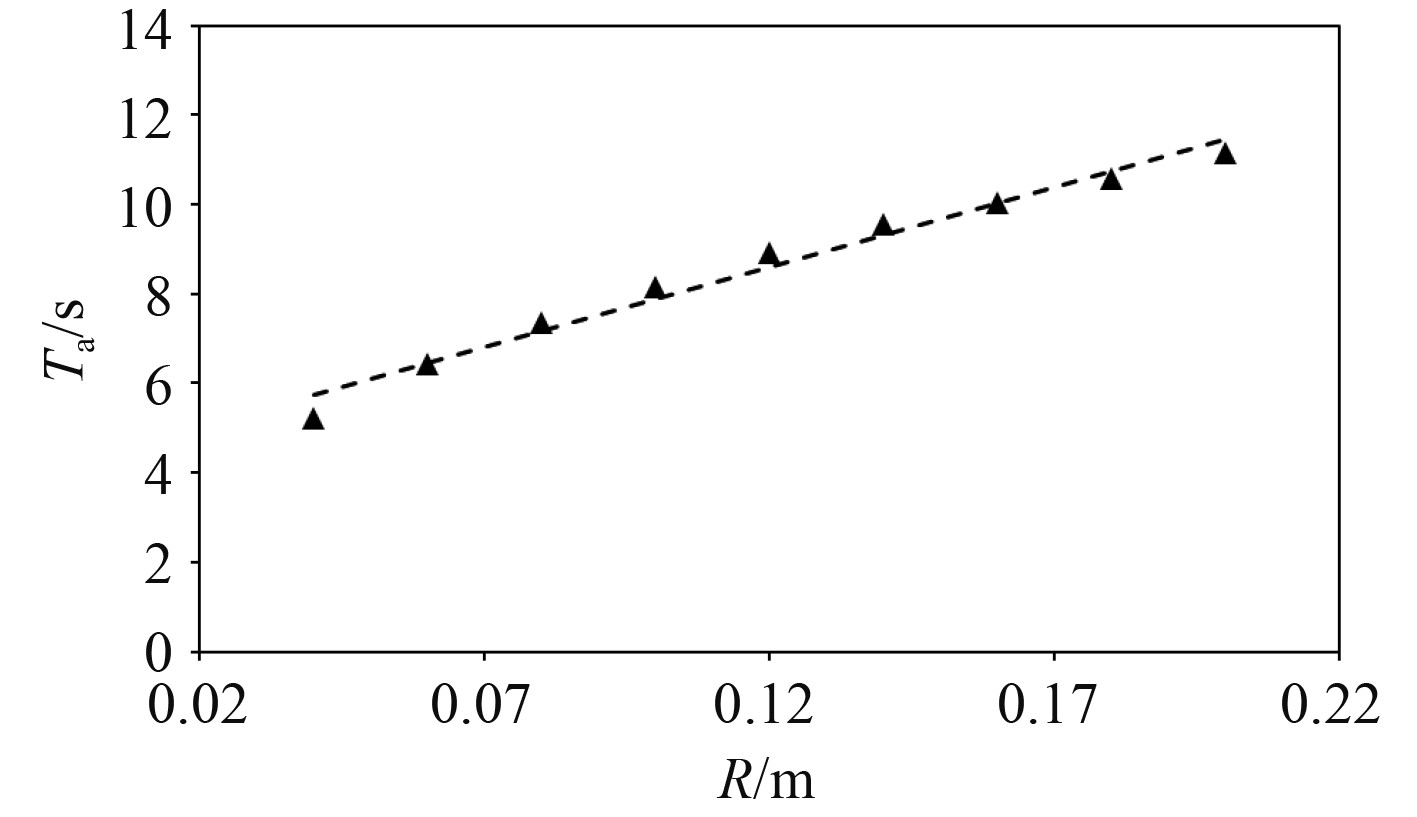
2.4 不同尺度圆球上浮总时间分析根据圆球上浮运动的特点,将圆球上浮距离确定为5 m时做截止,完成该段距离所需的上浮时间即为上浮总时间。不同直径圆球上浮总时间如图12所示。
|
图 12 不同直径圆球上浮总时间 Fig. 12 The total floating time of balls with different diameters |
可以看出,圆球的上浮总时间随尺度变化曲线一条光顺曲线,上浮总时间随着圆球尺度增大而增大,呈现出一定的相关性。分析圆球上浮运动的特点可知,上浮距离足够大时可以将圆球的上浮运动看作是速度大小与圆球上浮时稳定速度相等的匀速运动进行处理,据此可以推导出2个不同尺度圆球上浮总时间之间的关系,用
| $ \frac{{{t_{a1}}}}{{{t_{a2}}}} = {\raise0.7ex\hbox{${\frac{{{l_1}}}{{{v_1}}}}$} \mathord{\left/ {\vphantom {{\frac{{{l_1}}}{{{v_1}}}} {\frac{{{l_2}}}{{{v_2}}}}}}\right.} \lower0.7ex\hbox{${\frac{{{l_2}}}{{{v_2}}}}$}} = \frac{{{l_1}}}{{{l_2}}}\frac{{{v_2}}}{{{v_1}}} = \lambda \frac{1}{{\sqrt \lambda }} = \sqrt \lambda。$ | (6) |
当2个满足相似条件的圆球作上浮运动时,若2个圆球几何尺度之比为
以圆球状浮体作为研究对象,研究尺度、密度比对其上浮运动性能的影响。建立静水中圆球上浮运动数值模拟方法,通过模型试验对比测试结果,验证数值方法的可靠性。对多个满足相似条件的不同尺度圆球的上浮运动进行了模拟计算,以这些圆球上浮时的稳定速度和上浮总时间为指标,分析了圆球上浮运动性能的尺度相关性,得到如下结论:
1)圆球在稳定上浮阶段的阻力系数大致为常数1,不随雷诺数或圆球密度比的变化而发生变化;
2)当满足相似条件时,2个圆球在上浮时的稳定速度满足如下关系:若2个圆球的尺度之比为
3)当满足相似条件时,2个圆球的上浮总时间满足如下关系:若2个圆球的尺度之比为
| [1] |
孟晓宇, 田琬. 国外援潜救生装备系统发展现状[J]. 舰船科学技术, 2012, 34(10): 137-143. MENG X Y, TIAN W. Development status of foreign submarine rescue equipment system[J]. Ship Science and Technology, 2012, 34(10): 137-143. |
| [2] |
王世明, 吴爱平, 马利娜. 剖面探测浮标上浮运动研究[J]. 船舶工程, 2010, 32(6): 57-59+81. WANG S M, WU A P, M L. Study on the floating motion of profile detection buoy[J]. Naval Engineering, 2010, 32(6): 57-59+81. |
| [3] |
孙斌, 黄祥兵. 潜艇大型集体逃生舱上浮速度控制仿真计算[J]. 中国舰船研究, 2020, 15(S1): 42-49+60. SUN B, HUANG X B. Simulation calculation of floating speed control of large collective escape pod of submarine[J]. Chinese Journal of Ship Research, 2020, 15(S1): 42-49+60. |
| [4] |
黄祥兵, 黄兴玲, 董云飞. 潜艇集体逃生舱上浮水动力性能[J]. 海军工程大学学报, 2013, 25(3): 78−81. HUANG X B, HUANG X L, DONG Y F. Dynamic performance of floating water on the collective escape compartment of submarine[J]. Journal of Naval University of Engineering, 2013, 25(3): 78−81. |
| [5] |
黄祥兵, 董云飞, 黄兴玲. 减速翼对潜艇集体逃生舱最大上浮速度的影响研究[C]//中国国际船艇展暨高性能船学术报告会,中国造船工程学会,上海船舶工业行业协会,中国船舶工业行业协会, 上海, 中国, 2013: 1−5. HUANG X B, DONG Y F, HUANG X L. Study on the influence of deceleration wing on the maximum floating speed of the collective escape pod of submarine[C]//China International Boat Show & High Performance Ship Academic Presentation, China Shipbuilding Engineering Society, Shanghai Shipbuilding Industry Association, China Shipbuilding Industry Association, Shanghai, China, 2013: 1−5. |
| [6] |
唐鑫, 黄祥兵, 黄兴玲. 多尺度的潜艇集体逃生舱运动过程数值模拟[J]. 中国舰船研究, 2014, 9(4): 25−29. TANG X, HUANG X B, HUANG X L. Numerical simulation of the motion process of the collective escape capsule of submarines at multiple scales[J]. Chinese Journal of Ship Research, 2014, 9(4): 25−29. |
| [7] |
廖欢欢. 潜体应急上浮过程的水动力分析[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [8] |
李昆鹏, 魏成柱, 梁晓锋. 多面体网格在滑行艇数值仿真计算中的应用[J]. 舰船科学技术, 2020, 42(3): 33-37. LI K P, WEI C Z, LIANG X F. Application of polyhedral mesh in numerical simulation calculation of taxiing boat[J]. Ship Science and Technology, 2020, 42(3): 33-37. |
| [9] |
宋磊, 任再美, 陈林, 等. 一种船用推扭传感器设计及研究[J]. 舰船科学技术, 2020, 42(13): 82-85. SONG L, REN Z M, CHEN L, et al. Design and research of a kind of marine push-torsion sensor[J]. Ship Science and Technology, 2020, 42(13): 82-85. |
| [10] |
高勇, 裴金亮, 鲍文春. 一种考虑尾空泡影响的航行体流体动力数值仿真计算模型[J]. 船舶力学, 2018, 22(1): 31-37. GAO Y, PEI J l, BAO W c. A numerical simulation model of hydrodynamic forces considering the influence of tail cavitation[J]. Ship Mechanics, 2018, 22(1): 31-37. DOI:10.3969/j.issn.1007-7294.2018.01.004 |
| [11] |
覃梓真, 吴必军, 张芙铭. 不等截面串联双管浮体模型波浪能量转换特性研究[J]. 太阳能学报, 2022, 43(12): 476−481. QIN Z Z, WU B J, ZHANG F M. Study on wave energy conversion characteristics of unequal section tandem double-tube floating model[J]. Journal of Solar Energy, 2022, 43(12): 476−481. |
| [12] |
ZHANG L, KONG B, LIN S Y, et al. Research on the vibration-absorptive design of the independent escape capsule[J]. Ocean Engineering, 2021, 219: 108296.
|
 2024, Vol. 46
2024, Vol. 46
