2. 中国舰船研究院,北京 100101
2. China Ship Research and Development Academy, Beijing 100192, China
水下航行体低频声学特征传播问题是海洋工程中一个重要的基础性研究课题,尤其是针对远场低频特征的相关研究近年来逐渐成为了热点与难点。通过分析低频特征有利于掌握水下航行体的许多信息,对水下目标探测与鉴别起到积极作用。
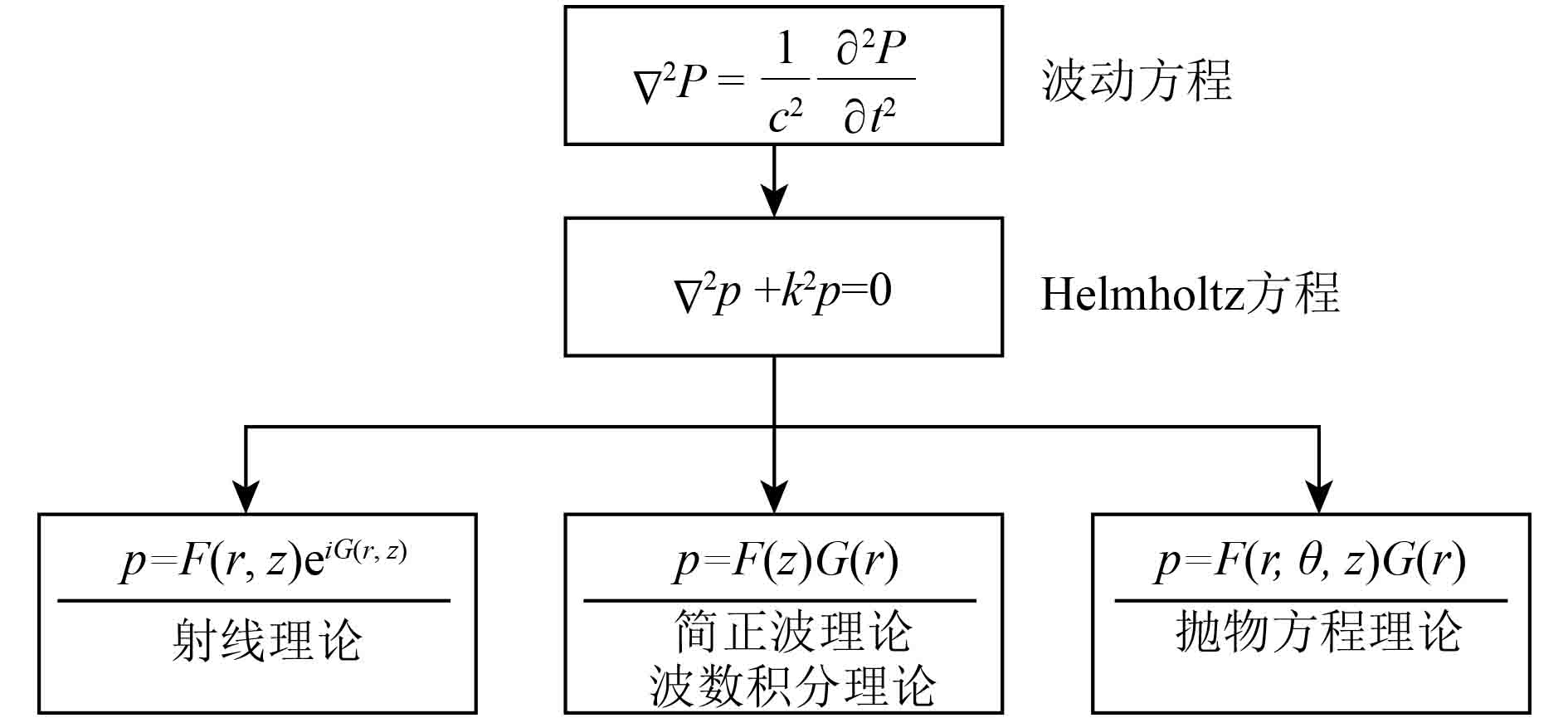
当前解决水下远距离声传播问题的主要理论可分为波动理论和射线理论,由此衍生出各种传播模型,例如简正波法、波数积分法、射线声学法以及抛物方程法等,如图1所示。但上述传播模型大多适用于特定条件下的二维声场计算问题,由于典型南海环境与声信道影响因素众多、影响关系复杂,内波活动频繁造成三维海洋效应显著,因此单一传播模型无法有效应对当前实际面临的三维水声环境,这也使得目前对海洋声特征产生、传播和演化规律依然掌握不清。因此,找到一种与典型南海环境相适应的传播计算模型是目前面临的又一难点。本文对当前使用的几种水下声传播计算方法进行综述,并展望了未来声传播计算方法的发展方向,希望对于改进当前典型南海环境下,目标特征低频远场声传播计算方法的不足产生积极意义。
|
图 1 水声传播仿真计算模型分类 Fig. 1 Classification of simulation calculation model for underwater sound propagation |
射线声学理论以几何近似的声场仿真方法为基础,该方法认为声场是通过声线传递能量,声线簇彼此叠加形成了所观测到的声场环境,因而更适用于高频声传播问题的求解。Jones[1]针对线性边界提出了海洋分层介质中声线折射轨迹计算方法。Lawrence[2]提出了一种改进射线方法,该方法适用于处理水平分层环境下的低频声传播问题,其计算结果精度与简正波方法计算结果精度相当。Hovem等[3 − 5]针对经典射线理论无法有效处理焦散区声场计算这一问题,引入稳相积分近似、频率修正、高斯声束等方法,解决了焦散区及低频声传播计算困难的问题。随着研究的深入,海洋声场研究逐渐由标量场扩展到矢量场。Harrison[6]给出了水平分层海洋介质环境下,声场的空间相关系数积分表达式垂直指向性解析表达式,杨娟等[7 − 9]研究了声场中声压和各向质点振速间的相关性,将射线声学理论推广到了矢量场。张仁和等[10 − 11]通过引入波束位移射线简正波理论与水平分段耦合处理方法,提出了改进的波束位移射线简正波理论,能够更好地适应浅海环境下的声场预报问题。
射线理论具有物理意义简单直观、易于处理复杂边界条件等优点,但在处理低频声传播问题和非水平分层介质问题时较为繁琐。同时,射线理论虽然也可求解三维海洋环境下的声传播问题,但在三维环境下需考虑声线水平方向的折射,增加了本征声线求解的难度,同时声线轨迹也更难进行描述。
1.2 简正波理论简正波理论是将声场表示成若干个离散的波导简正波模态叠加的声传播计算方法。早期Pekeris[12]将简正波理论用于解决海洋分层介质中的声传播问题,但该理论难以处理海洋环境随水平距离变化的声传播问题。A. D. Pierce等[13 − 14]基于速度势函数的波动方程提出了一种适用于海洋环境随水平距离变化的耦合简正波理论。Abawi[15]基于声压和质点位移的运动方程推导出一种仅有一个单独耦合矩阵的耦合简正波表达式,有效降低了耦合系数矩阵的复杂度。张仁和等 [16 − 18]引入单参数和双参数广义相积分近似方法改进了传统简正波理论基础,提出了能够有效解决深海声场会聚区问题的广义相积分(WKBZ)方法。考虑到浅海环境下非波导简正波的影响,张仁和等在广义相积分方法上加以改进,提出了一种适用于浅海环境的波束位移射线简正波理论。经数值仿真方法与实验测试数据对比验证,该理论与深海WKBZ的仿真结果均具备较高的准确性,这2种方法在提高计算效率的条件下,仍具有较高精度。
简正波理论目前仍是一种主流的计算方法。传统简正波方法以距离无关假设为基础,难以处理复杂海洋环境声传播问题。改进的绝热简正波理论将各号简正波间的能量交换作用项近似省略,显著降低了简正波方法的计算量,因此具备计算速度快的优点,但仅适用于海洋介质参数在水平方向缓慢变化的声传播问题[19]。耦合简正波理论则是考虑到海洋介质参数的水平非均匀性,通过引入各号简正波耦合系数,显著提高了在复杂海洋环境下,声传播问题求解的准确性和稳定性。因此耦合简正波理论描述的水下声场图像物理意义明确,具备计算精度高等优点,但耦合效应的存在使该方法的计算量很大,计算速度很慢,尤其是针对地形变化较为剧烈的环境,需减小步长以提高计算精度,从而计算效率大大降低[20]。
1.3 波数积分理论波数积分理论是一种利用数值方法直接对波动方程中的波数变量进行积分变换进而求解声传播规律的方法。Pekeris[12]首先将波数积分理论应用于水下声传播问题中。Gilbert等[21]根据广义格林函数方法,获得了单向波动方程的显式步进解。Seong[22]将波数积分与Galerkin边界元相结合,提出了SAFRAN模型,将波数积分理论应用于距离相关的海洋环境。Goh等[23]提出了基于全局多散射解或单散射步进解的谱超元方法,提供了一种准确求解波动方程双向解的方法并建立了适用于弹性液体分层的波导声传播问题声场计算软件 CORE。于晓林等[24]针对浅海负跃层环境下的声传播问题,将计算结果中的Airy函数进行归一化处理,得到一种无条件稳定的波数积分方法。
波数积分理论在求解过程中没有进行近似处理,全程利用数值积分方法进行求解,因而计算结果的准确性较好。但在求解深度分离方程时,会遇到计算不稳定问题,虽通过改进方法可保证算法在某些海洋环境下具备稳定的计算结果,但该理论在处理更复杂环境中,声传播问题时仍难以保证计算精度。
1.4 抛物方程理论抛物方程理论是基于抛物方程近似得到的一种声传播计算方法,其优点是处理声传播问题快速、灵活,能够有效处理海洋介质参数随距离变化的声传播问题。Tappert[25]在水声领域首先引入了该理论,基于分裂-步进傅里叶数值方法建立了早期抛物方程理论,但缺点是无法处理宽角声传播问题。Thomson等[26]在早期抛物方程理论加以改进,使该理论的适用范围扩展至宽角声传播问题。这种方法虽具有较高计算效率,但不能保证计算结果的稳定性[27]。Schultz等基于算子方法结合根式算子线性有理近似[28 − 30]和有限差分[31 − 32]数值方法改进了抛物方程方法,将抛物方程理论的适用范围扩展至大角度声传播问题,利用数值仿真证明了其稳定性。Collins[33 − 34]提出了一种弹性抛物方程法,该方法利用高阶Pade近似,能够将传播角扩大到接近90°。Küsel等[35]为解决海底边界变化较快的声传播问题,利用单向散射修正理论改进了抛物方程模型。Arnold等[36]将声传播数值计算方法推广至不规则流体-弹性体界面,包括处理不规则边界问题,确保数值数值求解稳定性等,并推进了三维数值计算模型的发展。Abawi等 [37 − 40]提出的简正波-抛物方程理论,该理论在沿深度方向上采用简正波理论进行求解,能够克服抛物方程理论不适用于高频、近场计算的缺陷,显著提高了二维声场计算效率,并将该方法应用范围扩展至三维声传播问题。
抛物方程理论针对海洋介质参数随距离变化以及三维变化的声传播问题具有较好适用性,但由于模型假设的限制,该理论难以处理近场、高频下的声传播问题。通过引入本地简正波,显著降低了抛物方程理论在垂向细化时的计算量,使得该理论适用于更复杂的海洋环境以及更高频率。
1.5 现有声传播方法优缺点学者们通过合理的假设和近似,建立了一系列声传播损失计算模型,用于研究海洋环境因素对水下声传播的影响机理。射线理论基于高频近似假设,能较好处理高频声传播问题,但难以有效解决焦散区及低频声传播问题。耦合简正波理论,在使用上不受频率限制,且物理图像清晰、精度高,各号简正波之间存在着相互耦合作用,但耦合系数的求解伴随着大量的计算,因而耦合简正波的计算效率不高。抛物方程理论是一种基于有限差分方法,对波动方程进行求解的理论,该方法具有很好的稳定性,适用于求解复杂海洋环境下低频远场声传播问题。但它的主要缺点是不适用于高频和大深度海洋环境声传播问题,在处理这类问题时,其时间复杂度和占用的内存空间会指数级增加,因而难以处理深海高频环境下的声传播问题。声传播理论模型都有各自的适用条件和适用范围,海洋作为一个与时间和空间有关的声传播介质,其复杂性导致难以准确研究海水中的声传播规律。目前,研究人员通过提高声传播计算方法的时间复杂度、计算准确度等方面提高现有理论的问题求解能力;另一方面,借助高性能的硬件设备,实现水声传播损失的并行计算方法[41]。
2 海洋环境对声传播损失计算影响研究综述 2.1 复杂海洋地形随着深海水下目标探测及远程脉冲声传播在水声通信中的应用,深海声传播的研究受到高度重视。Spiesberger[42]发现当接收器位于声道轴时,随着声源远离声道轴深度,传播损失在迅速增加。随着深海声学理论的发展及人们认识的加深,国内外学者开始探究各类复杂海洋环境下的声传播规律。深海中的地形水平变化与深海声道影响结合,会出现一些特殊的声传播现象。Chapman等[43]分析了不同深度的爆炸声源围绕Dickins山的声传播现象,研究了声波的到达路径及海底山的反射机制,发现海底山的坡面存在反射遮挡效应,与平坦海底地形相比声波在经过海山时,传播损失增大了20~30 dB。Dosso等[44]在大陆坡海域设计实验,测量结果表面声波沿下坡传播时,传播损失相较于平坦海底最大可减少15 dB,验证了斜坡增强效应,并基于射线理论对其进行解释说明。Tappert等[45]发现当声源固定在大陆架斜坡的浅海海底时,声波会先沿着斜坡坡面进行传播,传播至深海声道轴深度附近后,会与斜坡分离并沿着深海声道轴远距离传播,最远可达4 000 km以上,并用“泥流效应”解释了现象形成机理和稳健性。Qin等[46]在实验中发现接收的信号能量多集中在声道轴深度附近的现象。二维条件下的深海海底山声传播问题与海底斜坡声传播问题类似,Li等[47]研究分析了深海海底山声传播规律,证明了海底山坡面存在反射增强效应和遮挡效应。目前,研究重点多为大陆架斜坡和海底山环境下的声传播问题,而对深海低频声波与海洋耦合机理下的声传播研究较少。
2.2 三维海洋环境实际海洋环境是关于海洋边界和海水介质的三维环境。在研究声传播问题时,声波在海水中的水平折射、声场能量耦合与声场衍射等三维声场效应无法忽略。二维声场计算模型无法满足实际三维传播问题的需求,因此,便有许多学者开始关注三维海洋环境中水声传播问题。Heaney等[48]在佛罗里达东海岸进行水下声实验,清楚观测到深海变化引起的方位偏移和声线水平折射导致的水平多途三维声传播现象。Lee[49]首先根据抛物方程理论建立了For3D声场计算模型,该模型缺点是对海底边界考虑并不充分,在声场计算过程中无法满足能量守恒的要求。Brooke等[50]为解决匹配场处理的问题,建立了基于抛物方程方法的PECan声场计算模型,该模型是一种N×2D/3D声传播模型。Sturm[51]为解决三维高斯型海湾环境下脉冲声传播问题,提出了一种三维浅海波导下宽带脉冲声传播的数值解法。彭朝晖等[39]在耦合简正波-抛物方程理论基础上,发展并提出了三维耦合简正波-抛物方程模型CMPE3D。这种理论具有计算速度快、精度高的优点,同等精度下其计算速度可有效提高约100倍。Lin等[52 − 53]改进了三维柱坐标抛物方程模型,提高了其计算精度。钱治文等[54]为提高中低频段的计算精度和浅海环境下适应性,提出了一种三维浅海波导下的有限元-抛物方程法。
为验证声传播损失计算模型在三维海洋环境下的收敛性和稳健性,Chiu等[55]利用三维海洋环境抛物方程计算模型,对实测的三维海洋环境下声传播损失数据进行分析处理,验证了水下声传播具有三维效应。Lee等[56]为评估模型计算结果是能否满足精度的要求,提出了三维抛物方程模型的预测-校正理论。Sturm等[57]针对楔形海底地形开展实验验证,与三维抛物方程方法计算结果进行对比,验证了声传播模型计算结果的可靠性和准确性。
3 声传播损失计算方法的发展趋势 3.1 低频声传播特性及物理成因研究影响水声传播的主要海洋环境因素及物理原因,揭示低频声波与海洋耦合机理,特别是中尺度、大尺度直至海盆级区域范围内声波传播与海洋中尺度现象等动力学过程及复杂海底的耦合作用[58]。针对水声探测需求,重点研究典型的深海完全声道和非完全声道环境下,存在复杂海底地形和时空变化海洋环境条件下的低频声传播特性;针对深海远程信息传输信号检测需求,研究数百千米至上千千米尺度上的深海声场随距离及环境的演变规律。了解海盆尺度上的环境噪声演变趋势,探索利用低频、远距离、宽带声传播数据来理解和认识不同尺度海洋学现象的基本演变规律。
3.2 复杂海洋环境下声场时-空-频相干特性及机理在声传播机理认识的基础上,研究和掌握海洋动力学过程影响低频声信号空时相关性和特征稳健性的物理机制[59]。研究确定性海洋环境条件下声场的时间相关特性以及声场的垂直相关、水平纵向相关特性,重点关注低频远程传播到达结构、信号起伏特性及其与收发距离和频率的关系,掌握复杂海洋环境声场的时-空-频变化特征规律,揭示海深会聚区和声影区声场空间频率干涉特征的主要控制因素。探索在深海海域利用声场的时空-频相干特性提高阵列信号处理增益的方法,并通过声学实验来验证方法的有效性与适用性,研究在直达声区、会聚区和声影区内不同声呐系统的探测性能,为深海复杂环境水声目标探测方法研究奠定基础。
3.3 高纬度海域及两极冰区环境下的声场模型研究研究高纬度海域及两极区域表面声道与海面存在冰盖环境下,水下远程传播规律及冰下噪声场特性[60],发展基于无人平台的冰下声学环境实时监测技术及基于声学层析的北冰洋环流实时监测方法[61],为高纬度海域水声环境保障奠定技术基础。同时,发展适合于高纬度海域的水下探测技术与水声通信技术,提高我国在极地海域的海洋声学认知水平及保障应用能力。
4 结 语对于水下大型航行体的远场低频特征声传播问题,国内外诸多学者相继提出了射线理论、简正波理论等声传播损失计算方法。但实际海洋环境是复杂多变的,如海底地形与深海声道结合产生的遮挡效应和斜坡增强效应、声波在斜坡和海沟等复杂海底环境下传播产生的三维水平折射效应等。随着研究的深入,声场计算模型也从二维过渡至三维,研究学者相继对现有理论加以改进,建立了适用于三维水平折射现象、深海海洋混响等传播损失计算模型,提高了声传播计算方法在复杂海洋环境下的适用性和鲁棒性。但对声场计算模型的研究多集中在大陆架斜坡和海底山海域,在深海低频声波与海洋耦合机理,特别是中尺度、大尺度直至海盆级区域范围内,声波传播与海洋中尺度现象等动力学过程及复杂海面与海底的耦合作用方面有待深入。
综上所述,水下航行体低频声传播损失计算方法历经数十年发展在理论和试验验证方面都取得了长足进步,但在处理低频以及复杂海洋环境下的声传播问题仍存在一些不足之处。未来,水下航行体声传播损失研究将更加聚焦于低频声传播特性、声场时-空-频相干特性以及两极冰区环境下的声传播规律等问题,进一步提高传播损失计算方法在复杂海洋环境下的准确性和稳定性是重点研究方向。
| [1] |
JONES D S. High-frequency refraction and diffraction in general media[J]. Philosophical Transactions of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1963, 255(1058): 341-387. DOI:10.1098/rsta.1963.0007 |
| [2] |
LAWRENCE M W. Ray theory modeling applied to low-frequency acoustic interaction with horizontally stratified ocean bottoms[J]. Journal of the Acoustical Society of America, 1985, 78(2): 649-658. DOI:10.1121/1.392433 |
| [3] |
HOVEM J M . Ray trace modeling of underwater sound propagation[J]. Ray Trace Modeling, 2013: 39−49.
|
| [4] |
FOREMAN T L. An exact ray theoretical formulation of the Helmholtz equation[J]. Journal of the Acoustical Society of America, 1989, 86(1): 234-246. DOI:10.1121/1.398339 |
| [5] |
ITURBE I , ROUX P , NICOLAS B , et al. Shallow water acoustic tomography performed from a double beamforming algorithm: simulation results[J]. IEEE Journal of Oceanic Engineering, 2009, 34(2): 140-149.
|
| [6] |
HARRISON C H. Formulas for ambient noise level and coherence[J]. Journal of the Acoustical Society of America, 1996, 99(4): 2055-2066. DOI:10.1121/1.415392 |
| [7] |
杨娟, 惠俊英, 王德俊, 等. 低频矢量声场建模及其应用研究[J]. 声学技术, 2006, 25(1): 16-21. |
| [8] |
韩晶, 黄建国, 曹海旺. 海洋信道仿真软件HJRAY及其在水声通信中的应用[J]. 系统仿真学报, 2007, 019(1): 35-37,97. |
| [9] |
任超, 黄益旺, 夏峙. 宽频带海洋环境噪声矢量场空间相关特性建模[J]. 物理学报, 2022, 71(2): 131-141. |
| [10] |
张仁和, 李风华. 浅海声传播的波束位移射线简正波理论[J]. 中国科学:A辑, 1999, 29(3): 241-251. |
| [11] |
鄢锦, 张仁和. 海面波浪对空气中声源激发的浅海声场的影响[J]. 自然科学进展, 2003, 13(3): 21-25. |
| [12] |
PEKERIS C L . Theory of propagation of explosive sound in shallow water[J]. Geological Society of America Memoirs, 1948, 27: 1−116
|
| [13] |
PIERCE A D. Extension of the method of normal modes to sound propagation in an almost‐stratified medium[J]. The Journal of the Acoustical Society of America, 1965, 37(1): 19-27. DOI:10.1121/1.1909303 |
| [14] |
RUTHERFORD S R, HAWKER K E. Consistent coupled mode theory of sound propagation for a class of nonseparable problems[J]. Journal of the Acoustical Society of America, 1981, 70(2): 554-564. DOI:10.1121/1.386744 |
| [15] |
ABAWI A T. An energy-conserving one-way coupled mode propagation model[J]. Journal of the Acoustical Society of America, 2002, 111(1): 160-167. DOI:10.1121/1.1419088 |
| [16] |
张仁和, 何怡, 刘红. 水平不变海洋声道中的WKBZ简正波方法[J]. 声学学报, 1994, 19(1): 1-12. |
| [17] |
YAN J, ZHANG R. The WKBZ mode approach to sound propagation in two-axis underwater channel[J]. Progress in Natural Science (English Version), 1997, 22: 209-216. |
| [18] | ZHOUS H, ZHANG R H, GONG M, et al. Applications of WKBZ mode approach to matched-field localization in deep water channels[J]. Progress in Natural Science, 1997, (3): 280−286. |
| [19] |
NAGL A, ÜBERALL H, HAUG A J, et al. Adiabatic mode theory of underwater sound propagation in a range‐dependent environment[J]. Journal of the Acoustical Society of America, 1978, 63(3): 739-749. DOI:10.1121/1.381782 |
| [20] |
KNOBLES D P, STOTTS S A, KOCH R A. Low frequency coupled mode sound propagation over a continental shelf[J]. Journal of the Acoustical Society of America, 2003, 113(2): 781-787. DOI:10.1121/1.1534847 |
| [21] |
GILBERT K E, EVANS R B. A Green’s function method for one-way wave propagation in a range-dependent ocean environment[M]//Ocean Seismo-Acoustics: Low-Frequency Underwater Acoustics. Boston, MA: Springer US, 1986: 21−28.
|
| [22] |
SCHMIDT H. Numerical modeling in ocean seismo-acoustics[C]//OCEANS 91 Proceedings. IEEE, 1991, 1: 84−92.
|
| [23] |
GOH J T, SCHMIDT H. A hybrid coupled wave‐number integration approach to range‐dependent seismoacoustic modeling[J]. Journal of the Acoustical Society of America, 1996, 100(3): 1409-1420. DOI:10.1121/1.415988 |
| [24] |
于晓林, 许伟杰, 杨春梅, 等. 一种可稳定计算负跃层浅海环境下声场的波数积分方法[J]. 声学技术, 2022, 41(4): 497-504. |
| [25] |
TAPPERT F D . The parabolic approximation method[J]. Wave Propagation and Underwater Acoustics, 1977, 70: 224−287.
|
| [26] |
THOMSON D J, CHAPMAN N R. A wide‐angle split‐step algorithm for the parabolic equation[J]. Journal of the Acoustical Society of America, 1983, 74(6): 1848-1854. DOI:10.1121/1.390272 |
| [27] |
COLLINS M D, CEDERBERG R J, KING D B, et al. Comparison of algorithms for solving parabolic wave equations[J]. The Journal of the Acoustical Society of America, 1996, 100(1): 178-182. DOI:10.1121/1.415921 |
| [28] |
SCHULTZ P. Fundamentals of geophysical data processing[J]. Acoustics Speech & Signal Processing IEEE Transactions on, 1979, 27(5): 564-565. |
| [29] |
BOTSEAS G, LEE D, GILBERT K E. IFD (Implicit Finite-Difference). Wide Angle Capability, 1983: 1−25.
|
| [30] |
Greene, Robert R. The rational approximation to the acoustic wave equation with bottom interaction[J]. Journal of The Acoustical Society of America, 1984, 76(6): 1764-1773. DOI:10.1121/1.391561 |
| [31] |
LEE Ding. Finite‐difference solution to the parabolic wave equation[J]. Journal of the Acoustical Society of America, 1981, 70(3): 795-800. DOI:10.1121/1.386918 |
| [32] |
DING L , MCDANIEL S T . A finite-difference treatment of interface conditions for the parabolic wave equation: The horizontal interface[J]. Journal of the Acoustical Society of America, 1982, 73(5): 1441-1447.
|
| [33] |
COLLINS M D. A higher-order parabolic equation for wave propagation in an ocean overlying an elastic bottom[J]. Journal of the Acoustical Society of America, 1989, 86(4): 1459-1464. DOI:10.1121/1.398706 |
| [34] |
COLLINS M D . Higher-order and elastic parabolic equations for wave propagation in the ocean[LR], US Government Technology Report, 1990.
|
| [35] |
KÜSEL E T, SIEGMANN W L, COLLINS M D. A single-scattering correction for large contrasts in elastic layers[J]. Journal of the Acoustical Society of America, 2007, 121(2): 808-813. DOI:10.1121/1.2404627 |
| [36] |
ARNOLD A , EHRHARDT M . Discrete transparent boundary conditions for wide angle parabolic equations in underwater acoustics[J]. Journal of Computational Physics, 2000, 145(2): 611-638.
|
| [37] |
ABAWI A T, KUPERMAN W A, COLLINS M D. The coupled mode parabolic equation[J]. Journal of the Acoustical Society of America, 1997, 102(1): 233-238. DOI:10.1121/1.419819 |
| [38] |
彭朝晖, 李风华. 基于WKBZ理论的耦合简正波-抛物方程理论[J]. 中国科学(A辑), 2001(2): 165-172. |
| [39] |
彭朝晖, 张仁和. 三维耦合简正波-抛物方程理论及算法研究[J]. 声学学报, 2005, 30(2): 97-102. |
| [40] |
秦继兴, KATSNELSON Boris, 彭朝晖, 等. 三维绝热简正波-抛物方程理论及应用[J]. 物理学报, 2016, 65(3): 144-152. |
| [41] |
CASTOR K, STURM F. Investigation of 3D acoustical effects using a multiprocessing parabolic equation based algorithm[J]. Journal of Computational Acoustics, 2008, 16(2): 137-162. DOI:10.1142/S0218396X08003543 |
| [42] |
SPIESBERGER J L. Acoustic identification of a single transmission at 3115 km from a bottom-mounted source at Kauai[J]. Journal of the Acoustical Society of America, 2004, 115(4): 1497-1504. DOI:10.1121/1.1650014 |
| [43] |
CHAPMAN N R, EBBESON G R. Acoustic shadowing by an isolated seamount[J]. Journal of the Acoustical Society of America, 1983, 73(6): 1979-1984. DOI:10.1121/1.389562 |
| [44] |
DOSSO S E, CHAPMAN N R. Measurement and modeling of downslope acoustic propagation loss over a continental slope[J]. Journal of the Acoustical Society of America, 1987, 81(2): 258-268. DOI:10.1121/1.394945 |
| [45] |
TAPPERT F D, SPIESBERGER J L, WOLFSON M A. Study of a novel range-dependent propagation effect with application to the axial injection of signals from the Kaneohe source[J]. Journal of the Acoustical Society of America, 2002, 111(2): 757-762. DOI:10.1121/1.1432983 |
| [46] |
QIN J X, ZHANG R H, LUO W Y, et al. Sound propagation from the shelfbreak to deep water[J]. Science China Physics, Mechanics & Astronomy, 2014, 57: 1031-1037.
|
| [47] |
LI W, LI Z L, ZHANG R H, et al. The effects of seamounts on sound propagation in deep water[J]. Chinese Physics Letters, 2015, 32(6): 064302. DOI:10.1088/0256-307X/32/6/064302 |
| [48] |
HEANEY K D, CAMPBELL R L. Three-dimensional parabolic equation modeling of mesoscale eddy deflection[J]. Journal of the Acoustical Society of America, 2016, 139(2): 918-926. DOI:10.1121/1.4942112 |
| [49] |
LEE D, BOTSEAS G, SIEGMANN W L. Examination of three‐dimensional effects using a propagation model with azimuth‐coupling capability (FOR3D)[J]. Journal of the Acoustical Society of America, 1992, 91(6): 3192-3202. DOI:10.1121/1.402856 |
| [50] |
BROOKE G H, THOMSON D J, EBBESON G R. PECan: A Canadian parabolic equation model for underwater sound propagation[J]. Journal of Computational Acoustics, 2001, 9(1): 69-100. DOI:10.1142/S0218396X01000425 |
| [51] |
STURM F. Numerical study of broadband sound pulse propagation in three-dimensional oceanic waveguides[J]. Journal of the Acoustical Society of America, 2005, 117(3): 1058-1079. DOI:10.1121/1.1855791 |
| [52] |
LIN Y T, COLLIS J M, DUDA T F. A three-dimensional parabolic equation model of sound propagation using higher-order operator splitting and Padé approximants[J]. Journal of the Acoustical Society of America, 2012, 132(5): EL364-EL370. DOI:10.1121/1.4754421 |
| [53] |
STURM F. Leading-order cross term correction of three-dimensional parabolic equation models[J]. Journal of the Acoustical Society of America, 2016, 139(1): 263-270. DOI:10.1121/1.4939735 |
| [54] |
钱治文, 商德江, 孙启航, 等. 三维浅海下弹性结构声辐射预报的有限元-抛物方程法[J]. 物理学报, 2019, 68(2): 145-158. |
| [55] |
CHIU Y S, CHANG Y Y, HSIEH L W, et al. Three-dimensional acoustics effects in the ASIAEX SCS experiment[J]. Journal of Computational Acoustics, 2009, 17(1): 11-27. DOI:10.1142/S0218396X09003835 |
| [56] |
LEE D, CHEN C F. A new procedure to achieve required accuracy in computational ocean acoustics: theoretical development[J]. Journal of Computational Acoustics, 2012, 20(4): 1250012. DOI:10.1142/S0218396X12500129 |
| [57] |
STURM F, KORAKAS A. Comparisons of laboratory scale measurements of three-dimensional acoustic propagation with solutions by a parabolic equation model[J]. Journal of the Acoustical Society of America, 2013, 133(1): 108-118. DOI:10.1121/1.4770252 |
| [58] |
LI S, YUAN S, LIU S, et al. Characteristics of low-frequency acoustic wave propagation in ice-covered shallow water environment[J]. Applied Sciences, 2021, 11(17): 7815. DOI:10.3390/app11177815 |
| [59] |
李整林, 余炎欣. 深海声学研究进展[J]. 科学通报, 2022, 67(2): 125-134. |
| [60] |
殷敬伟, 马丁一, 张宇翔, 等. 极地海冰声波导建模综述[J]. 物理学报, 2022, 71(8): 162-172. |
| [61] |
李启虎, 黄海宁, 尹力, 等. 北极水声学研究的新进展和新动向[J]. 声学学报, 2018, 43(4). DOI:10.15949/j.cnki.0371-0025.2018.04.002 |
 2024, Vol. 46
2024, Vol. 46

