传统能源在船舶应用上有很多限制,特别是会造成污染且传统能源不可再生,因而新能源船舶是未来船舶的重要发展方向。新能源船舶同样也是采用电机和螺旋桨推进,使用舵来控制方向,这样就形成了依靠2个控制量来控制船舶的3个方向运动,即属于欠驱动控制系统问题。新能源船舶未来的应用场景倾向于环境测量、海洋资源探测等,为了实现这一目的,未来将会发展更为先进的无人新能源船舶。
目前国内研究较多的是无人艇路径跟踪的自抗扰控制方法,从研究对象上看,对新能源船舶的研究较少,在自抗扰控制技术上,20世纪90年代韩京清[1]第一次提出了自抗扰理论,通过测量外部扰动来实现系统控制的动态补偿,并设计了多种自抗扰控制器,具有非常不错的鲁棒性和控制效果。张荣彬[2]针对船用汽轮机提出了一种线性自抗扰控制方法,并提出了一种LADRC转速控制器。乌云嘎[3]对自主水下航行器的自抗扰控制方法进行了研究,实现了对扰动的测量及在线补偿。无人新能源船舶在运动特性以及实践中具有一些不同的特点,因而本文针对无人新能源船舶路径跟踪以及自抗扰控制方法进行研究,为无人新能源船舶的控制提供更多借鉴。
1 新能源船舶运动分析 1.1 新能源船舶受力分析为研究新能源船舶路径跟踪自抗扰控制方法,首先需要对新能源船舶在海上的运动情况进行分析。路径跟踪中考虑新能源船舶在海上有3个自由度的平面运动,分别是横荡、纵荡以及首摇。新能源船舶作为刚体,可以认为外在的所有力作用在船舶上时等同于作用在A点,若为力矩,则作用在对应的坐标轴上。新能源船舶受力分析如图1所示。

|
图 1 新能源船舶受力分析 Fig. 1 Force analysis of new energy ships |
建立新能源船舶运动方程:
| $ \left\{\begin{array}{l}{N}_{H}+{N}_{J}+{N}_{K}=({I}_{LL}+{J}_{LL}),\\ {M}_{H}+{M}_{J}+{M}_{K}=({m}+{{m}}_{y}){\dot{v}}_{r}+({m}+{{m}}_{x}){\dot{u}}_{r}r,\\ {Q}_{H}+{Q}_{J}+{Q}_{K}=({m}+{{m}}_{x}){\dot{u}}_{r}-({m}+{{m}}_{y}){\dot{v}}_{r}r。\end{array}\right. $ |
其中:H、J、K分别为螺旋桨、方向舵以及外界条件;N、M分别为船舶在x方向和y方向所受的外力;Q为所受的力矩;ur和vr分别为x方向和y方向船舶对水的速度;m为船舶质量;mx和my分别为船舶质量在x方向和y方向的分量;r为船舶首向角速度;JLL为附加惯性力矩;ILL为绕竖直方向的惯性矩。
惯性距ILL满足下列表达式:
| $ {I}_{LL}=\left[ \begin{array}{ccc} m_{11} & 0 &0 \\ 0& m_{22}&0 \\ 0& 0 & m_{33} \end{array} \right]=\left[ \begin{array}{ccc} m+{\lambda}_{11} &0 &0 \\ 0& m+{\lambda}_{22} &0 \\ 0& 0 & m+{\lambda}_{33} \end{array} \right] \text{。} $ |
在对新能源船舶路径跟踪时需要时刻获取当前新能源船舶的位置误差,位置误差可以通过GPS反馈来获取,当获取位置误差后,使用李雅普诺夫函数对船舶路径跟踪误差进行表达,规定李雅普诺夫函数:
| $ V = \frac{1}{2}(X_e^2 + Y_e^2 + Z_e^2) \text{。} $ |
其中,Xe、Ye、Ze为新能源船舶在X、Y、Z方向上的误差分量,可以获取新能源船舶路径跟踪误差方程:
| $\left\{ \begin{gathered} {{\dot x_e}} = {y_e}{d_1}(s) \dot s + W\cos {\theta _e}\cos {\phi _e} - {z_e}{d_2}(s)\dot s,\\ {{\dot y_e}} = W\cos {\theta _e}\sin {\phi _e} - {x_e}{d_2}(s)\dot s + {z_e}{d_1}(s)\dot s,\\ {{\dot z_e}} = W\sin {\theta _e}\sin {\phi _e} + {x_e}{d_2}(s)\dot s - {y_e}{d_1}(s)\dot s。\\ \end{gathered} \right. $ |
其中,s为新能源船舶的设计速度,通过对李雅普诺夫函数进行求导并代入到路径跟踪误差方程中进行求解,获取新能源船舶速度表达式为:
| $ \dot s = W\cos {\theta _e}\cos {\phi _e} + {X_e}{K_s} \text{。} $ |
其中,Ks为大于0的常数。
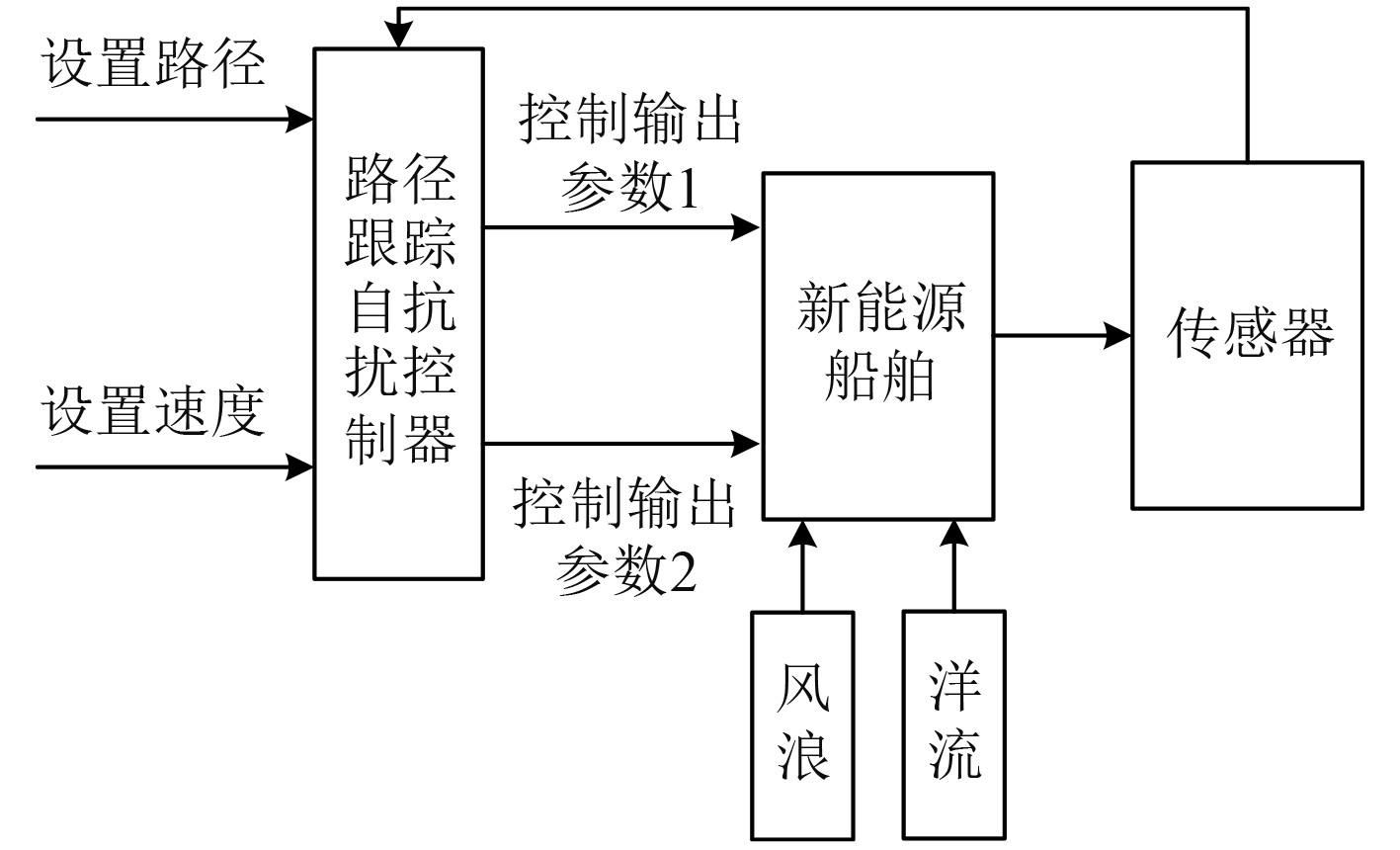
2 路径跟踪自抗扰控制器设计 2.1 整体设计新能源船舶路径跟踪自抗扰控制器包括舵角控制器、首向控制器、纵向速度控制器等,以舵角自抗扰控制器为例进行说明。新能源船舶路径跟踪自抗扰控制原理如图2所示。在给定路径和速度下,路径跟踪自抗扰控制器会输出多个控制参数,让新能源船舶按照一定的速度前进,在这个过程中新能源船舶受到风浪以及洋流的影响产生扰动,此时传感器会将获取的船舶参数(速度、船首向、舵角等)反馈到路径跟踪自抗扰控制器,形成闭环控制。
|
图 2 新能源船舶路径跟踪自抗扰控制原理 Fig. 2 The principle of path following active disturbance rejection control of new energy ships |
新能源船舶路径跟踪自抗扰控制包括对舵角、速度、船首向的控制[4],本文以舵角自抗扰控制为例进行说明。图3为舵角自抗扰控制器结构,包括跟踪微分器、动态稳定器、动态补偿器、扩张状态观测器等。其中跟踪微分器为后续控制提供一个过渡信号和该过渡信号的微分信号,即为目标值和当前值之间提供一条变化曲线,该变化曲线为惯性曲线,不会出现超调的情况。动态稳定器一方面接收跟踪微分器输出的目标信号,进而输出控制信号到新能源船舶,另外一方面又接收新能源船舶的反馈信号,实现自身闭环控制。在动态稳定器和新能源船舶之间有一个动态补偿器,动态补偿器是通过实时获取新能源船舶的输出(首向角、纵向速度、舵角等),然后根据当前的新能源船舶状态提供动态补偿,使得最终输出和目标之间的误差尽量小[5 − 6]。

|
图 3 舵角自抗扰控制器结构 Fig. 3 Rudder angle active disturbance rejection controller structure |
扩张状态观测器对新能源船舶路径跟踪自抗扰控制中的各类变量进行跟踪,并且将观测量反馈到动态稳定器和动态补偿器,能够在外界发生扰动时快速更正输出,是实现路径跟踪自抗扰控制的关键步骤之一。假设β1、β2、β3为设计的观测器增益,x1、x2、x3为系统中需要观测的状态变量,则存在下列变换关系:
| $ \begin{gathered} {x_1}(s) = \frac{{\beta _1^{}s + \beta _2^{}s + \beta _3^{}}}{{{L}\times(s)}}Y(s) + \frac{{bs}}{{{L}\times(s)}}U(s),\\ {x_2}(s) = \frac{{\beta _2^{}{s^2} + \beta _3^{}s}}{{{L}\times(s)}}Y(s) + \frac{{bs(s + \beta _1^{})}}{{{L}\times(s)}}U(s),\\ {x_3}(s) = \frac{{\beta _3^{}{s^2}}}{{{L}\times(s)}}Y(s) - \frac{{b\beta _3^{}}}{{{L}\times(s)}}U(s) 。\\ \end{gathered} $ |
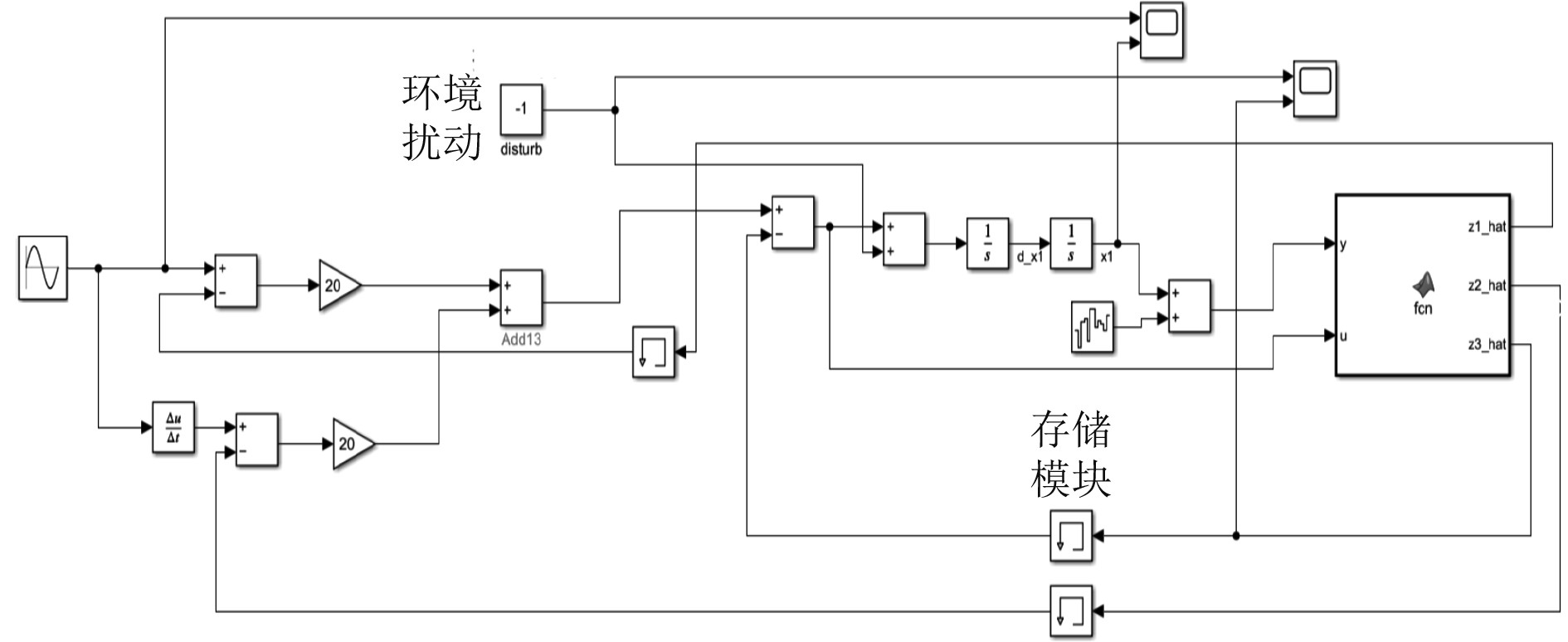
为了尽可能准确观测新能源船舶在运动中的各类变量,需要在应用中不断调整β1、β2、β3的值。在Matlab中构建扩张状态器的仿真模型,如图4所示。
|
图 4 Matlab扩张状态观测器仿真 Fig. 4 Matlab extended state observer simulation |
在路径跟踪中传统的PID也可以实现,因而在一些无人小车的路径跟踪中,有很多学者使用改进PID或者模糊PID来加以实现。对于新能源船舶而言,其路径跟踪受到外界干扰的影响,特别是很多干扰还是非线性的,PID算法控制的核心是通过反馈来消除误差,虽然具有较高的稳定性,但是动态性能较差,且非常容易出现超调。在加入跟踪微分器后可以有效解决这个问题,同时考虑到新能源船舶的运动特性,使用二阶跟踪微分器,其表达式为:
| $ \begin{split} y(s)=&\frac{1}{{T}_{2}-{T}_{1}}(\frac{1}{{T}_{1}s+1}-\frac{1}{{T}_{2}s+1})v(s)=\\ &\frac{s}{{T}_{1}{T}_{2}{s}^{2}+({T}_{1}+{T}_{2})s+1}v(s)\text{,} \end{split} $ |
将上式离散化,得到以下结果:
| $ \begin{gathered} {x_1}(k + 1) = {x_1}(k) + {T_2}{x_2}(k),\\ {x_1}(k + 1) = {x_2}(k) - {T_s}(\frac{1}{{{T^2}}}({x_1}(k) - v(k)) + \frac{2}{{{T^{}}}}{x_2}(k)) ,\\ y(k) = {x_2}(k) 。\\ \end{gathered} $ |
在Matlab中建立跟踪微分器的仿真,如图5所示。在船舶舵角控制信号中加入噪声信号,使用跟踪微分器对该信号进行处理并得到最后的结果,可以发现跟踪微分器具有良好的抗噪能力。

|
图 5 Matlab跟踪微分器仿真 Fig. 5 Matlab tracking differentiator simulation |
设置新能源船舶路径跟踪自抗扰控制仿真条件,建立的Matlab仿真程序如图6所示。

|
图 6 Matlab路径跟踪自抗扰控制仿真 Fig. 6 Matlab path tracing active disturbance rejection control simulation |
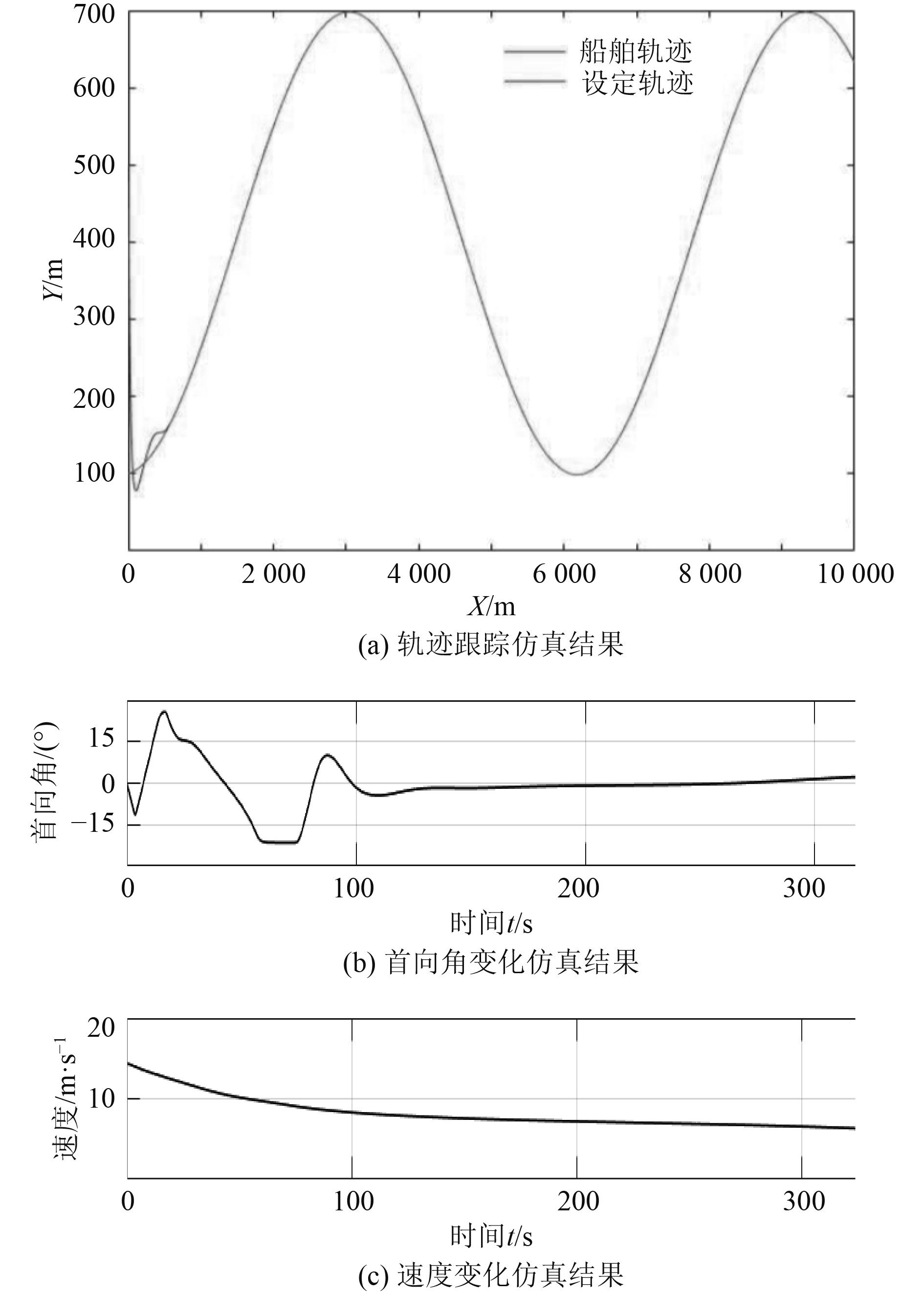
为了简化分析,航行路径设置为正弦函数,新能源船舶初始位置为(0,500),初始首向角度为0°,速度为0 m/s,得到的结果如图7所示。可以发现在路径跟踪上,设定轨迹的起始点和船舶初始位置不同,因而在运动开始后,新能源船舶会以一个小角度向起始位置靠近,同时在新能源船舶运动过程中是为了尽可能沿着设定轨迹行进,不考虑时间因素,因而船舶轨迹在靠近设定轨迹起始点后没有进行过多调整,而是开始直接跟随设定的正弦波航迹运动,并在短暂调整后设定轨迹和船舶轨迹几乎完全重合,证明在仿真条件下能够几乎零误差地跟随设定轨迹。图7(b)和图7(c)分别为新能源船舶的首向角变化以及速度变化。
|
图 7 新能源船舶自抗扰控制仿真结果 Fig. 7 Simulation results of active disturbance rejection control of new energy ships |
新能源船舶是船舶制造未来重要的发展方向,无人新能源船舶能够实现高效率的海洋资源探索。本文在对新能源船舶运动分析的基础上,设计了新能源船舶路径跟踪自抗扰控制器。
1)研究了新能源船舶路径跟踪自抗扰控制原理,以舵角自抗扰控制器为例进行说明,设计了舵角自抗扰控制器的结构;
2)设计了扩张状态观测器和跟踪微分器,并在Matlab下进行了仿真;
3)在一定的初始条件下使用Matlab对新能源船舶自抗扰控制进行仿真,得到了轨迹跟踪、首向角变化以及速度变化的仿真结果。仿真结果表明设计的控制器能够对设定轨迹进行跟随,具有较好的稳定性。
| [1] |
韩京清, 张荣. 二阶扩张状态观测器的误差分析[J]. 系统科学与数学, 1999(4): 465-471. HAN Jing-qing, ZHANG Rong. Error analysis of second-order expanded state observer[J]. Journal of Systems Science and Mathematical Sciences, 1999(4): 465-471. |
| [2] |
张荣彬, 郭永飞. 船用汽轮机转速线性自抗扰控制研究[J]. 仪器仪表用户, 2023, 30(11): 45-49. ZHAGN Rong-bin, GUO Yong-fei. Research on linear active disturbance rejection control of marine steam turbine speed[J]. Instrument & Meter Users, 2023, 30(11): 45-49. DOI:10.3969/j.issn.1671-1041.2023.11.012 |
| [3] |
乌云嘎, 徐会希, 姜志斌. 基于RBF神经网络的新型AUV自抗扰控制方法[J]. 舰船科学技术, 2023, 45(18): 85-91. WU Yun-ga, XU Hui-xi, JIANG Zhi-bin. Novel AUV active disturbance rejection control method based on rbf neural network[J]. Ship Science and Technology, 2023, 45(18): 85-91. |
| [4] |
刘长良, 杨超杰, 刘卫亮, 等. 非最小相位系统的改进自抗扰控制及参数整定方法[J]. 华北电力大学学报(自然科学版), 1−7. LIU Chang-liang, YANG Chao-jie, LIU Wei-liang, et al. Improved active disturbance rejection control and parameter tuning method for non-minimum phase system[J]. Journal of North China Electric Power University (Natural Science Edition), 1−7. |
| [5] |
杨义祥, 李壮举. 基于改进型自抗扰控制器的PMSM控制系统分析[J]. 制造业自动化, 2023, 45(8): 72-76. YANG Yi-xiang, LI Zhuang-ju. Analysis of PMSM control system based on improved active disturbance rejection controller[J]. Manufacturing Automation, 2023, 45(8): 72-76. DOI:10.3969/j.issn.1009-0134.2023.08.017 |
| [6] |
赵源, 戴晓强, 王莹, 等. 基于自抗扰水面无人艇路径跟踪导航与控制方法研究[J]. 战术导弹技术, 2023(4): 95-102+118. ZHAO Yuan, DAI Xiao-qiang, WANG Ying, et al. Research on path tracking, navigation and control method of unmanned surface vehicle based on active disturbance rejection[J]. Tactical Missile Technology, 2023(4): 95-102+118. |
 2024, Vol. 46
2024, Vol. 46
