0 引　言

水下无线传感器网络（Underwater Wireless Sensor Networks，UWSNs）是一种在水下工作的网络监测系统，其发展和研究备受关注。UWSNs中节点部署事关网络成本和服务质量。覆盖率作为节点部署性能重要评价指标，覆盖率越高，传感器网络性能越优异。因此，如何实现传感器节点高覆盖率部署尤为重要。同时，覆盖效率以及节点部署地快速性影响整个传感器网络的寿命，也是传感器节点部署过程中需要考虑的要素。考虑到UWSNs在海洋勘探及监测等领域的广泛应用，UWSNs覆盖优化研究的重要性凸显。

人工蜂群算法（Artificial Bee Colony Algorithm，ABC）作为群智能优化算法的一种，其在二维无线传感器网络覆盖优化应用较多，且取得了较好的优化效果。Dao等^[1]提出了一种最优部署覆盖模型，并利用改进的ABC算法调节传感器节点间的距离，以降低区域冗余率。Yue等^[2]针对人工蜂群算法收敛速度慢，容易陷入最优的缺点，采用自由搜索算法信息素敏感性模型代替传统的轮盘赌选择模型，并证明了所提出的改进算法可用于无线传感器网络覆盖优化上。Liu等^[3]考虑覆盖范围优化和节点部署的问题，在感知模型的基础上，融合了二元覆盖率模型和改进的人工蜂群算法。该算法在迭代次数较少时，具备的高覆盖率特性在仿真实验中得到验证。但是，ABC应用于UWSNs节点覆盖优化很少有公开的文献。Mini等^[4]利用基于群智能的人工蜂群算法，找出了三维地形中的最优部署位置。考虑到人工蜂群算法在二维覆盖优化应用时取得较好的效果，所以该算法在三维水下无线传感器网络覆盖优化研究中具有较多值得探索的可能性。但考虑到人工蜂群算法，在二维覆盖优化问题上，存在着易陷入局部最优、收敛慢的缺陷，面临应用于三维复杂环境覆盖优化问题，该缺陷更甚，这也是单一使用群智能优化算法普遍存在的弊端。

目前，采用虚拟力算法（Virtual Force Algorithm，VFA）进行UWSNs覆盖优化研究同样已取得了具有很大应用价值的成果。Liu等^[5]为了提高水下无线传感器网络的网络覆盖范围，提出了一种基于虚拟力的分布式节点部署算法。通过与其他基于虚拟力的节点部署算法比较，证明该算法优越性。Li等^[6]提出应用于3D传感器网络空间的改进虚拟力算法，以获得更好的传感器分布，并通过仿真实验验证了改进算法的有效性。Zhang等^[7]剖析了节点覆盖机理，设计自适应虚拟力参数控制策略，利用改进的虚拟力算法开展三维空间覆盖率优化部署研究。同时，在解决传感器节点覆盖优化问题上，虚拟力算法也展现出收敛速度快等优点。目前，UWSNs覆盖优化虽然已有大量的研究工作，但在如何快速、高效进行节点高覆盖率重部署，仍然有较大的研究空间。

本文针对水下无线传感器网络监测区域覆盖率低的问题，引入人工蜂群寻优思想并结合虚拟力算法。针对传统人工蜂群算法在解决水下无线传感器网络覆盖优化问题中存在的初始节点部署不均、算法寻优过程缓慢且精度不足和易陷入局部最优的缺陷，分别引入Tent混沌映射、虚拟力算法和柯西-高斯变异策略。针对提出的改进人工蜂群结合虚拟力算法，开展水下无线传感器网络覆盖优化仿真实验研究。

1 网络覆盖模型

假定在长×宽×高（$ L \times W \times H $）的三维水下传感同构网络的监测区域Q中，随机部署$ N $个感知半径为$ {R_s} $和通信半径为$ {R_c} $的传感器节点。假设UWSNs节点集合为$ pos = \left\{ {{p_1},{p_2}, \cdots ,{p_N}} \right\} $，集合$ pos $中第$ i $个节点坐标为$ {p_i} = \left( {{x_i},{y_i},{z_i}} \right) $，$ i \in \left[ {1,2, \cdots ,N} \right] $。为了方便计算网络覆盖范围，将监测区域Q离散化为$ M $个等体积的网格单元，且网格点位于网格单元的几何中心，即监测区域内含有$ M $个网格点。格点的坐标集合$ A = \left\{ {A_1},{A_2},{A_3}, \cdots , {A_M} \right\} $，令$ {A_s} = \left( {{x_s},{y_s},{z_s}} \right) $为集合$ A $中第$ s $个格点的三维空间坐标，且$ s \in \left[ {1,2, \cdots ,M} \right] $。传感器节点感知模型采用布尔模型，监测区域格点是否处于传感器节点感知范围内作为该格点是否被覆盖的评判指标。监测区域格点与传感器节点之间的欧氏距离可表示为：

$ d({p_i},{A_s}) = \sqrt {{{\left( {{x_i} - {x_s}} \right)}^2} + {{\left( {{y_i} - {y_s}} \right)}^2} + {{\left( {{z_i} - {z_s}} \right)}^2}} 。$

(1)

监测区域格点$ {A_s} $只有在传感器节点$ {p_i} $的感知半径$ {R_s} $内才能被监测到。即被感知概率$ {P_{cov}}({p_i},{A_s}) $为^[8]：

$ {P_{cov}}({p_i},{A_s}) = \left\{ {\begin{array}{*{20}{l}} 1 ，{{\mathrm{if}}\;d\left( {{p_i},{A_s}} \right) \leqslant {R_s}}，\\ 0 ，{{\mathrm{otherwise}}} 。\end{array}} \right.$

(2)

则水下无线传感器网络协同工作时，所有传感器节点$ pos $对格点$ {A_s} $的联合感知概率$ {P_{cov}}\left( {pos,{A_s}} \right) $可表示为^[9]：

$ {P_{cov}}\left( {pos,{A_s}} \right) = 1 - \prod\limits_{i = 1}^N {\left( {1 - {P_{cov}}\left( {{p_i},{A_s}} \right)} \right)} 。$

(3)

在优化过程中，采用如下的衡量指标：

1）网络覆盖率$ {C_{cov}} $定义为所有节点覆盖的网格点总数与该区域内网格点总数之比。$ {C_{cov}} $值越大，节点部署的性能越优越。其计算公式可表示为：

$ {C_{cov}} = \frac{{\displaystyle\sum\limits_{j = 1}^M {{P_{cov}}\left( {pos,{A_s}} \right)} }}{M}。$

(4)

2）覆盖效率$ CE $为节点覆盖的区域体积与节点总感知体积的比值，间接用来评价节点利用率和覆盖冗余度。可按照下式计算：

$ CE{\text{ = }}\frac{{{C_{cov}} \times L \times W \times H}}{{N \times ({{4{\text{π}} {R_s}^3} / 3})}} 。$

(5)

2 IABC-VFA算法

传统人工蜂群算法是源于蜜蜂群体觅食行为的智能算法^[10]。该算法中，蜜蜂通过雇佣蜂、跟随蜂和侦查蜂进行交流觅食。在蜜源搜索过程中，每类蜂分工明确，其中雇佣蜂和跟随蜂进行蜜源开采，侦察蜂进行新蜜源搜索。

对于求解UWSNs高覆盖率优化问题，蜜蜂找寻花蜜量最大的过程即是高覆盖率优化的过程，蜜源的位置即传感器节点位置代表目标函数的可行解，蜜蜂所带的花蜜量代表所求函数的适应度值，即覆盖率值。

针对水下无线传感器网络覆盖优化的特定问题，传统人工蜂群算法仍存在初始节点部署不均、算法寻优过程缓慢且精度不足和易陷入局部最优的缺陷，这些缺陷制约着传感器覆盖率的提升。

2.1 引入Tent混沌映射的蜜源初始化

在蜜源初始化阶段，按照式（6）产生初始种群，且该过程具有随机性。该种群具有2个方面特征：1）含有$ N $个可行解；2）每个解$ {p_{id}} $是1个$ d \in \left[ {1,2, \cdots ,D} \right] $维的向量。

$ {p_{id}} = l + rand(0,1) \cdot (u - l)。$

(6)

式中：$ i \in \left[ {1,2, \cdots ,N} \right] $，$ d \in \left[ {1,2, \cdots ,D} \right] $，$ D $为维度数；$ {p_{id}} $为初始的蜜源位置；$ rand $为$ \left( {0,1} \right) $的一个随机数；$ u $和$ l $分别为解的变量上界和下界^[11]。

传统的人工蜂群算法种群初始化以随机方式生成，无法确保种群在搜索空间中的均匀分布，为了解决这一问题，引入Tent混沌映射^[12]，并利用其产生的混沌序列初始化种群。Tent混沌映射可表示为^[13]：

$ H' = \left\{ \begin{aligned} & {2H, 0 \leqslant H \leqslant 0.5}，\\ & {2\left( {1 - H} \right),0.5 \leqslant H \leqslant 1}。\end{aligned} \right. $

(7)

该阶段蜜源的更新公式为：

$ {p_{id}} = l + H' \times \left( {u - l} \right)。$

(8)

种群初始化阶段引入Tent混沌映射进行传感器节点初始部署，提升了节点在监测区域内部署的均匀性。

2.2 引入虚拟力算法的跟随蜂阶段

在雇佣蜂阶段，雇佣蜂在当前蜜源邻域内以式（9）展开新蜜源搜索，并依据搜索结果更新适应度函数的最优值。

$ {p'_{id}} = {p_{id}} + {\varphi _{id}}({p_{id}} - {p_{kd}})。$

(9)

式中：$ {p'_{id}} $为通过改变$ {p_{id}} $的1个参数获得的新蜜源；$ k \in \left\{ {1,2, \cdots ,N\left| {k \ne i} \right.} \right\} $为随机选择的；$ {\varphi _{id}} $为[-1,1]之间的随机数^[14]。

在跟随蜂阶段，跟随蜂采用和雇佣蜂相同的搜索方式进行更新蜜源，分析传递的共享信息。同时，依靠轮盘赌和贪婪策略更新蜜源，并由下式确定雇佣蜂被选择概率：

$ PR\left( i \right) = \frac{{fitness\left( {{p_i}} \right)}}{{\displaystyle\sum\limits_{n = 1}^N {fitness\left( {{p_i}} \right)} }}。$

(10)

式中，$ fitness\left( {{p_i}} \right) $为第$ i $个解的适应度值^[15]。

传统的人工蜂群算法寻优过程缓慢且精度不足，为解决这一问题，引入虚拟力算法^[7]。该算法以节点分布的密集程度作为判别标准，通过定义引力和斥力实现节点自主移动，从而完成节点优化部署。当节点低于阈值时，则节点在引力作用下同向移动，以此来减少水下传感器网络的覆盖空洞。反之，节点受斥力背向移动，以减少网络的覆盖重叠。

在虚拟力算法模型中，假定任意一个水下无线传感器节点的感知搜索范围是以节点为球心的球形区域，并在如下所述的作用力下，动态调整传感器节点位置。

1）节点间的相互作用力

传感器网络随机部署后的节点间分布过于稀疏或过于密集时，节点间会在相互作用下发生自主移动。两节点间的距离$ {d_{ij}} $可表示为：

$ {d_{ij}} = \left\| {{p_i} - {p_j}} \right\|。$

(11)

式中：$ {p_i} $和$ {p_j} $分别为第$ i $、$ j $个节点坐标，表示为$ \left( {{x_i},{y_i},{z_i}} \right) $和（$ {{x_j},{y_j},{z_j}} $）。

节点间的相互作用力的表达式如下：

$ \,\,\,{\vec F_{ij}} = \left\{ {\begin{array}{*{20}{l}} {（ {{\omega _a}（ {{d_{ij}} - {d_{th}}} ）,{\alpha _{ij}}} ）,{\rm{if}}\,\,{d_{th}} < {d_{ij}} < {R_c}} ,\\ {0,\quad \quad \quad {\rm{if}}\,\,{d_{ij}} > {R_c}}, \\ {（ {{\omega _r}（ {{d_{th}} - {d_{ij}}} ）,{\alpha _{ij}} + {\text{π}} } ）,{\rm{if}}\,\,{d_{ij}} < {d_{th}}\,} ,\\ {0,\quad \quad \quad {\kern 1pt} {\rm{if}}\,\,{d_{ij}} > {R_c}}。\end{array}} \right. $

(12)

式中：$ {\vec F_{ij}} $和$ {\alpha _{ij}} $分别为第$ i $、$ j $两节点间的相互作用力及方位角；$ {\omega _a} $和$ {\omega _r} $分别为节点间虚力的引力和斥力系数；$ {d_{th}} $为节点间距离阈值；$ {R_c} $为节点通信半径。

2）监测区域边界的斥力

为了保证节点在受限的监测区域内移动，提高节点移动的有效性，通过定义监测区域的边界斥力约束传感器节点移动的自由性。监测区域的边界对节点的作用力$ {\vec F_{ib}} $可表示为^[7]：

$ {\vec F_{ib}} = \left\{ \begin{aligned} & {\left( {\omega \left( {{d_b} - {d_{ib}}} \right),\,{\alpha _{ib}} + {\text{π}} } \right)\,,\,\,\,{\mathrm{if}}\,{d_{ib}} < {d_b}}，\\ & { 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\qquad\qquad\;\;\qquad {\mathrm{otherwise}}} 。\end{aligned} \right. $

(13)

式中：$ {d_b} $为节点与监测区域边界之间的安全距离阈值，且$ {d_b} = {d_{th}}/2 $；$ {d_{ib}} $为节点到监测区域边界的距离；$ \omega $为节点与监测区域边界之间虚拟力的斥力系数；$ {\alpha _{ib}} $为节点$ i $与监测区域边界之间的方位角。

综上，节点所受的虚拟合力$ \vec F $为：

$ \vec F = \sum\limits_{j = 1,j \ne q}^q {{{\vec F}_{ij}}} + {\vec F_{ib}}。$

(14)

式中，$ q $为节点$ i $的相邻节点数。

因此，在虚拟合力$ F $的作用下，传感器节点将从位置原始位置$ O\left( {{x_i},{y_i},{z_i}} \right) $自主移动到目标位置$ O'\left( {{{x'}_i},{{y'}_i},{{z'}_i}} \right) $。节点移动的计算公式如下：

$ {x'_i} = \left\{ {\begin{array}{*{20}{c}} {{x_i},\,\,\,\,\quad \quad \quad \quad \quad \quad \,\,\,\quad \qquad \qquad \,\,{\mathrm{if}}\left| {{{\vec F}_{xyz}}} \right| = 0} ，\\ {{x_i} + \frac{{{{\vec F}_x}}}{{{{\vec F}_{xyz}}}} \times {\rm{Max}}Step \times {\ell ^{ - \,\frac{1}{{{{\vec F}_{xyz}}}}}},\,\,\,{\mathrm{otherwise}}} 。\end{array}} \right.\,\, $

$ {y'_i} = \left\{ {\begin{array}{*{20}{c}} { {y_i},\,\,\,\quad \quad \quad \,\, \quad \quad \quad \quad \qquad \qquad\,\,{\mathrm{if}}\left| {{{\vec F}_{xyz}}} \right| = 0}, \\ {{y_i} + \frac{{{{\vec F}_y}}}{{{{\vec F}_{xyz}}}} \times {\rm{Max}}Step \times {\ell ^{ - \frac{1}{{{{\vec F}_{xyz}}}}}},\,\,\,{\mathrm{otherwise}}} 。\end{array}} \right.\,\, $

(15)

$ {z'_i} = \left\{ {\begin{array}{*{20}{llllll}} { {z_i},\,\,\,\quad \,\,\,\,\quad \quad \quad \quad \quad \quad\qquad \qquad \,\,{\mathrm{if}}\left| {{{\vec F}_{xyz}}} \right| = 0}，\\ {{z_i} + \frac{{{{\vec F}_z}}}{{{{\vec F}_{xyz}}}} \times {\rm{Max}}Step \times {\ell ^{ - \frac{1}{{{{\vec F}_{xyz}}}}}},\,\,\,{\mathrm{otherwise}}} 。\end{array}} \right.\,\, $

式中：$ {\vec F_x} $、$ {\vec F_y} $和$ {\vec F_z} $为虚拟力在$ x $、$ y $和$ z $轴上的投影；$ {\vec F_{xyz}} $为节点上虚拟力合力，$ {\vec F_{xyz}} = \sqrt {{{\vec F}_x}^2 + {{\vec F}_y}^2 + {{\vec F}_z}^2} $；$ {\rm{Max}}Step $为单次最大移动距离^[16]。

引入虚拟力算法的跟随蜂阶段蜜源更新公式可表达为：

$ {p''_{id}} = \vec F\left( {{{p'}_{id}}} \right)。$

(16)

式中：$ {p'_{id}} $为雇佣蜂阶段的更新蜜源位置；$ \vec F $为节点所受的合力；$ {p''_{id}} $为引入虚拟力算法后更新的蜜源位置。

虚拟力算法的引入，刺激传感器自主移动，并且在移动过程中统筹兼顾所部署的所有传感器节点更优部署。

2.3 引入柯西-高斯变异策略的迭代后期

在侦察蜂阶段，当雇佣蜂所处位置的附近搜索次数超过预设定的搜索次数阈值仍没找到具有更高适应度值的蜜源时，完成向侦察蜂的身份转变，由式（6）重新选择新蜜源。

传统人工蜂群算法迭代后期，算法易陷入局部最优，为了解决这一问题，引入柯西-高斯策略，通过选择当前适应度函数值最高的蜂群个体$ {p_{bd}} $进行变异，然后择优迭代。柯西-高斯变异策略更新蜜源的公式可表示为^[17]：

$ {p'''_{id}} = {p_{bd}}\left[ {1 + {\alpha _1}cauchy(0,{\sigma ^2}) + {\alpha _2}Gauss(0,{\sigma ^2})} \right] ，$

(17)

$ \sigma = \left\{ {\begin{array}{*{20}{llllllll}} { 1,{\kern 1pt}\quad f\left( {{p_{bd}}} \right) < f\left( {{p_{id}}} \right)} ，\\ {exp\left( {\dfrac{{f\left( {{p_{bd}}} \right) < f\left( {{p_{id}}} \right)}}{{\left| {f\left( {{p_{bd}}} \right)} \right|}}} \right),\quad {\mathrm{otherwise}}} ，\end{array}} \right. $

(18)

$ {\alpha _1} = 1 - {{{t^2}} \mathord{\left/ {\vphantom {{{t^2}} {{T^2}}}} \right. } {{T^2}}}，$

(19)

$ {\alpha _2} = {{{t^2}} \mathord{\left/ {\vphantom {{{t^2}} {{T^2}}}} \right. } {{T^2}}}。$

(20)

式中：$ {p_{bd}} $为当前最优蜂群个体的坐标；$ {p'''_{id}} $为变异后蜂群个体坐标；$ {\sigma ^2} $为柯西-高斯变异策略的标准差；$ cauchy(0,{\sigma ^2}) $为柯西分布的随机变量；$ Gauss(0,{\sigma ^2}) $为高斯分布的随机变量；$ {\alpha _1} $和$ {\alpha _2} $为随着迭代次数自适应参数；$ {p_{id}} $为当前第$ i $个蜜源的坐标；$ t $为第$ t $次迭代；$ T $为最大迭代次数。

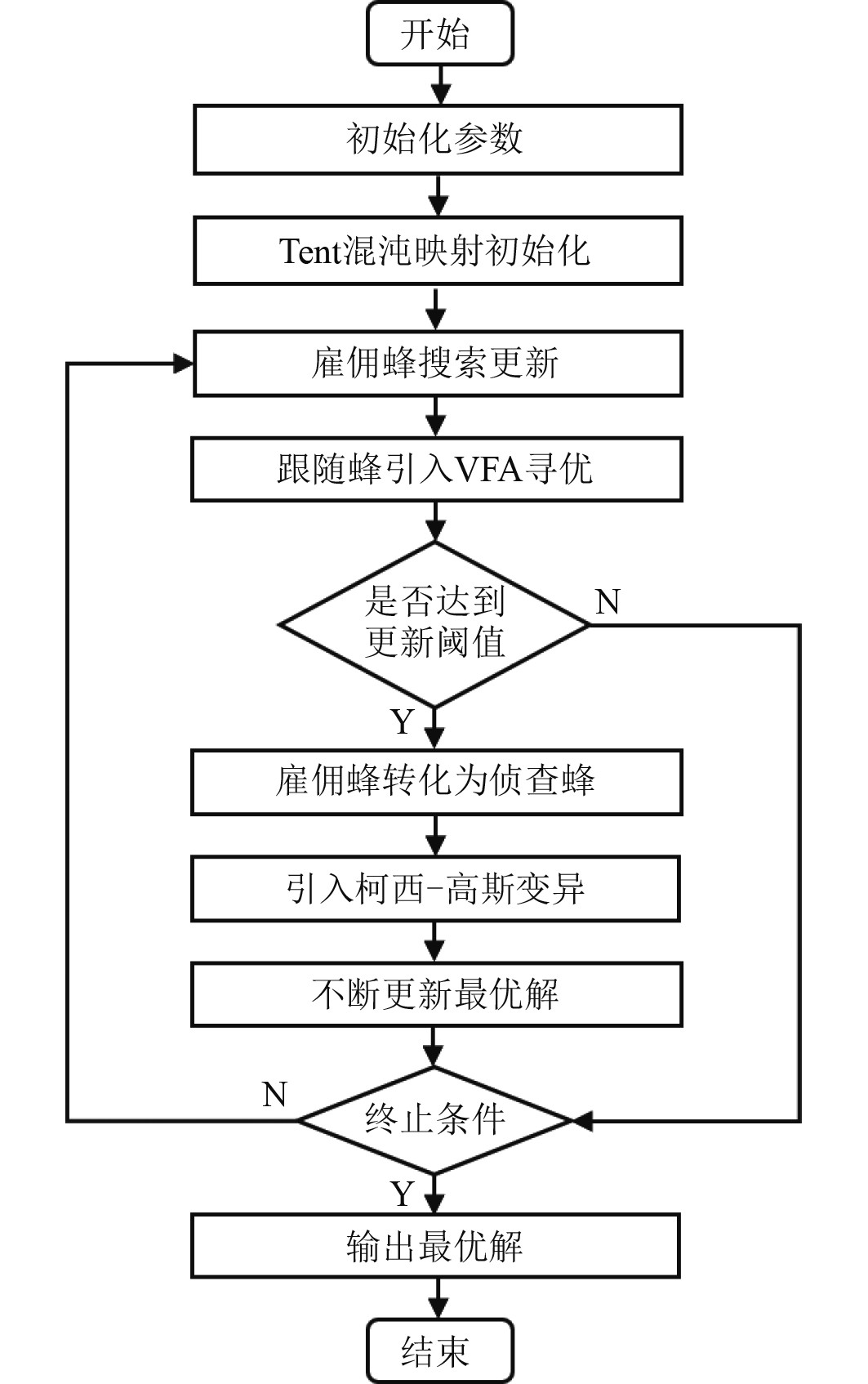
运用柯西-高斯变异策略在最优解位置进行扰动变异操作得出新解，使其跳出局部最优，提高最优解的质量。通过对传统人工蜂群算法缺陷的改进，结合虚拟力算法，形成了IABC-VFA算法。所提的IABC-VFA算法流程如图1所示。

3 仿真实验

为了验证所提出的改进人工蜂群结合虚拟力算法（IABC-VFA）在UWSNs覆盖优化应用上的性能，开展仿真实验研究。依托Matlab仿真实验平台，分别采用本文提出的IABC-VFA、3D-IVFA和DABVF开展仿真实验。假定监测区域为50 m×50 m×50 m的正立方体区域，为了保证对比要素一致性，在仿真实验采取随机部署传感器节点的初始化方案。仿真实验计算参数如表1所示。

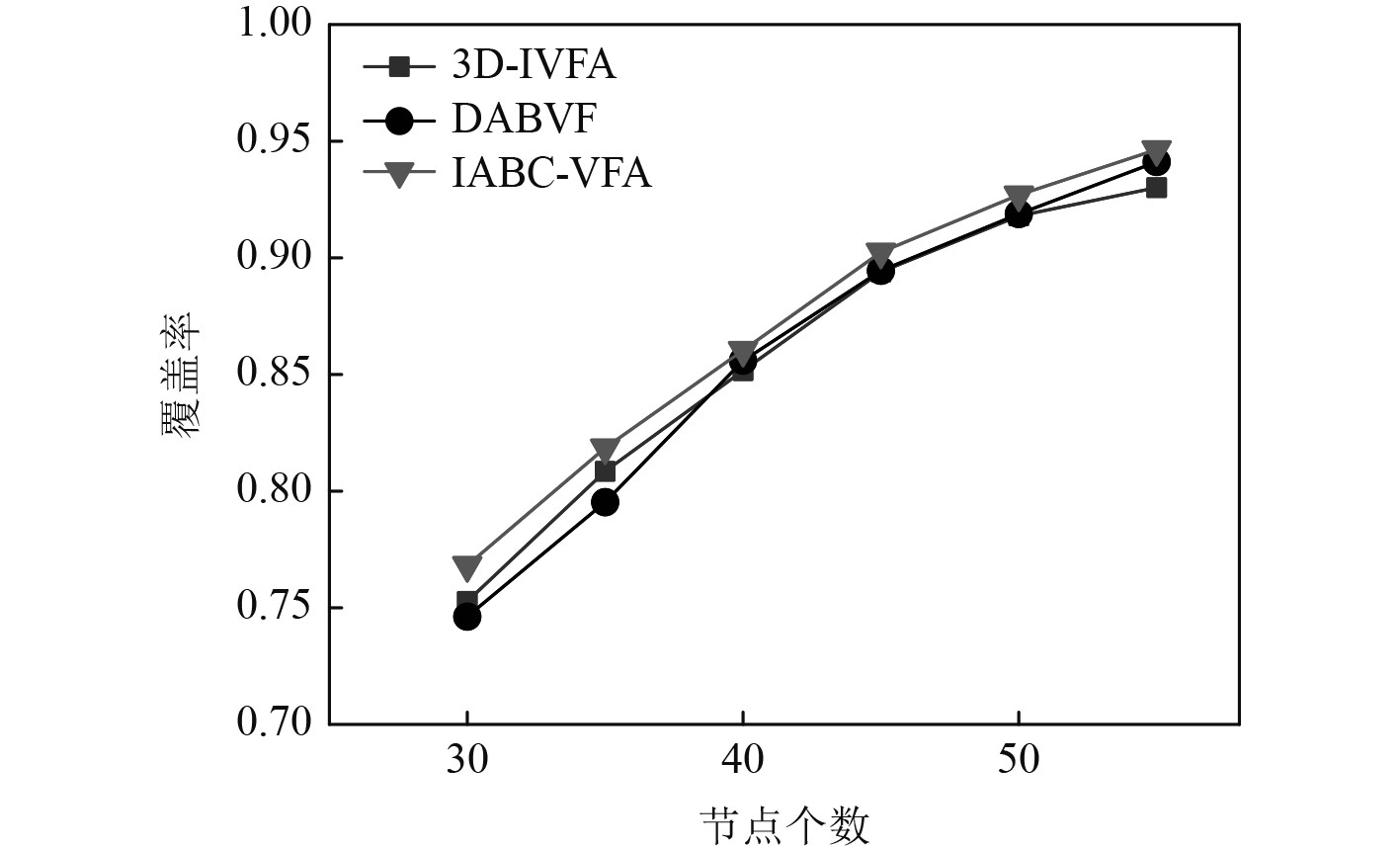
为了探索验证节点个数对于覆盖率的影响，本文节点个数的选取在30~55区间内，均匀采样6个工况，并开展仿真实验研究。由图2可知，随着节点布置个数的增加，3种算法的节点覆盖率都呈现增加趋势，但是增加趋势不断减缓。产生该现象的原因是在该节点个数范围内，节点个数与覆盖冗余的正相关性。当在监控区域内布置的传感器节点数目相同时，本文提出的IABC-VFA算法覆盖率均高于3D-IVFA算法和DABVF算法。由图3可知，IABC-VFA算法中传感器节点的覆盖效率也高于3D-IVFA算法和DABVF算法，表明经IABC-VFA算法的节点部署方案，节点分布更合理，节点利用效率更高。

图4为3种算法覆盖率收敛曲线。可知，所提的IABC-VFA用较少的迭代步可达到近似收敛，明显优于3D-IVFA和DABVF，且IABC-VFA算法始终保持较高的覆盖率，IABC-VFA算法覆盖率可达到90.25%。在3D-IVFA算法和DABVF算法覆盖率收敛曲线存在较多波动段，波动段的产生源于节点的位置不断调整，也意味着节点能量的消耗。相比之下，本文提出的IABC-VFA算法，波动段较少，节点移动的能耗少且能实现较高的覆盖率。

4 结　语

考虑到传统ABC算法在水下无线网络覆盖问题上的不足，本文提出了基于的IABC-VFA网络覆盖算法。该算法具有如下主要特点：1）引入Tent混沌映射产生混沌序列，提升了节点在监测区域内部署的均匀性；2）采用虚拟力算法提高算法寻优速度和精度；3）引入柯西-高斯变异策略解决算法迭代后期易陷入局部最优的问题。通过仿真实验，开展了所提出的IABC-VFA算法性能验证。实验结果表明，IABC-VFA算法比3D-IVFA、DABVF算法覆盖率分别提高了1.30%和1.63%，能够为水下传感网络构建提供一定基础。