2. 中国舰船研究院,北京 100101
2. China Ship Research and Development Academy, Beijing 100101, China
在传统的海上雷达探测系统中,发射机与接收机的间隔通常较长,存在严重的杂波干扰。因此,对低旁瓣天线的要求很高。阵列天线的波束形成能力直接影响系统的快速捕获和跟踪性能。如果不处理面元,会导致阵列方向图中的第一旁瓣高度过低进而无法达到雷达天线所需的旁瓣参数需要。而且目标点和轨迹信息的共享效率低,难以满足未来海上探测目标的需求。最小均方(LMS)自适应滤波算法可在噪声干扰下形成波束并将主波束引导到目标信号。该算法通过调整波束形成设备的状态来减少参考信号和输出信号之间的误差,并使用其适应性来跟踪目标信号。然而,在苛刻的信号接收条件下,LMS算法的收敛难度将增加。Di[1]通过引入SDM方法,以增大计算复杂度为代价降低了线性阵列的旁瓣高度。Mohammed等[2]使用每个用户的最大信号泄漏率来最小化总发射功率。Guo等[3]通过引入相位扰动思想来降低阵列的旁瓣高度。该方法与遗传算法的原理相近,但容易导致局部过优化问题。
遗传算法(GA)是一种典型的基于全局概率的搜索方法。其基本原理类似于自然界中的自然选择规律。通过对编码染色体进行多轮操作,使得群体满足目标函数的要求,生成最优解。由于传统的遗传算法存在早熟、收敛速度慢、需要大量计算等问题,其在智能天线应用领域当中表现不佳。为此,需对传统遗传算法进行改进。Ma等[4]提出了一种能够应用于传感器阵列波束图的优化的模拟退火遗传算法。在Zhang等[5]中,改进了适应度函数,分别为子阵列级和元素级添加了窗口,以优化波束形成算法。Yuan等[6]将凸优化方法与基本遗传算法相结合来优化向量权重,用于解决具有高旁瓣的圆形阵列图案问题。
针对初始种群的生成和交叉操作,本文改进传统遗传算法,提出一种优化遗传算法,其可以替代LMS算法,将天线阵列的主波束引导到运动目标,并根据参考目标信号同步更新波束形成装置。这种算法将自适应思想引入,以达到全局最优为目标,使得算法的收敛速度明显提升,最终能够获得高度较低的旁瓣。本文提出的优化遗传算法在应用于波束形成时通过全局范围内自适应地找到最优权重向量,得到最优波束方向图。
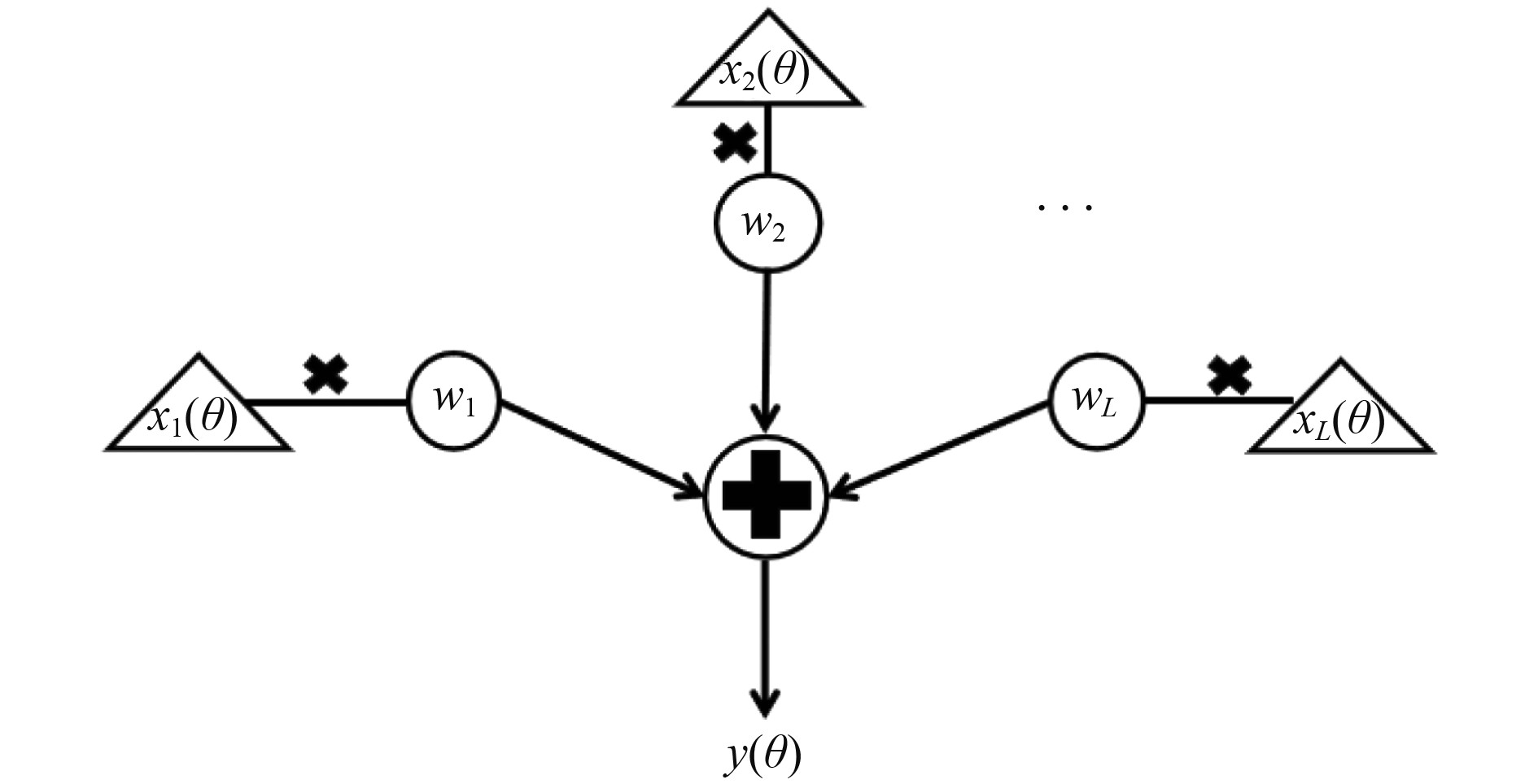
1 优化模型构建 1.1 天线阵列模型本文以一维均匀直线等幅天线阵列为研究对象。天线阵列波束形成的一般模型如图1所示。图中有
|
图 1 波束形成装置的一般模型 Fig. 1 General model of beam forming device |
| $ y(\theta)=W^{{\mathrm{T}}} X,$ | (1) |
假设传感器阵列最大输出为
| $ G(\theta)=10 \lg \frac{|y(\theta)|^{2}}{\left|y\left(\theta_{0}\right)\right|^{2}}。$ | (2) |
由于基于不同权重向量
假设信号为窄带信号,入射波长为

|
图 2 信号模型示意图 Fig. 2 Schematic diagram of signal model |
在建立的天线阵列模型结构下,对于从
| $ x_{r}(t)=a_{r}(\theta, \phi) s(t),$ | (3) |
仅考虑信号存在于X, Y平面内,假设
| $ X=\left[x_{1}(t), x_{2}(t), \ldots, x_{\mathrm{m}}(\mathrm{t})\right]^{{\mathrm{T}}}=s(t) a(\phi),$ | (4) |
当有d个信号
| $ X=\sum_{k=1}^{d} s_{k}(t) \alpha\left(\phi_{k}\right)+\sum_{k=1}^{m} n_{k}(t)。$ | (5) |
其中,
则信号接收模型为:
| $ X(t)=A S(t)+N。$ | (6) |
基于最陡下降法,LMS算法主要通过对接收信号之间的互相关估计与每一轮迭代的相对误差进行计算从而不断迭代更新输出信号的加权值[7]。首先,LMS算法会设置一个初始化的权重向量使得输出信号方向为0°。然后在每一次迭代中,阵列输出信号如下:
| $ y(t)=w^{{\mathrm{H}}} x(t),$ | (7) |
其中,计算目标信号方向与输出信号方向的误差为:
| $ \varepsilon^{i}=y^{i}(n)-d(n),$ | (8) |
将误差进行反馈并更新权重向量:
| $ w(n+1)=w(n)+2 \mu x(n) e^{{\mathrm{H}}}(n) 。$ | (9) |
进行多次迭代后,算法会逐渐收敛。对于控制收敛速度的参数
遗传算法是一种基于自适应的全局最优概率寻优方法,无需引入微分等数学手段,只需解出目标函数和匹配函数的寻优方向即可[8]。
利用遗传算法进行自适应波束形成的关键是对加权系数w优化运算。首先在设置好的天线阵列基础上,确定主瓣指向角度θ。接下来进行权重向量的优化。
步骤1 初始种群的生成与算法编码。首先产生初始种群,即初始待优化的权重向量
步骤2 个体适应度值选择与计算。利用式
步骤3 交叉。设置交叉概率
步骤4 变异。设置变异概率
步骤5 将步骤4中得到的新个体代入式(1)和式(2)计算以判断产生的波束图是否满足实际需要。如果满足则算法结束,否则返回步骤2进一步优化。
在判断达到波束图的性能指标后,得到最优化的权重向量:
| $ {\boldsymbol{\omega}}=\left[w_{1}, w_{2}, \ldots, w_{t}\right]。$ | (10) |
最终将最优权重向量
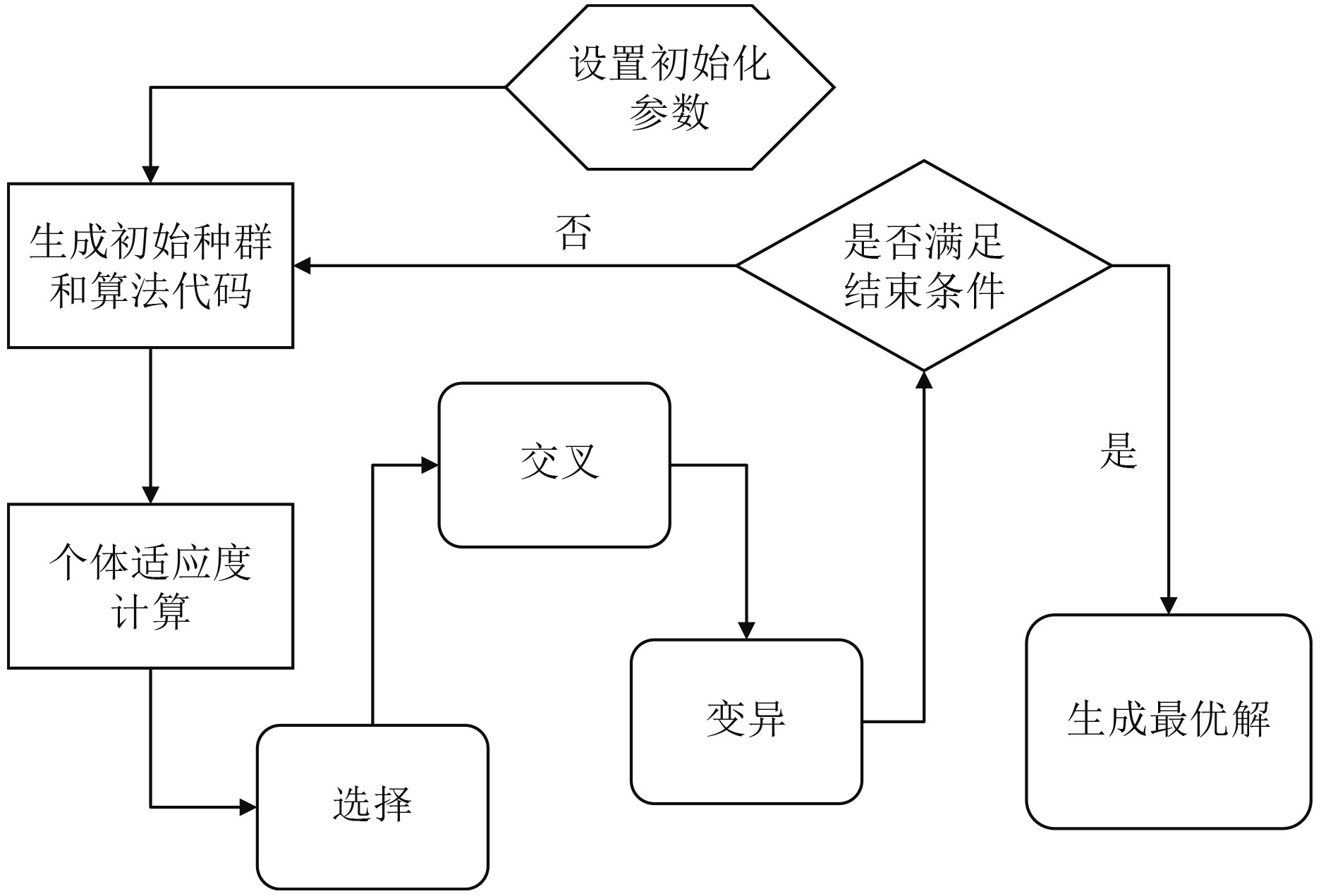
|
图 3 基于遗传算法的波束形成流程图 Fig. 3 Flow chart of beamforming based on genetic algorithm |
本文在文献[9]的基础上,提出一种优化的初始种群规划生成方法。此方法分为2个步骤:
步骤1 将变量所在的区间分成多个子空间;
步骤2 在每个子空间内分别随机生成初始种群的个体。
通过这种方法生成的初始个体将会较均匀地分布在整个空间上,实现提高算法收敛速度的提升,让算法更易于收敛于全局最优。
2.3.2 优化交叉本文提出一种基于判断的交叉操作改进方法。
步骤1 建立多个缓存分组。设置可发生交叉操作的门限值为
步骤2 将种群个体按照两两一组的方式进行分组。
步骤3 对每组内2个个体的相似度按下式进行比较,从而判断能否进行交叉操作。
| $ e(i)=T_{1}(i)-T_{2}(i)。$ | (11) |
式中,
步骤4 当2个个体间的相似变量比例占总数的一半以上时,将它们置入不同的缓存分组中。当所有两两个体分组比较完成后,分别将不同缓存分组中的个体取出并在每组内重复步骤2~步骤4。
步骤5 当所有剩余未交叉个体两两之间的相似变量比均超过一半,结束。
通过上述步骤,对传统的遗传算法进行交叉运算改进,有效地克服传统的遗传算法在局部最优和收敛速度上的不足,从而使算法的优化效率得到进一步提高。
3 仿真实验为了比较不同算法之间的性能差异,基本模拟参数设置相同。天线阵列为不考虑元件之间线性耦合具有15个元件的均匀线性阵列。2个元件之间的间距为
令适应度函数为F,则目标函数为:
| $ F=M S L L 。$ | (12) |
式中,MSLL为最大相对旁瓣电平,可表示为MSLL=
| $ U=\left\{\theta \mid-90^{\circ} \leqslant \theta \leqslant-\frac{\theta^{\prime}}{2} \text { or } \frac{\theta^{\prime}}{2} \leqslant \theta \leqslant 90^{\circ}\right\}。$ | (13) |
实验参数设置交叉概率
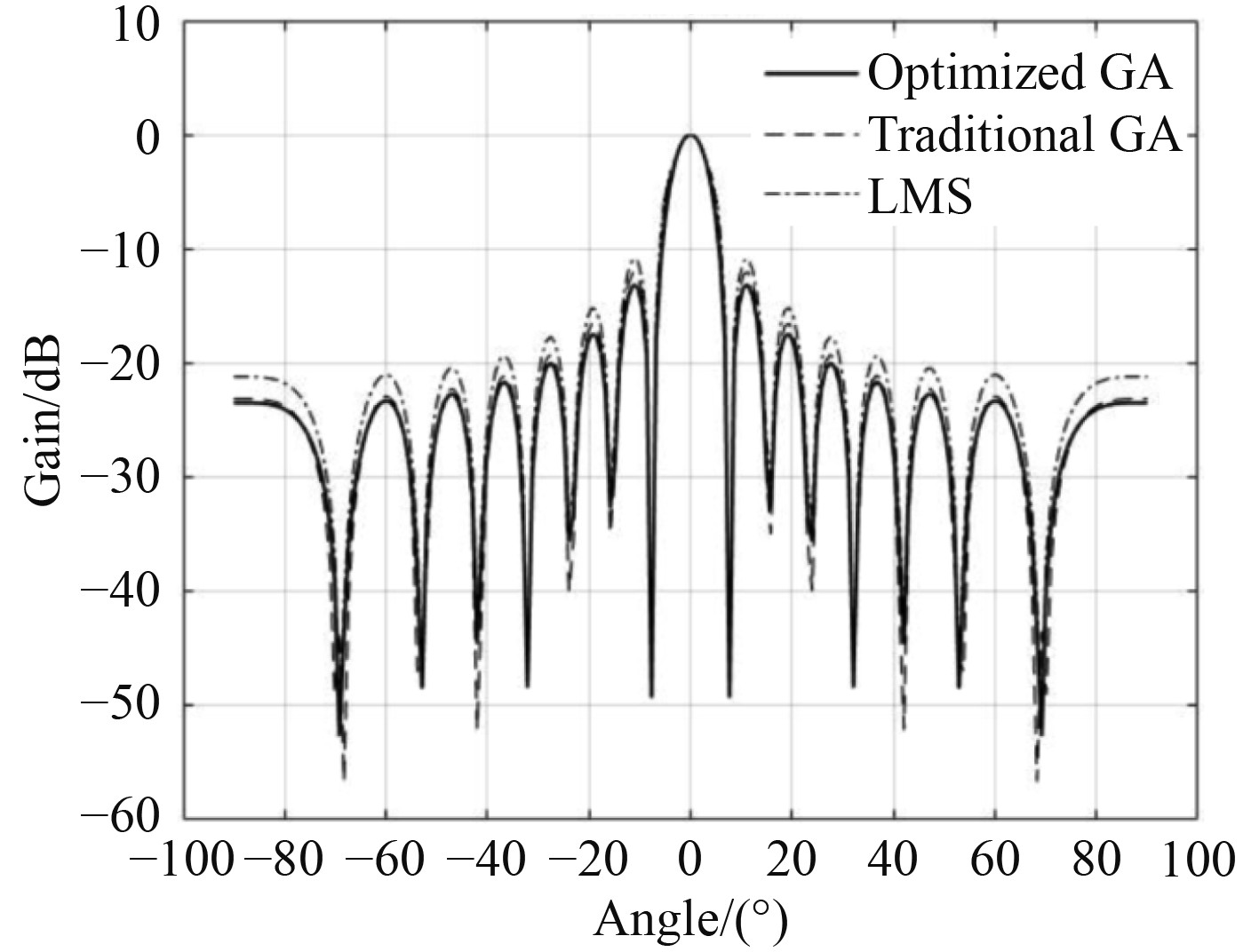
|
图 4 DOA为0°的方向图 Fig. 4 0° DOA pattern |
从图4可知,经典算法LMS算法的旁瓣高度不高于−10.8 dB,传统遗传算法的旁瓣高度不高于−12.2 dB,而优化遗传算法的旁瓣高度约为−13.9 dB。如图5所示,经典的LMS算法在大约250次迭代后,收敛到最优解;传统的遗传算法在120次迭代后,也收敛到最优;而优化的遗传算法仅在大约80次迭代后,即可收敛到最优。结果表明,与经典算法LMS和传统遗传算法相比,本文提出的优化遗传算法具有更优秀的旁瓣抑制效果,收敛到最优解的速度更快,验证了该算法的正确性、有效性和高效率。

|
图 5 算法迭代过程比较 Fig. 5 Comparison of algorithm iteration process |
随着海上雷达技术和设备的智能化,智能天线和波束形成技术在海上通信中的重要性逐渐凸显。具有快速收敛和高旁瓣抑制的智能算法可在海上雷达检测和通信中获得更好的结果。
本文通过对遗传算法的研究,结合遗传算法的特点,提出一种优化遗传算法。该方法主要优化了传统遗传算法中的初始种群规划和交叉操作。基于雷达阵列模型和信号模型,对LMS算法、遗传算法和本文提出的优化遗传算法进行了仿真实验。实验结果表明,优化后的遗传算法具有更好的旁瓣抑制效果,更快的收敛速度,提高了智能天线的工作效率。对该算法的有效性进行了验证,为以后在智能天线方面的深入研究打下良好基础。
| [1] |
DI Jingying. Study on transmiting beamforming at subarray level for phased array [D]. Harbin: Harbin Institute of Technology, 2016: 2−5.
|
| [2] |
MOHAMMED F, NOR F A , MAHAMOD I, et al. Power allocation in cooperative NOMA MU-MIMO beamforming based on maximal SLR precoding for 5G[J]. Journal of Communications, 2019, 14(8): 676-683. |
| [3] |
GUO Hua, YUE Leihui, JIN Guangrui, et al. Pattern synthesis of subarrayed linear array antenna[J]. Electronic Design Engineering, 2020, 28(13): 119-122. |
| [4] |
MA Yezi. Analytical method of transmiting beampattern synthesis and its applications[C]. Chengdu: School of Information and Communication Engineering, 2020: 4-8.
|
| [5] |
ZHANG Haisheng, YU Yong, SHI Yahui. Analysis of wide-ban two-dimensional arraying method for digital beam-forming[J]. Electronic Information Warfare Technology, 2019, 34(5): 62-66. |
| [6] |
YUAN Fei, YANG Bo, HUANG Zhongrui. A hybrid SLL suppression algorithm for sparse array under the constraint of amplitude range ratio[J]. Modern Radar, 2018, 7(7): 57-60. |
| [7] |
DAYODELE S. OLUWOLE, VIRANJAY M. Srivastava,. "Analysis and synthetic model of adaptive beamforming for smart antenna systems in wireless communication," Journal of Communications, 2018, 13(8): 436−442.
|
| [8] |
PATRICIA DA S A, GUILHERME F GO, SEBASTIÃO SIMÕES C. A robust optimization for damage detection using multi-objective genetic algorithm, neural network and fuzzy decision making[J]. Inverse Problems in Science and Engineering, 2020, 28(1): 21-27. DOI:10.1080/17415977.2019.1583225 |
| [9] |
LIU Hao, ZHAO Lulu, LIANG Guang, et al. A phase-only beamforming method based on improved genetic algorithm[J]. Electronic Design Engineering, 2018, 26(5): 169-172. |
 2024, Vol. 46
2024, Vol. 46
