0 引　言

海底门是船舶海水系统与海水接触的开口，海水通过船体外壳上海底门格栅进入海底阀箱内腔，随后进入通海阀及海水管路，成为船舶的冷却水、压载水以及消防水来源。海底门（海水吸入箱、海底阀箱）可根据海水总管、格栅及管路附件来设计^[1]，在满足全船海水供给量前提下需考虑声学设计。若船舶以水下探测、捕捞、科考为主要业务，以使用水声设备来实现其功能，水下噪声过高会严重影响多波束声呐的使用性能。此外，环保组织越来越重视船舶水下噪声对水中生物的影响^[2]，因此需对此类船舶的水下噪声限值进行规定，中国船级社在2018年发布了《船舶水下辐射噪声指南》，并依据此规范为船舶提供入级服务，授予民船水下辐射噪声附加标志Underwater Noise N（N=1，2，3，N=1最安静）^[3]。海底门可直接向海水中辐射噪声，是船舶水下噪声的重要来源之一，因此海底门的水下噪声研究具有重要的工程意义。

为了降低船舶海底门噪声，董自虎等^[4]对通海阀的流道结构进行改进，通过增加阀瓣开启行程、对局部结构进行倒角等措施，避免了流场局部出现驻点，大大减小了速度梯度和压力梯度，改善整个流场，达到了降噪减阻的效果。孙启等^[5]采用有限元和声学自动匹配层（AML）技术，对海底门水下声场进行计算，采用增加导板及海水总管入口流通面积等措施，未能降低海底门噪声，增大深入海底门的海水总管长度会使流噪声辐射量增加。张静^[6]研究海底阀箱流-固耦合特性，简化海底阀箱模型的干模态及湿模态，给出了附连水质量对海底阀箱干模态的影响规律。仿真计算出流场分布、不同抽水速度的定常力，研究不同壁厚在流激作用下的强迫振动幅频响应，对海底阀箱进行低噪声设计。

本文对海底门声传递损失、结构湿模态进行分析，获得海底门的共振频率。对流场及水动力噪声进行计算，云图显示压力峰值条带沿着格栅对角线方向分布，频谱分析显示海底门水动力噪声以低频贡献为主。将海底门钢格栅替换为水下多孔介质时，不同频率范围内的水动力噪声均有所降低。当海底门的入口处由钢替换成水下多孔介质时，总声压级水平降低12.9 dB，说明水下多孔介质在海底门降噪上有较大潜力。共振频率计算方法及水下多孔介质材料应用为海底门低噪声设计提供了参考。

1 控制方程

对于海底门流场问题，考虑到实际工程应用中关心的是各湍流要素的时均值，故本文基于非定常雷诺平均N-S方程（URANS方程），不可压缩流动的连续性方程：

$ \frac{{up\partial \overline {{u_i}} }}{{up\partial {x_i}}} = 0 。$

(1)

动量方程：

$\begin{split} \rho \frac{{up\partial \overline {{u_i}} }}{{up\partial t}} + \rho \overline {{u_j}} \frac{{up\partial \overline {{u_i}} }}{{up\partial {x_j}}} =& \rho \overline {{F_i}} - \frac{{up\partial \overline p }}{{up\partial {x_i}}} +\\& \frac{up\partial }{{up\partial {x_j}}}\left(\mu \frac{{up\partial \overline {{u_i}} }}{{up\partial {x_j}}} - \rho \overline {u_i'u_j'} \right) + {S_i}。\end{split} $

(2)

式中：$ \overline {{u_i}} $与$ u_i' $为${x_i}$方向时均速度和脉动速度；$ {x_j} $为方向；$ \overline p $为时均压力；$ \overline {{F_i}} $为质量力强度；$ \rho $为流体密度；$ t $为时间；$ {S_i} $为动量源项，代表多孔介质对流动的作用。$ \rho \overline {u_i'u_j'} $为雷诺应力项，是未知的，为使方程封闭引入Realizable k-ε湍流模型对雷诺应力项进行建模。

针对水动力噪声分析，本文采用FW-H方程处理。FW-H方程为Ffowcs-Williams和Hawkings利用广义函数推导而来，是一个非齐次波动方程：

$ \begin{gathered} \frac{1}{{c_0^2}}\frac{{{up\partial ^2}p'(x,t)}}{{up\partial {t^2}}} - {\nabla ^2}p'(x,t) = \\ {\text{ }}\frac{up\partial }{{up\partial t}}({\rho _0}{U_n})\delta (f) - \frac{{{up\partial ^2}}}{{up\partial {x_i}}}\left\{ {{L_i}\delta (f)} \right\}- \\ {\text{ }} \frac{{{up\partial ^2}}}{{up\partial {x_i}up\partial {x_j}}}[{T_{ij}}H(f)] 。\\ \end{gathered} $

(3)

其中：

$ {U_n} = (1 - \frac{\rho }{{{\rho _0}}}){v_n} + \frac{{\rho {u_n}}}{{{\rho _0}}} ，$

(4)

$ {L_i} = [({p^{}} - {p_0}){\delta _{ij}} - {\tau _{ij}} - \rho u_i^{}(u_j^{} - v_j^{})]{n_j} ，$

(5)

$ {T_{ij}} = \rho {u_i}{u_j} + [(p - {p_0}) - c_{}^2(\rho - {\rho _0})]{\delta _{ij}} - {\tau _{ij}} 。$

(6)

等式依次为物体运动引起体积变化的单极子声源、壁面对流体作用的起伏产生偶极子声源和表面以外流体中的体声源^[7]。$ {c_0} $为远场声速；${u_i}$为${x_i}$方向的流体速度分量；${u_j}$为${x_j}$方向的流体速度分量；${u_n}$沿着壁面法线方向的流体速度分量；${v_i}$为${x_i}$方向的壁面速度分量；$ {v_j} $为${x_j}$方向的壁面速度分量；${v_n}$为着壁面法线方向的壁面速度分量；n为壁面法线方向矢量；$ f $为壁面函数；${\tau _{ij}}$为亚格子应力；$\delta (f)$为狄拉克函数；$H(f)$为Heaviside函数，$p'$为远场声压($p' = p - {p_0}$)；$\rho $为周围介质密度；${\rho _0}$为远场密度；${T_{ij}}$为Lighthill应力张量。

水下多孔介质介质是一种很好的流体控制材料，当流体经过多孔介质时，其速度低且稳定，速度梯度小不利于形成湍流^[8]。因此，对多孔介质区域流动的模拟是通过在动量方程（2）中加入一个给定的动量源项S_i来实现的。该源项由粘性损失（第1项）和惯性损失项（第2项）构成，其表达式为：

$ {S_i} = - \left( {\mathop \sum \limits_{j = 1}^3 {D_{ij}}\mu {v_j} + \mathop \sum \limits_{j = 1}^3 {C_{ij}}\frac{1}{2}\rho |v|{v_j}} \right)。$

(7)

式中：$ |v| $为速度大小；$ {D_{ij}} $和$ {C_{ij}} $分别为系数矩阵。动量源项通过改变压力梯度从而对多孔介质区域产生阻碍，其产生的压降与速度（速度平方）大小成正比关系。

对各向同性多孔介质，上式可简化为：

$ {S_i} = - \left( {\frac{\mu }{\alpha }{v_i} + {C_2}\frac{1}{2}\rho |v|{v_i}} \right)。$

(8)

其中：$ \mu $为动力粘度；$ \alpha $为多孔介质的渗透性；$ {C_2} $为惯性阻力系数。当模拟层流状态下的多孔介质，忽略对流加速度和扩散即$ {C_2} $取0，主要考虑第1项，则可简化为达西定律：

$ {S_i} = \nabla P = \frac{\mu }{\alpha }\vec v。$

(9)

$ {\Delta }P $为压降分量，在笛卡尔坐标系下，在x, y, z方向的压降分量$ {{\Delta }}{P_x} $、$ {{\Delta }}{P_y} $、$ {{\Delta }}{P_z} $如下：

$ \begin{gathered} {{\Delta }}{P_x} = \mathop \sum \limits_{j = 1}^3 \frac{\mu }{{{\alpha _{xj}}}}{v_j}{{\Delta }}{n_x}, \\ {{ \Delta }}{P_y} = \mathop \sum \limits_{j = 1}^3 \frac{\mu }{{{\alpha _{yj}}}}{v_j}{{\Delta }}{n_y},{\text{ }} \\ {{\Delta }}{P_z} = \mathop \sum \limits_{j = 1}^3 \frac{\mu }{{{\alpha _{zj}}}}{v_j}{{\Delta }}{n_z}。\\ \end{gathered} $

(10)

其中：$ {1 \mathord{\left/ {\vphantom {1 {{\alpha _{ij}}}}} \right. } {{\alpha _{ij}}}} $为不同方向的粘性阻力系数；$ {v_j} $为下x、y、z方向的速度；$ {\Delta}{n_x} $、$ {\Delta}{n_{\text{y}}} $、$ {\Delta}{n_z} $为x、y、z方向上多孔介质的厚度。

2 计算模型

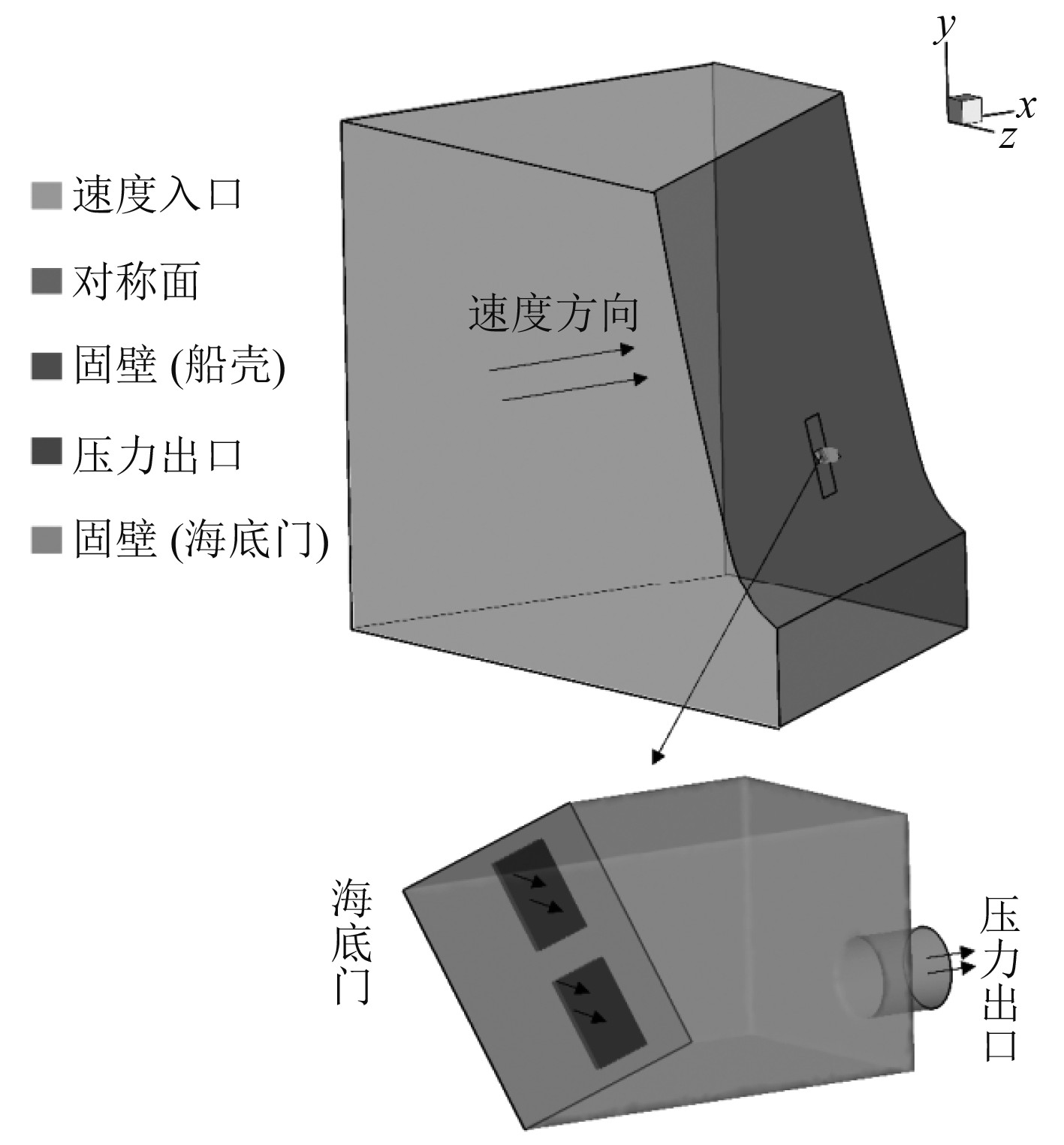
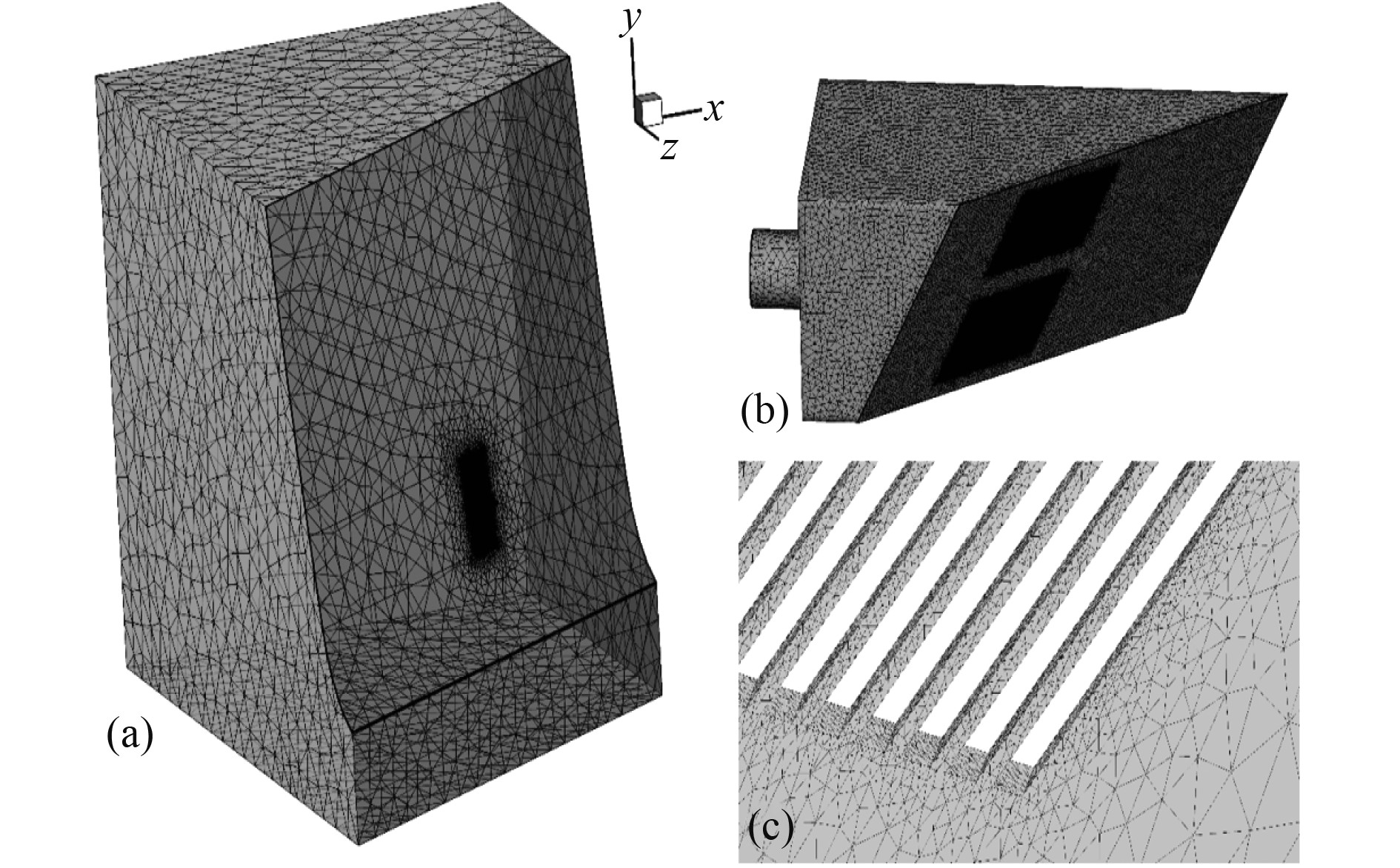
选用安装在船体舷侧的海底门作为研究对象，CFD模型的计算域与边界条件如图1所示。海底门安装在船壳内侧，水流经过格栅进入海底门阀箱内腔，再进入船体内部的海水系统。此海底门有2个格栅，格栅区域的尺寸为0.65 m×0.83 m，单个格栅条的宽度为0.005 m，2个格栅条之间的间距为0.011 m。在船壳的外部和海底门内部建立流体域，两部分流体域通过海底门入口格栅空隙相连接。为了节约计算资源，采用对称边界条件，只计算船壳一舷流动情况。水流在入口处以指定速度15 kn流入计算域，在出口处采用压力出口边界条件，船壳和海底门壁面被设定为无滑移壁面。为了减少网格数量，提高计算效率，采用了非结构网格对流场进行离散。图2(a)为整体网格视图，图2(b)为局部网格视图。为了更好地捕捉边界层流动，在固体壁面添加边界层网格，对海底门格栅区域网格加密，见图2(c)，模型共计5232079个单元。

3 海底门声场、共振、流场及水动力噪声分析 3.1 海底门阀箱声腔共振分析

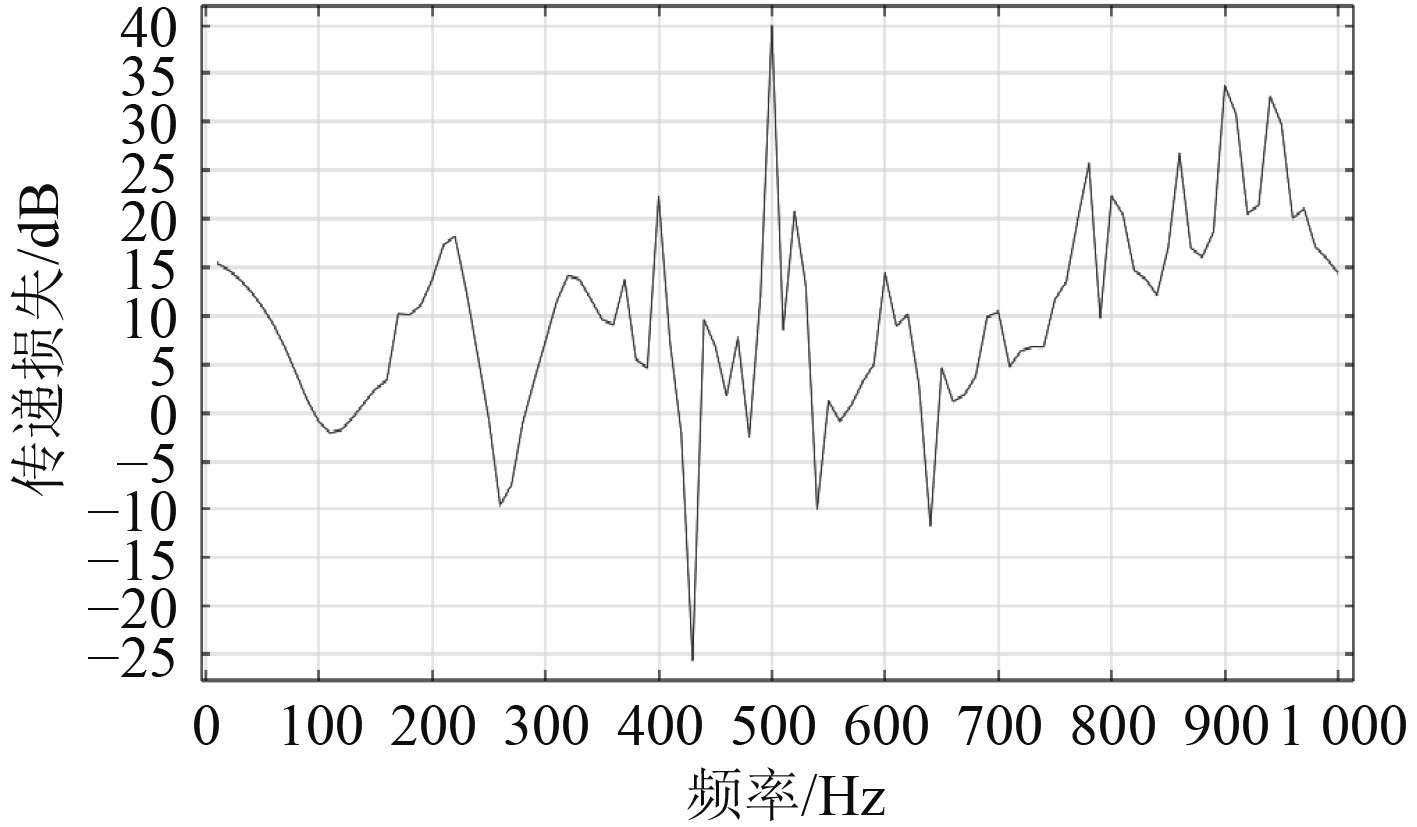
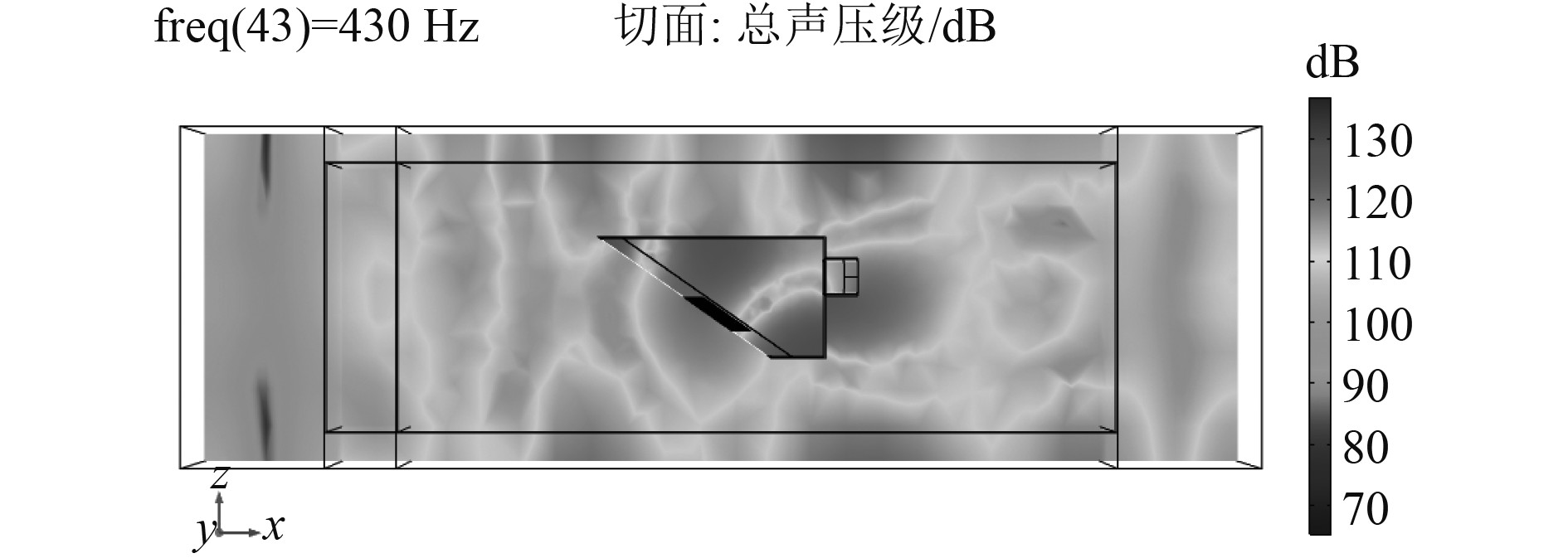
为研究某船用海底门阀箱内腔的声场发生共振的可能，对海底门区域划分声学有限元网格，一个波长至少6个单元节点，声学区域一侧设置完美匹配层（PML）模拟无反射边界条件。在声学区域另一侧设置声源段，提供沿入口方向压力幅值为1 m/s平面波激励，海底门阀箱的声传递损失曲线如图3所示。流动状态下的声传递损失基本为正，在500 Hz附近传递损失较大，在负波峰430 Hz附近会出现声压变大现象，图4为430 Hz时声压级云图。为避免海底门腔体共振，海水泵等运转设备激励频率应避开430 Hz左右共振频率，或者通过改变海底门阀箱尺寸使腔体共振避开海水泵等运转设备激励频率。

3.2 海底门结构共振分析

因海底门浸入在海水里，常规的结构干模态计算不符合应用实际。为研究海底门发生结构共振的可能，需考虑周围流体对共振频率的影响，对海底门结构湿模态分析，此模型为原始模型（baseline），采用钢质船体外壳、阀箱及格栅。首先建立流体域和海底门结构域的声-固耦合模型，再建立结构与流体的接触对，对格栅面网格进行加密，网格长度为0.02 m，其余网格尺寸默认设置为0.8 m，保证计算频率的一个波长段分布至少10个节点以上。

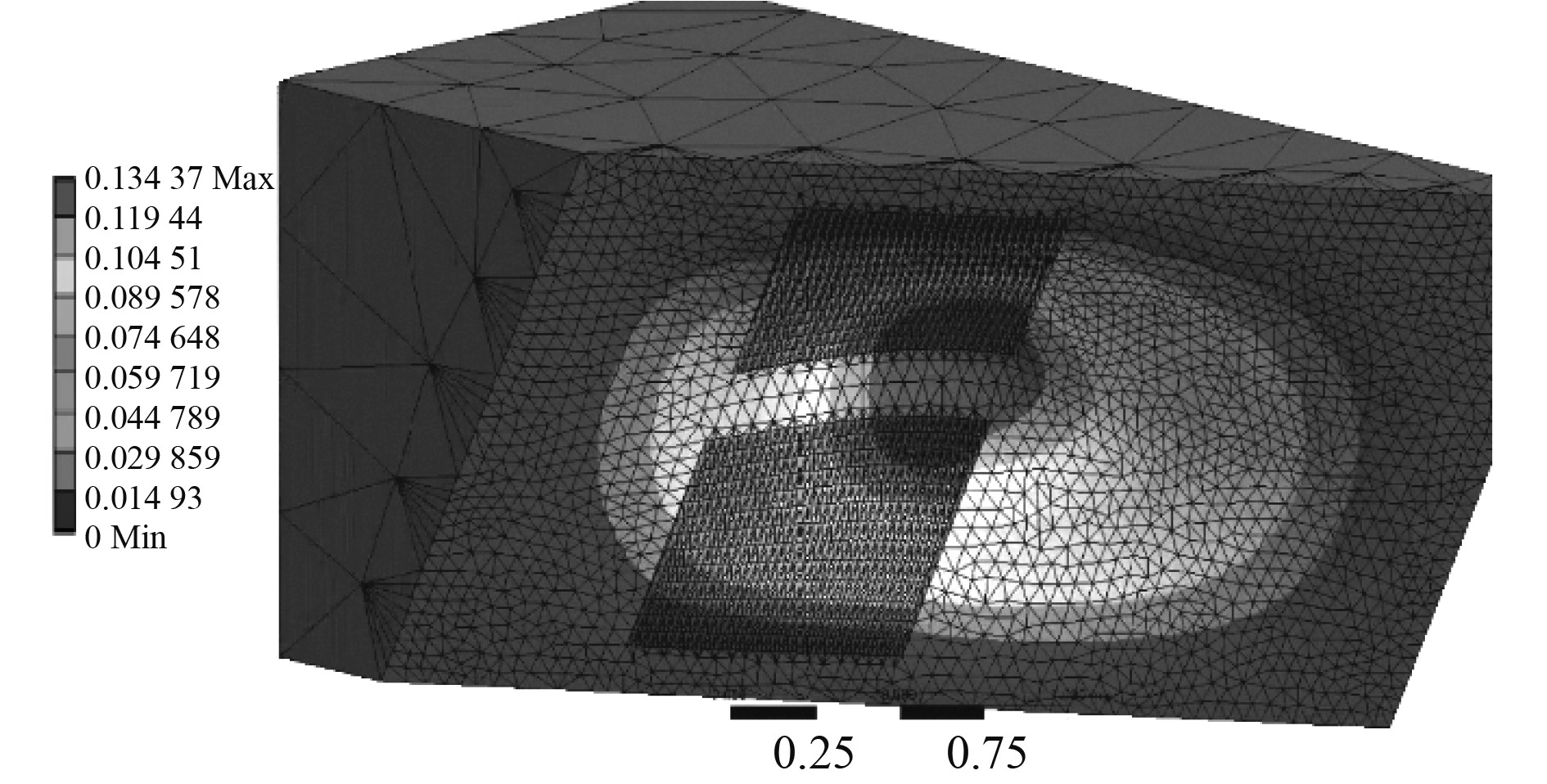
声-固耦合模型计算的海底门前6阶湿模态频率分别为29.284 Hz、39.965 Hz、45.774 Hz、54.024 Hz、58.208 Hz、61.009 Hz，第一阶湿模态振型如图5所示。为避免发生海底门结构共振，海水泵等运转设备激励频率应避开此湿模态共振频率，或者通过改变海底门结构尺寸，使结构共振频率避开海水泵等运转设备频率。

3.3 海底门流场分析

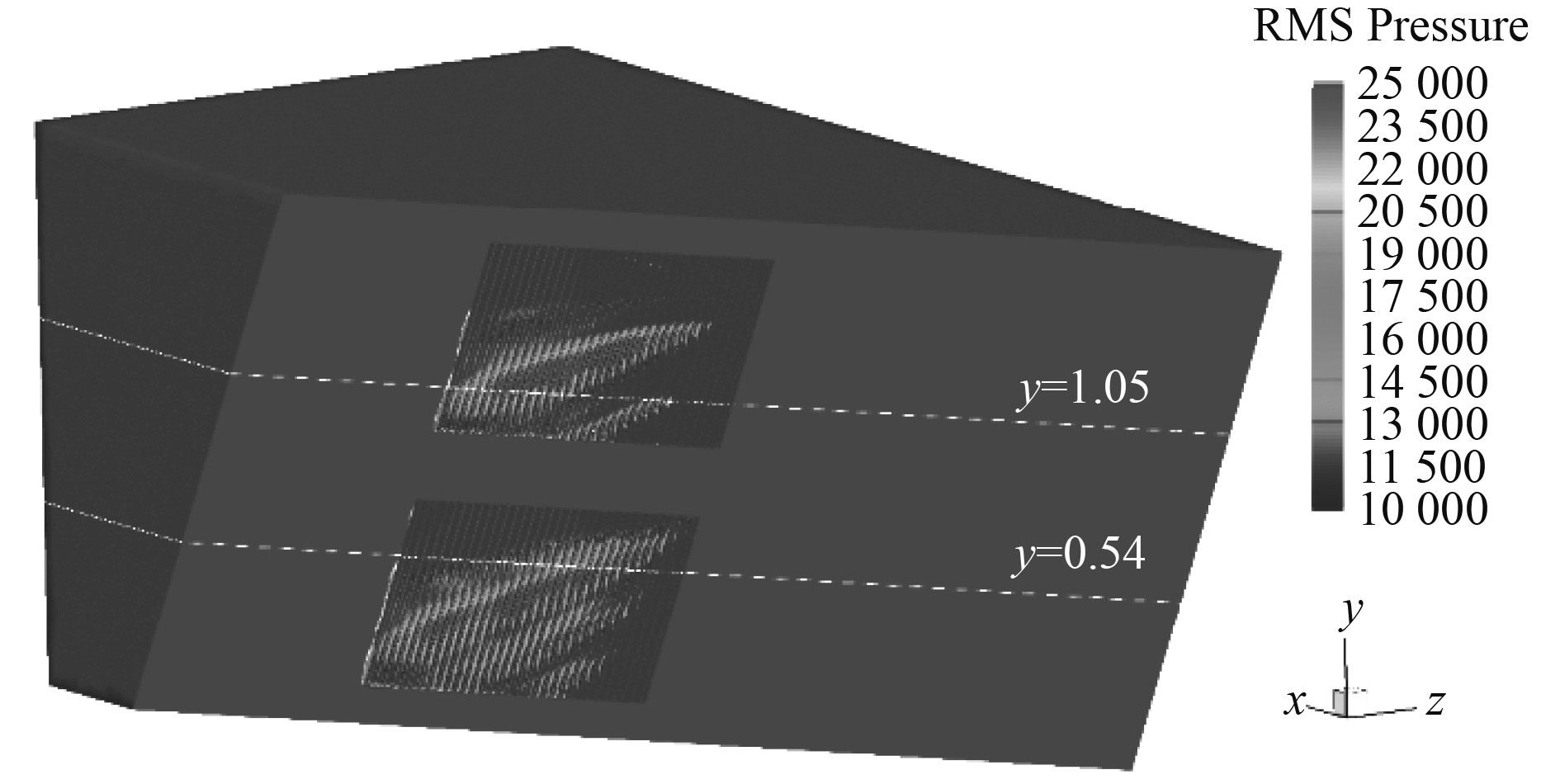
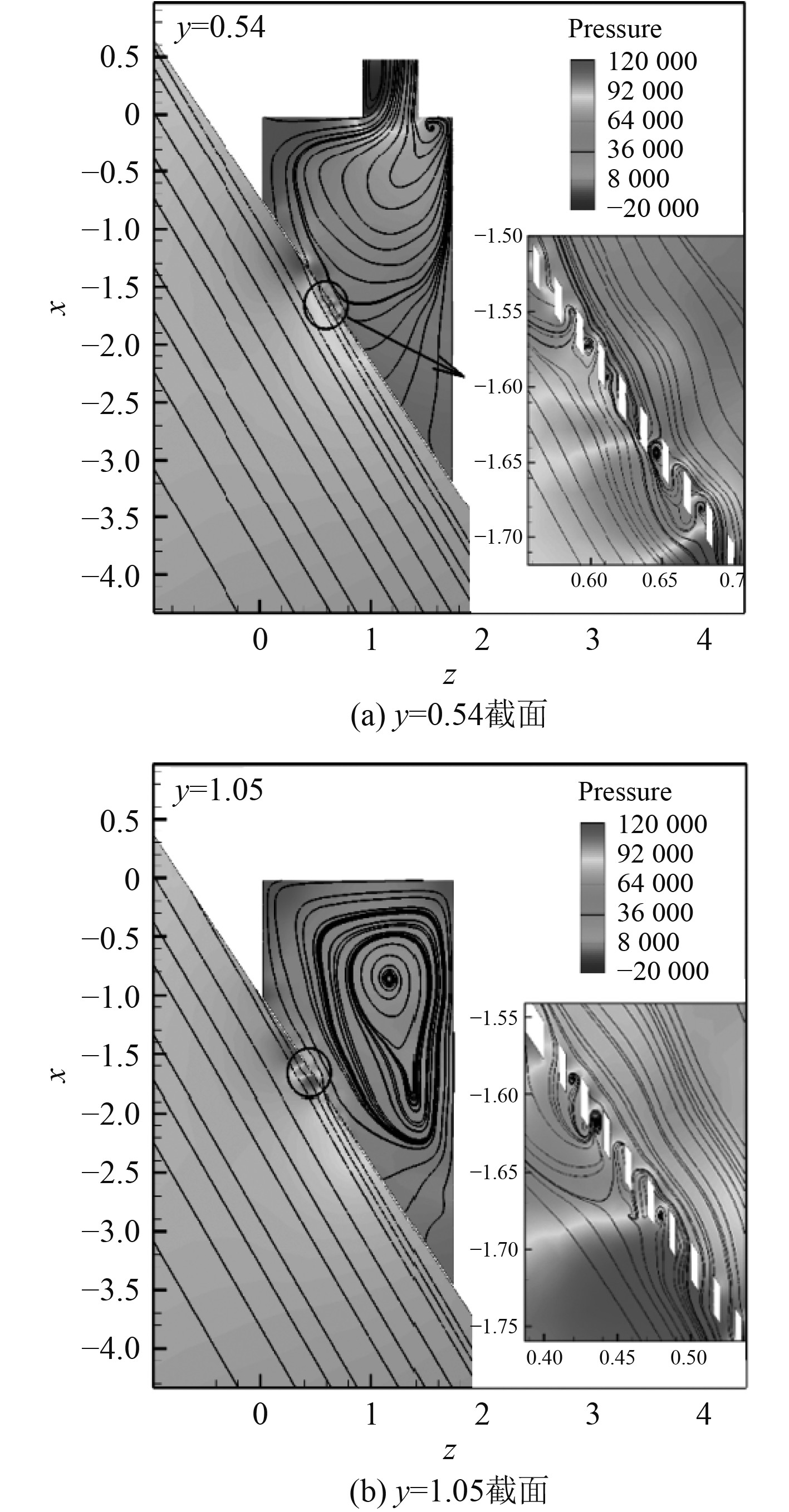
对海底门流体域划分网格，进行流场计算，图6为海底门入口格栅处的均方根压力云图。可知，海底门中的压力峰值主要集中在格栅上，且压力峰值沿着格栅的对角线方向分布。上方的格栅上出现了2条沿着对角线分布的峰值条带，而下方的格栅有3条显著的压力峰值条带，范围显著增大。为了解格栅处压力脉动产生的根源，分别切取y=0.54和y=1.05处的2个截面，图7（a）、图7（b）分别展示上述2个截面上的流线图和压力云图，水流经海底门格栅缝流入，在海底门腔体中形成了一个大尺度的漩涡。由于格栅的存在，水流流动受到了显著的阻碍，在格栅背面出现了显著的流动分离现象，导致格栅上出现明显的压力峰值条带。

3.4 海底门水动力噪声分析

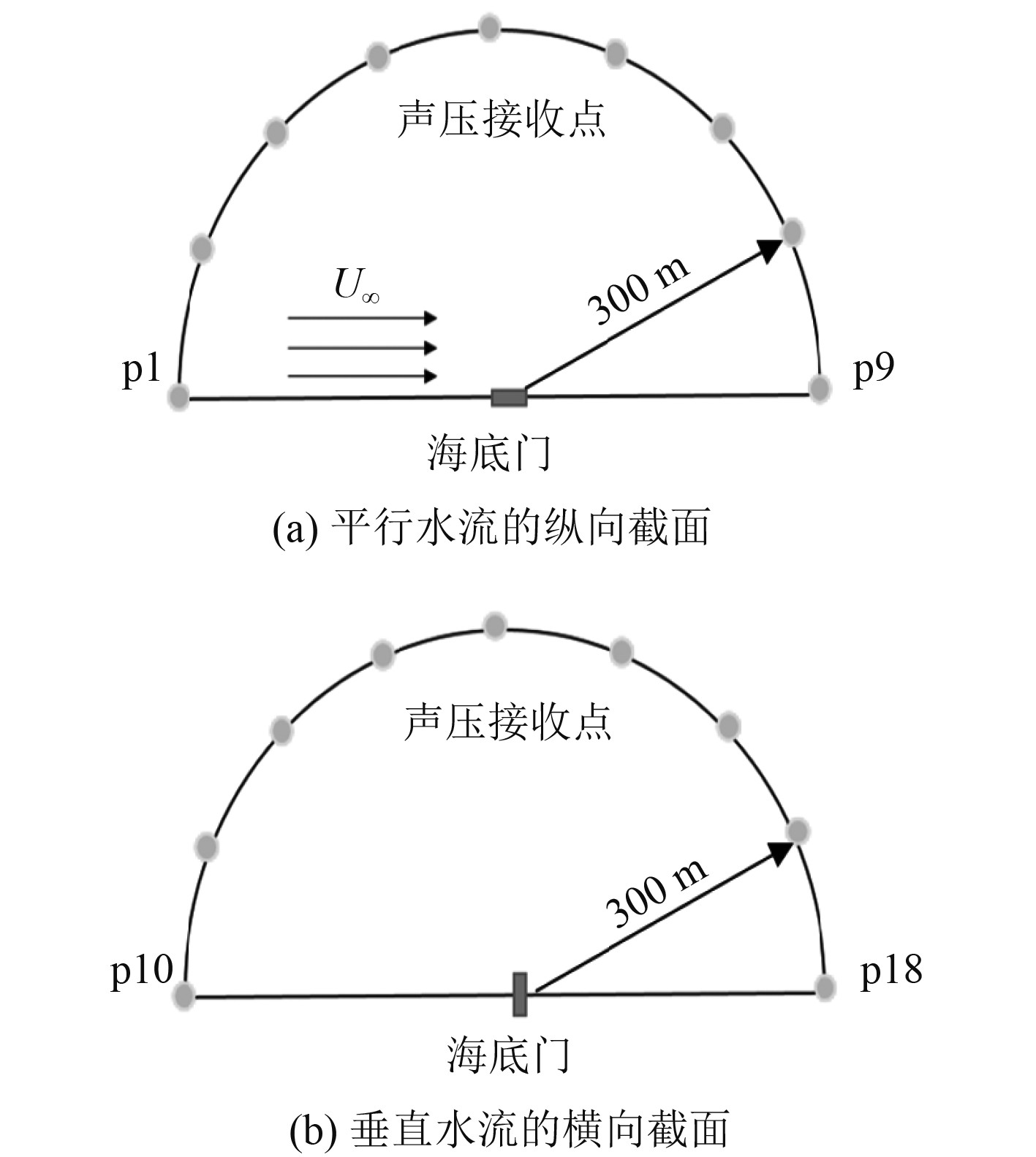
采用URANS、Realizable k-ε湍流模型和FW-H方法进行计算，时间步长设置为1×10⁻⁴ s，计算步数为5000步，计算频率达到5 kHz，频率步长为2 Hz，选择声压级作为评判噪声的水平，参考声压10⁻⁶ Pa。水动力声压接收点与海底门的相对位置如图8所示，各截面设定9个声压接收点以获得不同方位的声学特征。

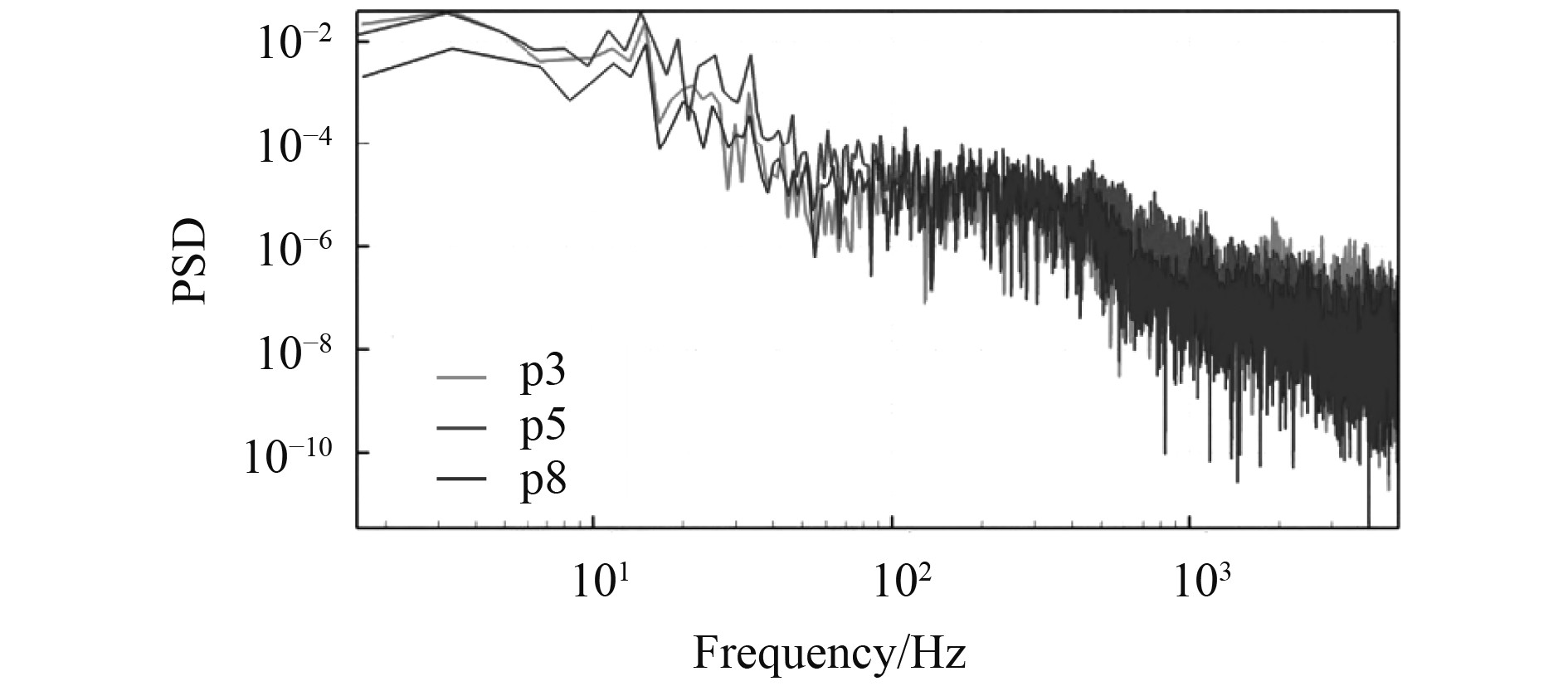
提取频率范围为2 Hz~5 kHz的水下噪声，将流场计算收敛后的数据采用快速傅里叶变换，且将时间域的声压信号转换为频域的声压信号后进行功率谱密度PSD分析。图9为典型声压接收点（p3、p5、p8）功率谱密度（PSD），p5点在海底门的正前方，频谱图声压级明显高于另外2个监测点。在40 Hz以下频谱数值较大，说明海底门格栅的水动力噪声以低频段贡献为主。总声压级能够展示噪声的指向性，而指向性是衡量声源方向特性的指标。图10为原始模型（baseline）在2个截面上的声指向性特征图。可知，2个截面上辐射噪声的特征基本相同，呈现出2侧小中间大的趋势，海底门平面正前方的监测点（p5、p15）总声压级最大，达到近116 dB，两侧的监测点（p1、p9、p10和p18）的最小。整体来看，纵向截面总声压级略低于横向界面，纵向截面平均总声压级为111.74 dB，横向截面平均总声压级为109.22 dB。

4 水下多孔介质降噪优化

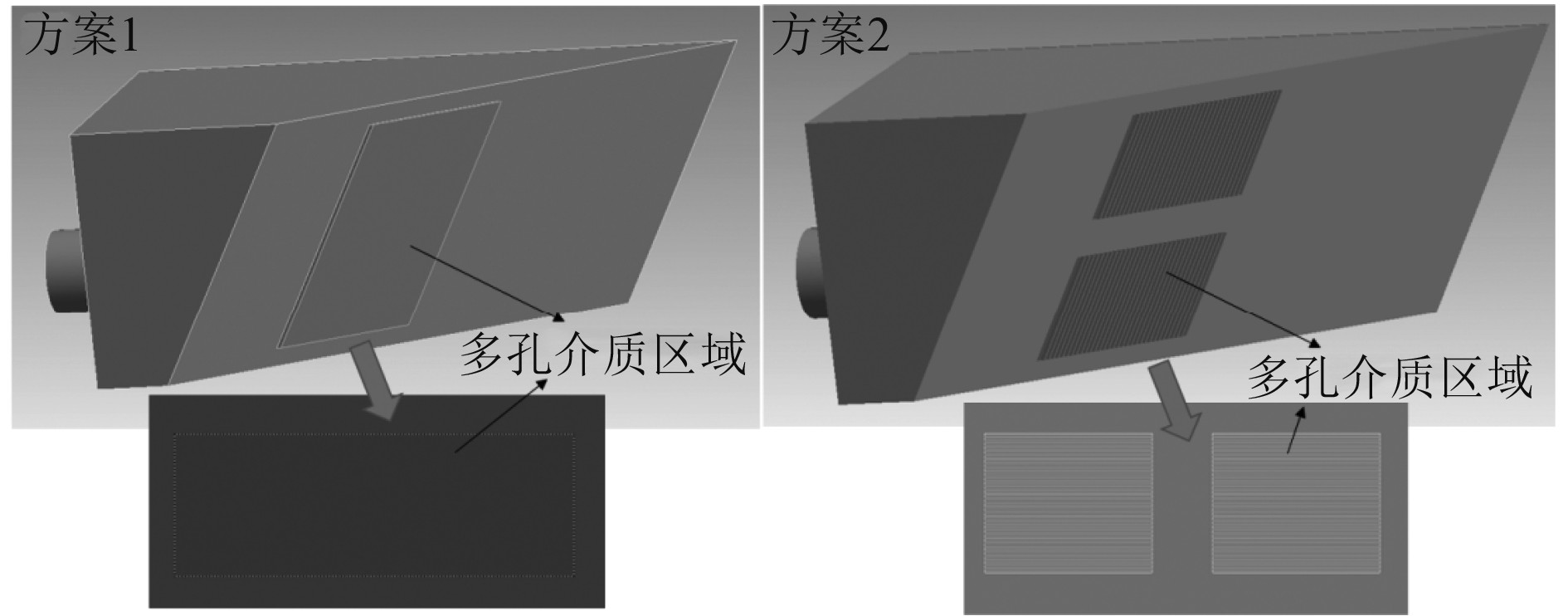
海底门原始模型（baseline）采用钢质格栅，拟对海底门进行降噪。方案1（porous1）：将原始模型的整个海底门入口区域全部采用水下多孔介质材料替换；方案2（porous2）：将原始模型的钢制格栅条采用水下多孔介质材料替换，如图11所示。方案3（rounding）：将原始模型的钢制格栅条进行半径2.5 mm倒圆角处理。

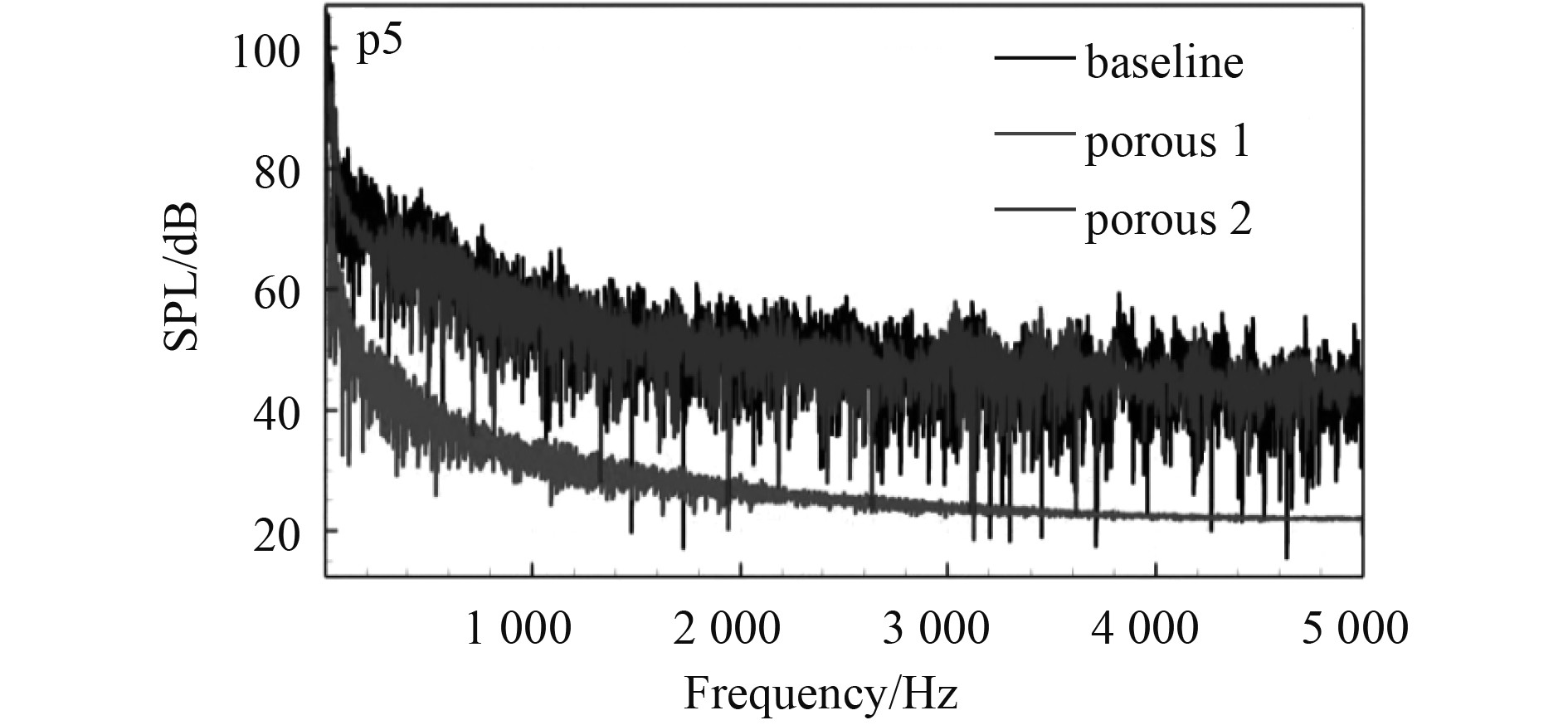
将多孔介质设定为各项同性，x、y、z方向的粘性阻力系数为2.111×10⁸，孔隙率为80%。首先，将3种降噪方案中远场声压接收点处的总声压级结果与原始模型进行对比，绘制出2个截面在极坐标下的总声压级指向性图（见图10）。3种方案与原始模型的远场辐射噪声存在一些共同特征，在2个截面上，总声压级最大的位置依然是在模型正前方。原始模型平均声压级110.5 dB，方案1平均声压级为97.6 dB，方案2平均声压级为107.1 dB，方案3平均声压级为110.8 dB。2种水下多孔介质材料模型方案的噪声相较于原模型均有所降低，其中方案1平均降噪为12.9 dB，方案2平均降噪为3.4 dB。而方案3对海底门的水动力噪声未产生积极效果，相比于原始方案，部分典型声压接收点的总声压级增加明显，说明对格栅条倒圆角并未起到降噪效果。图12为典型声压接收点（p5）的声压级（SPL）频谱曲线，对比可知，方案1（porous1）水下多孔介质材料应用对整个频率范围的噪声都有明显的抑制效果。水下噪声在低频段较大，随着频率升高快速衰减，频率升高越多，声压衰减幅度降低。

5 结　语

本文以某船用海底门为研究对象，对舷侧海底门的声场、湿模态、流场及流噪声进行数值计算，总结如下：

1）基于URANS，结合Realizable k-ε湍流模型和FW-H方法，对海底门流场及流噪声进行分析，数值计算表明，海水经海底门格栅缝流入阀箱，格栅背面出现了显著的流动分离，压力峰值条带沿格栅面对角线分布，海底门水动力噪声在低频段明显较大。

2）分别对海底门进行声传递损失及湿模态分析，得到声腔共振频率和海底门结构共振频率。在海底门低噪声设计时，应避开此在共振频率范围内的海水泵激励，或者通过改变海底门结构，使共振频率避开海水泵等运转设备频率。

3）海底门格栅条倒圆角并未起到降噪效果，当海底门入口替换成为水下多孔介质材料时，总声压级降低12.9 dB。当仅将格栅换成水下多孔介质时，总声压级降低3.4 dB，说明水下多孔介质材料在海底门降噪上有着较大的潜力。