0 引　言

多相永磁同步电机由于转矩脉动小，容错能力强，可使用低功率等级器件实现低压大功率调速等优点，被广泛应用于船舶电力推进系统 ^{[1 − 2]}。双Y移30°永磁同步电机（Dual Three- Phase Permanent Magnet Synchronous Motor，DTP-PMSM）作为船舶电力推进电机，在控制时需实时的转子位置信息，当机械的位置传感器系统在极端工况下出现故障时，无位置传感器控制可提高系统的容错能力，进一步增加设备的可靠性^{[3 − 4]}。

目前永磁同步电机的无位置传感器方法主要分为两类。一类是基于电机基波激励模型中与转速有关的量进行转子位置和速度估算，常见的有滑膜观测器^[5]，扩展卡尔曼滤波^[6]，模型参考自适应^[7]等。但电机在低速运行时，信噪比很低，有用的信息很难获取，因此此类算法更适用于电机中高速运行阶段。

另外一类是向电机注入高频信号，利用电机的凸极特性进行转子位置估算，此类方法不依赖电机基波模型，可实现电机在零低速阶段的无位置传感器控制^{[8 − 10]}。刘颖等^[11]提出了一种基于高频电流注入的无位置传感器控制方法，在估计同步旋转坐标系直轴上注入高频电流，然后检测交轴电流环PI输出的电压来估计转子位置。但PI控制难以跟踪高频电流，进而影响转子位置的估算。在高频电压注入的方法中，张烨璐等^[12]采用低速高频注入和高速滑膜观测器结合的复合算法进行DTP-PMSM全速范围内的无位置传感器控制，在低速时采用的旋转高频电压注入法主要依赖于电机转子的凸极性，对于表贴式电机并不适用。徐斌等^[13]采用了高频脉振电压注入法，高频电压信号从$ d $轴注入，利用磁饱和效应构造“饱和凸极”，通过对“凸极”进行跟踪来估算转子位置，适用于无结构凸极性电机。周中坚等^[14]提出了一种改进的高频脉振电压注入算法，直接从两相静止轴系$ \alpha 、\beta $轴的高频响应电流中提取转子的位置信息，分析了带通滤波器对系统信号幅值和相位的影响，但没有考虑低通滤波器对系统带宽和结构的影响。上述基于高频注入进行无位置传感器控制的方法，都需使用滤波器对高频的响应电流进行处理，而滤波器的多次使用会降低电流环和无位置观测器的带宽，造成估计延迟，影响控制系统的动态性能^[15]。

针对上述问题，本文提出一种基于高频方波注入法的DTP-PMSM低速无传感器控制策略，将信号注入周期和磁场定向控制（Field Oriented Controller，FOC）周期进行分离，在高频注入周期给同步旋转坐标系的$ d $轴注入高频方波信号，利用正交锁相环直接对$ \alpha {\text{ - }}\beta $两相静止坐标系上的高频响应电流进行处理，估算出转子位置信息，整个无位置传感器控制过程中均无需使用数字滤波器，提高了系统的动态性能和控制精度。

1 DTP-PMSM高频注入数学模型

基于矢量空间解耦（Vector Space Decomposition,VSD）坐标变换，将双三相永磁同步电机的六维空间向量经过坐标变换映射到3个相互正交的子平面，$ \alpha - \beta $子平面参与机电能量转换，将其转换到同步旋转坐标系$ d - q $，在d轴注入高频信号；$ x - y $子平面包含谐波分量，给定参考电流为0，设计电流环加以抑制；因为双三相电机2套绕组中性点隔离，对应到$ {o_1} - {o_2} $子平面的分量都为0，所以在控制时不予以考虑。

DTP-PMSM在同步旋转坐标$ d、q $轴上的电压方程为：

$ \left\{ \begin{gathered} {u_d} = R{i_d} + {L_d}\frac{{\mathrm{d}}}{{{{\mathrm{d}}t}}}{i_d} - {\omega _e}{L_q}{i_q}，\\ {u_q} = R{i_q} + {L_q}\frac{{\mathrm{d}}}{{{{\mathrm{d}}t}}}{i_q} + {\omega _e}{L_d}{i_d} + {\omega _e}{\psi _f} 。\end{gathered} \right. $

(1)

式中：$ R $为定子电阻；$ {u}_{d}、{u}_{q} $为$ d、q $轴的定子电压；$ {i}_{d}、{i}_{q} $为定子电流；$ {L}_{d}、{L}_{q} $为$ d、q $轴电感分量；$ {\omega _e} $为电角速度；$ {\psi _f} $为永磁体磁链。

当电机在零低速运行时，与转子角速度$ {\omega _e} $有关的项可忽略，对式（1）在高频信号注入情况下进行化简，得到：

$ \left[ \begin{gathered} {u_{dh}} \\ {u_{qh}} \\ \end{gathered} \right]{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{L_{dh}}}&0 \\ 0&{{L_{qh}}} \end{array}} \right]\frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left[ \begin{gathered} {i_{dh}} \\ {i_{qh}} \\ \end{gathered} \right]。$

(2)

式中：$ {u}_{dh}、{u}_{qh}、{i}_{dh}、{i}_{qh} $分别为$ d、q $轴的高频电压分量和电流分量，$ {L}_{dh}、{L}_{qh} $为$ d、q $轴定子高频电感。

2 传统脉振高频电压注入法

图1为表贴式DTP-PMSM基于传统脉振高频电压注入法的无位置传感器控制框图，向同步旋转坐标系的d轴注入高频电压信号，因为电感的非线性饱和，电机会呈现饱和凸极性，从估计同步旋转轴系提取高频响应电流进行处理，获得转子位置估算值，简单分析其实现过程。

两相静止坐标系$ \alpha {\text{ - }}\beta $，实际同步旋转坐标系$ d - q $和估计同步旋转坐标系$ \hat d - \hat q $这3个坐标系之间的关系如图2所示。

图中，$ {\hat \theta _e} $为估计转子位置角，$ {\theta _e} $为实际转子位置角，$ {\tilde \theta _e} $为位置角差，即$ {\tilde \theta _e} = {\theta _e} - {\hat \theta _e} $。可得在$ \hat d - \hat q $中，高频电流和电压的方程为：

$ \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left[ \begin{gathered} {{\hat i}_{dh}} \\ {{\hat i}_{qh}} \\ \end{gathered} \right] = {T^{ - 1}}\left( {{{\tilde \theta }_e}} \right)\frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left[ \begin{gathered} {i_{dh}} \\ {i_{qh}} \\ \end{gathered} \right]，$

(3)

$ \left[ \begin{gathered} {{\hat u}_{dh}} \\ {{\hat u}_{qh}} \\ \end{gathered} \right] = {T^{ - 1}}\left( {{{\tilde \theta }_e}} \right)\left[ \begin{gathered} {u_{dh}} \\ {u_{qh}} \\ \end{gathered} \right] $

(4)

式中：$ {\widehat{u}}_{dh}、{\widehat{u}}_{qh}、{\widehat{i}}_{dh}、{\widehat{i}}_{qh} $分别为$ \widehat{d}、\widehat{q} $轴的高频电压分量和电流分量；$ T\left( {{{\tilde \theta }_e}} \right) $为$ \hat d - \hat q $坐标向$ d - q $坐标变换的矩阵，$ T\left( {{{\tilde \theta }_e}} \right){\text{ = }}\left[ {\begin{array}{*{20}{c}} {\cos {{\tilde \theta }_e}}&{\sin {{\tilde \theta }_e}} \\ { - \sin {{\tilde \theta }_e}}&{\cos {{\tilde \theta }_e}} \end{array}} \right] $。

由式（2）～式（4）可得估计同步旋转坐标系$ \hat d - \hat q $中高频电压与电流信号的关系式如下：

$ \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left[ \begin{gathered} {{\hat i}_{dh}} \\ {{\hat i}_{qh}} \\ \end{gathered} \right] = {T^{ - 1}}\left( {{{\tilde \theta }_e}} \right)\left[ {\begin{array}{*{20}{c}} {\frac{1}{{{L_{dh}}}}}&0 \\ 0&{\frac{1}{{{L_{qh}}}}} \end{array}} \right]T\left( {{{\tilde \theta }_e}} \right)\left[ \begin{gathered} {{\hat u}_{dh}} \\ {{\hat u}_{qh}} \\ \end{gathered} \right]。$

(5)

估计同步旋转坐标系的$ \hat q $轴无需注入高频余弦信号，仅在$ \hat d $轴上注入。

$ \left\{ \begin{gathered} {{\hat u}_{dh}} = {u_h}\cos {\omega _h}t ，\\ {{\hat u}_{qh}} = 0。\end{gathered} \right. $

(6)

式中：$ {u_h} $表示注入电压信号幅值，$ {\omega _h} $为高频电压信号的频率。代入式（8）可得高频注入下$ \hat d - \hat q $响应电流为：

$ \left[ \begin{gathered} {{\hat i}_{dh}} \\ {{\hat i}_{qh}} \\ \end{gathered} \right]{\text{ = }}\frac{{{u_h}\sin {\omega _h}t}}{{{\omega _h}\left( {{L^2} - \Delta {L^2}} \right)}}\left[ \begin{gathered} L + \Delta L\cos 2{{\tilde \theta }_e} \\ \Delta L\sin 2{{\tilde \theta }_e} \\ \end{gathered} \right] 。$

(7)

式中，$ L = {{\left( {{L_{dh}} + {L_{qh}}} \right)} \mathord{\left/ {\vphantom {{\left( {{L_{dh}} + {L_{qh}}} \right)} 2}} \right. } 2}\Delta L = {{\left( {{L_{dh}} - {L_{qh}}} \right)} \mathord{\left/ {\vphantom {{\left( {{L_{dh}} - {L_{qh}}} \right)} 2}} \right. } 2} $。

将$ q $轴得到的高频响应电流$ {\hat i_{qh}} $与信号$ \sin \left( {{\omega _h}t} \right) $相乘，通过低通滤波器处理，得到转子位置误差信号，如下式：

$ \varepsilon = LPF\left( {{{\hat i}_{qh}}\sin {\omega _h}t} \right) = {k_\varepsilon }\sin 2{\tilde \theta _e}。$

(8)

式中，$ {k_\varepsilon } = {{{u_h}\left( {{L_q} - {L_d}} \right)} \mathord{\left/ {\vphantom {{{u_h}\left( {{L_q} - {L_d}} \right)} {2{\omega _h}{L_q}{L_d}}}} \right. } {2{\omega _h}{L_q}{L_d}}} $。误差信号再经过锁相环（Phase locked loop，PLL），然后得到转子的位置信息。

3 改进高频方波电压注入法

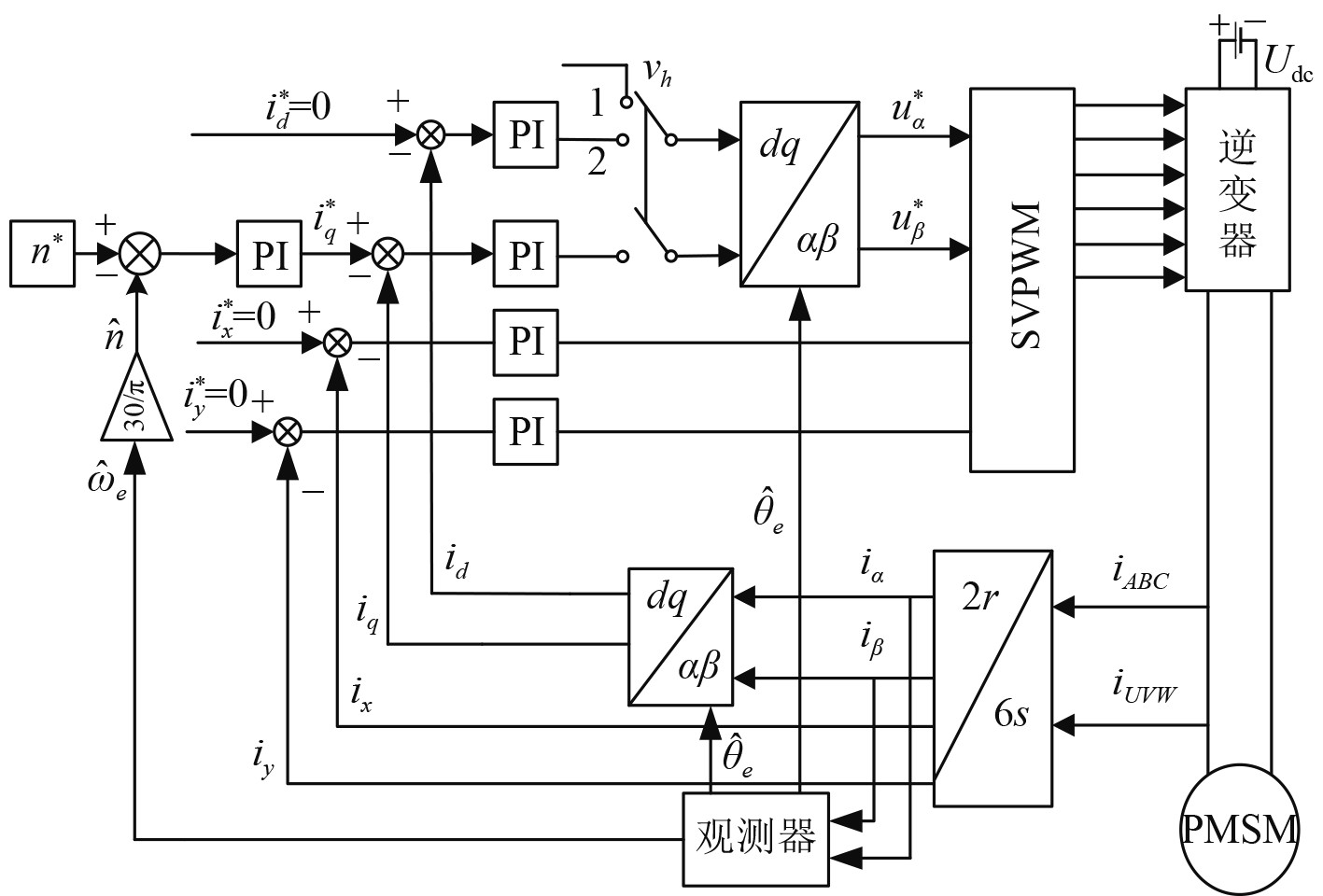
本文提出基于高频方波电压注入的DTP-PMSM低速阶段无传感器控制算法，框图如图3所示。

3.1 注入法原理分析

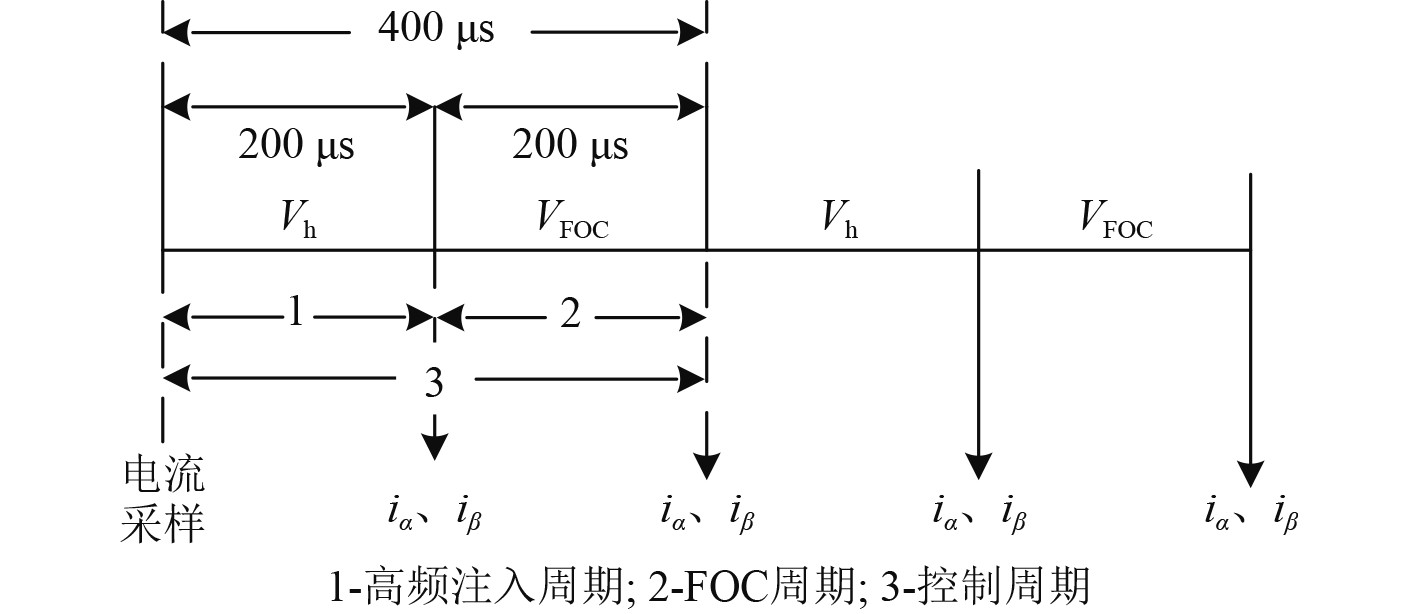
如图4所示，当开关位置在1时，向$ d $轴注入幅值一定的方波电压$ {V_h} $，$ q $轴电压为0，电机处于高频注入周期；当开关位置在2时，电机切换到FOC周期，此时，$ d $轴无高频电压注入，$ d、q $电压为电流环PI的输出值。高频注入周期与FOC周期交替进行，高频注入获得转子位置信息，提供给FOC对电机进行控制，实现了高频注入电压和控制电压的分离。并且得到的$ \alpha 、\beta $高频电流响应只与电感值有关，不依赖电机的凸极性，适用于表贴式永磁同步电机。控制交替时间见图4。

在高频注入周期前后对$ \alpha 、\beta $轴电流进行采样，从而估计出转子位置。本文中采样频率与开关频率相等，均为5 kHz，即周期为200 μs，高频注入末点即FOC起始点，得到转子位置信息的电流环PI控制器产生响应对电机进行控制，高频注入周期和FOC周期均为200 μs，控制周期为400 μs。

在高频注入环节输入观测器的高频电流不含有基波分量，所以无需滤波器滤除即可估计转子位置，而电流环PI只在FOC周期开始点有电流响应，不会响应太高频率的信号，因此在位置估计和电流环节均无需使用数字滤波器。

根据图2可得，在$ \hat d - \hat q $轴注入高频电压时，$ \alpha {\text{ - }}\beta $轴的高频响应电流公式为：

$ \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left[ \begin{gathered} {i_{\alpha h}} \\ {i_{\beta h}} \\ \end{gathered} \right] = {T^{ - 1}}\left( {{{\hat \theta }_e}} \right)\frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left[ \begin{gathered} {{\hat i}_{dh}} \\ {{\hat i}_{qh}} \\ \end{gathered} \right]。$

(9)

式中：$ T\left( {{{\hat \theta }_e}} \right) $为$ \alpha {\text{ - }}\beta $坐标向$ \hat d - \hat q $坐标变换的矩阵，$ T\left( {{{\hat \theta }_e}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {{\hat \theta }_e}}&{\sin {{\hat \theta }_e}} \\ { - \sin {{\hat \theta }_e}}&{\cos {{\hat \theta }_e}} \end{array}} \right] $。

将式（5）代入式（9），可得：

$ \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left[ \begin{gathered} {i_{\alpha h}} \\ {i_{\beta h}} \\ \end{gathered} \right] = {T^{ - 1}}\left( {{{\hat \theta }_e}} \right){T^{ - 1}}\left( {{{\tilde \theta }_e}} \right)\left[ {\begin{array}{*{20}{c}} {\frac{1}{{{L_{dh}}}}}&0 \\ 0&{\frac{1}{{{L_{qh}}}}} \end{array}} \right]T\left( {{{\tilde \theta }_e}} \right)\left[ \begin{gathered} {{\hat u}_{dh}} \\ {{\hat u}_{qh}} \\ \end{gathered} \right]。$

(10)

对于表贴式永磁电机交直轴电感近似相等，即$ {L_{dh}} = {L_{qh}} = {L_s} $，200 μs的开关周期下，$ {{{\mathrm{d}}i} \mathord{\left/ {\vphantom {{di} {dt}}} \right. } {{\mathrm{d}}t}} $可近似为$ {{\Delta i} \mathord{\left/ {\vphantom {{\Delta i} {\Delta t}}} \right. } {\Delta t}} $，式（10）可简化为：

$ \left[ \begin{gathered} \Delta {i_{\alpha h}} \\ \Delta {i_{\beta h}} \\ \end{gathered} \right] = \frac{{\Delta t}}{{{L_s}}}\left[ {\begin{array}{*{20}{c}} {\cos {{\hat \theta }_e}}&{ - \sin {{\hat \theta }_e}} \\ {\sin {{\hat \theta }_e}}&{\cos {{\hat \theta }_e}} \end{array}} \right]\left[ \begin{gathered} {{\hat u}_{dh}} \\ {{\hat u}_{qh}} \\ \end{gathered} \right]。$

(11)

式中：$ {\hat \theta _e} $为转子位置估计角，$ \Delta t $为一个高频注入周期。

高频注入周期内的注入电压可表示为式（2），$ {V_h} $为注入的电压幅值。

$ \left[ \begin{gathered} {{\hat u}_{dh}} \\ {{\hat u}_{qh}} \\ \end{gathered} \right] = \left[ \begin{gathered} {V_h} \\ {\text{0}} \\ \end{gathered} \right]。$

(12)

将式（12）代入式（11），可得高频注入后两相静止$ \alpha 、\beta $轴上的响应电流为：

$ \left[ \begin{gathered} \Delta {i_{\alpha h}} \\ \Delta {i_{\beta h}} \\ \end{gathered} \right] = \frac{{{V_h}\Delta t}}{{{L_s}}}\left[ \begin{gathered} \cos {{\hat \theta }_e} \\ \sin {{\hat \theta }_e} \\ \end{gathered} \right]。$

(13)

当估计角度误差足够小，即$ {\theta _e} - {\hat \theta _e} $趋近于0时，上式可写为：

$ \left[ \begin{gathered} \Delta {i_{\alpha h}} \\ \Delta {i_{\beta h}} \\ \end{gathered} \right] \approx \frac{{{V_h}\Delta t}}{{{L_s}}}\left[ \begin{gathered} \cos {\theta _e} \\ \sin {\theta _e} \\ \end{gathered} \right]。$

(14)

从式（13）可看出，$ \alpha 、\beta $轴提取的高频电流只于电感值有关，不依赖电机的凸极特性。

3.2 转子位置观测器

高频响应电流经过正交锁相环估算出转子位置角和转速，具体结构如图5所示。

根据图5可得转子位置误差信号为：

$ \varepsilon = \Delta {i_{\beta h}}\cos {\hat \theta _e} - \Delta {i_{\alpha h}}\sin {\hat \theta _e} = \frac{{{V_h}\Delta t}}{{{L_s}}}\sin \left( {{\theta _e} - {{\hat \theta }_e}} \right)。$

(15)

当实际角和估计角$ {\theta _e} - {\hat \theta _e} $误差很小时，上式可简化为：

$ \varepsilon \approx \frac{{{V_h}\Delta t}}{{{L_s}}}\left( {{\theta _e} - {{\hat \theta }_e}} \right) = {k_\varepsilon }\left( {{\theta _e} - {{\hat \theta }_e}} \right) 。$

(16)

式中，$ {k_\varepsilon } = \dfrac{{{V_h}\Delta t}}{{{L_s}}} $。

锁相环的闭环传递函数为：

$ \frac{{{{\hat \theta }_e}}}{{{\theta _e}}} = \frac{{{k_\varepsilon }{k_p}s + {k_\varepsilon }{k_i}}}{{{s^2} + {k_\varepsilon }{k_p}s + {k_\varepsilon }{k_i}}}。$

(17)

可看出$ {k_\varepsilon }{\text{ = }}{{{V_h}\Delta t} \mathord{\left/ {\vphantom {{{V_h}\Delta t} {{L_s}}}} \right. } {{L_s}}} $为正数，根据劳斯-霍尔维兹定理，当$ {k_\varepsilon }{k_p} $、$ {k_\varepsilon }{k_i} $均为正数的时候系统是稳定的，锁相环能够锁住角度，转子位置的估算值也能收敛于实际值。

4 仿真分析

基于Matlab/Simulink平台搭建DTP-PMSM无位置传感器控制系统模型，包括基于传统高频脉振电压注入和改进基于高频方波电压注入的模型。在低速阶段模拟船舶运行过程中常见的转速突变和负荷突变工况分别进行仿真，某船电机参数如表1所示。

4.1 转速突变仿真

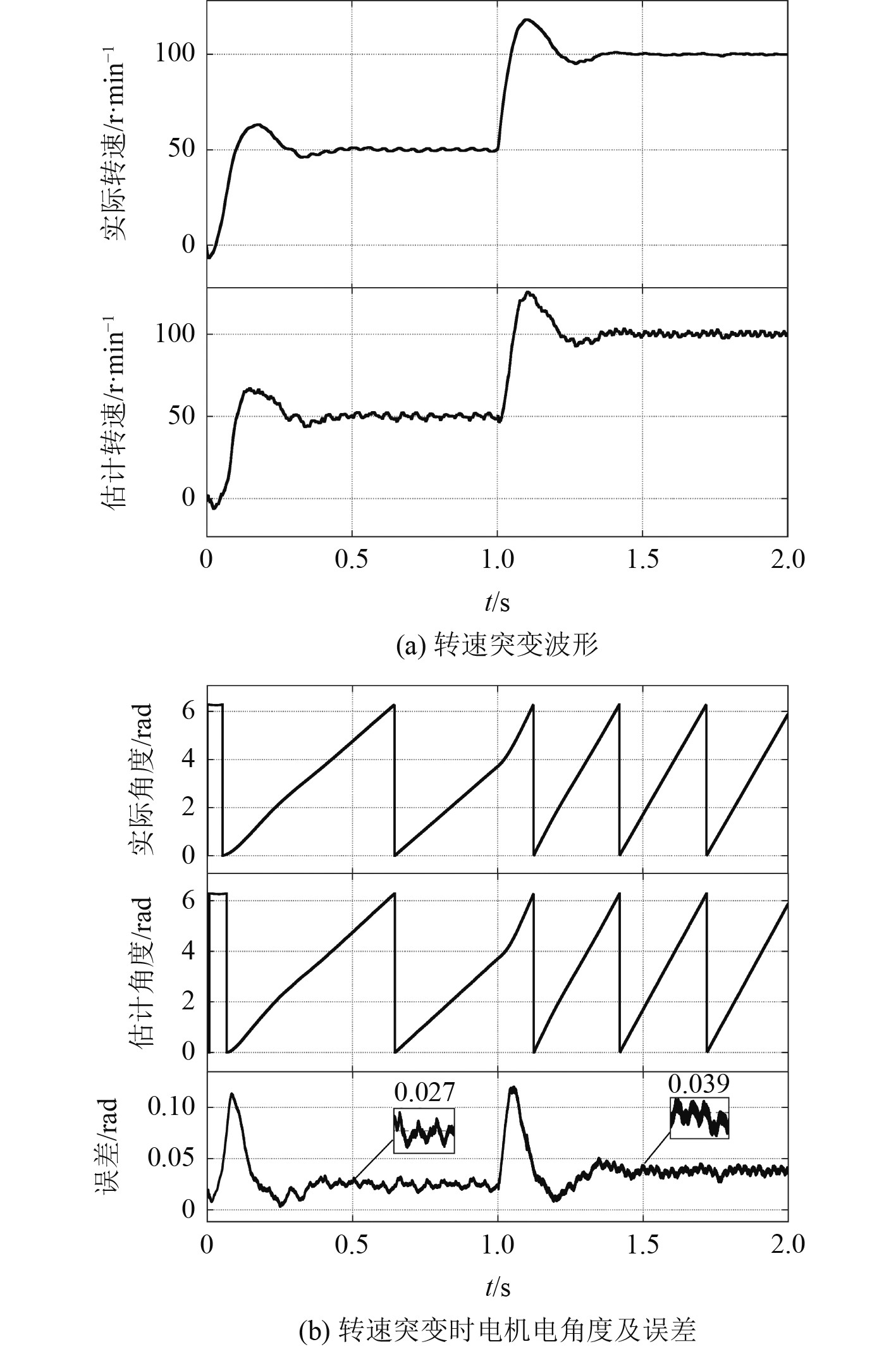
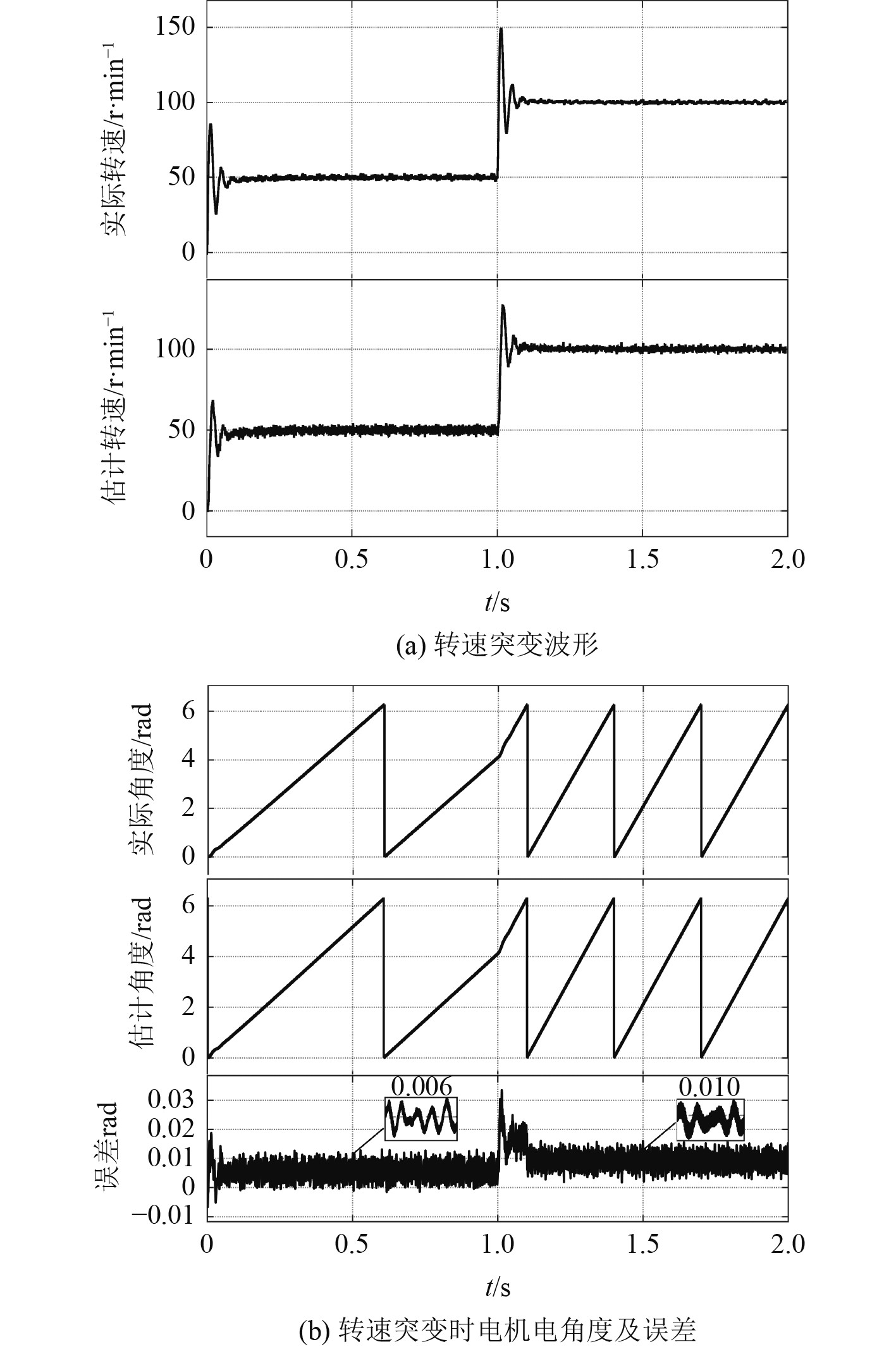
给定电机起动转速为50 r/min，在1.0 s时突加到100 r/min，负载恒定为100 N·m，图6（a）和图7（a）分别为基于传统高频注入和改进高频方波注入得到的电机转速突变下，实际转速和估计转速的对比波形。图6（b）和图7（b）分别为转速突变下电机转子的实际角度，估计角度和角度估计误差。

从图6可看出，转速突变时基于传统高频脉振电压注入的电机可有效估算转子位置和转速。与图7的转速和位置角波形对比可看出，传统方法存在一定的响应延迟，在转速突变后需约0.4 s才能重新追踪到转子位置并恢复稳定，而改进方法只需0.1 s；传统方法在50 r/min时，转子位置估计误差约为0.027 rad，100 r/min时误差约为0.039 rad，而改进方法在50 r/min时，角度估计误差为0.006 rad，100 r/min时为0.01 rad。可看出模型在低速阶段转速突变时改进高频方波注入法，在系统响应速度和角度估计精度上均好于传统高频脉振注入法。

4.2 负荷突变仿真

设置电机转速恒定在50 r/min，给定初始负载转矩为100 N·m，0.5 s突加到300 N·m，1.5突减到200 N·m，图8（a）和图9（a）分别为基于传统高频注入和改进高频方波注入得到的电机电磁转矩波形，图8（b）和图9（b）为负载突变下转子位置角的实际值、估计值和估算误差。

从图8和图9可看出，当电机低速阶段负荷发生突变时，基于2种方法的模型都能够有效地估计转子位置信息，但相比较改进的高频方波注入法，基于传统高频脉振电压注入法控制的电机在负荷突变后会出现较大波动，负荷突增时电磁转矩超调量约为23%，而且需约0.4 s才恢复稳定，远大于改进方法约16%的超调量和0.1 s的响应时间。改进的高频方波电压注入法在负荷突变过程中，转子位置角误差基本稳定在0.01 rad，远小于传统高频注入的0.037 rad。

经过对比仿真分析可看出，针对表贴式DTP-PMSM低速无位置传感器控制，无论是转速突变还是负荷突变的工况下，改进高频方波电压注入法与传统高频脉振电压注入法相比，因为减少了滤波器的使用，能够以更快的响应速度来追踪转子实际位置，具有更好的动态性能和稳定精度。

5 结　语

针对传统高频脉振电压注入法应用于表贴式双三相永磁同步电机时，存在凸极特性不明显和滤波器过多使用造成的滞后效应叠加、动态性能下降等问题。本文提出一种将高频方波注入周期和磁场定向控制周期分离的方法，直接从两相静止坐标轴$ \alpha 、\beta $上提取高频响应电流$ {i}_{\alpha h}、{i}_{\beta h} $，经过正交锁相环来估计转子位置信息，整个控制过程也避免了数字滤波器的使用。通过仿真分析，对比这2种方法在转速突变和负荷突变2种船舶常见工况下得到的参数波形，验证了改进方法在转子位置估算性能上优于传统方法，有着更好的动态性能和估算精度。该方法可提升船舶电力推进系统低速运行时电机控制的性能，具有一定的实际应用意义。