2. 江苏大学,江苏 镇江 212013
2. Jiangsu University, Zhenjiang 212013, China
为缓解传统能源供需紧张关系,应对能源危机及严峻的环境问题,研究者们提出了通过浮式风力机俘获位于深远海的丰富风资源,并利用其进行发电的设想[1]。国外早在20世纪与21世纪初就已开始布局海上浮式风机。2003 年,荷兰代夫特大学联合多家公司,提出各种形式的浮式风机基础结构,如圆台形浮体(pill-box),三角平台(triple floater),四边形平台(Quadruple floater),经过可行性论证后,认为三角平台为海上浮式风机平台的最优方案[2]。随后,美国、日本、挪威等国多以Spar形式、TLP (张力腿)、三角形半潜平台为研究对象,并得出这3种结构形式基础的固有周期位于常规波浪能量范围之外,具有良好的运动性能结论[3-4]。
国内在浮式风电项目上发展较晚,近年来实际装机的大型浮式风机仅有2座,分别为“三峡引领”号和“扶摇”号,皆为三角形半潜平台。这2座浮式风机项目均呈现出尺度大、单机容量大和抗强台风的特点,这也是目前深远海浮式风机设计的趋势[5]。
平台稳定性研究方面,Collu[6]参考石油平台的相关规范建立了浮式风机平台的稳性评价标准和规范体系,总结了相近行业的稳性研究方法,为浮式风机规范的制定提供了参考。李青等[7]基于Windfloat半潜式浮式风机,探究不同结构参数(立柱直径、立柱间距以及吃水深度等)下的Windfloat平台模型稳性、附加质量、辐射阻尼与一阶波浪激励力的变化规律。
本文基于前人的理论和经验,设计了一种V型浮式风机平台构型,该构型能有效减少钢材利用率,提升经济性能,且由于减少了一道连接舱,更便于操作安装。进一步地,通过NAPA软件计算结构的稳定性,验证了结构设计合理可靠。
1 基本理论及规范 1.1 风倾力矩计算规范浮式风机所受风倾力矩需考虑风机产生的气动推力和风作用在塔柱上产生的风压载荷,风倾力矩可根据式(1)计算[8],其中气动推力的大小可根据图1选取(未达到切出风速时)。

|
图 1 NREL 5MW风机气动推力 Fig. 1 NREL 5MW wind turbine thrust |
| $ M{\text{ = }}{F_h}{H_h} + {F_{{\mathrm{wind}}}}{H_z} 。$ | (1) |
式中:
当风速达到切出风速风力机停机时,其气动推力计算式如下:
| $ {F_h} = \frac{1}{2}{C_{DD}}\rho {V_r}^2A。$ | (2) |
式中:
利用规范计算恒定风力时的风载荷,通常取1小时内的平均风速代替稳定风载荷进行计算。规范中,风压系数
| $ p_{\mathrm{wind}}=0.61c_sc_hv_{ref}^2。$ | (3) |
式中:
相应的风力
| $ F\mathrm{_{wind}}=p_{\mathrm{wind}}A\mathrm{_{wind}}。$ | (4) |
式中:
海上浮式平台需满足一定的稳性要求,如图2所示。图中,

|
图 2 完整稳性曲线示意图 Fig. 2 Diagram of the intact stability curve |
表1给出了IMO的2009 MODU CODE对柱稳式平台(半潜式钻井平台属于柱稳式平台)完整稳性提出的相关要求。1)对柱稳式平台,至进水角处复原力矩曲线下的面积至少应比至同一限制角处风压倾侧力矩曲线下的面积大30%,即面积比
|
|
表 1 IMO完整稳性要求 Tab.1 IMO requirements of intact stability |
典型的计算工况主要为拖航工况(Transit),工作工况(Operation)和自存工况(Survival),其风速要求如表2所示[10]。
|
|
表 2 典型工况 Tab.2 List of typical test cases |
传统的运输船舶或海上工程船舶,长宽比较大,船舶在纵向上的稳定性远高于横向稳定性。但对于半潜式平台,横向和纵向的长度比接近,无法确定平台最危险的倾斜方向,故需对每个角度的倾斜轴均进行稳性评估。倾斜轴的示意图如图3所示。

|
图 3 倾斜轴示意图 Fig. 3 Diagram of inclination axis |
倾斜轴:过漂心,平台围绕其发生横倾的水平轴,与风向垂直。
危险轴:在平台倾斜过程中,位能(残余稳性)变化速率最小的倾斜轴称为危险轴。
方位角:倾斜轴相对于x轴的角度,用来表示不同角度的倾斜轴,顺时针为正。
横倾角:表示在确定的方位角下绕倾斜轴转动的倾斜角度。
2 稳性计算准确性分析 2.1 OC4 DeepCwind平台参数本文利用总体设计软件NAPA进行浮式风机的稳性计算,为了验证计算结果的准确性,试算了OC4 DeepCwind模型的完整稳性,并将计算结果与文献[11]结果进行对比,在相同工况下验证本文计算的准确性。
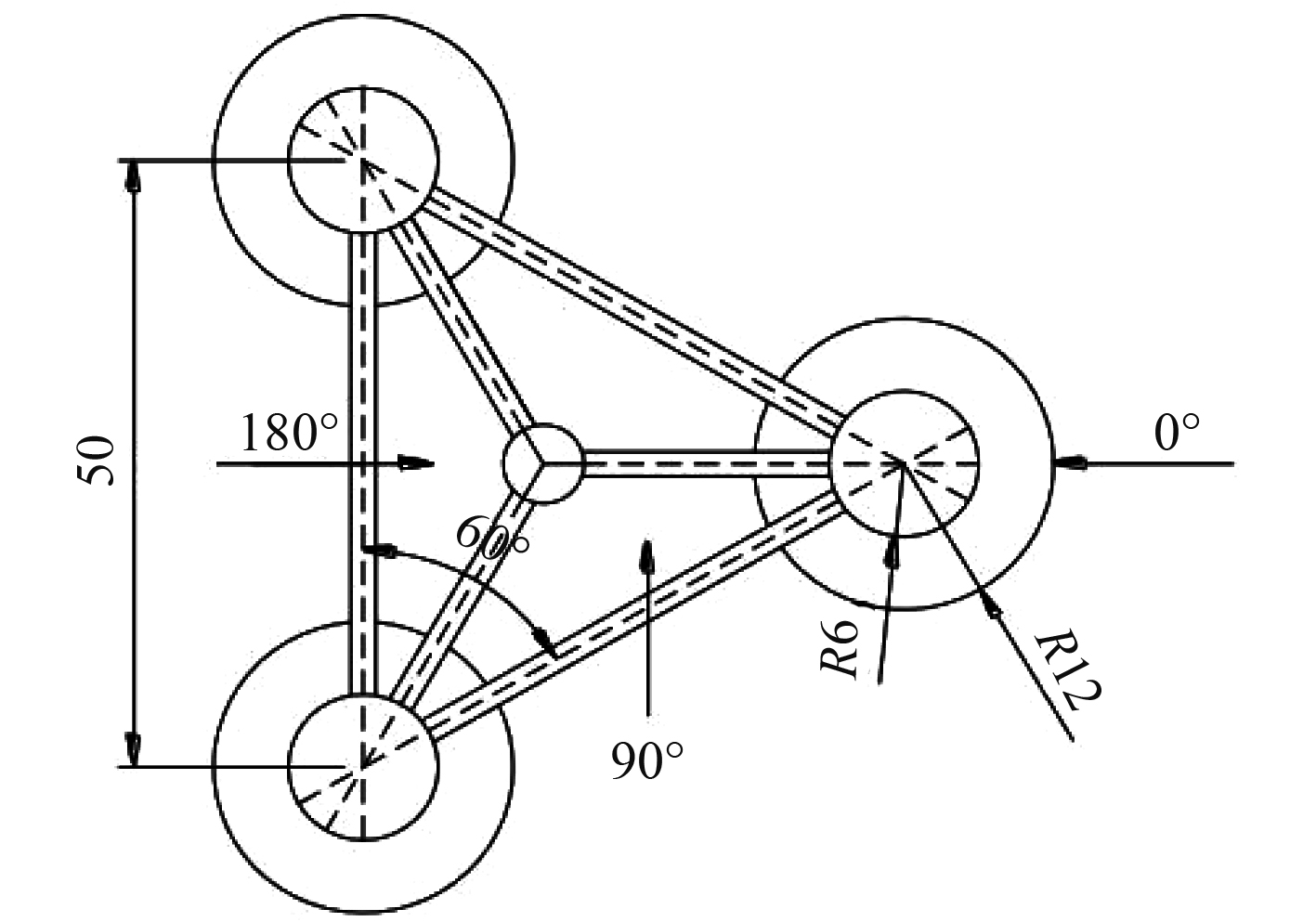
OC4 DeepCwind模型为美国国家可再生能源实验室(NREL)设计的一种5兆瓦级半潜式浮式风机平台,它由3个立柱以及中间的中柱组成,由多根细长杆件连接。三立柱底部设置有垂荡板,风机和塔架布置于中柱上。其模型和尺度参数如图4所示。
|
图 4 OC4平台示意图 Fig. 4 Diagram of the OC4 platform |
稳性结果对比如图5所示。核验工况为自存工况(Survival)下0º倾斜轴的完整稳性结果,工况如表3所示。从结果可看出,在风暴自存工况0º倾斜轴时,复原力臂(GZ)计算值与文献值基本吻合,表明本文的稳性计算数值方法具有较高的准确性。风倾力臂(L)同样吻合良好,表明利用规范理论计算风倾力矩准确可靠。

|
图 5 稳性结果对比 Fig. 5 Comparison of stability results |
|
|
表 3 工况表 Tab.3 List of test cases |
进一步校核稳性衡准可发现,复原力臂与风倾力臂下面积比为1.32,符合1.3的限值,静平衡角(第一交角)为13.3º,低于限值为17º,复原力臂从0º到第二交角均为正值,同样符合规范要求。可见风暴自存工况0º倾斜轴下,OC4-DeepCwind平台的完整稳性符合规范要求。
3 浮式风机平台设计 3.1 模型设计本文选取NREL 5MW风机,设计了一种V型底座的5兆瓦级浮式风机平台,浮式风机的整体模型及尺度参数如图6所示。从图中可看出,该V型浮式风机平台为三立柱式半潜式平台,由主柱AH、偏柱BH、底部垂荡板CH、底部连接舱DH和钢管架组成,主柱与底部垂荡板和连接舱构成V型结构,可有效减少钢材用量和焊接件数量,结构施工和安装更为简易;钢管架可增强结构的整体强度,改善模型的耐波性能。模型坐标系统已在图6中标出,坐标原点位于模型中心,指定后续计算0º工况为x轴正向,90º和180º工况如图6(c)所示,平台静水力参数如表4所示。

|
图 6 V型浮式风机示意图 Fig. 6 Diagram of V-type floating wind turbine |
|
|
表 4 静水力参数 Tab.4 Hydrostatic parameters |
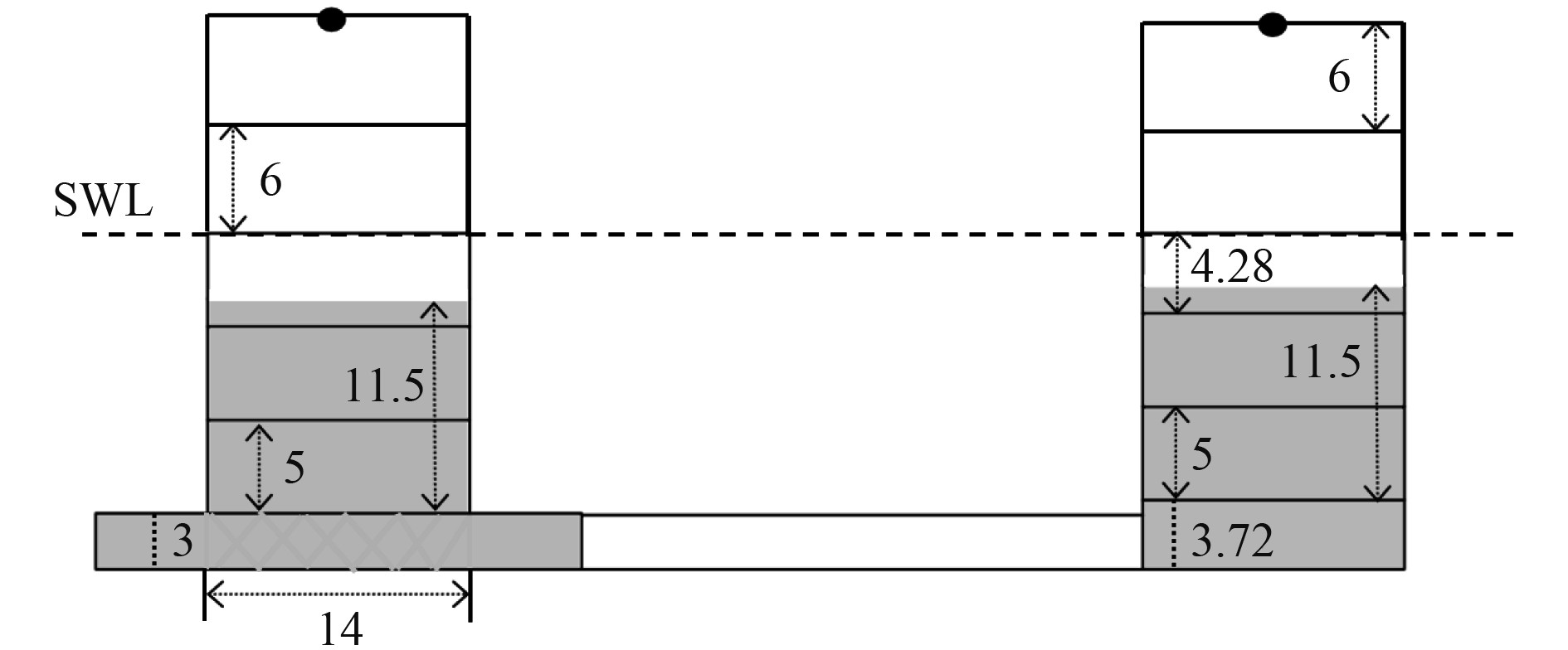
为了使浮式平台达到额定的吃水,需设置相关的分舱和压载,且由于该浮式风机为偏置型风机塔架,重心向风机侧偏移,需通过压载来平衡重心位置。图7为V型浮式风机压载及分舱开口示意图,右边为主柱AH,左边为偏柱BH。从图中可看出,主柱AH底部设置有混凝土压载舱,高度3.72 m,上部设置3个压载水舱,偏柱BH设置3个压载水舱,高度均为5 m,压载水总高11.5 m。偏柱下方为垂荡板CH,其中心位置设置一个圆柱形舱室,直径14 m,高度3 m(尺度均不计壁厚),舱室内部设置混凝土压载。圆柱形舱室外壁与垂荡板内壁围成圆环形封闭舱室,并在其中布置压载水降低整体重心。3个立柱吃水以上部分设置2个舱室,其中顶部为设备舱,需在此处设置舱口盖、透气孔、通风孔等风雨密开口。设备开口对后续的稳性计算极为重要,其开口坐标如表5所示。
|
图 7 压载及分舱开口示意图 Fig. 7 Diagram of ballast and subdivision openings |
|
|
表 5 开口坐标 Tab.5 Coordinate of opening |
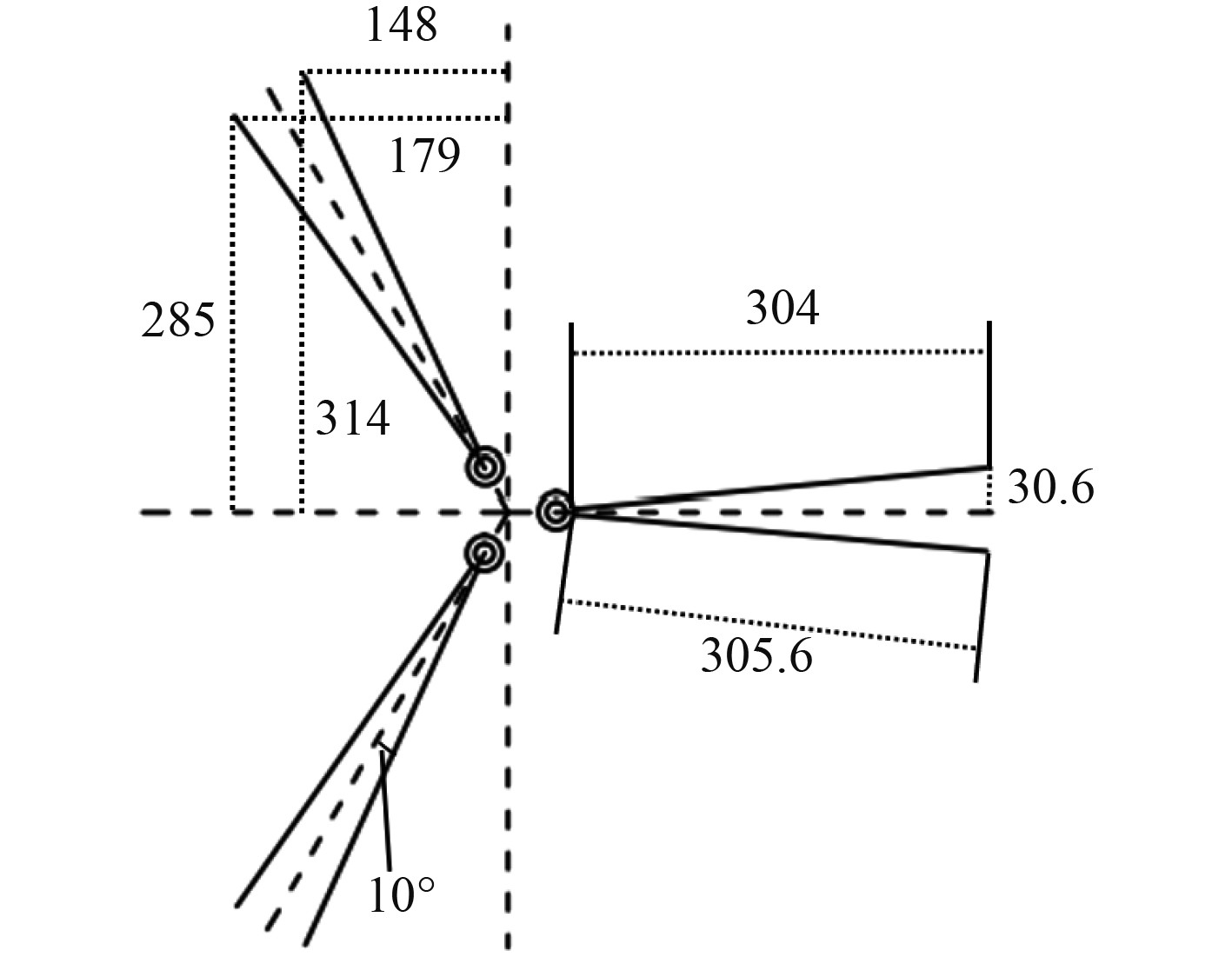
系泊系统提供相应的慢漂回复力,合理的布置系泊系统能够有效提升结构稳定性。V型浮式风机系泊设置如图8所示,表6给出了系泊布置的主要参数。
|
图 8 系泊系统示意图 Fig. 8 Diagram of the mooring system |
|
|
表 6 系泊系统参数 Tab.6 Mooring system parameters |
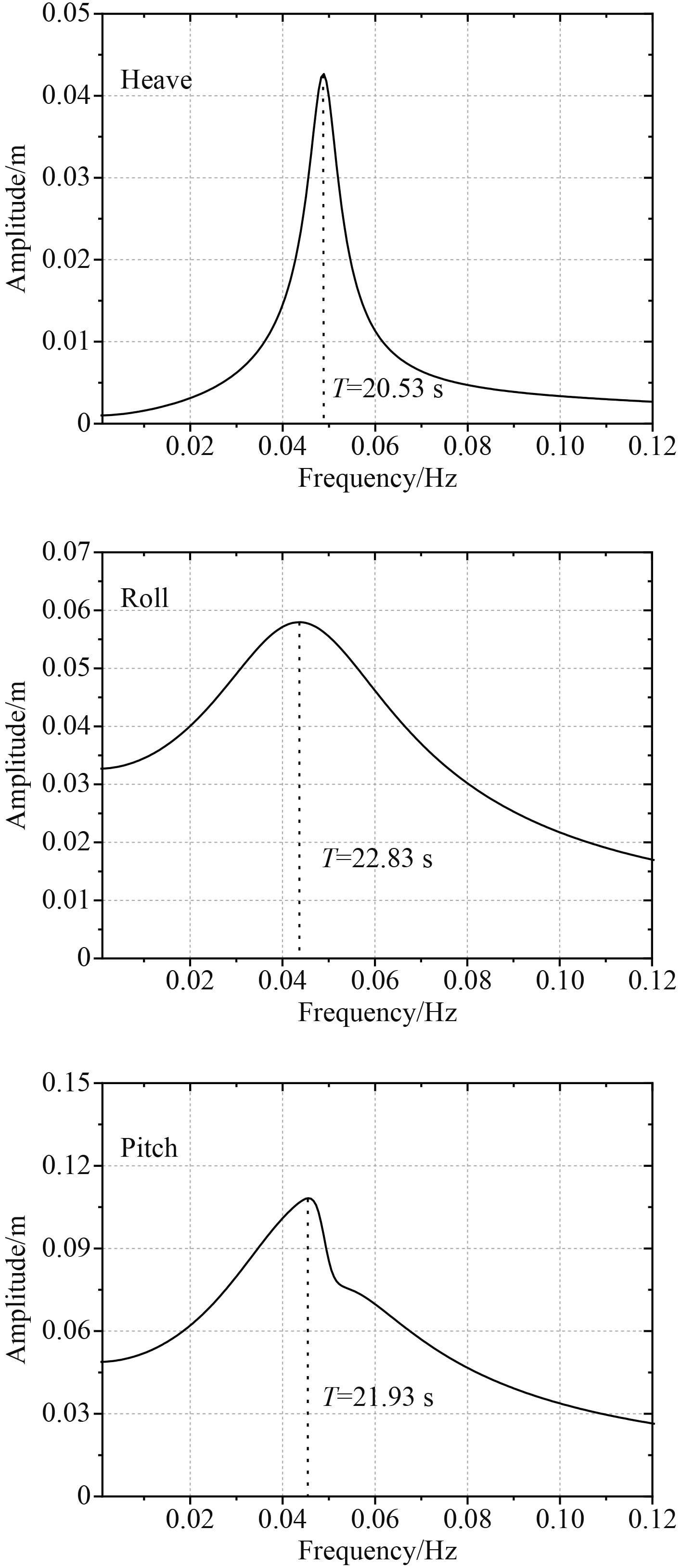
通过自由衰减测试得到各个自由度的固有周期,这可用来预测浮式平台的耐波性能。给定平台一个初始位移(摇摆),并关闭其他自由度,使平台自由衰减至平衡位置。通常半潜式平台垂荡(Heave)、横摇(Roll)和纵摇(Pitch)自由度的固有周期应大于或接近20 s,这样可避开波浪的能量集中范围。本文设计的V型浮式风机自由衰减的振幅谱,如图9所示。可以看出,3个自由度的振幅能量集中于固有周期附近,其中垂荡的固有周期T = 20.53 s,横摇的固有周期T = 22.83 s,纵摇的固有周期T = 21.93 s。从结果可知,该V型浮式风机平台设计可靠,固有周期较大,能够避开波浪的能量集中范围,耐波性较佳。
|
图 9 自由衰减振幅谱 Fig. 9 Free decaying amplitude spectrum |
浮式平台稳性校核需要考虑3种不同的工况,分别为拖航工况(Transit)、工作工况(Operation)和自存工况(Survival)。拖航工况为平台在无压载或小压载情况下拖航至工作区域中的稳性校核工况;工作工况和自存工况为特定风速下进行的稳性校核工况,风速要求见表2。
本文主要针对工作工况和自存工况的平台稳定性进行校核。需注意的是,NREL 5MW风力机的额定风速为11.4 m/s,此时基础平台受到巨大的气动推力和气动扭矩,极易致使平台倾覆,故本文工作工况的校核风速应设置为11.4 m/s。
由于平台的对称性,倾斜轴只需在0º ~ 90º之间,每隔15º设置一道。
工况设置如表7所示。
|
|
表 7 工况表 Tab.7 List of test cases |
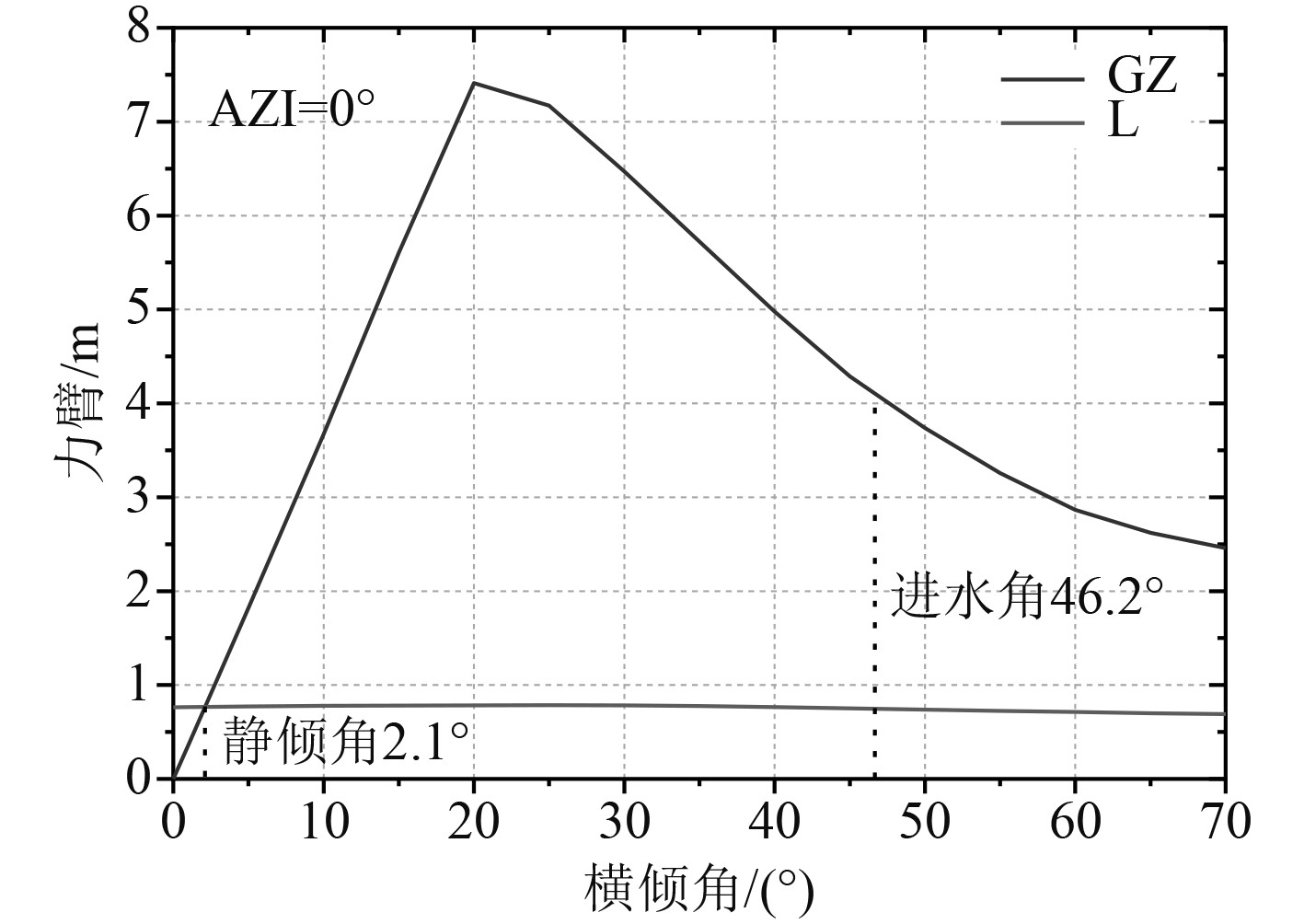
当风速达到额定风速时,发电功率达到额定的5 MW功率,此时轮毂中心气动推力最大(见图1)。当风速达到11.4 m/s时,气动推力可达到780 kN。塔架和平台出水部分还需承受风压载荷,2种倾覆力矩叠加下的稳性校核曲线,如图10所示。图中结果为V型平台在工作工况0º倾斜轴下的稳性曲线,其中“·”代表复原力臂(GZ),“−”代表风倾力臂(L)。从结果可计算得到该工况条件下,复原力矩曲线与风倾力矩曲线下(0º到进水角)的面积比φ = 6.45,静倾角θ1 = 2.1º,初稳性高GM = 20.86,复原力臂在0º到进水角之间均为正值,这符合表1的规范要求。
|
图 10 工作工况稳性校核曲线 Fig. 10 Stability curve of operation condition |
其他倾斜轴下的稳性数据如表8所示。可以看出,V型浮式风机平台在各个倾斜轴下稳性均符合规范要求,稳性余量较大,稳性良好。进一步对比分析发现,倾斜轴为30°时面积比φ最小为5.43,其他倾斜轴下稳性数据均优于30°轴,故30º倾斜轴为该平台的稳性危险轴。
|
|
表 8 工作工况稳性校核数据 Tab.8 Stability data of operation condition |
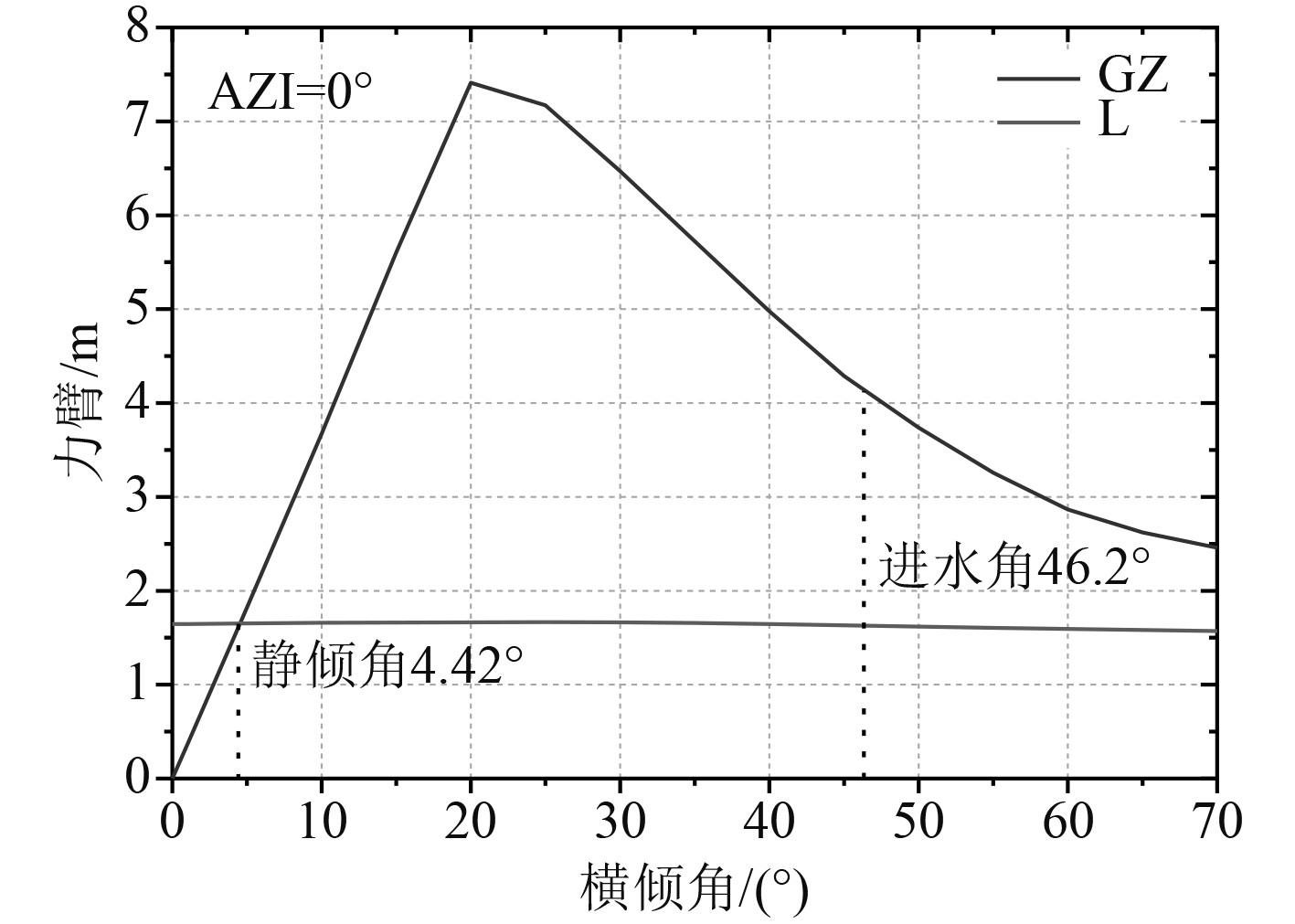
海洋结构物需抵御来自海上的各种极端海况,规范对极端海况下结构的稳定性提出了相关要求,需保证结构在100 kn(51.4 m/s)风速下,具有足够的稳性使结构不致倾覆。图11给出了V型浮式风机平台自存工况下,0º倾斜轴稳性校核曲线。从图中可计算得到该工况下,0º到进水角之间面积比φ = 3.02,静倾角θ1 = 4.42º,GM = 20.86,完全符合规范要求。
|
图 11 自存工况稳性校核曲线 Fig. 11 Stability curve of survival condition |
其他倾斜轴角度下稳性数据如表9所示。可以看出,V型浮式风机平台在自存工况各个倾斜轴下面积比φ均大于1.3的限值,静倾角θ1均小于17°,GZ在0º到进水角之间均为正值,且初稳性高较大,稳性符合规范的要求。
|
|
表 9 自存工况稳性校核数据 Tab.9 Stability data of survival condition |
进一步分析稳性结果可得到同样在30º倾斜轴时面积比φ最小,仅为2.68。此倾斜轴为该平台危险轴,需格外注意平台在该倾斜轴下的横倾运动。
4.4 自存工况许用重心高度许用重心高度(AVCG)是指平台在当前吃水压载下恰能满足稳性要求时的重心高度,即平台设计时重心高度不能超过许用重心高度的最小值,否则就会造成稳性不足的情况。
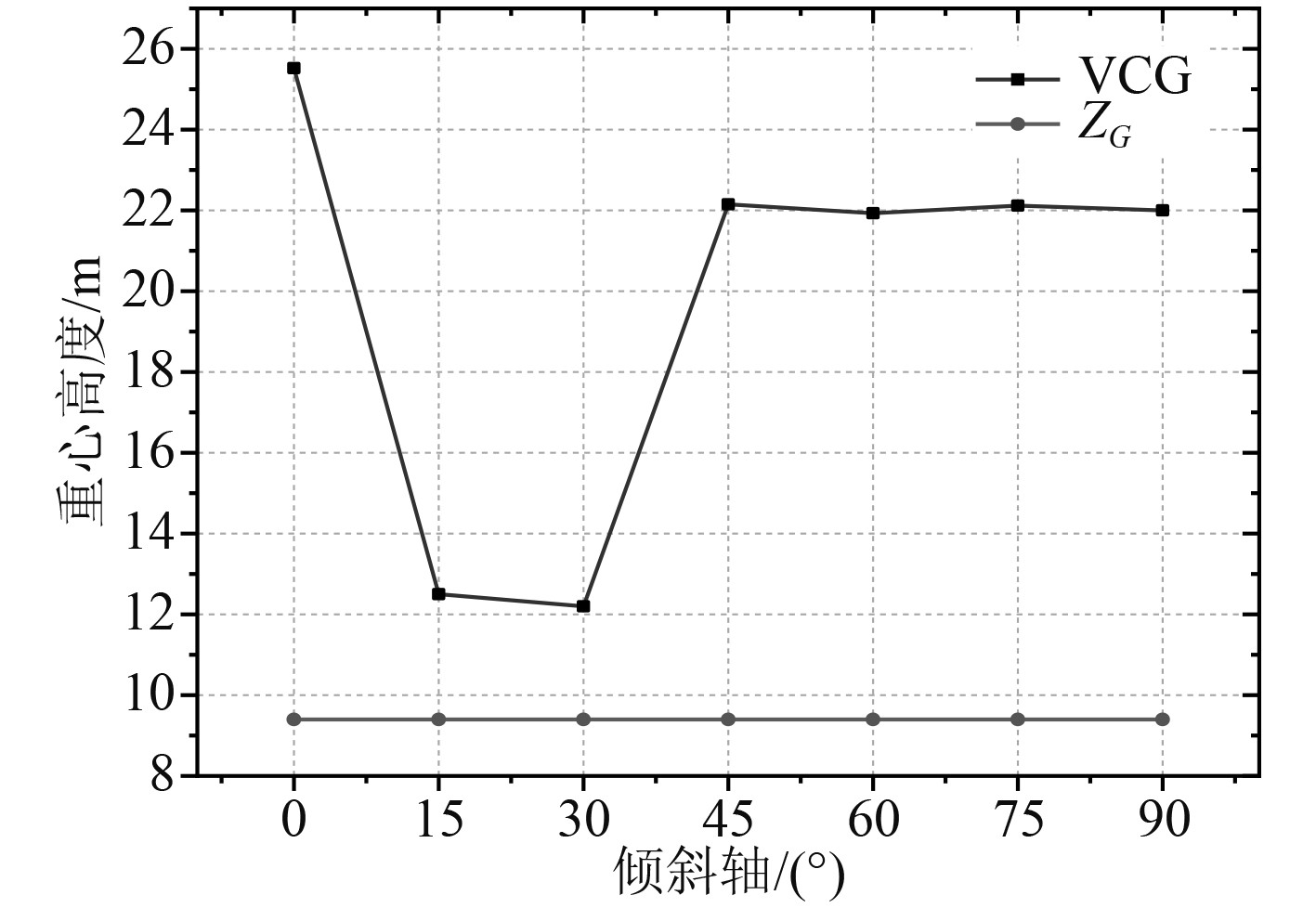
根据V型浮式风机平台的设计和完整稳性的计算,绘制自存工况下平台的许用重心高度曲线,如图12所示。图中一条线表示平台当前重心高度ZG(距基线),一条线表示其许用重心高度VCG(距基线)。可看出平台当前重心高度在各个倾斜轴下均低于许用重心高度,平台设计合理。进一步分析发现,平台最小许用重心高度出现在危险轴30º时,对应了此倾斜轴下稳性相对较差的现象,此时平台的重心高度不得大于12.2 m。
|
图 12 许用重心高度曲线 Fig. 12 Curve of allowable vertical center of gravity |
本文基于静力学原理计算分析浮式风机平台在工作海域中的结构完整稳性,通过OC4模型的稳性数据与文献结果的对比分析,验证了稳性计算的准确性。进一步,设计了一种搭载NREL 5MW风机的V型浮式风机平台,计算其在工作工况(风速U = 11.4 m/s)和自存工况(风速U = 51.4 m/s)下的结构完整稳性,结果如下:
1)V型浮式风机平台在工作工况和自存工况的各个倾斜轴下均能保证面积比φ > 1.3、静倾角θ1 < 17º、GZ在0º倾角到进水角之间均为正值,且初稳性高较大。这保证了平台足够的稳性,符合规范的要求,可以证明V型浮式风机平台设计的合理性。
2)V型浮式风机平台稳性危险轴为30º倾斜轴,此时平台复原力矩和风倾力矩曲线下面积比φ相对较小,平台稳性相对较差,后续计算需注意该倾斜轴下的横倾运动。
3)V型浮式风机平台在本文的设计吃水下,其许用重心高度(距基线)为12.2 m,实际装载设计后重心高度(距基线)为9.4 m,未超过许用重心高度,平台设计合理。
| [1] |
BALTROP N. Multiple unit floating offshore windfarm[C]// In Proceedings of a BWEA/DTI Seminar Great Britain: Prospects of Offshore Wind Energy: The State of the Art and Future Opportunities. , pages paper–9, October 1993.
|
| [2] |
ANDREW R, Henderson, Bernard Bulder, Rene Huijsmans, et al. Feasibility study of floating windfarms in shallow offshore sites[J]. Wind Engineering, 2003, 27(5): 405-418. DOI:10.1260/030952403322771002 |
| [3] |
RODDIER D , CERMELLI C , AUBAULT A , et al. WindFloat: A floating foundation for offshore wind turbines[J]. Journal of Renewable & Sustainable Energy, 2010, 2(3): 53.
|
| [4] |
ALEXANDRE A , PERCHER Y , CHOISNET T , et al. Coupled analysis and numerical model verification for the 2MW floatgen demonstrator project with IDEOL platform[C]//ASME 2018 1st International Offshore Wind Technical Conference, 2018.
|
| [5] |
王波. 全球首台抗台风型漂浮式海上风电机组建成[J]. 能源研究与信息, 2021, 37(3): 159.
|
| [6] |
COLLU M, MAGGI A, GUALENI P, et al. Stability requirements for floating offshore wind turbine (FOWT) during assembly and temporary phases: overview and application[J]. Ocean Engineering, 2014, 84: 164−175.
|
| [7] |
李青, 张礼贤, 高山, 等. 不同结构参数下漂浮式海上风机水动力性能分析[J]. 中南大学学报(自然科学版), 2022, 53(10): 4165−4173
|
| [8] |
中国船级社. 海上移动平台入级规范[S]. 北京: 人民交通出版社, 2012.
|
| [9] |
Sevastianov NB. Theoretical and practical models for probabilistic estimation of vessels stability[C]//Proceeding of International Workshop OPRADNOYE-1993, 1: 5.
|
| [10] |
高占胜, 蔡烽, 迟卫, 等. 风浪中舰船稳性计算[J]. 舰船科学技术, 2004, 26(3): 9−12.
|
| [11] |
任重进, 杨勇, 王力群, 等. 半潜漂浮式风机稳性数值分析[J]. 船海工程, 2019, 48(3): 95−98+104.
|
 2024, Vol. 46
2024, Vol. 46
