半潜式海洋平台作为一种典型的浮式结构物,因甲板面积大、稳定性高等优点被广泛应用于军民领域。目前,半潜式海洋平台已发展到第7代[1],工作水域已从浅水发展到超深水海域,但随之而来的是作业环境的越发恶劣,复杂的环境和多变的载荷致使疲劳成为半潜海洋平台结构发生破坏的主要模式之一。
在目前海洋工程领域,全时域法通常被认为是最精准的疲劳评估方法[2]。Xu等[3]基于时域分析法量化了波浪非线性对半潜式浮式平台疲劳损伤的影响。盛振国等[4]为解决风与浪对海洋工程结构的联合效应,提出一种风浪载荷叠加分析法,并对某5 MW大型海上风机进行时域范围的疲劳损伤计算,验证了该方法的可行性。
虽然时域分析法疲劳计算精度高,但完整时域分析过于耗时,对于全海况下的长期预报更是难以完成,从节约成本和提高疲劳分析效率角度出发,频域疲劳评估方法是更好的选择。谢文会等[5]利用频域谱分析法对半潜式平台的疲劳特征进行研究,得到半潜平台在不同海域下应力长期分布的Weibull形状参数。Du等[6]利用频域谱分析法对某单桩海洋平台进行疲劳计算,但结果发现频域谱分析法的结果与时域法结果相差3.4倍。研究表明[7],频域谱分析法评估结果偏差较大的主要原因是将随机过程的交变应力峰值认为服从Rayleigh窄带分布,但在实际的海洋结构物中,交变应力通常是一个宽带随机过程,用窄带分布模型进行疲劳寿命预测结果偏于保守。
为了对海洋结构物进行疲劳评估,同时克服时域法和频域法中各自缺点,本文提出一种频域-时域的混合疲劳评估方法,以某半潜式海洋平台为例,对该平台不同区域的热点进行疲劳评估,并分析不同浪向角和短期海况对疲劳损伤的贡献。
1 频域-时域混合疲劳评估方法基本思想 1.1 基本原理频域-时域混合疲劳评估分两部分进行,第1部分在频域中实现,第2部分在时域中实现,具体流程如图1所示。其基本思想为:将不规则的应力时历过程认为是一系列规则应力时历的叠加,利用傅里叶逆变换(IFFT)将频域法中的应力谱重建为应力时历,通过雨流计数法统计热点应力幅值与均值,最后基于Palmgren-Miner累积准则和S-N曲线得出疲劳累积损伤度。

|
图 1 频域-时域混合法流程图 Fig. 1 The flow chart of hybrid frequency-time domain method |
将波浪输入看成一个均值为0的平稳遍历随机过程,单边功率谱密度函数可描述为:
| $ {G_x}(f) = \frac{2}{T}{\left| {X({f_n},T)} \right|^2}。$ | (1) |
式中:
| $ X({f_n},T) = \Delta t\sum\limits_{k = 0}^{N - 1} {{x_k}} {e^{ - j2{\text{π}} {f_n}k/N}},\,\,\,\,\,\,n = 0,1, \cdots ,N/2。$ | (2) |
式(1)、式(2)联立,得下式:
| $ G({f_n}) = \frac{2}{{N\Delta t}}{\left| {\Delta t\sum\limits_{k = 0}^{N - 1} {{x_k}} {e^{ - j2{\text{π}} {f_n}k/N}}} \right|^2},\,\,\,n = 0,1, \cdots ,N/2。$ | (3) |
若单边功率谱密度已知,则频谱信号幅值
| $ \left| {X({f_n})} \right| = \sqrt {\frac{N}{{2\Delta t}}{G_X}({f_n})},\,\,\,\,\,n = 0,1, \cdots ,N/2。$ | (4) |
将式(4)傅里叶变化得下式:
| $ \left| {X({f_n})} \right| = \sqrt {\frac{N}{{2\Delta t}}{G_X}({f_n})} \,{e^{j{\phi _n}}}{{ = }}\left| {X({f_n})} \right|\,{e^{j{\phi _n}}},n = 0,1, \cdots ,N/2。$ | (5) |
其中:Φn为频谱信号的相位角,
最后,利用IFFT得到随机过程的离散时间序列X(t),表达式为:
| $ X(t) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {X({f_n})} {e^{j2{\text{π}} nt/N}},n = 0,1, \cdots ,N{{ - }}1。$ | (6) |
以某半潜式海洋平台为研究对象,结构为双浮筒、四立柱、四横撑和无斜撑设计,平台基本参数如表1所示。
|
|
表 1 半潜式海洋平台基本参数 Tab.1 Basic parameters of semi-submersible marine platform |
取自存工况为计算工况,平台受到的波浪载荷基于三维水动力理论直接计算,利用SESAM/Hydro D软件完成水动力载荷计算。考虑到海洋平台结构的对称性,浪向角设为0°~180°,间隔取15°,浪向在0°~180°等概率分布。考虑到热点应力功率谱密度函数的积分精度问题[8],计算频率设为0.1~2.0 rad/s,步长间隔为0.05 rad/s。
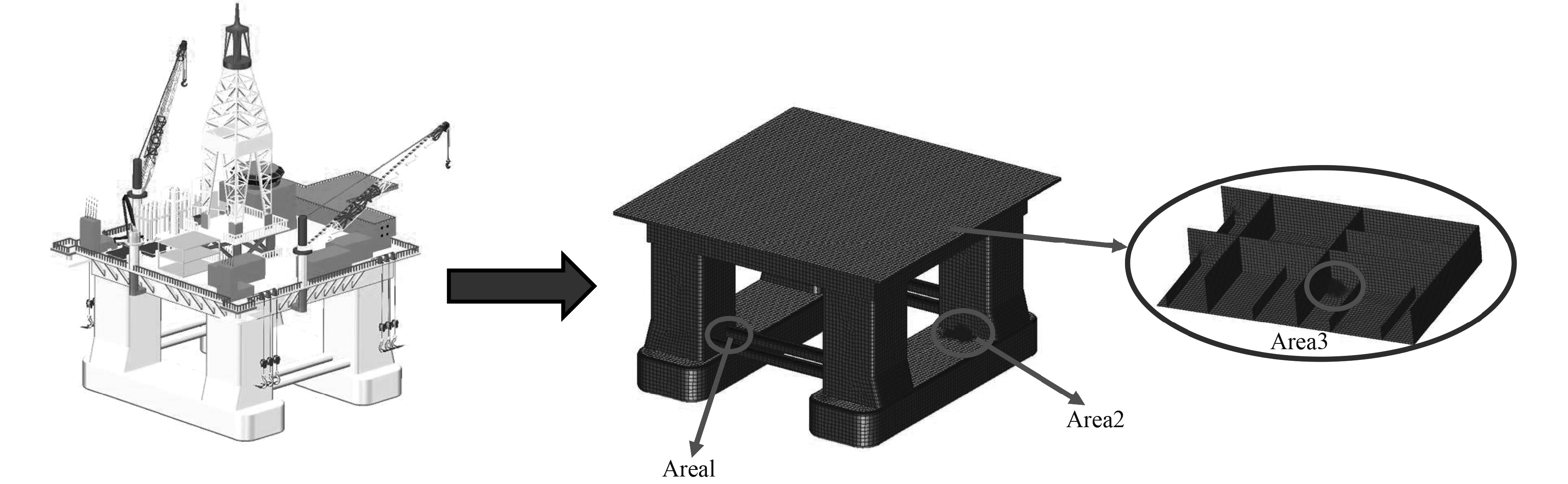
基于MSC.Patran建立半潜平台有限元模型,根据半潜平台的总体强度计算结果,选取3个连接区域作为疲劳评估的重点区域,共计7个热点,热点网格的细化原则参考CCS的疲劳评估规范[9],示意图如图2所示,表2为具体的评估热点。
|
图 2 疲劳评估热点区域 Fig. 2 Fatigue assessment hotspot areas |
|
|
表 2 疲劳评估热点选取 Tab.2 Hot spots of fatigue assessment |
将不同工况下,平台运动产生的惯性力和波浪动压力施加到有限元模型上得到应力响应,图3为Area1区域3个热点的应力响应传递函数曲线。

|
图 3 Area1区域的应力响应传递函数 Fig. 3 The stress transfer function of Area1 |
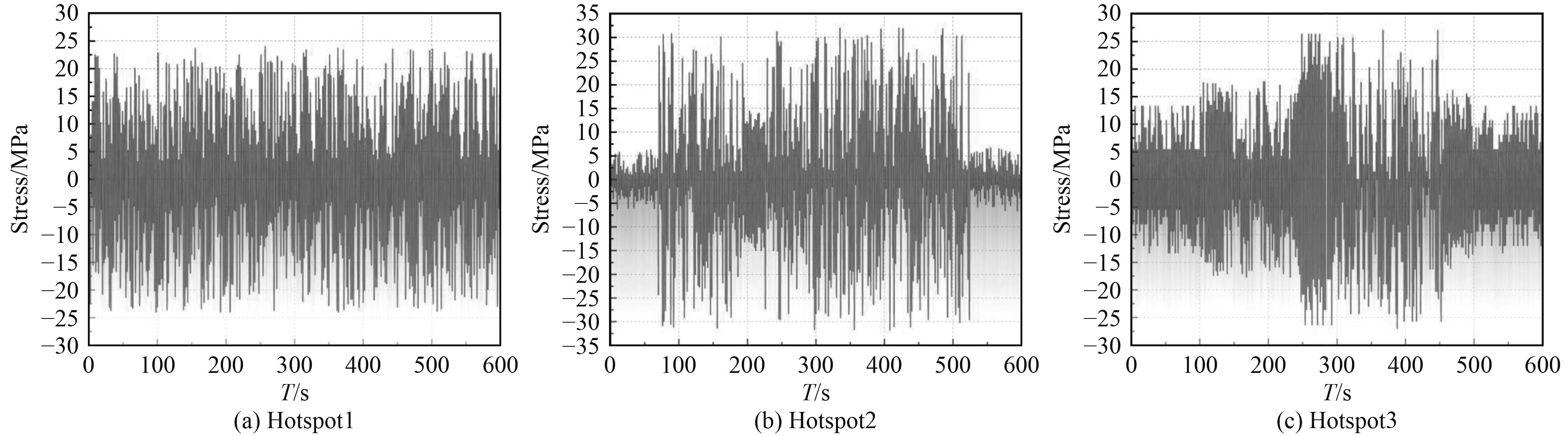
海洋平台作业海域为南海海域,南海海域波浪散布图见文献[10]。热点应力响应传递函数通过式(7)可得应力响应谱,进行信号转换,将频域响应谱转换成时域的应力时历,图4给出Area1区域热点在HS=3.5 m、Tz=8.5 s海况下,转化得到的应力时历结果,HS为有义波高,Tz为短期海况的特征周期。
|
图 4 在Hs=3.5 m,Tz=8.5 s海况下Area1区域的应力时历 Fig. 4 The stress history of Area1 under Hs=3.5 m,Tz=8.5 s |
| $ {G}_{XX}({\omega }_{e})={\left|{H}_{\sigma }({\omega }_{e})\right|}^{2}\cdot{G}_{\eta \eta }({\omega }_{e})。$ | (7) |
式中:
利用四峰谷值的雨流计数程序统计热点应力时历内的应力循环水平Si及循环次数ni。参考文献[11],每个海况计算时长定为3 h,计算步长设为0.5 s。图5给出Area1区域的3个热点在Hs=3.5 m、Tz=8.5 s海况下得到的3 h内热点应力时历计数结果。

|
图 5 Area1区域热点雨流计数结果 Fig. 5 The result of rainflow cycle counting of hotspots in Area1 |
统计得到热点应力水平后,结合Palmgren-Miner累积损伤理论和S-N曲线即可得到船体热点的疲劳损伤度。S-N曲线选择HSE(1995)[12]的C、D两根曲线,第i个海况下的累积损伤度Di计算如下:
| $ {D}_{i}={\displaystyle \sum _{s}\left(\frac{365\times 24\times {p}_{i}}{3}\cdot\frac{{n}_{s}}{{N}_{s}}\right)}。$ | (8) |
式中:pi为第i海况出现的概率;ns为该海况下的应力循环次数;Ns为总循环次数。
将各短期海况下热点的累积损伤度Di进行线性叠加,最终得到平台在自存工况下各热点总疲劳损伤度D,具体结果如表3所示。
|
|
表 3 各热点疲劳累积损伤度 Tab.3 The Fatigue cumulative damage of each hotspot |
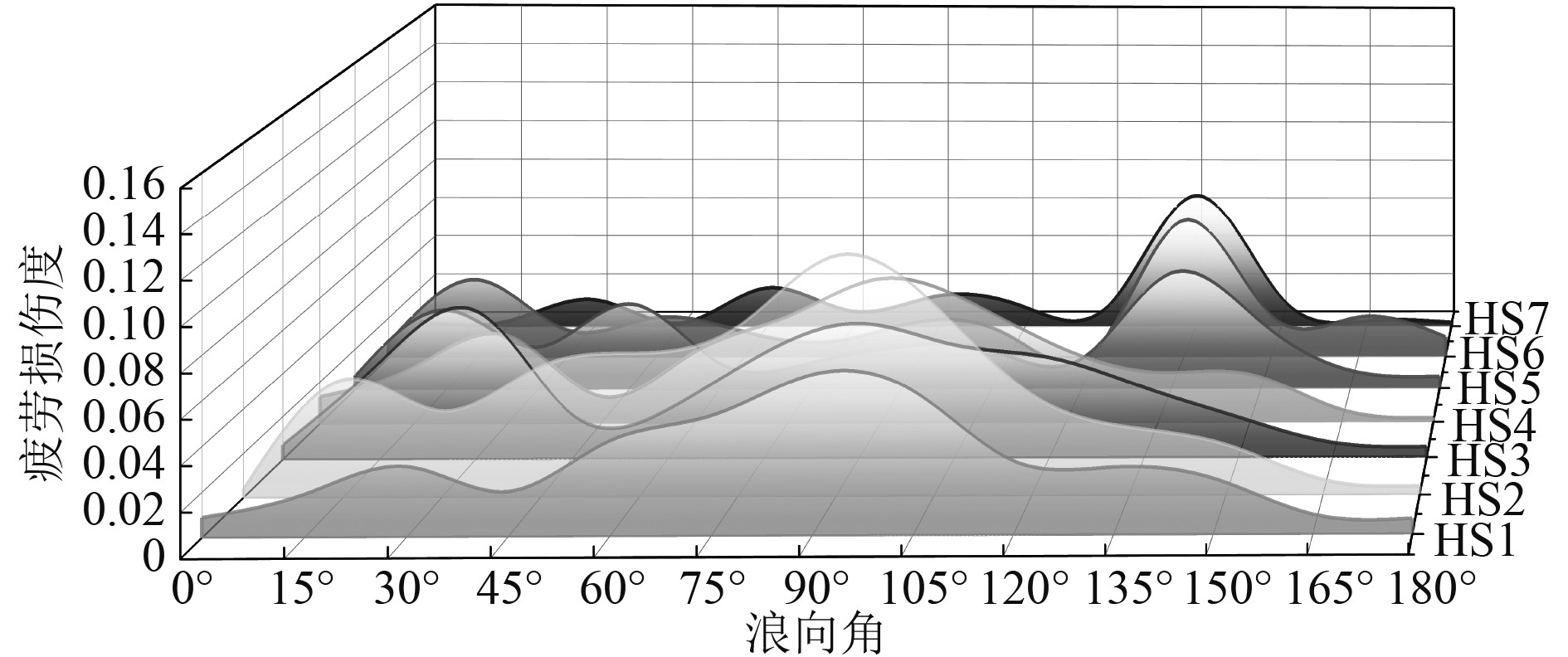
由于波浪谱函数会随浪向角、海况和船速的变化而变化,研究在航速的一定情况下,不同浪向角对平台热点疲劳损伤的影响,各热点在各浪向角下的疲劳结果如图6所示。从结果可发现,对Area1和Area2区域疲劳贡献最大的浪向为90°,对Area3区域疲劳贡献最大的浪向为135°。总体来看,横浪和斜浪工况对海洋平台疲劳损伤影响最大,75°、90°和135°浪向下各热点产生的疲劳损伤分别占到了总疲劳损伤的19%、27%和23%,而迎浪和随浪工况对海洋平台热点的疲劳损伤贡献较小。
|
图 6 各热点在不同浪向角下的疲劳损伤 Fig. 6 Fatigue damage of the hotspots under different wave angles |
基于南海海浪谱,研究不同短期海况因素对平台热点疲劳的影响,图7为海洋平台热点的疲劳损伤度在各短期海况下的分布情况。从整体来看,在有义波高HS=2.5~5.5 m,周期Tz=4.5~9.5 s附近的短期海况对海洋平台的疲劳贡献较大。但不同结构区域又有所差异,对Area1区域热点疲劳贡献较大的海况集中在HS=3~5.5 m、Tz=6.5~9.5 s附近,对Area2区域热点疲劳贡献较大的海况集中在HS=3~5.5 m、Tz=5~9.5 s附近,对Area3区域热点疲劳贡献较大的海况集中在HS=2~5.5 m、Tz=4~9.5 s。

|
图 7 平台疲劳损伤度在各短期海况下的分布 Fig. 7 The distribution of fatigue damage in short-term sea state |
为解决频域法和时域法在海洋平台疲劳评估中各自的缺陷,本文提出一种频域-时域混合疲劳评估方法,并以某半潜式海洋平台为例进行疲劳计算。通过分析得到以下结论:
1)频域-时域混合法以谱分析法为基础,在求得应力响应谱后,基于IFFT得到热点应力时间历程,既避免了频域法中Rayleigh窄带模型给结果带来的误差,又克服了时域法中计算过于耗时的问题,可适用于实际工程计算。
2)不同浪向角对海洋平台的疲劳贡献度不同,对平台疲劳贡献最大的浪向与所选的评估区域有关。但从整体上看,当平台在自存工况时,横浪和斜浪对半潜平台的疲劳影响更大,而迎浪和随浪对半潜平台热点的疲劳损伤贡献较小。
3)海洋平台的疲劳评估结果依赖于工作海域的海浪分布特征,针对南海海域,对海洋平台疲劳贡献度最大的海况集中在有义波高HS=2.5~5.5 m,周期Tz=4.5~9.5 s附近,具体不同结构区域又存在部分差异,寻找对疲劳损伤贡献度最大的短期海况需与评估位置相结合。
| [1] |
王金峰, 王永刚, 周庆, 等. 半潜式平台关键连接结构节点形式对疲劳强度的影响[J]. 中国海洋平台, 2021, 36(5): 1-7. |
| [2] |
LI Z, MAO W, RINGSBERG J W, et al. A comparative study of fatigue assessments of container ship structures using various direct calculation approaches[J]. Ocean Engineering, 2014, 82: 65−74.
|
| [3] |
XU K, ZHANG M, SHAO Y, et al. Effect of wave nonlinearity on fatigue damage and extreme responses of a semi-submersible floating wind turbine[J]. Applied Ocean Research, 2019, 91: 10189. |
| [4] |
盛振国, 任慧龙, 甄春博, 等. 基于时域载荷的海上风机基础结构疲劳分析[J]. 华中科技大学学报(自然科学版), 2014, 42(4): 96-100. |
| [5] |
谢文会, 谢彬, 赵晶瑞, 等. 半潜式平台结构疲劳特征研究[J]. 舰船科学技术, 2020, 42(7): 131-135. |
| [6] |
DU Junfeng, LI Huajun, ZHANG Min, et al. A novel hybrid frequency-time domain method for the fatigue damage assessment of offshore structures[J]. Ocean Engineering, 2015, 98.
|
| [7] |
周陈炎, 张佳宁, 申亚洲, 等. 宽带随机载荷下船舶结构的两种疲劳直接计算方法[J]. 大连海事大学学报, 2018, 44(1): 41−47.
|
| [8] |
胡毓仁, 陈伯真. 船舶与海洋工程结构疲劳可靠性[M]. 北京: 人民交通出版社, 1996.
|
| [9] |
中国船级社. 海洋工程结构物疲劳强度评估技术指南[S]. 北京: 人民交通出版社, 2022.
|
| [10] |
GAO Xifeng, LIU Xiaoyong, XUE Xutian, et al. Fracture mechanics-based mooring system fatigue analysis for a spar-based floating offshore wind turbine[J]. Ocean Engineering, 2021, 108618.
|
| [11] |
彭丽华. 考虑雨流计数的频域疲劳计算方法[D]. 武汉: 武汉理工大学, 2018.
|
| [12] |
HSE. Offshore technology report[R]. UK: BOMEL Ltd. , 2001.
|
 2024, Vol. 46
2024, Vol. 46
