0 引　言

AUV由于其自主性强、运动灵活等特点，在海洋观测^{[1 − 3]}、水下组网^[4,5]、水下目标跟踪^[6,7]等领域发挥了重要作用。动力学模型作为机器人研究的一项重要内容，在AUV设计阶段的受力分析、控制算法设计、计算机仿真验证等方面有着重要作用。

文献[8−9]通过N-E（Newton-Euler）方程研究了四旋翼无人机的动力学问题。在建模过程中，将旋翼作为质点，仅提供升力而忽略旋翼自身转动以及旋翼与本体之间的相互作用。文献[10−12]从能量出发，推导出机械手、Delta机器人的L-E（Lagrange-Euler）方程。该方法需计算动能和势能，通过求解二阶微分方程获得最终的动力学模型，计算机求解效率较低。Kane动力学运算效率高、模型结构简单，非常适合处理多刚体建模问题，满足实时控制的需求。该方法已应用在无人自行车^[13]、船载Stewart平台^[14]、太空探测车^[15]、F直升机吊装系统^[16]、机械手^[17]的动力学建模问题中。

本文将Kane方程应用在X舵欠驱动AUV的动力学建模中，可避免N-E方程建模时，需考虑的舵与AUV本体之间的相互作用力，也不需计算L-E方程建模时用到的动能和势能以及求解二阶微分方程。该方法可清晰地展示哪些力对X舵欠驱动AUV的动力学模型有贡献，也可非常方便地将外界作用力添加到动力学方程中。

1 坐标系与旋转矩阵

X舵欠驱动AUV是由本体和X舵组成，坐标系如图1和图2所示。为了便于公式的推导，本文引入Z函数。

AUV本体相对于惯性坐标系的旋转矩阵为：

$\begin{aligned} & {}_b^ER = {\left( {{}_E^bR} \right)^{\mathrm{T}}} = \\ & \left[ {\begin{array}{*{20}{c}} {{Z_4}{Z_6}}&{ - {Z_2}{Z_5} + {Z_1}{Z_3}{Z_6}}&{{Z_1}{Z_5} + {Z_2}{Z_3}{Z_6}} \\ {{Z_4}{Z_5}}&{{Z_2}{Z_6} + {Z_1}{Z_3}{Z_5}}&{ - {Z_1}{Z_6} + {Z_2}{Z_3}{Z_5}} \\ { - {Z_3}}&{{Z_1}{Z_4}}&{{Z_2}{Z_4}} \end{array}} \right]。\end{aligned}$

(1)

X舵是由4个独立的舵组成（见图2），${y_i}( i = 1,{\text{ }}2, {\text{ }}3,{\text{ }}4 )$为舵的转轴，${O_i}\left( {i = 1,{\text{ }}2,{\text{ }}3,{\text{ }}4} \right)$为与舵固连的载体坐标系的原点，位于舵与本体的连接处。${x_i}( i = 1,{\text{ }}2, {\text{ }}3,{\text{ }}4 )$初始位置与图1中的$x$轴平行，方向一致。${\delta _i}( i = 1,{\text{ }}2,{\text{ }}3,{\text{ }}4 )$为舵角。

舵1可看作是载体坐标系$\left\{ b \right\}$绕$x$轴旋转$- {135^ \circ }$，绕${y_1}$轴旋转${\delta _1}$得到；舵2可看作是载体坐标系$\left\{ b \right\}$绕$x$轴旋转$- {45^ \circ }$，绕${y_2}$轴旋转${\delta _2}$得到；舵3可看作是载体坐标系$\left\{ b \right\}$绕$x$轴旋转${45^ \circ }$，绕${y_3}$轴旋转${\delta _3}$得到；舵4可看作是载体坐标系$\left\{ b \right\}$绕$x$轴旋转${135^ \circ }$，绕${y_4}$轴旋转${\delta _4}$得到。AUV本体相对于舵的旋转矩阵为${}_b^1R$、${}_b^2R$、${}_b^3R$、${}_b^4R$。

2 运动学分析

X舵欠驱动AUV本体有6个自由度，X舵有4个自由度，因此，广义坐标可写为：

$q = \left\{ {{x_g}，{y_g}，{z_g}，\phi ，\theta ，\psi ，{\delta _1}，{\delta _2}，{\delta _3}，{\delta _4}} \right\}。$

(2)

式中：${x_g},{y_g},{z_g}$为AUV本体重心相对于惯性坐标系的位置；${\delta _i}\left( {i = 1,{\text{ }}2,{\text{ }}3,{\text{ }}4} \right)$为舵角。广义速度为：

$\begin{aligned} & {u_1} = {\dot x_g},{\text{ }}{u_2} = {\dot y_g},{\text{ }}{u_3} = {\dot z_g},{\text{ }}{u_4} = \dot \phi ,{\text{ }}{u_5} = \dot \theta ,\\ & {\text{ }}{u_6} = \dot \psi ,{\text{ }}{u_7} = {\dot \delta _1},{\text{ }}{u_8} = {\dot \delta _2},{\text{ }}{u_9} = {\dot \delta _3},{\text{ }}{u_{10}} = {\dot \delta _4}。\end{aligned}$

(3)

2.1 AUV本体的运动学分析

AUV本体的角速度在载体坐标系$\left\{ b \right\}$下的矢量形式为：

$\begin{aligned} & {}^b{\omega _b} = p{n_x} + q{n_y} + r{n_z} = \left( {{u_4} - {Z_3}{u_6}} \right){n_x} + \\ & \left( {{Z_2}{u_5} +{Z_1}{Z_4}{u_6}} \right){n_y} + \left( { - {Z_1}{u_5} + {Z_2}{Z_4}{u_6}} \right){n_z}。\end{aligned}$

(4)

式中：$Z_{1}=\sin \varphi，Z_{2}=\cos \varphi，Z_{2}=\sin \theta，Z_{4}=\cos \theta$，$Z_{5}= \sin \psi,Z_{6}=\cos \psi$；${n_x}、{n_y}、{n_z}$均为与载体坐标系$\left\{ b \right\}$的3个坐标轴对应的单位矢量。

由偏角速度的计算公式${\tilde \omega _{b,i}} = {{{\partial ^b}{\omega _b}}/{\partial {u_i}}}$可知，偏角速度为：

$\begin{split} & {{\tilde \omega }_{b,1}} = 0,{\text{ }}{{\tilde \omega }_{b,2}} = 0,{\text{ }}{{\tilde \omega }_{b,3}} = 0,{\text{ }}{{\tilde \omega }_{b,4}} = {n_x},{\text{ }}{{\tilde \omega }_{b,5}} = \\ & \left( {{Z_2}{n_y} - {Z_1}{n_z}} \right) {{\tilde \omega }_{b,6}} = \left( {{Z_1}{Z_4}{n_y} + {Z_2}{Z_4}{n_z}} \right), \\ & {\text{ }}{{\tilde \omega }_{b,7}} = {{\tilde \omega }_{b,8}} = {{\tilde \omega }_{b,9}} = {{\tilde \omega }_{b,10}} = 0 ，\end{split}$

(5)

因此，AUV本体重心处的速度在载体坐标系$\left\{ b \right\}$下的矢量形式为：

$\begin{gathered} {}^b{v_g} = u{n_x} + v{n_y} + w{n_z} = \left( {{Z_4}{Z_6}{u_1} + {Z_4}{Z_5}{u_2} - {Z_3}{u_3}} \right){n_x} + \\ \left( {{Z_7}{u_1} + {Z_8}{u_2} + {Z_1}{Z_4}{u_3}} \right){n_y} + \left( {{Z_9}{u_1} + {Z_{10}}{u_2} + {Z_2}{Z_4}{u_3}} \right){n_z} 。\end{gathered}$

(6)

式中：$Z_{7}=-Z_{2} Z_{5}+Z_{1} Z_{2} Z_{6}；Z_{8}=Z_{2} Z_{6}+Z_{1} Z_{3} Z_{5}；Z_{0}=$$Z_{1} Z_{5}+Z_{2}Z_{3} Z_{6}；Z_{10}= -Z_{1} Z_{6}+Z_{2} Z_{2} Z_{3}$；$u、v、w$均为AUV本体重心处的速度在载体坐标系$\left\{ b \right\}$下的表示形式。

AUV本体浮心处的速度在载体坐标系$\left\{ b \right\}$下的矢量形式为：

$\begin{split} & {}^b{v_c} = {}^b{v_g} + {}^b{\omega_{\text{b}}} \times {}^b{r_{gc}} = [ {Z_4}{Z_6}{u_1} + {Z_4}{Z_5}{u_2} - {Z_3}{u_3} + \\ & {Z_{11}}{u_5} + {Z_{12}}{u_6} ]{n_x} + [ {Z_7}{u_1} + {Z_8}{u_2} + {Z_1}{Z_4}{u_3} -{z_{gc}}{u_4} -\\ & {x_{gc}}{Z_1}{u_5} + {Z_{13}}{u_6} ]{n_y} + [ {Z_9}{u_1} + {Z_{10}}{u_2} + {Z_2}{Z_4}{u_3} +\\ & {y_{gc}}{u_4} - {x_{gc}}{Z_2}{u_5} - {Z_{14}}{u_6}，]{n_z}。\end{split}$

(7)

式中：$Z_{11} = z_{\mathrm{gc}}Z_2 + y_{\mathrm{gc}}Z_1；Z_{12} = z_{\mathrm{gc}}Z_1Z_4 - y_{\mathrm{gc}}Z_2Z_4；$$Z_{13}= x_{\mathrm{gc}}Z_2Z_4+z_{\mathrm{gc}}Z_3Z_{14}=y_{\mathrm{gc}}Z_3+x_{\mathrm{gc}}Z_1Z_4$；${}^b{r_{gc}}$为重心到浮心的位置矢量；${x_{gc}}、{y_{gc}}、{z_{gc}}$均为${}^b{r_{gc}}$在载体坐标系$\left\{ b \right\}$下的坐标。

推进器与本体连接处位于载体坐标系$\left\{ b \right\}$的$x$轴上，速度为：

$\begin{split} & {}^b{v_T} = {}^b{v_g} + {}^b{\omega _{\text{b}}} \times {}^b{r_{g,T}} = \left[ {{Z_4}{Z_6}{u_1} + {Z_4}{Z_5}{u_2} - {Z_3}{u_3}} \right]{n_x} + \\ & \left[ {{Z_7}{u_1} + {Z_8}{u_2} + {Z_1}{Z_4}{u_3} - {x_{g,T}}{Z_1}{u_5} + {x_{g,T}}{Z_2}{Z_4}{u_6}} \right]{n_y} + \\ & \left[ {{Z_9}{u_1} + {Z_{10}}{u_2} + {Z_2}{Z_4}{u_3} - {x_{g,T}}{Z_2}{u_5} - {x_{g,T}}{Z_1}{Z_4}{u_6}} \right]{n_z} 。\end{split}$

(8)

式中，${x_{g,T}}$为推进器与本体连接处在载体坐标系$\left\{ b \right\}$下的坐标。

由偏速度计算公式${\tilde v_{g,i}} = {{\partial {}^b{v_g}} / {\partial {u_i}}}$，${\tilde v_{c,i}} = {{\partial {}^b{v_c}} / {\partial {u_i}}}$，${\tilde v_{T,i}} = {{\partial {}^b{v_T}}/ {\partial {u_i}}}$可知，X舵欠驱动AUV本体浮心、重心、推进器的偏速度为：

$\begin{split} & {{\tilde v}_{c,1}} = {Z_4}{Z_6}{n_x} + {Z_7}{n_y} + {Z_9}{n_z},{\text{ }}{{\tilde v}_{c,2}} = {Z_4}{Z_5}{n_x} + {Z_8}{n_y} + \\ & {Z_{10}}{n_z} , {{\tilde v}_{c,3}} = - {Z_3}{n_x} + {Z_1}{Z_4}{n_y} + {Z_2}{Z_4}{n_z},{\text{ }}{{\tilde v}_{c,4}} = - {z_{gc}}{n_y} +\\ & {y_{gc}}{n_z} , {{\tilde v}_{c,5}} = {Z_{11}}{n_x} - {x_{gc}}{Z_1}{n_y} - {x_{gc}}{Z_2}{n_z},{\text{ }}{{\tilde v}_{c,6}} = {Z_{12}}{n_x} + \\ &{Z_{13}}{n_y} - {Z_{14}}{n_z}{{\tilde v}_{c,7}} = {\text{ }}{{\tilde v}_{c,8}} = {{\tilde v}_{c,9}} = {{\tilde v}_{c,10}} = 0 。\end{split}$

(9)

$\begin{split} & {{\tilde v}_{g,1}} = {Z_4}{Z_6}{n_x} + {Z_7}{n_y} + {Z_9}{n_z},{\text{ }}{{\tilde v}_{g,2}} = {Z_4}{Z_5}{n_x} + {Z_8}{n_y} + \\ & {Z_{10}}{n_z} {{\tilde v}_{g,3}} = - {Z_3}{n_x} + {Z_1}{Z_4}{n_y} + {Z_2}{Z_4}{n_z},{\text{ }}{{\tilde v}_{g,4}} ={{\tilde v}_{g,5}} = \\ & {{\tilde v}_{g,6}} = {\text{ }}{{\tilde v}_{g,7}} = {\text{ }}{{\tilde v}_{g,8}} = {\text{ }}{{\tilde v}_{g,9}} = {\text{ }}{{\tilde v}_{g,10}} = 0, \end{split}$

(10)

$\begin{split} & {{\tilde v}_{T,1}} = {Z_4}{Z_6}{n_x} + {Z_7}{n_y} + {Z_9}{n_z},{\text{ }}{{\tilde v}_{T,2}} = {Z_4}{Z_5}{n_x} + {Z_8}{n_y} + \\ & {Z_{10}}{n_z} {{\tilde v}_{T,3}} = - {Z_3}{n_x} + {Z_1}{Z_4}{n_y} + {Z_2}{Z_4}{n_z},{\text{ }}{{\tilde v}_{T,5}} = \\ & - {x_{g,T}}{Z_1}{n_y} - {x_{g,T}}{Z_2}{n_z} {{\tilde v}_{T,6}} = {x_{g,T}}{Z_2}{Z_4}{n_y} - \\ &{x_{g,T}}{Z_1}{Z_4}{n_z},{\text{ }}{{\tilde v}_{T,4}} = {\text{ }}{{\tilde v}_{T,7}} = {\text{ }}{{\tilde v}_{T,8}} = {\text{ }}{{\tilde v}_{T,9}} = {\text{ }}{{\tilde v}_{T,10}} = 0 。\end{split}$

(11)

AUV本体重心处的加速度的矢量形式为：

${}^b{a_g} = \frac{{{\mathrm{d}}{}^b{v_g}}}{{{\mathrm{d}}t}} = {Z_{15}}{n_x} + {Z_{16}}{n_y} + {Z_{17}}{n_z} 。$

(12)

式中：$Z_{15}Z_4Z_6\dot u_1+Z_4Z_5\dot u_2-Z_3\dot u_3；Z_{16}=Z_7\dot u_1+Z_8\dot u_2+$$Z_1Z_4\dot u_3, Z_{17}= Z_9\dot u_1+Z_{10}\dot u_2+Z_2Z_4\dot u_3$。

AUV本体角加速度的矢量形式为：

${}^b{\alpha _b} = \frac{{{\mathrm{d}}{}^b{\omega _b}}}{{{\mathrm{d}}t}} = {Z_{18}}{n_x} + {Z_{19}}{n_y} + {Z_{20}}{n_z}。$

(13)

式中：${Z_{18}} = {\dot u_4} - {Z_4}{u_5}{u_6} - {Z_3}{\dot u_6}$；${Z_{19}} = - {Z_1}{u_4}{u_5} +{Z_2}{\dot u_5} +$${Z_2}{Z_4}{Z_6}{u_4} \ -\ {Z_1}{Z_3}{Z_5}{u_6} \ +\ {Z_1}{Z_4}{\dot u_6}$；${Z_{20}} = - {Z_2}{u_4}{u_5} - {Z_1}{\dot u_5} -$${Z_1}{Z_4}{u_4}{u_6} - {Z_2}{Z_3}{Z_5}{u_6} + {Z_2}{Z_4}{\dot u_6}$。

2.2 X舵的运动学分析

X舵的角速度分别为：

$\begin{split} & {}^i{\omega _i} = {}_b^iR{}^b{\omega _b} + {\dot \delta _i}{n_{i,y}} = {}^i{\omega _{i,x}}{n_{i,x}} +\\ & {}^i{\omega _{i,y}}{n_{i,y}} + {}^i{\omega _{i,z}}{n_{i,z}}\left( {i = 1,2,3,4} \right)。\end{split}$

(14)

式中：${}^i{\omega _{i,x}}$、${}^i{\omega _{i,y}}$、${}^i{\omega _{i,z}}$为X舵的角速度${}^i{\omega _i}$在坐标系$\left\{ {{O_i}} \right\}$下的分量。

偏角速度可表示为：

${\tilde \omega _{i,r}} = {{\partial {}^i{\omega _i}} / {\partial {u_r}}}{\text{ }}\left( {i = 1,{\text{ }}2,{\text{ }}3,{\text{ }}4} \right)，$

(15)

X舵重心处的速度为：

$\begin{split} ^iv_{ig}=& {}_b^iR^bv_g+_b^iR\left(^b\omega\times^br_{g,O_i}\right)+^i\omega_i\times^ir_{O_i,ig}= \\ &{} ^iv_{ig,x}n_{i,x}+^iv_{ig,y}n_{i,y}+^iv_{ig,z}n_{i,z}\left(i=1,2,3,4\right)。\end{split}$

(16)

式中：${}^i{v_{ig,x}}$、${}^i{v_{ig,y}}$、${}^i{v_{ig,z}}$为X舵重心处的速度${}^i{v_{ig}}$在坐标系$\left\{ {{O_i}} \right\}$下的分量。

X舵重心处的偏速度为：

${\tilde v_{ig,r}} = {{\partial {}^i{v_{ig}}} \mathord{\left/ {\vphantom {{\partial {}^i{v_{ig}}} {\partial {u_r}}}} \right. } {\partial {u_r}}}，\left( {i = 1,2,3,4} \right)，$

(17)

舵的角加速度为：

${}^i{\alpha _i} = \frac{{{\mathrm{d}}{}^i{\omega _i}}}{{{\mathrm{d}}t}} = {}^i{\alpha _{i,x}}{n_{i,x}} + {}^i{\alpha _{i,y}}{n_{i,y}} + {}^i{\alpha _{i,z}}{n_{i,z}}，\left( {i = 1,2,3,4} \right)。$

(18)

式中：${}^i{\alpha _{i,x}}$、${}^i{\alpha _{i,y}}$、${}^i{\alpha _{i,z}}$为X舵的角加速度${}^i{\alpha _i}$在坐标系$\left\{ {{O_i}} \right\}$下的分量。

舵重心处的加速度为：

${}^i{a_{ig}} = \frac{{{\mathrm{d}}{}^i{v_{ig}}}}{{{\mathrm{d}}t}} = {}^i{a_{ig,x}}{n_{i,x}} + {}^i{a_{ig,y}}{n_{i,y}} + {}^i{a_{ig,z}}{n_{i,z}}，\left( {i = 1,2,3,4} \right)。$

(19)

式中：${}^i{a_{ig,x}}$、${}^i{a_{ig,y}}$、${}^i{a_{ig,z}}$为X舵重心处的加速度${}^i{a_{ig}}$在坐标系$\left\{ {{O_i}} \right\}$下的分量。

3 动力学分析 3.1 AUV本体的动力学分析

AUV本体的质量为${m_b}$，惯性张量为${}^b{I_b}$，受到惯性力$F_b^ *$、惯性矩$T_b^ *$、重力${G_b}$、浮力${B_b}$、水动力${F_{\text{b}}}$^[18]、水动力矩${T_b}$^[18]、推进器推力$T$、舵对AUV本体的反作用力矩${T_{ - i}}\left( {i = 1,2,3,4} \right)$（方向为${n_{iy}}( i =$1, 2, 3, 4）的影响。

AUV本体的惯性力和惯性矩为：

$\begin{gathered} F_b^ * = - {m_b}{}^b{a_g} = F_{b,x}^ * {n_x} + F_{b,y}^ * {n_y} + F_{b,z}^ * {n_z} ，\\ T_b^ * = - {}^b{I_b}{}^b{\alpha _b} - {}^b{\omega _b} \times {}^b{I_b} \cdot {}^b{\omega _b} = T_{b,x}^ * {n_x} + T_{b,y}^ * {n_y} + T_{b,z}^ * {n_z} 。\end{gathered}$

(20)

式中：$F_{b,x}^ * 、F_{b,y}^ * 、F_{b,z}^ *$为惯性力$F_b^ *$在载体坐标系$\left\{ b \right\}$下的分量；$T_{b,x}^ * 、T_{b,y}^ * 、T_{b,z}^ *$为惯性矩$T_b^ *$在载体坐标系$\left\{ b \right\}$下的分量。

AUV本体的惯性力和惯性矩对广义惯性力的贡献$F_{M,r}^ * = F_b^ * \cdot {\tilde v_{g,r}} + T_b^ * \cdot {\tilde \omega _{b,r}}$，可以表示为：

$\begin{split} & F_{M,1}^ * = {Z_4}{Z_6}F_{b,x}^ * + {Z_7}F_{b,y}^ * + {Z_9}F_{b,z}^ * ,{\text{ }}F_{M,2}^ * = {Z_4}{Z_5}F_{b,x}^ * + \\ & {Z_8}F_{b,y}^ * + {Z_{10}}F_{b,z}^ * F_{M,3}^ * = - {Z_3}F_{b,x}^ * + {Z_1}{Z_4}F_{b,y}^ * + {Z_2}{Z_4}F_{b,z}^ * , \\ &{\text{ }}F_{M,4}^ * = T_{b,x}^ * ,{\text{ }}F_{M,5}^ * = {Z_2}T_{b,y}^ * - {Z_1}T_{b,z}^ * F_{M,6}^ * ={Z_1}{Z_4}T_{b,y}^ * +\\ & {Z_2}{Z_4}T_{b,z}^ * ,{\text{ }}F_{M,7}^ * = F_{M,8}^ * = F_{M,9}^ * = F_{M,10}^ * = 0。\\[-1pt] \end{split}$

(21)

施加在AUV本体上的水动力和水动力矩对广义主动力的贡献$F_{b,r}^{} = F_b^{} \cdot {\tilde v_{g,r}} + T_b^{} \cdot {\tilde \omega _{b,r}}$为：

$\begin{split} & {F_{{{b}},1}} = {Z_4}{Z_6}{F_{b,x}} + {Z_7}{F_{b,y}} + {Z_9}{F_{b,z}},{\text{ }}{F_{b,2}} = {Z_4}{Z_5}{F_{b,x}} + \\ & {Z_8}{F_{b,y}} + {Z_{10}}{F_{b,z}}{F_{b,3}} = - {Z_3}{F_{b,x}} + {Z_1}{Z_4}{F_{b,y}} + {Z_2}{Z_4}{F_{b,z}},\\ & {F_{h,4}} = {T_{b,x}},{F_{b,5}} = {Z_2}{T_{b,y}} - {Z_1}{T_{b,z}}{F_{b,6}} = {Z_1}{Z_4}{T_{b,y}} +\\ &{Z_2}{Z_4}{T_{b,z}},{\text{ }}{F_{b,7}} = {F_{b,8}} = {F_{b,8}} = {F_{b,10}} = 0 。\end{split}$

(22)

AUV本体重力对广义主动力的贡献$F_{G,r}^{} = G_b^{} \cdot {\tilde v_{g,r}}$为：

$\begin{split} &{F_{G,1}} = {Z_4}{Z_6}{G_{b,x}} + {Z_7}{G_{b,y}} + {Z_9}{G_{b,z}},{\text{ }}{F_{G,2}} = {Z_4}{Z_5}{G_{b,x}} + \\ & {Z_8}{G_{b,y}} + {Z_{10}}{G_{b,z}}{F_{G,3}} = - {Z_3}{G_{b,x}} + {Z_1}{Z_4}{G_{b,y}} + {Z_2}{Z_4}{G_{b,z}},\\ &{\text{ }}{F_{G,r}} = 0\left( {r = 4,{\text{ }}5,{\text{ }} \cdots ,{\text{ }}10} \right) ，\\[-1pt] \end{split}$

(23)

式中，${G_{b,x}}、{G_{b,y}}、{G_{b,z}}$均为重力${G_b}$在载体坐标系$\left\{ b \right\}$下的分量。

AUV本体浮力对广义主动力的贡献$F_{B,r}^{} = B_b^{} \cdot {\tilde v_{c,r}}$为：

$\begin{split} & {F_{B,1}} = {Z_4}{Z_6}{B_{b,x}} + {Z_7}{B_{b,y}} + {Z_9}{B_{b,z}},{\text{ }}{F_{B,2}} = {Z_4}{Z_5}{B_{b,x}} + \\ & {Z_8}{B_{b,y}} + {Z_{10}}{B_{b,z}} {F_{B,3}} = - {Z_3}{B_{b,x}} + {Z_1}{Z_4}{B_{b,y}} + {Z_2}{Z_4}{B_{b,z}},\\ &{F_{G,r}} = 0\left( {r = 4,5,{\text{ }} \cdots ,{\text{ }}10} \right) ，\end{split}$

(24)

式中，${B_{b,x}}、{B_{b,y}}、{B_{b,z}}$均为浮力${B_b}$在载体坐标系$\left\{ b \right\}$下的分量。

推进器推力对广义主动力的贡献$F_{T,r}^{} = T \cdot {\tilde v_{T,r}}$为：

$\begin{gathered} {F_{T,1}} = {Z_4}{Z_6}T,{\text{ }}{F_{T,2}} = {Z_4}{Z_5}T,{\text{ }}{F_{T,3}} = - {Z_3}T, \\ {F_{T,4}} ={F_{T,5}} = {F_{T,6}} = {F_{T,7}} = {F_{T,8}} = 0，\end{gathered}$

(25)

舵对AUV本体的反作用力矩${T_{ - i}}\left( {i = 1,2,3,4} \right)$对广义主动力的贡献$F_{ - i,r}^{} = T_{ - i}^{} \cdot {\tilde \omega _{b,r}}$为：

$\begin{split} & {F_{ - 1,1}} = {F_{ - 1,2}} = {F_{ - 1,3}} = {F_{ - 1,4}} = {F_{ - 1,7}} = {F_{ - 1,8}} = {F_{ - 1,9}}= \\ & {F_{ - 1,10}} = 0,{\text{ }}{F_{ - 1,5}} = - {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{Z_2}{T_{ - 1}} + {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{Z_1}{T_{ - 1}},\\ & {\text{ }}{F_{ - 1,6}} =- {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{T_{ - 1}}\left( {{Z_1}{Z_4} + {Z_2}{Z_4}} \right){F_{ - 2,1}} = {F_{ - 2,2}} =\\ & {F_{ - 2,3}} = {F_{ - 2,4}} = {F_{ - 2,7}} = {F_{ - 2,8}} ={F_{ - 2,9}} = {F_{ - 2,10}} =\\ & 0{F_{ - 2,5}} = {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{Z_2}{T_{ - 2}} + {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{Z_1}{T_{ - 2}},{\text{ }}{F_{ - 2,6}} =\\ & {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{T_{ - 2}}\left( {{Z_1}{Z_4} - {Z_2}{Z_4}} \right) {F_{ - 3,1}} = {F_{ - 3,2}} ={F_{ - 3,3}} = \\ & {F_{ - 3,4}} = {F_{ - 3,7}} = {F_{ - 3,8}} = {F_{ - 3,9}} = {F_{ - 3,10}} = 0,{F_{ - 3,5}} = \\ & {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{Z_2}{T_{ - 3}} - {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{Z_1}{T_{ - 3}}, {\text{ }}{F_{ - 3,6}} ={{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{T_{ - 3}}\\ & \left( {{Z_1}{Z_4} + {Z_2}{Z_4}} \right) {F_{ - 4,1}} = {F_{ - 4,2}} = {F_{ - 4,3}} ={F_{ - 4,4}} = \\ & {F_{ - 4,7}} = {F_{ - 4,8}} = {F_{ - 4,9}} = {F_{ - 4,10}} = 0 {F_{ - 4,5}} = \\ & - {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{Z_2}{T_4} - {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{Z_1}{T_{ - 4}},{\text{ }}{F_{ - 4,6}} = \\ & {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. } 2}{T_{ - 4}}\left( { - {Z_1}{Z_4} + {Z_2}{Z_4}} \right) 。\\[-1pt] \end{split}$

(26)

AUV本体的广义主动力为：

$\begin{split} {F_{M,r}} = &{F_{b,r}} + {F_{G,r}} + {F_{B,r}} + {F_{T,r}} + {F_{ - 1,r}} + {F_{ - 2,r}} +\\ & {F_{ - 3,r}} + {F_{ - 4,r}},{\text{ }}\left( {r = 1,2, \cdots ,10} \right)。\end{split}$

(27)

3.2 X舵的动力学分析

第$i$个舵的质量为${m_i}\left( {i = 1,2,3,4} \right)$，惯性张量为${}^i{I_{i,g}}$，施加在第$i$个舵上的力主要有惯性力$F_i^ *$、惯性力矩$T_i^ *$、重力$G_i^{}$、浮力$B_i^{}$、水动力$F_{{{h}},i}^{}$、水动力矩$T_{{{h}},i}^{}$，舵机施加在舵上的扭矩$T_i^{}$（方向为${n_{i,y}}$）。重心和浮心重合。

舵的惯性力和惯性矩为：

$\begin{gathered} F_i^ * = - {m_i}{}^i{a_{ig}} = F_{i,x}^ * {n_{i,x}} + F_{i,y}^ * {n_{i,y}} + F_{i,z}^ * {n_{i,z}} ，\\ T_i^ * = - {}^i{I_{i,g}}{}^i{\alpha _i} - {}^i{\omega _i} \times {}^i{I_{i,g}} \cdot {}^i{\omega _i} = T_{i,x}^ * {n_{i,x}} + T_{i,y}^ * {n_{i,y}} + T_{i,z}^ * {n_{i,z}} 。\end{gathered}$

(28)

式中：$F_{i,x}^ * 、F_{i,y}^ * 、F_{i,z}^ *$均为惯性力$F_i^ *$在载体坐标系$\left\{ i \right\}$下的分量；$T_{i,x}^ *、T_{i,y}^ * 、T_{i,z}^ *$均为惯性矩$T_i^ *$在载体坐标系$\left\{ i \right\}$下的分量。

X舵对广义惯性力的贡献为：

$F_{X,r}^ * = \sum\limits_{i = 1}^4 {\left( {F_i^ * \cdot {{\tilde v}_{ig,r}} + T_i^ * \cdot {{\tilde \omega }_{i,r}}} \right)，\left( {r = 1,2, \cdots ,10} \right)}，$

(29)

X舵的重力和浮力对广义主动力的贡献为：

$F_{{G_X},r}^{} = \sum\limits_{i = 1}^4 {G_i^{} \cdot {{\tilde v}_{ig,r}}，\left( {r = 1,2, \cdots ,10} \right)}，$

(30)

$F_{{B_X},r}^{} = \sum\limits_{i = 1}^4 {B_i^{} \cdot {{\tilde v}_{ig,r}}，\left( {r = 1,2, \cdots ,10} \right)}。$

(31)

X舵的水动力和水动力矩为：

$\begin{gathered} {F_{h,i}} = {X_{{\delta _i}{\delta _i}}}\delta _i^2{u^2}{n_x} + {Y_{{\delta _i}}}\delta _i^{}{u^2}{n_y} + {Z_{{\delta _i}}}\delta _i^{}{u^2}{n_z} ，\\ {T_{h,i}} = {K_{{\delta _i}}}\delta _i^{}{u^2}{n_x} + {M_{{\delta _i}}}\delta _i^{}{u^2}{n_y} + {N_{{\delta _i}}}\delta _i^{}{u^2}{n_z}。\end{gathered}$

(32)

式中：${X_{{\delta _i}{\delta _i}}}、{Y_{{\delta _i}}}、{Z_{{\delta _i}}}、{K_{{\delta _i}}}、{M_{{\delta _i}}},{N_{{\delta _i}}}$为与舵相关的水动力系数。

X舵的水动力对广义主动力的贡献为：

$F_{{H_X},r}^{} = \sum\limits_{i = 1}^4 {\left( {F_{h,i}^{} \cdot {{\tilde v}_{ig,r}} + T_{h,i}^{} \cdot {{\tilde \omega }_{i,r}}} \right)，\left( {r = 1,2, \cdots ,10} \right)} ，$

(33)

X舵上的扭矩对广义主动力的贡献为：

$F_{{T_X},r}^{} = \sum\limits_{i = 1}^4 {T_i^{} \cdot {{\tilde \omega }_{i,r}}，\left( {r = 1,2, \cdots ,10} \right)}，$

(34)

X舵的广义主动力为：

${F_{X,r}} = {F_{{G_X},r}} + {F_{{B_X},r}} + {F_{{H_X},r}} + {F_{{T_X},r}}，$

(35)

X舵欠驱动AUV的动力学方程为：

$F_{{{M}},r}^ * + F_{{{X}},r}^ * + F_{{{M}},r}^{} + F_{{{X}},r}^{} = 0{\text{ }}\left( {r = 1,2, \cdots ,10} \right)。$

(36)

4 仿真验证

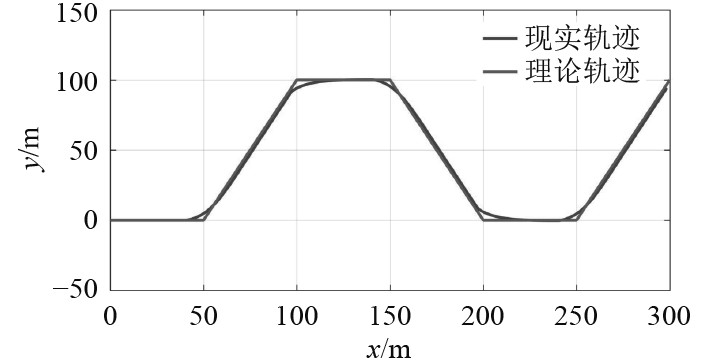
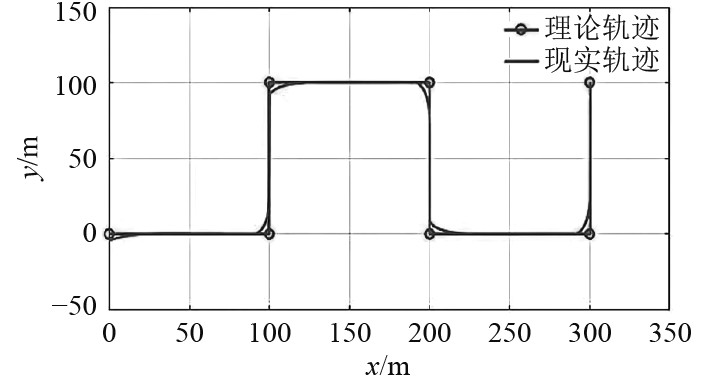
为了验证模型的有效性，利用Matlab/Simulink中的S函数，求解式（36），状态量为广义坐标，输入为推进器推力、舵角，输出为广义坐标。在Matlab/Simulink环境下设计滑模控制器，搭建仿真验证平台，分别对垂直面（见图3）和水平面（见图4）的路径跟踪问题进行仿真验证，仿真结果与AUV运动规律一致，表明该建模方法有效。

5 结　语

本文详细介绍偏速度、偏角速度、广义惯性力、广义主动力的计算方法，展示凯恩动力学的建模步骤，推导出X舵欠驱动AUV的凯恩动力学模型。该建模方法分别计算AUV本体和X舵的广义主动力和广义惯性力，可非常方便地添加AUV本体和X舵的相互作用，也可清晰地展示作用在X舵欠驱动AUV上的力对动力学模型的影响。仿真结果表明该建模方法有效。