0 引　言

作为人类探索和开发海洋的工具，自主水下航行器(Autonomous Underwater Vehicle, AUV)引起了世界各国研究人员的广泛关注。在过去的几十年里，AUV越来越多地应用于科学、工业、商业和军事领域，主要应用包括海洋学测绘、深海勘探^[1]、海上油气开发、管道维护^[2]、海上救援、水下目标跟踪^[3]和巡逻^[4]等。为了确保AUV能够执行这些水下任务，设计高效、鲁棒性强的运动控制系统至关重要。轨迹跟踪控制是AUV运动控制领域中一项复杂的任务^[5]，考虑到AUV系统所受到的约束以及复杂的外界干扰等，实现精确的AUV轨迹跟踪任务更加艰难。

针对自主水下航行器的轨迹跟踪控制问题，很多学者开展了相应研究。高剑等^[6]将跟踪误差分解为位置跟踪和航向角跟踪2个级联系统，分别设计控制器实现AUV的水平面轨迹跟踪控制。严浙平等^[7]针对时变干扰下AUV水平面的轨迹跟踪问题，基于反步法和滑模控制设计了具有较强鲁棒性的轨迹跟踪控制器。武建国等^[8]针对AUV在环境干扰下的三维轨迹跟踪问题，综合非线性干扰观测器设计了反步滑模控制器，并通过李雅普诺夫证明了系统的稳定性。杜佳璐等^[9]通过构造一种新的超螺旋有限时间收敛扩张状态观测器，对系统受到的总扰动进行观测，设计了AUV在复杂扰动情况下的轨迹跟踪控制器。Taha Elmokadem等^[10]设计了终端滑模控制器，保证了AUV在多重不确定性和由洋流和波浪引起外部干扰下的鲁棒性，实现了AUV轨迹跟踪的快速收敛和高稳态跟踪精度。

上述研究方法的常见结构是在运动学阶段产生期望的速度，在动力学阶段考虑系统所受干扰和不确定性，从而完成控制器的设计。但上述研究所设计的期望速度并没有考虑到系统所受的速度约束，而忽略速度约束会降低控制器的性能，甚至会导致控制系统的不稳定。因此，在AUV的轨迹跟踪控制中考虑速度约束很有必要。

模型预测控制(Model Predictive Control, MPC)作为一种最优控制算法，最大优点是可直接处理系统约束，是解决AUV约束问题的有效方法。本文基于MPC算法设计了优化的运动学控制器，可得到满足速度约束的期望速度。考虑到系统受到的复杂环境扰动，设计干扰观测器(Disturbance Observer, DO)进行实时估计，结合水下无人航行器三自由度动力学模型，设计了精确跟踪期望速度的动力学控制器。最后，进行了数值仿真以评估控制性能。仿真结果表明，欠驱动AUV能够在复杂外界干扰及存在速度约束的情况下实现精确的轨迹跟踪。

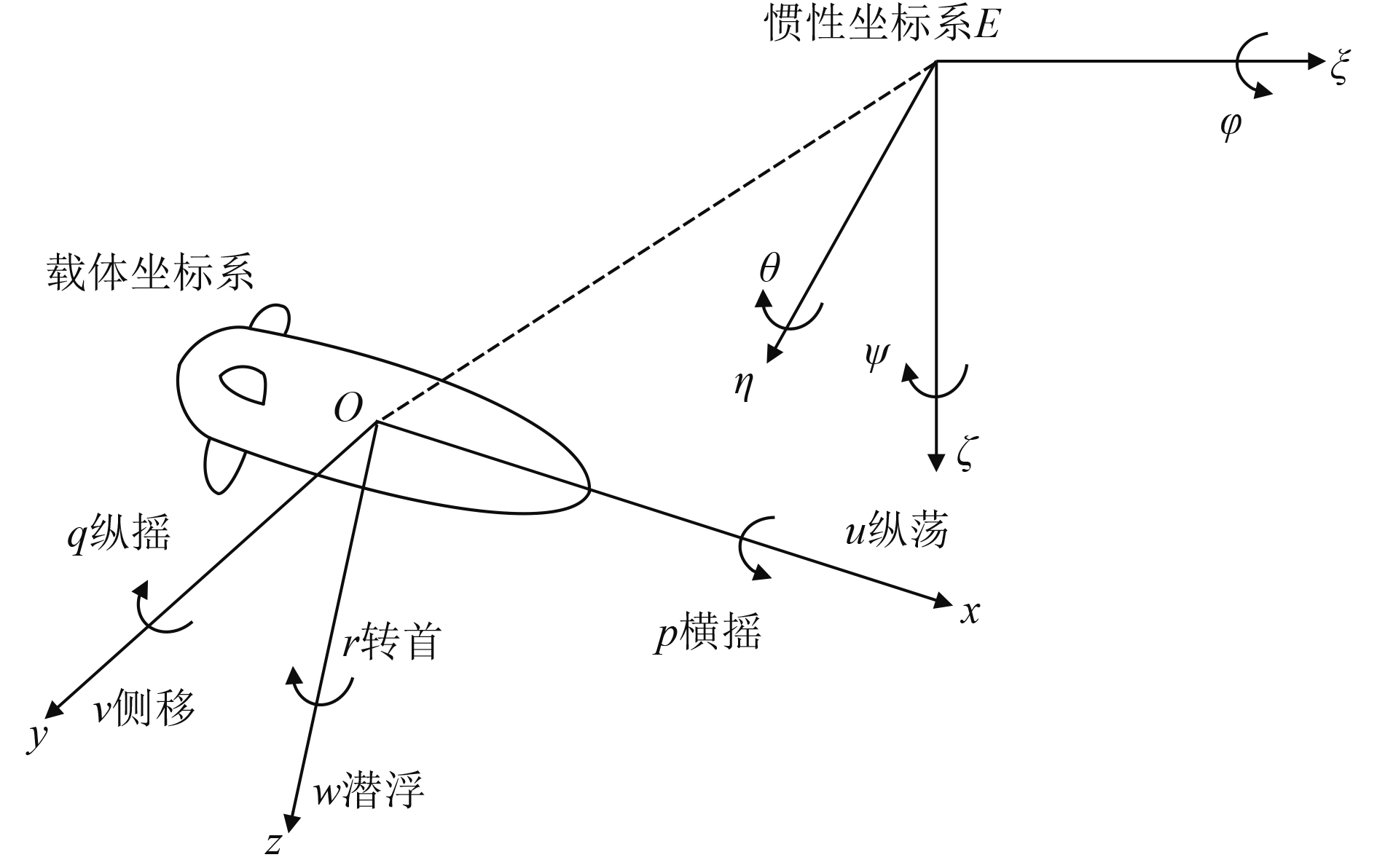
1 AUV数学模型 1.1 AUV运动学模型

为了研究AUV的运动模型，将AUV运动近似为流体中刚体的一般运动。根据坐标系原点位置，可建立惯性坐标系$ E - \xi \eta \zeta $和载体坐标系$ O - xyz $，惯性坐标系是以地球上某一点为原点，载体坐标系原点固定在AUV上，如图1所示。

本文考虑AUV的水平面轨迹跟踪控制，即忽略AUV垂荡、横摇和俯仰3个方向上的运动，做如下假设：

假设1　AUV艇体左右对称，即AUV转动惯量满足$ {I_{xy}} = {I_{yx}} = 0 $。

假设2　AUV的载体坐标系原点固定在重心处，即$ {x_g} = {y_g} = 0 $。

则欠驱动AUV水平面运动学方程可表示为：

$ {\boldsymbol{\dot \eta }} = {\boldsymbol{J(\eta )v}} 。$

(1)

式中：$ {\boldsymbol{\eta }} = {[x,y,\varphi ]^{\mathrm{T}}} $为固定坐标系下AUV的位置和姿态；首向角$\varphi $为AUV载体坐标系相对于固定坐标系的角度；${\boldsymbol{v}} = {[u,v,r]^{\mathrm{T}}}$为载体坐标系下定义速度信息，其中，u、v、r分别为纵向速度、横向速度及首向角速度。${\boldsymbol{J(\eta )}}$为载体坐标系到惯性坐标系下的转换矩阵，定义为：

$ {\boldsymbol{J(\eta )}} = \left[ {\begin{array}{*{20}{c}} {\cos \varphi }&{ - \sin \varphi }&0 \\ {\sin \varphi }&{\cos \varphi }&0 \\ 0&0&1 \end{array}} \right]。$

(2)

1.2 AUV动力学模型

对于欠驱动AUV，未知环境扰动下的三自由度动力学方程为^[11]：

$ {\boldsymbol{M\dot v + C}}({\boldsymbol{v}}){\boldsymbol{v + D}}({\boldsymbol{v}}){\boldsymbol{v + g}}({\boldsymbol{\eta }}){\boldsymbol{ = \tau + d}} 。$

(3)

式中：$ {\boldsymbol{M}} $为AUV广义质量矩阵，$ {\boldsymbol{M}} = {{\boldsymbol{M}}_{{RB}}} + {{\boldsymbol{M}}_{A}} $，$ {{\boldsymbol{M}}_{{RB}}} $为刚体惯性质量矩阵，$ {{\boldsymbol{M}}_{A}} $为水动力附加质量矩阵，$ {{\boldsymbol{M}}_{{RB}}} = {\mathrm{diag}}(m,m,{I_z}) $，$ {{\boldsymbol{M}}_{A}} = {\mathrm{diag}}( - {X_{\dot u}}, - {Y_{\dot v}}, - {N_{\dot r}}) $，$ {\boldsymbol{C}}({\boldsymbol{v}}) $为科里奥利向心力矩阵；$ {\boldsymbol{C}}({\boldsymbol{v}}) = {{\boldsymbol{C}}_{{RB}}}({\boldsymbol{v}}) + {{\boldsymbol{C}}_{A}}({\boldsymbol{v}}) $，$ {{\boldsymbol{C}}_{{RB}}}({\boldsymbol{v}}) $为刚体向心力矩阵，$ {{\boldsymbol{C}}_{A}}({\boldsymbol{v}}) $为水动力向心力矩阵。其中：

$ {{\boldsymbol{C}}_{{RB}}}({\boldsymbol{v}}) = \left[ {\begin{array}{*{20}{c}} 0&0&{ - mv} \\ 0&0&{mu} \\ {mv}&{ - mu}&0 \end{array}} \right] ，$

(4)

$ {{\boldsymbol{C}}_{A}}({\boldsymbol{v}}) = \left[ {\begin{array}{*{20}{c}} 0&0&{{Y_{\dot v}}v} \\ 0&0&{ - {X_{\dot u}}u} \\ { - {Y_{\dot v}}v}&{{X_{\dot u}}u}&0 \end{array}} \right]。$

(5)

式中，$ {\boldsymbol{D}}({\boldsymbol{v}}) $为水动力阻尼矩阵，表示AUV上流体的粘性力，表达式为：

$ {\boldsymbol{D}}({\boldsymbol{v}}) = \left[ {\begin{array}{*{20}{c}} {{X_u}{\text{ + }}{X_{\left| u \right|u}}\left| u \right|}&0&0 \\ 0&{{Y_v}{\text{ + }}{Y_{\left| v \right|v}}\left| v \right|}&0 \\ 0&0&{{N_r}{\text{ + }}{N_{\left| r \right|r}}\left| r \right|} \end{array}} \right]。$

(6)

$ {\boldsymbol{g}}({\boldsymbol{\eta }}) $为由重力和浮力引起的恢复力矩阵，此处为零矩阵。

$ {\boldsymbol{\tau }} = {[{\tau _u},0,{\tau _r}]^{\mathrm{T}}} $为执行器产生的控制输入矩阵；$ {\boldsymbol{d}} = {[{d_u},{d_v},{d_r}]^{\mathrm{T}}} $为有界的外界干扰矩阵。

上述式中，$ m $为AUV质量，$ {I_z} $为惯性张量，$ {X_u}、{Y_v}、{N_r}、{X_{\dot u}}、{Y_{\dot v}}、{N_{\dot r}}、{X_{\left| u \right|u}}、{Y_{\left| v \right|v}}、{N_{\left| r \right|r}} $均为可测量的水动力系数。

2 基于MPC-DO的控制器设计

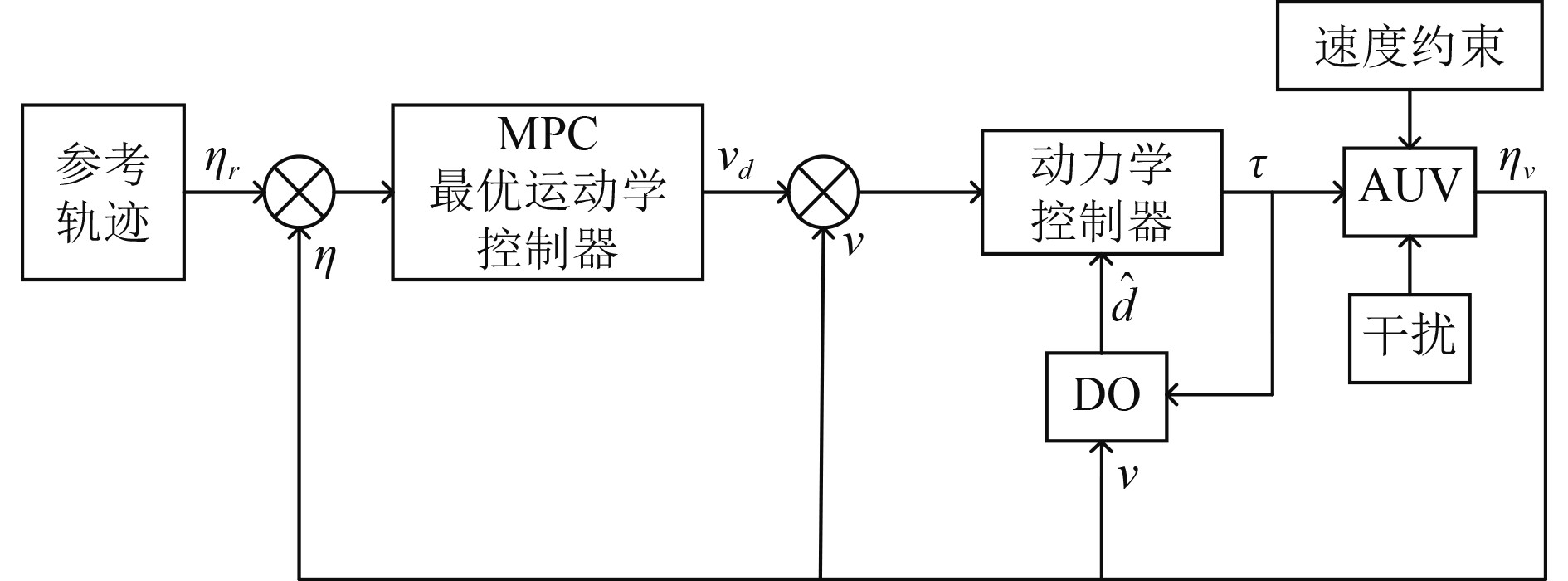
本文的目标是实现存在速度约束和复杂扰动下AUV的精确轨迹跟踪，控制系统设计包括基于MPC的运动学控制器和基于DO的动力学控制器。运动学控制器生成具有相应约束的期望速度，以保证AUV位姿跟踪误差的收敛性。动力学控制器利用系统实际控制输入实现AUV的速度逐渐收敛到期望的速度指令，即确保AUV速度跟踪误差的收敛。设计的欠驱动AUV轨迹跟踪控制方案，如图2所示。

2.1 基于MPC的运动学控制器

定义$ {p}_{r}={[{x}_{r},{y}_{r }]}^{{\mathrm{T}}} $描述AUV在惯性坐标系下的参考位置，并做如下假设：

假设3　AUV参考位置${{\boldsymbol{p}}_r}$光滑可导且有界，其一阶导数$ {{\boldsymbol{\dot p}}_r} $和二阶导数${{\boldsymbol{\ddot p}}_r}$存在且有界。

可得AUV参考的姿态、参考纵向速度、参考横向速度及参考首向角速度分别为^[12]：$ {\varphi _r}(t) = {\mathrm{arc}}\tan 2({\dot y_r},{\dot x_r}) $，$ {u_r}(t) = \sqrt {{{\dot x}^2}_r{\text{ + }}{{\dot y}^2}_r} $，$ {v_r}(t) = 0 $，$ {r_r}(t) = ({\dot x_r}{\ddot y_r} - {\dot y_r}{\ddot x_r})/({\dot x^2}_r{\text{ + }}{\dot y^2}_r) $。其中，$ {\mathrm{arctan2}} $为四象限反正切函数。则AUV参考的轨迹可表示为：${{\mathbf{\eta }}_{\boldsymbol{r}}} = {[{x_r},{y_r},{\varphi _r}]^{\mathrm{T}}}$，参考的速度可表示为$ {v}_{r}={[{u}_{r},{v}_{r },{r}_{r}]}^{{\mathrm{T}}} $。

对AUV运动学模型(1)在${{\mathbf{\eta }}_r}$处线性化，再用采样周期$T$离散化，可得离散误差跟踪模型为^[13]：

$ \tilde {\mathbf{\eta }}(k + 1) = {\tilde {\boldsymbol{A}}_k}\tilde {\boldsymbol{\eta}}(k) + {\tilde {\boldsymbol{B}}_k}\tilde {\boldsymbol{u}}(k)。$

(7)

式中：$\tilde{\boldsymbol{ \eta }}(k{\text{ + }}1) = {\mathbf{\eta }}(k{\text{ + }}1) - {{\boldsymbol{\eta }}_{\mathbf{r}}}(k{\text{ + }}1)$，$\tilde{\boldsymbol{ \eta }}(k) = {\boldsymbol{\eta }}(k) - {{\boldsymbol{\eta }}_{\boldsymbol{r}}}(k)$，$ \tilde{\boldsymbol{ u}}(k) = {\boldsymbol{v}}(k) - {{\boldsymbol{v}}_r}(k) $，分别为$k + 1$时刻的位姿跟踪误差、k时刻的位姿跟踪误差、k时刻的速度跟踪误差。

$ {\tilde {\boldsymbol{A}}_k} = {\boldsymbol{I}} + \frac{{\partial ({\boldsymbol{J(\eta )v}})}}{{\partial {\boldsymbol{\eta }}}} \cdot T = \left[ {\begin{array}{*{20}{c}} 1&0&{( - {u_r}\sin {\varphi _r} - {v_r}\sin {\varphi _r})T} \\ 0&1&{({u_r}\cos {\varphi _r} - {v_r}\cos {\varphi _r})T} \\ 0&0&1 \end{array}} \right]，$

(8)

$ {\tilde{\boldsymbol{ B}}_k} = \frac{{\partial ({\boldsymbol{J(\eta )v}})}}{{\partial {\boldsymbol{\eta }}}}\cdot T = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\cos {\varphi _r}T} \\ {\sin {\varphi _r}T} \\ 0 \end{array}}&{\begin{array}{*{20}{c}} 0 \\ 0 \\ T \end{array}} \end{array}} \right]。$

(9)

在上述跟踪误差模型的推导过程中，因欠驱动AUV在横向方向上缺少推进器，故此处假设$ v(t) = 0 $。但考虑到AUV系统的耦合特性，实际的横向速度并不为0，$ v(t) = 0 $的假设会导致首向角存在跟踪误差。因此，有必要对参考首向角进行补偿。补偿机制为：${\varphi _c} = {\varphi _r} - {\mathrm{arctan}}(v,u)$，在下文中，${{\mathbf{\eta }}_r}$中${\varphi _r}$的值将会被${\varphi _c}$的值所代替，以实现精确的轨迹跟踪。

为使AUV速度平缓变化，本文将控制增量作为控制输入，改进的状态空间模型可重新表示为：

$ \tilde{\boldsymbol{ \xi }}(k{\text{ + }}1) = {{\boldsymbol{A}}_k}\tilde{\boldsymbol{ \xi }}(k){\text{ + }}{{\boldsymbol{B}}_k}{\boldsymbol{\Delta \tilde u}}(k)，$

(10)

${\boldsymbol{\chi}}(k) ={\boldsymbol{C}}_k \tilde{\boldsymbol{ \xi }}(k)。$

(11)

式中：$\tilde{\boldsymbol{ \xi }}(k) = \left[ {\begin{array}{*{20}{c}} {\tilde{\boldsymbol{ \eta }}(k)} \\ {\tilde{\boldsymbol{ u}}(k - 1)} \end{array}} \right]$；${\boldsymbol{\Delta \tilde u}}(k) = \tilde{\boldsymbol{ u}}(k) - \tilde{\boldsymbol{ u}}(k - 1)$；${{\boldsymbol{A}}_k} = $$ \left[ {\begin{array}{*{20}{c}} {{{\tilde{\boldsymbol{ A}}}_k}}&{{{\tilde{\boldsymbol{ B}}}_k}} \\ {{{\boldsymbol{0}}_{2 \times 3}}}&{{{\boldsymbol{I}}_{2 \times 2}}} \end{array}} \right]$；${{\boldsymbol{B}}_k} = \left[ {\begin{array}{*{20}{c}} {{{\tilde{\boldsymbol{ B}}}_k}} \\ {{{\boldsymbol{I}}_{2 \times 2}}} \end{array}} \right]$；$ {{\boldsymbol{C}}_k} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_{3 \times 3}}}&{{{\boldsymbol{0}}_{3 \times 2}}} \end{array}} \right] $。基于该模型可推断出系统未来的动态特性，假设所有状态是可测量的，设置${N_p}$为预测时域，${N_c}$为控制时域，则在k时刻预测的系统输出和输入分别为：

$ {\boldsymbol{Y}}(k) = [{\boldsymbol{\chi }}(k{\text{ + }}1/k),{\boldsymbol{\chi }}(k{\text{ + }}2/k), \cdots ,{\boldsymbol{\chi }}(k{\text{ + }}{N_p}/k)]，$

(12)

$ {\boldsymbol{\Delta U}}(k) = [{\boldsymbol{\Delta \tilde u}}(k/k),{\boldsymbol{\Delta \tilde u}}(k{\text{ + }}1/k), \cdots ,{\boldsymbol{\Delta \tilde u}}(k{\text{ + }}{N_c} - 1/k)]。$

(13)

式中，${\boldsymbol{\chi }}(k{\text{ + }}i/k)、{\mathbf{\Delta \tilde u}}(k{\text{ + }}i/k)$分别为式(10)和式(11)在k时刻预测$k{\text{ + }}i$时刻的输出和输入，则基于MPC可得系统在k时刻的预测输出表达式${\boldsymbol{Y}}(k)$为：

$ {\boldsymbol{Y}}(k) = {\boldsymbol{\varPsi \tilde \xi }}(k/k){\text{ + }}{\boldsymbol{\Theta \Delta U}}(k)。$

(14)

$ {\boldsymbol{\varPsi }} = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{C}}_k}{{\boldsymbol{A}}_k}}&{{{\boldsymbol{C}}_k}{\boldsymbol{A}}_k^2}& \cdots &{{{\boldsymbol{C}}_k}{\boldsymbol{A}}_k^{{N_p}}} \end{array}} \right]^{\mathrm{T}}}，$

(15)

$ {\boldsymbol{\Theta}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{C}}_k}{{\boldsymbol{B}}_k}}&{\boldsymbol{0}}& \cdots &{\boldsymbol{0}} \\ {{{\boldsymbol{C}}_k}{{\boldsymbol{A}}_k}{{\boldsymbol{B}}_k}}&{{{\boldsymbol{C}}_k}{{\boldsymbol{B}}_k}}& \cdots &{\boldsymbol{0}} \\ \vdots & \vdots & \ddots & \vdots \\ {{{\boldsymbol{C}}_k}{\boldsymbol{A}}_k^{{N_p} - 1}{{\boldsymbol{B}}_k}}&{{{\boldsymbol{C}}_k}{\boldsymbol{A}}_k^{{N_p} - 2}{{\boldsymbol{B}}_k}}& \cdots &{{{\boldsymbol{C}}_k}{\boldsymbol{A}}_k^{{N_p} - {N_c} - 1}{{\boldsymbol{B}}_k}} \end{array}} \right]。$

(16)

基于式(14)，可得到如下的代价函数：

$ J(k) = {{\boldsymbol{Y}}^{\mathrm{T}}}(k){\boldsymbol{QY}}(k) + {\boldsymbol{\Delta }}{{\boldsymbol{U}}^{\mathrm{T}}}(k){\boldsymbol{R\Delta U}}(k) + \rho \times {\varepsilon ^2}。$

(17)

式中：${\boldsymbol{Q}}$和${\boldsymbol{R}}$为权重矩阵；$\rho $为权重系数；$\varepsilon $为松弛因子，在代价函数中加入松弛因子，可防止执行过程中出现没有可行解的情况^[14]。

为了使用QP(Quadratic Programming)求解最优问题，得到使代价函数$J(k)$最小的最优序列${\boldsymbol{\Delta U}}(k)$，将式(14)代入式(17)化简成标准的二次型形式：

$ J(k) = {[{\boldsymbol{\Delta }}{{\boldsymbol{U}}^{\mathrm{T}}}(k),\varepsilon ]^{\mathrm{T}}}{\boldsymbol{H}}(k)[{\boldsymbol{\Delta }}{{\boldsymbol{U}}^{\mathrm{T}}}(k),\varepsilon ]{\text{ + }}{\boldsymbol{G}}(k)[{\boldsymbol{\Delta }}{{\boldsymbol{U}}^{\mathrm{T}}}(k),\varepsilon ] 。$

(18)

式中：$ {\boldsymbol{H}}(k) = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\Theta }}^{\mathrm{T}}}{\boldsymbol{Q\Theta }}{\text{ + }}{\mathbf{R}}}&0 \\ 0&\rho \end{array}} \right] $，${\boldsymbol{G}}(k) = \left[ {\begin{array}{*{20}{c}} {2e_k^{\mathrm{T}}{\boldsymbol{Q\Theta }}}&0 \end{array}} \right]$，${e_k}$为预测时域内的跟踪误差。

对于实际的AUV控制系统，速度约束必不可少，本文对速度的上下界及速度增量的上下界进行如下约束：

$ {\tilde{\boldsymbol{ u}}_{\min }} \leqslant \tilde{\boldsymbol{ u}}(k{\text{ + }}i/k) \leqslant {\tilde{\boldsymbol{ u}}_{\max }},i = 0,1,2, \cdots ,{N_c} - 1，$

(19)

$ {\boldsymbol{\Delta }}{\tilde{\boldsymbol{ u}}_{\min }} \leqslant {\boldsymbol{\Delta \tilde u}}(k{\text{ + }}i/k) \leqslant {\boldsymbol{\Delta }}{\tilde{\boldsymbol{ u}}_{\max }},i = 0,1,2, \cdots ,{N_c} - 1。$

(20)

通过对满足约束式(19)和式(20)的代价函数(18)求解，得到最佳控制序列${[{\boldsymbol{\Delta }}{{\boldsymbol{U}}^ * }(k),{\varepsilon ^ * }(k)]^{\mathrm{T}}} =$$ [{\boldsymbol{\Delta }}{\tilde{\boldsymbol{ u}}^ * }(k/k), {\boldsymbol{\Delta }}{\tilde{\boldsymbol{ u}}^ * }(k + 1/k), \cdots ,{\boldsymbol{\Delta }}{\tilde{\boldsymbol{ u}}^ * }(k{\text{ + }}{N_c} - 1/k),{\varepsilon ^ * }(k)] $。此时解的最优性可保证误差跟踪系统(17)的稳定性。详细证明过程参考文献[15]，本文简要证明如下：

$\begin{split}{\text{选择}} V(k) = & J_1^ * (k) = \min {J_1}(k) = \\ & \min \left\{ \sum\limits_{i = 1}^{{N_p}} \left\| {{\boldsymbol{\eta}}(k + i/k) - {{\boldsymbol{\eta}}_r}(k + i/k)} \right\|_{\boldsymbol{M}}^2 + \right. \\ & \left. \sum\limits_{i = 0}^{{N_c} - 1} {\left\| {\Delta \tilde {\boldsymbol{u}}(k + i/k)} \right\|_{\boldsymbol{N}}^2 + \rho \cdot{\varepsilon ^2}} \right\}，\end{split}$

(21)

作为备选的Lyapunov函数，显然$ k \ne 0 $时，$ V(k) \geqslant $ 0。同时$ V(k) \leqslant {J_1}(k) $，定义：

$ \begin{split} {J_1}(k + T) = & \sum\limits_{i = 1}^{{N_p}} \left\| {{\boldsymbol{\eta }}(k + 1 + i)/k + 1) - {{\boldsymbol{\eta }}_r}(k + 1 + i/k + 1)} \right\|_{\boldsymbol{M}}^2 + \\ & \sum\limits_{i = 0}^{{N_c} - 1} {\left\| {{\boldsymbol{\Delta \tilde u}}(k + 1 + i/k + 1)} \right\|_{\boldsymbol{N}}^2 + \rho \cdot \varepsilon {{(k + 1)}^2}} = \\ & \sum\limits_{i = 2}^{{N_p}} \left\| {{{\boldsymbol{\eta }}^ * }(k + i)/k) - {{\boldsymbol{\eta }}_r}(k + i/k)} \right\|_{\boldsymbol{M}}^2 + \\ & \sum\limits_{i = 1}^{{N_c} - 1} {\left\| {{\boldsymbol{\Delta }}{{\tilde{\boldsymbol{ u}}}^ * }(k + i/k)} \right\|_{\boldsymbol{N}}^2 + \rho \cdot \varepsilon {{(k)}^2}} = \\ & V(k) - \left\| {{{\boldsymbol{\eta }}^ * }(k + 1)/k) - {{\boldsymbol{\eta }}_r}(k + 1/k)} \right\|_{\boldsymbol{M}}^2 - \\ & \left\| {{\boldsymbol{\Delta }}{{\tilde{\boldsymbol{ u}}}^ * }(k/k)} \right\|_{\boldsymbol{N}}^2。\\[-1pt] \end{split} $

(22)

显然，$ {J_1}(k{\text{ + }}T) \leqslant V(k) $，进一步得出，$ V(k{\text{ + }}1) \leqslant V(k) $，误差跟踪系统(7)的稳定性证明完毕。

参考文献[16]，可得满足速度约束的运动学控制器输出，即AUV期望的跟踪速度为：

$ {{\boldsymbol{v}}_d} = {\boldsymbol{\Delta }}{\tilde{\boldsymbol{ u}}^ * }(k/k){\text{ + }}\tilde{\boldsymbol{ u}}(k - 1/k){\text{ + }}\tilde{\boldsymbol{ u}}(k)\text{，} {{\boldsymbol{v}}_d} = [{u_d},{r_d}] 。$

(23)

式中：$ {u_d}、{r_d} $分别为AUV期望的纵向速度和期望的首向角速度。

2.2 基于DO的动力学控制器设计

在设计DO时，进行如下假设：

假设4　AUV所遭受的外界扰动未知但有界且扰动的变化率有界。

基于AUV动力学方程，设计非线性扰动观测器如下^[17]：

$ {\boldsymbol{\hat d}} = {\boldsymbol{\beta }}{\text{ + }}{{\boldsymbol{K}}_{\boldsymbol{0}}}{\boldsymbol{Mv}}，$

(24)

$ {\boldsymbol{\dot \beta }} = - {{\boldsymbol{K}}_{0}}{\boldsymbol{\beta }} - {{\boldsymbol{K}}_0}( - {\boldsymbol{C}}({\boldsymbol{v}}){\boldsymbol{v}} - {\boldsymbol{D}}({\boldsymbol{v}}){\boldsymbol{v}}{\text{ + }}{\boldsymbol{\tau }}{\text{ + }}{{\boldsymbol{K}}_0}{\boldsymbol{Mv}})。$

(25)

定义扰动观测误差为：

$ \tilde{\boldsymbol{ d}} = {\boldsymbol{\hat d}} - {\boldsymbol{d}}。$

(26)

对式(24)两边求导，由动力学模型式(7)、式(25)、式(26)可得：

$ \begin{split} {\boldsymbol{\dot {\hat d}}} = & {\boldsymbol{\dot \beta }} + {{\boldsymbol{K}}_0}{\boldsymbol{M\dot v}} =\\ & - {{\boldsymbol{K}}_0}{\boldsymbol{\beta }} - {{\boldsymbol{K}}_0}( - {\boldsymbol{C}}({\boldsymbol{v}}){\boldsymbol{v}} - {\boldsymbol{D}}({\boldsymbol{v}}){\boldsymbol{v}} + {\boldsymbol{\tau }} + {{\boldsymbol{K}}_0}{\boldsymbol{Mv}}) + \\ & {{\boldsymbol{K}}_0}( - {\boldsymbol{C}}({\boldsymbol{v}}){\boldsymbol{v}} - {\boldsymbol{D}}({\boldsymbol{v}}){\boldsymbol{v}} + {\boldsymbol{\tau }} + {\boldsymbol{d}}) = \\ & {{\boldsymbol{K}}_0}({\boldsymbol{d}} - ({\boldsymbol{\beta }} + {{\boldsymbol{K}}_0}{\boldsymbol{Mv}})) = {{\boldsymbol{K}}_0}\tilde{\boldsymbol{ d}}，\end{split} $

(27)

对式(26)两边求导，并将式(27)代入可得干扰估计误差动力学模型：

$ {\boldsymbol{\dot {\tilde d}}} = {\boldsymbol{\dot d}} - {\boldsymbol{\dot {\hat d}}} = {\boldsymbol{\dot d}} - {{\boldsymbol{K}}_0}\tilde{\boldsymbol{ d}}，$

(28)

在假设4成立的情况下，干扰估计误差动力学模型(28)为输入到状态稳定。证明如下：

选择备选的Lyapunov函数

$ {V_1} = \frac{1}{2}{\tilde{\boldsymbol{ d}}^{\mathrm{T}}}\tilde{\boldsymbol{ d}}，$

(29)

对式(29)两边公式求导，并代入式(28)可得：

$ {\dot V_1} = - {\tilde{\boldsymbol{ d}}^{\mathrm{T}}}{{\boldsymbol{K}}_0}\tilde{\boldsymbol{ d}}{\text{ + }}{\tilde{\boldsymbol{ d}}^{\mathrm{T}}}{\boldsymbol{\dot d}} \leqslant - {\lambda _{\min }}({{\boldsymbol{K}}_0}){\left\| {\tilde{\boldsymbol{ d}}} \right\|^2}{\text{ + }}\left\| {\tilde{\boldsymbol{ d}}} \right\|\left\| {{\boldsymbol{\dot d}}} \right\|。$

(30)

式中，$ {\lambda _{\min }}() $为矩阵的最小特征值。

显然，当$ \left\| {\tilde{\boldsymbol{ d}}} \right\| \geqslant \dfrac{{\left\| {{\boldsymbol{\dot d}}} \right\|}}{{{\lambda _{\min }}({{\boldsymbol{K}}_0}){\alpha _0}}} $时，$ {\dot V_1} \leqslant - (1 - {\alpha _0})\left\| {\tilde{\boldsymbol{ d}}} \right\| $。式中，$ {\alpha _0} \in (0,1) $，为正常数。

由假设4可知，$ \left\| {{\boldsymbol{\dot d}}} \right\| $是有界的，故系统(28)为输入到状态稳定的，且观测误差$ \tilde{\boldsymbol{ d}} $满足：

$ \left\| {\tilde{\boldsymbol{ d}}} \right\| \leqslant \max \left\{ {\left\| {\tilde{\boldsymbol{ d}}({t_0})} \right\|{e^{ - (1 - {\alpha _0})(t - {t_0})}},\frac{{\left\| {{\boldsymbol{\dot d}}} \right\|}}{{{\lambda _{\min }}({{\boldsymbol{K}}_0}){\alpha _0}}}} \right\}。$

(31)

系统的速度跟踪误差可表示为$ {\hat u_e} = u - {u_d}, $ ${\hat r_e} = r - {r_d} $，则结合AUV动力学模型可得速度跟踪误差动力学为：

$ \left[ {\begin{array}{*{20}{c}} {{{\dot {\hat u}}_e}} \\ {{{\dot {\hat r}}_e}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_u}{\text{ + }}{\tau _u}/{m_{11}}{\text{ + }}{d_u} - {{\dot u}_d}} \\ {{f_r}{\text{ + }}{\tau _r}/{m_{33}}{\text{ + }}{d_r} - {{\dot r}_d}} \end{array}} \right]。$

(32)

式中：$ {f_u} $、$ {f_r} $为已知的动力学模型；$ {d_u} $、$ {d_r} $为未知的复合干扰。

设计动力学控制律为：

$ \left\{\begin{gathered} {\tau _u} = {m_{11}}[ - {f_u} - {{\hat d}_u} - {k_u} \cdot{{\hat u}_e}]，\\ {\tau _r} = {m_{33}}[ - {f_r} - {{\hat d}_r} - {k_r}\cdot{{\hat r}_e}]。\end{gathered} \right.$

(33)

式中，$ {k_u} $和$ {k_r} $为正常数。

将动力学控制律(33)代入(32)中，则速度跟踪误差系统转换为：

$ {\boldsymbol{\dot e}} = - {{\boldsymbol{K}}_k}{\boldsymbol{e}} - {{\boldsymbol{d}}_e} - {{\boldsymbol{d}}_a}。$

(34)

式中：$ {\boldsymbol{e}} = {[{\hat u_e},{\hat r_e}]^{\mathrm{T}}} $；$ {{\boldsymbol{d}}_e} = {[{d_u} - {\hat d_u},{d_r} - {\hat d_r}]^{\mathrm{T}}} $；$ {{\boldsymbol{d}}_a} = {[{\dot u_d},{\dot r_d}]^{\mathrm{T}}} $。

在动力学控制律(33)作用下，速度跟踪误差系统(34)为输入到状态稳定，证明如下：

选择备选的Lyapunov函数

$ {V_2} = \frac{1}{2}{{\boldsymbol{e}}^{\mathrm{T}}}{\boldsymbol{e}}，$

(35)

对式(35)两边同时求导可得：

$\begin{split} {\dot V_2} = & - {{\boldsymbol{e}}^{\mathrm{T}}}{{\boldsymbol{K}}_k}{\boldsymbol{e}} - {\boldsymbol{d}}_e^{\mathrm{T}}{\boldsymbol{e}} - {\boldsymbol{d}}_a^{\mathrm{T}}{\boldsymbol{e}} \leqslant - {\lambda _{\min }}({{\boldsymbol{K}}_k}){\left\| {\boldsymbol{e}} \right\|^2} + \left\| {{{\boldsymbol{d}}_e}} \right\|\left\| {\boldsymbol{e}} \right\| + \\ &\left\| {{{\boldsymbol{d}}_a}} \right\|\left\| {\boldsymbol{e}} \right\| \leqslant - {\lambda _{\min }}({{\boldsymbol{K}}_k}){\left\| {\boldsymbol{e}} \right\|^2} + \left\| {\tilde{\boldsymbol{ d}}} \right\|\left\| {\boldsymbol{e}} \right\| + \left\| {{{\boldsymbol{d}}_a}} \right\|\left\| {\boldsymbol{e}} \right\|。\\[-1pt] \end{split}$

(36)

显然，当$ \left\| {\boldsymbol{e}} \right\| \geqslant \frac{{\left\| {\tilde{\boldsymbol{ d}}} \right\|{\text{ + }}\left\| {{{\boldsymbol{d}}_a}} \right\|}}{{{\lambda _{\min }}({{\mathbf{K}}_k}){\alpha _1}}} $时，$ {\dot V_2} \leqslant - (1 - {\alpha _1}){\lambda _{\min }}({{\boldsymbol{K}}_k})\left\| {\boldsymbol{e}} \right\| $。式中，$ {\alpha _1} \in (0,1) $，为正常数。

由(31)可知，$ \left\| {\tilde{\boldsymbol{ d}}} \right\| $是有界的，故系统(33)为输入到状态稳定的，且速度跟踪误差$ {\boldsymbol{e}} $满足$ \left\| {\boldsymbol{e}} \right\| \leqslant \max \left\{ {\left\| {{\boldsymbol{e}}({t_0})} \right\|{e^{ - (1 - {\alpha _1})(t - {t_0})}}, \frac{{\left\| {\tilde{\boldsymbol{ d}}} \right\|{\text{ + }}\left\| {{{\boldsymbol{d}}_a}} \right\|}}{{{\lambda _{\min }}({{\boldsymbol{K}}_k}){\alpha _1}}}} \right\} $。

3 仿真分析

验证本文提出的基于MPC-DO的轨迹跟踪控制方案有效性，同时为了突出本文控制方法的优越性，将本文的控制结果和采用反步法得到的结果进行对比。以REMUS作为仿真对象，使用的模型参数参考文献[18]。

选择采样时间$ T = 0.1 $ s，仿真总时间为50 s。控制器参数为：$ {{\boldsymbol{K}}_{0}} = {\mathrm{diag}}(2,2,2) $,$ {{\boldsymbol{K}}_k} = {\mathrm{diag}}(10,0,10) $，控制时域$ {N_c} = 30 $，预测时域$ {N_p} = 60 $，松弛因子$ \rho = 10 $，权重矩阵$ {\boldsymbol{Q}} = 10 \cdot {I_{180 \times 180}} $，$ {\boldsymbol{R}} = 100 \cdot {I_{60 \times 60}} $，$ {\tilde{\boldsymbol{ u}}_{\min }} = \left[ { - 1, - 0.5} \right] $，$ {\tilde{\boldsymbol{ u}}_{\max }}\left[ {1,0.5} \right] $，${\mathbf{\Delta }}{\tilde{\boldsymbol{ u}}_{\min }}\left[ { - 0.1, - 0.02} \right]$，${\boldsymbol{\Delta }}{{\boldsymbol{\tilde u}}_{\max }} = \left[ {0.1,0.02} \right]$。AUV初始位置和姿态角定义为$ x(0) = $ 0 m，$ y(0) = $ 2.5 m，$ \varphi (0) ={\text{π}} /4 $，初始速度为$ u(0) = $ 0 m/s，$ v(0) = $ 0 m/s，$ r(0) = $ 0 rad/s。

选择圆形参考轨迹方程为：

$ \left\{ {\begin{array}{*{20}{l}} {{x_r} = 5 \times \sin (0.2 \times t)}，\\ {{y_r} = 4 - 5 \times \cos (0.2 \times t)}。\end{array}} \right. $

(37)

仿真中考虑了复合扰动，分别为常数扰动、未知周期性扰动以及符合高斯分布的随机噪声。

$ \left\{ {\begin{array}{*{20}{c}} {{\mathrm{d}}u = 0.2 + 0.2 \times \sin (0.1 \times t) + 0.1 \times \sqrt {0.1} \times {\mathrm{rand}}n(1)} ，\\ {{\mathrm{d}}v = 0.2 + 0.2 \times \sin (0.1 \times t) + 0.1 \times \sqrt {0.1} \times {\mathrm{rand}}n(1)} ，\\ {{\mathrm{d}}r = 0.2 + 0.2 \times \sin (0.1 \times t) + 0.1 \times \sqrt {0.1} \times {\mathrm{rand}}n(1)}。\end{array}} \right. $

(38)

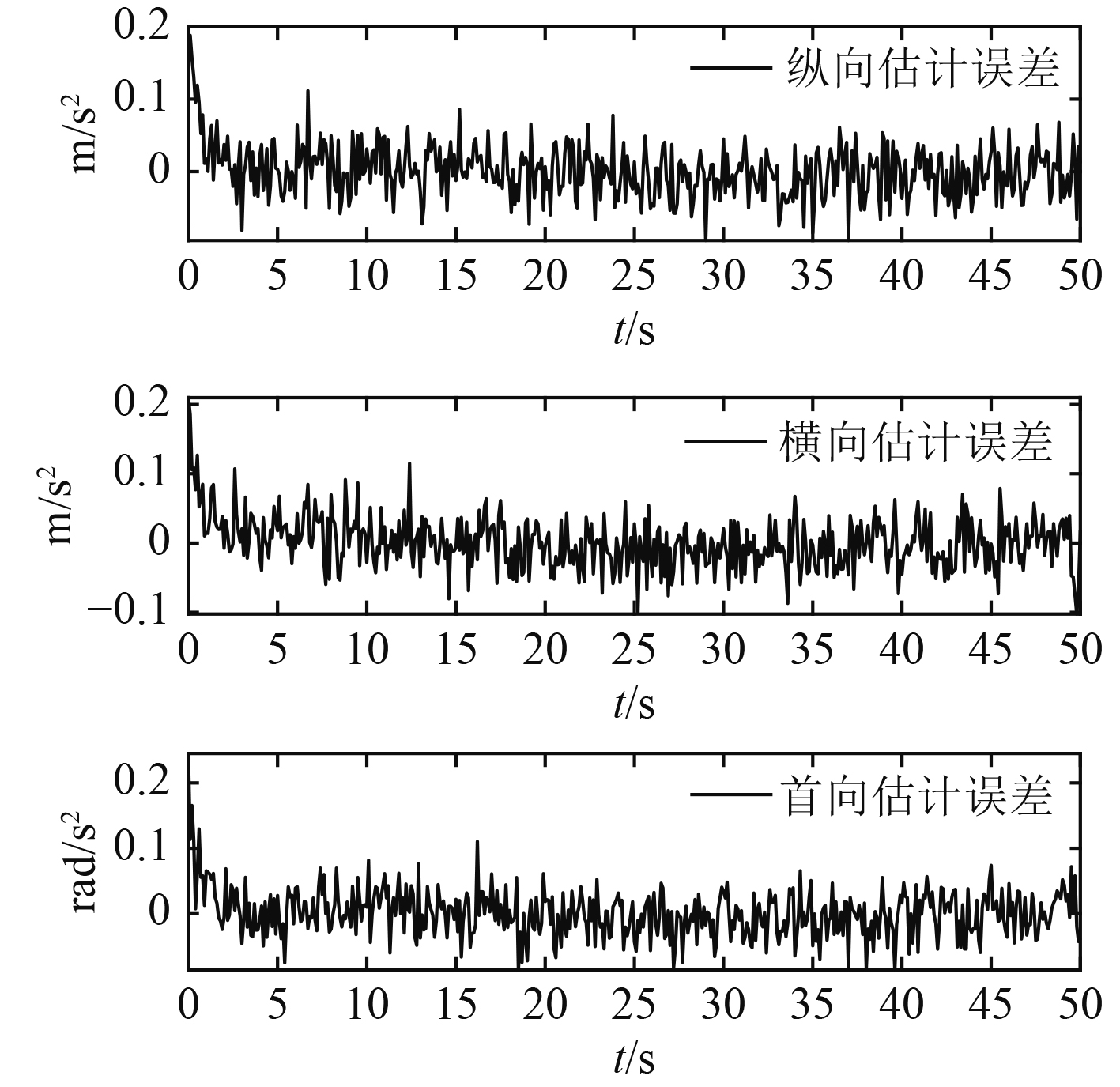
图3为复合扰动的观测误差图，采用标准差来评估观测器的估计性能，对$ {\mathrm{d}}u、{\mathrm{d}}v、{\mathrm{d}}r $观测误差的标准差分别为0.0367、0.0375、0.0364。结果表明，在存在随机噪声的情况下，所设计的非线性干扰观测器仍能准确估计AUV受到的复合扰动，实时准确的干扰估计将用于系统控制器设计，增强系统的抗干扰能力。

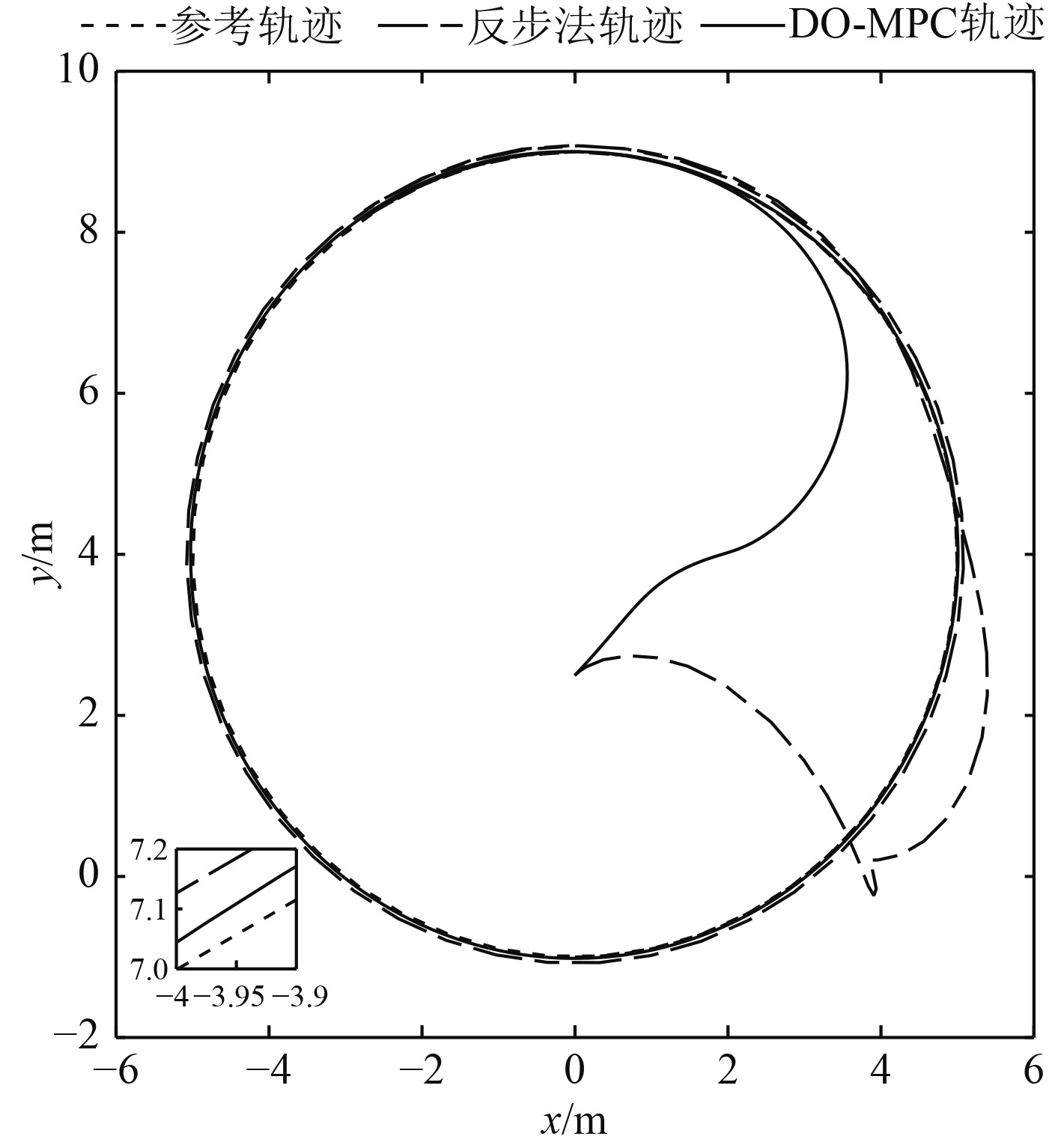
AUV在2种不同控制方案下的运动轨迹图和期望轨迹图如图4所示，轨迹跟踪误差图如图5所示。可以看出，反步法和基于MPC-DO控制方案都可对期望轨迹进行较精确的跟踪。但面对较大的初始误差，反步法提供了大的期望速度，出现了较大超调现象，而基于MPC-DO控制方案考虑了实际系统的速度约束，提供了满足系统约束的、较小的期望速度，可使AUV更加平稳的跟踪期望轨迹。同样可看出，基于MPC-DO控制方案的轨迹跟踪控制相较于反步法，有着更小的跟踪误差，可实现更为精确的跟踪。

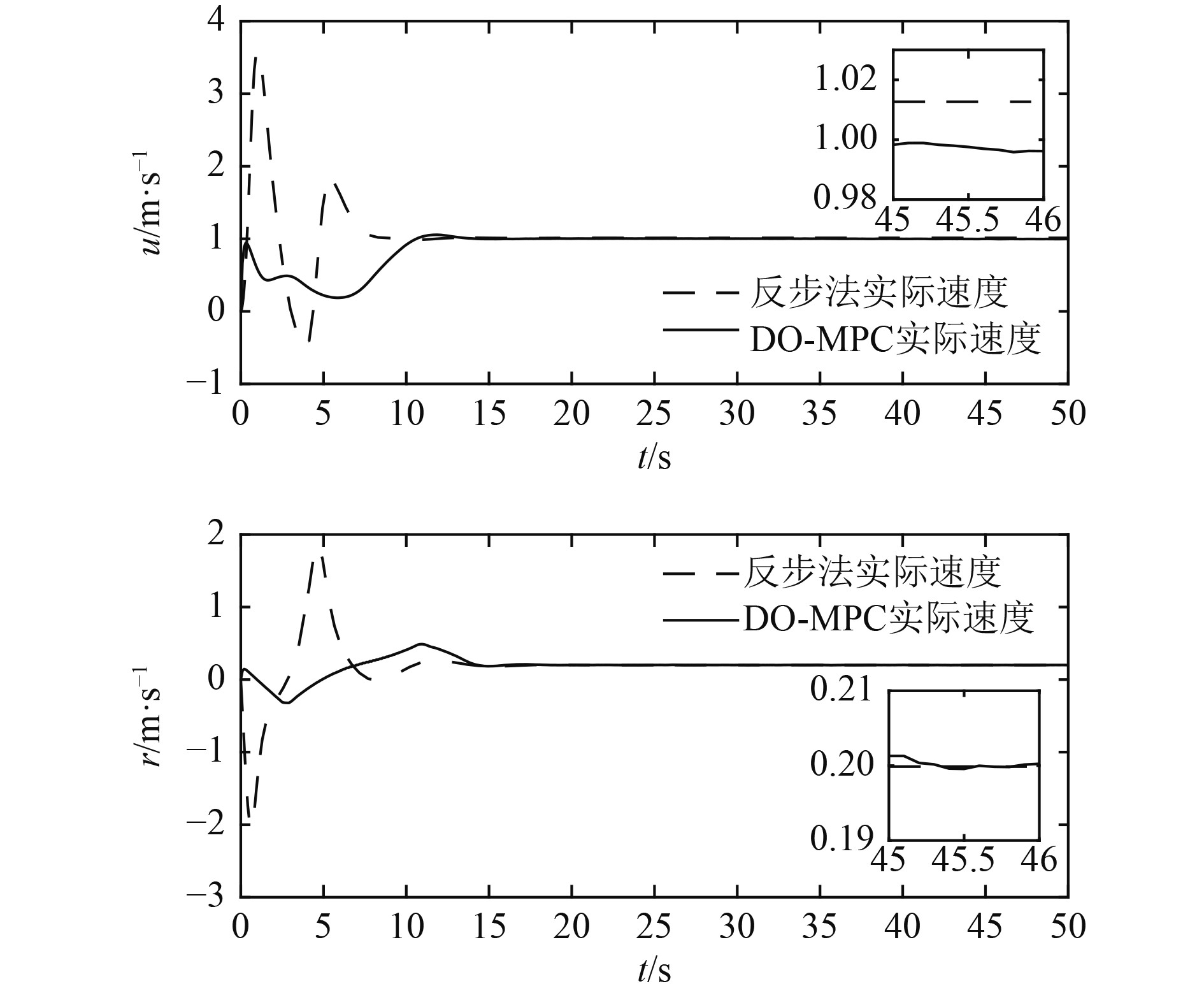
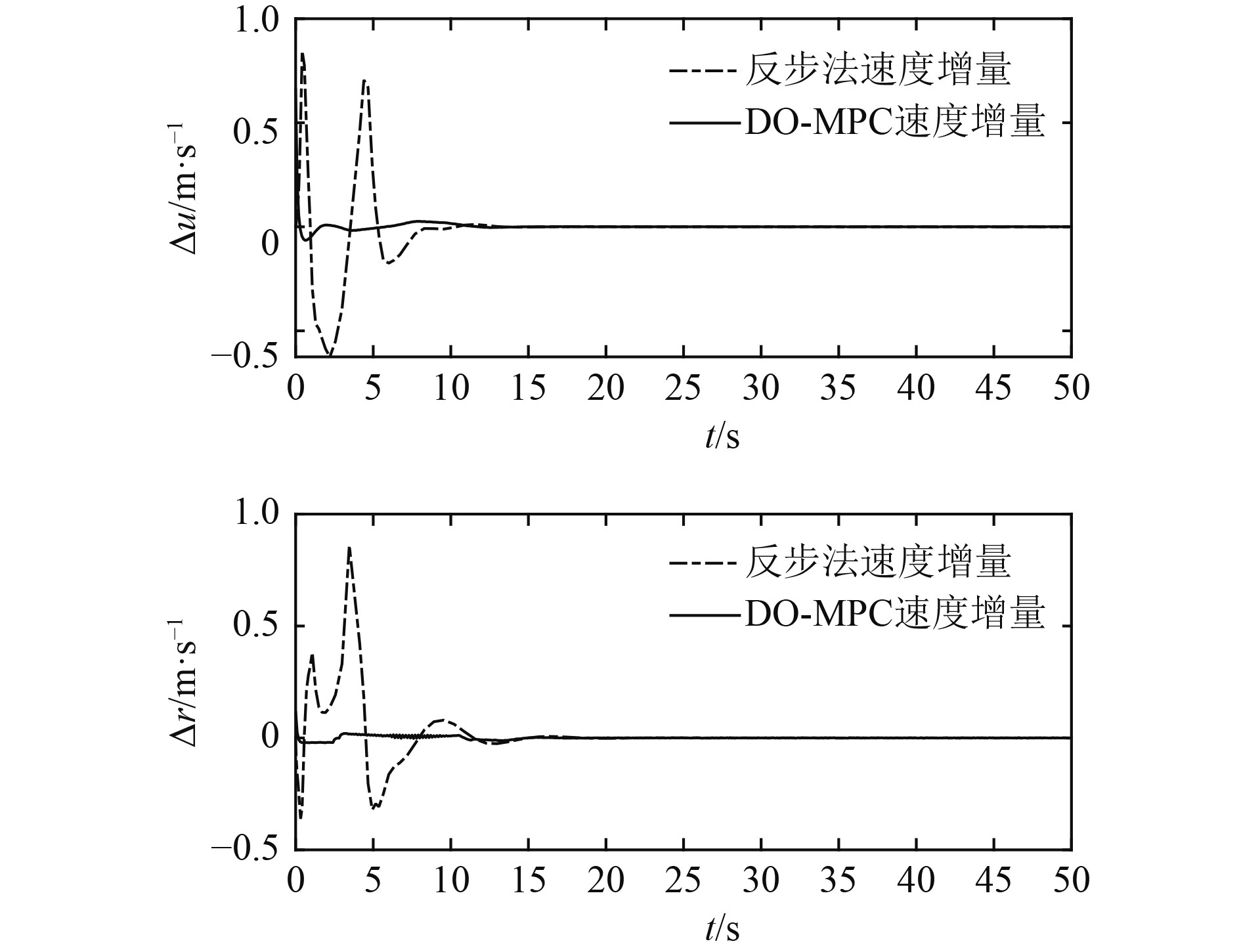
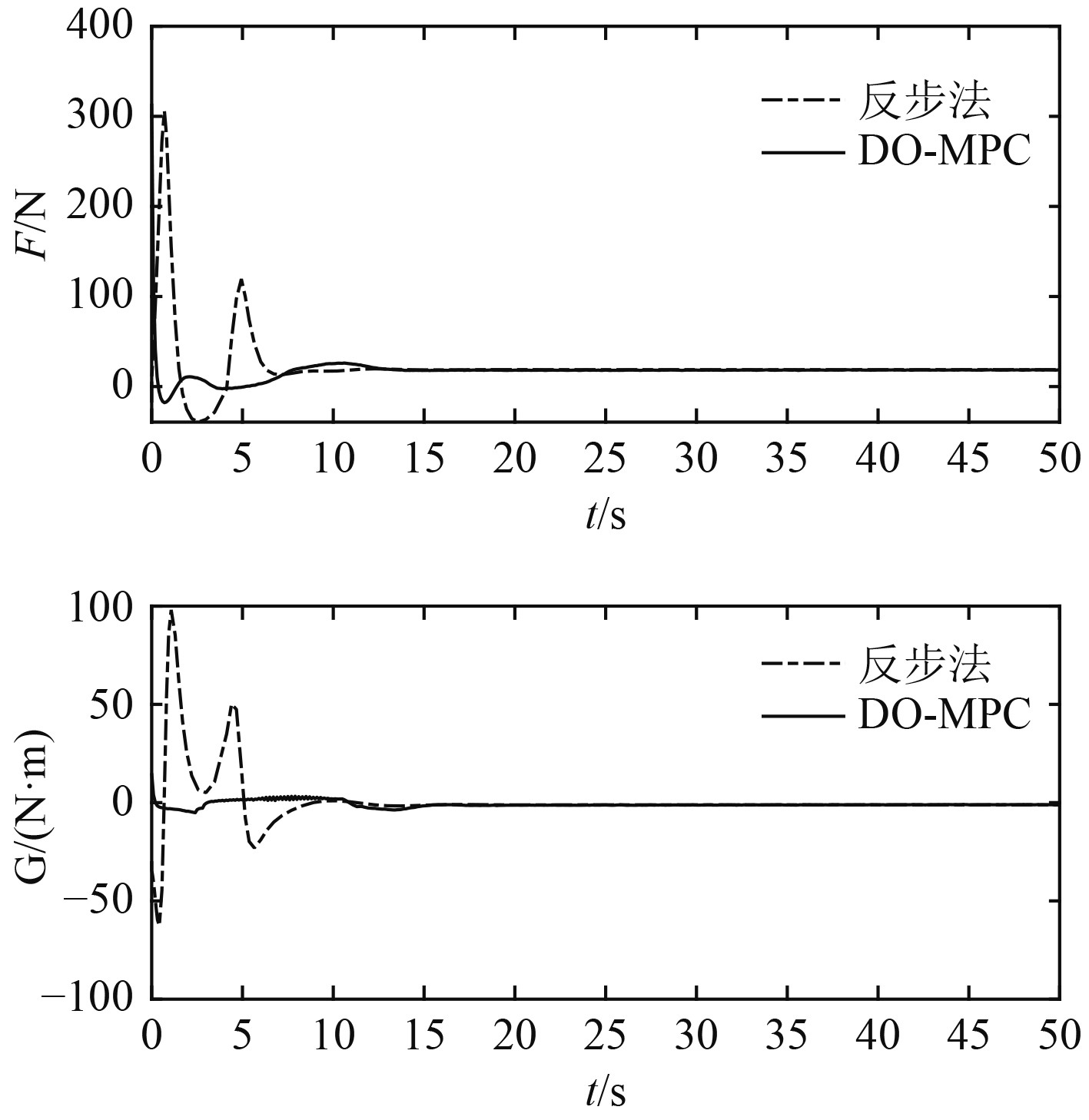
速度跟踪误差如图6所示，速度变化增量如图7所示，控制输入如图8所示。由图6和图7可知，2种控制方案都可实现速度的收敛。

但在前10 s，面对较大的位姿误差，反步法会产生很大的期望速度和尖锐的速度跳变现象。反步法最大纵向速度绝对值达到3.59 m/s，最大首向角速度绝对值达到−2 rad/s，最大纵向速度增量达到0.85 m/s²，最大首向角速度增量达到0.86 rad/s²，甚至出现小于0的纵向速度，这些在实际的AUV系统中，可能无法满足。

基于MPC-DO的控制方案考虑了速度约束和速度增量约束，基于MPC的运动学控制器会提供一个最优的满足相应约束的期望速度。此时，AUV的纵向速度被限制在0～1 m/s之间，首向角速度被限制在−0.5～0.5 rad/s之间，纵向速度增量基本在−0.1～0.1 m/s²之间，首向角速度增量基本在0 rad/s²上下，可使AUV实现更平稳的运动，更符合实际AUV系统的物理限制。

4 结　语

针对欠驱动AUV存在外界干扰和速度约束的轨迹跟踪问题，提出一种基于干扰观测器和模型预测控制算法的控制方案，通过理论分析和仿真结果验证了该方案的可行性。仿真结果表明，基于MPC的运动学控制器可有效解决实际系统中存在的速度约束问题，基于DO的动力学控制器可实现对期望速度的精确跟踪。