0 引　言

水下机器人因为“小、快、灵”的特性，受到世界范围内各个研究机构广泛关注。在复杂的海洋场景中，单台水下机器人很难对环境和目标态势实时感知和决策，由多台异构机器人组成的无人集群系统则可以利用多种高精度传感器和负载设备相互配合，提高空间和时间上的利用率，弥补单台机器人性能上的缺陷。当其中某台或者多台水下机器人发生意外而无法正常运行时，整个异构无人集群可能会崩溃，从而导致任务失败。为提高机器人面对不同作业任务的适应性，基于模块化可重构思想进行设计非常有效。根据环境和任务要求，通过搭载不同子单元模块的方法实现构型变换，不仅可以降低机器人的前期制造成本和时间代价，更有利于对单个机器人进行维修和性能扩展^[1]。

水下机器人集群在进行搜索任务过程中，如何形成并保持所设定的队形也是目前热点问题之一。韩光洁等^[2]提出了一种基于强化学习和粒子群优化算法的有效奖励机制，为多AUV系统在三维水下环境中的实时救援分配提供了一种新的策略。Elkhider等^[3]研究了多种异构AUV系统的控制方法，并考虑了时间延迟和避障问题，用于协调领航者周围或限定空间内的跟随者。由此可以发现，当前水下机器人编队方法的发展并不局限于单一算法的改进，更倾向于多种控制方法共同使用，取长补短，使编队运动更加高效。

本文结合近海的搜救、打捞、巡逻等应用场景，设计开发由成本低廉、任务分工明确、协同高效的水下机器人组成的异构集群系统。采用基于领航者-虚拟结构和滑模变结构方法，提出针对定深搜救的协同编队控制律，并使用李雅普诺夫稳定性理论证明。最后采用已自主开发的模块化可重构水下机器人作为研究对象，在引入物理引擎的可视化仿真平台中进行验证。

1 模块化水下机器人设计 1.1 整体构型

本文以模块化可重构思想为理念对水下机器人进行设计，在制造和使用成本上具有明显优势。如图1所示，单推进器式水下机器人整体采用对称结构，转向系统由水平舵和垂直舵组成，主体结构包括一个或多个耐压舱模块和由固体浮力材料制成的首尾部模块。为尽可能保证艇体外形的包络体积最大、水阻力最小，将耐压舱直接作为维持结构稳定的核心，电池组和电控元器件分别安置于耐压舱的前后两端。首部设计为椭圆形，无线通信模块、旋钮开关和充电接口设置在其空腔内部。

1.2 耐压舱设计与实验

耐压舱作为水下机器人内部结构的骨架，对保证系统运动稳定具有重要作用。本文所设计水下机器人可适用于近东海的平均深度范围内，以一般航速进行长续航、大范围航行。为保证机器人在满足要求的情况下正常工作，应使其至少可承受1.1倍的水压。如图2所示，以单节的水下机器人耐压舱为例，基于GB/T 38106-2019《压力容器用铝及铝合金》，可得可靠性计算公式为：

$ \frac{{{R_i}}}{{{R_o}}} \leqslant \sqrt {1 - \frac{{2P}}{{\left[ \sigma \right]}}} \text{，} $

(1)

其中：$ {R_i} $为水下机器人耐压舱的外半径；$ {R_o} $为内半径；$ P $为机器人在水下所受最大压力；$ \sigma $为选定材料的屈服极限。

将表1铝合金6061材料性能参数代入式(1)，计算可得该外壳可靠性完全满足设计要求。

如图3所示，在仿真中可得水下机器人耐压舱外壳最大变形仅为0.036 2 mm，位于中间部分，不会造成漏水或者挤压耐压舱内部元器件而导致损坏；最大压强为47.4 MPa，小于6061铝合金的屈服极限55.1 MPa。

为进一步验证水下机器人艇体耐压舱外壳的可靠性，模拟水下高压环境进行实体测试。所使用的水压试验装置内径为0.7 m，有效容积为0.27 m²，最高可提供20 MPa的负载。为保证耐压壳的安全性，目前实体测试仅模拟到近海平均水深100 m范围，即承受1.1 MPa静压力。

在某专业耐压性测试装置中进行测试，第1阶段模拟水深压力0.6 MPa，保压10 min；第2阶段模拟水深压力1.1 MPa，保压20 min。保压结束显示，耐压舱外壳无变形，无渗水，密封完好。数据表明，与前文理论计算和仿真验证获得的结果相似，可以证明可靠性。

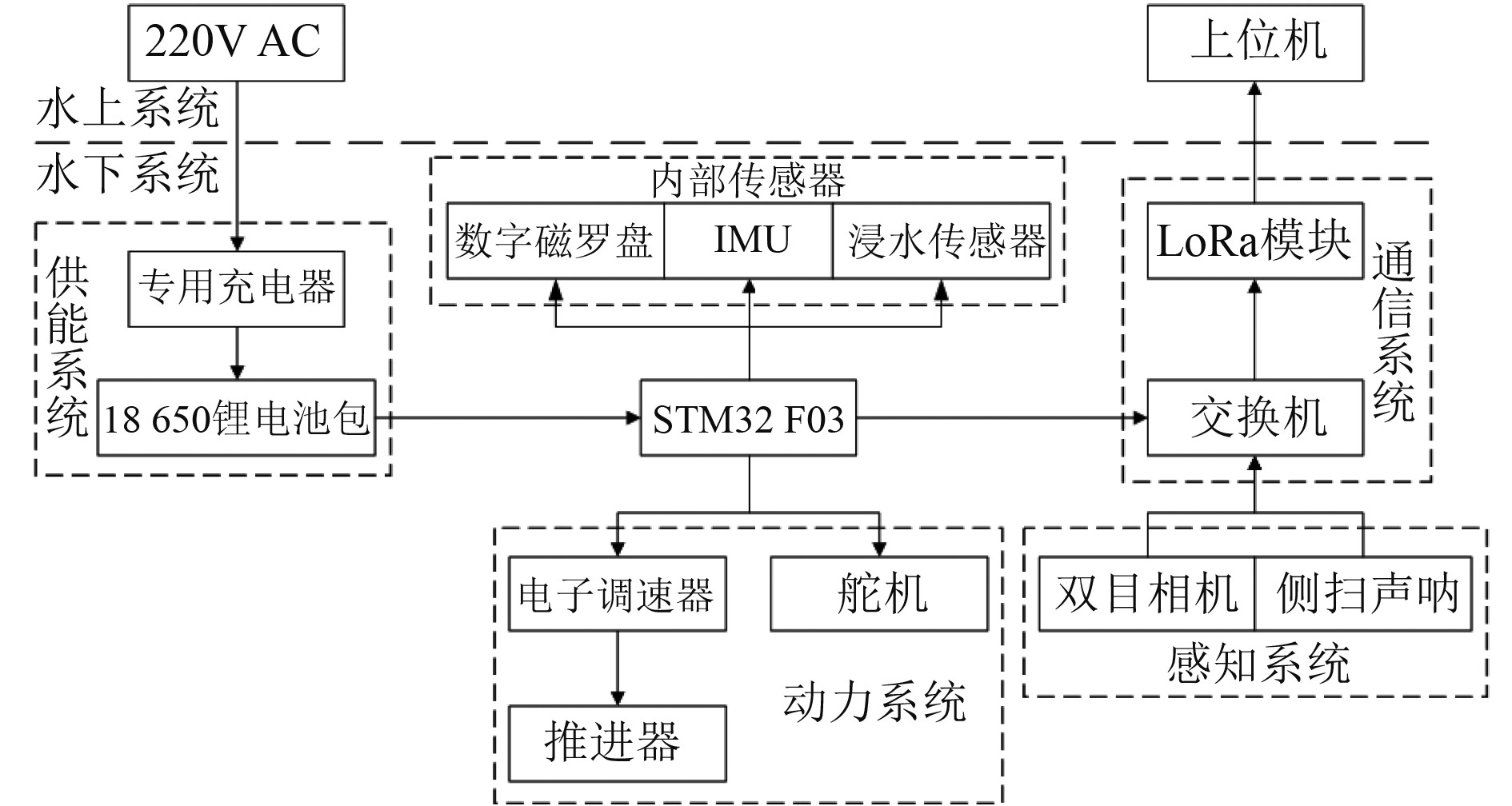
1.3 电控系统设计

所设计水下机器人电控系统核心为STM32系统，图4为电控系统逻辑框架，可以体现硬件组成以及各部分间的逻辑关系，其中主要有供能系统、动力系统、通信系统和感知系统等。

STM32微控制器通过LoRa无线模块将从水下双目相机或侧扫声呐的目标和环境信息传递到上位机，同时上位机将对应的控制指令发送回控制器，以此控制水下机器人运动。机器人在布入工作之前，利用专用充电器对18650锂电池包充电，随后可通过电源转换模块将其转换成系统所需的5～48 V直流电，给各元器件供电。IMU和数字磁罗盘分别用以获取机器人3个自由度方向的位移值和角度值。浸水传感器用以检测舱内是否发生漏水，一旦发生漏水，立即向上位机发出警报，防止造成损失。为水下机器人提供动力的执行机构主要是安装在尾部的推进器和舵机，分别控制前进和转向，其中推进器通过电子调速器来驱动电机完成STM32发送的指令。

1.4 可重构方案

在实际水下任务中，往往需要根据不同任务需求和场景快速组成不同的水下机器人集群系统，对各机器人单体的作业功能、航行速度等属性具有不同要求。为了使所设计水下机器人可以适用于多种场合，便于实现可重构，有必要划分一系列相对独立的子功能单元模块。当单台或者多台水下机器人需要更换或者损坏时，也只需要更换受损的子单元模块即可马上重新投入任务中去，图5为所设计水下机器人部分已完成的重构构型。

将子单元模块按定性属性和定量属性进行分类，定性属性指可实现功能、结构尺寸、操作方法等无法用具体量值描述的特征；定量属性指负载、航速、续航数值等。按重构方案在库中查询所要求定性属性和定量属性，即可选出满足要求的子单元模块。部分基于任务需求的模块化水下机器人重构方案如表2所示。

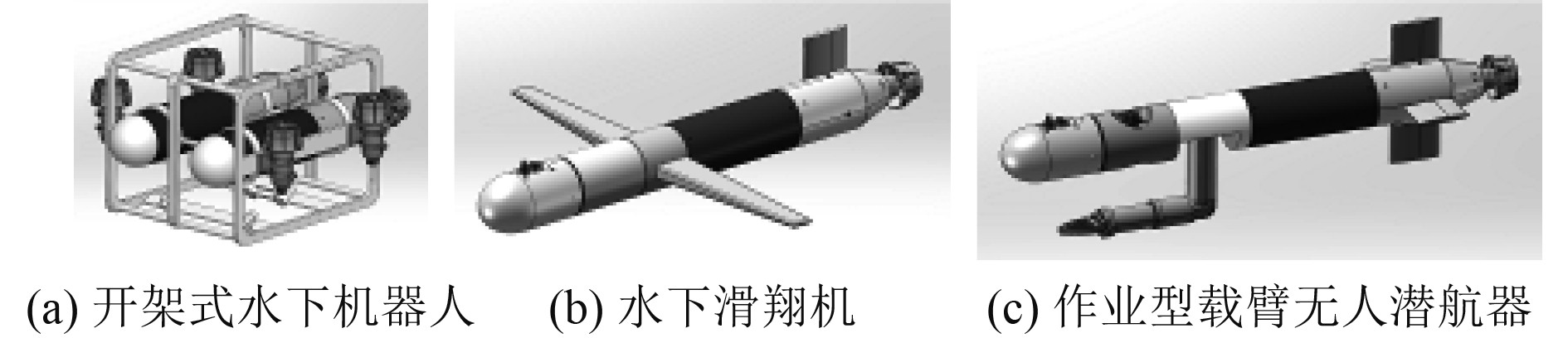
如图6所示，以面向近海搜索救援任务为例，依据重构方案设计的水下异构无人集群系统，包括全驱动、可实现灵活运动和搜索的开架式水下机器人，对救援目标进行精准作业；能在大范围内快速航行的水下滑翔机，用以搜索和监视状态异常的船舶和港口设备；作业型的载臂无人潜航器，主要应用于海洋事故中掩埋物的破拆、抓取和清理等作业。

2 异构水下机器人集群编队控制 2.1 集群编队方案

相较于传统的同构水下机器人集群，异构水下机器人集群在航行时往往因为构型的不同，而受到的干扰力大小和方向相差较大，从而很大程度影响协同编队任务的精度和稳定性。本文通过将虚拟结构法和领航跟随者法结合，根据领航者状态确定虚拟结构点的期望状态，简化了编队运动控制问题，同时保持整体队形的稳定与各机器人的高精度移动。假设异构水下机器人集群系统由$ n $台机器人组成，结合定深搜索过程中的水下机器人特性，建立平面运动学和动力学模型，第$ i $个水下机器人可以描述为：

$ {\dot \eta _i} = J\left( {{\eta _i}} \right){{\boldsymbol{v}}_i} \text{，} $

(2)

$ {M_i}\left( {{{\boldsymbol{v}}_i}} \right){\dot {\boldsymbol{v}}_i} + {C_i}\left( {{{\boldsymbol{v}}_i},{{{\dot {\boldsymbol{v}}}}_i}} \right){{\dot {\boldsymbol{v}}}_i} + {D_i}\left( {{{{\boldsymbol{v}}}_i},{{{\dot {\boldsymbol{v}}}}_i}} \right){{\dot {\boldsymbol{v}}}_i} = {\tau _i}。$

(3)

其中：$ {\eta _i} = \left[ {{x_i},{y_i},{\psi _i}} \right] $为水下机器人在惯性坐标系下的水平面位姿；$ {{\boldsymbol{v}}_i} = \left[ {{u_i},{v_i},{r_i}} \right] $为载体坐标系下的速度矢量；$ {\tau _i} $为水下机器人的控制输入，旋转矩阵$ J\left( {{\eta _i}} \right) \in {{{R}}^{3 \times 3}} $满足$ J\left( {{\eta _i}} \right){J^{\text{T}}}\left( {{\eta _i}} \right) = {I^{3 \times 3}} $。

$ J\left( {{\eta _i}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _i}}&{ - \sin {\psi _i}}&0 \\ {\sin {\psi _i}}&{\cos {\psi _i}}&0 \\ 0&0&1 \end{array}} \right] \text{，} $

(4)

惯性矩阵$ {{\boldsymbol{M}}_i}\left( {{{\boldsymbol{v}}_i}} \right) $可表示为：

$ {{\boldsymbol{M}}_i}\left( {{{\boldsymbol{v}}_i}} \right) = \left[ {\begin{array}{*{20}{c}} {m - {X_{\dot u}}}&0&0 \\ 0&{m - {Y_{\dot v}}}&0 \\ 0&0&{{I_z} - {N_{\dot r}}} \end{array}} \right] \text{，} $

(5)

科式力和向心力矩阵$ {{\boldsymbol{C}}_i}\left( {{{\boldsymbol{v}}_i},{{\dot {\boldsymbol{v}}}_i}} \right) $可表示为：

$ {{\boldsymbol{C}}_i}\left( {{{\boldsymbol{v}}_i},{{\dot {\boldsymbol{v}}}_i}} \right) = \left[ {\begin{array}{*{20}{c}} 0 & 0 & { - \left( {m - {Y_{\dot v}}} \right)v} \\ 0 & 0 & {\left( {m - {X_{\dot u}}} \right)u} \\ {\left( {m - {Y_{\dot v}}} \right)v} & { - \left( {m - {X_{\dot u}}} \right)u} & 0 \end{array}} \right] \text{，} $

(6)

阻尼项系数矩阵$ {{\boldsymbol{D}}_i}\left( {{{\boldsymbol{v}}_i},{{\dot {\boldsymbol{v}}}_i}} \right) $可表示为：

$\begin{split} & {{\boldsymbol{D}}_i}\left( {{{\boldsymbol{v}}_i},{{\dot {\boldsymbol{v}}}_i}} \right) = \\ & \left[ {\begin{array}{*{20}{c}} { - {X_u} - {X_{u\left| u \right|}}\left| u \right|}&0&0 \\ 0&{ - {Y_v} - {Y_{v\left| v \right|}}\left| v \right|}&0 \\ 0&0&{ - {N_r} - {N_{r\left| r \right|}}\left| r \right|} \end{array}} \right] \text{。}\end{split} $

(7)

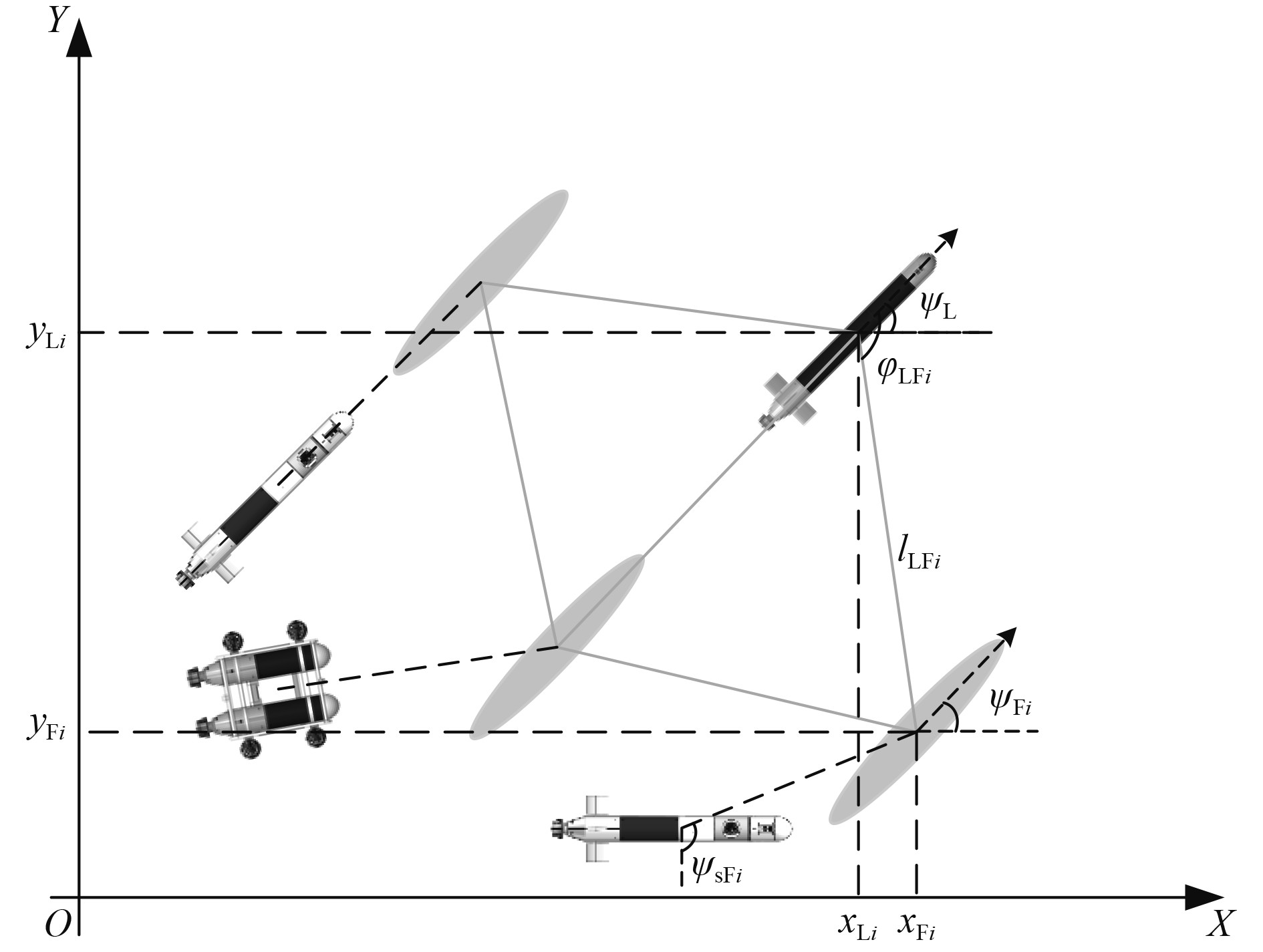
如图7所示，假设在任务过程中保持所示的菱形编队模式，其中灰色椭圆为刚性虚拟结构中水下机器人的期望位姿。在领航者-虚拟结构模型中，领航者根据目标点位置进行追踪，在惯性坐标系中可以表示为$ {\eta _{\text{L}}} = {\left[ {{x_{\text{L}}},{y_{\text{L}}},{\psi _{\text{L}}}} \right]^{\text{T}}} $；跟随者位姿和其所跟踪的期望位姿可以分别表示$ {\eta _{{\text{sF}}i}} = {\left[ {{x_{{\text{sF}}i}},{y_{{\text{sF}}i}},{\psi _{{\text{sF}}i}}} \right]^{\text{T}}} $和$ {\eta _{{\text{F}}i}} = {\left[ {{x_{{\text{sF}}i}},{y_{{\text{sF}}i}},{\psi _{{\text{sF}}i}}} \right]^{\text{T}}} $。在事先人为设置的刚性虚拟结构下，可得跟随者水下机器人的期望位姿与领航者位姿的关系式为：

$ \left\{ \begin{gathered} {x_{{\text{F}}i}} = {x_{\text{L}}} - {l_{{\text{LF}}i}}\cos \left( {{\psi _{\text{L}}} + {\varphi _{{\text{LF}}i}}} \right)，\\ {y_{{\text{F}}i}} = {y_{\text{L}}} - {l_{{\text{LF}}i}}\sin \left( {{\psi _{\text{L}}} + {\varphi _{{\text{LF}}i}}} \right) ，\\ {\psi _{{\text{F}}i}} = {\psi _{\text{L}}}。\\ \end{gathered} \right. $

(8)

其中，$ {l_{{\text{LF}}}} $和$ {\varphi _{{\text{LF}}}} $分别是刚性虚拟结构中领航者和第$ i $个虚拟结构点的平面距离和角度。

惯性坐标系下，跟随者水下机器人的误差模型可以表示为：

$ \left\{ \begin{gathered} {{\tilde x}_{{\text{F}}i}} = {x_{{\text{F}}i}} - {x_{s{\text{F}}i}} ，\\ {{\tilde y}_{{\text{F}}i}} = {y_{{\text{F}}i}} - {y_{s{\text{F}}i}}，\\ {{\tilde \psi }_{{\text{F}}i}} = {\psi _{{\text{F}}i}} - {\psi _{s{\text{F}}i}} 。\\ \end{gathered} \right. $

(9)

其中：$ {\tilde x_{{\text{F}}i}} $和$ {\tilde y_{{\text{F}}i}} $分别为惯性坐标系下各水下机器人实际位置和期望位置在$ X $和$ Y $轴的误差；$ {\tilde \psi _{{\text{F}}i}} $为偏航角误差。

2.2 协调编队控制器

该集群编队方案主要可分为两步，首先是基于任务要求的刚性虚拟结构分析，计算出各个虚拟结构中水下机器人的期望位姿；然后根据得到的期望位姿，对各个跟随者水下机器人进行轨迹跟踪控制。控制器设计的目的是根据水下机器人的数学模型，使其在期望速度的情况下，达到期望位置或在期望路径上运动。

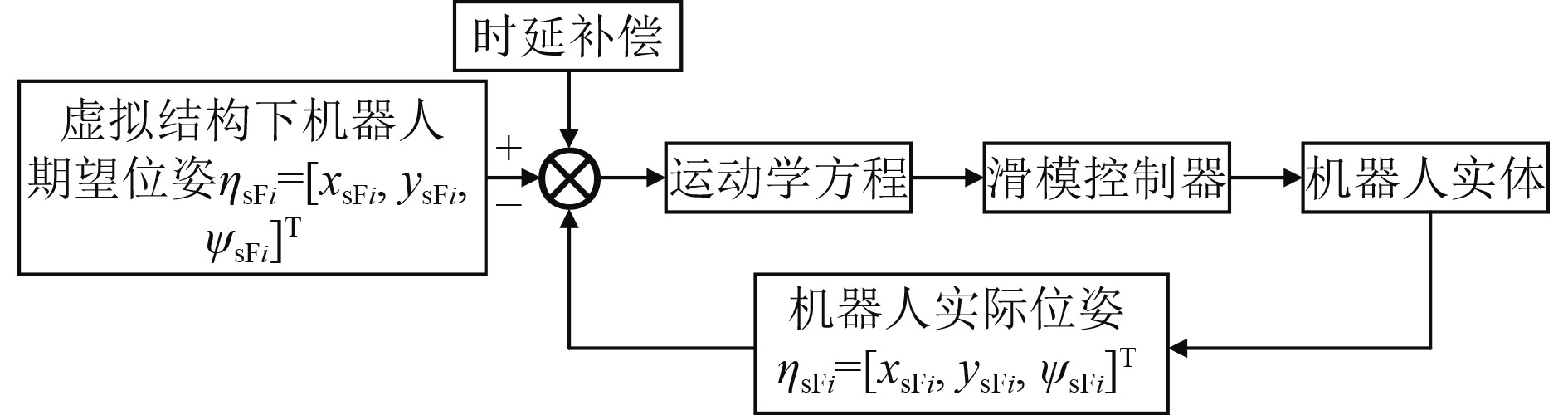
本文设计的控制器框架如图8所示。将刚性虚拟结构中水下机器人的期望位姿输入到运动学方程中，可计算出当前时刻的各机器人的期望位姿和速度矢量，并更新状态。异构水下机器人集群编队航行时往往因为构型不同的问题，受扰动影响较大，同时针对大幅值、慢时变的水下复杂环境特性^[4]，设计基于指数趋近律的滑模控制器^[5]，减少外界扰动对系统的影响。同时考虑水声信道会带来通信时延甚至丢包的情况，利用最小均方误差法对位置信息进行拟合，预测轨迹信息。

首先选取线性滑模面为：

$ {\boldsymbol{s}} = ce + \dot e \text{。} $

(10)

其中：$ {\boldsymbol{s}} = {\left[ {{s_1},{s_2}, \ldots {s_n}} \right]^{\text{T}}} $为控制系统滑模面矢量；$ {\boldsymbol{c}} = {\text{diag}}\left\{ {{c_1},{c_2}, \ldots {c_n}} \right\} $为滑模面参数矩阵。

为减少不确定性和时变环境扰动的影响，抑制滑模控制抖振情况，把指数趋近律引入式（10），设置滑模控制律：

$ {\dot s_i} = \frac{{{\text{d}}{s_i}}}{{{\text{d}}t}} = - \varepsilon {{\mathrm{sgn}}} \left( {{s_i}} \right) - k{s_i},\varepsilon > 0,k > 0 \text{。} $

(11)

其中，$ k{s_i} $为指数趋近项。等速趋近律$ {{\mathrm{sgn}}} \left( {{s_i}} \right) $为：

$ {{\mathrm{sgn}}} \left( {{s_i}} \right) = \left\{ {\begin{array}{*{20}{l}} 1，&{{s_i} > 0} ，\\ 0，&{{s_i} = 0}，\\ { - 1}，&{{s_i} < 0}。\end{array}} \right. $

(12)

结合式（3）、式（9）和式（11）可得滑模控制律为：

$ \begin{split} u =& \tau = {\boldsymbol{M}}\left( \eta \right)\left( {c\dot e + \varepsilon {{\mathrm{sgn}}} \left( s \right) + ks + {{\ddot \eta }_d}} \right) +\\ &{\boldsymbol{C}}\left( {v,\dot v} \right)\left( {ce - s + {{\dot \eta }_d}} \right) {\boldsymbol{D}}\left( {v,\dot v} \right)\left( {ce - s + {{\dot \eta }_d}} \right) + {\boldsymbol{D}}\left( \eta \right)。\end{split} $

(13)

为证明控制系统稳定，选取Lyapunov函数为：

$ {{V = }}\frac{{s{s^{\mathrm{T}}}}}{2} \text{，} $

(14)

两边同时微分可得：

$ \dot V = \sum\limits_{i = 1}^n {{s_i}{{\dot s}_i}} = {s^{\text{T}}}\dot s \text{。} $

(15)

结合式（11）和式（15）可得：

$ \dot V = - \varepsilon \left| {{s^{\text{T}}}{{\mathrm{sgn}}} \left( s \right)} \right| - k{s^{\text{T}}}s 。$

(16)

易证得$ \dot V \leqslant 0 $，当且仅当$ s = 0 $时，$ \dot V = 0 $。即该控制方法满足Lyapunov稳定条件，系统趋于稳定。

针对水声信道容易产生信号衰减速度快的特点，利用最小均方误差法对位姿信息进行拟合。

$ \left[ {\begin{array}{*{20}{c}} {{x_{{\text{F}}{\mathrm{in}}}}(t)} \\ {{y_{{\text{F}}{\mathrm{in}}}}(t)} \\ {{\psi _{{\text{F}}{\mathrm{in}}}}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{a_0}}&{{a_1}}& \ldots &{{a_m}} \\ {{b_0}}&{{b_1}}& \ldots &{{b_m}} \\ {{c_0}}&{{c_1}}& \ldots &{{c_m}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1 \\ t \\ \vdots \\ {{t^m}} \end{array}} \right] 。$

(17)

假设从编队开始时刻$ {t_0} $到当前时刻$ {t_{{\text{rece}}}} $共接收$ n $个位姿信息$ {\eta _{{\text{F}}{\mathrm{in}}}} $，期望位姿的数据代入式（17）可以得出3个关于时间$ t $的函数$ {x_{{\text{F}}in}}(t) $、$ {y_{{\text{F}}{\mathrm{in}}}}(t) $和$ {\psi _{{\text{F}}{\mathrm{in}}}}(t) $。对于各个水下机器人，在目前时刻$ {t_{{\text{rece}}}} $接收到发送时刻$ {t_{{\text{send}}}} $发出的目标轨迹$ \eta _{{\text{F}}{\mathrm{in}}}^{{\text{send}}} = \left[ {x_{{\text{F}}{\mathrm{in}}}^{{\text{send}}},y_{{\text{F}}{\mathrm{in}}}^{{\text{send}}},\psi _{{\text{F}}{\mathrm{in}}}^{{\text{send}}}} \right] $，可得当前的期望轨迹应该为$ \eta _{{\text{F}}in}^{{\text{rece}}} = \left[ {x_{{\text{F}}in}^{{\text{rece}}},y_{{\text{F}}in}^{{\text{rece}}},\psi _{{\text{F}}in}^{{\text{rece}}}} \right] $。在下一个目标信息到达之前，使用最小均方误差进行估计预算，并将结果传入机器人进行编队控制，同时更新当前位姿信息。

3 可视化仿真实现

利用实验室已有的开架式水下机器人和作业型载臂无人潜航器^[6]替代，组成异构水下机器人集群（见图9）。为验证前文方法的有效性，基于Webots仿真软件二次开发和集成，并引入根据模型和实验获得的物理引擎参数，对异构水下机器人集群及编队方法进行可视化仿真。

在仿真中，异构水下机器人集群整体运动保持菱形结构，各机器人与领航者微型水下机器人的期望距离为$ {\text{5 m}} $，初始位置为$ \left( {0,0} \right) $、$ \left( { - 4,0} \right) $、$ \left( {0, - 4} \right) $和$ \left( { - 2, - 1} \right) $，执行搜索探测任务的微型水下机器人位于集群前方位置，2台作业型载臂无人潜航器位于集群两侧位置，开架式水下机器人位于末尾做精确作业和感知任务。设定微型水下机器人以$ 0.707\;{\text{m/s}} $航速缓慢运动，运动轨迹为$ y = x $，并以$ {{T = 5\; {\mathrm{s}}}} $为周期向其他机器人广播。

根据图10异构水下机器人集群的运动轨迹可以明显看出，在本文所使用的编队方法作用下，集群可以快速形成队形，并稳定保持。

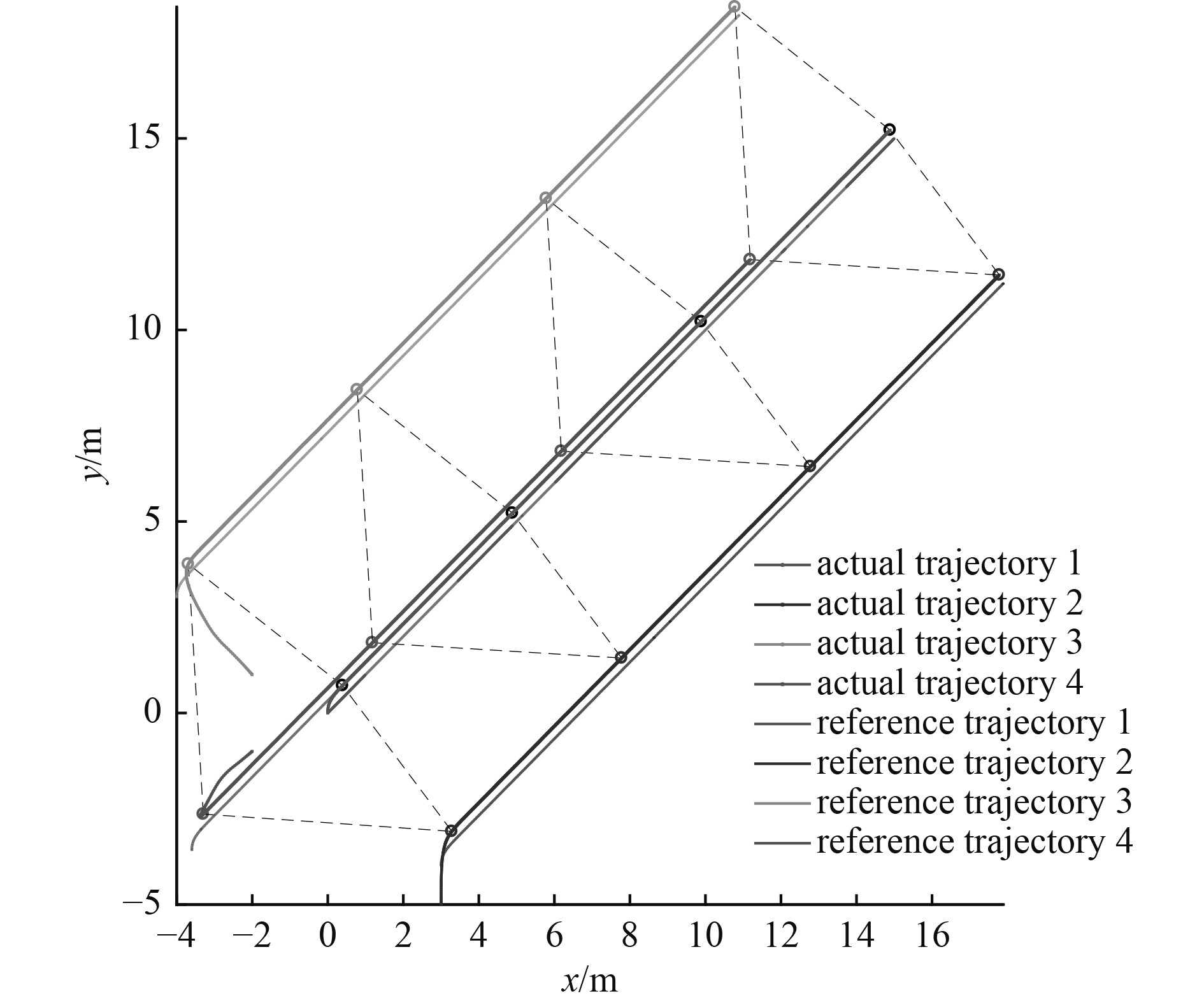
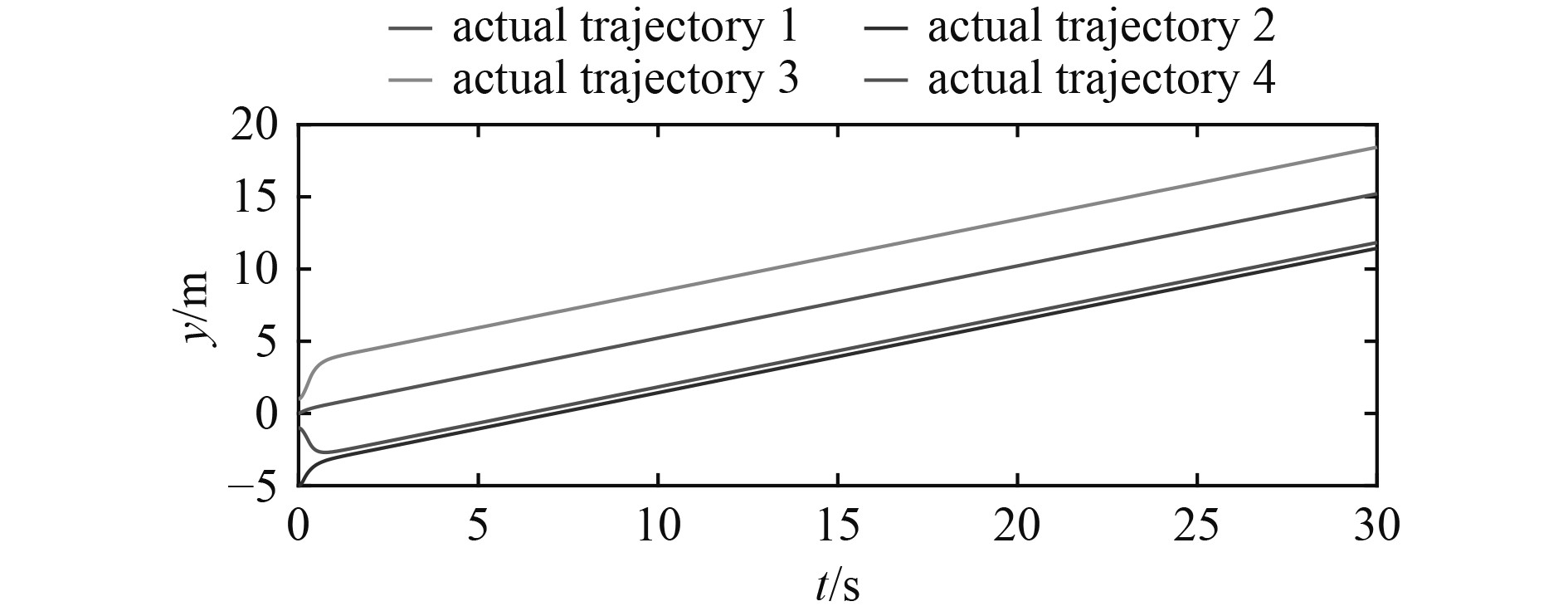
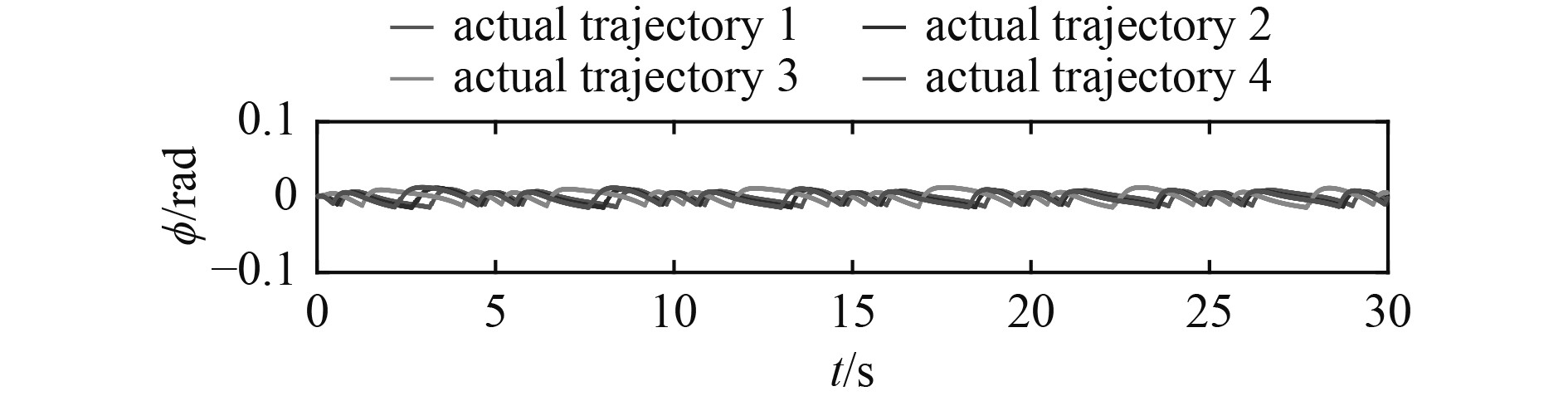
集群横向和纵向的运动轨迹结果如图11和图12所示，其偏航角姿态控制如图13所示。从仿真结果曲线可知，所设计的控制器效果明显，能够以较高的精度实现水下机器人集群的编队运动，相比于刚性虚拟结构下的期望轨迹，该编队方法在形成和保持队形中误差小于5%。但由于机器人结构特性和外界干扰参数的不确定性，在偏航角姿态控制上存在一定抖振。

4 结　语

本文针对近海环境的特点和不同的水下典型任务需求，利用模块化可重构思想设计了多种型号的水下机器人。对于异构水下机器人集群在工作中扰动参数不确定的问题，将领航-跟随者和虚拟结构法相结合，采用滑模控制方法与李雅普诺夫理论设计控制律函数，使各水下机器人能够保持刚性队形而达到近同速稳定运动。最终在引入物理引擎的可视化仿真平台中进行验证，结果证明所设计编队控制策略可以满足近海环境下异构水下机器人集群的实际需求。下一步将研制更多水下机器人重构构型，并考虑灵活变换队形和动态避障，优化编队控制策略，在实际近海环境中进行验证。