2. 中国船舶科学研究中心,江苏 无锡 214082;
3. 深海技术科学太湖实验室,江苏 无锡 214082
2. China Ship Scientific Research Center, Wuxi 214082, China;
3. Taihu Laboratory of Deepsea Technological Science, Wuxi 214082, China
船舶空调通风系统一般采用定风量运行方式,易造成能源浪费。变风量送风技术(VAV)可避免风机长期满负荷运行造成的能源浪费,同时降低空调通风系统噪声。该技术在陆上建筑领域研究充分而在船舶上的研究基础薄弱,目前仅有少量豪华客船、特种船舶采用了变风量空调系统,但限于技术基础,并没有取得令人满意的效果[1-2]。
船舶航行环境复杂多变,除了成本因素外,变风量空调系统在船舶领域应用较少的另一个重要原因是其调控难度大。变风量空调系统中存在多个控制回路,包括“舱室温度—送风量”控制回路、“送风温度—冷冻水流量”控制回路、“监测静压—风机频率”控制回路、“CO2浓度—新风阀开度”控制回路等。各回路之间相互耦合,在实际的调控过程中任一回路的参数变动都将影响其他回路,变风量空调系统具有多变量、强耦合、非线性的特点[3-4]。系统的耦合性增加了调控难度,如要取得良好的控制效果,应对系统进行解耦设计。目前相关研究主要集中在建筑领域,在船舶工程领域关注很少[5 − 11]。此外,现有研究多是从解耦设计技术的角度开展研究,而对于实际工程应用中的调试方法鲜有涉及。
本文针对船用变风量空调系统的多回路耦合问题开展解耦及调试技术研究,选取典型单元船舶空调系统为研究对象,从解耦设计技术及工程调试方法2个方面进行论述。首先在解耦设计技术上,对各控制回路进行数学建模,开展解耦设计,通过仿真的方式验证解耦效果;在工程调试方法上,提出多回路串联延时调控方法,经验证在未进行解耦设计的情况下仍能实现各个回路的有效调控,有利于工程实际应用。
1 系统耦合特性分析受到航行环境及人员流动的影响,船舶舱室热负荷时刻变化,变风量空调系统通过调节送风量对室温进行调节,区域送风量的变化势必会影响总风量;总风量影响表冷器负载,在冷冻水流量尚未发生改变时会导致送风温度变化,送风温度波动又会进一步影响舱室温度;送风量改变使得管道内监测点静压值变化,为使静压实测值跟随设定值,需对风机转速进行调节,而风机转速的变化又将影响送风量,进一步影响送风温度以及室内温度。此外,对多个舱室的温度控制同样存在耦合现象,当某一舱室的负荷减小,室内温度下降时,其末端装置的风阀开度就会减小,这将导致送风系统阻力的升高,送风管压力增大,进而导致其他舱室的送风量增加。此时相应舱室的末端装置为了保持室内温度,就会关小风阀以减小送风量,造成静压进一步升高。当系统静压超过设定值后,静压控制器就会降低送风机的转速,使系统静压回落到原来的设定值,各个末端风阀又逐渐开大。由此产生末端风阀不断关小、开大的情况,不仅会引起系统不稳定,也会产生噪声过大的问题。
1.1 数学建模对耦合特性进行分析,建立各控制回路的数学模型,分析输入、输出及干扰量的关系。描述一个系统的数学模型包括微分方程和传递函数2种方式,变风量空调系统的各个控制回路符合相应的物理定律,可采用机理分析法进行数学建模,该方法物理意义明确,能清晰看出各变量之间的关系。
1.1.1 室温控制回路舱室温度实际上反映的是室内热量,与输入热量、输出热量有关,根据能量守恒,温度控制的热平衡方程为:
| $ {C_r}\frac{{{\mathrm{d}}{t_r}}}{{{\mathrm{d}}t}} = Q - c\rho {G_a}({t_r} - {t_s})。$ | (1) |
式中:Cr为舱室的热容,kJ/℃;c为空气的比热容,kJ/(kg·℃);
| $ {C_r}\frac{{\Delta {\rm{d}}{t_r}}}{{{\rm{d}}t}} = \Delta Q - \left[ {c\rho \Delta {G_a}({t_r} - {t_s}) + c\rho {G_a}(\Delta {t_r} - \Delta {t_s})} \right]。$ | (2) |
式(2)在工作点附近展开,并进行拉普拉斯变换得:
| $ {C_r}s\Delta {t_r}(s) = \Delta Q(s) - c\rho \Delta {G_a}(s)({t_r} - {t_s}) - c\rho {G_a}(\Delta {t_r}(s) - \Delta {t_s}(s))。$ | (3) |
令
| $ \Delta {t_r}(s) = \frac{{{b_1}}}{{Ts + 1}}\Delta {G_a}(s) + \frac{{{b_2}}}{{Ts + 1}}\Delta {t_s}(s) + \frac{{{b_3}}}{{Ts + 1}}\Delta Q(s)。$ | (4) |
根据能量守恒,表冷器的热交换关系式为:
| $ {M_c}{C_c}\frac{{{\mathrm{d}}{t_c}}}{{{\mathrm{d}}t}} = {G_a}{\rho _a}{C_a}({t_{ai}} - {t_{ao}}) - {G_w}{\rho _w}{C_w}({t_{wi}} - {t_{wo}})。$ | (5) |
其中,出风温度tao与tc一致,tai与新风和回风有关,
| $\begin{split} & {M_c}{C_c}\frac{{{\mathrm{d}}{t_c}}}{{{\mathrm{d}}t}} = {G_a}{\rho _a}{C_a}\left(\frac{{{G_{an}}}}{{{G_a}}}{t_{an}} + \frac{{{G_{ar}}}}{{{G_a}}}{t_r} - {t_c}\right) - \\ & {G_w}{\rho _w}{C_w}({t_{wi}} - {t_{wo}})。\end{split} $ | (6) |
可看到送风温度与冷冻水流量和送风量Ga均有关系,与冷冻水流量的传递函数可直接得到,而与送风量呈非线性关系,需通过泰勒级数展开得到。最终得到的传递函数为:
| $ \Delta {t_c}(s) = \frac{{{b_1}}}{{Ts + 1}}\Delta {G_w}(s) + \frac{{{b_2}}}{{Ts + 1}}\Delta {G_a}(s)。$ | (7) |
其中,
选取典型风机特性曲线,根据风机风压与风量、频率的关系以及静压与管路阻抗的关系,可得静压测点压力的计算公式为:
| $ \begin{split} {P_s} = P - S{Q^2} = - 5.65485 \times {10^{ - 5}}{Q^2} + \\ 0.53747Q(\frac{f}{{50}}) + 1.42892{(\frac{f}{{50}})^2} - 87{Q^2}。\end{split} $ | (8) |
再根据风量与频率的关系以及额定工况风量可最终得到静压与频率的传递函数。
2 解耦设计从以上分析可看出,各回路的控制方程中各变量是耦合在一起的,增大了系统调控难度,要实现系统解耦就必须利用解耦补偿器使控制系统的开环和闭环传递函数矩阵成为对角矩阵,将一个有耦合影响的多变量过程化成无耦合的单变量过程。实际上,解耦环节也是耦合,其作用是补偿原有的耦合作用。
2.1 解耦方法传统的解耦方法包括对角矩阵解耦法、前馈补偿解耦法、反馈解耦法等。
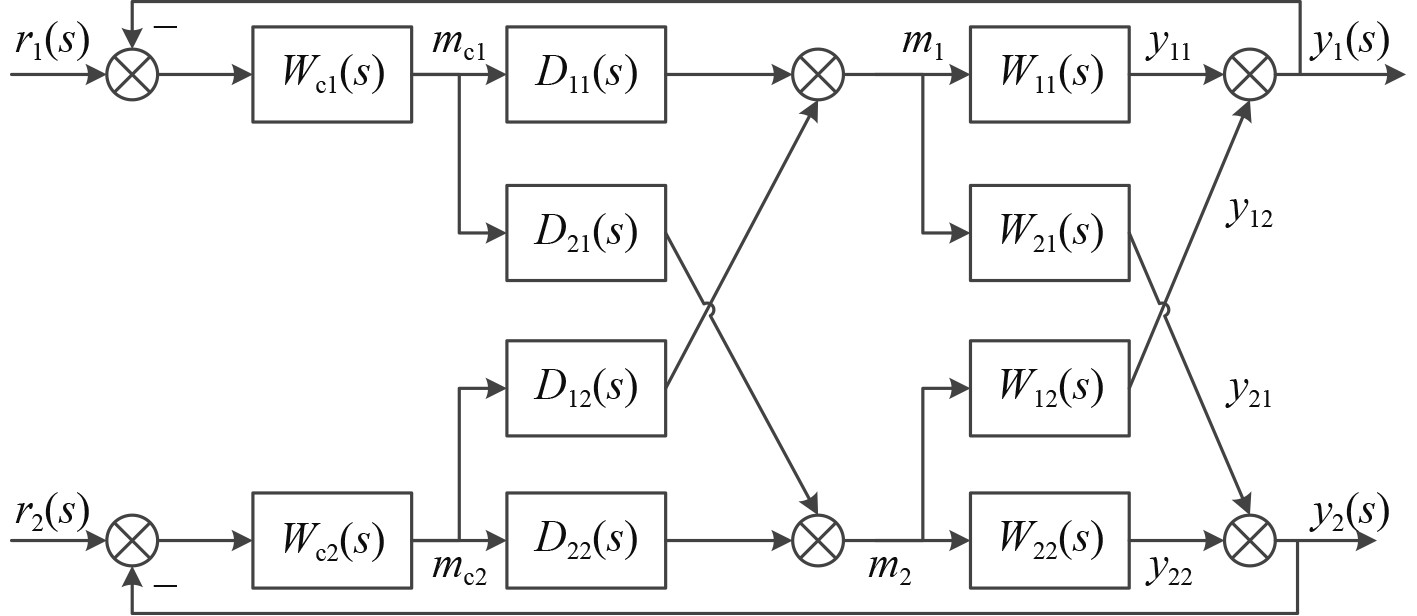
2.1.1 对角解耦对角解耦就是通过解耦使耦合对象的传递函数变为对角矩阵,其控制框图如图1所示。
|
图 1 对角矩阵法解耦控制框图 Fig. 1 Block diagram of diagonal matrix decoupling control |
耦合对象的传递函数为:
| $ {W_0}(s) = \left[ {\begin{array}{*{20}{c}} {{W_{11}}(s)}&{{W_{12}}(s)} \\ {{W_{21}}(s)}&{{W_{22}}(s)} \end{array}} \right]。$ | (9) |
结构网络的传递函数矩阵为:
| $ {D_0}(s) = \left[ {\begin{array}{*{20}{c}} {{D_{11}}(s)}&{{D_{12}}(s)} \\ {{D_{21}}(s)}&{{D_{22}}(s)} \end{array}} \right]。$ | (10) |
目标矩阵为:
| $ {W_ \wedge }(s) = \left[ {\begin{array}{*{20}{c}} {{W_{11}}(s)}&0 \\ 0&{{W_{22}}(s)} \end{array}} \right]。$ | (11) |
根据要求实现的目标为:
| $ \begin{split} \left[ {\begin{array}{*{20}{c}} {{Y_1}} \\ {{Y_2}} \end{array}} \right] &= \left[ {\begin{array}{*{20}{c}} {{W_{11}}(s)}&{{W_{12}}(s)} \\ {{W_{21}}(s)}&{{W_{22}}(s)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{D_{11}}(s)}&{{D_{12}}(s)} \\ {{D_{21}}(s)}&{{D_{22}}(s)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{M_{c1}}} \\ {{M_{c2}}} \end{array}} \right] \\ & = \left[ {\begin{array}{*{20}{c}} {{W_{11}}(s)}&0 \\ 0&{{W_{22}}(s)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{M_{c1}}} \\ {{M_{c2}}} \end{array}} \right] 。\\[-1pt] \end{split} $ | (12) |
即经过解耦后,保留原传递函数矩阵中对角线元素,由此可计算得到解耦矩阵为:
| $ \begin{aligned} & {D_0}(s) = W_0^{ - 1}(S){W_ \wedge }(s) =\\ &{\left[ {\begin{array}{*{20}{c}} {{W_{11}}(s)}&{{W_{12}}(s)} \\ {{W_{21}}(s)}&{{W_{22}}(s)} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{W_{11}}(s)}&0 \\ 0&{{W_{22}}(s)} \end{array}} \right] 。\end{aligned}$ | (13) |
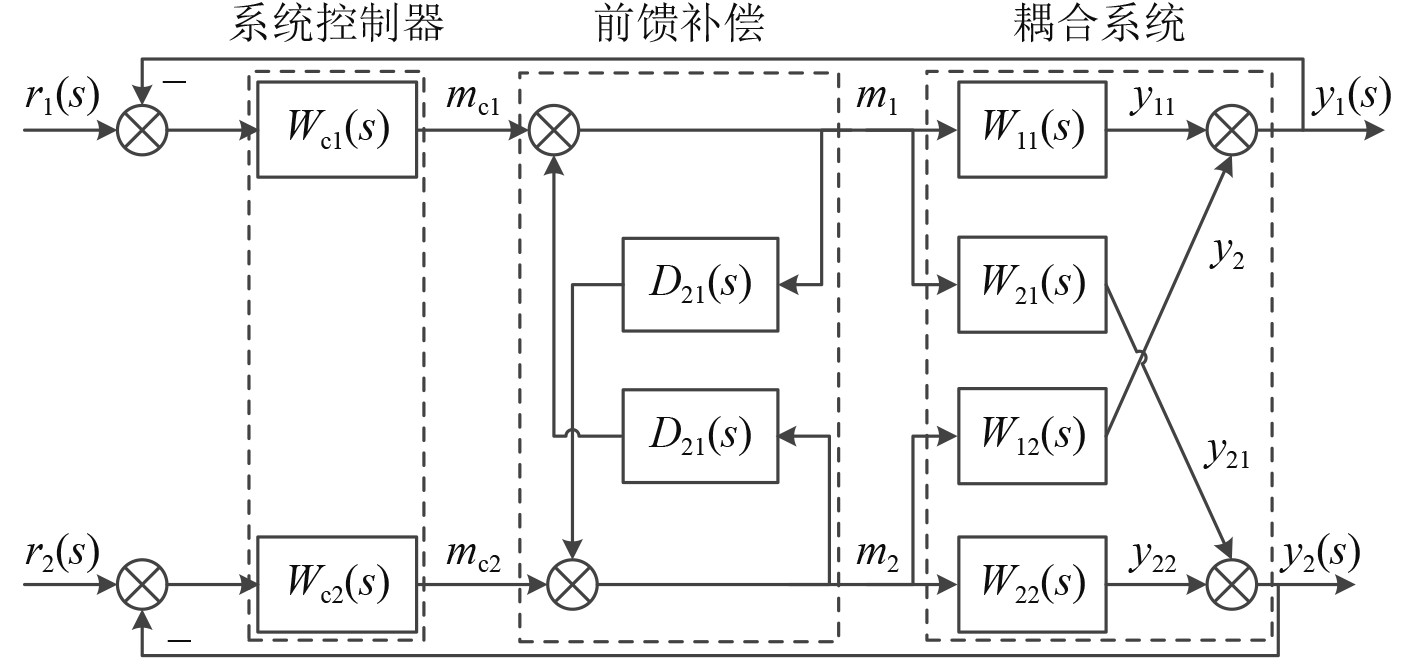
前馈补偿解耦法是根据不变性原理设计解耦网络,从而解除系统的耦合关联,其系统框图如图2所示。
|
图 2 前馈补偿解耦法控制框图 Fig. 2 Control block diagram of feed-forward compensation decoupling method |
如不存在耦合,则当输入为0、干扰量不为0时,相应通道的输出应为0,由此根据不变性原理有
| $ \begin{gathered} {y_{11}} + {y_{12}} = 0({m_2} \ne 0),\\ {y_{21}} + {y_{22}} = 0({m_1} \ne 0)。\end{gathered} $ | (14) |
即
| $ \begin{gathered} {W_{12}}(s) + {D_{12}}(s){W_{11}}(s) = 0,\\ {W_{21}}(s) + {D_{21}}(s){W_{22}}(s) = 0。\end{gathered} $ | (15) |
从而可得到解耦器的数学模型为:
| $ \begin{gathered} {D_{12}}(s) = - \frac{{{W_{12}}(s)}}{{{W_{11}}(s)}},\\ {D_{21}}(s) = - \frac{{{W_{21}}(s)}}{{{W_{22}}(s)}}。\end{gathered} $ | (16) |
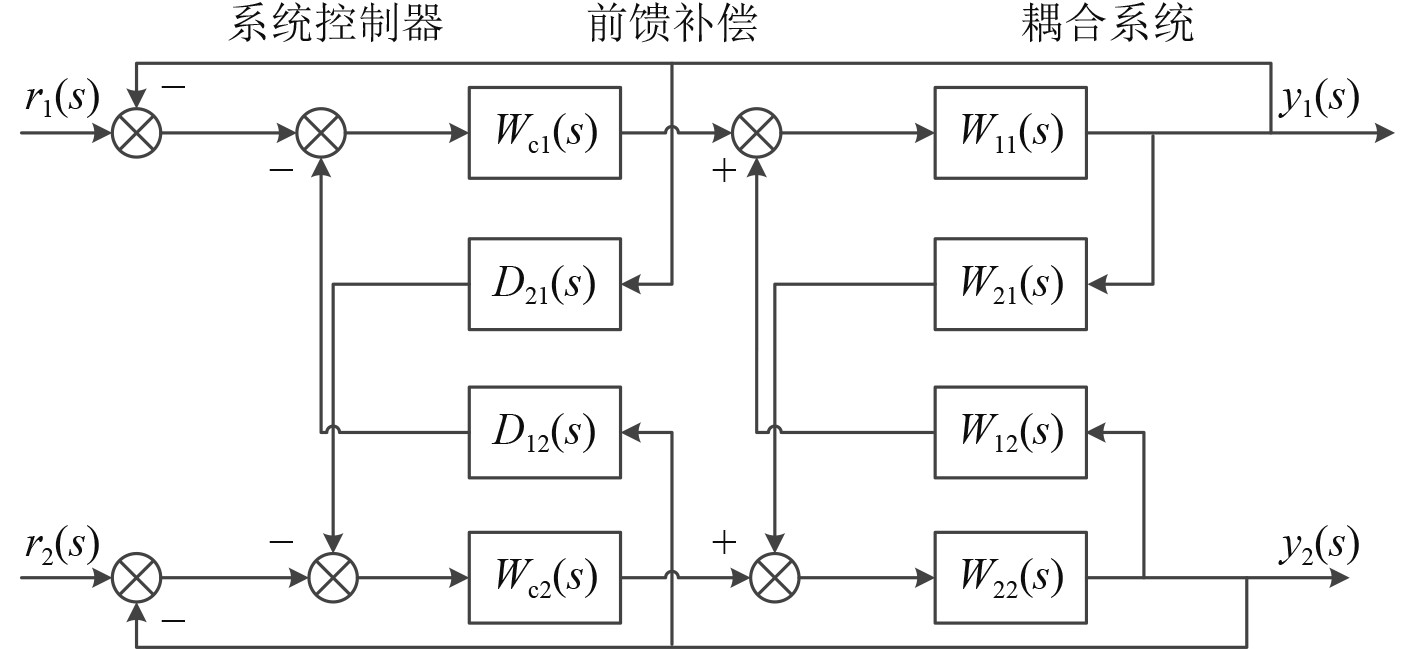
反馈解耦控制中,解耦控制器配置在系统的反馈通道上,而不是在系统的前向通道上,如图3所示。
|
图 3 反馈补偿解耦法控制框图 Fig. 3 Control block diagram of feedback compensation decoupling method |
要实现系统对输出的解耦,应有:
| $ \begin{gathered} - {Y_1}(s){D_{21}}(s){W_{c2}} + {Y_1}(s){W_{21}}(s) = 0,\\ - {Y_2}(s){D_{12}}(s){W_{c1}} + {Y_2}(s){W_{12}}(s) = 0。\end{gathered} $ | (17) |
反馈控制器的传递函数为:
| $ \begin{gathered} {D_{21}}(s) = \frac{{{W_{21}}(s)}}{{{W_{c2}}(s)}},\\ {D_{12}}(s) = \frac{{{W_{12}}(s)}}{{{W_{c1}}(s)}} 。\end{gathered} $ | (18) |
此时,系统的输出为:
| $ \begin{gathered} {Y_1}(s) = \frac{{{W_{c1}}(s){W_{11}}(s){R_1}(s)}}{{1 + {W_{c1}}(s){W_{11}}(s)}},\\ {Y_2}(s) = \frac{{{W_{c2}}(s){W_{22}}(s){R_2}(s)}}{{1 + {W_{c2}}(s){W_{22}}(s)}} 。\end{gathered} $ | (19) |
可见解耦后的系统等效为2个相互独立的单输入单输出系统。
2.2 解耦设计前馈补偿和对角矩阵解耦具有相同的解耦效果,在几种方法中前馈补偿解耦模型较简单、易于实现,还可以实现对扰动信号的解耦,是目前工业过程控制中应用最普遍的一种解耦方法,本文亦采用前馈补偿解耦方法对变风量空调系统进行解耦设计。在此仅分析其中的2个回路,即舱室温度及送风温度控制回路,根据上文中对各个控制回路的数学建模,得到系统传递函数矩阵为:
| $\begin{split} & \left[ {\begin{array}{*{20}{c}} {{t_r}} \\ {{t_s}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{\text{ - 71}}{\text{.43}}}}{{{\text{357s + 1}}}}{\text{ - }}\frac{{\text{1}}}{{{\text{357s + 1}}}}\frac{{{\text{59}}}}{{{\text{231s + 1}}}}}&{\frac{{\text{1}}}{{{\text{357s + 1}}}}\frac{{{\text{11}}}}{{{\text{231s + 1}}}}} \\ {\frac{{{\text{ - 59}}}}{{{\text{231s + 1}}}}}&{\frac{{{\text{10}}}}{{{\text{231s + 1}}}}} \end{array}} \right]\cdot\\ & \left[ {\begin{array}{*{20}{c}} {{G_a}} \\ {{G_w}} \end{array}} \right]。\\[-1pt]\end{split} $ | (20) |
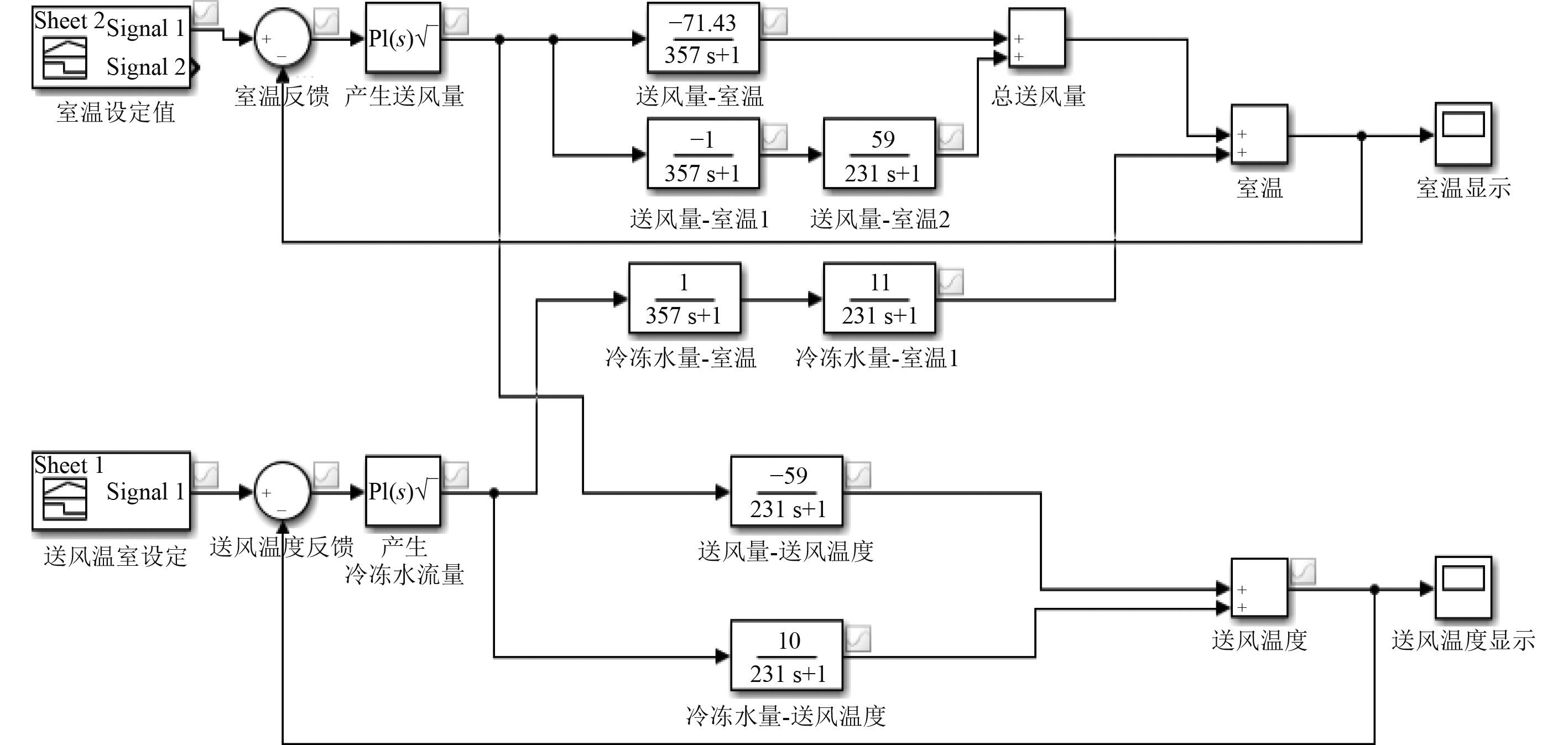
基于Simulink建立系统的仿真模型如图4所示。
|
图 4 系统耦合仿真模型 Fig. 4 System coupling simulation model |
设定舱室温度为26℃,送风温度为16℃,对模型进行仿真。从图5可看出,该控制回路能对室温及送风温度进行调节,最终稳定在设定值。由于系统中不存在设定值波动,因此未能显现出耦合性。

|
图 5 仿真结果(无温度变动) Fig. 5 Simulation results (no temperature change) |
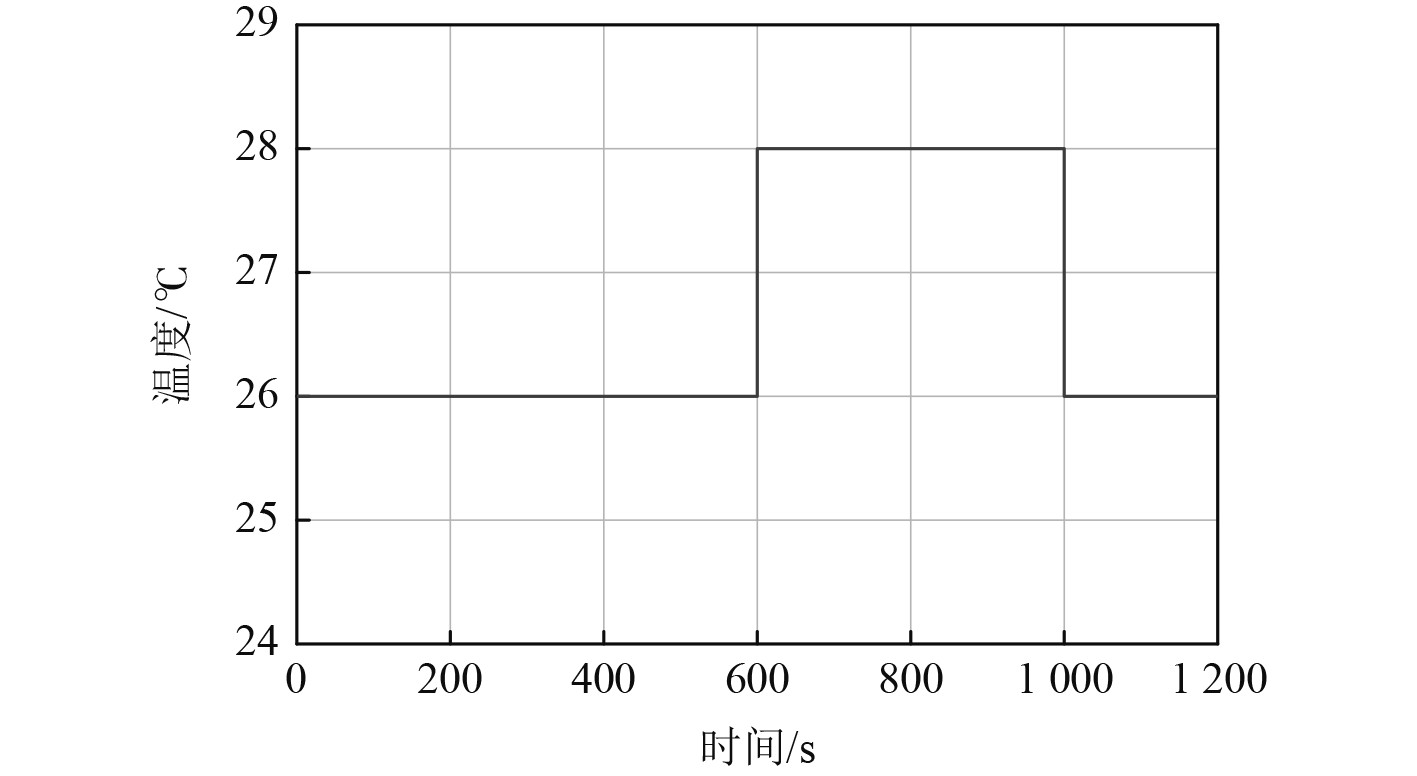
令舱室温度设定值波动,在600−1 000 s时间范围内温度设定值变为28 ℃(见图6),该输入条件下对系统仿真得到的结果如图7所示。可以看出,当室温设定值改变,系统经过一段时间的调节能够跟随设定值,但即使未改变送风温度设定值,由于室温控制回路的波动也会导致送风温度变化,即产生回路耦合的影响。
|
图 6 室温设定值 Fig. 6 Room temperature setting value |

|
图 7 回路耦合现象(有温度变动) Fig. 7 Loop coupling (with temperature variation) |
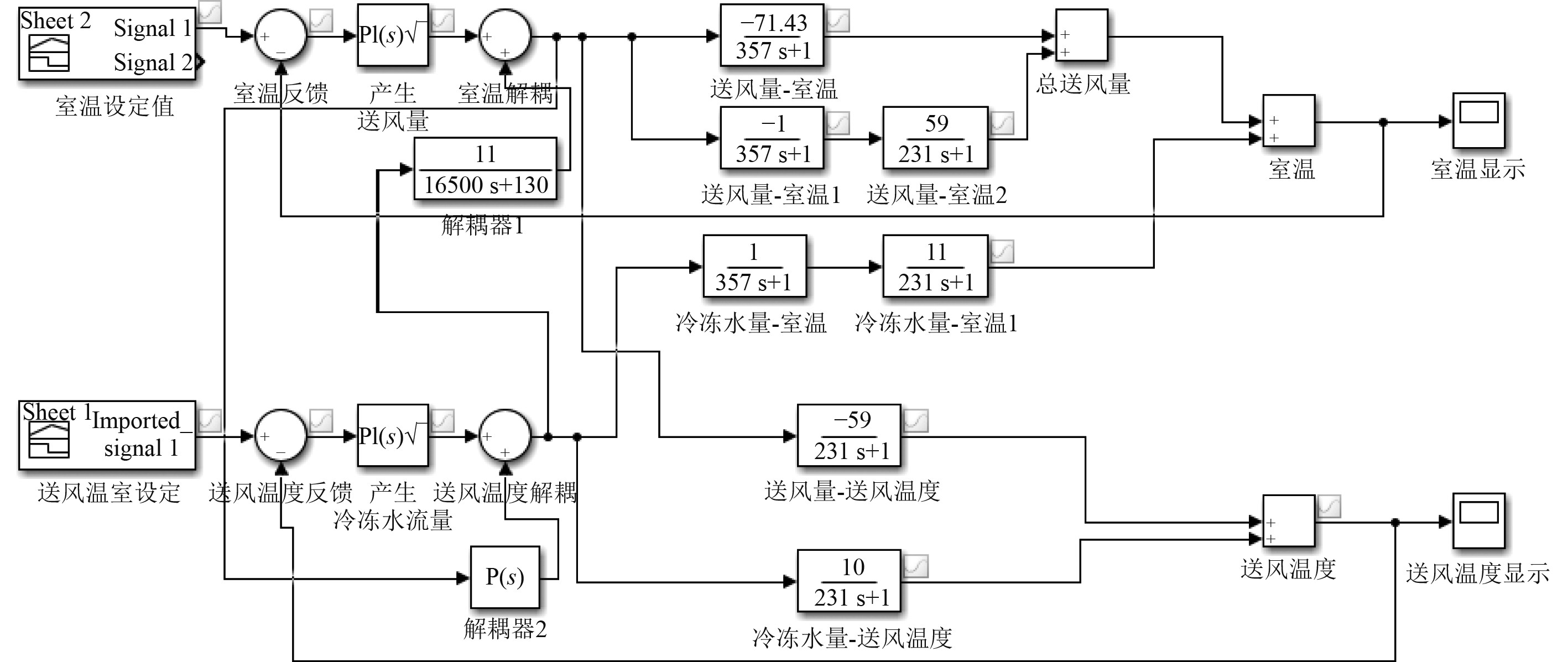
为了消除耦合的影响,在不改变系统原始结构的情况下,加入解耦控制器对系统进行补偿解耦,根据前馈补偿解耦方法建立的解耦仿真模型如图8所示。可以看出,实际上解耦就是在相应的耦合通道上加入补偿器,利用其补偿效果抵消耦合产生的干扰效应。
|
图 8 系统解耦仿真模型 Fig. 8 System decoupled simulation model |
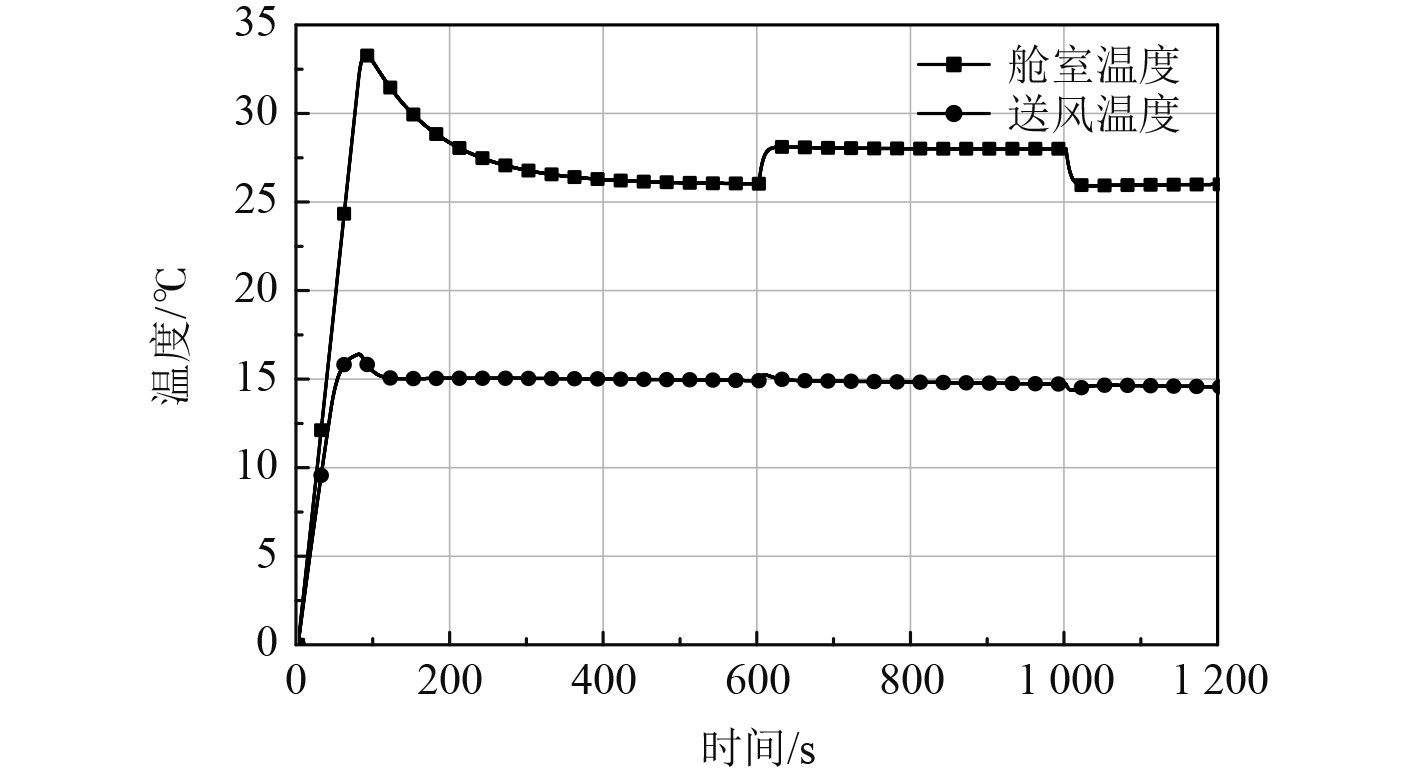
在室温设定值存在波动的情况下,对系统进行仿真,得到结果如图9所示。与图7的仿真结果对比可看出,加入解耦器后能明显降低室温控制回路波动对送风温度的影响,降低系统调控的难度。
|
图 9 解耦后(有温度变动) Fig. 9 After decoupling (with temperature change) |
以上所述解耦法适用于变风量空调系统的设计阶段,对于设计技术要求较高。实际工程中,大多数的变风量空调系统是在原有的定风量空调系统基础上通过设备改进而实现的,这一过程中难以进行解耦设计。针对实际工程中的变风量空调系统调控问题,本文提出一种多回路串联延时调控的方法,该方法不要求对系统进行完全解耦,而是着眼于系统调控过程。其基本思路是将各个控制回路看作串联,上游控制回路完成调节并稳定后再进行下游控制回路的调节,直至完成全部调节。
3.1 建 模基于Trnsys软件建立空调通风系统的控制回路,采用变静压方法进行变风量控制,控制目标为舱室温度,调节的参数包括风机频率、静压设定值、出风口阀位等,从舱室温度设定到风机频率调节的整个流程如图10所示。控制器根据舱室温度设定值与实际值对比计算所需风量,并对出风口阀门开度进行调节,为保证节能将静压值设定在能够满足要求的最低限值,静压设定值稳定15 min后再对风机频率进行调节。

|
图 10 变风量空调系统延时调控过程 Fig. 10 Delayed regulation process of VAV air conditioning system |
仿真模型中的风量控制采用PID控制器,根据舱室温度设定值与实测值的偏差确定舱室送风量。PID控制器数学模型如下式:
| $ U(t) = {k_p}\{ e(t) + \frac{T}{{{T_i}}}\sum\nolimits_{\tau = 1}^t {e(\tau )} + \frac{{{T_d}}}{T}[e(t) - e(t - 1)]\} 。$ | (21) |
式中:U(t)为控制变量;kp为比例系数;e为偏差;Ti为积分时间;Td为微分时间。传递函数为:
| $ G(s) = \frac{{U(s)}}{{E(s)}} = {k_p}(1 + \frac{1}{{{T_i}s}} + {T_D}s) 。$ | (22) |
PID控制器的设计核心是参数整定,整定方法包括公式整定法、工程整定法和试凑法等,目前常用的是工程整定法,根据被控对象的传递函数获得阶跃响应图,利用工程经验对PID参数进行整定。
3.2 多回路串联延时调控效果仿真对系统进行仿真,对比无延时和有延时2种情况下的风机频率变化,如图11所示。可知,当不设置延时调控时静压设定值随着阀门开度的调节实时变化,导致风机频率一直大幅度波动,对系统运行稳定性不利。而加入延时调控后,风机频率的波动曲线平缓,有利于系统的稳定,可降低调控难度。

|
图 11 风机运行频率变化过程 Fig. 11 Change process of fan operating frequency |
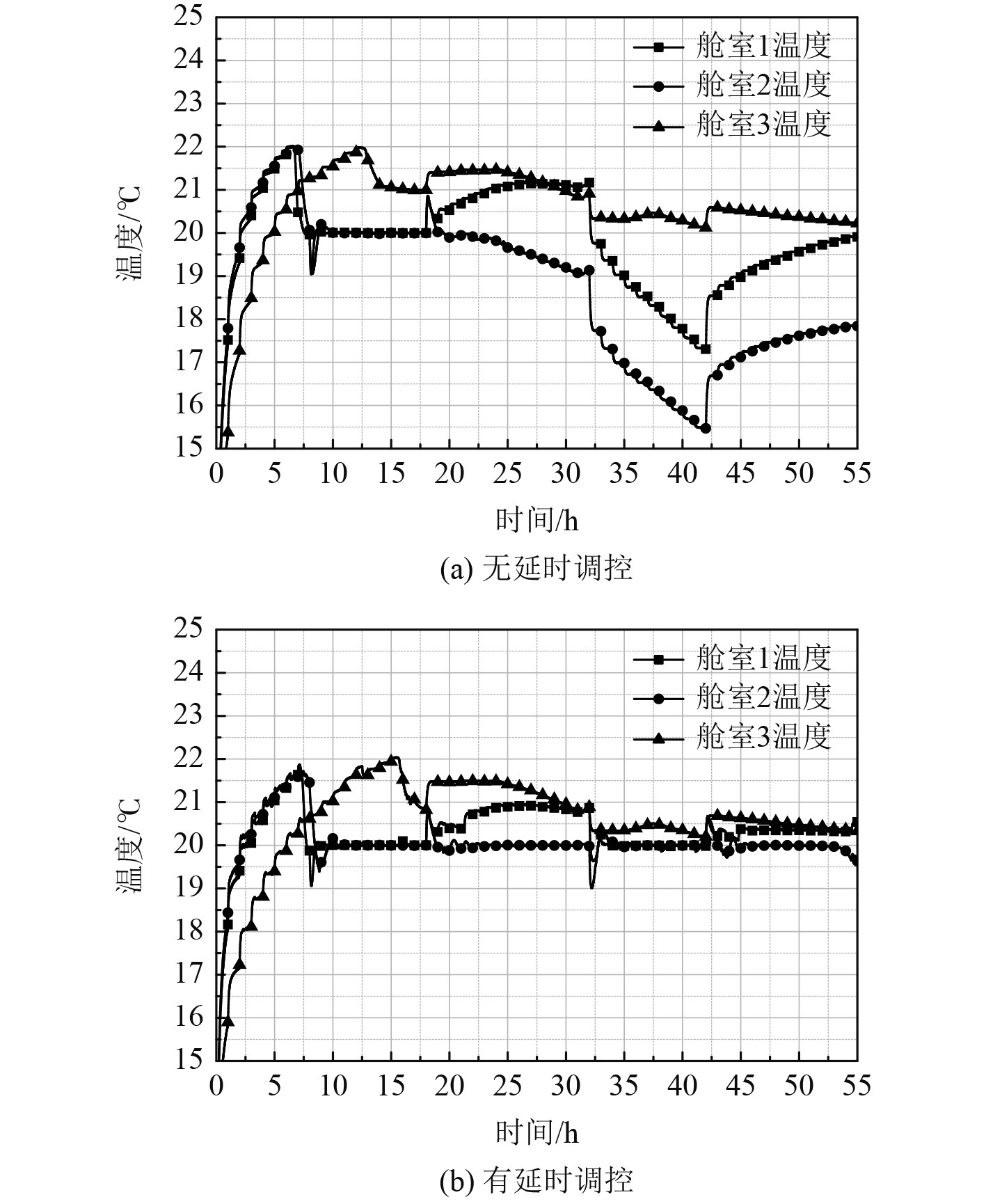
2种情况下的舱室温度变化如图12所示。可看出有延时的调控由于避免了风机工况的剧烈波动,因此对舱室温度的控制效果也更好,反应速度快、温度偏差小,验证了多回路串联延时调控方法的有效性。
|
图 12 舱室温度变化过程 Fig. 12 Cabin temperature change process |
为验证变风量送风技术在降低舱室噪声、提高空调系统节能性上的优势,进行变风量空调系统台架试验。设定各舱室目标温度,控制系统根据舱室实测温度与设定值的偏差调节末端阀门开度实现风量调节。
试验结果如表1 所示,可看到变风量调控方法能实现变风量系统的调控功能,实现舱室温度的精准调控(偏差±1℃)。同时降低部分负荷条件下的风机频率与压缩机转速,相对定风量系统显著降低系统能耗与噪声,验证了变风量送风技术的优势。
|
|
表 1 试验结果对比 Tab.1 Comparison of test results |
本文对船用变风量空调系统的解耦及调控技术进行了研究,旨在降低调控难度,改善系统稳定性,得到以下结论:
1)变风量空调系统中存在的多回路耦合现象是导致调控困难、应用效果不理想的重要原因,在一定程度上限制了变风量空调系统的推广和应用。对变风量空调系统解耦技术及调控方法的研究既有必要又有意义。
2)利用前馈解耦的方法对变风量空调系统进行解耦设计,经验证有效地消除了多回路间的耦合现象,解耦后的系统调控难度大大降低。
3)为适应实际工程应用,提出多回路串联延时调控方法。该方法无需对系统进行解耦设计即可实现有效调控,是工程中提高系统稳定性的可行方法。
| [1] |
陈文华, 黄伟稀, 梁赟. 船舶空调系统及设备节能运行技术研究[J]. 流体机械, 2021, 49(1): 97-104. |
| [2] |
黄伟稀, 陈文华, 何涛, 等. 船用变风量空调系统调控技术研究综述[J]. 舰船科学技术, 2021, 43(17): 1-6. |
| [3] |
顾凯, 付东翔, 王亚刚. 基于自抗扰控制器的变风量空调解耦控制[J]. 信息技术, 2014(1): 24-27. DOI:10.3969/j.issn.1009-2552.2014.01.008 |
| [4] |
梁芯萌, 张九根, 谢金鑫, 等. 基于改进内模解耦控制的空调系统优化[J]. 暖通空调, 2019, 49(9): 91-96. |
| [5] |
袁柯婷. 变风量空调温度与温度解耦控制方法研究[D]. 西安: 西安科技大学, 2021.
|
| [6] |
雷艳杰. 船用变风量空调系统的控制方法研究[D]. 厦门: 集美大学, 2011.
|
| [7] |
陈宗帅, 李绍勇, 贺冬辰, 等. 基于改进单神经元PID算法的变风量空调系统三参数前馈解耦控制[J]. 制冷与空调(四川), 2020, 34(6): 655-663. |
| [8] |
倪再玥, 张九根, 陈哲, 等. 变风量空调系统的内膜解耦控制[J]. 计算机工程与设计, 2020, 41(10): 2996-3001. DOI:10.16208/j.issn1000-7024.2020.10.048 |
| [9] |
孙崇国, 杨世忠, 李善伟. 基于自抗扰的变风量空调房间温湿度解耦控制[J]. 电工技术, 2020(1): 38-40. DOI:10.19768/j.cnki.dgjs.2020.01.013 |
| [10] |
闫秀联, 颜菲菲, 闫秀英. 变风量空调系统温湿度解耦控制[J]. 制冷与空调(四川), 2019, 33(3): 298-302+342. |
| [11] |
李徐嘉, 高峰. 某型船用变风量空调系统风量控制方法研究[J]. 广东造船, 2021, 40(4): 45-48. DOI:10.3969/j.issn.2095-6622.2021.04.013 |
 2024, Vol. 46
2024, Vol. 46
