2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. Key Laboratory of Ship Vibration and Noise, Wuhan 430033, China
在噪声主动控制中,按照整体系统是否需要参考信号输入可以将ANC(Active Noise Control)系统分为前馈ANC系统和反馈 ANC系统。反馈ANC系统的误差信号同时用来调节自适应滤波器参数和估计参考信号,稳定性和环境适应能力较弱,适用于参考信号难以获取的场合。前馈控制系统用参考传感器获取的信号作为控制器的输入,误差传感器信号只用来调节自适应滤波器参数,有更好的稳定性和适应性[1]。但是前馈ANC系统中作动器产生的次级噪声会反馈到参考传感器处,干扰参考传感器采集初级噪声信号,使得参考信号与实际信号失配,导致控制效果变差[2]。
对于前馈主动控制系统,曾文杰[3]设计了基于发动机转速信号的车内前馈噪声主动控制系统,避免了声反馈现象的出现。陈辉[4]提出基于神经网络通道辨识的改进FxLMS算法,对非线性传递通道达到更精确的建模。高永生[5]对FuLMS算法仿真分析其性能,并基于DSP系统搭建了试验平台。谷飞鸿[6]提出了一种宽窄带混合的前馈主动控制系统,但是大大增加了计算量。梁超[7]设计一种前反馈混合的主动控制系统。张欢[8]对前馈系统中不同的通道建模方法进行比较。Kim[9]提出MFuLMS算法,提高了系统的稳定性。Lu[10]提出一种FRLMS算法,具有更快的收敛速度。
目前对于液体管路脉动前馈主动控制的相关研究较少,本文以DN25液压管路为试验对象,对传统FxLMS算法进行改进,设计一种具有声反馈补偿和窄带通滤波功能的自适应滤波算法,最后对算法性能进行验证。
1 宽带前馈FxLMS控制算法原理分析液体管路脉动宽带前馈ANC系统原理如图1所示。管路可以简化为一维系统,总共有3条声学传递路径,参考传感器到误差传感器的路径表示为

|
图 1 前馈ANC系统脉动传递通道示意图 Fig. 1 Schematic diagram of pulsation transmission channel of feedforward ANC system |
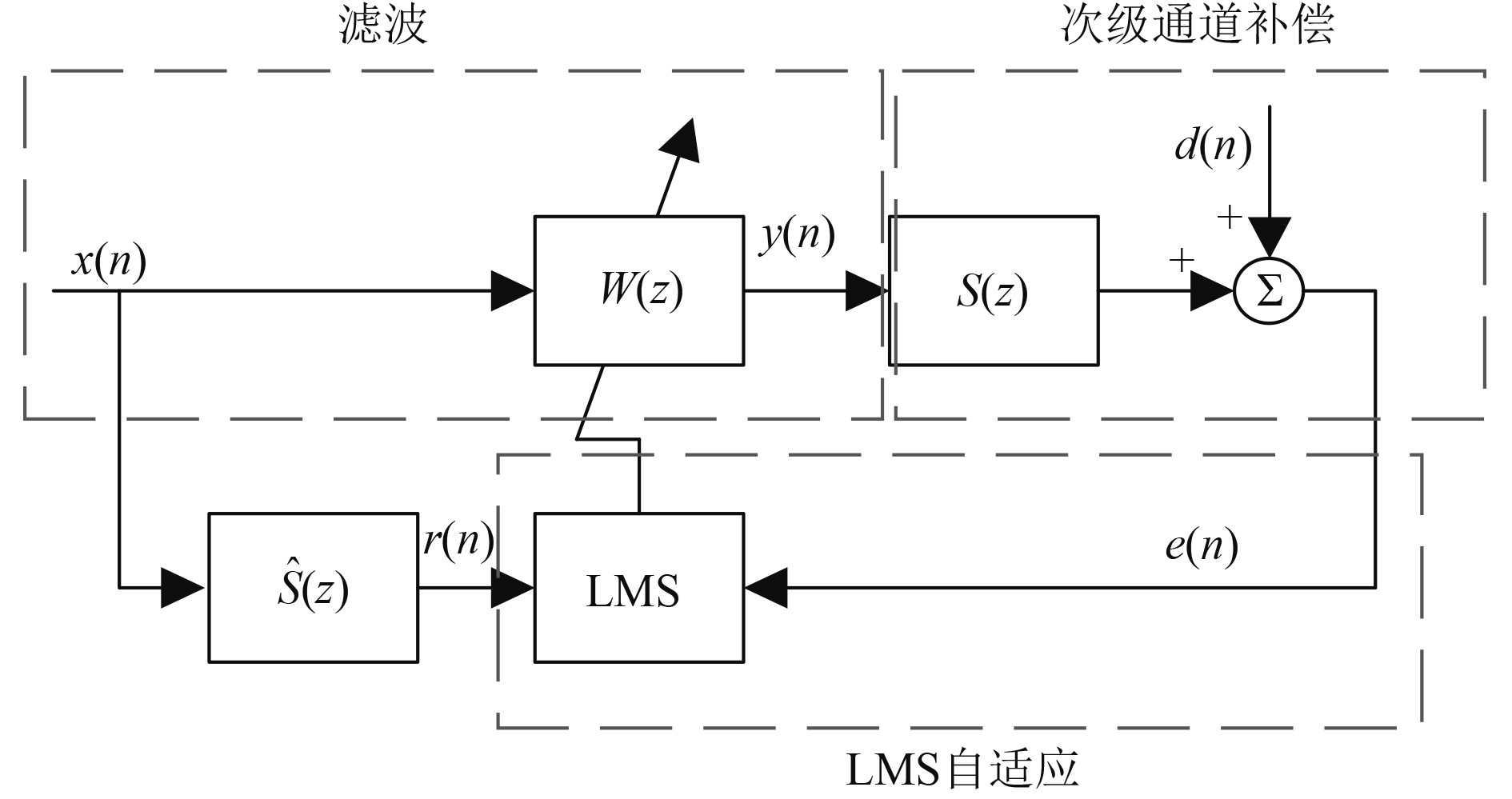
如图2所示,FxLMS算法的信号流程图主要包括3个相互关联的基本部分,即滤波部分、次级通道补偿部分和LMS自适应部分
|
图 2 液体管路脉动宽带前馈ANC系统原理图 Fig. 2 Schematic diagram of liquid line pulsating broadband feedforward ANC system |
参考传感器采集到参考信号
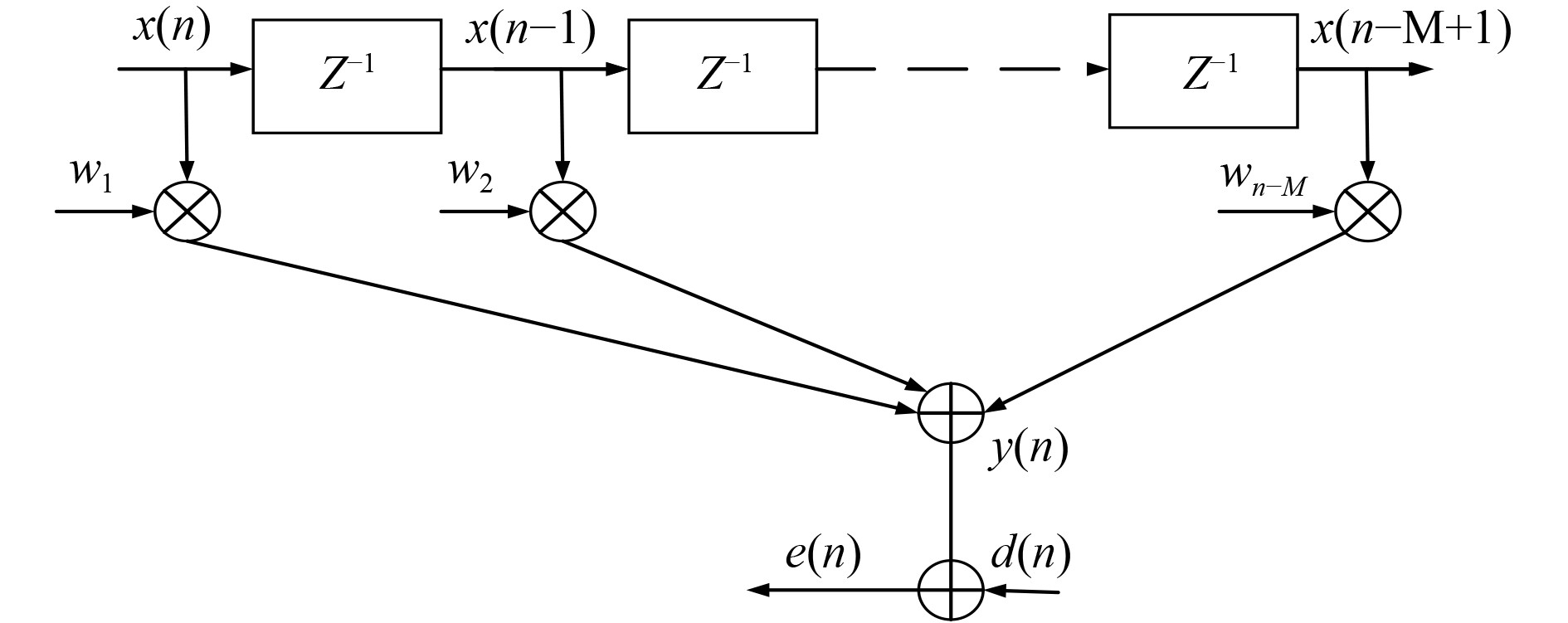
|
图 3 维纳滤波器原理图 Fig. 3 Wiener filter schematic |
假设第
| $ {\boldsymbol{W}}\left( n \right) = {\left[ {\begin{array}{*{20}{c}} {{w_1}\left( n \right)}&{{w_2}\left( n \right)}& \cdots &{{w_M}\left( n \right)} \end{array}} \right]^{\text{T}}} ,$ | (1) |
式中,
参考信号
| $ {\boldsymbol{X}}\left( n \right) = {\left[ {\begin{array}{*{20}{c}} {x\left( n \right)}&{x\left( {n - 1} \right)}& \cdots &{x\left( {n - M + 1} \right)} \end{array}} \right]^{\text{T}}},$ | (2) |
其中,上标T为转置矩阵。
滤波器向作动器输出的信号
| $ y\left( n \right) = {{\boldsymbol{X}}^{\text{T}}}\left( n \right){\boldsymbol{W}}\left( n \right),$ | (3) |
控制后的误差信号
| $ e\left( n \right) = d\left( n \right) - y\left( n \right)。$ | (4) |
维纳滤波器的作用是找到一组最优的权系数
在实际应用中,作动器产生的次级脉动要经过次级通道
次级通道辨识原理如图4所示,采用N阶滤波器对次级通道传递函数进行估计。控制器输出随机白噪声信号作为激励信号给作动器,传递到误差传感器处作为期望信号,经过模拟滤波器作为输出信号,两者叠加得到误差信号,通过LMS算法不断对滤波器参数进行更新至误差信号收敛到最小。
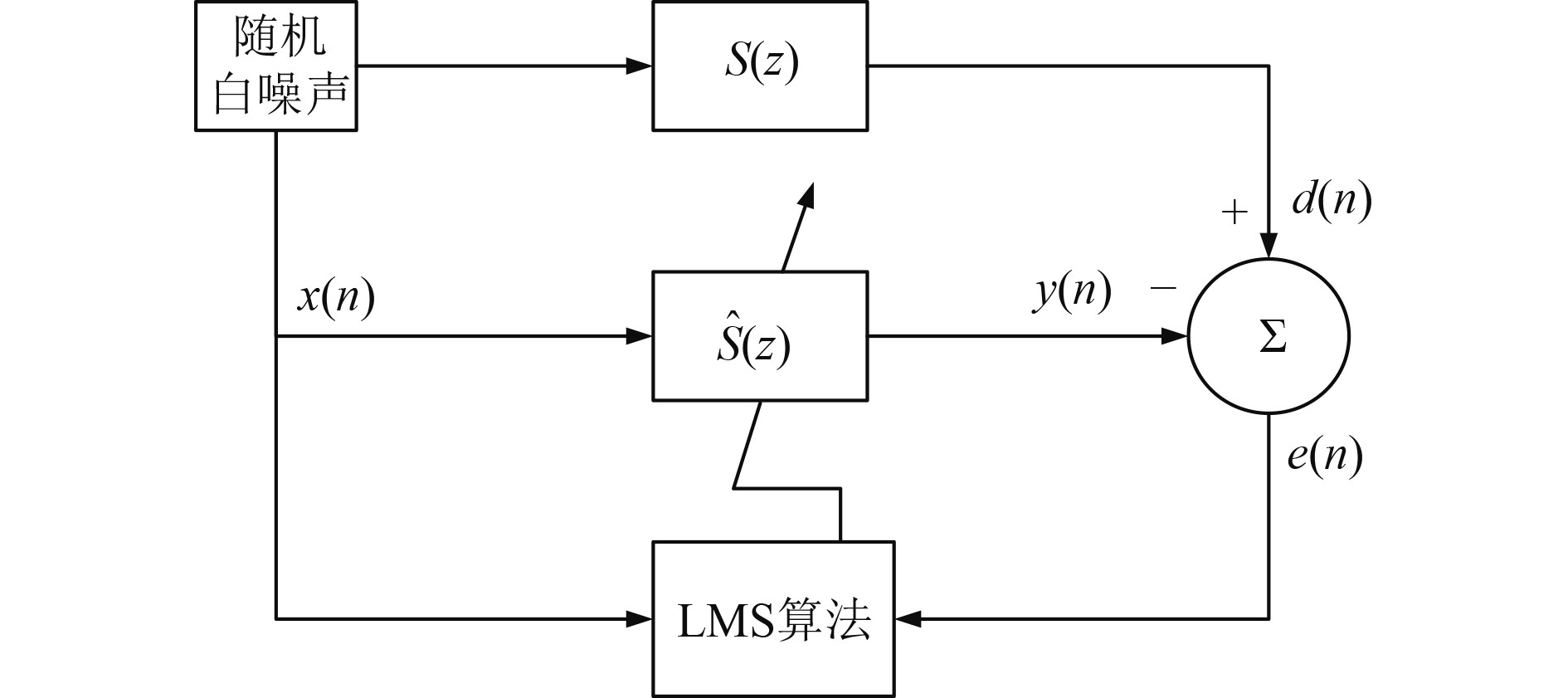
|
图 4 次级通道辨识原理图 Fig. 4 Schematic diagram of secondary channel identification |
设次级通道
| $ \mathop S\limits^{} (z) = \mathop {{s_0}}\limits^{} + \mathop {{s_1}}\limits^{} {z^{ - 1}} + \cdots \mathop {{s_{N - 1}}}\limits^{} {z^{1 - N}} ,$ | (5) |
| $ \mathop S\limits^ \wedge (z) = \mathop {{s_0}}\limits^ \wedge + \mathop {{s_1}}\limits^ \wedge {z^{ - 1}} + \cdots \mathop {{s_{N - 1}}}\limits^ \wedge {z^{1 - N}} 。$ | (6) |
式中,
当辨识误差收敛到足够小,近似为:
| $ \hat{S}(z)=S(z) 。$ | (7) |
在自适应收敛的过程中,LMS算法是对最陡下降法的随机实现,即控制器权系数的迭代公式为:
| $ {\boldsymbol{W}}\left( {n + 1} \right) = {\boldsymbol{W}}\left( n \right) - 2\mu e\left( n \right)\hat S\left( z \right)x\left( n \right) 。$ | (8) |
式中,
在每一个新的输入样本
在参考信号可以获取的情况下,前馈主动控制系统的效果会比反馈控制的效果要好。由试验测试发现,管路系统的脉动噪声源为泵源,脉动噪声以低频线谱为主。针对管路脉动噪声的特征,在宽带前馈FxLMS算法的基础上,利用布置于噪声源附近的传感器采集参考信号,提出一种有频率追踪和声反馈补偿功能的窄带前馈自适应滤波算法,算法原理如图5所示。

|
图 5 优化算法原理图 Fig. 5 Principle diagram of optimization algorithm |
参考传感器采集到信号
布置于噪声源附近的参考传感器会同时接收噪声源和作动器产生的脉动波,2种信号的耦合会使得参考信号与管内实际脉动信号失配,即声反馈现象。
自适应的输出信号为:
| $ y(n) = W(n)x(n) + W(n)y(n)h(n) ,$ | (9) |
其中,
化简可得:
| $ y(n) = \frac{{W(n)x(n)}}{{1 - W(n)h(n)}} ,$ | (10) |
式(10)的Z变换为:
| $ Y(z) = \frac{{W(z)X(z)}}{{1 - W(z)H(z)}}。$ | (11) |
在某些频率下,
通道建模采用附加白噪声法进行离线建模,建模的原理如图6所示,采用N阶滤波器对声反馈通道传递函数进行估计,辨识过程中,残余误差信号
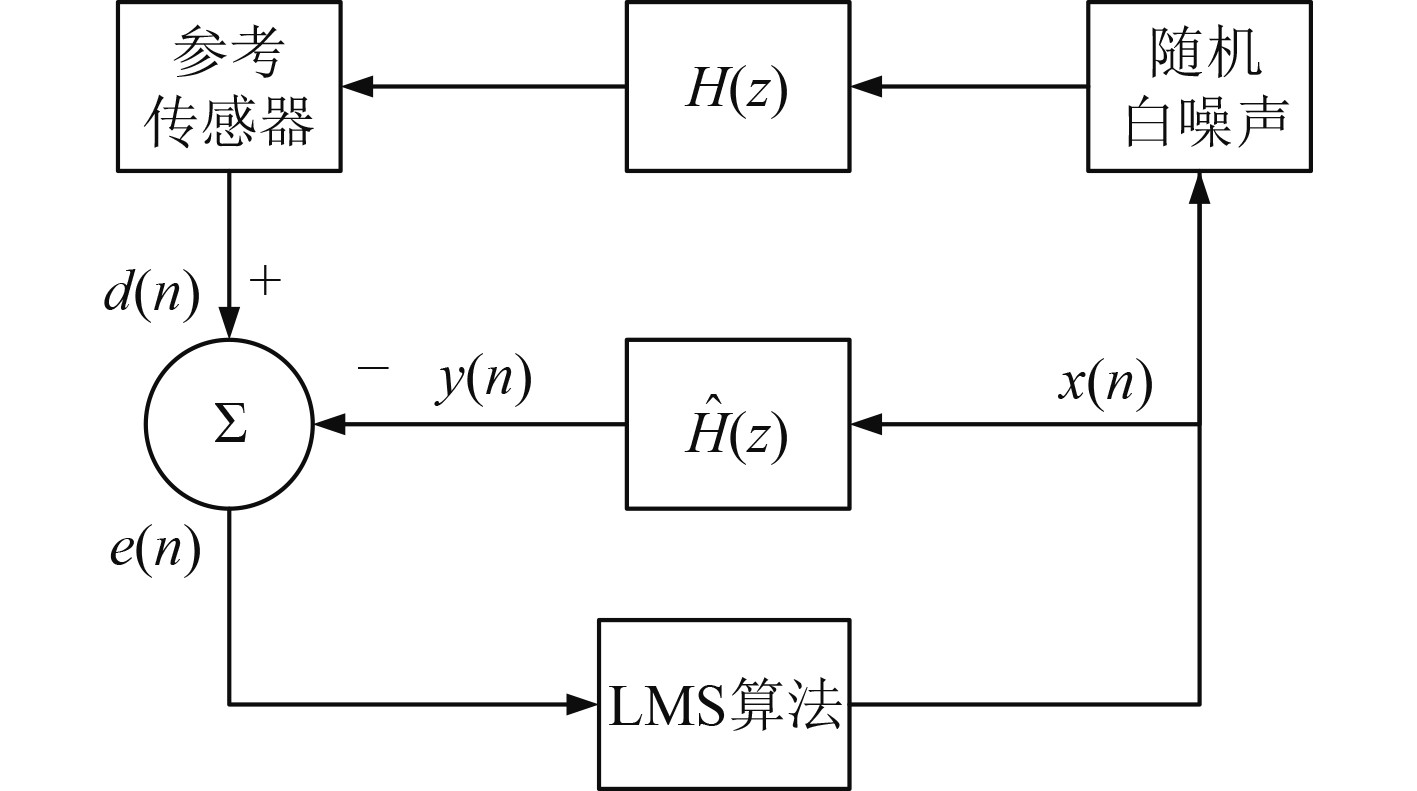
|
图 6 声反馈通道辨识原理图 Fig. 6 6 Principle diagram of acoustic feedback channel identification |
设声反馈通道
| $ \mathop H\limits^{} (z) = \mathop {{h_0}}\limits^{} + \mathop {{h_1}}\limits^{} {z^{ - 1}} + \cdots \mathop {{h_{N - 1}}}\limits^{} {z^{1 - N}} ,$ | (12) |
| $ \mathop H\limits^ \wedge (z) = \mathop {{h_0}}\limits^ \wedge + \mathop {{h_1}}\limits^ \wedge {z^{ - 1}} + \cdots \mathop {{h_{N - 1}}}\limits^ \wedge {z^{1 - N}} 。$ | (13) |
建模误差为:
| $ e(n) = \left[ {H(z) - \mathop H\limits^ \wedge (z)} \right]x(n),$ | (14) |
按照式(15)更新滤波器的参数:
| $ \mathop {{h_{}}}\limits^ \wedge \left( {n + {\text{1}}} \right) = \mathop {{h_{}}}\limits^ \wedge \left( n \right) + 2\mu e(n)x(n) ,$ | (15) |
对不同频率的声反馈通道进行离线辨识建模,得到各频率点声反馈通道的FIR滤波器系数矩阵,表达式为:
| $ h(w) = \left[ {\begin{array}{*{20}{c}} {h({w_1})}&{h({w_2})}& \cdots &{h({w_N})} \end{array}} \right]。$ | (16) |
对于不同频率的脉动线谱进行主动控制时,输入切换后的频率,程序将使用该频率的滤波器系数矩阵,如图7所示。

|
图 7 滤波器系数选择原理图 Fig. 7 Schematic diagram of filter coefficient selection |
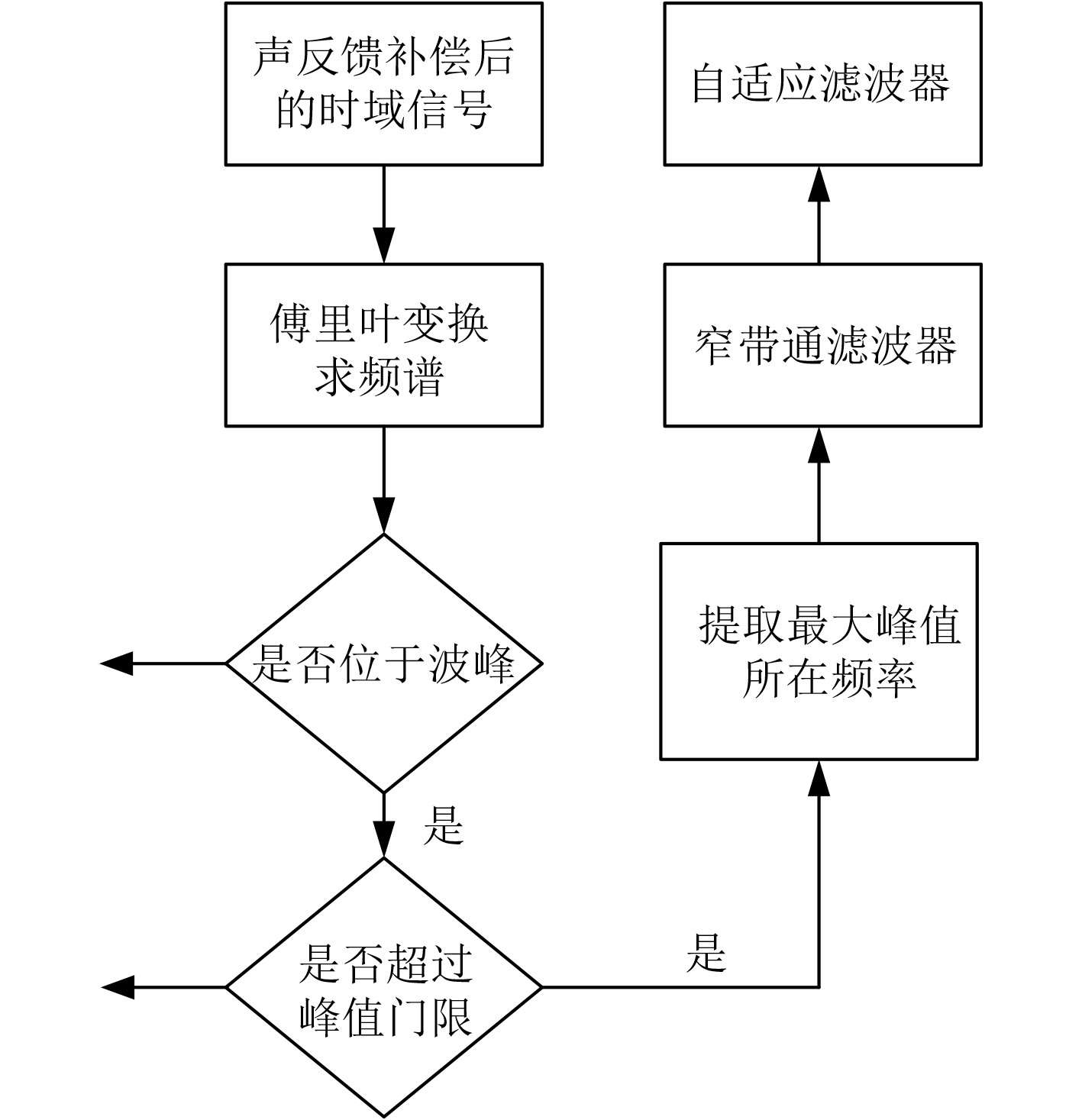
窄带通滤波流程图如图8所示。将系统看作线性系统,对采集到的时域信号进行傅里叶变换,得到系统频率响应函数可表示为:
|
图 8 窄带通滤波流程图 Fig. 8 Narrow bandpass filtering flow chart |
| $ H({{\text{e}}^{jw}}) = \sum\limits_{n = 0}^\infty {h(n){{\text{e}}^{ - jwn}}} = A\frac{{\prod\limits_{i = 1}^m {\left( {{{\text{e}}^{jw}} - {a_i}} \right)} }}{{\prod\limits_{i = 1}^n {\left( {{{\text{e}}^{jw}} - {b_i}} \right)} }} 。$ | (17) |
当频率
| $ P({{\text{e}}^{jw}}) \geqslant {P_T}({{\text{e}}^{jw}}) ,$ | (18) |
设计窄带通滤波器对信号进行滤波,表达式为:
| $ H({\text{e}}^{jw})\left\{\begin{array}{l}{\text{e}}^{-jwM/2}\text{},{w}_{1}\leqslant \left|w\right|\leqslant {w}_{2},\\ \text{0},\text{}{\rm{others}}。\end{array}\right. $ | (19) |
提取最大功率谱峰值所在频率作为窄带通滤波器的中心频率
设计一种具有峰值频率提取和声反馈补偿功能的改进FxLMS算法,相比传统的FxLMS算法,理论上对于低频线谱的噪声信号控制效果更好搭建试验台架,对比2种算法的控制效果,验证算法的优劣。
3.1 试验系统及组成管路脉动低频线谱主动控制算法试验系统原理和如图9所示。紧靠泵出口依次布置参考传感器、压电作动器、误差传感器,压电控制器控制压电作动器产生次级脉动,电机转速控制器调节电机的转速。试验时,调节电机的转速为180 r/min、300 r/min、420 r/min、540 r/min,待转速完全稳定以后,30 Hz、50 Hz、70 Hz、90 Hz为管路脉动噪声对应的幅值最大的线谱频率。试验过程中,分别用宽带前馈FxLMS算法和优化算法对4个工况的脉动线谱噪声进行主动控制,比较二者的脉动衰减效果。

|
图 9 控制算法优化对比试验系统 Fig. 9 Control algorithm optimization comparison test system |
1)收敛步长
调节电机转速为350 r/min,不同收敛步长时脉动线谱的衰减量随时间变化情况如图10所示,步长越小的算法脉动衰减速度越慢,步长越大的算法衰减速度越快,但是步长大的算法在控制中出现不稳定的风险越大。

|
图 10 350 r/min线谱收敛速度对比图 Fig. 10 Comparison of convergence speed of 350 r/min line spectrum |
2)滤波器长度
调节电机转速为400 r/min,不同滤波器长度时脉动线谱的衰减量随时间变化情况如图11所示,滤波器长度越大时脉动衰减速度越快,滤波器长度越小的算法衰减速度越慢,但是滤波器长度越大的算法在控制中出现不稳定的风险越大。

|
图 11 400 r/min线谱收敛速度对比图 Fig. 11 Comparison of convergence speed of 400 r/min line spectrum |
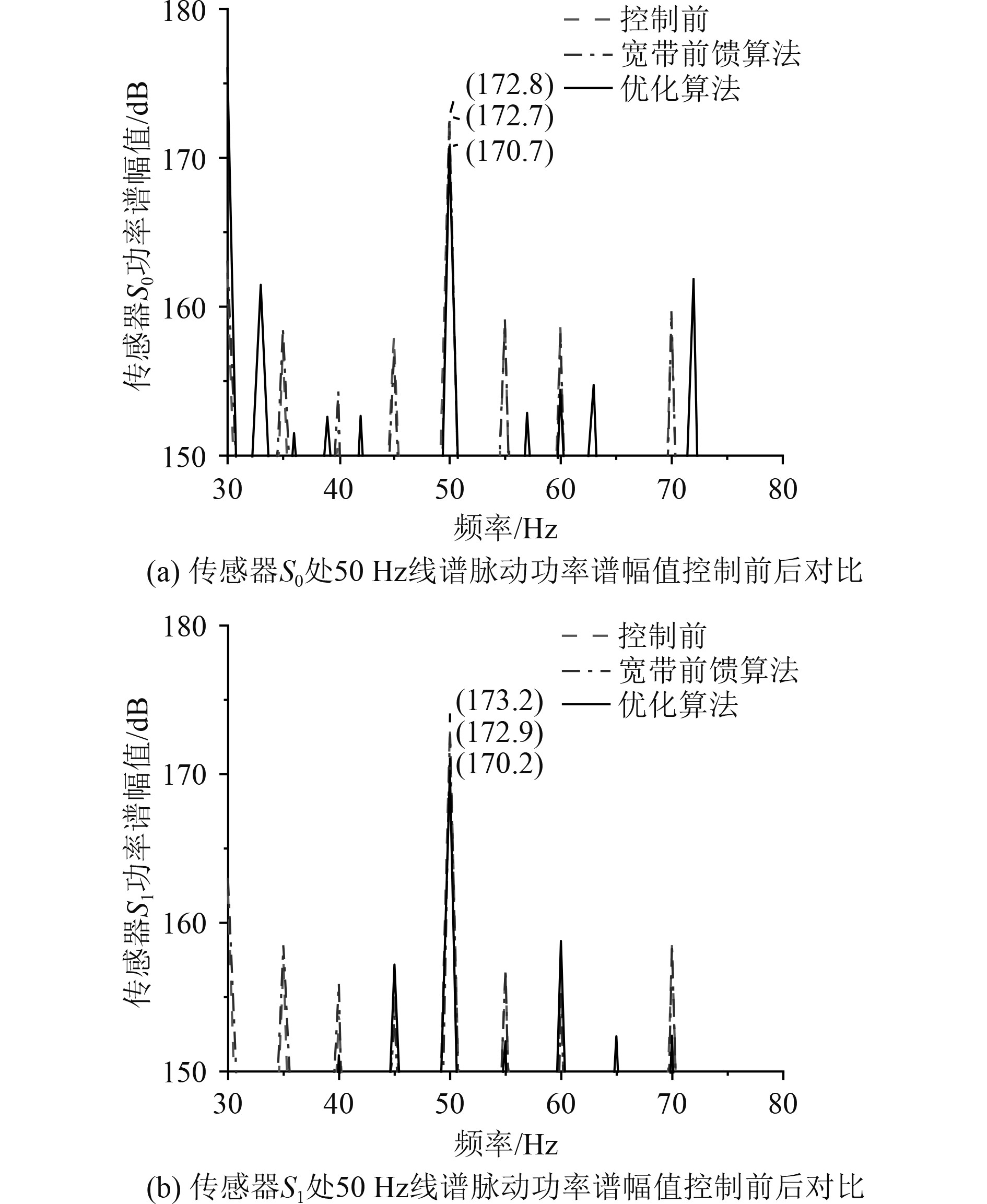
在泵源以180 r/min、300 r/min、420 r/min、540 r/min的转速稳定运行以后,传感器S0、传感器S1分别采集控制前、宽带前馈算法控制后、优化算法控制后的管路压力脉动信号,进行功率谱分析。对比30 Hz、50 Hz、70 Hz、90 Hz频率传递线谱噪声控制后功率谱幅值变化情况。
|
图 13 50 Hz线谱脉动衰减效果对比图 Fig. 13 50 Hz line spectrum pulsation attenuation effect comparison chart |
|
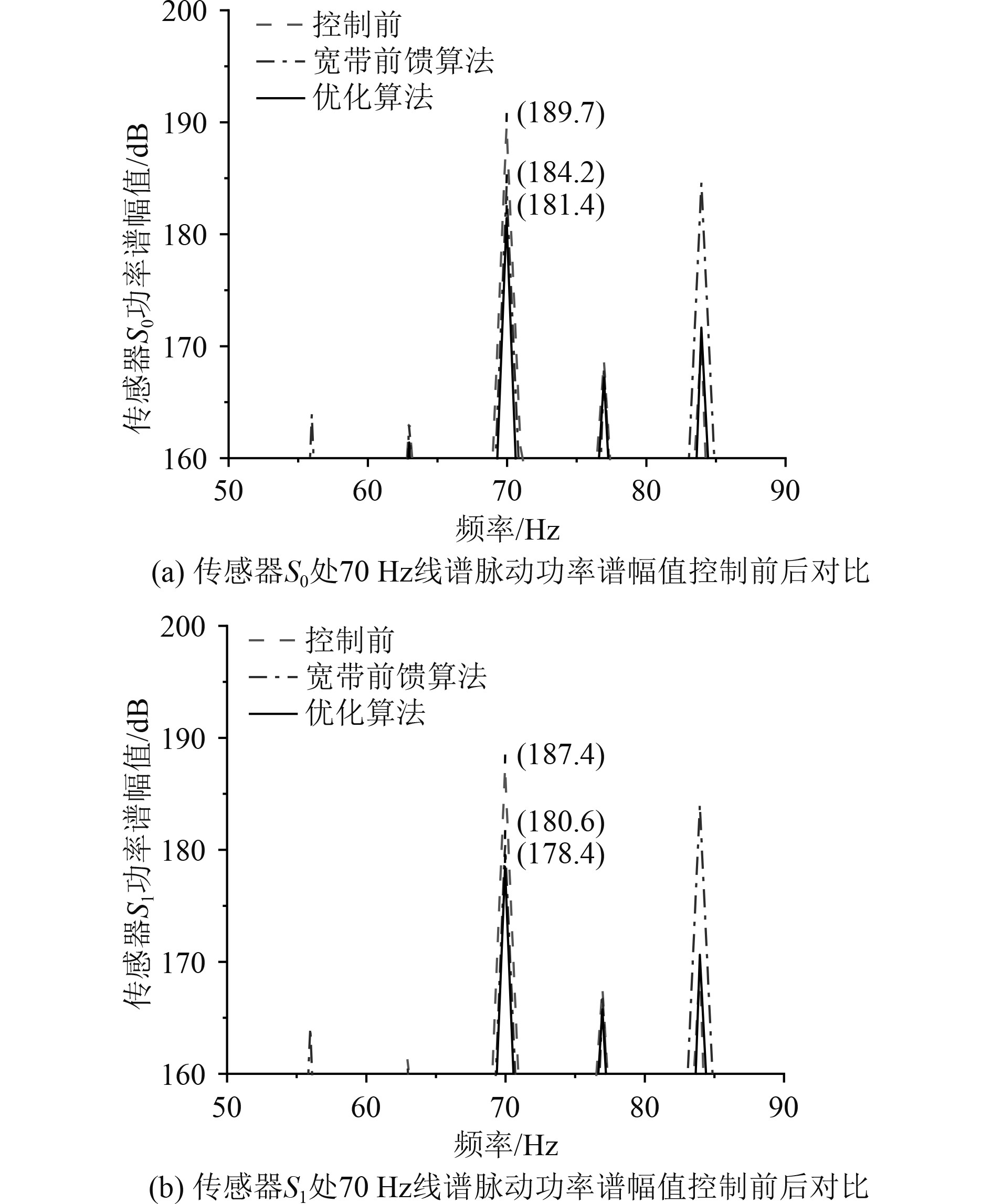
图 14 70 Hz线谱脉动衰减效果对比图 Fig. 14 70 Hz line spectrum pulsation attenuation effect comparison chart |
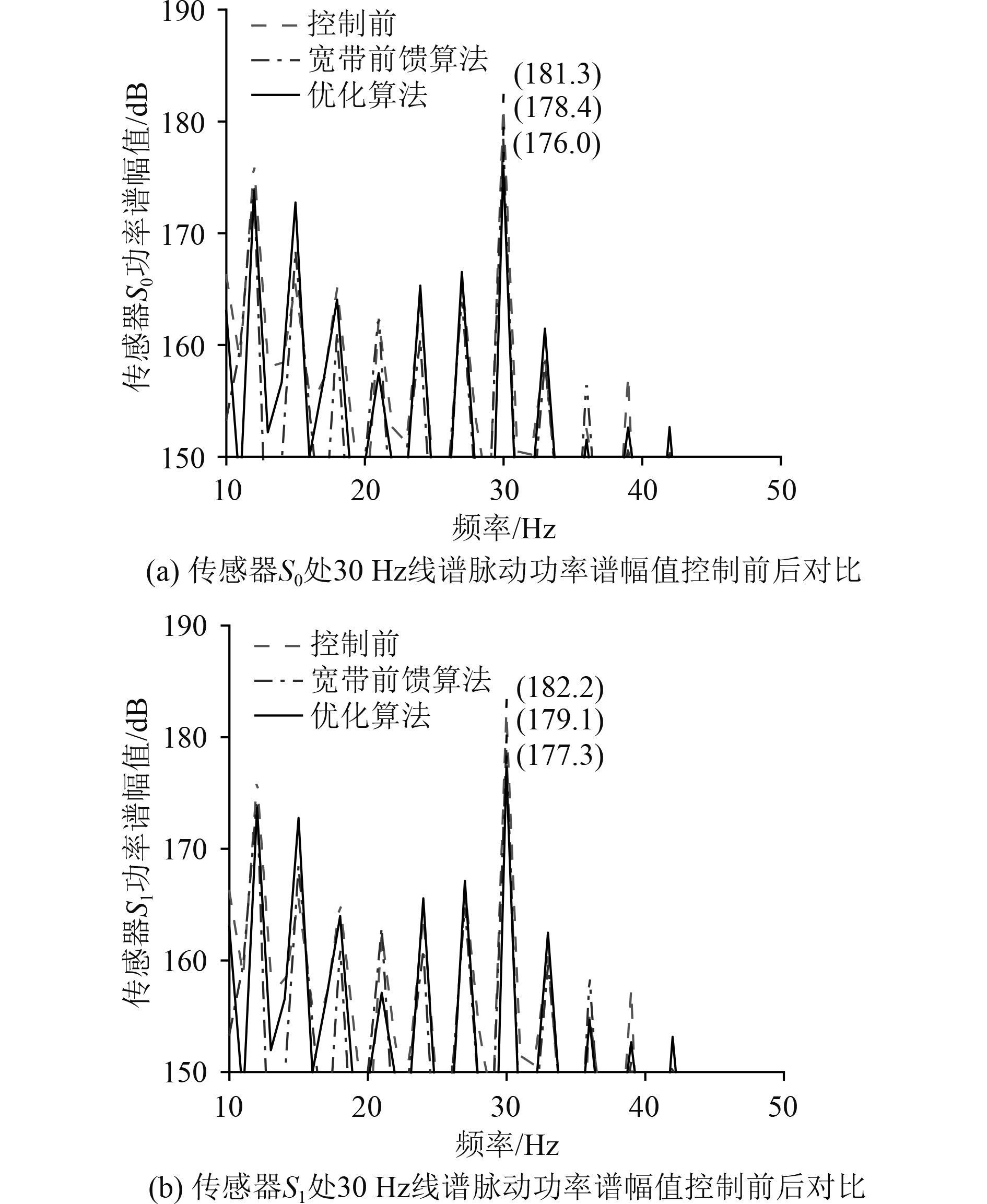
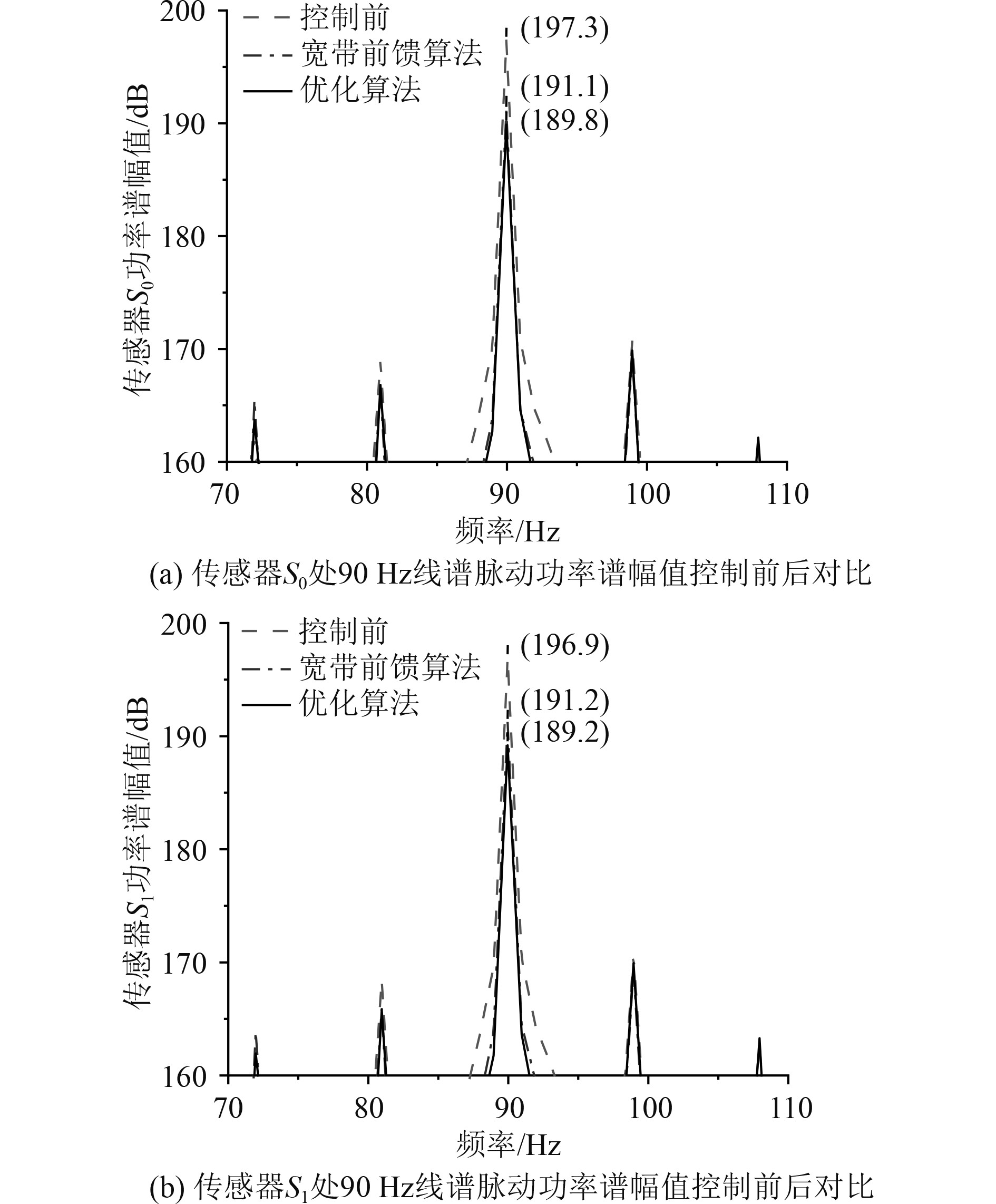
分析控制前后线谱功率谱幅值变化可得,2种控制效果均能对线谱噪声进行脉动衰减,且优化算法脉动衰减效果比宽带前馈算法更好。如图12 ~ 图15所示,宽带前馈算法在频率70 Hz的控制中,虽然70 Hz的线谱幅值降低了,但是在85 Hz的线谱幅值反而升高了十几分贝,超过了降低后的70 Hz线谱噪声,说明传统算法对于线谱的控制过程有可能产生新的线谱,导致噪声不降反增。而优化算法在对原有线谱进行控制的时候,没有出现新增的线谱,说明优化算法的稳定性和脉动衰减效果都比宽带前馈算法更佳。
|
图 12 30 Hz线谱脉动衰减效果对比图 Fig. 12 30 Hz line spectrum pulsation attenuation effect comparison chart |
|
图 15 90 Hz线谱脉动衰减效果对比图 Fig. 15 90 Hz line spectrum pulsation attenuation effect comparison chart |
通过对比表1中数据可得,宽带前馈算法对不同频率的线谱噪声的脉动衰减量约为1 ~ 6 dB,经过线谱频率提取和窄带通滤波的优化算法的脉动衰减量约为3 ~ 9 dB,在测试的频率中,优化后算法的脉动衰减量全都比优化前要高约1 ~ 3 dB。
|
|
表 1 不同脉动线谱控制前后功率谱衰减量 Tab.1 Power spectrum attenuation before and after different pulsation line spectrum control |
对管路脉动的主动控制算法优化开展研究,基于管路脉动的传递特性,对宽带前馈FxLMS算法进行了优化,设计了一种适用于液体管路的窄带控制算法。对脉动线谱进行频率特性分析,提取峰值频率提取,以此为中心频率进行窄带通滤波;通过离线辨识作动器到参考传感器的传递函数,根据不同频率点储存传函矩阵,对相应的线谱控制时调用传函补偿,消除了作动器对参考传感器的不利耦合影响。搭建试验台架,进行算法优化前后脉动衰减效果的对比试验,得到了以下结论:
宽带前馈算法对管路脉动线谱可以取得约为3 dB的脉动衰减效果,但是会导致控制线谱以外其他线谱增大的现象。优化算法能对脉动线谱进行跟踪控制,取得约为6 dB的脉动衰减效果,且不会新增其他线谱,比宽带前馈算法提升3 dB的脉动衰减量。在实际工程应用中,对于变工况的管路脉动线谱,优化算法可以根据泵源特性进行自适应调整控制,取得更好的脉动衰减效果。
| [1] |
陈克安. 有源噪声控制[M]. 北京: 国防工业出版社, 2003.
|
| [2] |
马进, 邹海山, 邱小军. 存在声反馈的前馈有源噪声控制系统性能分析[J]. 声学学报, 2016, 41(5): 686-693. MA J, ZOU H-S, QIU S-J. Performance analysis of feedforward active noise control system in the presence of acoustic feedback[J]. Journal of Acoustics, 2016, 41(5): 686-693. DOI:10.15949/j.cnki.0371-0025.2016.05.018 |
| [3] |
曾文杰. 基于FXLMS算法的车内噪声主动控制技术研究[D]. 镇江: 江苏大学, 2017.
|
| [4] |
陈辉. 车内路噪自适应主动控制技术研究[D]. 长春: 吉林大学, 2019.
|
| [5] |
高永升, 李忠利, 杨淑君, 等. 基于Fu-LMS算法的前馈式噪声主动控制系统研究[J]. 仪表技术与传感器, 2021(3): 112-116. GAO Y S, LI Z L, YANG S J, et al. Research on feed-forward active noise control system based on Fu-LMS algorithm[J]. Instrumentation Technology and Sensors, 2021(3): 112-116. DOI:10.3969/j.issn.1002-1841.2021.03.023 |
| [6] |
谷飞鸿. 基于宽窄带混合控制算法的车内主动噪声控制系统研究[D]. 长春: 吉林大学, 2020.
|
| [7] |
梁超. 车内前反馈混合结构主动噪声控制系统与应用[D]. 长春: 吉林大学, 2021.
|
| [8] |
张欢. 管道噪声主动控制系统通道建模的研究[D]. 西安: 陕西科技大学, 2019.
|
| [9] |
KIM H W, PARK H S, LEE S K, et al. Modified-filtered-u LMS algorithm for active noise control and its application to a short acoustic duct[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 475-484. DOI:10.1016/j.ymssp.2010.09.001 |
| [10] |
LU J, SHEN C, QIU X, et al. Lattice form adaptive infinite impulse response filtering algorithm for active noise control[J]. The Journal of the Acoustical Society of America, 2003, 113(1): 327-335. DOI:10.1121/1.1529665 |
 2024, Vol. 46
2024, Vol. 46

