2. 中国石油大学(华东),山东 青岛 266400
2. China University of Petroleum, Qingdao 266400, China
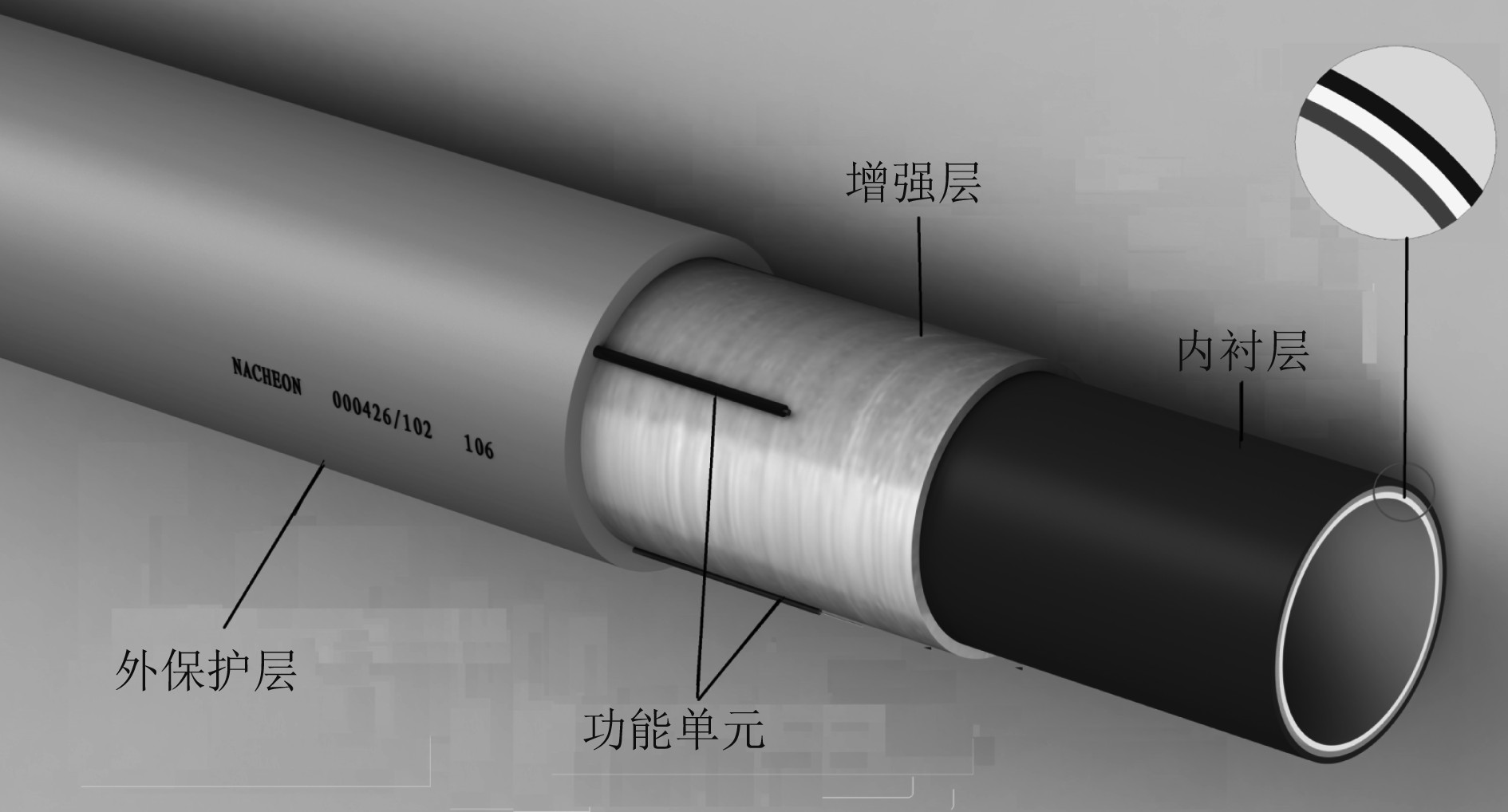
近年来,随着海洋油气资源开采深度的增加,一种新型的纤维增强热塑性复合材料管材(FRTP)应运而生。相对于传统钢制管道,FRTP由于具有较小弯曲刚度和较轻自身质量使其能更好地承受波浪、海流、顶部浮体结构运动引起的复杂荷载。FRTP是由热塑性聚合物挤出管和多层纤维增强复合材料带缠绕粘结组成,其截面结构从内到外,分别是内衬层、中间增强层和外保护层,如图1所示。增强层由多层增强纤维带(相邻两层呈正负角度交替分布)缠绕而成,而且各层之间通过加热融合的方式粘结在一起。内衬层的主要作用是输送内部油气或水等流体介质,并起保护作用;外保护层主要作用是防止海水入侵,并且对管道起保护作用,减轻外部冲击引起FRTP的损坏;纤维增强层主要作用是承受管道大部分内压、外压、弯曲和拉伸等荷载,是主要的承载结构。由于海洋环境荷载具有循环作用的特点,海洋立管的悬挂点和触地区域是疲劳热点区域,对于应用在海洋油气开发领域柔性管的疲劳问题不容忽视。
|
图 1 FRTP结构简图 Fig. 1 FRTP structure diagram |
目前,关于纤维增强复合材料管的疲劳实验研究主要集中在热固性复合材料管。Kaynak等[1]发现±55°玻璃纤维/环氧树脂复合材料管道在轴向循环荷载作用下的宏观和微观损伤机理,得到了管道的S-N曲线,研究了加载频率与管道疲劳性能的关系。Joseph等[2]对玻璃纤维/环氧树脂复合材料管在单轴循环加载下的疲劳行为进行研究,其确定相应的S-N曲线,建立损伤模型和确定累积损伤量。Gemi和Tarakçioğlu等[3-4]研究了±75°和±55°玻璃纤维/环氧树脂复合材料管在循环内压荷载作用下的疲劳破坏行为,观察了管道的白化、泄漏和最终失效等损伤过程,得到了复合材料管的S-N曲线。Tasyürek[5]研究了带有裂纹的碳纳米/玻璃纤维/环氧树脂复合材料管的疲劳性能,通过电镜发现碳纳米能够提高管道环氧树脂和纤维之间的层间强度和疲劳性能。Ellyin[6]对玻璃纤维/环氧树脂复合材料管进行了轴向荷载和内压荷载作用下的双轴疲劳试验,讨论了复合材料管的轴向和周向剩余刚度变化规律,研究了管道疲劳寿命和其失效机理。Perreux[7]对直径为60 mm的±55°玻璃纤维/环氧树脂复合材料管开展了疲劳试验,研究加载频率对管道损伤速率及管道寿命的影响。研究结果表明,由于管道蠕变/疲劳的相互作用,随着加载频率的增加,管道疲劳寿命增加。Quaresimin[8]针对玻璃/环氧树脂复合材料管在拉-扭疲劳荷载下管道损伤的产生和演化展开研究,发现损伤的发生和演化受多轴加载条件的影响较大,其中剪切应力分量加速了管道损伤的产生和演化。
本文以纤维增强热塑性复合材料管(FRTP)为研究对象,开展拉-拉单轴疲劳实验模型,以刚度衰减20%为疲劳失效判据,获得了FRTP的S-N曲线。利用Fortran语言编写UMAT子程序对Abaqus有限元软件进行二次开发,建立FRTP三维有限元模型,对FRTP的疲劳过程进行预测。
1 失效准则针对纤维增强复合材料的7种失效形式[9],本文采用修正的三维Hashin疲劳失效准则作为FRTP的疲劳失效准则,其对应的表达方式如下:
纤维拉伸失效(σ11 > 0)
| $ {\left( {\frac{{{\sigma _{11}}}}{{{X_T}}}} \right)^2} = 1,$ | (1) |
纤维压缩失效(σ11 < 0)
| $ {\left( {\frac{{{\sigma _{11}}}}{{{X_C}}}} \right)^2} = 1,$ | (2) |
基体拉伸失效(σ22 > 0)
| $ \left(\frac{\sigma_{22}}{Y_{T}}\right)^{2}+\left(\frac{\tau_{12}}{S_{12}}\right)^{2}+\left(\frac{\tau_{23}}{S_{23}}\right)^{2}=1,$ | (3) |
基体压缩失效(σ22 < 0)
| $ \left(\frac{\sigma_{22}}{Y_{C}}\right)^{2}+\left(\frac{\tau_{12}}{S_{12}}\right)^{2}+\left(\frac{\tau_{23}}{S_{23}}\right)^{2}=1 ,$ | (4) |
拉伸分层失效(σ33 > 0)
| $ \left(\frac{\sigma_{\mathrm{3B}}}{Z_{T}}\right)^{2}+\left(\frac{\tau_{\mathrm{1B}}}{S_{\mathrm{BB}}}\right)^{2}+\left(\frac{\tau_{\mathrm{ZB}}}{S_{2 \mathrm{~B}}}\right)^{2}=1 ,$ | (5) |
压缩分层失效(σ33 < 0)
| $ \left(\frac{\sigma_{33}}{Z_{\mathrm{C}}}\right)^{2}+\left(\frac{\tau_{\mathrm{1B}}}{S_{\mathrm{BB}}}\right)^{2}+\left(\frac{\tau_{\mathrm{ZB}}}{S_{2 \mathrm{~B}}}\right)^{2}=1 ,$ | (6) |
纤维基体剪切失效(σ11 < 0)
| $ \left(\frac{\sigma_{11}}{X_{\mathrm{C}}}\right)^{2}+\left(\frac{\tau_{12}}{S_{12}}\right)^{2}+\left(\frac{\tau_{13}}{S_{13}}\right)^{2}=1 。$ | (7) |
式中:σij与τij(i, j = 1, 2, 3)为材料主方向上的应力分量;X为材料的纵向强度;Y为材料的横向强度;Z为材料的法向强度;T和C分别表示拉伸和压缩;Sij(i = 1, 2, 3, j = 1, 2, 3)为材料平面内的剪切强度。当材料的任意单元满足任意一种失效形式的表达式时,认为材料的这个单元发生疲劳失效。
以拉伸荷载为例,将等寿命方程E(n)/E(0) = 1−Qnv乘以应变,则有:
| $ \frac{X(n, s)}{X_{T}}=1-Q n^{e} 。$ | (8) |
FRTP增强层所用玻纤带的具体参数如表1所示。
|
|
表 1 玻纤带极限强度参数 Tab.1 Ultimate strength parameters of glass fiber ribbon |
本文使用的纤维增强热塑性复合管由内衬层、增强层和外保护层3层组成。管道增强层由8层玻璃纤维带缠绕而成,其缠绕角度为±55°,玻纤带为各向异性材料,其纤维材料为玻璃纤维,基体材料是高密度聚乙烯(HDPE);管道内衬层和外保护层的材料是高密度聚乙烯(HDPE),为各向同性材料。实验所用管道实验段的长度为366.0 mm,内径为62.0 mm,外径分别为48.0 mm,其中内衬层、增强层和外保护层的厚度分别为3 mm、2 mm和2 mm,管道等效密度996.64 kg/m−3,具体参数如表2所示,FRTP力学性能参数如表3所示。
|
|
表 2 FRTP规格参数 Tab.2 FRTP specification parameters |
|
|
表 3 FRTP各层力学性能参数 Tab.3 Mechanical property parameters of FRTP layers |
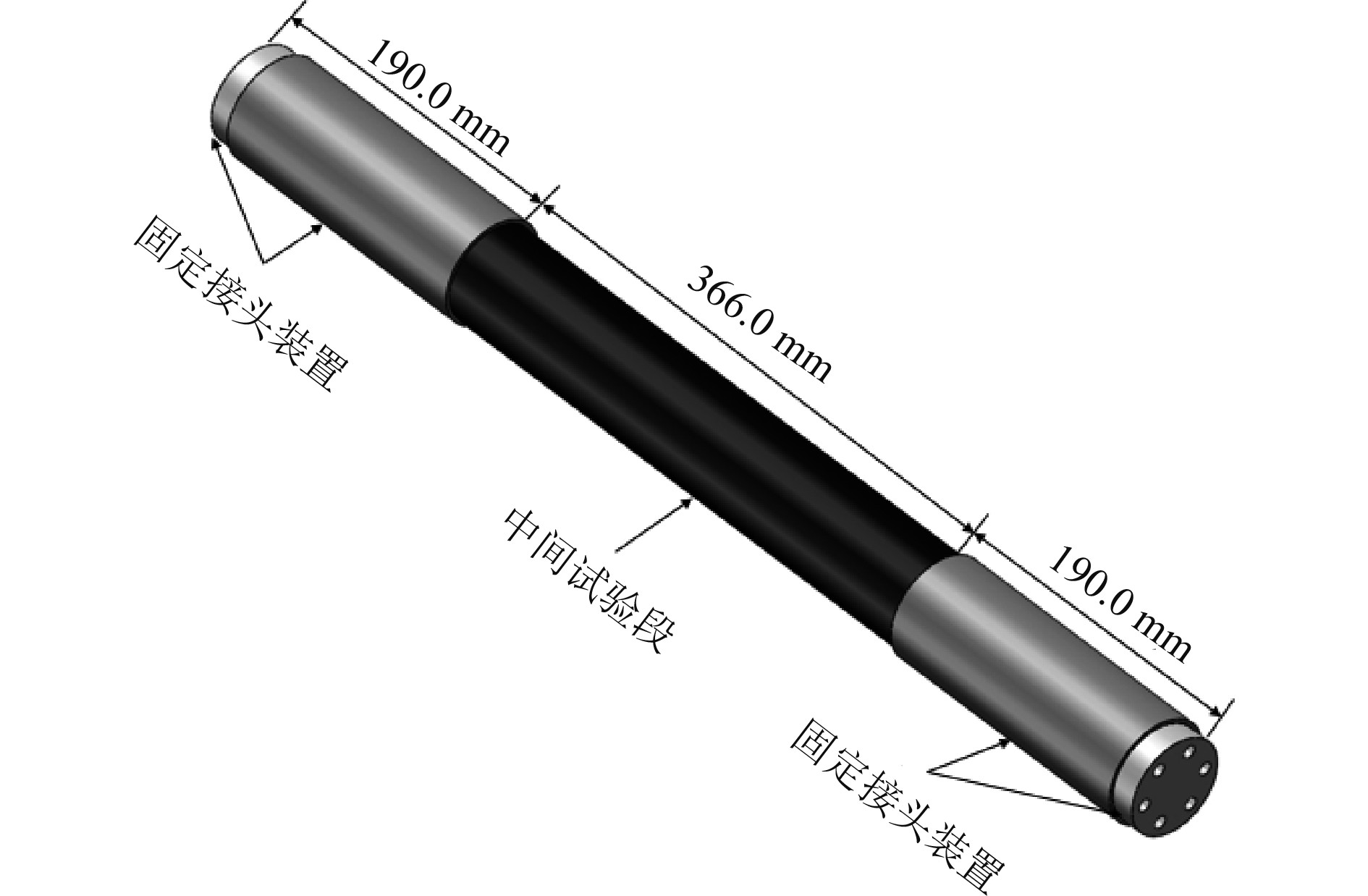
对FRTP进行拉-拉单轴疲劳实验,实验方案的设计依据为ISO 13003: 2003[10]和DNVGL-RP- F119[11]。研究采用的疲劳实验设备为多功能电液伺服加载机,加载机通过控制器能够设定荷载大小、波形和加载频率,荷载波形有三角波和正弦波,加载机最大能够提供50 kN加载力。为将管道固定在加载装置上,管道两端设计有190.0 mm的接头装置,如图2所示。设置4种应力水平,分别为σmax = 80% σs、65% σs、55% σs、40% σs,σmax为样管的最大循环应力,σs为样管的屈服应力。循环荷载类型为拉-拉单轴疲劳荷载,荷载加载波形为正弦波,应力比R = 0.1,即σmin / σmax = 0.1。图3为疲劳实验荷载加载方式,实验时按照斜波的方式将荷载加载到最大荷载与最小荷载的平均值Fmean = (Fmax + Fmin) / 2,然后将荷载以正弦波的方式对样管进行加载。ISO 13003: 2003[10]建议实验的加载频率为1~25 Hz,因此设定正弦波的幅值ΔF = (Fmax − Fmin) / 2、加载频率f = 1 Hz。
|
图 2 FRTP试件外观几何尺寸 Fig. 2 Geometric dimensions of FRTP specimen appearance |

|
图 3 疲劳实验荷载加载方式 Fig. 3 Load loading method for fatigue experiment |
为了描述研究所用样管的疲劳损伤及寿命情况,参考Yang[12]提出的复合材料剩余刚度预测模型:
| $ \frac{E(n)}{E(0)}=1-Q n^{E} 。$ | (9) |
式中:E(n)为材料在n次循环荷载是的刚度;E(0)为材料初始刚度;Q = a1 + a2 v,v = a3 + BS,S为荷载应力水平;a1、a2和a3为材料常数。
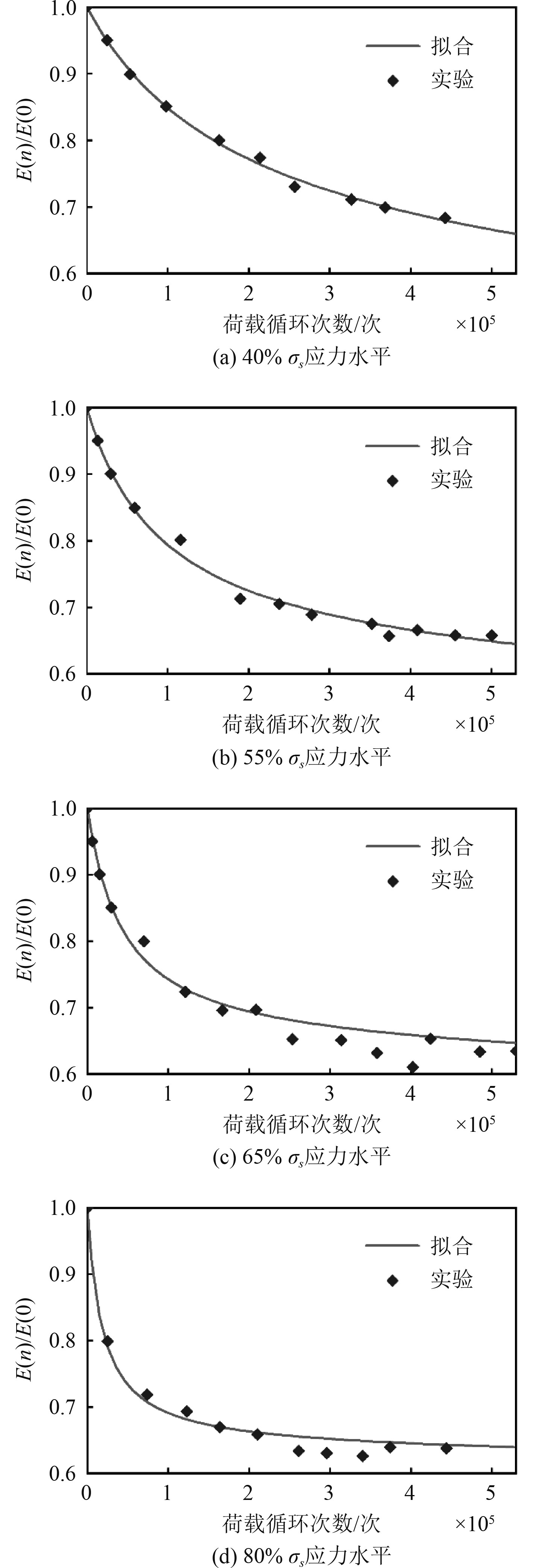
利用式(9)所得实验数据,通过最小二乘法得到样管在拉-拉疲劳荷载下的剩余刚度模型,参数a1、a2、a3和B在表4中给出。图4为剩余刚度模型的刚度变化规律和与实验中刚度变化规律,二者吻合较好。可以看出:随着荷载循环次数增加,管道刚度逐渐减小;荷载应力水平越高,管道刚度衰减越快;管道刚度衰减速率前期较大,后来逐渐减小。
|
|
表 4 拟合所得各参数值 Tab.4 Parameter values obtained by fitting |
|
图 4 各应力水平下剩余刚度拟合模型与实验数据 Fig. 4 Residual stiffness fitting model and experimental data at various stress levels |
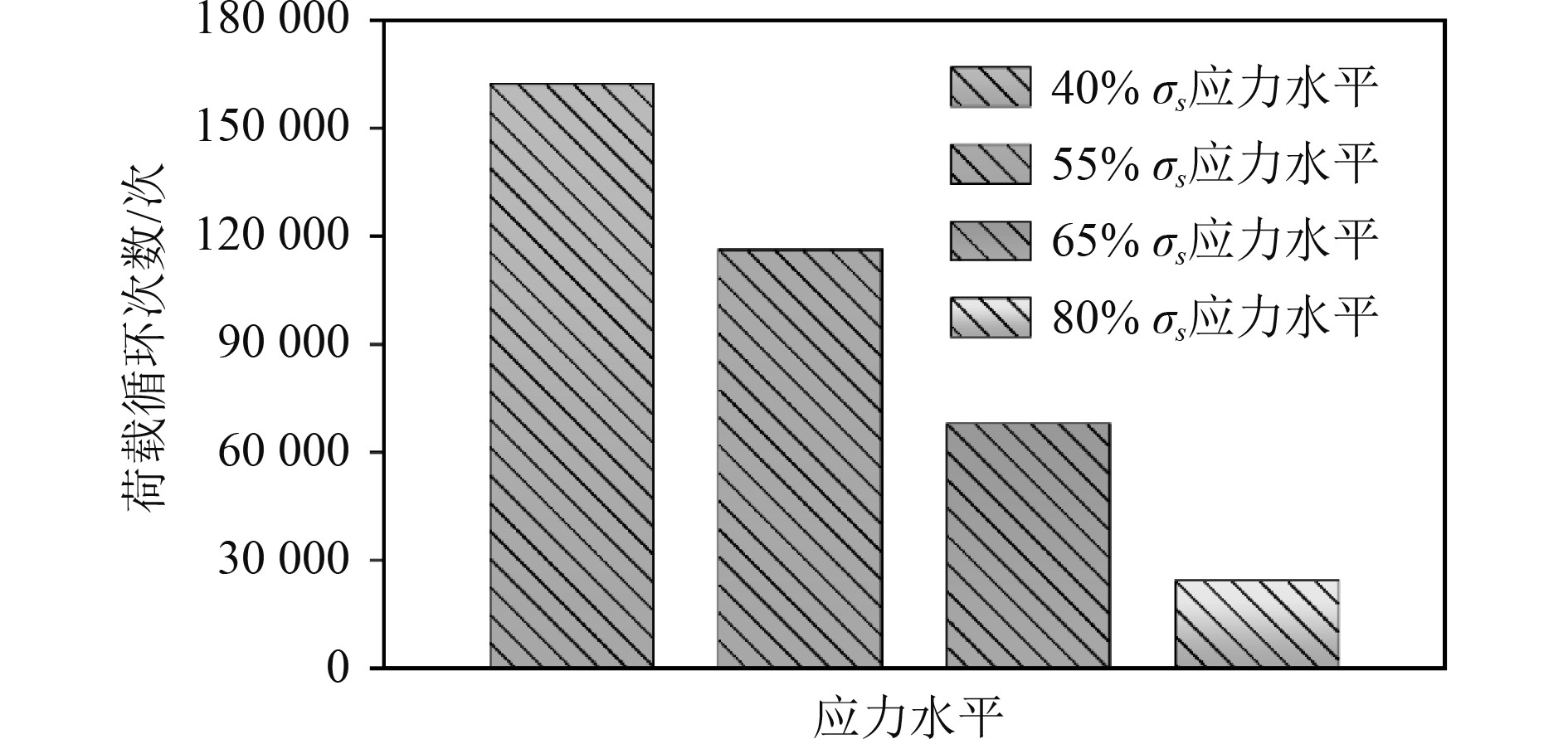
图5为实验所得FRTP在4种应力水平下的疲劳剩余刚度曲线。随着循环荷载周次的增加,管道的刚度逐渐降低。ISO 13003: 2003[10]建议将复合材料试样的刚度降低20%时的循环荷载周次作为复合材料的疲劳寿命。由图5可知,尽管管道没有发生疲劳断裂失效,但刚度衰减已超过35%,可视为疲劳失效。图6为各应力水平下管道失效的加载次数。可以看出,样管应力水平越低,其在失效时所对应的循环荷载周次越高,即材料遭受的循环荷载越小,其疲劳寿命越高。80% σs应力水平下FRTP疲劳寿命为24300次,40% σs应力水平下FRTP疲劳寿命为162215次,是前者的6.68倍。

|
图 5 剩余刚度曲线 Fig. 5 Residual stiffness curve |
|
图 6 各应力水平下失效时的加载次数 Fig. 6 Loading times at failure at various stress levels |
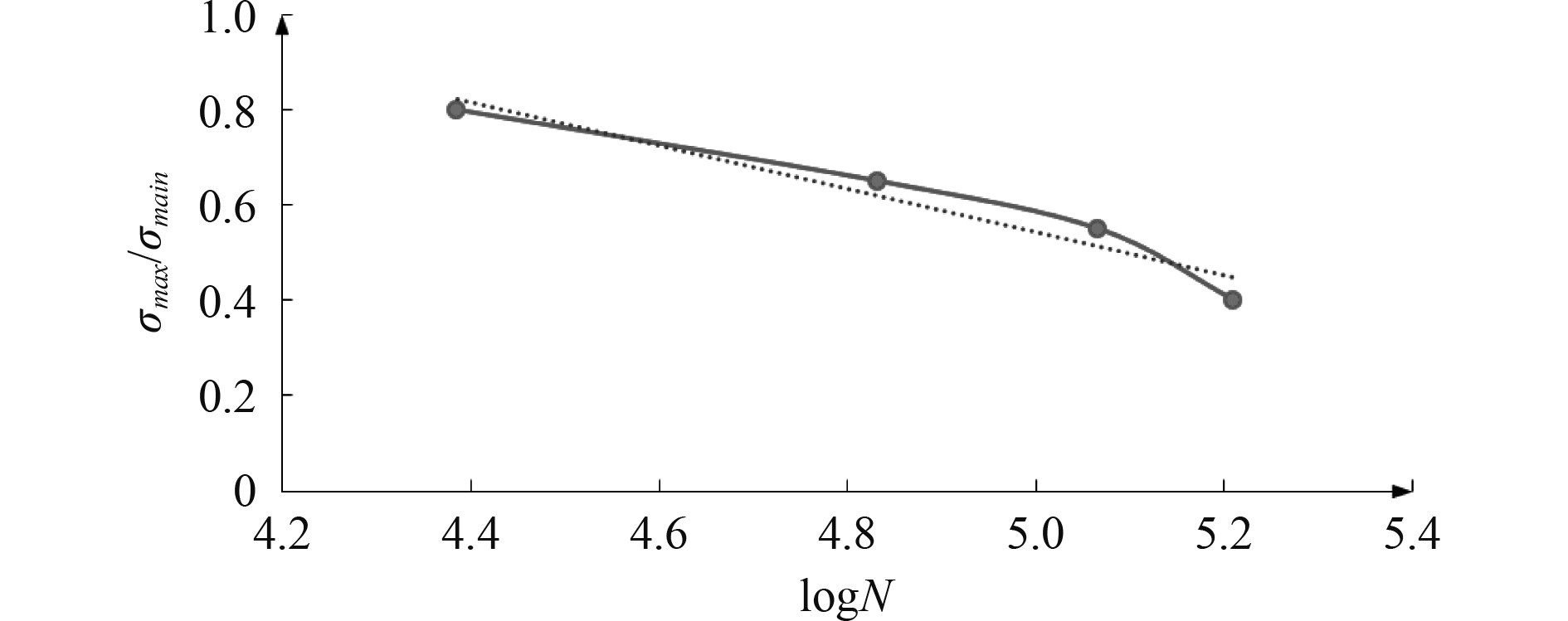
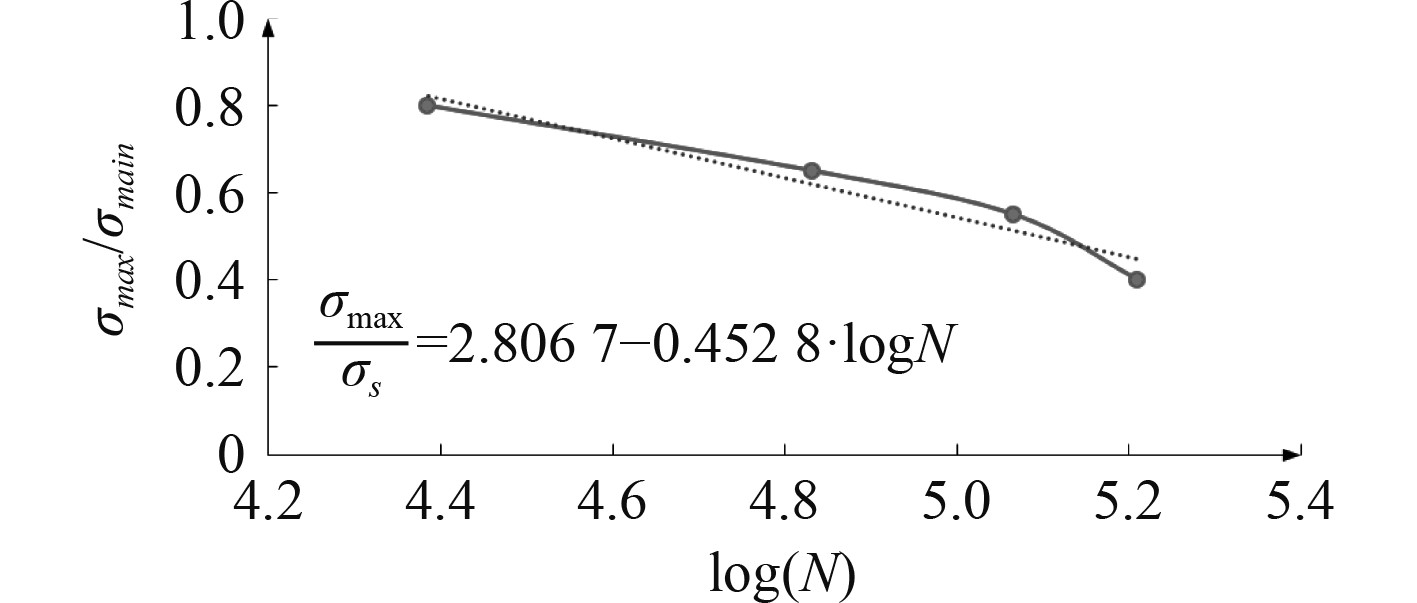
以刚度退化20%为失效判据,得到管道在疲劳失效时的循环荷载次数N。将循环应力归一化得到σmax / σs,对N取对数函数得到logN,最终得到归一化的S-N曲线,以斜截式的形式表示如下:
| $ \frac{\sigma_{\text {max }}}{\sigma_{\alpha}}=a-b-\log N 。$ | (10) |
| $ \frac{\sigma_{ \text{max }}}{\sigma_{s}}=2.806\;7-0452\;8\cdot \log N 。$ | (11) |
式中:σmax为最大循环应力;σs为样管屈服应力;N为失效时循环次数;a为拟合曲线截距;b为拟合曲线的斜率。图7为疲劳实验得出的S-N曲线图,以σmax/ σs为纵坐标,log N为横坐标,得到一条近似直线的S-N曲线。将曲线进行拟合成类似式(3)的数学表达式,得到S-N曲线的表达式。
|
图 7 S-N曲线 Fig. 7 S-N curve |
根据表2几何参数,建立管道三维有限元模型,如图8所示。整个FRTP的有限元模型分为内衬层、中间增强层和外保护层3部分组成。有限元模型使用的单元类型为8节点实体减缩积分单元C3D8R,模型共有140000个网格单元。模型的材料参数在Abaqus中输入并在UMAT中调用,具体参数见表3。
|
图 8 FRTP有限元模型 Fig. 8 FRTP finite element model |
为了与实验模型保持一致性,有限元模型的荷载及边界条件与实验模型完全相同。由于FRTP管道为粘结性柔性管道,管道的层间通过热融合的方式粘结在一起,层间没有相互滑移运动,所以在有限元中分别将管道的内衬的外表面与中间增强层内表面、中间增强层的外表面与外保护层的内表面用Tie接触方式绑定在一起。针对管道所受的拉伸疲劳荷载工况,将有限元模型一端固支约束,另一端施加沿管道轴向(Z方向)的集中力,并将该端其他5个自由度的位移设为0,确保管道的只受单轴拉伸荷载。
2.3.2 有限元模型验证图9为40% σs、55% σs、65% σs和80% σs应力水平下FRTP位移的有限元及实验结果对比图,图中位移表征FRTP在荷载作用下发生变形的大小。对比各应力水平下FRTP变形结果发现,随着荷载循环周次的增加,FRTP的变形值逐渐增大;实验模型的变形值相比有限元模型的变形值偏大,但误差在15%以内,在允许误差范围之内。这是由于有限元模型是理想化模型,实验模型各项力学性能指标由于生产制造带来的缺陷相对于理想化模型偏小。整体上看,FRTP变形量随着荷载循环周次的变化规律在实验模型及有限模型中表现出良好的一致性,这表明有限元模型中所使用的用户自定义子程序UMAT编写正确,保证了有限元模型结果的正确性。

|
图 9 不同应力水平下FRTP位移与荷载循环次数的关系 Fig. 9 Relationship between FRTP displacement and number of load cycles under different stress levels |
图10为4种应力水平下FRTP在不同寿命期间的应变云图,各种应力水平下应变云图所选的循环次数与应力云图所选循环次数相同。为了更好反映出FRTP在不同寿命时期的应变变化规律,将6个寿命时期的应变云图放在同一标尺下。可以看出,FRTP应变较大的位置与应力较大的位置都出现在外表面扣压接头与中间实验管段的交界处。此外,在4种不同应力水平下,当FRTP遭受越高应力水平的疲劳荷载时,其应变值越大。FRTP在40% σs应力水平的疲劳荷载作用下,循环荷载周次为208320次时,其应变值为1.018×10−2;FRTP在80% σs应力水平的疲劳荷载作用下,循环荷载周次为198720次时,其应变值为2.352×10−2,是前者的2.31倍。在同一应力水平下,随着荷载循环周次的增加,FRTP的刚度逐渐衰减,其应变值逐渐增大。以40% σs应力水平为例,循环荷载周次为1时,其应变值为8.013×10−3,循环荷载周次为312480次时,其应变值为1.083×10−2,是前者的1.35倍。

|
图 10 不同应力水平下FRTP不同寿命时期的应变云图 Fig. 10 Strain cloud chart of FRTP at different life periods under different stress levels |
图11为4种应力水平下FRTP在不同寿命时期的位移云图,各应力水平所选的循环次数与应力应变云图所选循环次数相同。可以看出,随着荷载循环周次的增加,由于刚度的逐渐衰减,同一应力水平下的FRTP的最大位移值逐渐增大,这表明FRTP在循环荷载的作用下所发生的变形在逐渐增大。以55% σs应力水平为例,循环荷载周次为1时,其变形值为2.814 mm,循环荷载周次为247680次时,其变形值为3.988 mm,是前者的1.42倍。此外分析不同应力水平下的FRTP位移云图可知,处在较高应力水平荷载下的FRTP,其变形值增大得越快。以55% σs应力水平和65% σs应力水平为例,55% σs应力水平疲劳荷载下的FRTP在疲劳荷载循环周次为1时,其变形值为2.814 mm,在疲劳荷载循环周次为165120次时,其变形值为3.785 mm,变形值是开始时的1.35倍;65% σs应力水平疲劳荷载下的FRTP在疲劳荷载循环周次为1时,其变形值为3.541 mm,在疲劳荷载循环周次为152640次时,其变形值为4.939 mm,变形值是开始时的1.41倍。从位移分布云图可以看出,在施加约束一侧,距离端部190 mm内的单元位移相等,其数值为0;在施加荷载一侧,距离端部190 mm内的单元位移相等,其数值为最大值,这与实验模型的结果一致。

|
图 11 不同应力水平下FRTP不同寿命时期位移云图 Fig. 11 Displacement cloud map of FRTP at different life periods under different stress levels |
经过有限元模型与实验模型的对比可以发现,有限元模型与实验模型显现出了良好的一致性,针对60% σs应力疲劳荷载下的FRTP进行数值仿真模拟,对其进行疲劳预测。图12为60% σs应力水平下不同寿命时期的应变云图,可看出随着荷载循环周次的增加,管道的应变值逐渐增加,这是管道刚度衰减的体现。在第1次循环荷载周次时,管道最大应变值是1.128×10−2,在第237600次循环荷载周次时,最大应变值为1.609×10−2,应变值增大了42.6%。

|
图 12 60% σs应力水平下不同寿命时期应变云图 Fig. 12 Strain of different life periods under 60% σs stress levels |
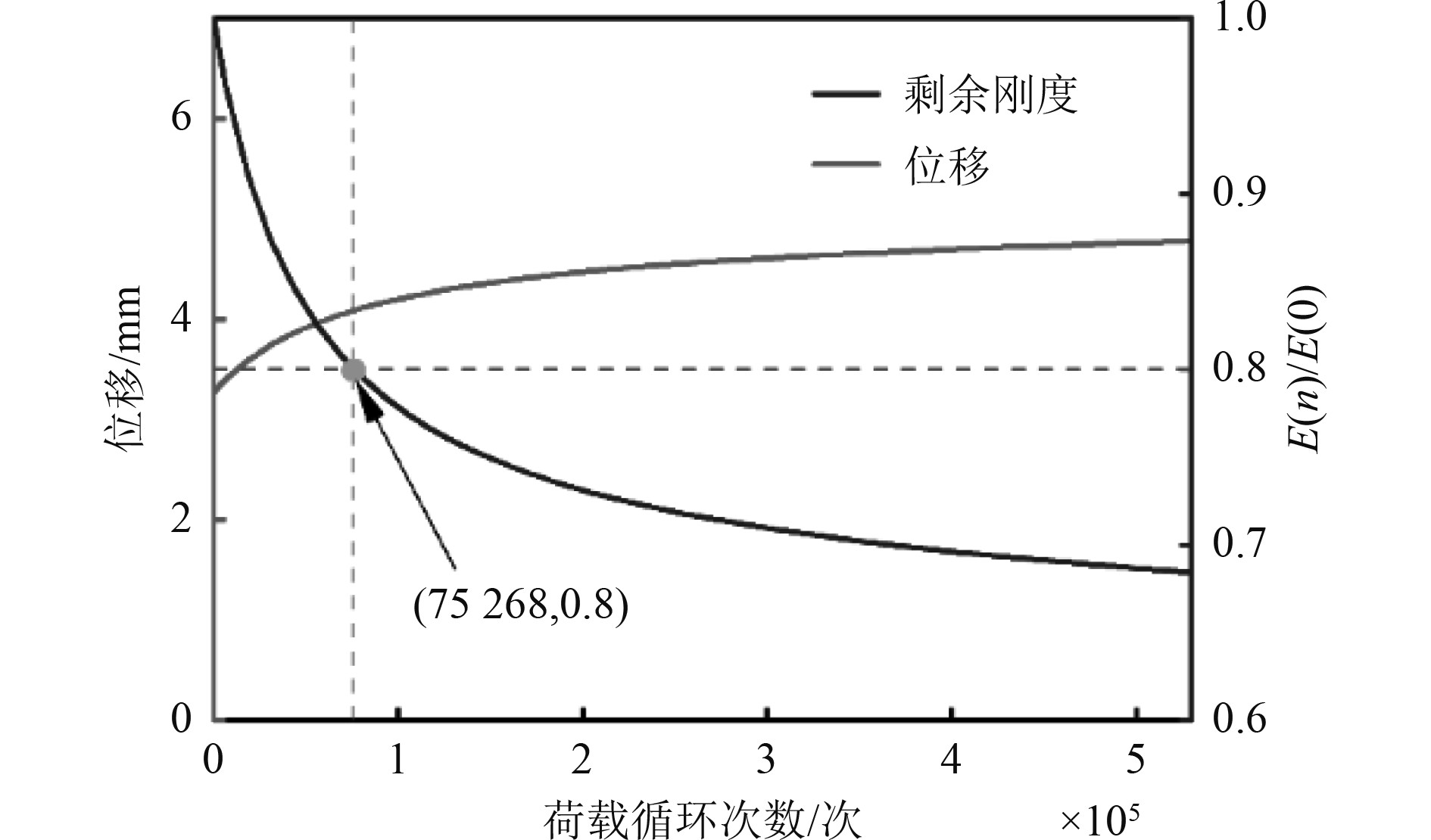
图13为60% σs应力水平下管道位移变化及剩余刚度变化曲线。可以看出,管道在荷载循环周次为75268次时,其刚度衰减20%;管道刚度随着荷载循环次数增加而减小,变形值随着荷载循环次数增加而变大,但是其变化速率都逐渐减小,与其他应力水平下的情况一致。
|
图 13 60% σs应力水平下不同寿命时期位移及刚度变化 Fig. 13 Changes in displacement and stiffness during different life periods under 60% σs stress levels |
本文以FRTP为研究对象,通过疲劳实验和有限元数值模拟研究了FRTP的拉伸疲劳性能,具体结论如下:
1)疲劳实验过程中,随着荷载循环次数增加,管道刚度逐渐衰减,即使最大应力水平(80% σs)下循环100万周次,管道也没有出现整体断裂现象,但是刚度衰减了35%。以FRTP刚度衰减20%作为其疲劳失效判据,得到了管道疲劳寿命曲线(即S-N曲线):
2)提出了FRTP疲劳刚度衰减模型,通过编制UMAT子程序对60% σs应力水平下拉-拉单轴FRTP进行疲劳预测。
3)FRTP在4种应力水平疲劳荷载作用下的刚度随着荷载循环周次的增大而减小,管道应变值和变形值随着荷载循环周次的增大而增大;加载前期,荷载应力水平越高,管道刚度衰减速率越大。
| [1] |
KAYNAK C, MAT O. Uniaxial fatigue behavior of filament-wound glass-fiber/epoxy composite tubes[J]. Composites Science and Technology, 2001, 61: 1833-1840. DOI:10.1016/S0266-3538(01)00084-7 |
| [2] |
JOSEPH E, PERREUX D. Fatigue behaviour of glass-fibre/epoxy-matrix filament-wound pipes: Tension loading test and result[J]. Composite Science and Technology, 1994, 52(4): 469-480. DOI:10.1016/0266-3538(94)90029-9 |
| [3] |
GEMI L, TARAKÇIOĞLU N, AKDEMIR A, et al. Progressive fatigue failure behavior of glass/epoxy (±75°)2 filament-wound pipes under pure internal pressure[J]. Materials and Design, 2009, 30(10): 4293-4298. DOI:10.1016/j.matdes.2009.04.025 |
| [4] |
TARAKÇIOĞLU N, GEMI L, YAPICI A. Fatigue failure behavior of glass/epoxy ±55 filament wound pipes under internal pressure[J]. Composites Science and Technology, 2005, 65(3/4): 703-708. |
| [5] |
TASYÜREK M, TARAKÇIOĞLU N. Enhanced fatigue behavior under internal pressure of CNT reinforced filament wound cracked pipes[J]. Composites Part B, 2017, 124: 23-30. DOI:10.1016/j.compositesb.2017.05.050 |
| [6] |
ELLYIN F, MARTENS M. Biaxial fatigue behavior of a multidirectional filament-wound glass-fiber/epoxy pipe[J]. Composites Science and Technology, 2001, 61(4): 491-502. DOI:10.1016/S0266-3538(00)00215-3 |
| [7] |
PERREUX D, JOSEPH E. The effect of frequency on the fatigue performance of filament-wound pipes under biaxial loading: experimental results and damage model[J]. Composites Science and Technology, 1997, 57(3): 353-64. DOI:10.1016/S0266-3538(96)00155-8 |
| [8] |
QUARESIMIN M, CARRARO P A. Damage initiation and evolution in glass/epoxy tubes subjected to combined tension-torsion fatigue loading[J]. International Journal of Fatigue 2014, 63: 25-35.
|
| [9] |
吴将. 起圈织物增强复合材料细观力学及冲击性能研究[D]. 南京: 南京航空航天大学, 2018.
|
| [10] |
ISO 13003: 2003. Fiber-reinforced plastics-determination of fatigue properties under cyclic loading conditions[S]. GENEVA: ISO, 2003.
|
| [11] |
DNVGL-RP-F119. Thermoplastic composite pipes[S]. NORGE:DNVGL, 2015.
|
| [12] |
YANG J N, LEE L J., SHEN D Y. Modulus reduction and fatigue damage of matrix dominated composite laminates[J]. Composite Structures, 1992, 21: 91-100. DOI:10.1016/0263-8223(92)90044-D |
 2024, Vol. 46
2024, Vol. 46
