圆柱壳是工程中最基本的结构单元之一,因具有良好的承载能力,并且制作简单,所以广泛应用于航空航天及海洋等多种领域[1 - 2]。典型的薄壁圆柱壳结构的径厚比很大,而且极易因承受巨大的轴向压力载荷而存在屈曲的风险,屈曲也正是该类结构在实际工程中主要的失效模式[3]。如海洋平台的桩腿多采用薄壁圆柱壳结构[4],桩腿由于受到来自平台较大的轴向压缩载荷而存在屈曲风险。多年来,众多学者已对圆柱壳结构的稳定性进行了大量研究,早在20世纪末Teng[5]就全面评述了薄壳屈曲领域的研究进展和趋势。Zhao等[6]通过实验和数值方法研究了几何缺陷对薄壁圆柱壳受压屈曲行为的影响。Himayat[7]进行了薄壁圆柱壳在轴向压缩下,具有大挠度效应和几何缺陷的非线性屈曲分析,结果表明非线性和几何缺陷的影响是造成理论和实验结果不匹配的原因。承载能力在薄壁圆柱壳结构稳定性的评价中具有重要意义,一直以来都是工程力学中的重难点。
提高薄壁圆柱壳在均匀轴向压缩载荷下承受力的典型方法是对柱壳进行各种形式加筋。Li等[8]基于实验和数值结果发现,承受轴向压缩载荷的环形加筋圆柱壳相比于未加筋的圆柱壳可获得更高的临界载荷。Fan等[9]系统研究了不同结构参数对加筋圆柱壳缺陷敏感性和设计屈曲载荷的复杂影响,基于能垒法对加筋圆柱壳进行优化,有效地提高加筋圆柱壳的承载效率。Zhou等[10]提出一种新颖的两尺度拓扑优化方法,通过所提出的优化方法获得的具有最优模式的临界屈曲载荷增加了21.7%。由于桩腿常年浸泡在海水中,容易受到海水的腐蚀而影响其承载能力,采用分层结构是一种简单有效的解决腐蚀问题的方法。Patel[11] 提出用海水和海砂制成的混凝土填充双层不锈钢圆柱,其具有高耐腐蚀性的显著特征。通过试验和数值结果进行比较,表明随着混凝土强度的增加,圆形双层不锈钢混凝土短柱的极限强度和初始刚度都有显著提高。
然而,关于钢结构中轴压环向加筋圆柱壳设计在实际工程中难以实现。目前,针对轴向压缩下层状结构的研究也主要集中在双层混凝土钢管,而双截面构件的突出特征将导致复合柱的有效占地面积显著增加。关于两层贴合的双层圆柱壳在轴向压缩下的屈曲行为的研究较少,本文研究一种既能提高其承载强度又能实现耐腐蚀的双层结构。
1 双层圆柱壳的试验研究不锈钢圆柱壳有单层和双层2种模型,其中双层圆柱壳由2个单层不锈钢柱壳组成,如图1(a)所示,外壳和内壳的厚度分别为to和ti,之间的初始间隙为δ,外壳的外径为D,2个壳体的长度均为L。单层圆柱壳即为双层不锈钢圆柱壳的外壳,如图1(b)所示。

|
图 1 圆柱壳的几何模型 Fig. 1 Geometric model of cylindrical shells |
制作这2种圆柱壳的材料是用激光从不同规格的长圆柱钢管上切割下来的,这种切割方法相较于传统砂轮切割误差更小。2种规格的圆柱钢管的尺寸如图2所示,其中单层圆柱壳即为图2(b)所示的不锈钢柱壳,试验试样共3个。双层圆柱壳则采用橡胶成形技术制作,制作过程所采用的模具如图3所示。
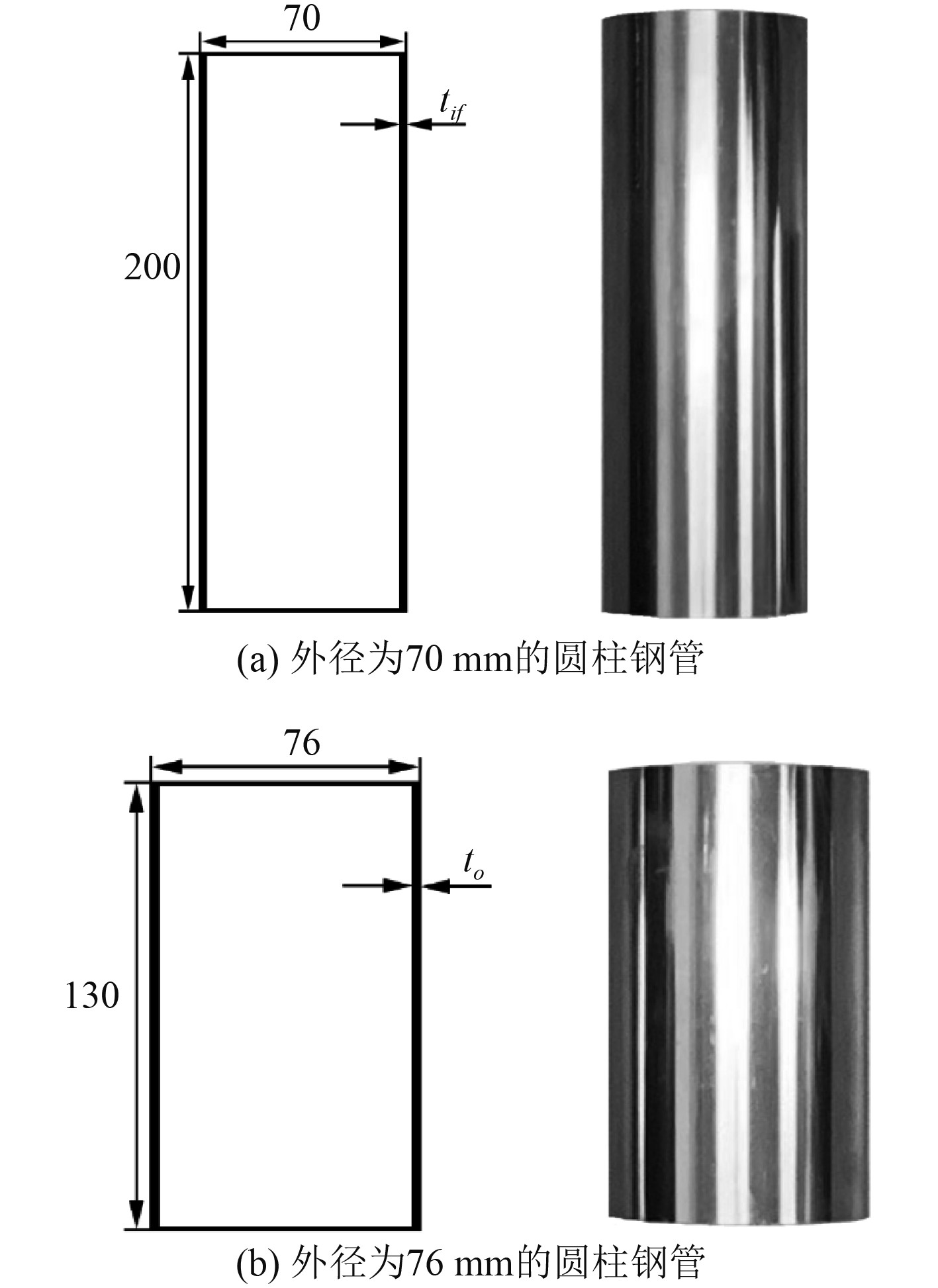
|
图 2 2种规格圆柱钢管的几何尺寸与实物图 Fig. 2 Geometric dimensions and physical maps of cylindrical steel pipes of two specifications |
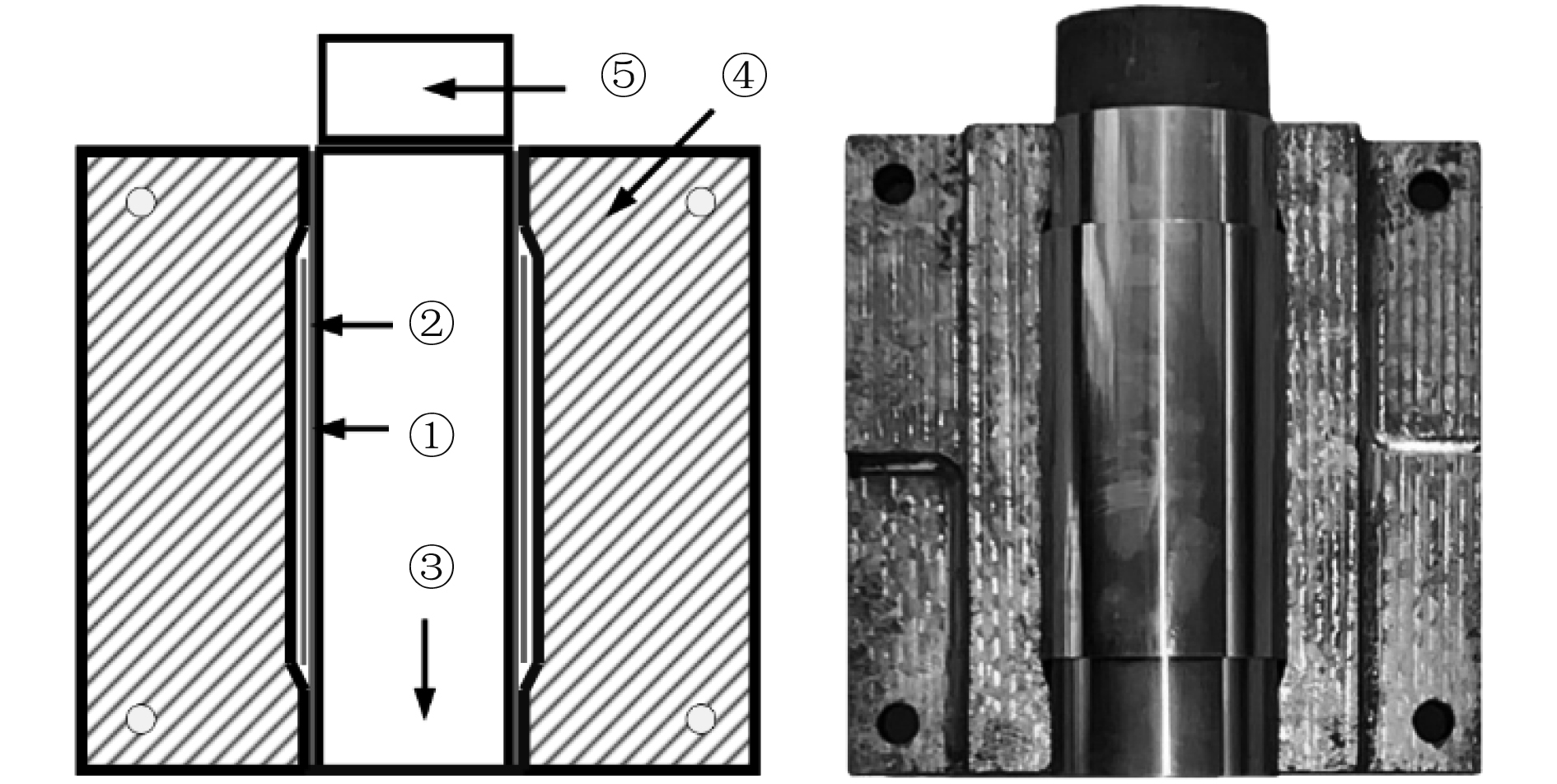
|
图 3 模具的几何、实物图 Fig. 3 Geometric and physical maps of the mold |
首先,将不锈钢壳体①套入直径较大的壳体②中,并将橡胶③塞入壳体①内;其次,三者以组合形式放入模具④后用螺栓螺母将模具锁死;再次,挤压压头⑤,橡胶③受到来自压头⑤的轴向力后发生弹性变形进而挤压壳体①使其与壳体②贴合,因壳体②的外径被设计成与模具内径相同,所以几乎不会发生塑性变形;最后,取出两层圆柱壳后切除壳体①两端多出壳体②的部分,双层柱壳制作完成。重复上述步骤得到双层圆柱壳共 3 个。
1.2 双层圆柱壳的几何测量进行轴压试验之前,采用超声波测厚仪测量3个单层试样的厚度。由于超声波测量仪无法精确测量出双层试样的厚度,因此改用微米级测厚规测量3个双层试样的厚度。每个试样上总共有88个测量点,均匀分布在轴向和圆周方向上(11×8),厚度测量结果列在表1中。
|
|
表 1 实测试样的厚度参数 Tab.1 Wall thickness data obtained from measurements |
从表1的测量结果可以看出,3个单层试样的平均厚度相差很小,最大与最小平均壁厚的差0.002 mm,且厚度标准差都不超过0.01,制作精度都较高。3个双层试样的平均壁厚在1.956~1.999 mm之间,最大的厚度标准差为0.033,制作质量也相对较好。
由于外层柱壳的外径与模具内径相同,所以在挤压过程中几乎不会发生塑性变形,而内层柱壳由于受到橡胶的挤压,外径变大和长度的伸长从而导致壁厚变薄,胀形前后的几何形状如图4所示。

|
图 4 双层圆柱壳胀形前后几何对比图 Fig. 4 Geometry before and after the fabrication of the DL cylindrical shell |
由于胀形前后柱壳的质量守恒,经过胀形后,内层柱壳发生了变形的这部分高度的质量(即图4中Lf段)等于未胀形之前该部分质量与上端因变形而发生了收缩部分(即图4中Ls段)的质量之和,其中内层柱壳未发生变形的部分同外层柱壳一样视为厚度不发生变化,于是可通过式(1)和式(2)联立方程组计算出经过橡胶胀形后的内层柱壳发生变形部分的厚度和两层柱壳之间的间隙值,公式如下:
| $ \mathrm{{\text{π}} }\times \left[D-2\left({t}_{o}+\delta \right)\right]\times {L}_{f}\times {t}_{i}={\text{π}} \times d \times \left({L}_{f}+{L}_{s}\right)\times {t}_{if},$ | (1) |
| $ {t}_{o}+{t}_{i}+\delta =t。$ | (2) |
式中:D为双层圆柱壳的外径,即模具的内径为76 mm;ti为内层柱壳胀形后的厚度;Lf为内层柱壳受挤压产生变形的一段长度,即150 mm;d为内层柱壳胀形前的外径,即70 mm;tif为内层柱壳胀形前的厚度;Ls为内层柱壳受到橡胶的挤压而发生收缩的收缩量。计算结果如表2所示,表中的外层壳体厚度to和胀形前内层壳体厚度tif均为测量的平均值,收缩量Ls采用精度为0.001 mm的游标卡尺测量后取其平均值。
|
|
表 2 双层试样经理论计算后的几何参数 Tab.2 The thickness and clearance of DL cylindrical shells calculated by theoretical equations |
使用光学扫描仪对所有试样的外表面进行光学测量,目的是使由制造过程引起的初始几何缺陷包含在几何形状中,以获取真实的外表面轮廓。用三维检测软件GOM Inspect将扫描数据和用三维软件绘制出的CAD数据进行对比,得到扫描模型与理想模型之间的几何形状的偏差,如图5所示。
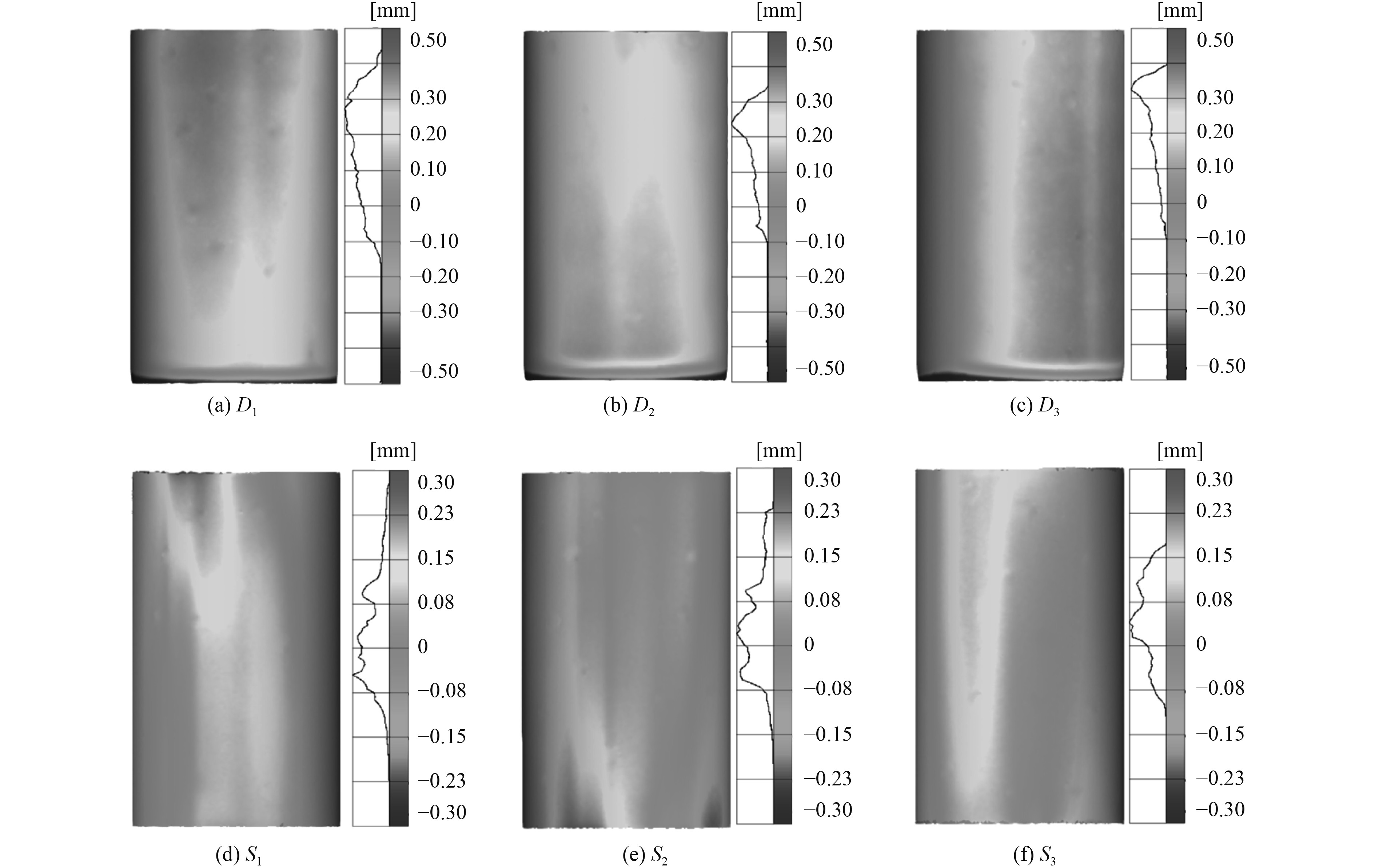
|
图 5 圆柱壳外表面与其完美几何形状之间的误差图 Fig. 5 The deviation of the geometries between the scanned models and the ideal |
可以看出,单层试样的加工误差总体低于双层试样,因此图5中单层试样显示的误差范围(–0.30~0.30 mm)较双层试样(–0.50~0.50 mm)小。之所以双层试样制造质量较单层低,主要是因为双层试样是在单层圆柱壳的基础上,采用橡胶成形技术手工制造而成的,由于橡胶的挤压,钢管在模具中受到了摩擦力的作用而发生了向过度位置滑动的现象,导致双层圆柱壳在模具中的下端部分向内微微弯曲,图5中的双层圆柱壳的上下端均与放入模具中的方向一致,于是图5中双层圆柱壳均为下端呈现出少量蓝色。即便如此,双层圆柱壳的真实形状与其理想形状之间的偏差也主要在−0.2~0.45 mm之间,其值很小。
1.3 双层圆柱壳的轴压试验试验采用万能压缩试验机(型号:CMT-5305;试验力:300 kN;试验力测量范围:0.2%~100%FS;试验力分辨力:1/300000 FS;有效压缩空间:800 mm;位移分辨力:0.015 μm;大变形分辨力:0.008 mm)。因为试验机的压头能够带来足够大的压紧力,所以试验过程无需对试样采取任何约束。为了采集到完整的试验数据,可快速下降压头直到即将与试样的上端面接触时,降低压头下降速率,当二者刚刚发生接触时将压头的压缩速率调整至最小1 mm/min,压缩变形量设置为4 mm,数据调整完成后开始进行轴压试验,即试样端部开始受力时试验正式开始。
试样在轴压试验过程中的载荷位移曲线如图6所示。所有试样的曲线均可大致分为2个阶段:第1阶段,曲线呈现出理想线性屈曲特征,该阶段为圆柱壳的前屈曲阶段;第2阶段,曲线达到峰值后开始出现转折下降,即圆柱壳进入后屈曲阶段。需说明的是,除了试样S2,其他5个试样均在开始阶段呈现出轻微的非线性特征。这是因为压头刚与圆柱壳接触时,受试样的加工精度的影响,无法使压头与试样的端部完美贴合。试样S2则是因进行轴压试验时的操作不当导致未能采集到完整的试验数据。各试样通过试验获得的极限强度也在表3中列出,根据试验极限强度可知,双层圆柱壳的平均极限强度约为单层的1.85倍。

|
图 6 圆柱壳轴压试验载荷位移曲线图 Fig. 6 Load-displacement curves of the cylindrical shells obtained by axial compression test |
|
|
表 3 圆柱壳的试验极限载荷值 Tab.3 The ultimate strength of cylindrical shells obtained by axial compression test |
将扫描得到的圆柱壳外表面模型导入到HYPERMESH软件中进行网格划分,网格尺寸为2mm,每层圆柱壳外表面网格数量约为7500个,该网格数量经网格收敛性分析后确定。单元类型主要为四边形单元S4,少部分为三角形单元S3。由于双层圆柱壳无法得到内层实际模型,于是采用HYPERMESH软件将外层网格进行复制后,按照0.972的比值进行缩小得到柱壳内层网格。然后,创建GAP单元,选择单元类型为GAPUNI一维单元连接内外壳一一对应的节点。为了模拟柱壳一端受到均匀轴向压缩力的环境,在圆柱壳一端设置一个参考点,参考点略高出该端的边缘且位于圆柱的中心轴上,并将设置好的参考点与柱壳该端的边缘进行耦合(Coupling)约束。数值分析所采用的材料参数为:杨氏模量E=191 052 MPa,泊松比v=0.3,屈服强度
采用Abaqus有限元分析软件分别对单、双层圆柱壳进行和非线性屈曲分析,每个单层圆柱壳的厚度分别为表1中对应的厚度测量值的平均值,双层圆柱壳外层厚度为表2第2列对应的厚度测量值的平均值,内层厚度为表2第3列经式(1)和式(2)计算所得胀形后的厚度。初始载荷值为10 000 N,约束定义为释放上端参考点处轴向位移,其他自由度固定,下端6个自由度全部限制。有限元模型如图7所示。
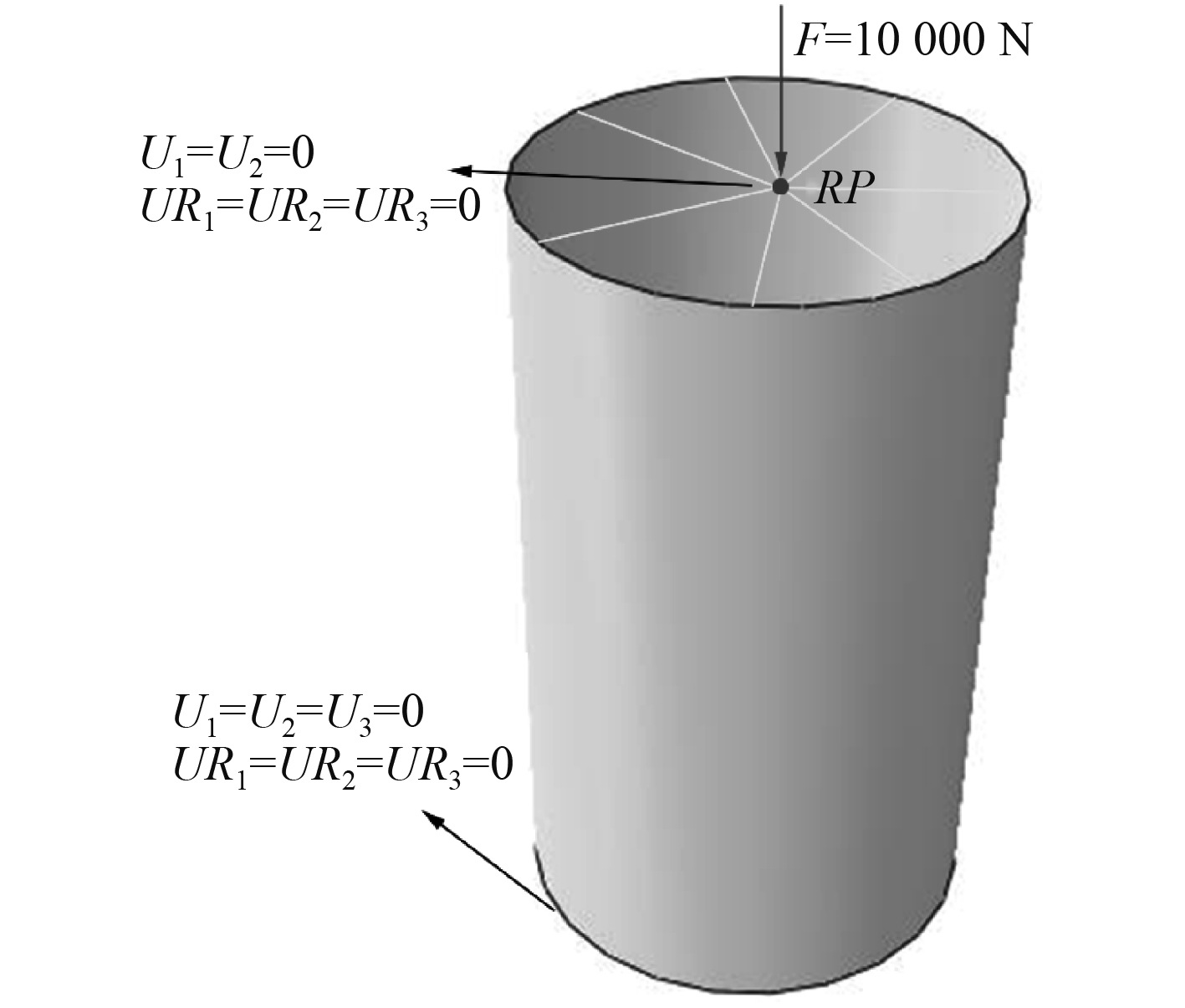
|
图 7 均匀轴压下薄壁圆柱壳有限元模型的约束及边界条件 Fig. 7 Constraints and boundary conditions of finite element models of the cylindrical shell under uniform axial compression |
非线性屈曲分析采用Riks弧长法,其基本参数为:初始弧长为0.01,最大弧长为0.5,最小弧长为1×10−30,总弧长为1,最大迭代步数为150。经非线性计算的6个圆柱体的临界载荷列于表4。可以看出,所有试样的屈曲临界载荷与试验值之间的最大误差为
|
|
表 4 圆柱壳数值计算结果 Tab.4 Critical load of cylindrical shells obtained by finite element method |
使用有限元法获得的6个圆柱壳参考点处的载荷位移曲线如图8所示。图中每个试样试验失稳图和有限元失稳图的上端均为施加轴向载荷的一端,从图中可看出轴压圆柱壳的真实屈曲变形与有限元模拟的屈曲变形基本一致,用有限元法得到的载荷-位移曲线与试验过程采集到的曲线的整体趋势基本一致,圆柱壳前屈曲阶段的载荷-位移曲线斜率的差异是因数值分析时边界条件的设置无法被完美地还原。另外需说明的是,图5中的单层圆柱壳的上端均与轴压试验中的上端一致,而图5中的双层圆柱壳的上端均为制作过程的上端,其中试样D1和D3制作过程的底端为轴压试验中的上端,D2制作过程的上端即为试验过程的上端。于是结合图5和图8可发现试验后的圆柱壳均在端部发生环状鼓起现象,并且发生环状鼓起的一端均为圆柱壳缺陷相对较大的一端。

|
图 8 圆柱壳参考点处载荷位移曲线图 Fig. 8 Load-displacement curves at the reference point of the cylindrical shells |
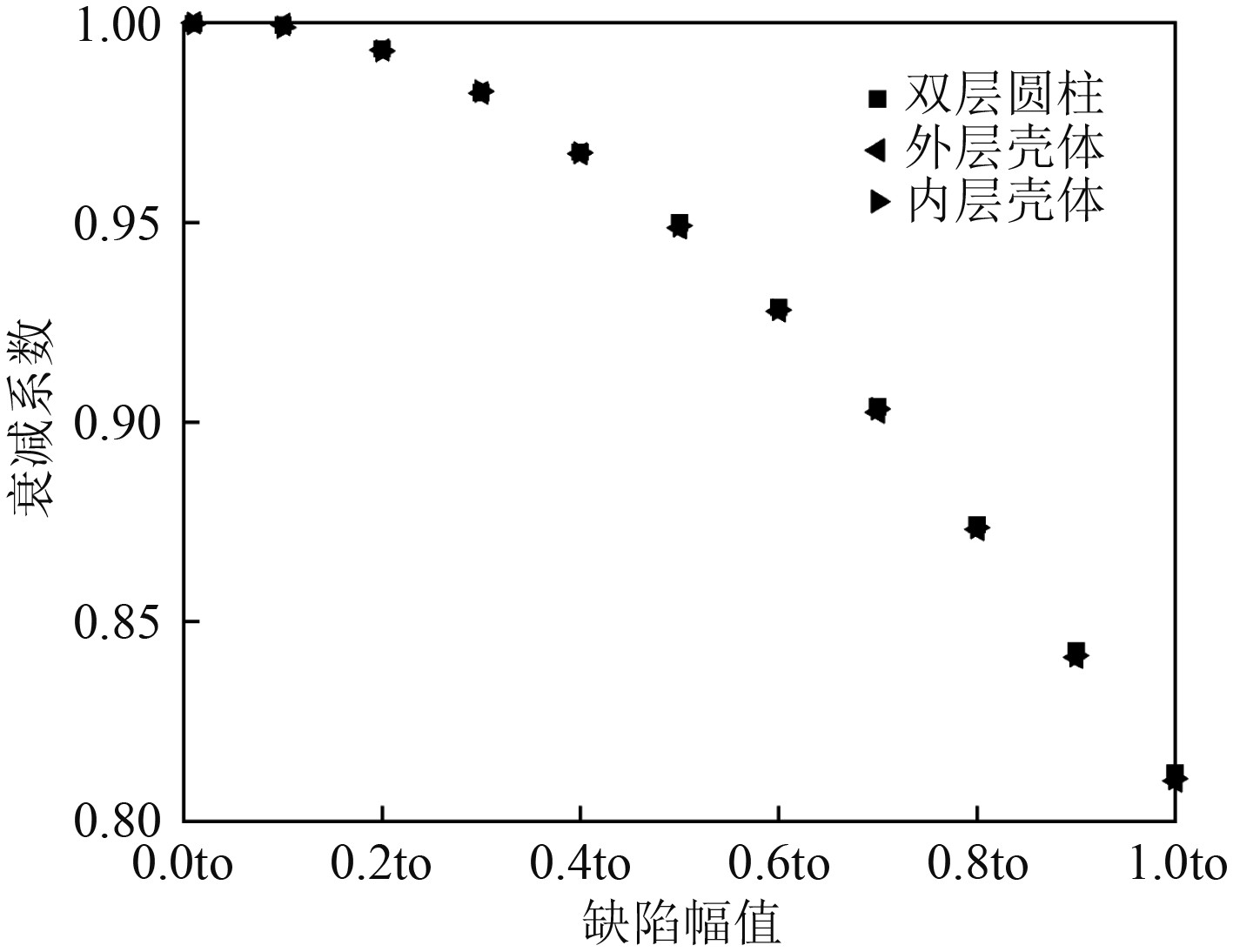
通过有限元法对双层圆柱壳的理想模型进行非线性屈曲分析,计算不同的缺陷幅值下内、外和双层圆柱壳的临界载荷F,建模方法相同,理想模型的高度为130 mm,半径为38 mm,内、外层均采用向内附厚的方式,外层的厚度为0.970 mm,内层的厚度为0.909 mm,外层壳体厚径比(0.970/38)比内层壳体厚径比(0.909/37)多0.001。缺陷形状从线性屈曲模式中引入,得到的计算结果列于表5,表中Fd为双层圆柱壳的临界载荷,Fo为外层壳体的临界载荷,Fi为内层壳体的临界载荷。从表5可看出,外层壳体获得比内层壳体更高的临界载荷,且双层圆柱壳的临界载荷总是略微高于内层的2倍,所以双层圆柱壳的极限强度可用较弱那一层的2倍来进行保守评估。
|
|
表 5 双层圆柱壳各缺陷值下的数值计算结果 Tab.5 Nonlinear buckling loads of the DL, outer and inner shells at different imperfection amplitudes |
根据表5的数据绘制出如图9所示的散点图。图中,横坐标为不同的缺陷幅值,纵坐标为不同缺陷幅值下所对应的内、外和双层柱壳的衰减系数,衰减系数被认为是引入了缺陷值的几何形状与未引入缺陷值的完美几何形状的临界载荷的比值。从图9可看出,双层圆柱壳是缺陷敏感结构,且双层壳体的缺陷敏感性与内层的缺陷敏感性越趋于一致。
|
图 9 不同缺陷幅值的内、外和双层圆柱壳的衰减系数 Fig. 9 Attenuation coefficients for inner, outer, and DL cylindrical shells at different imperfect amplitudes |
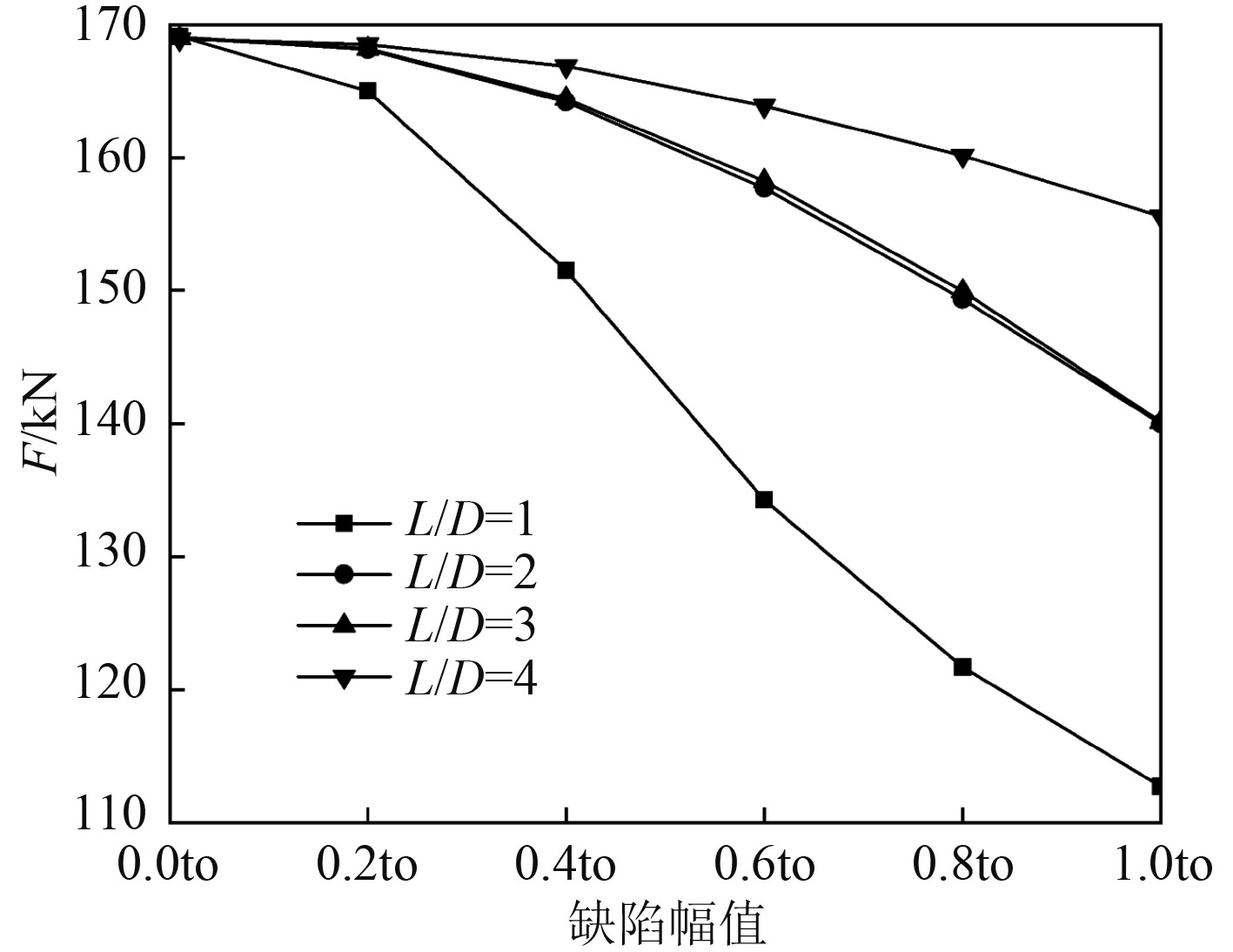
通过有限元法对理想模型进行非线性屈曲分析,计算不同长径比的双层圆柱壳在不同缺陷值下临界载荷F,理想模型的直径以及厚度参数与上文中研究双层圆柱壳缺陷敏感性的模型参数一致,长径比为1、2、3、4的双层圆柱壳所对应的长度分别为76 mm、152 mm、228 mm和304 mm,结果分别列于表6。
|
|
表 6 不同长径比的双层圆柱壳在不同缺陷值下的数值计算结果 Tab.6 Nonlinear buckling loads of DL cylindrical shells with different length-to-diameter ratios at different imperfect amplitudes |
由表6的数据绘制成图10的点线图,可看出双层圆柱壳的长径比越大,增加同样的缺陷幅值,双层圆柱壳的临界载荷下降越慢,于是可得出双层圆柱壳的缺陷敏感性随着长径比的增加而降低。
|
图 10 不同长径比的圆柱壳的临界载荷与缺陷值的关系 Fig. 10 Critical loads and imperfection amplitudes of DL cylindrical shells with different length-to-diameter ratios |
文献[12]通过给出不同的屈服强度
| $ \beta =\frac{{\sigma }_{yp}}{{\sigma }_{cr}}。$ | (3) |
其中,
| $ {\sigma }_{cr}=\frac{E}{\sqrt{3(1-{v}^{2})}}\times \frac{t}{R}。$ | (4) |
式中:E为弹性模量;t为厚度;v为泊松比;R为半径。
得到的经过弹塑性修正后的理想均匀轴压圆柱壳屈曲载荷
| $ {N}_{cr}={{N}_{cr}}^{plastic}=2{\text{π}} Rt\cdot{\sigma }_{yp},(\beta \leqslant 0.2)。$ | (5) |
其中,
从数值结果分析中得出的双层圆柱壳的临界载荷总是略微高于内层临界载荷的2倍,所以理想均匀轴压双层圆柱壳临界载荷
| $ {N}_{dcr}=2{\{{F}_{o},{F}_{i}\}}_{\min}。$ | (6) |
本文所研究的3个双层圆柱壳的外层、内层柱壳经计算得
| $ {{{N}_{cr}=N}_{cr}}^{plastic}=4{\left\{{R}_{o}{t}_{o}\text{,}{R}_{i}{t}_{i}\right\}}_{\min}\times {\text{π}} \times {\sigma }_{yp}。$ | (7) |
式中:
将6个试样的理论计算结果列于表7,并和试验结果进行对比。由表7可知,6个试样的理论值总是略高于试验值,单层圆柱壳S3试样的误差最大为
|
|
表 7 圆柱壳的数值与试验对比结果 Tab.7 Nonlinear buckling critical load of cylindrical shells versus the ultimate strength of the test |
本文通过采用轴压试验、数值分析和理论计算3种方法分析双层圆柱壳的轴向承载能力,双层圆柱壳采用2个材料相同的单层柱壳制作而成,并与单层的极限强度进行对比得到层状结构对其承载能力的影响。另外,采用数值分析法探究双层圆柱壳的缺陷敏感性。得出以下结论:
1)单层和双层不锈钢圆柱壳的测量结果表现出了其制作精度良好,具有较高的重复性。双层结构可较大提高圆柱壳在轴压下的承载能力,双层圆柱壳的试验平均极限强度大约是单层圆柱壳极限强度的1.85倍。在厚度相同的情况下,用有限元法获得的双层圆柱壳的非线性屈曲临界载荷为单层的0.912倍。
2)双层和单层圆柱壳都具有不稳定的后屈曲特性,由于柱壳两端会出现较大的环向力、端部的平整度存在不足和几何缺陷的影响,单、双层圆柱壳均在两端随机发生环状鼓起现象,数值模型用于验证试验的屈曲形状,结果显示试验和数值结果之间有良好的相关性。
3)对理想圆柱壳进行非线性屈曲分析,结果表明双层圆柱壳是缺陷敏感结构,双层圆柱壳的缺陷敏感性与内层壳体的缺陷敏感性趋于一致,且双层圆柱壳的缺陷敏感性随着长径比的增加而降低。通过对双层圆柱壳进行缺陷敏感性分析得到可理论预测出其临界载荷约为较弱那一层的临界载荷的2倍,试验结果、数值分析和理论预测具有较高一致性。
由于双层圆柱壳的每层厚径比相差很小,并且单独对双层圆柱壳的外(内)层壳体进行缺陷敏感性分析时,忽略了内(外)层壳体对它的影响,所以其准确性有待提高。今后将对内、外层壳体厚度不同的双层圆柱壳进行数值分析并通过试验验证。
| [1] |
MAGNUCKI K, JASION P, RODAK M. Strength and buckling of an untypical dished head of a cylindrical pressure vessel[J]. International Journal of Pressure Vessels and Piping, 2018, 161: 17-21. DOI:10.1016/j.ijpvp.2018.02.003 |
| [2] |
MAGNUCKI K, LEWINSKI J, CICHY R. Strength and buckling problems of dished heads of pressure vessels—contemporary look[J]. Journal of Pressure Vessel Technology, 2018, 140(4).
|
| [3] |
JIAO P, CHEN Z, TANG X, et al. Design of axially loaded isotropic cylindrical shells using multiple perturbation load approach–simulation and validation[J]. Thin-Walled Structures, 2018, 133: 1-16. DOI:10.1016/j.tws.2018.09.028 |
| [4] |
NEGRO V, LÓPEZ-GUTIÉRREZ J S, ESTEBAN M D, et al. Monopiles in offshore wind: Preliminary estimate of main dimensions[J]. Ocean Engineering, 2017, 133: 253-261. DOI:10.1016/j.oceaneng.2017.02.011 |
| [5] |
JIN, GUANG, TENG. Buckling of thin shells: recent advances and trends[J]. Applied Mechanics Reviews, 1996.
|
| [6] |
ZHAO C, NIU J, ZHANG Q, et al. Buckling behavior of a thin-walled cylinder shell with the cutout imperfections[J]. Mechanics of Advanced Materials and Structures, 2019, 26(18): 1536-1542. DOI:10.1080/15376494.2018.1444225 |
| [7] |
ULLAH H. Buckling of thin-walled cylindrical shells under axial compression[J]. International Journal for Numerical Methods in Engineering, 2009, 79(11): 1332-1353. DOI:10.1002/nme.2612 |
| [8] |
LI Z, PASTERNAK H, JAEGER-CANAS A. Buckling of ring-stiffened cylindrical shell under axial compression: Experiment and numerical simulation[J]. Thin-Walled Structures, 2021, 164: 107888. DOI:10.1016/j.tws.2021.107888 |
| [9] |
FAN H, LI L, GU W, et al. Buckling design of stiffened cylindrical shells under axial compression based on energy barrier approach[J]. Thin-Walled Structures, 2022, 179: 109667. DOI:10.1016/j.tws.2022.109667 |
| [10] |
ZHOU Y, TIAN K, XU S, et al. Two-scale buckling topology optimization for grid-stiffened cylindrical shells[J]. Thin-Walled Structures, 2020, 151: 106725. DOI:10.1016/j.tws.2020.106725 |
| [11] |
PATEL V I, LIANG Q Q, HADI M N S. Numerical analysis of circular double-skin concrete-filled stainless steel tubular short columns under axial loading[C]//Structures, Elsevier, 2020, 24: 754−765.
|
| [12] |
焦鹏. 局部轴压下薄壁圆柱壳结构的屈曲行为及设计方法研究[D]. 杭州: 浙江大学, 2021.
|
 2024, Vol. 46
2024, Vol. 46
