2. 中国空气动力研究与发展中心,四川 绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang 621000, China
航行体高速入水时,其表面局部低压区域的水流会发生汽化,进而与空气等其他气体形成空泡,称为空化现象。空化是一种独特的流固耦合现象,被广泛应用于水下武器减阻研究等领域[1]。
目前,国内外航行体入水大多数研究更多关注于复杂环境及复合结构对空泡特性的影响[2 − 8]。邹志辉等[9]开展了喷气协助航行体入水实验,探讨了不同喷气量、入水角度对空泡形态、射流长度等的影响。鱼怡澜等[10]开展了超空泡航行体入水的数值模拟,获得了航行体空泡演变、尺寸、载荷及压力变化规律。马庆鹏等[11]针对球体不同速度下的入水过程开展了实验研究,得到了球体入水空泡的发展演化过程,分析了入水速度与表面沾湿状态对球体入水空泡演化的影响。赵成功等[12]利用高速摄像技术开展了具有不同头型航行体的斜入水实验研究,发现了高速斜入水时航行体附着的空腔是对称的,不受重力影响。
综上所述,航行体入水空化演变过程中,空化阶段的演变机理及划分标准研究对航行体跨介质飞行研究有着重要作用,加之入水角度对空化阶段的演变机理影响较为复杂,目前针对该问题研究非常有限。因此本文以Mrying型航行体模型作为研究对象,基于Realizable k-ε湍流模型和VOF多相流模型,考虑自然空化作用,引入6 DOF算法以及动网格技术,对航行体不同俯仰角跨介质入水过程开展数值模拟研究,研究不同俯仰角下航行体入水的空化演变过程,分析空泡内流体分布的变化趋势,提出航行体在跨介质入水空化演变阶段的划分依据,揭示不同俯仰角对航行体入水后各空化阶段的影响,为空化演变机理研究提供准确的过程界定描述方法。
1 数值计算方法采用体积分数(VOF)多相流模型描述气、汽、液形成的多相流动,同时假设流体为不可压缩,忽略入水过程中由于流体粘性产生的热效应,基于N-S方程,其基本控制方程[10]如下:
1)质量守恒方程
| $ \frac{{up\partial {\rho _m}}}{{up\partial t}} + \frac{up\partial }{{up\partial {x_i}}}({\rho _m}{u_i}) = 0 。$ | (1) |
2)动量守恒方程
| $\begin{aligned} &\dfrac{up\partial }{{up\partial t}}({\rho _m}{u_i}) + \dfrac{up\partial }{{up\partial {x_j}}}({\rho _m}{u_i}{u_j}) = - \dfrac{{up\partial p}}{{up\partial {x_i}}} + \\ &\dfrac{up\partial }{{up\partial {x_i}}}\left[ {({\mu _m} + {\mu _t})\left( {\dfrac{{up\partial {u_i}}}{{up\partial {x_j}}} + \dfrac{{up\partial {u_j}}}{{up\partial {x_i}}}} \right)} \right]。\end{aligned}$ | (2) |
3)能量守恒方程
| $ \frac{up\partial }{{up\partial t}}\left( {{\rho _m}T} \right) + \frac{up\partial }{{up\partial {x_i}}}\left( {{\rho _m}{u_i}T} \right) = \frac{up\partial }{{up\partial {x_j}}}\left( {\frac{{{k_i}}}{{{c_p}}}\frac{{up\partial T}}{{up\partial {x_i}}}} \right) + {S_T}。$ | (3) |
采用Schnerr-Sauer[13]空化模型对空化问题求解,其中汽相体积分数满足以下方程:
| $\begin{split} & \frac{{up\partial {\alpha _v}}}{{up\partial t}} + \frac{{up\partial \left( {{\alpha _v}{u_i}} \right)}}{{up\partial {x_i}}} = {F_{vap}}\frac{{2{\alpha _{nuc}}\left( {1 - {\alpha _v}} \right){\rho _v}}}{{{R_B}}}\times \\ & \sqrt {\frac{2}{3}\frac{{{p_v} - p}}{{{\rho _1}}}} - {F_{cond}}\frac{{2{\alpha _v}{\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{p - {p_v}}}{{{\rho _1}}}} 。\end{split}$ | (4) |
采用Realizable k-ε 湍流模型,其方程形式[10]为:
| $\begin{aligned} & \frac{up\partial }{{up\partial t}}\left( {\rho k} \right) + \frac{up\partial }{{up\partial {x_j}}}\left( {\rho k{u_j}} \right) = \frac{up\partial }{{up\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{up\partial k}}{{up\partial {x_j}}}} \right] + {G_k} + \\ & {G_b} - \rho \varepsilon - {Y_M} + {S_k} 。\end{aligned}$ | (5) |
| $ \begin{split} & \frac{up\partial }{{up\partial t}}\left( {\rho \varepsilon } \right) + \frac{up\partial }{{up\partial {x_j}}}\left( {\rho \varepsilon {u_j}} \right) = \frac{up\partial }{{up\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{up\partial \varepsilon }}{{up\partial {x_j}}}} \right] + \\ & \rho {C_1}S\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} + {C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b} + {S_\varepsilon }。\\[-3pt] \end{split} $ | (6) |
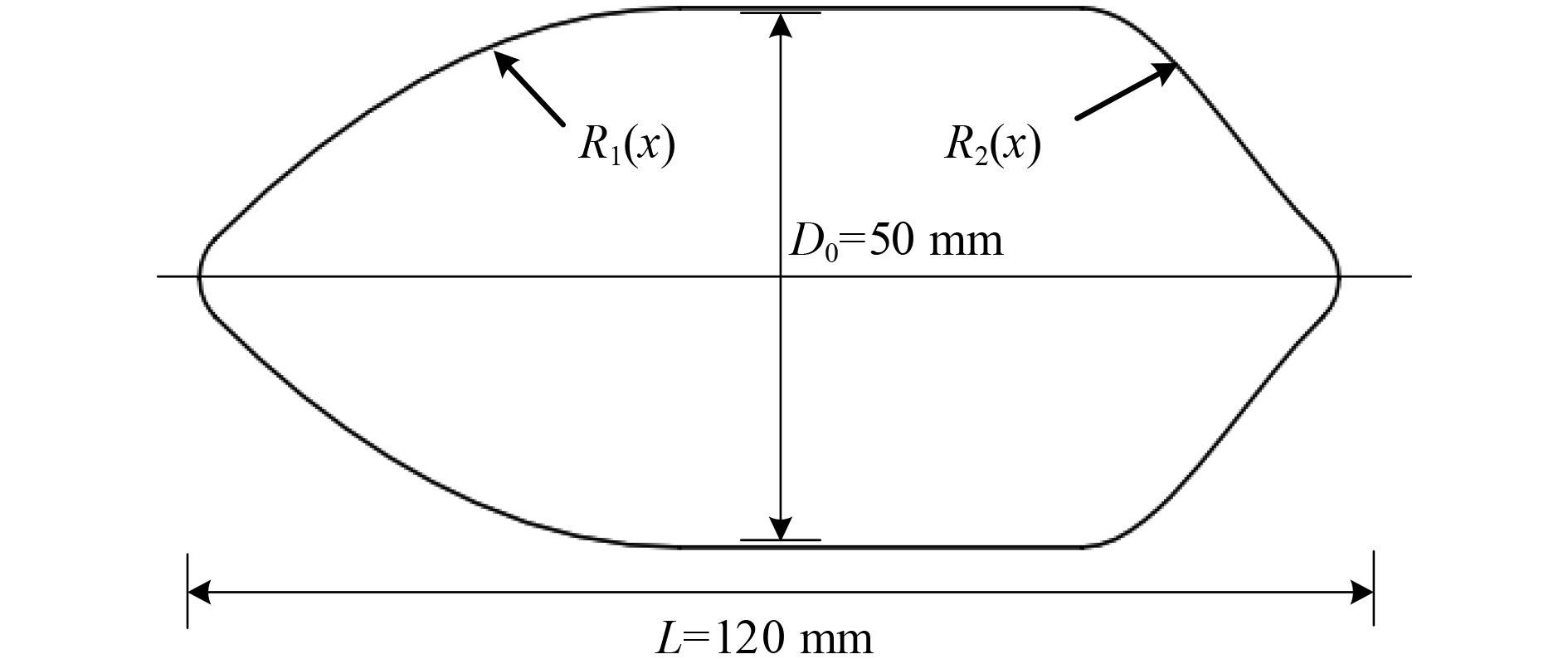
基于广泛应用的Mrying航行体模型AUV,设计航行体结构,其首尾两段的曲线方程分别为R1(x)、R2(x)[14]。其几何结构参数为:直径D0=50 mm,总体长度L=120 mm。航行体质量m=1.22 kg;材料采用316 L不锈钢,密度为ρ=7.89 g/cm3,如图1所示。
|
图 1 航行体结构示意图 Fig. 1 Schematic diagram of vehicle |
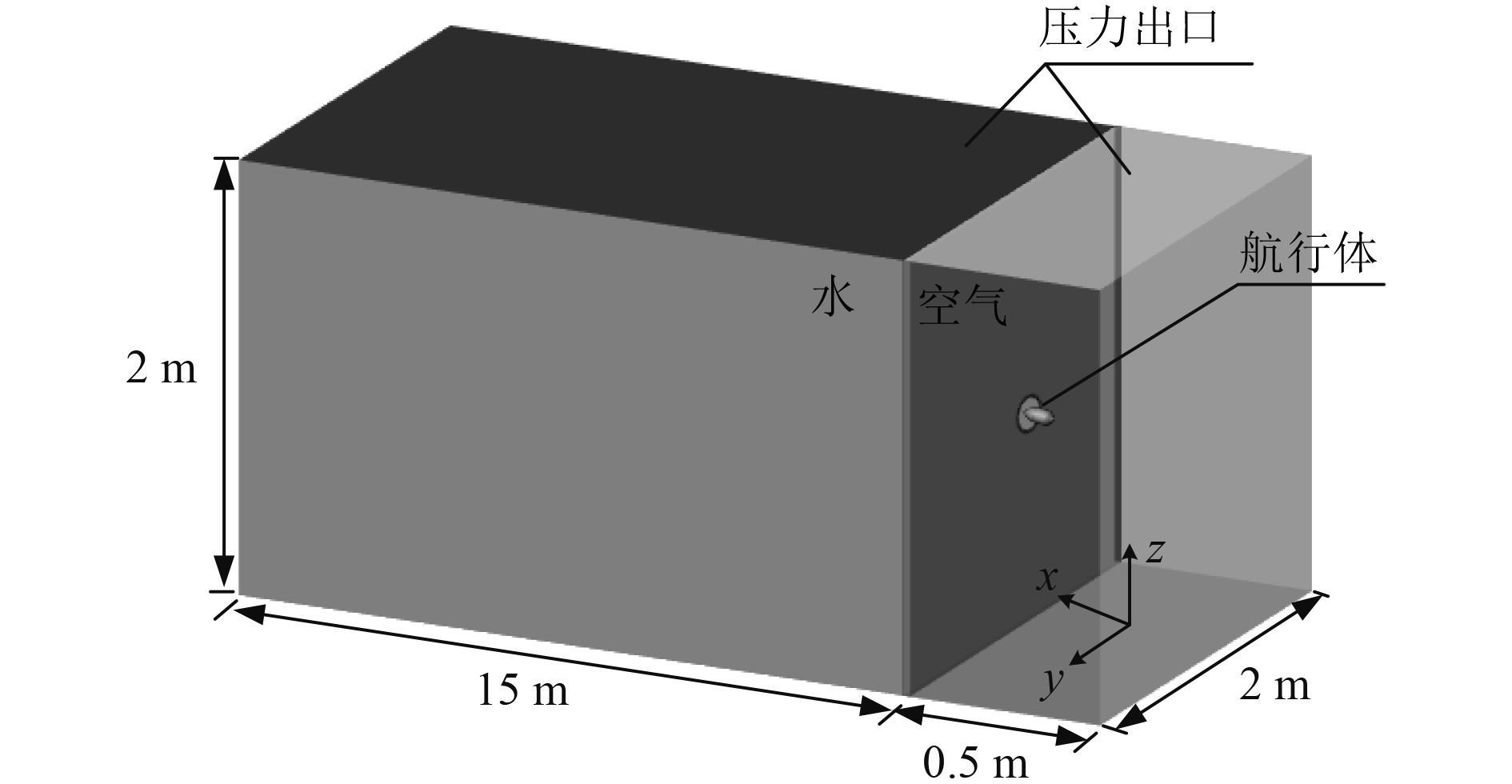
设计水域尺寸为2 m×2 m×15 m,空气域尺寸为0.5 m×2 m×2 m,采用挡板隔开两流域,计算模型不考虑其厚度。挡板中间设置直径为300 mm 圆孔作为航行体入水的入口,考虑到航行体高速通过入口的时长不超过0.5 ms,水域的水来不及流出,故不设置隔水薄膜。计算模型中,计算域的上方为压力出口与空气相连通,右侧为压力进口,其余设置为壁面,重力方向为负z方向,弹尖位置设为坐标原点,航行体距离入水口为0.1 m,计算域如图2所示。
|
图 2 计算域示意图 Fig. 2 Sketch of computational domain |
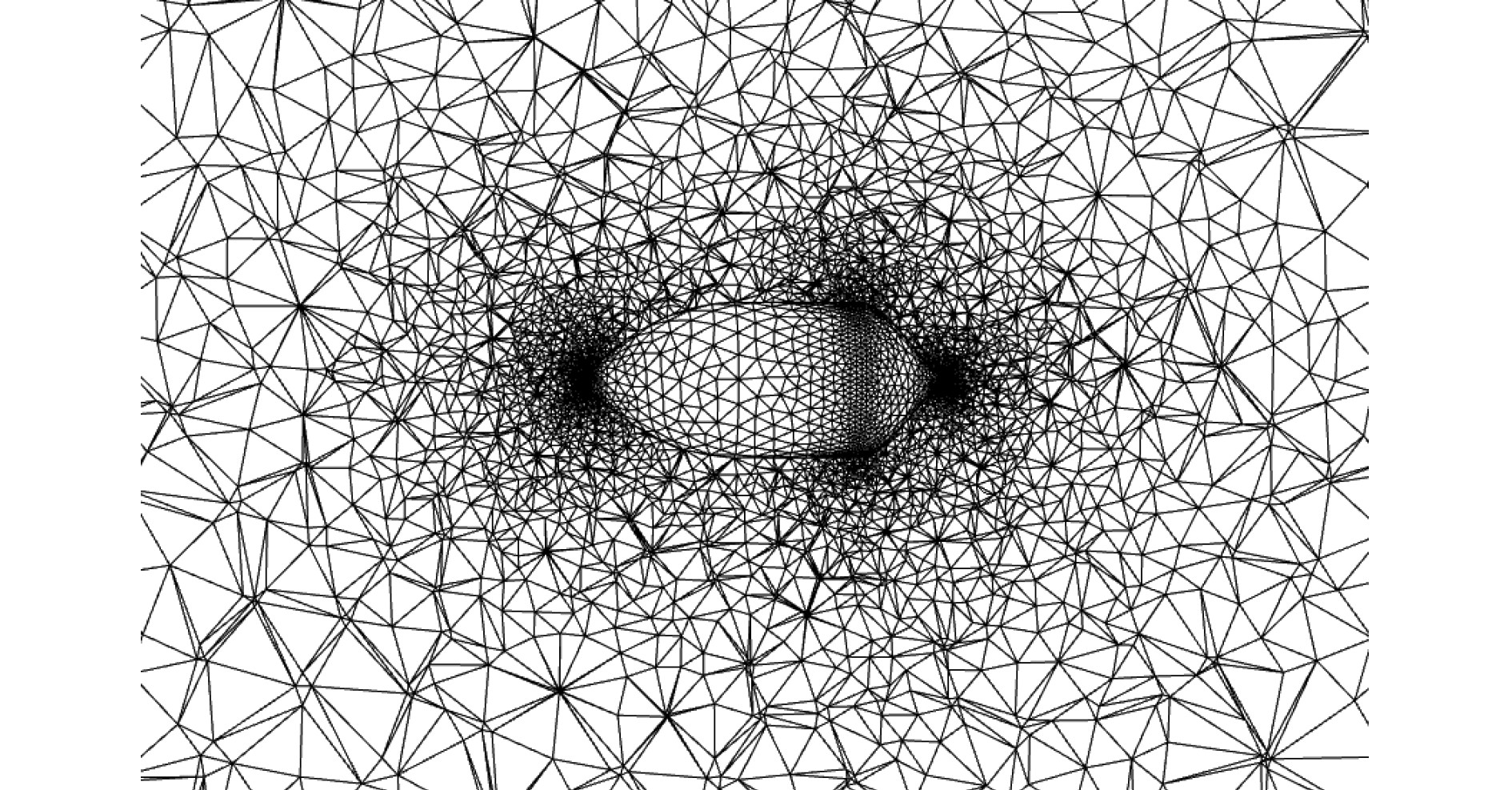
对整体计算域采用四面体非结构化网格,单元尺寸设为70 mm,为提高多相耦合流场的计算精度,加密航行体接触界面网格,尺寸为5 mm,网格单元共计715783,如图3所示。采用弹簧光顺法与局部重构法相结合的动网格技术,航行体接触界面的重构单元尺寸设为5 mm,再结合6 DOF算法对航行体模型的六自由度运动进行计算。
|
图 3 计算域网格划分示意图 Fig. 3 Sketch of computational domain for mesh |
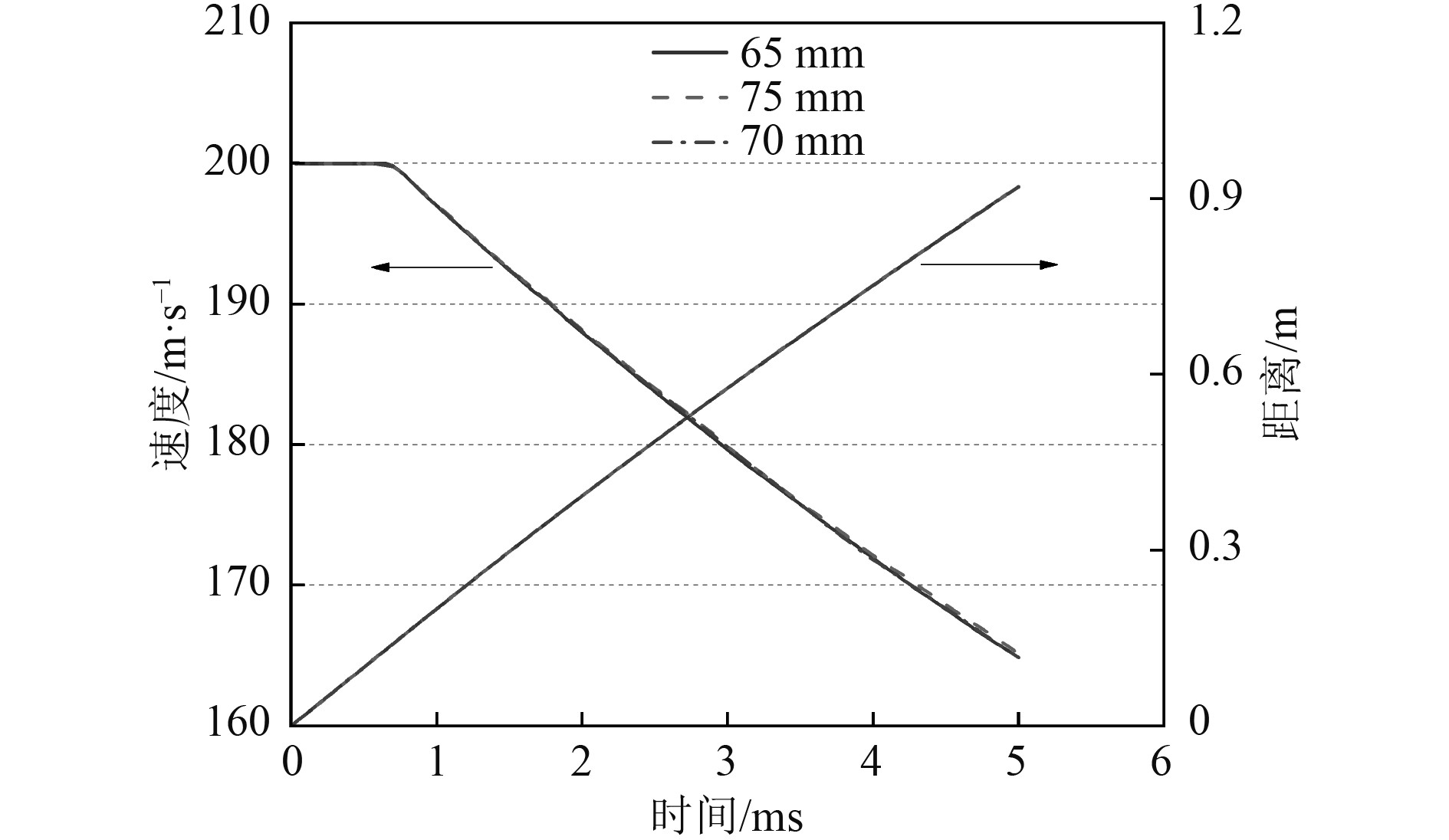
以v=200 m/s的速度入水进行网格尺寸无关性验证。网格单元尺寸分别为65、70、75 mm,网格总数量分别为861892、715783、575015,计算得到了不同网格尺寸下,航行体入水的速度及深度随时间的变化曲线,如图4所示。通过观察对比可得出,不同网格尺寸下,航行体入水的速度及深度随时间的变化基本一致,综合考虑计算效率后选择使用单元尺寸70 mm网格进行计算。
|
图 4 不同网格尺寸下航行体速度与航行距离随时间变化 Fig. 4 Variation of vehicle velocity and travel distance with time for different grid sizes |
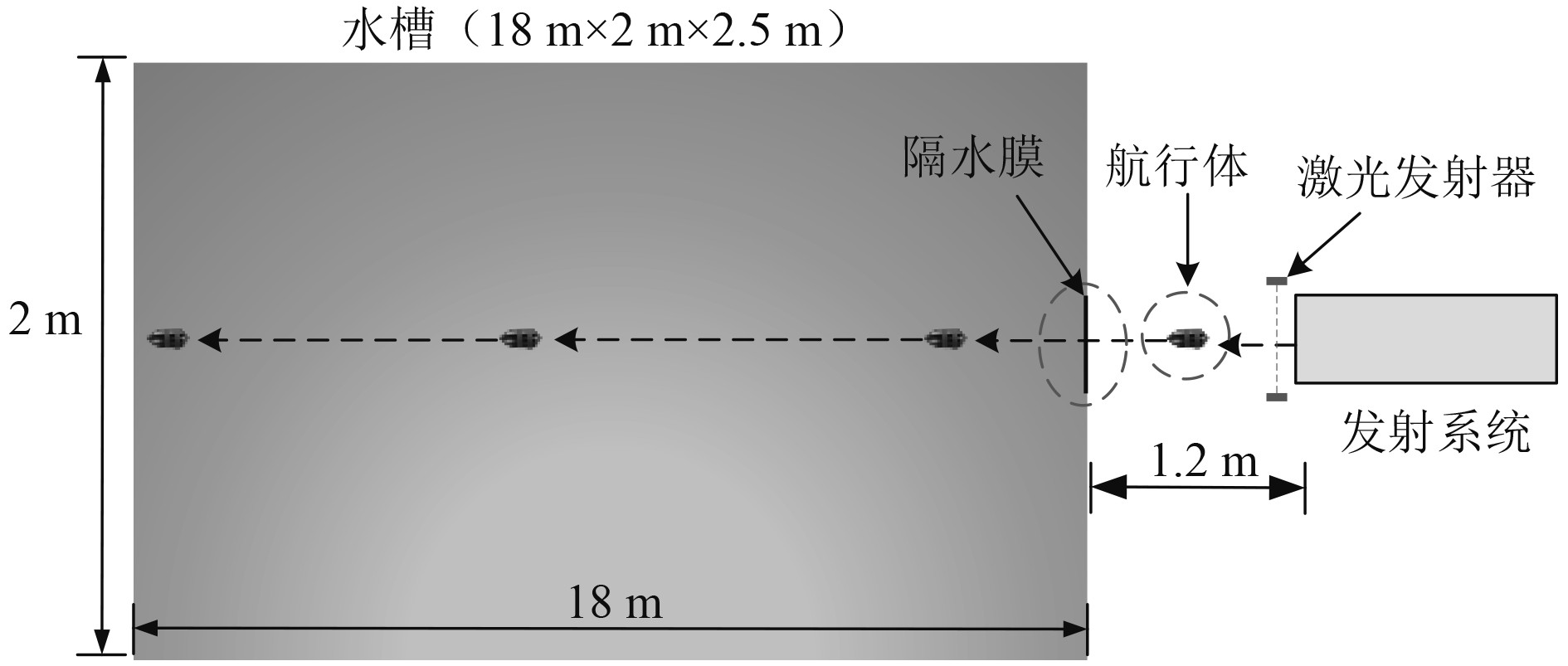
为了验证航行体跨介质入水数值算法的准确性,搭建航行体发射入水测试系统,结构原理如图5所示。采用一级气体压缩的方式弹射航行体,通过高速成像系统捕获入水过程。
|
图 5 航行体入水实验示意图 Fig. 5 Vehicle's water entry test |
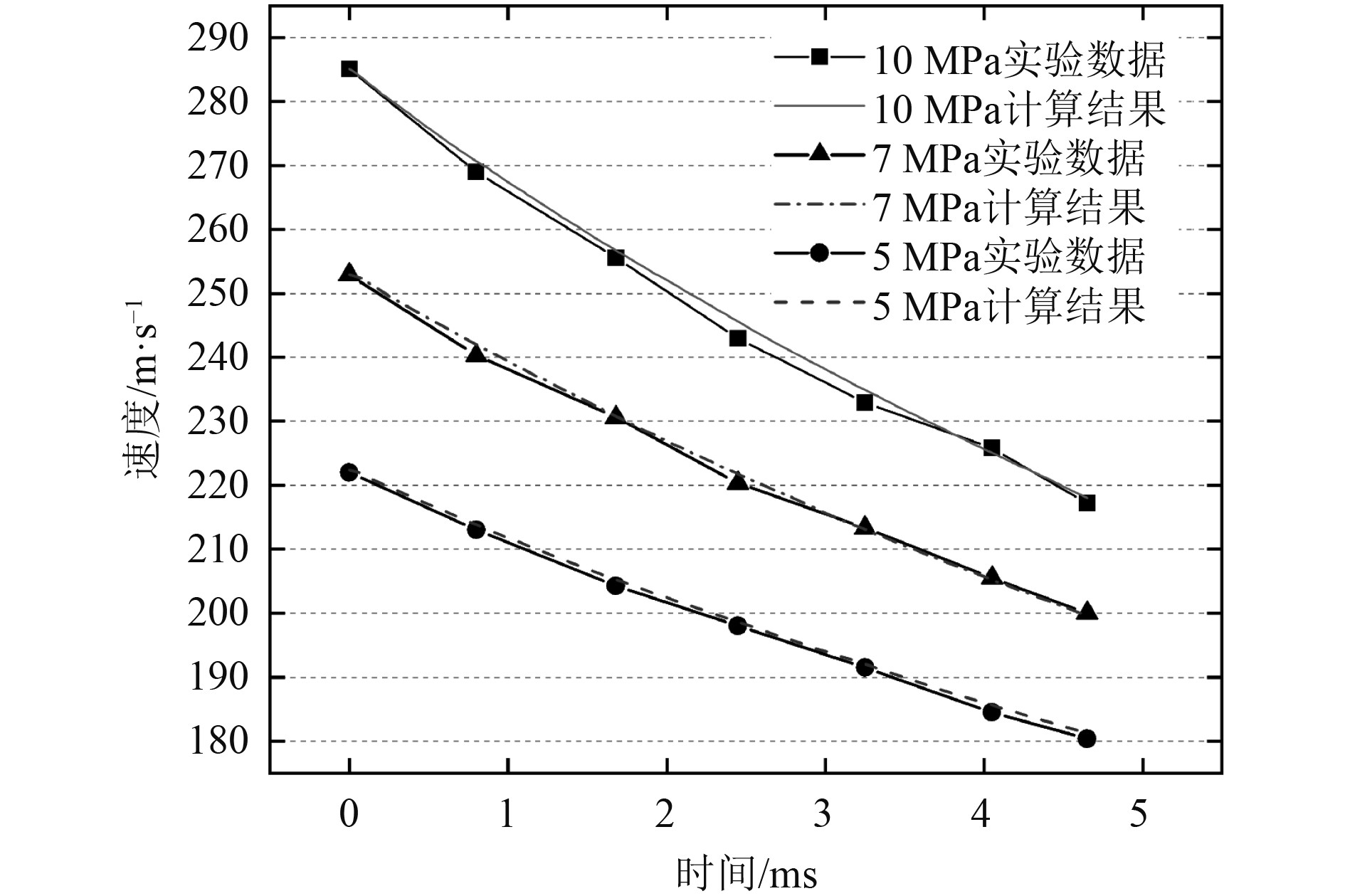
在此基础上对航行体分别以222、252和285 m/s的速度进行入水测试与数值模拟,在入水后0.66 m航程内以0.8 ms间隔的7个航段的平均速度,与仿真结果对比,如图6所示。
|
图 6 实验结果与仿真结果对比 Fig. 6 Comparison of simulated and experimental results |
相较于实验测试结果,仿真计算入水后在速度222、252和285 m/s的偏差均值分别为0.36%、0.52%、0.86%,仿真计算结果与实验测试结果高度吻合。因此,建立的航行体以不同俯仰角入水计算模型准确。
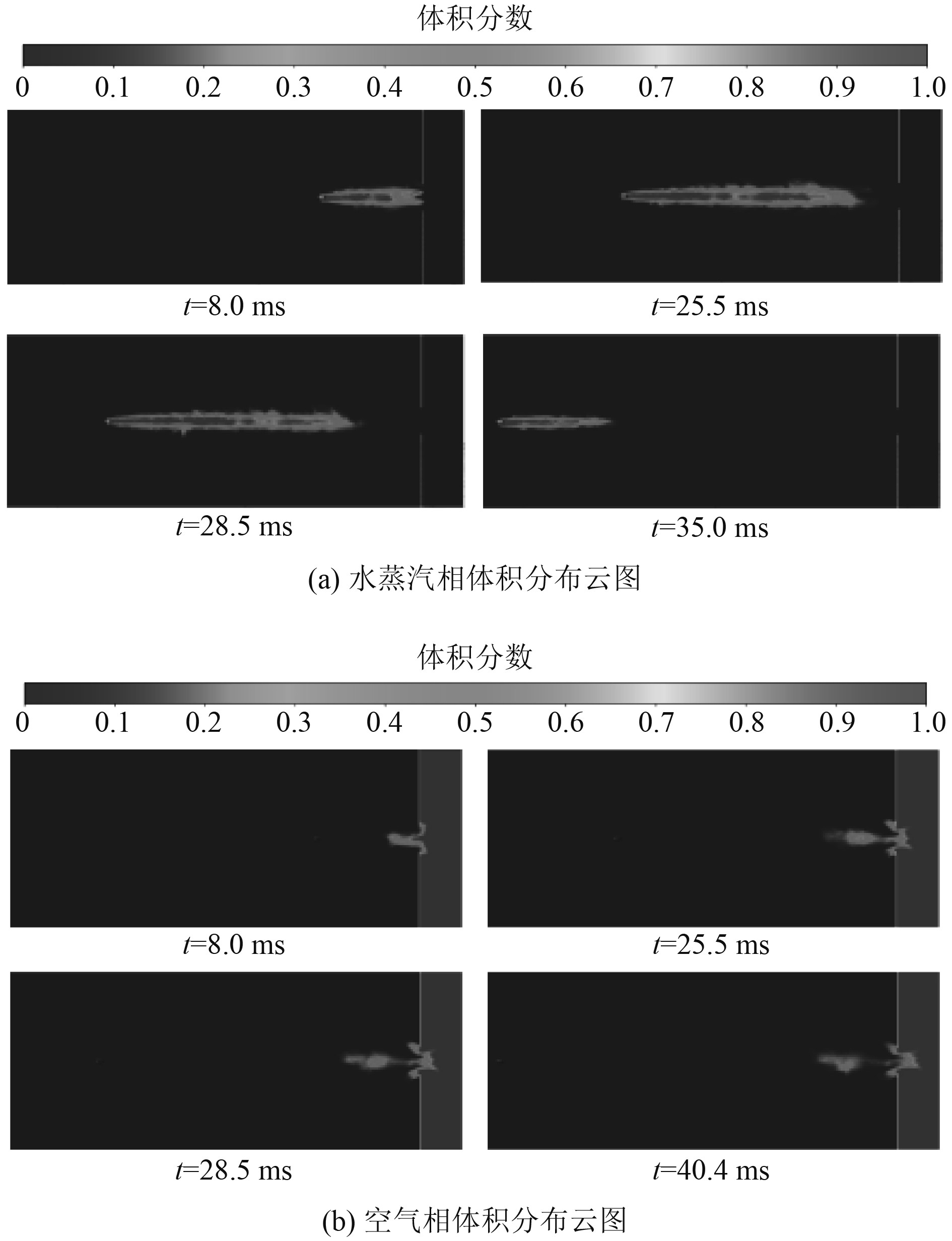
3 计算结果与分析讨论 3.1 空化过程演变机制在多相流耦合的影响下,水下航行体的空泡内流体分布在不断发生改变,在空泡流体随时间演变的作用下,空化过程表现出多种阶段变化。图7为Myring航行体模型在200 m/s速度下,以俯仰角φ=0°入水的水蒸汽、空气双相体积分布云图。
|
图 7 水蒸气、空气体积分布云图 Fig. 7 Contour of volume fractions of vapor and air |
在局部低压区域的影响下,航行体入水后立刻发生空化现象,并短时间内由局部空化发展为超空化状态。在空泡发展的过程中,空泡内水蒸汽体积持续增大并占据空泡的主体部分,水槽外的空气则涌入空泡尾部,与水蒸汽共同组成空泡。随后空泡完成了表面闭合及深度闭合,空泡内水蒸汽与空气发生分离,空泡内流体分布发生了显著变化。
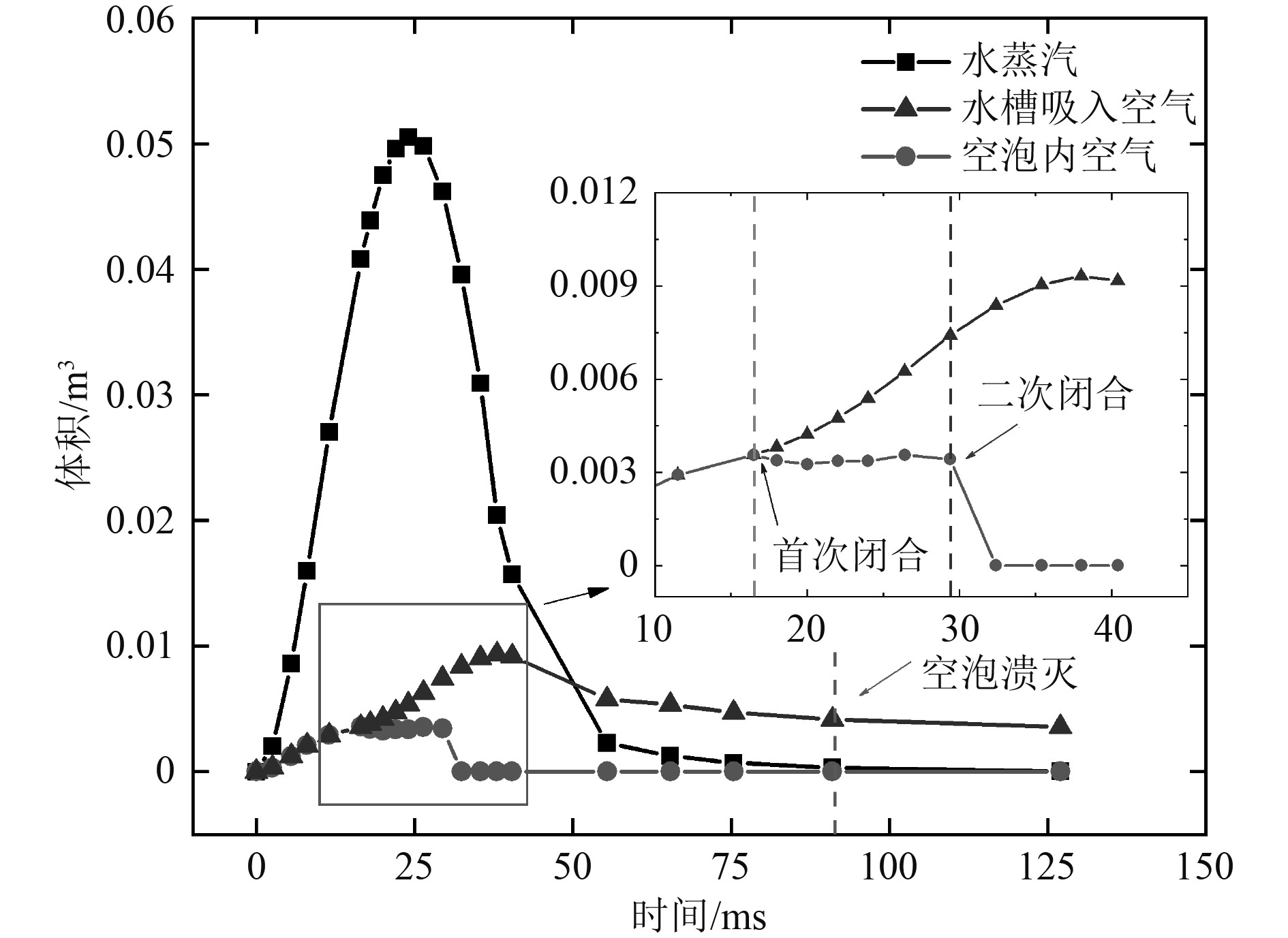
依据空泡内流体分布的变化可对空化过程进行演变阶段划分,对空泡内的水蒸汽、空气以及水槽内的空气进行量化分析,如图8所示。
|
图 8 水蒸汽、空气及水域吸入空气体积随时间变化 Fig. 8 Variation of volume of vapor,cavity air and inhaled air with time |
在空化演变过程中,由于航行体的速度不断减小,空泡内水蒸汽体积呈现先增后减的趋势,并在t=24 ms时达到峰值。依据水蒸汽的体积变化趋势,可将空化过程从整体上划分为空泡生长环节和空泡消散环节。空泡内空气体积呈现增加到饱和再到骤降的变化趋势,空泡内的空气与水槽内的空气在入水初期体积变化相同,但在t=16.5 ms时空泡完成表面闭合,二者在变化趋势上发生分离,空泡空气进入饱和阶段;在t=29.4 ms时,空泡完成深度闭合,空泡内水蒸汽与空气分离,空泡内流体仅剩水蒸汽。依据空泡内空气体积变化趋势,可将空化过程进一步划分为4个阶段:空泡表面闭合阶段、空泡饱和阶段、空泡深度闭合阶段、空泡溃灭阶段。
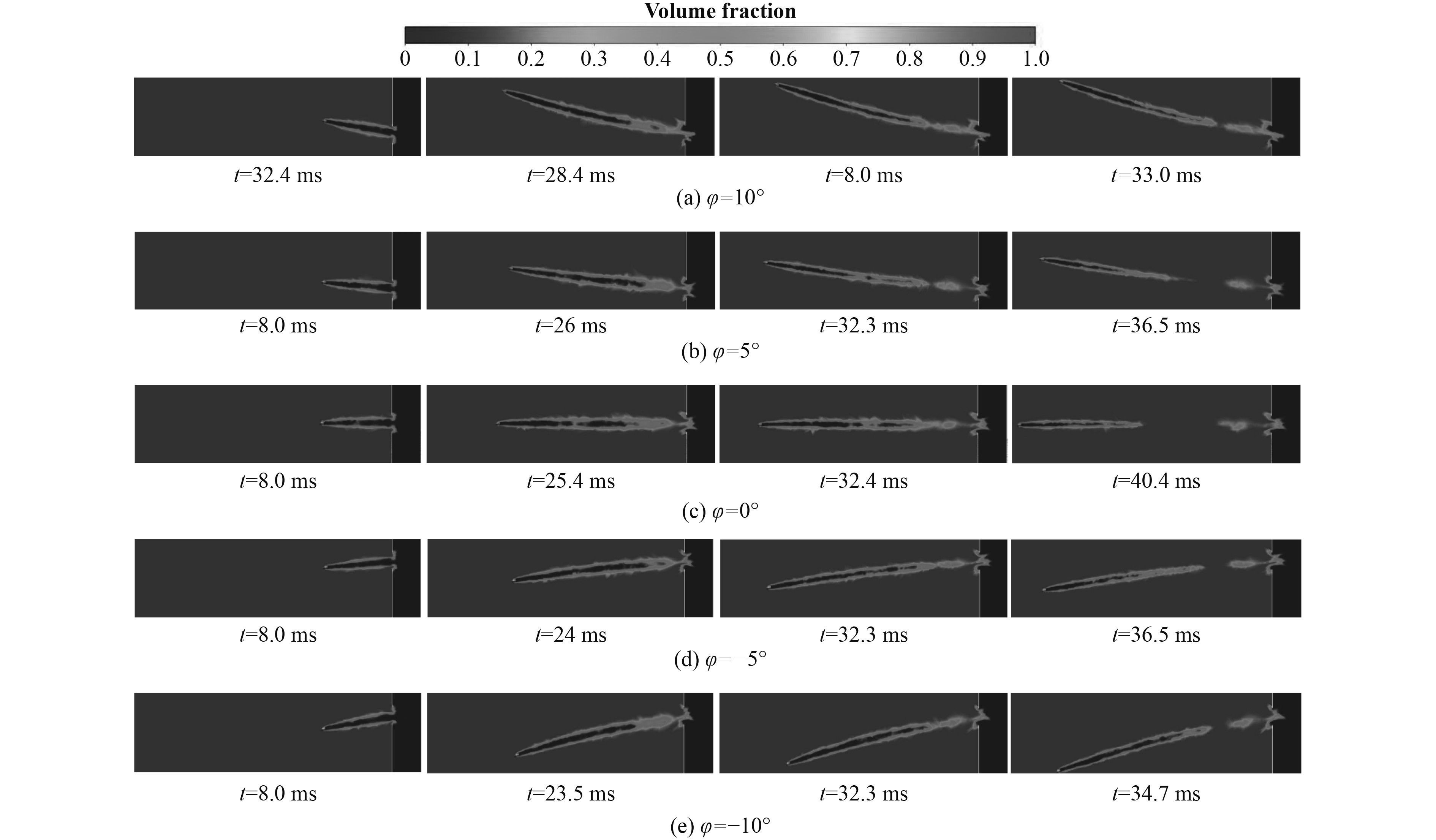
3.2 空化过程演变机制基于航行体以俯仰角φ=0°入水分析的基础上,开展俯仰角φ=–10°、φ=–5°、φ=0°、φ=+5°、φ=+10°入水角度下,空泡内流体分布特性研究,航行体在不同俯仰角下入水的水相体积分布,如图9所示。
|
图 9 不同俯仰角下航行体入水水相体积分布云图 Fig. 9 Contour of volume fractions of water at different angle of entry of the vehicle |
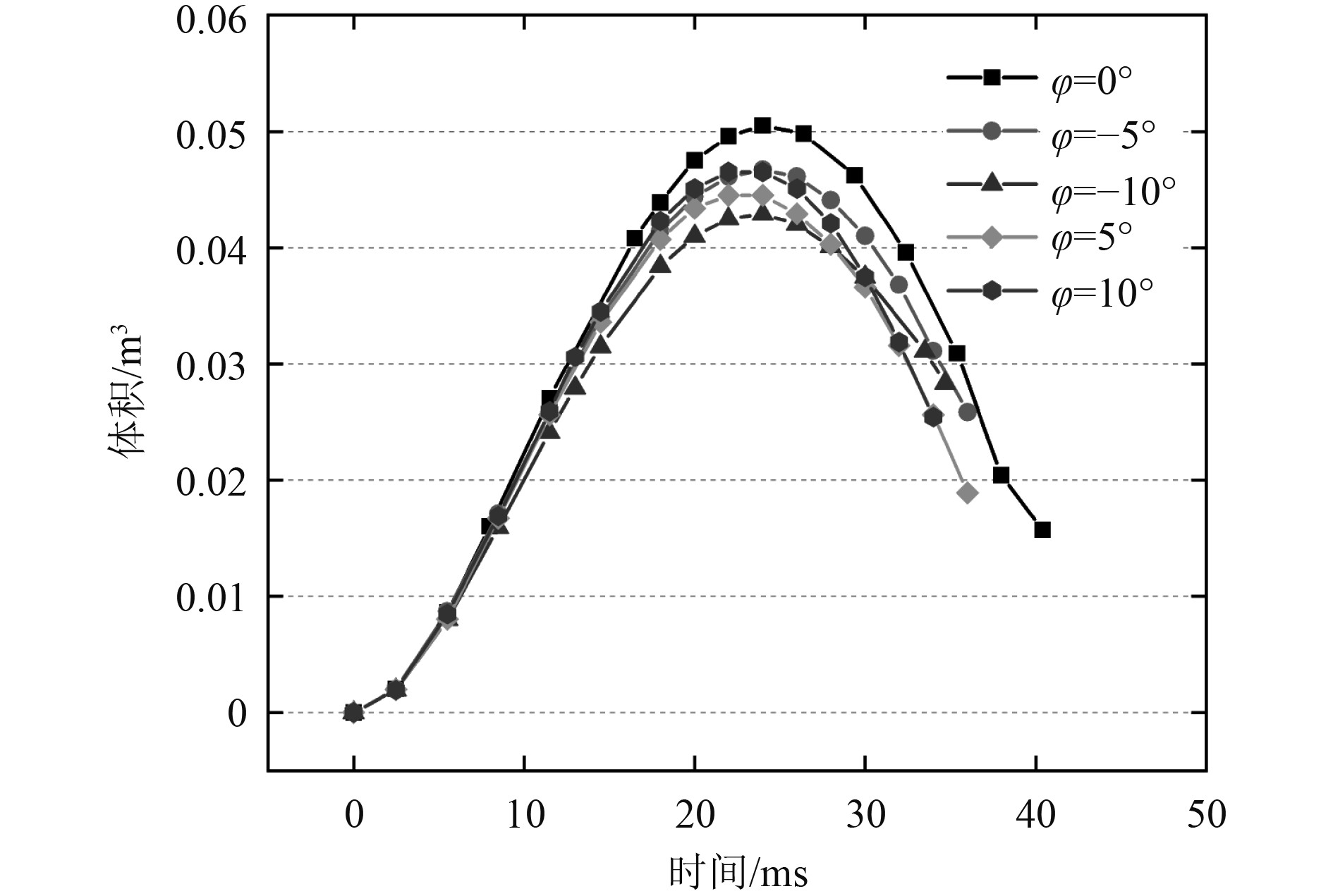
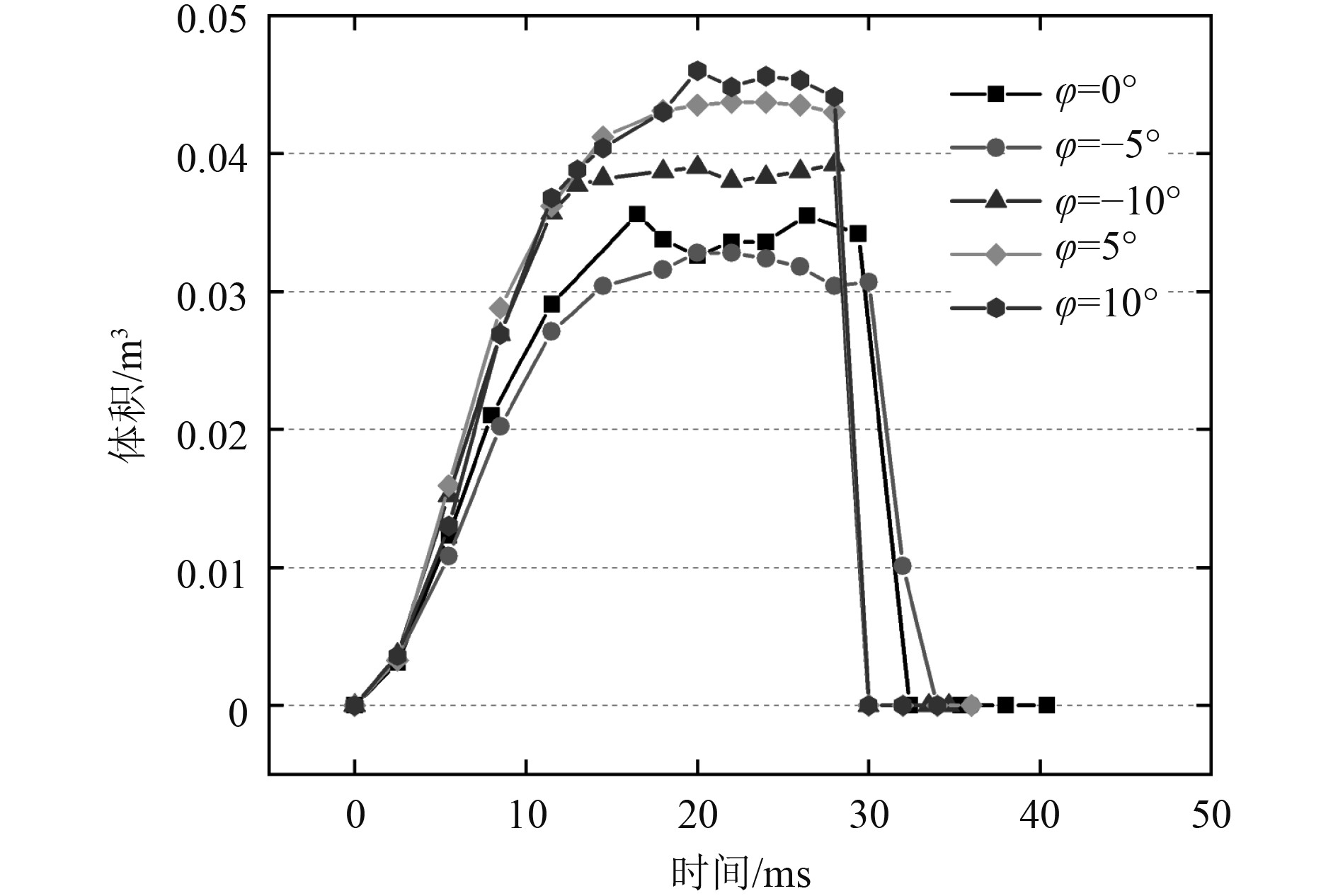
随着俯仰角度的增加,空泡外型的整体曲率不断增加,空化各阶段持续时间产生的差异显著,空泡内流体分布不断发展。随着入水角度由–10°~10°的不断增大,空泡表面闭合时间逐渐延长,空泡深度闭合时间变化微小;在–10°~–5°范围内,空泡溃灭速率更为缓慢。在俯仰角的影响下,航行体空泡表现出非定常发展特性,空泡内的流体分布产生明显变化,如图10和图11所示。
|
图 10 空泡内水蒸汽体积随时间变化 Fig. 10 Variation of volume of vapor inside the cavity with time |
|
图 11 空泡内空气体积随时间变化 Fig. 11 Variation of volume of air inside the cavity with time |
航行体在以俯角(即φ=−5°、−10°)入水的空化过程中,入水角度越大,空泡内的水蒸汽体积增长越慢,空泡生成速率越低,水蒸汽体积含量峰值越小。航行体在以仰角(即φ=5°、10°)入水的空化过程中,在0°~5°范围内,泡内水蒸汽体积峰值随入水角度的增大而减小,在5°~10°范围内相反。
航行体在以俯角入水的空化过程中,在0~5°范围内,空泡内空气饱和体积变化微小,在5°~10°范围内则随入水角的增大而增大。航行体在以仰角入水的空化过程中,空泡内空气体积随入水角度的增大而增大,各俯仰角入水下的具体数值对应如表1 所示。
|
|
表 1 空泡内流体体积参数表 Tab.1 Fluid volume parameters inside the cavity in the table |
表1 中的V1为空泡内水蒸汽饱和体积、V2为空气饱和体积、Vc为空泡最大体积、C为空气体积占比。
通过对不同俯仰角下空泡内流体体积参数的分析对比,发现当航行体入水存在俯仰角时,空泡最大体积会减小,泡内空气体积占比会增加。在–10°~10°范围内,空泡内空气体积占比范围为6%~9%,其中,0°时空泡体积最大,空泡内空气体积占比最小。
3.3 多角度空化阶段演变特性为探究入水俯仰角度对空化演变阶段的一般影响规律,对图10和图11数据处理后获得的无量纲时间[15]如表2所示。
|
|
表 2 无量纲时间数据表 Tab.2 Dimensionless time in the table |
表2中的t1为空泡表面闭合阶段、t2为空泡生长环节、t3为空泡深度闭合阶段、
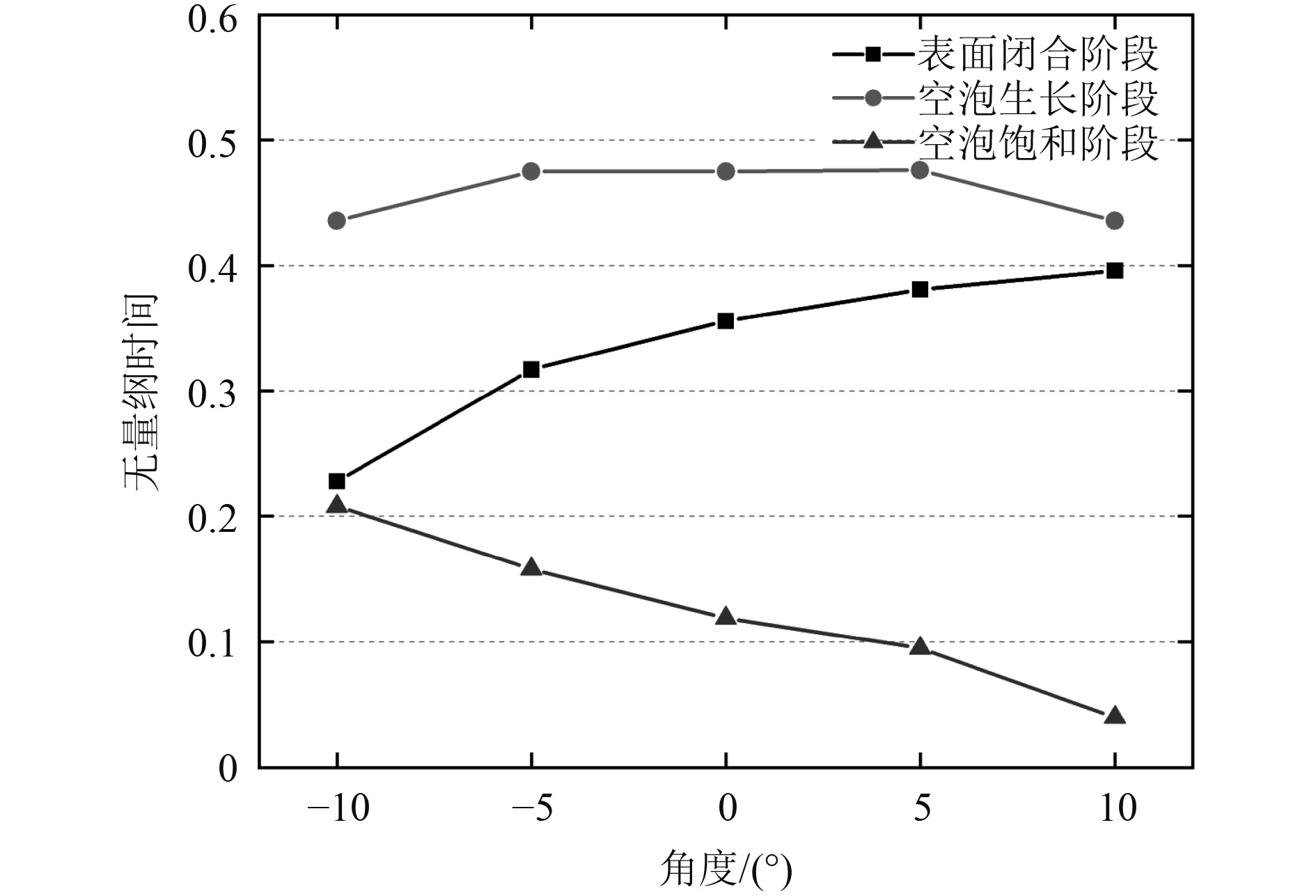
在空化演变的过程中,当航行体的入水角度在−5°~5°范围内时,空泡生长阶段的无量纲时间无明显变化,随着入水角度的进一步增加,空泡生长阶段的无量纲时间减小,整体曲线以0°为中心呈对称分布,如图12所示。此外,随着航行体入水角度由−10°向10°逐渐变化,空泡表面闭合无量纲时间呈对数趋势增长,空泡饱和阶段无量纲时间则近似线性递减。
|
图 12 空化阶段无量纲时间随角度变化 Fig. 12 Variation of dimensionless time of cavity with deg |
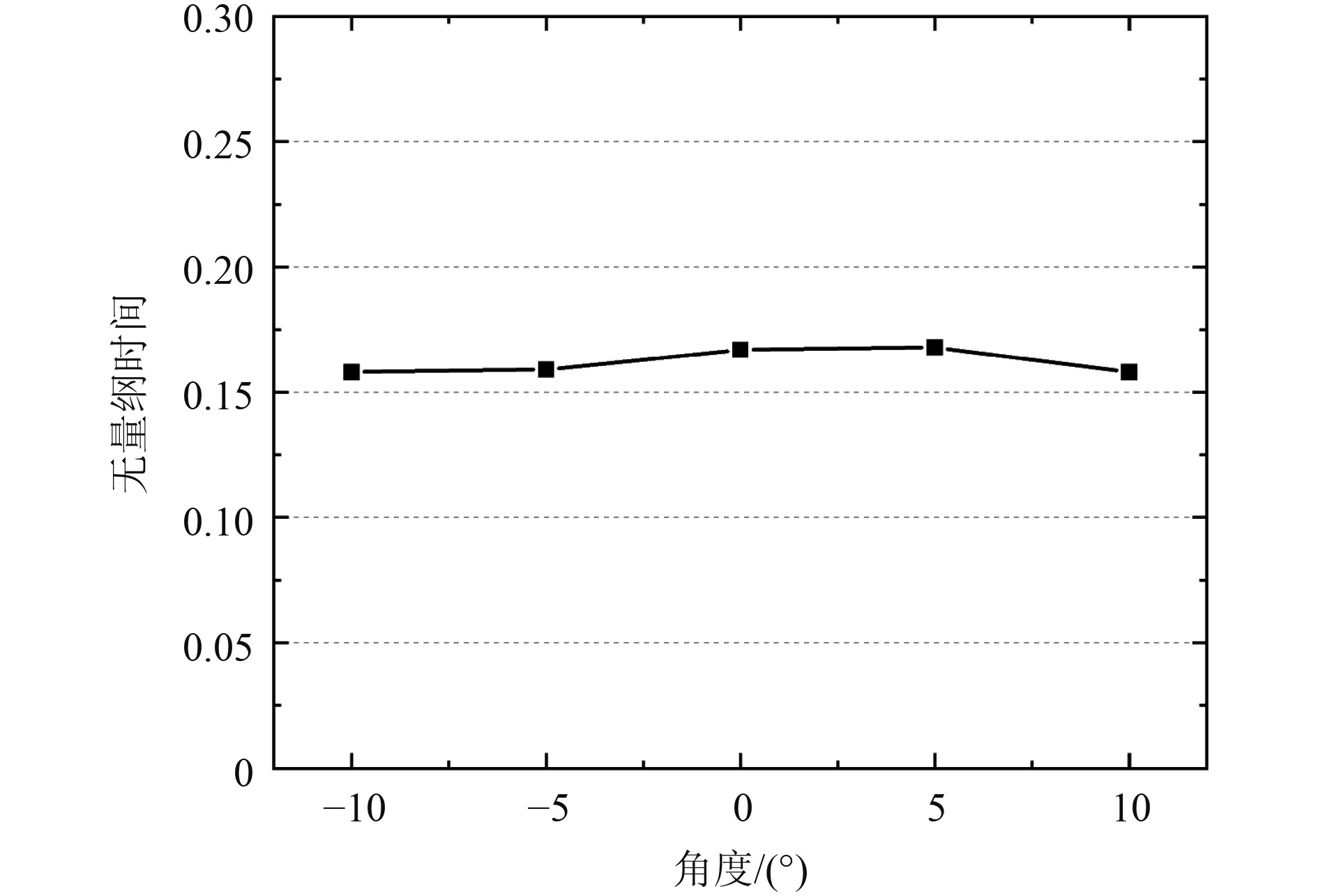
通过分析空泡深度闭合阶段无量纲时间随角度的变化趋势发现,随着航行体入水角度的增大,空泡深度闭合阶段无量纲时间基本不受入水俯仰角的影响,如图13所示。
|
图 13 空泡深度闭合阶段无量纲时间随角度变化 Fig. 13 Variation of dimensionless time of deep closure with deg |
本文基于Realizable
1)空化演变过程中,空泡内流体分布特性变化显著,依据水蒸汽体积变化规律可将空化过程划分为空泡生长环节和空泡消散环节;依据空泡内空气体积变化趋势,空泡演变过程可清晰界定为4个阶段,分别为空泡的表面闭合阶段、饱和阶段、深度闭合阶段和溃灭阶段。
2)在入水速度一定的情况下,随航行体入水俯仰角增大空泡生成速率降低、空泡内的水蒸汽体积增长率减小、水蒸汽体积含量峰值变小、空泡饱和阶段的空气体积变大,空泡内空气体积占比范围为6%~9%。
3)空泡表面闭合无量纲时间随入水俯仰角从–10°变化到10°呈对数趋势增长,空泡饱和无量纲时间近似线性递减,空泡生长环节无量纲时间和空泡深度闭合无量纲时间基本不受俯仰角变化影响,其中空泡生长环节的无量纲时间变化曲线以0°入水俯仰角为中心呈对称分布。
| [1] |
王浩宇, 李木易, 程少华, 等. 航行体高速入水问题研究综述[J]. 宇航总技术, 2021, 5(3): 65-70. WANG H Y, LI M Y, CHENG SH H, et al. Review of vehicle′s high-speed water entry[J]. Astronautical Systems Engineering Technology, 2021, 5(3): 65-70. |
| [2] |
BOTTOMLEY G H. The impact of a model seaplane floaton water [J]. Report s and Memoranda, 1919.
|
| [3] |
WATANABE S. Resistance of impact on water surface. Part V-sphere[J]. Scientific papers of the Institute of Physical and Chemical Research of Japan, 1934, 23(484): 202-208. |
| [4] |
WORTHINGTON A M, COLER S. Impact with a liquid surface, studied by the aid of instantaneous photography[J]. Philosophical Transactions of the Royal Society a Mathematical Physical and Engineering Sciences, 1900, 194(252-261): 175-199. |
| [5] |
董鹏, 崔自宪, 丁晓冬. 粗糙表面水下航行体阻力特性分析[J]. 舰船科学技术, 2022, 44(23): 1-5. DONG P, CUI Z X, DING X D. Resistance analysis of underwater vehicle with tough surface[J]. Ship Science and Technology, 2022, 44(23): 1-5. |
| [6] |
程栋, 卢丙举, 朱珠. 航行体出筒过程中弹翼横向偏移研究[J]. 舰船科学技术, 2022, 44(19): 178-183. LI CHENG D, LU B J, ZHU Z. Lateral displacement of wing on process launching submersible tactical vehicle[J]. Ship Science and Technology, 2022, 44(19): 178-183. |
| [7] |
谢超, 樊华, 周景军, 等. 超空泡航行体自导作用距离需求分析[J]. 舰船科学技术, 2022, 44(8): 79-83. XIE C, FAN H, ZHOU J J, et al. Analysis of necessary homing distance of supercavitating vehicle[J]. Ship Science and Technology, 2022, 44(8): 79-83. |
| [8] |
胡芳芳, 陈静, 涂卫民, 等. 围壳对水下航行体水动力系数的影响特性研究[J]. 舰船科学技术, 2022, 44(7): 31-36. HU F F, CHEN J, TU W M, et al. Numerical study on effect of sail on hydro-coefficient of the underwater vehicle[J]. Ship Science and Technology, 2022, 44(7): 31-36. |
| [9] |
邹志辉, 李佳, 杨茂, 等. 喷气协助航行体入水空泡流动特性实验研究[J]. 弹道学报, 2022, 34(1): 1-8+97. ZOU ZH H, LI J, YANG M, et al. Experimental investigation on cavity flow characteristics of water entry of vehicle with gas jet cavitator[J]. Journal of Ballistics, 2022, 34(1): 1-8+97. |
| [10] |
鱼怡澜, 施瑶, 潘光, 等. 超空泡航行体高速入水空泡与载荷特性数值分析[J]. 西北工业大学学报, 2022, 40(3): 584-591. YU Y L, SHI Y, PAN G, et al. Numerical analysis of cavitation and load characteristics of supercavitating vehicle entering water at high speed[J]. Journal of Northwestern Polytechnical University, 2022, 40(3): 584-591. DOI:10.1051/jnwpu/20224030584 |
| [11] |
马庆鹏, 何春涛, 王聪, 等. 球体垂直入水空泡实验研究[J]. 爆炸与冲击, 2014, 34(2): 174−180. MA Q P, HE CH T, WANG C, et al. Experimental investigation on vertical water-entry cavity of sphere[J]. Explosion and Shock Waves, 2014, 34(2): 174−180. |
| [12] |
ZHAO CH G, WANG C, WEI Y J, et al. Experimental study on oblique water entry of vehicles[J]. Modern Physics Letters B, 2016, 30(28): 1650348. DOI:10.1142/S0217984916503486 |
| [13] |
SCHNERR G H, SAUER J. Physical and numerical modeling of unsteady cavitation dynamics[C]//Fourth International Conference On Multiphase Flow, New Orleans, LO, USA: I CMF New Orleans, 2001.
|
| [14] |
李龙, 张宏伟, 王延辉. 无人自治水下航行器外形及推进系统优化设计[J]. 机械设计, 2017, 34(5): 23-29. LI L, ZHANG H W, WANG Y H. Autonomous underwater vehicle appearance and propulsion system optimization design[J]. Journal of Machine Design, 2017, 34(5): 23-29. |
| [15] |
胡明勇, 张志宏, 刘巨斌, 等. 低亚声速射弹垂直入水的流体与固体耦合数值计算研究[J]. 兵工学报, 2018, 39(3): 560-568. HU M Y, ZHANG ZH H, LIU J B, et al. Fluid-solid coupling numerical simulation on vertical water entry of vehicle at low subsonic speed[J]. Act a Armamentarii, 2018, 39(3): 560-568. DOI:10.3969/j.issn.1000-1093.2018.03.018 |
 2024, Vol. 46
2024, Vol. 46
