导管螺旋桨又称导管桨,是如今船舶行业中应用较广的特种推进器之一,与普通螺旋桨的不同之处在于其在螺旋桨的外围增加了具有流线型剖面的导管[1]。因为其在重载荷船舶应用中效果较好,受到了工业界和国内外学者的广泛关注和研究。
目前对于导管螺旋桨的研究主要分为物理模型试验和仿真数值模拟2种主要方法。Kort等[2]较早地提出了在螺旋桨的外侧添加导管以实现对螺旋桨的优化。Feiten等[3]通过开展物理模型试验对导管螺旋桨的研究。叶元培等[4]对于双体导管螺旋桨的水动力性能进行了物理试验研究。Kervin等[5]在导管和螺旋桨的相互干扰的研究中首次使用了迭代法。Khatib等[6]在研究了导管与螺旋桨之间水动力的干扰问题时采用了升力面理论。杨晨俊等[7]对导管和螺旋桨分别使用了面元法和涡格法研究导管螺旋桨在定常下的水动力性能。赵强等[8]使用Fluent 软件实现了对导管螺旋桨定常流场下的数值仿真计算。胡健等[9]使用Fluent软件对加速导管和减速导管的水动力性能进行了研究。邱鹏等[10 − 11]使用STAR−CCM+软件模拟计算了导管桨粘性流场下的水动力性能以及基于重叠网格条件导管螺旋桨在非定常流场下的水动力性能。吴家鸣等[12]使用STAR−CCM+软件讨论了MRF法、RBM法和OM 法等3种CFD方法对导管螺旋桨推力的影响。
本文采用物理模型试验和CFD数值模拟相结合的方式,基于MRF法,采用计算流体软件STAR−CCM+研究导管螺旋桨在定常情况下的水动力性能,验证方法的可行性并进行网格收敛性的验证和湍流适用性的验证,同时分析导管桨的相关水动力性能。
1 导管桨敞水试验 1.1 试验模型本次研究的螺旋桨模型为可调距的4叶桨,直径152 mm,旋向右旋。导管桨基本参数如表1所示,导管桨的设计图及导管剖面图如图1所示。
|
|
表 1 导管桨主要参数 Tab.1 Main particulars of ducted propeller |
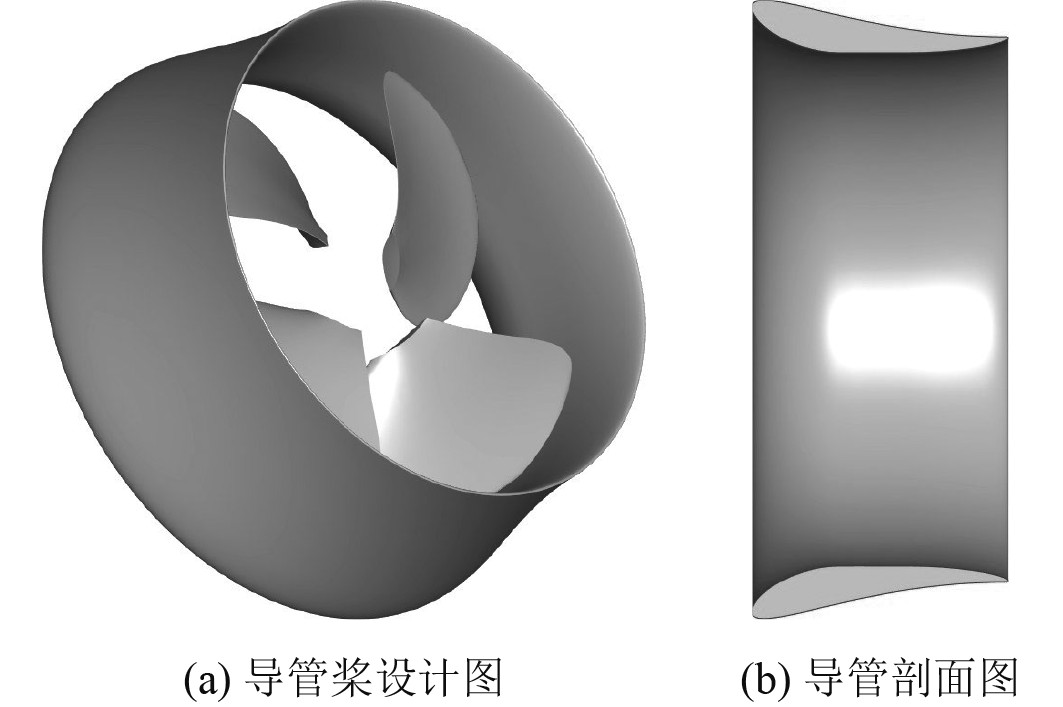
|
图 1 导管桨三维几何图 Fig. 1 The 3D model of ducted propeller |
试验对象的导管桨模型比尺为1∶21,为保证外形的精度和强度,导管和螺旋桨模型材料均为金属铝,采用数控加工,整体精度在0.05 mm,桨叶和导管的间隙为1 mm,符合规范要求。
1.2 试验设备导管桨模型敞水试验于大连理工大学船模拖曳水池进行,水池尺度为160.0 m ×7.0 m ×3.7 m(长×宽×水深),敞水试验使用H29-1敞水动力仪和R35-01单分量天平完成,并使用DH5922D数据采集仪以100Hz的采集频率进行信号采集。
1.3 试验过程导管桨敞水试验按照ITTC 建议程序 7.5-02-03-02.1[13] 进行,采用等转速法进行。试验前,测得拖曳水池水温为16.4 ℃,按照ITTC建议程序文件7.5-02-01-03查询出密度 ρ = 998.8802 kg/m3,运动粘性系数 ν =1.0979 × 10−6 m2/s。预先进行校验和标定,随后将敞水动力仪固定在水池的拖车上,将导管桨模型安装在敞水动力仪上,叶背向前,桨轴浸没于水下 300 mm处,满足大于 1.5D = 229 mm 的要求。
螺旋桨的雷诺数定义为:
| $ {{Re} _{0.7}} = \frac{{{C_{0.7}}\sqrt {V_A^2 + {{\left( {0.7\text{π} nD} \right)}^2}} }}{\nu } 。$ | (1) |
式中:C0.7为0.7R 处叶切面的弦长;VA为螺旋桨进速;n为螺旋桨旋转速度;D为螺旋桨直径;ν为水的运动粘性系数。当进速VA = 0,螺旋桨的雷诺数最低,试验时螺旋桨转速 n = 15 r/s 时,螺旋桨的雷诺数通过计算得到为3.1797 × 105。因此,选取 n = 15 r/s 可以保证雷诺数大于 ITTC 要求的临界值 3.0 ×105。
采用强迫自航法进行敞水试验,测得不同进速系数下的拖车速度VA、导管推力TD、螺旋桨推力Tp、扭矩Qt 等数据。
1.4 试验结果试验的螺旋桨进速VA取0~1.8 m/s,螺旋桨固定转速15 r/s ,通过试验测量得到导管桨的相关数据,根据相应公式可计算出相应值。
进速系数:
| $ J = \frac{{{V_A}}}{{nD}} ,$ | (2) |
导管推力系数:
| $ {K_{TD}}{\text{ = }}\frac{{{T_D}}}{{\rho {n^2}{D^4}}} ,$ | (3) |
螺旋桨推力系数:
| $ {K_{TP}}{\text{ = }}\frac{{{T_P}}}{{\rho {n^2}{D^4}}} ,$ | (4) |
导管桨总推力系数:
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}} = \frac{{{T_P} + {T_D}}}{{\rho {n^2}{D^4}}},$ | (5) |
导管桨的扭矩系数:
| $ {K_Q} = \frac{{\boldsymbol{Q}}}{{\rho {n^2}{D^4}}},$ | (6) |
导管桨的敞水效率:
| $ {\eta _0}{\text{ = }}\frac{J}{{2{\text{π}} }} \cdot \frac{{{K_T}}}{{{K_Q}}} 。$ | (7) |
其中:D为螺旋桨的直径;TP为螺旋桨推力;TD为导管推力;T为导管桨产生的总推力;Q为螺旋桨扭矩;VA表示螺旋桨的进速;n为螺旋桨转速;ρ为水的密度。将计算得到导管桨的敞水推力系数、扭矩系数以及敞水效率作图得到导管桨的敞水性征曲线,如图2所示。

|
图 2 导管桨敞水性征曲线 Fig. 2 Open water performance curve of ducted propeller |
采用CFD技术进行导管螺旋桨水动力性能的求解,用时均项和脉动项代替Navier-Stokes方程中的瞬时项,得到三维不可压缩流体RANS方程。
质量守恒方程:
| $ \frac{\partial {u}_{i}}{\partial {x}_{i}}=0\text{,}(i=1,2,3),$ | (8) |
动量守恒方程:
| $ \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial \rho }}{{\partial {x_i}}} + \mu \frac{\partial }{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {{u_i}^\prime {u_j}^\prime } } \right) 。$ | (9) |
式中:ui、uj 分别为i、j方向上的速度分量;ρ为密度;μ为动力粘度;
多参考系法(Multi Reference Frames, MRF)是多区域计算方法中一种稳定性好、易于收敛的稳态方法。参考系分为动参考系和静参考系。其中动参考系用于定义旋转组件的运动情况,而静参考系则用于定义相对旋转组件静止的模型的运动情况。在不同区域可以假设不同的旋转速度或者平移速度,将瞬态问题近似看成稳态进行。
由于多区域的存在,MRF方法需要对不同区域的物理量进行传递,保证整体流场是单值、协调、符合物理现实的。为了使两区域间的数据互通有无,更好地进行流场的信息传递,MRF法通过交界面Interface来实现。
对于导管螺旋桨来说,在导管螺旋桨工作时,导管固定不动,而螺旋桨旋转运动,可以将导管桨分为动和静2个计算区域。导管和螺旋桨之间虽然存在相对运动,但是导管是一个回转体,轴向均匀来流中不同位置的桨叶和导管之间的影响相同,可以把导管螺旋桨的分析当成定常问题处理。
3 导管桨的数值计算运用CFD 分析软件STAR−CCM+ 对导管桨模型的敞水性能和尾流特征等水动力性能进行数值仿真计算,并与试验所获得的数据进行对比,以验证方法的可行性和可靠性。为保证计算结果的说服性,计算模型的尺寸依然采用1∶21与试验模型保持一致。
3.1 计算模型与网格划分整个计算域分为包含桨叶和桨毂的旋转域以及包含导管和其余部分的静止域2个部分。计算域的坐标原点选取螺旋桨的中心,外流场静止域是一个直径为3D(D为螺旋桨直径),总长度为10D的圆柱,其入口距桨的中心为 3D,出口距桨的中心为 7D。内流场旋转域选择在导管内部,采用直径介于螺旋桨直径和导管内壁直径之间,长度为1.1D 的圆柱流域。旋转域和静止域均采用切割体网格形式,因导管和桨叶间隙非常小,为减少离散误差,且更好地模拟出导管螺旋桨的实际运动,对螺旋桨的随边和导边进行局部加密,对导管和叶梢间隙等复杂的区域也进行网格加密。整个计算域的示意图如图3所示,导管螺旋桨的部分网格如图4和图5所示。
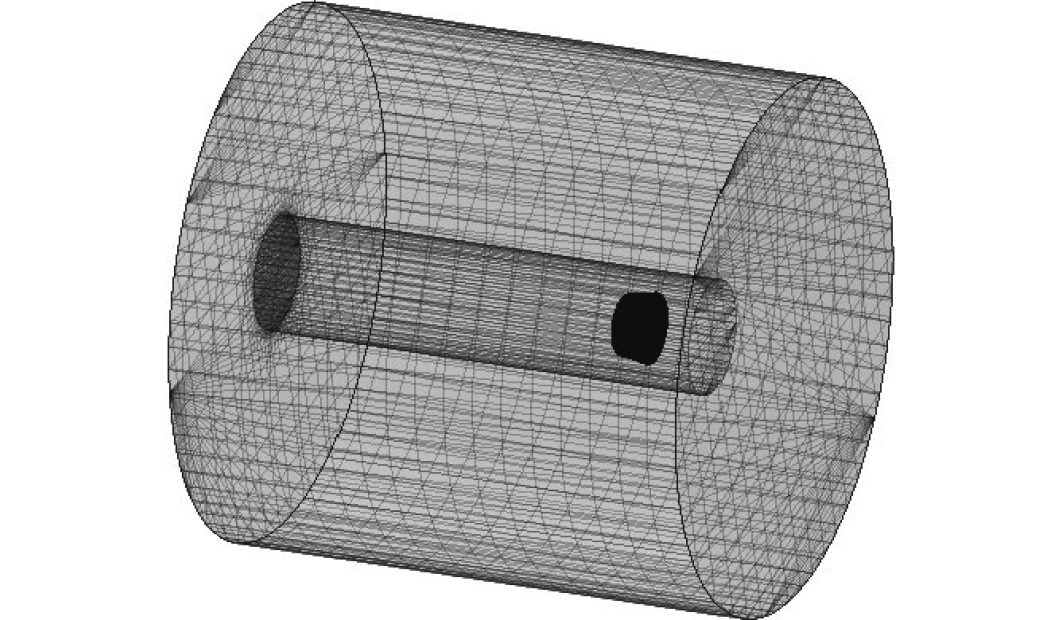
|
图 3 计算域示意图 Fig. 3 Schematic diagram of the computational domain |

|
图 4 导管螺旋桨表面网格 Fig. 4 Schematic diagram of the ducted propeller |
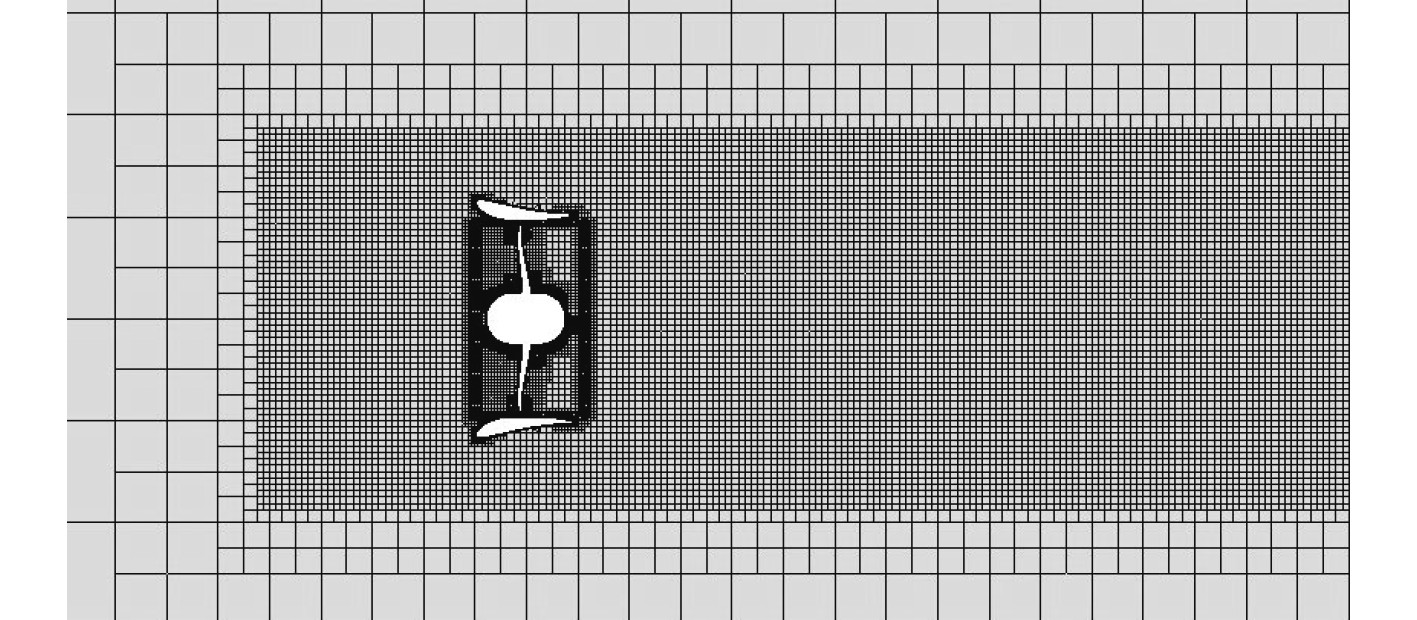
|
图 5 轴向纵剖面网格 Fig. 5 Vertical section grid diagram |
因为进速系数J = 0.525时导管螺旋桨模型试验的敞水效率为最高值,所以选取进速系数为0.525时进行分析,分别对此进速系数下不同网格数的推力系数KT,扭矩系数10KQ及敞水效率η0,进行对比分析,结果如表2所示。通过结果分析可以发现,在一定网格数目范围内,各项参数的计算结果总体误差都满足工程计算要求。当模型划分为粗网格时,此时网格数约为100万,由于网格尺度较大,对于导管附近的流场信息不易捕捉,使得导管螺旋桨的水动力性能较试验值误差较大;当模型划分为中等网格时,此时网格数约为240万,流场中的信息可以较为准确的进行捕捉,但是不够精确;当网格划分为细网格时,此时网格数约为560万,由于网格尺度合适,流场信息可以进行有效的传递,使得导管螺旋桨的水动力性能可以进行较为有效的模拟;当网格划分为极细网格时,此时网格数约为970万,由于网格尺度太小,对边界层、湍流及实际流场信息的模拟都不准确,使得导管螺旋桨的水动力性能的模拟结果误差较细网格时增大。经过综合考虑,取网格基本尺寸d = 0.067D = 10 mm,总体网格数量约为560万。
|
|
表 2 J = 0.525时不同网格数模拟结果对比 Tab.2 Comparison of the numerical results with different grid numbers as J = 0.525 |
计算域的入口以及流场区域的圆柱表面设置为速度进口,计算域的出口设置为压力出口,导管表面及螺旋桨表面设置为无滑移的壁面条件。螺旋桨的旋转域采用MRF法,旋转域绕X 轴旋转,旋转速度采用螺旋桨的旋转速度,在静止域和旋转域之间设置交界面,进行流场的信息传递,具体的设置如表3所示。
|
|
表 3 数值模型及求解器参数 Tab.3 Numerical model and the solver parameters |
本文还使用了在导管螺旋桨的CFD分析中常使用的Realizable k-ε湍流模型进行了模拟,以进速系数J = 0.525 时为例,将使用Realizable k-ε湍流模型的模拟结果与使用SST k-ω 湍流模型的模拟结果进行比较,结果如表4所示。由对比结果可以看出,使用SST k-ω 湍流模型的模拟结果和使用Realizable k-ε湍流模型的模拟结果的精度均在可接受的范围内,但SST k-ω 湍流模型相对来说更适用于此导管螺旋桨的模拟计算。
|
|
表 4 J = 0.525时不同湍流模型模拟结果对比 Tab.4 Comparison of the numerical results with different turbulent models as J = 0.525 |
为了进一步研究所采用的网格数与湍流模型的适应性是否良好,选取进速系数J = 0.525时的Y+ 值分布图,如图6所示。根据Y+ 值分布可以看出:螺旋桨整体区域的Y+ 值主要分布在0.2~0.6之间;导管的Y+值主要分布在0~0.12之间;导管螺旋桨整体的Y+ 值分布在0~0.6之间。本文选取湍流模型为SST k-ω,通常要求Y+ 值在0~1之间,所以所采用的网格划分得到的Y+值满足选取的湍流模型适应性的规定。因此,采用网格数目为560万网格,湍流模型为SST k-ω的方案进行导管桨敞水性能模拟的研究。
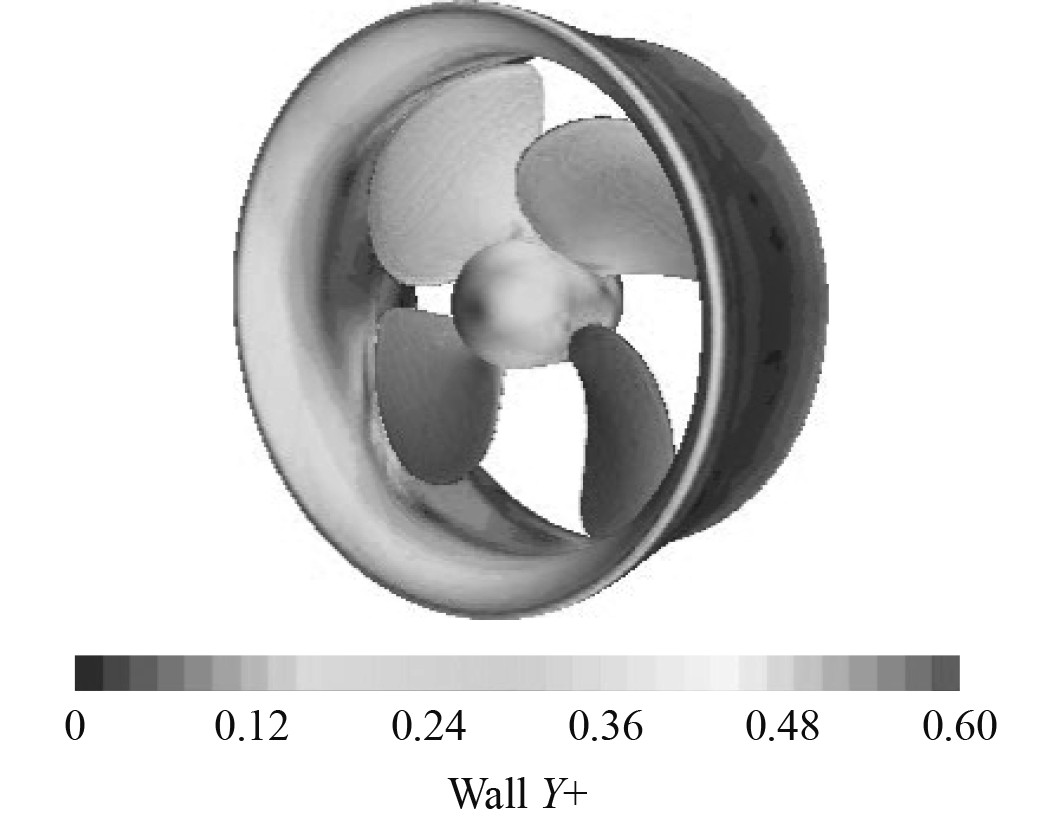
|
图 6 J = 0.525时导管螺旋桨Y+值分布 Fig. 6 Distribution of the ducted propeller Y+ as J = 0.525 |
使用数值方法对导管螺旋桨的敞水性能进行数值计算,图7 为不同进速系数下导管螺旋桨的敞水性能。其中,进速系数J、导管的推力系数KTD、螺旋桨的推力系数KTP、导管螺旋桨的总推力系数KT 、导管螺旋桨的扭矩系数KQ、导管螺旋桨的敞水效率η0的定义与式(2)~式(7)一致。将数值计算所得的结果与试验数据进行对比分析,得到推力系数KT、扭矩系数10KQ和敞水效率 η0的误差分析如表5~表7所示,计算值与试验值的拟合对比见图7。
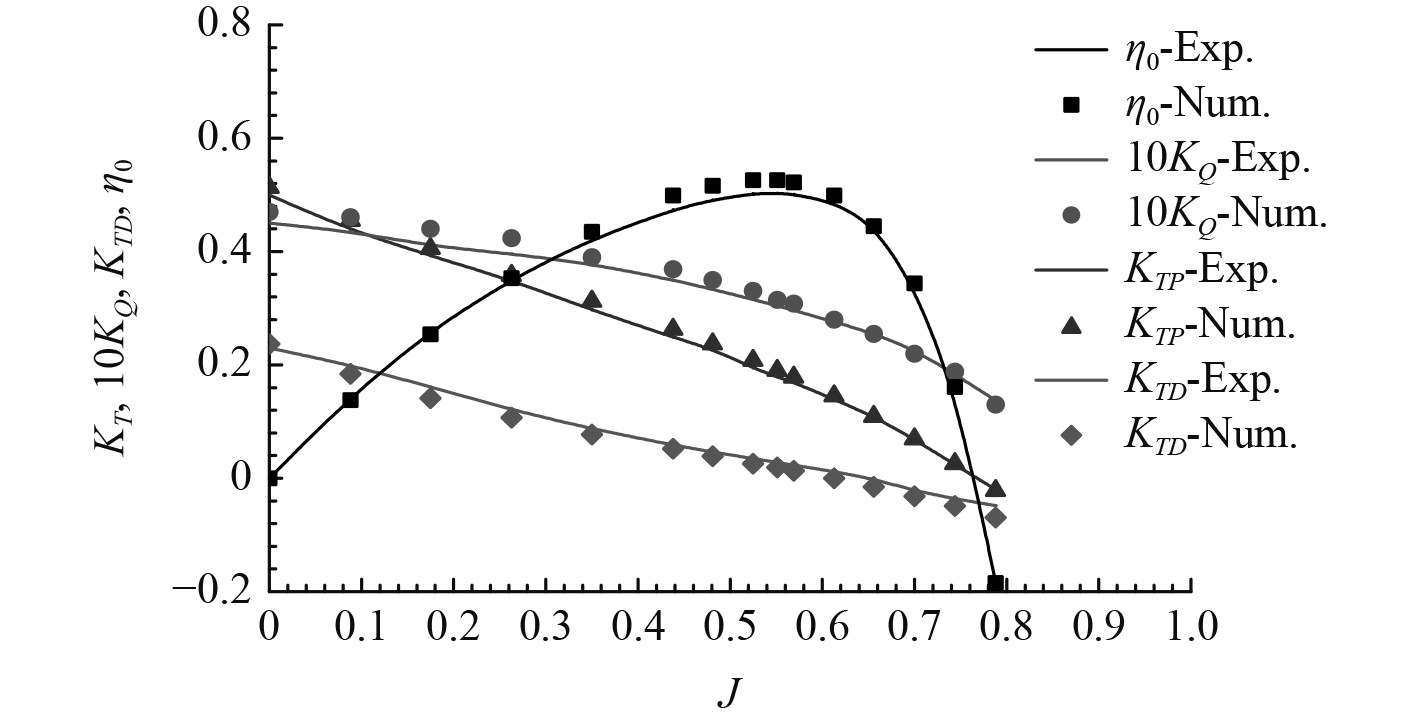
|
图 7 导管桨敞水性征的计算值与试验值比较 Fig. 7 Comparison of numerical and test results of the ducted propeller′s open water performance |
由图7及表5~表7的相关数据可以看出,导管螺旋桨的敞水效率η0、扭矩系数KQ、总推力系数KT以及导管推力系数KTD的CFD模拟结果与试验结果变化趋势基本一致。导管螺旋桨的总推力和扭矩普遍低于试验值,其中推力系数的平均误差在6 % 左右,扭矩系数的平均误差在4% 左右,敞水效率的平均误差在3%左右。分析误差的主要原因是软件本身的计算精度、以及网格划分质量的好坏都对计算结果的准确性有很大影响。但总的来说,计算值与试验值的吻合较好。因此,采用CFD 技术,借助STAR−CCM+ 软件进行导管桨的敞水性征的预报,其计算结果满足精度要求,在一定程度上满足工程实际应用的需求。
|
|
表 5 推力系数 KT误差分析 Tab.5 The error analysis of KT |
|
|
表 7 敞水效率η0误差分析 Tab.7 The error analysis of η0 |
|
|
表 6 扭矩系数 10KQ误差分析 Tab.6 The error analysis of 10KQ |
图8和图9分别为J = 0.525、来流速度1.2 m/s、螺旋桨转速15 r/s时的导管螺旋桨叶面与叶背方向上导管与螺旋桨的压力云图和导管螺旋桨纵剖面速度云图。
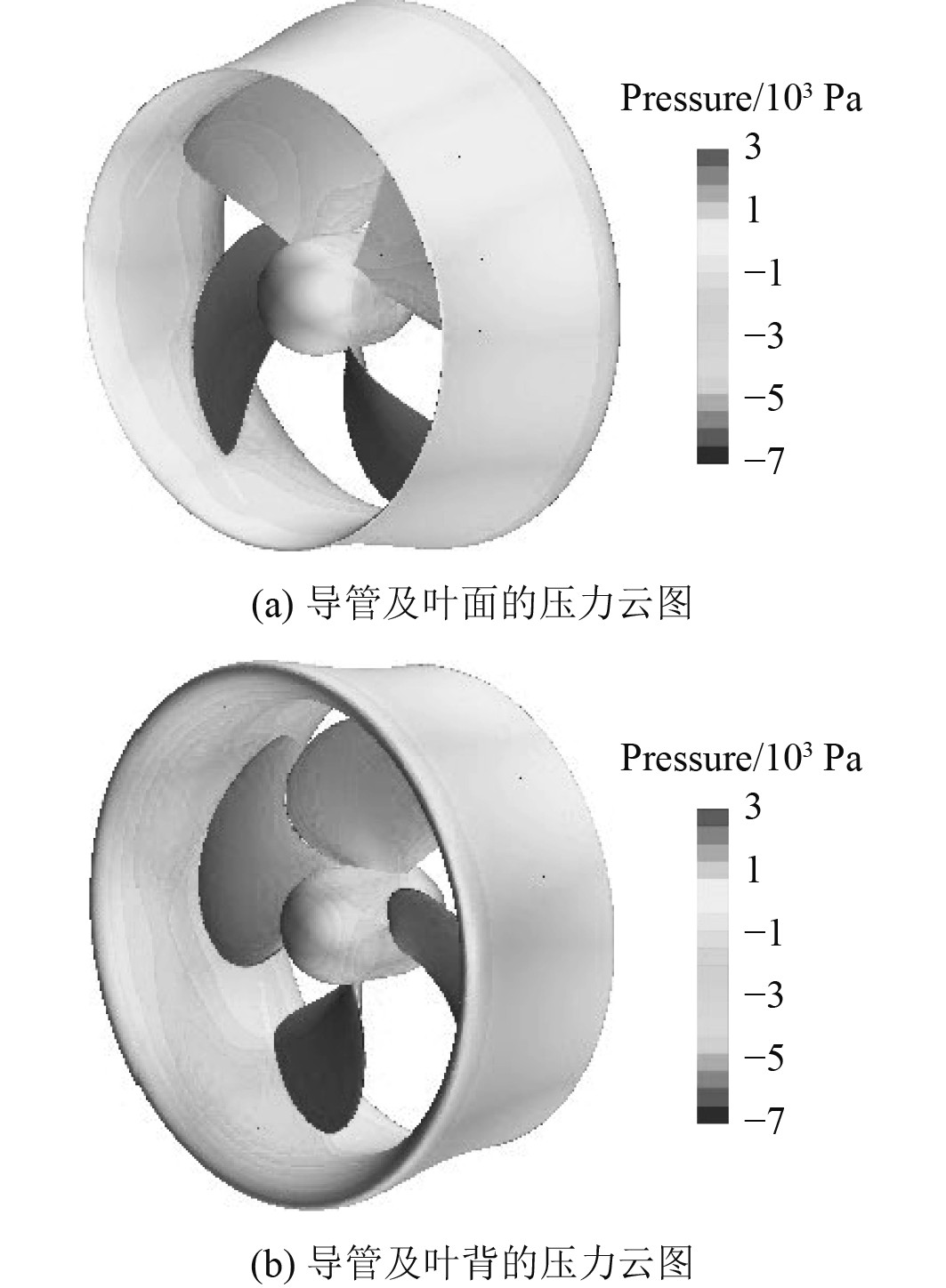
|
图 8 J = 0.525时导管桨压力云图 Fig. 8 Ducted propeller pressure cloud map as J = 0.525 |

|
图 9 J = 0.525时导管螺旋桨纵剖面速度云图 Fig. 9 Longitudinal section velocity cloud map as J = 0.525 |
结合图8和图9可以看出,当导管螺旋桨在运转时,流体在导边处速度小而压力大,在随边处速度大而压力小,当来流从导边流向随边时,叶面的压力值升高而叶背的压力值降低,使得桨的叶面方向为正压力区,而叶背方向为负压力区,从而形成了一个压力差为导管螺旋桨提供了推力。由速度分布还可以看出导管以外区域的场速度为1.2 m/s左右,与定义的来流速度相符且来流在导管的入口处被加速形成了一个椭球型区域,越靠近导管处加速越明显。
4.2 导管机理分析图10和图11分别为低进速系数J = 0.175、来流速度0.4 m/s、螺旋桨转速15 r/s和高进速系数J = 0.7、来流速度 1.6 m/s、螺旋桨转速15 r/s两种工况下导管的压力云图。图12为导管推力敞水性征曲线。

|
图 10 J = 0.175时导管压力云图 Fig. 10 The pressure cloud map of the duct as J = 0.175 |
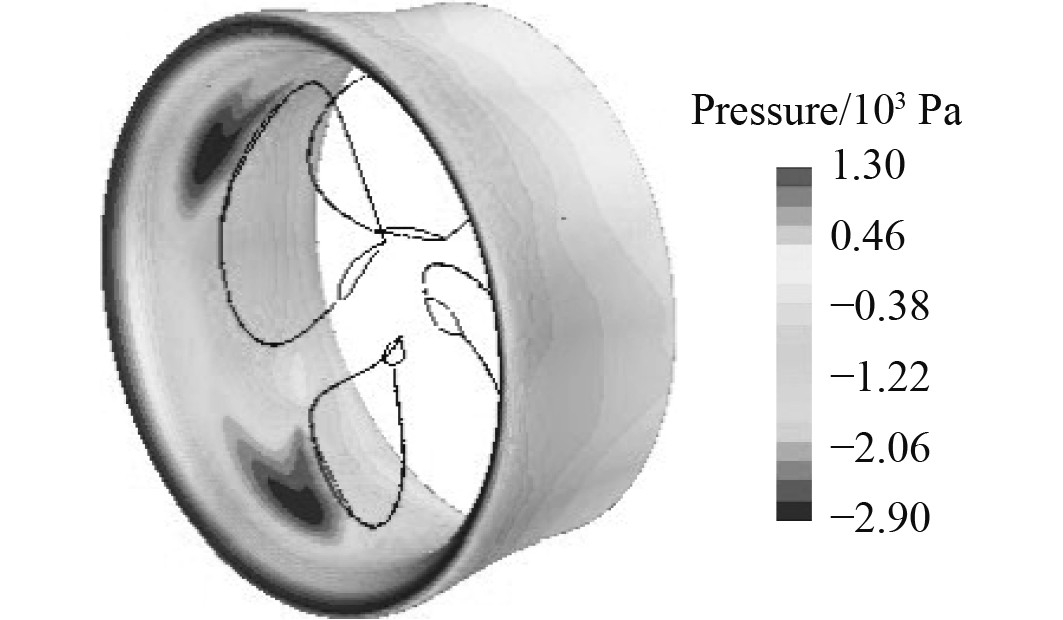
|
图 11 J = 0.7时导管的压力云图 Fig. 11 The pressure cloud map of the duct as J = 0.7 |
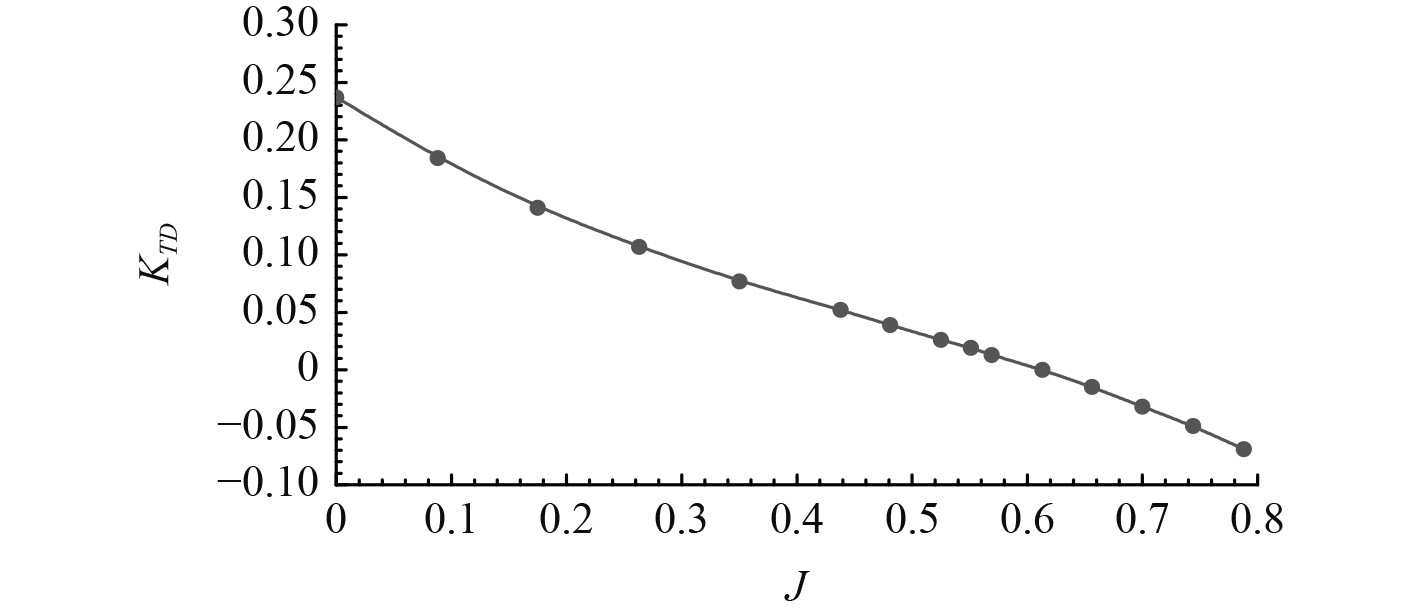
|
图 12 导管推力系数敞水性征曲线 Fig. 12 Open water performance curve of KTD |
由图10可知,在进速系数J = 0.175 时,导管外侧压力分布整体大于导管内侧压力。导管外侧压力分布均匀,而导管内侧压力分布复杂,叶梢前部的导管压力大于叶梢后部的导管压力,形成一个正向的推力。由图11可知,在进速系数J = 0.7 时,导管内侧的压力分布与低进速系数J = 0.175 时相反,叶梢前部的导管压力小于叶梢后部的导管压力,形成了一个反向的阻力。结合图12的导管推力系数敞水性征曲线可以看出,导管的推力随着进速系数的增加而逐渐降低,当进速系数取0.6左右时,导管推力系数由正变负,这说明导管此时不再起正向推进作用,而是变为阻力起到阻碍作用。
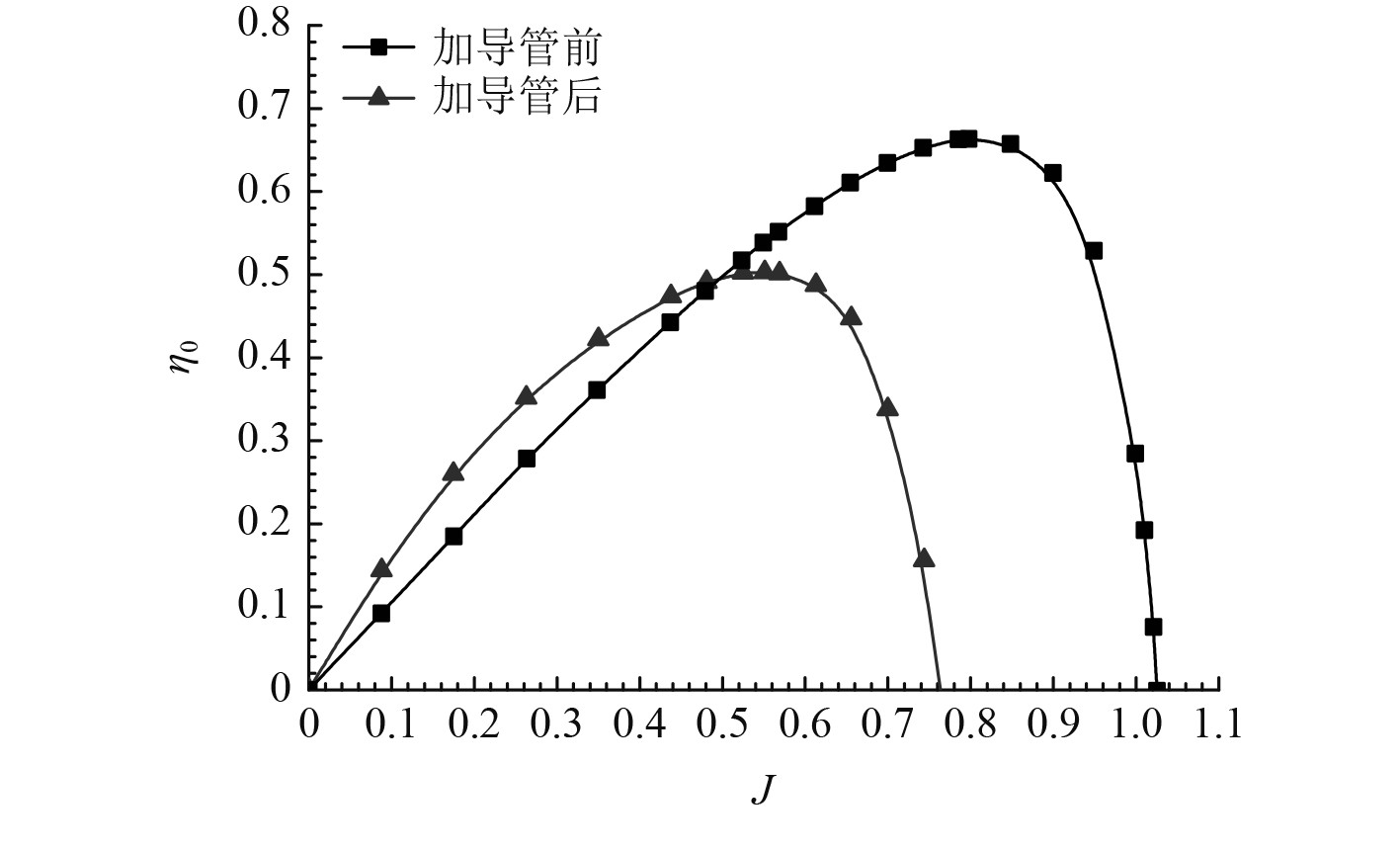
为了进一步探究导管对于螺旋桨敞水效率的影响,对去掉导管后的螺旋桨的敞水效率进行研究。按照数值方法,运用计算流体软件STAR−CCM+,网格划分方案采用细网格,湍流模型采用SST k-ω,求解器参数等其他设置与导管螺旋桨的模拟一致。通过计算得到螺旋桨的敞水效率,与导管桨的敞水效率进行对比分析,结果如图13所示。
|
图 13 导管桨在加装导管前后的敞水性能曲线对比 Fig. 13 The comparison of curve of the open water performance ofducted propeller |
可以看出,进速系数取0~0.55左右时导管对于螺旋桨的敞水效率有明显的促进作用,而进速系数取0.55~1左右时,导管对螺旋桨的敞水效率无促进作用,相反此时的敞水效率会低于加装导管之前。因此,导管螺旋桨适用于螺旋桨载荷较大,在低进速系数下工作的船舶,如顶推船、拖网渔船等。
5 结 语本文以特种推进器中较为熟知的导管螺旋桨为研究对象,通过导管桨模型试验和CFD仿真模拟相结合的方式研究了不同进速系数下导管螺旋桨的水动力性能,分析了流场特点并进行了验证分析,得到以下结论:
1)基于MRF技术,通过使用CFD仿真软件STAR−CCM+能够较为准确的计算导管螺旋桨的水动力性征,推力系数、扭矩系数和敞水效率与试验值吻合良好,能够满足实际工程中的设计需求。
2)SST k-ω湍流模型更适合导管螺旋桨的水动力性能的模拟,所模拟计算的结果与敞水试验数据能更好的吻合。
3)网格数在一定范围内,网格划分越细,导管螺旋桨的计算精度越高。但是需要注意的是,网格的划分如果过细会导致流场信息传递的不准确。
4)在低进速系数下,给螺旋桨安装合适的导管对螺旋桨的敞水效率提高明显,导管螺旋桨适用于在低进速系数下工作的重载船舶。
| [1] |
盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2009: 177–188.
|
| [2] |
JOHN A A, CARNEGIE, ALBERT M M. Kort Nozzle[P]. USA, 3499412, 1970.
|
| [3] |
FEITEN W, BAUER R, LAWITZKY G. Robust obstacle avoidance in unknown and cramped environments [C] // IEEE International Conference on Robotics and Automation, 1994: 2412−2417.
|
| [4] |
叶元培, 沈贻德. 双体导管螺旋桨系列试验研究[J]. 中国造船, 1979(2): 3-36. |
| [5] |
KERWIN J E, KINNAS S A. A surface panel method for the hydrodynamic analysis of ducted propellers[J]. Transactions. SNAME, 1987(95), 93−122.
|
| [6] |
KHATIB M. Sensor-based motion control for mobile robots [C] // 5th International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 2009.
|
| [7] |
杨晨俊, 王国强, 杨建民. 导管螺旋桨定常性能理论计算[J]. 上海交通大学学报, 1997, 31(11): 36-39. DOI:10.16183/j.cnki.jsjtu.1997.11.007 |
| [8] |
赵强. 导管螺旋桨水动力性能和船尾伴流场的 CFD 模拟[D]. 武汉: 武汉理工大学, 2011.
|
| [9] |
胡健, 王楠, 胡洋. 加速导管和减速导管的性能比较[J]. 北京航空航天大学学报, 2017, 43(2): 240-252. HU Jian, WANG Nan, HU Yang. Performance comparison of accelerating duct and decelerating duct[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(2): 240-252. DOI:10.13700/j.bh.1001-5965.2016.0140 |
| [10] |
邱鹏, 郑高, 李国诚. 基于 STAR-CCM + 的导管螺旋桨黏性流场计算方法研究[J]. 造船技术研究, 2019(3): 54-58, 64. |
| [11] |
邱鹏, 郑高. 基于重叠网格的导管桨非定常水动力性能数值模拟[J]. 舰船科学技术, 43(4): 73−77.
|
| [12] |
吴家鸣, 张强. 三种 CFD 方法计算敞水导管螺旋桨推力 特性结果观察[J]. 广州航海学院学报, 29(3): 56−61.
|
| [13] |
ITTC–Recommended Procedures and Guidelines, Revision 07[R]. 2017.
|
 2024, Vol. 46
2024, Vol. 46
