2. 浙江省海洋大数据挖掘与应用重点实验室,浙江 舟山 316022
2. Key Laboratory of Oceanographic Big Data Mining and Application of Zhejiang Province, Zhoushan 316022, China
船舶在夜晚可见度较低的海上航行过程中,最重要的就是航行安全问题。由于夜晚海上的可见距离较短,船舶在较短时间、较短距离内无法紧急避让其他船舶,可能导致船舶的碰撞。在夜晚可见度较低的海上,通过人的眼睛直接获取到的信息非常有限,即便观察到对向船舶,由于反应时间短仍会导致危险的发生。低照度图像增强技术能有效地对海上可见度较低场景下的船舶进行清晰化处理,通过提高低照度的船舶图像对比度,能够突出海上船舶的整体轮廓,减弱船舶周围海浪花对边缘提取的影响,并能为图像的整体亮度提高做支撑,使后续目标检测结果更加精确。因此,研究海上低照度船舶图像增强的方法具有重要意义。
目前,随着各类图像增强技术的应用,使得低照度图像得到了不同程度的增强。刘寿鑫等[1]针对低照度图像色彩偏暗,整体亮度较低以及光照不均等问题,提出了基于HSV色彩空间的低照度图像增强方法。田江丽等[2]提出低照度的船舶图像增强研究,通过建立低照度的船舶图像Retinex模型,将该模型参量引入低照度船舶图像,最后利用神经网络算法重建,完成低照度船舶图像增强计算。虽然这些方法能够提升低照度船舶图像增强处理效果,但都未考虑夜间海上非均匀光照以及船舶周围的海面反射光等对船舶可见度的影响。
本文针对海上低照度船舶图像增强出现的过度曝光、细节丢失以及边缘模糊等问题,提出一种融合同态滤波与多尺度Retinex的算法。
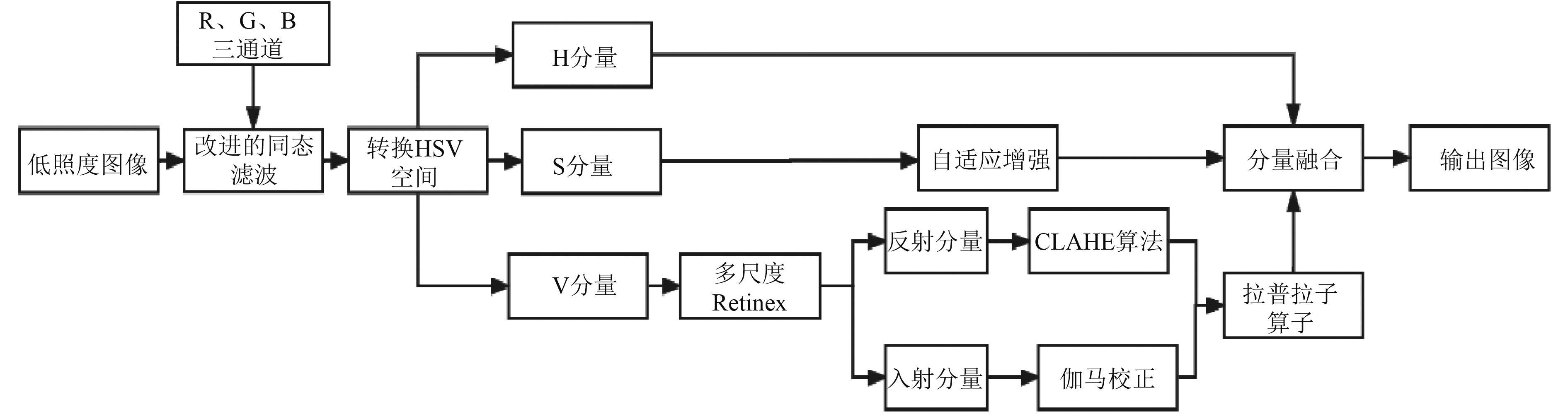
1 低照度船舶图像增强实现本文提出的算法流程图如图1所示。具体步骤如下:
|
图 1 算法流程图 Fig. 1 Algorithm flow chart |
步骤1 利用改进的单参数同态滤波对输入的低照度图像的R、G、B 三通道进行滤波,得到滤波后的图像;
步骤2 将步骤1得到的图像转为HSV并对饱和度分量S进行自适应增强,保留图像的色彩饱和度;采用MSR算法从亮度分量V分离出光照分量与反射分量;
步骤3 对步骤2得到的光照分量进行限制对比度直方图均衡化,避免光照分量的中由于部分灰度级丢失而产生的噪声放大,从而提升图像整体轮廓的清晰度;
步骤4 利用伽马变换对反射分量的部分灰度级过度增强现象进行抑制,限制海面反射光的过度曝光;
步骤5 利用拉普拉斯增强算子突出步骤3与步骤4得到的处理结果进行图像融合后得到V分量的边缘细节,最后将各分量融合并并转为RGB通道输出图像。
1.1 改进的同态滤波算法同态滤波算法可调整输入图像中的整体灰度范围并增强其对比度。原理为:入射分量的值越小,低频成分所削弱的越多,光照范围越少,则灰度级范围越小,从而导致高频部分不断增强,最终图像细节更加清晰。在一幅图像S(x, y)中,图像的反射分量对应高频部分(R(x, y)),图像的入射分量对应低频部分(I(x,y)),其公式如下:
| $ S\left( {x,y} \right) = I\left( {x,y} \right) \cdot R\left( {x,y} \right)。$ | (1) |
由于式(1)中的乘积不可分,故对式(1)两边同时取对数得:
| $ S'\left( {x,y} \right) = {\rm{In}}S\left( {x,y} \right) = {\rm{In}}I\left( {x,y} \right) + {\rm{In}} R\left( {x,y} \right)。$ | (2) |
频域表达式为:
| $ S\left( {U,V} \right) = I\left( {U,V} \right) + R\left( {U,V} \right) 。$ | (3) |
对式(3)两边用滤波函数处理得:
| $ S\left( {U,V} \right) \cdot H\left( {U,V} \right) = I\left( {U,V} \right) \cdot H\left( {U,V} \right) + R\left( {U,V} \right) \cdot H\left( {U,V} \right)。$ | (4) |
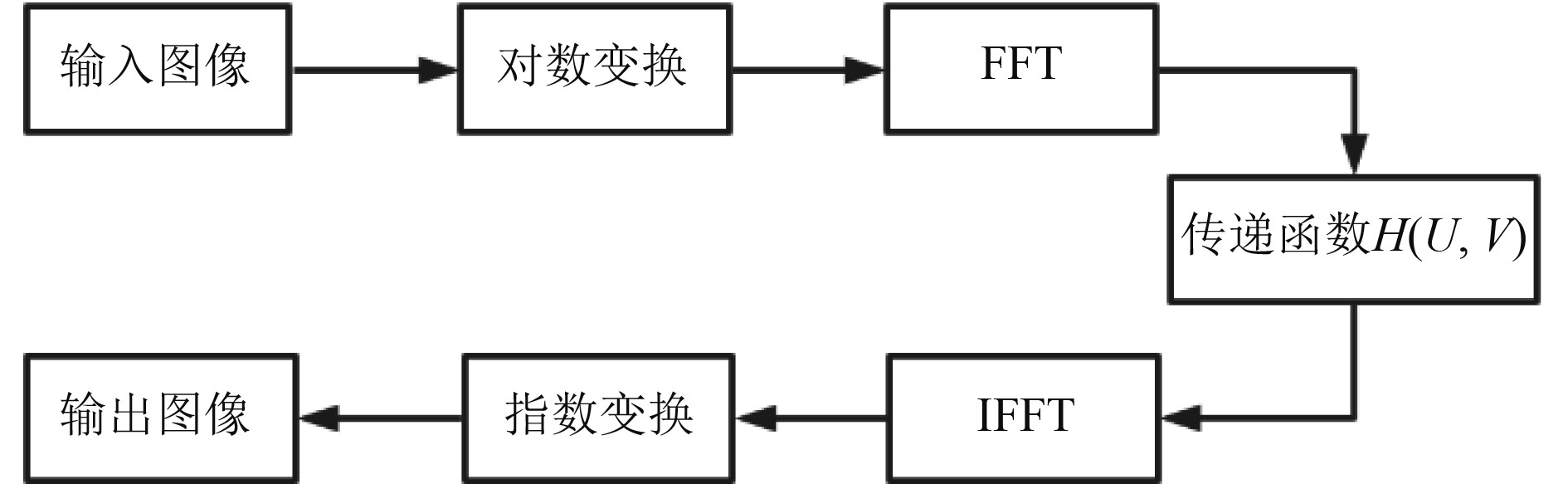
式(4)中的传递函数
|
图 2 同态滤波算法流程 Fig. 2 Homomorphic filtering algorithm flow |
本文算法中,采用的是巴特沃斯型传递函数,因其具有设计简单、振荡较小等特点。传统的巴特沃斯型传递函数表示为:
| $ H\left( {U,V} \right) = \left( {{r_H} - {r_L}} \right)/\left[ {1 + {{\left( {\frac{{{D_0}}}{{c \cdot D\left( {U,V} \right)}}} \right)}^{2n}}} \right] + {r_L} 。$ | (5) |
式中:
| $ D\left( {U,V} \right) = \sqrt {{{\left( {U - {U_0}} \right)}^2} + {{\left( {V - {V_0}} \right)}^2}}。$ | (6) |
但传统的巴特沃斯型传递函数中的参数过多,在实际研究中会针对图像增强的角度不同,在高低频增益和截至频率方面难以调节。因此,采用一种既能保证原来的滤波效果,又能减少传递函数的相关调节参数的单参数同态滤波[3]。该传递函数基于S型函数构造,其中S型函数剖面图与同态滤波具有类似结构,该S函数公式为:
| $ y = \frac{k}{{1 + {e^{ - ax}}}}。$ | (7) |
改进后的传递函数表示为:
| $ H\left( {U,V} \right) = 1/\left[ {1 + \exp \left( { - \alpha \cdot D\left( {U,V} \right)} \right)} \right] 。$ | (8) |
式中,
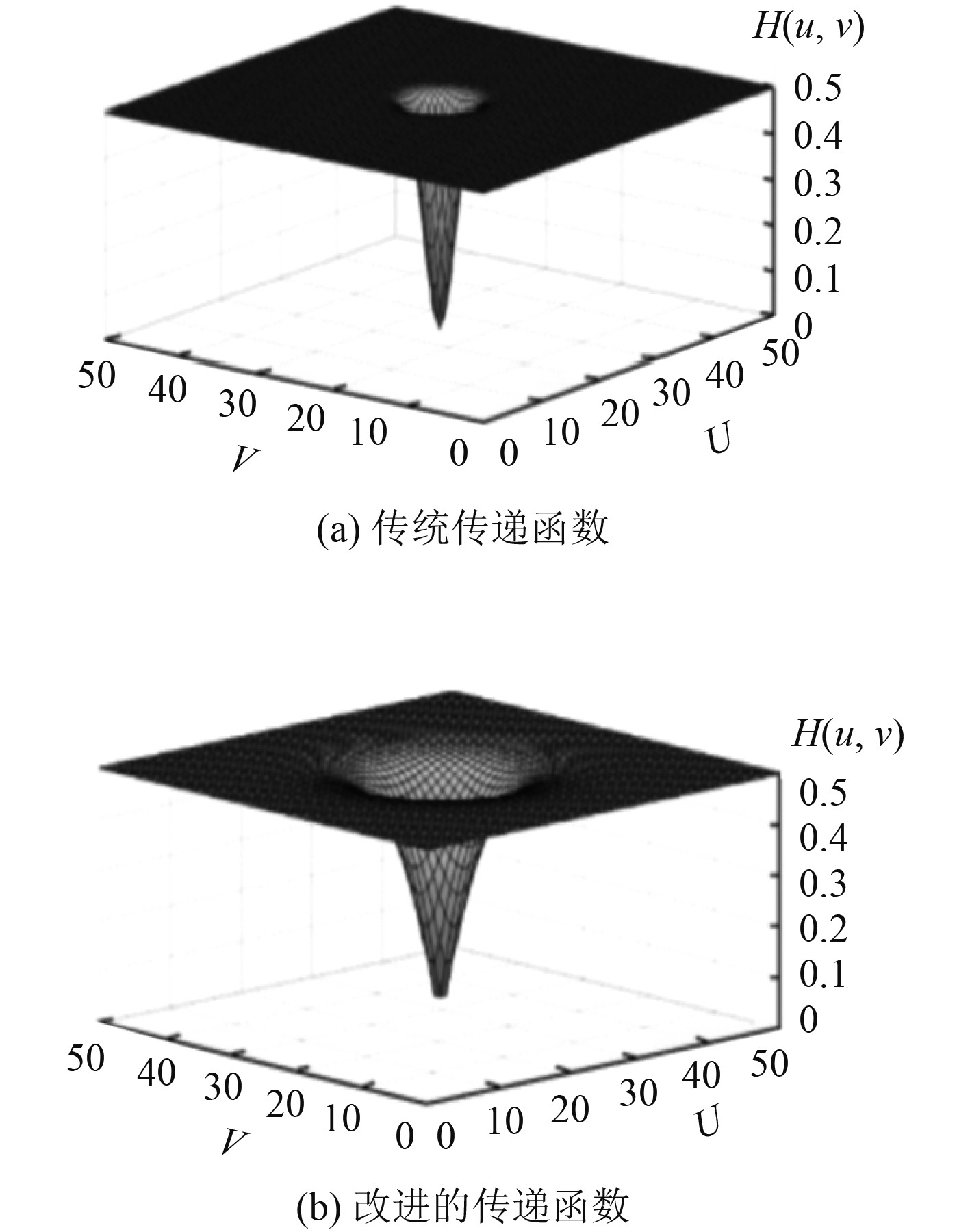
对比传统的巴特沃斯型同态滤波[4],该改进的同态滤波在低频分量上得到一定的增益。传统的高斯型同态滤波器通常为0,从而导致图像动态范围内出现过度压缩现象,该传递函数的剖面图如图3(a)所示。改进后同态滤波算法的中心频率与高频之间的过渡更缓慢,滤波效果更加均匀,避免了过度压缩对图像对比度的影响,改进的单参数传递函数剖面如图3(b)所示。
|
图 3 传统传递函数与改进后的剖面图对比 Fig. 3 Comparison between traditional transfer function and improved profile |
Retinex理论代表可见光图像是通过日常环境中光照分量和光照在物体表面所产生的反射分量组成的。一幅图像可以分解为:反射图像和入射图像。反射图像在频域中属于高频分量,相对变化较大;入射分量可视为环境中的照明,变化相对较缓,属于在频域中低频分量,也被称为光照分量[5]。其表达式为:
| $ S\left( {x,y} \right) = I\left( {x,y} \right) \cdot R\left( {x,y} \right)。$ | (9) |
对式(1)两边同时取对数,可得到关系式为:
| $ {\mathrm{In}}R\left( {x,y} \right) = {\mathrm{In}}S\left( {x,y} \right) +{\mathrm{ In}}I\left( {x,y} \right)。$ | (10) |
其中,光照分量I(x,y)估算出之后才能得出其反射分量R(x,y)。
对比SSR,MSR既保持图像高保真度与对图像的动态范围进行压缩,还可以实现色彩增强、颜色恒常性等[6]。其中,反射分量类似一幅图像的基本特征,但非常不真实,需加入一些明暗对比度以及一些晕影阳光等信息使得图像变得更加真实。因此,需去对照度分量进行处理,提升明暗亮度,最后将处理后的图像与反射分量重新组合后得到最终增强的图像。在该实验中,将其中的3个尺度设定为15、101、301。由此可知,MSR算法针对各种不同类型的输入图像能够自适应增强。
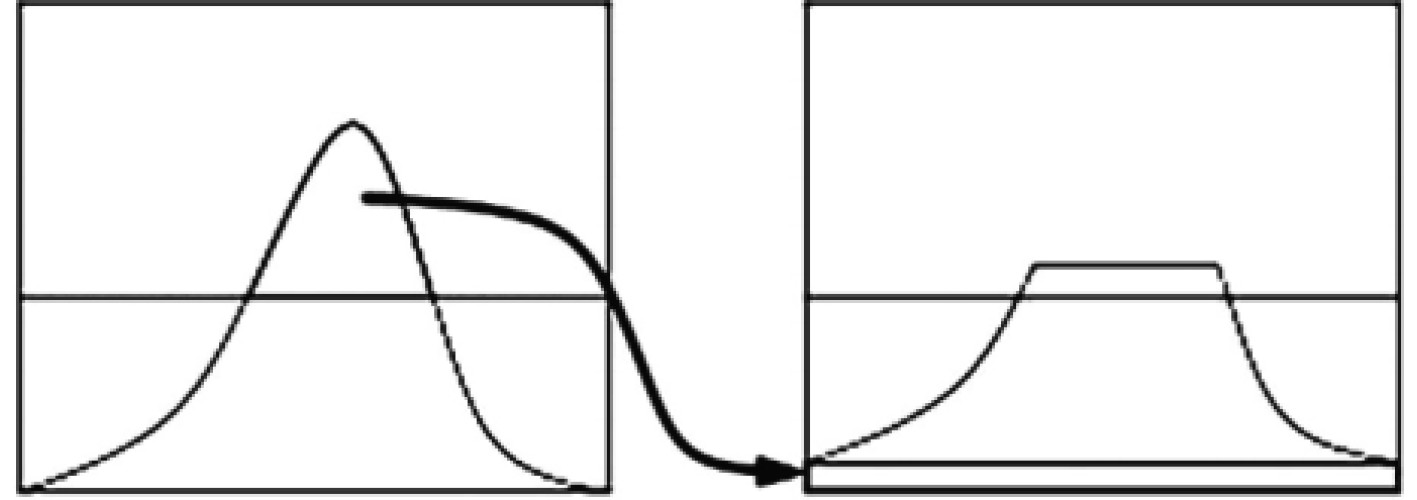
1.3 光照分量与反射分量增强设计 1.3.1 CLAHE算法CLAHE算法[7]是自适应直方图均衡化(AHE)算法的一种变体,全称为限制对比度自适应直方图均衡,其通过限制累积分布函数(CDF)限制对比度放大以达到减少图像背景噪声放大的问题,避免图像背景过分增强而导致图像过度曝光。通常,CLAHE算法在计算CDF之前会将图像生成的直方图预定值裁定出来,并将大于该预定值的部分均匀分布在整个灰度空间上,用于限制直方图的最大变化幅度,并确保该直方图的整体面积不变。原理示意图如图4所示。
|
图 4 CLAHE算法原理示意图 Fig. 4 Schematic diagram of principle of CLAHE algorithm |
伽马校正实质是将输入图像产生的伽马曲线进行图像非线性色调编辑。提升图像的暗部细节,对图像过度曝光或曝光不足导致的过暗情况进行矫正。伽马校正可表示为:
| $ Dt = c \cdot {\left( {D + \varepsilon } \right)^\gamma } 。$ | (11) |
式中:
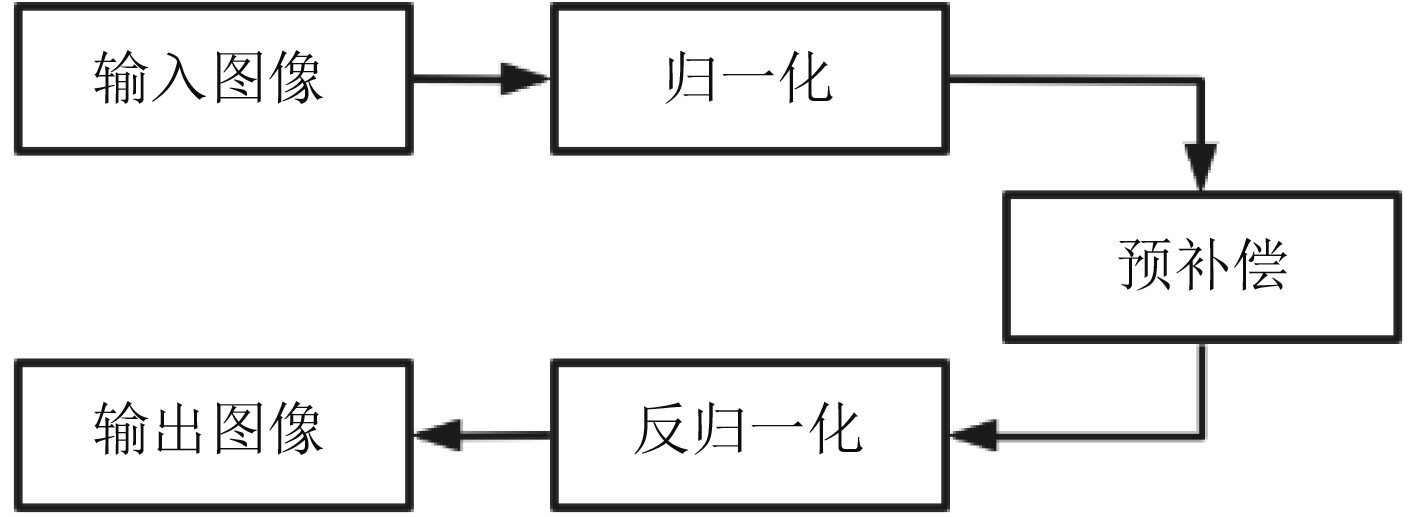
|
图 5 伽马校正流程 Fig. 5 Gamma correction process |
拉普拉斯增强算子[8]相较其他边缘检测算子而言,旋转不变性是其重要特性,是一种基于积分变换的简单算法。在图像处理中,由于图像式离散分布的并且有x和y两个方向,则拉普拉斯算子方程在垂直和水平2个方向上的离散形式[9]。
离散一阶微分方程为:
| $ \nabla f = f\left( {x + 1} \right) - f\left( x \right),$ | (12) |
离散二阶微分方程为:
| $ {\nabla ^2}f = f\left( {x + 1} \right) + f\left( {x - 1} \right) - 2f\left( x \right),$ | (13) |
则拉普拉斯离散方程可表示为:
| $ \begin{split} {\nabla ^2}f =\,& f\left( {x + 1,y} \right) + f\left( {x - 1,y} \right) + \\ & f\left( {x,y + 1} \right) + f\left( {x,y - 1} \right) - 4f\left( {x,y} \right)。\end{split} $ | (14) |
该边缘增强算子可使像素之间的灰度差异得到保留,突出图像中的急剧灰度变化部分,抑制灰度缓慢变化区域,从而提高灰度突变处的对比度,最终将拉普拉斯图像与图叠加,这样能同时突出边缘信息和图像背景中的有用信息。因此,本文依靠二阶拉普拉斯增强算子的无方向性优势对低照度的船舶影像进行边缘细节增强,具有更好的效果。
拉普拉斯增强算子在运用中通常以4邻域和8邻域作为卷积核模板,本文设定模板H为:
| $ H = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 1&{ - 4}&1 \\ 0&1&0 \end{array}} \right]。$ | (15) |
由于传统Retinex算法[10]处理后的图像被直接输出为最终图像,且得到图像局部区域会出现光晕、过曝或者不均匀性等,导致低照度图像中的暗区噪声突出。为解决上述出现的问题,将经过多尺度Retinex后估算出平均照度分量A,结合伽马校正后的反射分量R进行融合[11],求取最后的亮度分量I(x,y)。公式为:
| $ I\left( {x,y} \right) = \exp \left( \begin{gathered} \log \left( {{R_{}}\left( {x,y} \right) + 1} \right) \\ + \log \left( {A\left( {x,y} \right) + 1} \right) \\ \end{gathered} \right) - 1 。$ | (16) |
式中:R(x,y)为反射分量;A(x,y)为平均照度分量。
原始亮度图像与增强后的图像对比如图6所示。

|
图 6 亮度图像增强前后对比 Fig. 6 Contrast before and after brightness image enhancement |
为验证本文算法的可靠性,选取若干张海上低照度船舶实景图像,主要对比传统的高斯型同态滤波算法、CLAHE算法、多尺度Retinex算法(MSR)、文献[3]以及本文算法。对比实验硬件配置为Intel core i7-6700HQ、内存8 G、主频2.6 GHz;软件环境为windows10操作系统、Pycharm 2022.1版本辅助工具。
2.1 主观评价对邮轮和渔船这两类船舶的低照度图像进行实验,分别利用传统的同态滤波、CLAHE算法、多尺度Retinex算法以及本文提出的算法对图像进行增强处理,最终观察实验结果。图7为低照度船舶图像的增强效果图。图7(a)原图像中只能观察到船舶内的灯光,不能确定其整体轮廓;经过CLAHE算法增强后的图像如图7(b)所示,未能凸显边缘的暗部信息,并且整体的对比度较低,只能观察到船舶的整体轮廓;图7(c)经过传统同态滤波处理后的图像中的水面反射光过度曝光,船舶边缘细节模糊;图像经过多尺度Retinex算法处理后,图7(d)的整体效果提升明显,但存在水面反射光以及光照影响带来的过度增强,图像呈现过多光晕噪声现象。而本文算法有效抑制了水面以及周围光照的过度曝光现象,并保留了船舶的边缘细节,整体对比度效果更佳,同时保留了原图像的色彩,如图7(e)所示。

|
图 7 低照度船舶图像增强结果对比 Fig. 7 Comparison of enhancement results of low illuminance ship images |
主观评价结果通常有一定偏差。因此,为了验证本文算法对比其他低照度图像增强算法的有效性,分别采用图像的均值、信息熵(IE)、峰值信噪比(PSNR)作为增强效果的评价指标。图像的均值用于表示图像的整体亮度,均值越大对应的图像亮度越大;信息熵(IE)用于衡量一幅图像中的信息量大小,其值越大表示图像信息越丰富,细节信息越多。信息熵(IE)表示为:
| $ H = \sum\limits_{i = 0}^{255} {{p_i}\log {p_i}} ,$ | (17) |
式中,pi为灰度值为i的像素占比。
PSNR表示在一幅图像中可能产生的最大功率与噪声功率的比值,该指标可衡量噪声对图像的干扰程度,其比值越高,则表示干扰越小,图像提升的效果越佳。PSNR(峰值信噪比)计算公式为:
| $ PSNR=10\cdot \log_{10}\left(\frac{MAX_I^2}{MSE}\right)。$ | (18) |
式中:MAX−2为输出图像最大像素值的平方;MSE为均方误差。
| $ MSE = \frac{1}{{m \cdot n}}\sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {{{\left[ {I\left( {i,j} \right) - K\left( {i,j} \right)} \right]}^2}} }。$ | (19) |
以上3种图像质量评价指标的测定结果如表1所示(测定结果数值均保留小数点后三位)。
|
|
表 1 各类算法的均值对比 Tab.1 Comparison of mean values of various algorithms |
可知,传统的高斯型同态滤波、CLAHE算法、多尺度Retinex算法以及本文算法对海上复杂情况的低照度船舶图像增强效果都有明显提升。但从增强后图像的峰值信噪比、信息熵和均值的数值分析来看,本文提出的改进算法在控制过度增强、保留边缘细节、光晕问题以及整体清晰度方面表现更好,效果更佳。
3 结 语由于传统Retinex算法对海上复杂环境下,低照度船舶图像的增强带来过度曝光、光晕效应、边缘模糊等缺点,提出一种单参数同态滤波结合多尺度Retinex的算法。利用改进的同态滤波,结合单参数的传递函数,对原图像的RGB通道进行滤波处理,能提高图像处理的速度;采用CLAHE算法对反射分量的对比度进行增强;之后伽马校正入射分量,抑制过度增强的同时提升了暗部的细节;利用拉普拉斯边缘增强算子对处理后的V分量进行处理,有效保留了图像的边缘的高频部分细节信息,提升了整体的对比度。最后,本文对算法进行实验测试,实验结果表明,本文提出的改进算法有效克服了低照度船舶图像增强后,图像过度增强、光晕、边缘模糊等现象。虽然本文算法对低照度船舶图像增强效果较好,但存在过多的算法融合,使得海上船舶图像实时增强还存在时间复杂度的问题,在实际应用中有所限制。因此,未来将针对这一缺点进行优化研究。
| [1] |
刘寿鑫, 龙伟, 李炎炎, 等. 基于HSV色彩空间的低照度图像增强[J]. 计算机工程与设计, 2021, 42(9): 2552-2560. LIU S X, LONG W, LI Y Y, et al. Low illumination image enhancement based on HSV color space[J]. Computer Engineering and Design, 2021, 42(9): 2552-2560. |
| [2] |
田江丽, 李攀. 低照度的船舶图像增强研究[J]. 舰船科学技术, 2021, 43(2): 88-90. TIAN J L, LI P. Research on ship image enhancement under low illuminance[J]. Ship Science and Technology, 2021, 43(2): 88-90. |
| [3] |
王智奇, 李荣冰, 刘建业, 等. 基于同态滤波和直方图均衡化的图像增强算法[J]. 电子测量技术, 2020, 43(24): 75-80. WANG Z Q, LI R B, LIU J Y, et al. Image enhancement algorithm based on homomorphic filtering and histogram equalization[J]. Electronic Measurement Technology, 2020, 43(24): 75-80. DOI:10.19651/j.cnki.emt.2005346 |
| [4] |
程新. 基于同态滤波的图像增强算法研究[D]. 西安: 西安邮电大学, 2016.
|
| [5] |
闫保中, 韩旭东, 何伟. 基于Retinex理论改进的低照度图像增强算法[J]. 应用科技, 2020, 47(5): 74-78. YAN B Z, HAN X D, HE W. An improved low illumination image enhancement algorithm based on Retinex theory[J]. Applied Science and Technology, 2020, 47(5): 74-78. |
| [6] |
张江鑫, 杨惠. 基于同态高低通滤波与多尺度Retinex的低照度彩色图像增强[J]. 计算机应用与软件, 2021, 38(01): 232-237. ZHANG J X, YANG H. Low illumination color image enhancement based on homomorphic low-pass filtering and multiscale Retinex[J]. Computer Applications and Software, 2021, 38(01): 232-237. DOI:10.3969/j.issn.1000-386x.2021.01.039 |
| [7] |
李红, 王瑞尧, 耿则勋, 等. 基于多尺度梯度域引导滤波的低照度图像增强算法[J]. 计算机应用, 2019, 39(10): 3046-3052. LI H, WANG R Y, GENG Z X, et al. Low illumination image enhancement algorithm based on multi-scale gradient domain guided filtering[J]. Computer Applications, 2019, 39(10): 3046-3052. |
| [8] |
RASHEED M T,et al. An empirical study on retinex methods for low-light image enhancement[J]. Remote Sensing, 2022, 14(18): 4608-4608. DOI:10.3390/rs14184608 |
| [9] |
HU Yunxue, et al. Detail enhancement multi-exposure image fusion based on homomorphic filtering[J]. Electronics, 2022, 11(8): 1211-1211. DOI:10.3390/electronics11081211 |
| [10] |
JEON JONG JU, EOM IL KYU. Low-light image enhancement using inverted image normalized by atmospheric light[J]. Signal Processing, 2022: 108523.
|
| [11] |
崔圆斌, 田益民, 杜云飞, 等. 基于光照分量校正和补偿的低照度图像增强算法[J]. 数字印刷, 2021(6): 29-37. CUI Y B, TIAN Y M, DU Y F, et al. Low illumination image enhancement algorithm based on illumination component correction and compensation[J]. Digital Printing, 2021(6): 29-37. |
 2024, Vol. 46
2024, Vol. 46
