海底管道被广泛应用于海上油气开发领域,但海底管道所处载荷环境复杂,同时受到风、浪、流等外部交变载荷及内部交变压力载荷的作用,致使疲劳破坏成为海底管道主要的失效形式。海底管道无论从制造或是工作环境角度来说必然会存在裂纹缺陷,随着海洋石油及天然气开发程度的升级,海底管道(线)断裂泄漏的事故越来越频繁。因此,研究海底管道的疲劳裂纹扩展过程并预测海底管道的剩余疲劳寿命,对预防海底管道因疲劳破坏而引起的失效问题具有重要的实践意义。
国内外专家和学者对不同类型的海底管道疲劳问题进行研究,目前对海底管道进行疲劳分析的方法主要有基于累积损伤理论的S-N曲线法和断裂力学法。Wormsen等[1]通过实验得到管道材料在空气中和在有阴极保护措施的海水环境中的S-N曲线,利用损伤理论预报了海底管道疲劳寿命。为了确保海底管道在运行过程中的安全可靠,对已经存在裂纹缺陷的海底管道更需进行疲劳分析。在海底管道剩余寿命预报及裂纹扩展研究方面,赵雪健等[2]以Pairs公式为基础,考虑管道所受载荷、材料特性及裂纹尺寸等因素,基于Monte Carlo法完成对海底管道的疲劳寿命可靠性计算。黄如旭等[3]利用最大环向应力准则预测裂纹的偏折角度,并基于线弹性断裂力学和Ansys建立起三维裂纹扩展及寿命的数值预报方法。余建星等[4 − 5]基于线性断裂力学理论,研究点蚀作用下的海底管道疲劳裂纹扩展过程,分析了管道表面蚀坑-裂纹的应力强度因子,并对腐蚀和交变载荷耦合下的海底管道疲劳寿命进行预测。
为保障海底管道油气运输的安全,有必要对服役中的海底管道进行疲劳裂纹扩展寿命预报。本文首先利用有限元法和1/4节点位移法计算裂纹应力强度因子,随后基于Pairs公式的da法预报海底管道的疲劳扩展寿命。将数值预报结果与试验数据比较,验证此方法的准确性。最后,对影响海底管道疲劳裂纹扩展寿命数值预报结果的关键参数进行探讨。
1 基本理论Irwin[6]提出用应力强度因子K来表征裂纹尖端区域附近的应力场强弱程度,并将裂纹分成张开I型、滑开II型和剪切III型3类,其应力强度因子分别用KI、KII、KIII表示。
考虑到实际材料抵抗裂纹扩展能力不同,为描述裂纹的扩展过程,引入裂纹扩展速率的概念。在交变载荷(应力)循环ΔN次后,材料的裂纹扩展量为Δa,此时可用微分形式da/dN来表示应力循环一周裂纹的扩展增量。
自裂纹扩展速率概念提出至今,出现很多经典的裂纹扩展速率公式将da/dN与应力强度因子联系起来,其中应用最广泛的为Pairs公式:
| $ \frac{{{\mathrm{d}a}}}{{{\mathrm{d}}N}} = C{\left( {\Delta K} \right)^m} 。$ | (1) |
式中:C、m均为与材料有关的系数;ΔK为应力强度因子幅值,ΔK=Kmax-Kmin。
对式(1)两边进行积分得:
| $ N = \int {{\mathrm{d}}N} = \int_{{a_0}}^{{a_c}} {\frac{1}{{C{{(\Delta K)}^m}}}} {\mathrm{d}}a 。$ | (2) |
式中:N为应力循环次数;a0为裂纹初始尺寸;ac为裂纹临界尺寸。
2 关键参数求解方法结构的初始裂纹尺寸a0通常可根据ASME规定的无损检测方法得到,根据Pairs裂纹扩展公式,此时要对结构进行剩余疲劳寿命预测,需要求解2个关键参数,即应力强度因子K和裂纹临界尺寸ac。
2.1 应力强度因子K求解方法及验证关于应力强度因子K,采用有限元法与1/4节点位移法[3]进行计算。基于有限元法求出裂纹节点处的张开位移,通过1/4节点位移法进行应力强度因子K的计算,如下式:
| $ \begin{split} & {K_{\rm{I}}}{\text{ = }}\frac{{2\mu }}{{1 + k}}\sqrt {\frac{{2{\text{π}} }}{{{r_{AB}}}}} ({v_B} - {v_A}),\\ & {K_{\rm{II}}}{\text{ = }}\frac{{2\mu }}{{1 + k}}\sqrt {\frac{{2{\text{π}} }}{{{r_{AB}}}}} ({u_B} - {u_A}),\\ & {K_{\rm{III}}}{\text{ = }}\frac{{2\mu }}{{1 + k}}\sqrt {\frac{{2{\text{π}} }}{{{r_{AB}}}}} ({w_B} - {w_A})。\end{split} $ | (3) |
式中:A点为裂纹尖端点,B点为1/4节点处;k为材料参数,μ为剪切模量;rAB为1/4处节点到裂尖的距离;ν为x方向位移量;u为y方向位移量;w为z方向位移量。
由于裂纹尖端应力具有奇异性,有限元法计算时若用常规有限元网格进行划分,即便网格划分很小,对计算能力要求提高的同时,计算精度却不够理想。故通常数值计算时,对于裂纹尖端附近区域需使用奇异单元进行划分,其余区域则可使用一般网格划分。此节将基于Abaqus的有限元法对含半圆裂纹的平板进行应力强度因子计算,并将结果与Newman-Raju理论[7]计算值比较,验证有限元法的计算准确度。
平板参数为L×B×t(200 mm×60 mm×10 mm),一端刚性固定,一端施加100 MPa的拉应力,参考文献[8]奇异单元处理方法,裂纹附近区域网格大小设置为0.3a,裂纹尖端单元层数设置为3,裂纹尖端奇异单元长度设为0.1a,含裂纹平板有限元处理流程如图1所示。导入初始裂纹a0,裂纹尺寸形状比a/c=1/2,裂纹长度30 mm,有限元法裂纹前缘KI分布图,如图2所示。
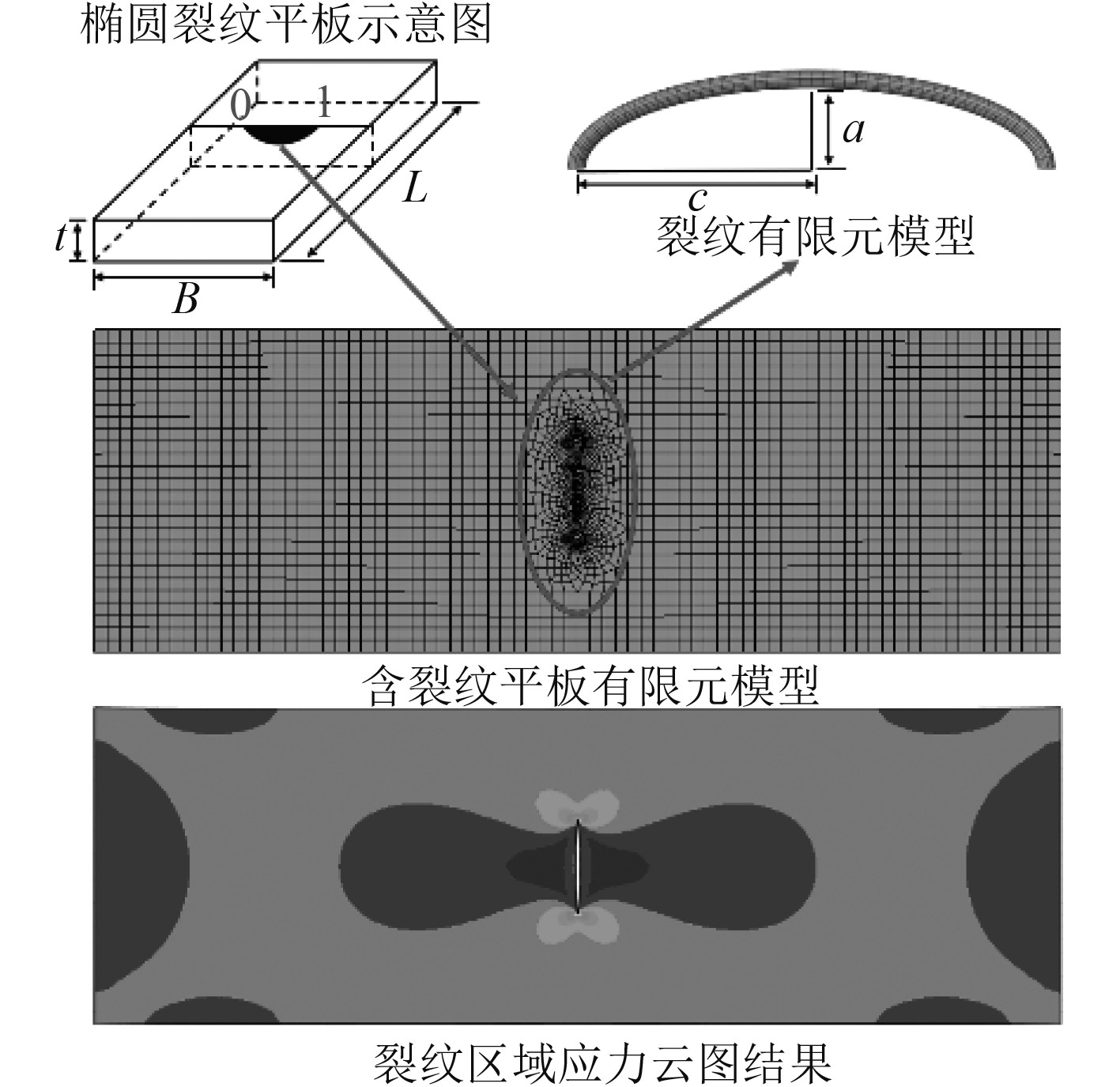
|
图 1 半圆裂纹平板有限元处理流程 Fig. 1 FEM process of the semi-circular crack plate |
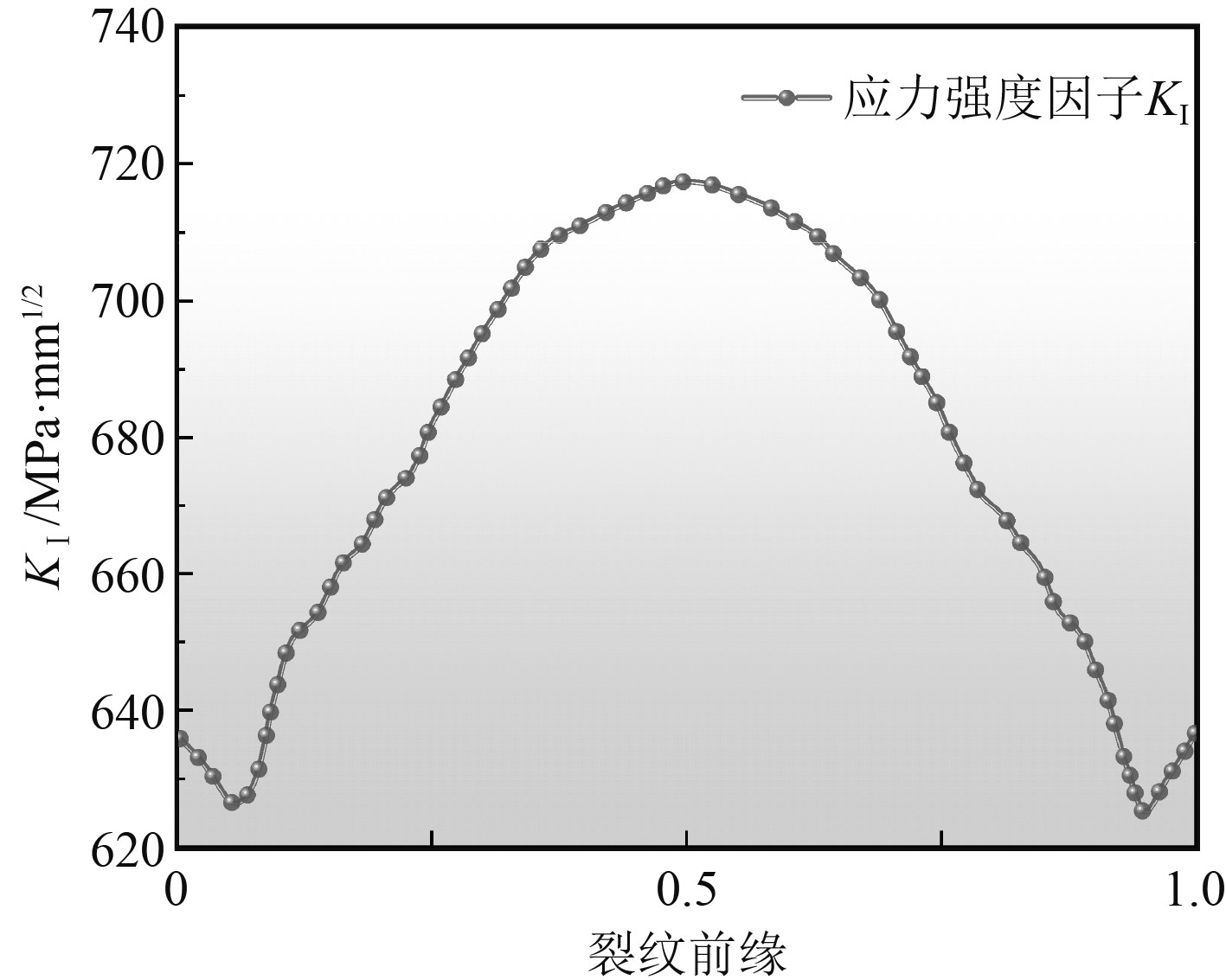
|
图 2 裂纹区域的应力强度因子KI Fig. 2 The value of KI in the cracked area |
由表1可知,基于Abaqus的有限元数值计算结果与Newman-Raju解析法结果误差仅为0.8%,说明基于有限元法与1/4节点位移法结合计算出来的应力强度因子结果相对可靠。对于工程中复杂的、不规则的结构,可利用上述方法来求解应力强度因子,对海洋管道应力强度因子K求解时也将采用此方法。
|
|
表 1 应力强度因子比较 Tab.1 Comparison of stress intensity factors |
裂纹临界尺寸是结构断裂疲劳寿命计算的边界,在剩余强度理论中对裂纹临界尺寸进行求解需要依据一定的判定准则。计算时依据亚临界裂纹扩展特性的断裂K准则,以I型裂纹为例建立应力强度因子的K判据:
| $ {K_{\rm{I}}} \geqslant {K_{\rm{IC}}}。$ | (4) |
当应力强度因子K达到KIC时,此时裂纹深度尺寸a对应的值即为裂纹临界尺寸ac。
3 海底管道疲劳裂纹扩展模式分析 3.1 海底管道参数海洋管道材料为X65钢,基本力学性能如表2所示。管道示意图如图3所示,局部放大图中0、1代表椭圆裂纹长度方向端点,应力强度因子记为Kc;0.5代表椭圆裂纹深度方向端点,应力强度因子记为Ka。
|
|
表 2 X56钢基本力学性能 Tab.2 Basic mechanical properties of X56 steel |
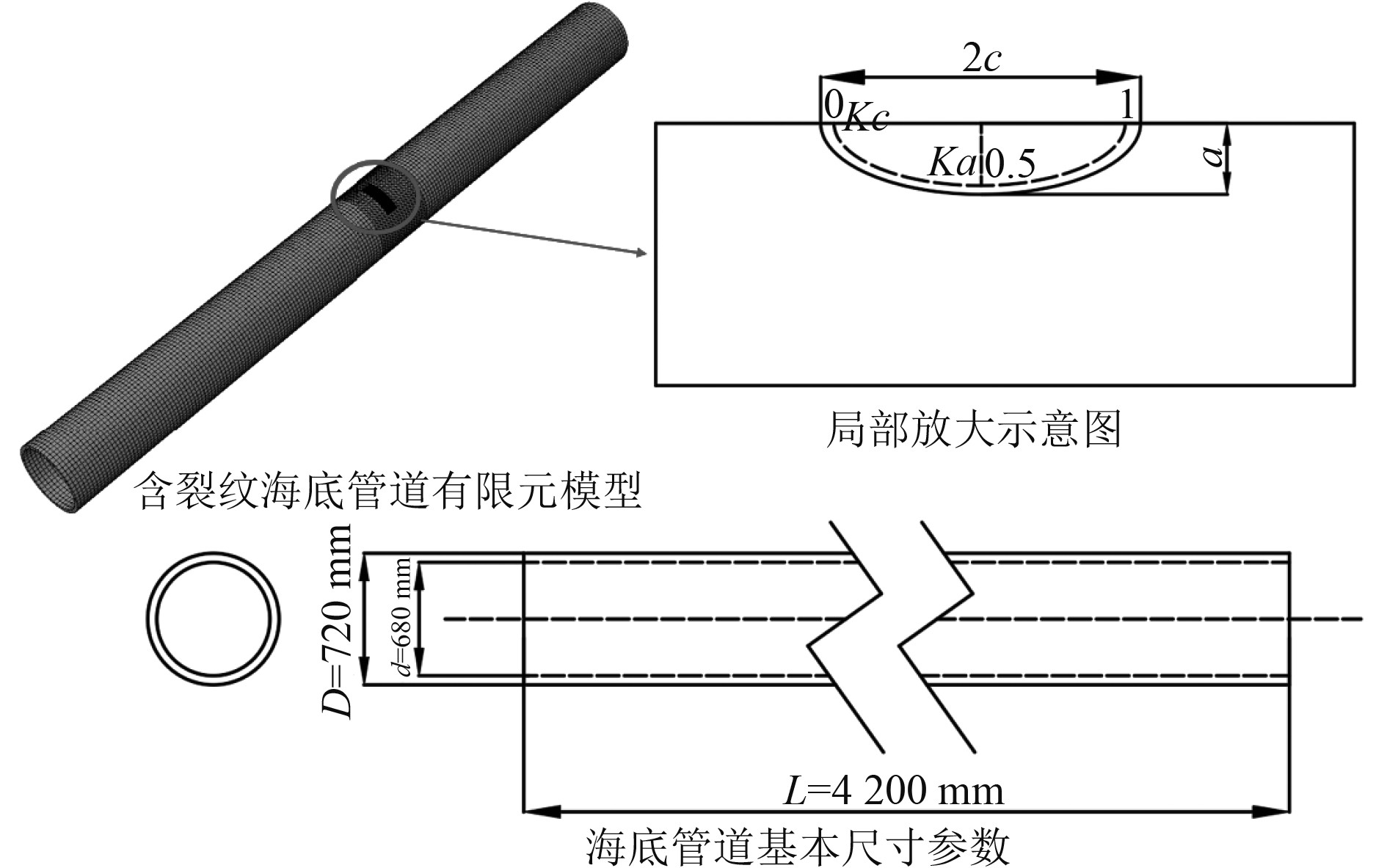
|
图 3 海底管道参数及建模示意图 Fig. 3 Subsea pipeline parameters and calculation model |
对于海底管道的裂纹扩展显然属于三维裂纹扩展,此时描述裂纹扩展的参数有:应力循环数N、椭圆裂纹深度a、椭圆裂纹长度c、裂纹扩展偏转角度θ。
根据保守估计法,假定裂纹形状保持几何相似,即a/c为常数。基于有限元法和1/4节点位移法求解管道裂纹初始尺寸a0为10~35 mm,裂纹尺寸比a/c=1/1~1/5下的应力强度因子K。以a/c=1/3为例,从图4裂纹前缘KIII的计算结果看,KIII值本身较小且KIIIa在不同初始裂纹尺寸下皆接近于0,在研究裂纹扩展时可忽略KIII值的影响。
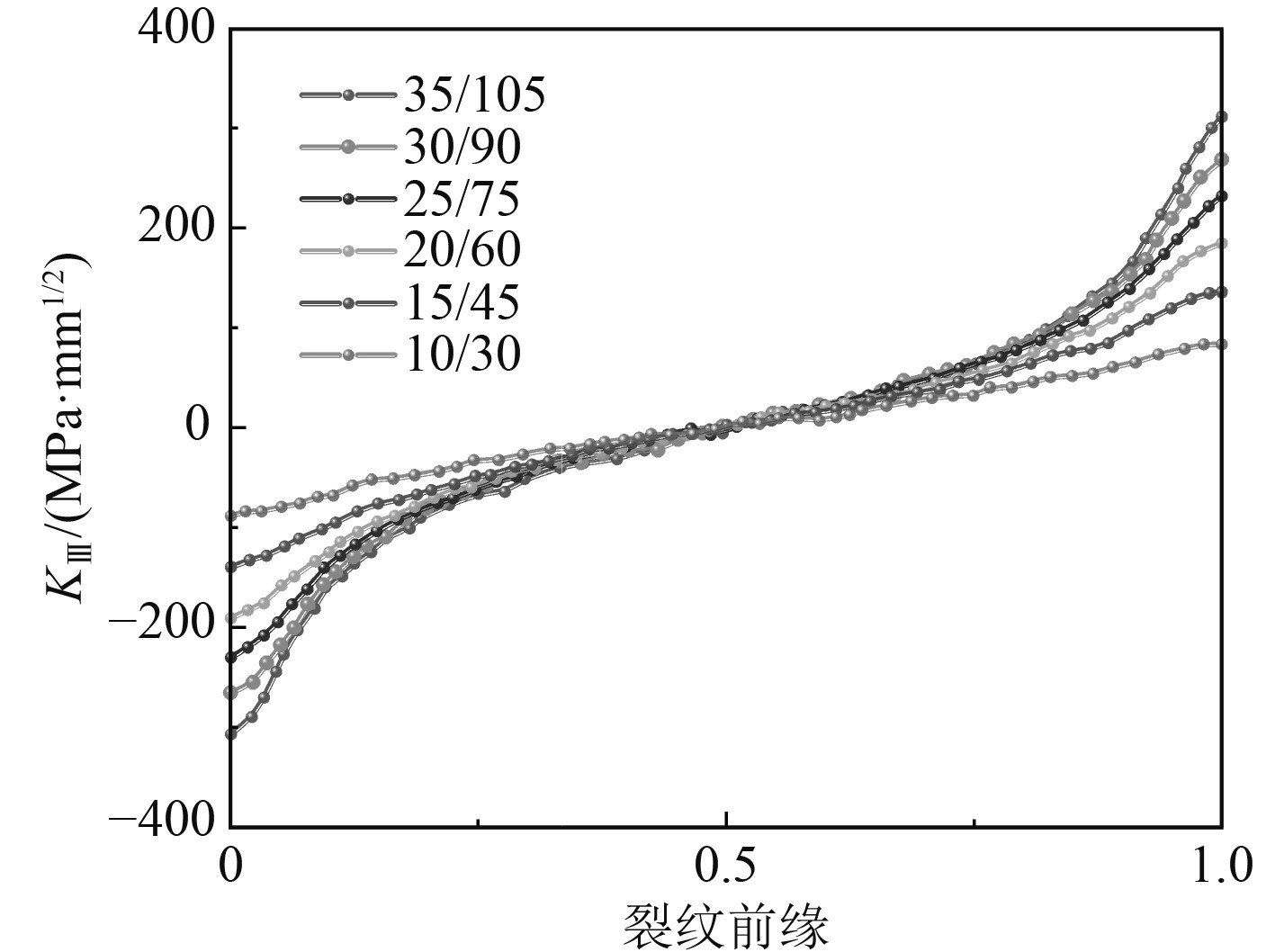
|
图 4 应力强度因子KIII分布图 Fig. 4 Distribution of stress intensity factor KIII |
基于I-II复合型裂纹最大环向应力准则(MTS准则)[9]研究三维裂纹扩展时的偏转角θ。根据此理论得裂纹扩展偏转角θ与KI、KII的关系,如下式:
| $ \theta {\text{ = arccos}}\frac{{3{K_{\rm{II}}}^2 \pm \sqrt {{K_{\rm{I}}}^4 + 8{K_{\rm{I}}}^2{K_{{\rm{II}}}}^2} }}{{{K_{\rm{I}}}^2 + 9{K_{{\rm{II}}}}^2}}。$ | (5) |
将有限元法得到的KI和KII值代入式(5),得到在形状比a/c=1/3下的6个不同初始裂纹前缘的裂纹偏转角,计算结果如图5所示。可以看出,随着裂纹尺寸的增加,裂纹扩展偏转角θ变小,在裂纹深度端点处变化尤为明显,说明裂纹深度端点的偏转角对初始裂纹尺寸最敏感,但最小值发生在裂纹表面长度方向端点附近。基于MTS准则得到的海洋管道裂纹扩展偏转角度并不大,幅值范围仅在0.04°~0.32°。在进行扩展寿命预报时,由于管道裂纹偏转角度不大,可假定裂纹扩展偏转角度为0,此时裂纹扩展模式将简化成I型裂纹扩展模式。
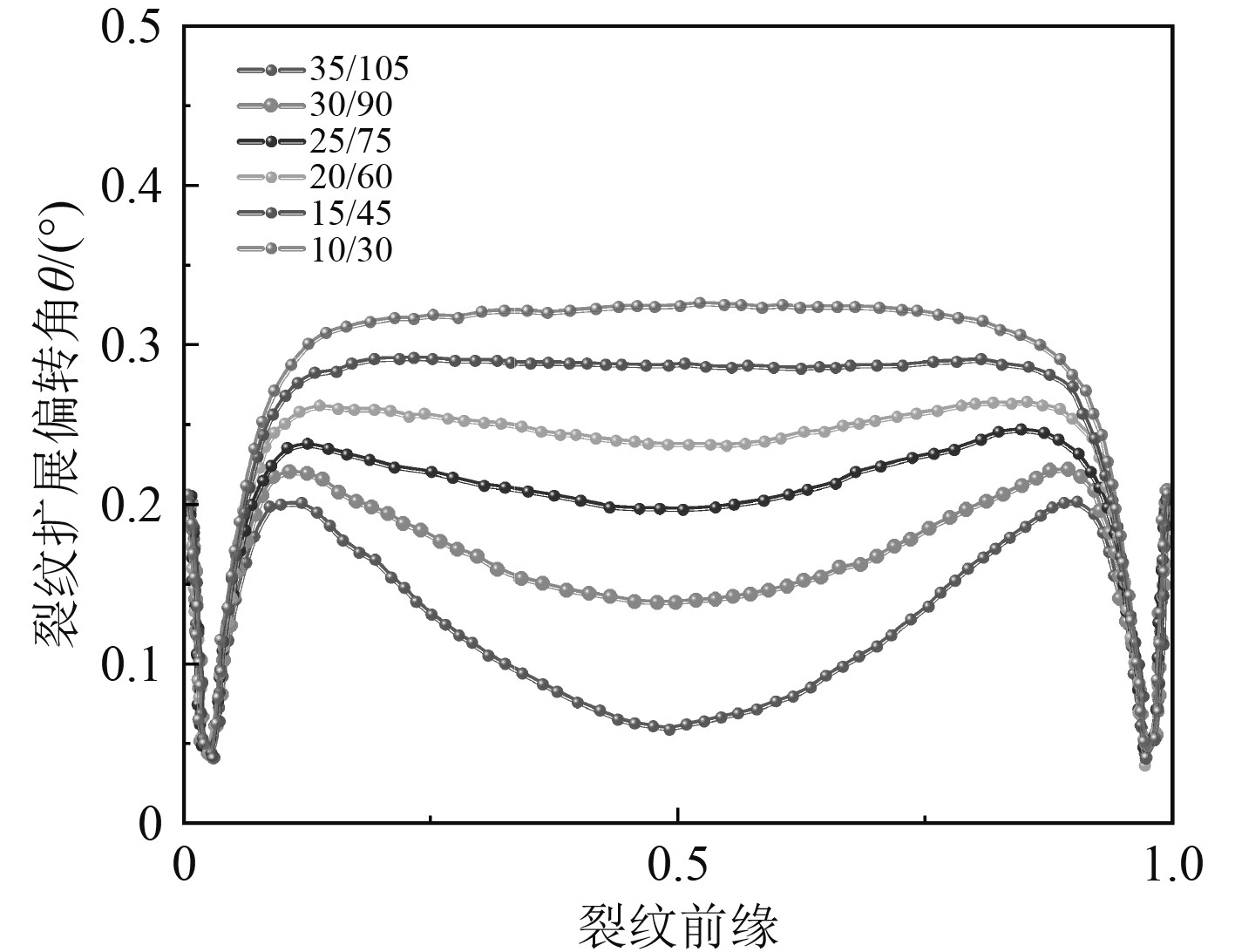
|
图 5 a/c=3海底管道裂纹偏转角度 Fig. 5 Crack deflection angle at a/c=3 |
疲劳扩展寿命数值预报采用da法,其基本思想:每次裂纹尺寸增加Δa,依据双自由度拟合法[7]和Pairs公式求解Δc和ΔN,当K≥KIC时循环停止,输出临界裂纹尺寸ac和裂纹扩展寿命N。利用文献[10]中的X56管道疲劳裂纹扩展试验结果来验证文章数值预报方法的准确度,试验结果如表3所示。数值计算选取初始裂纹尺寸a0、最大加载载荷Pmax和应力比R与试验设定值一致,裂纹形状比暂定a/c=1/3。计算时发现裂纹尺寸增量Δa取值不同,数值预报结果的误差很大,为研究Δa对数值预报的影响及Δa的合理取值,将裂纹尺寸增量Δa取值范围设为0.01~10 mm,计算在不同Δa下的海底管道裂纹扩展寿命,结果如表4所示。
|
|
表 3 X56管道的疲劳裂纹扩展试验数据 Tab.3 Fatigue crack propagation test data of X56 pipeline |
|
|
表 4 选择不同裂纹尺寸增量Δa时的疲劳裂纹扩展寿命 Tab.4 Fatigue crack propagation life at different crack size increments Δa |
可知,当Δa取值0.02mm时,疲劳扩展寿命预报值与试验值接近,误差为2.2%,说明本文海底管道疲劳裂纹扩展寿命计算方法具备一定的准确性。但也可发现该数值预报法的准确度非常依赖于裂纹尺寸增量Δa的取值,选用不同的裂纹尺寸增量时,预报结果相差很大。若以试验数据为精准解,当Δa选用0.01 mm和10 mm时,两者寿命误差达258.2%。Δa取值越小,计算迭代步数越小,计算寿命结果自然越精准,但计算所需耗时也大大增加,从表3能够看出最快与最慢计算耗时之比达到275倍。
显然,工程中若要对全管道进行剩余寿命预报,从计算成本角度考虑,裂纹尺寸增量Δa并不是越小越好。为了在工程预报计算中寻找一个合适的Δa,引入裂纹扩展离散度Vk概念[11],Vk=Δa/(ac-a0)。研究表明[11],若寿命结果要满足工程要求,裂纹扩展离散度应低于3%。
分析表4结果,当Δa≥0.5时寿命预报误差较大,不做考虑。比较Δa=0.01~0.5 mm间的计算精度误差和计算耗时减少率,如图6所示。可知,Δa=0.1 mm是明显的分界点,当Δa≥0.1时,计算耗时减少率相对平缓,但计算出的寿命误差率却成数倍增加;Δa≤0.1时,计算寿命误差率曲线斜率小,寿命误差率变化不大,但计算时间减少率曲线斜率大,计算时间成本大大增加。故综上考虑计算精度及耗时因素,预报疲劳扩展寿命时裂纹尺寸增量Δa取0.1 mm性价比最高,此时对应的裂纹扩展离散度Vk=0.85%,满足文献[11]所得结论。
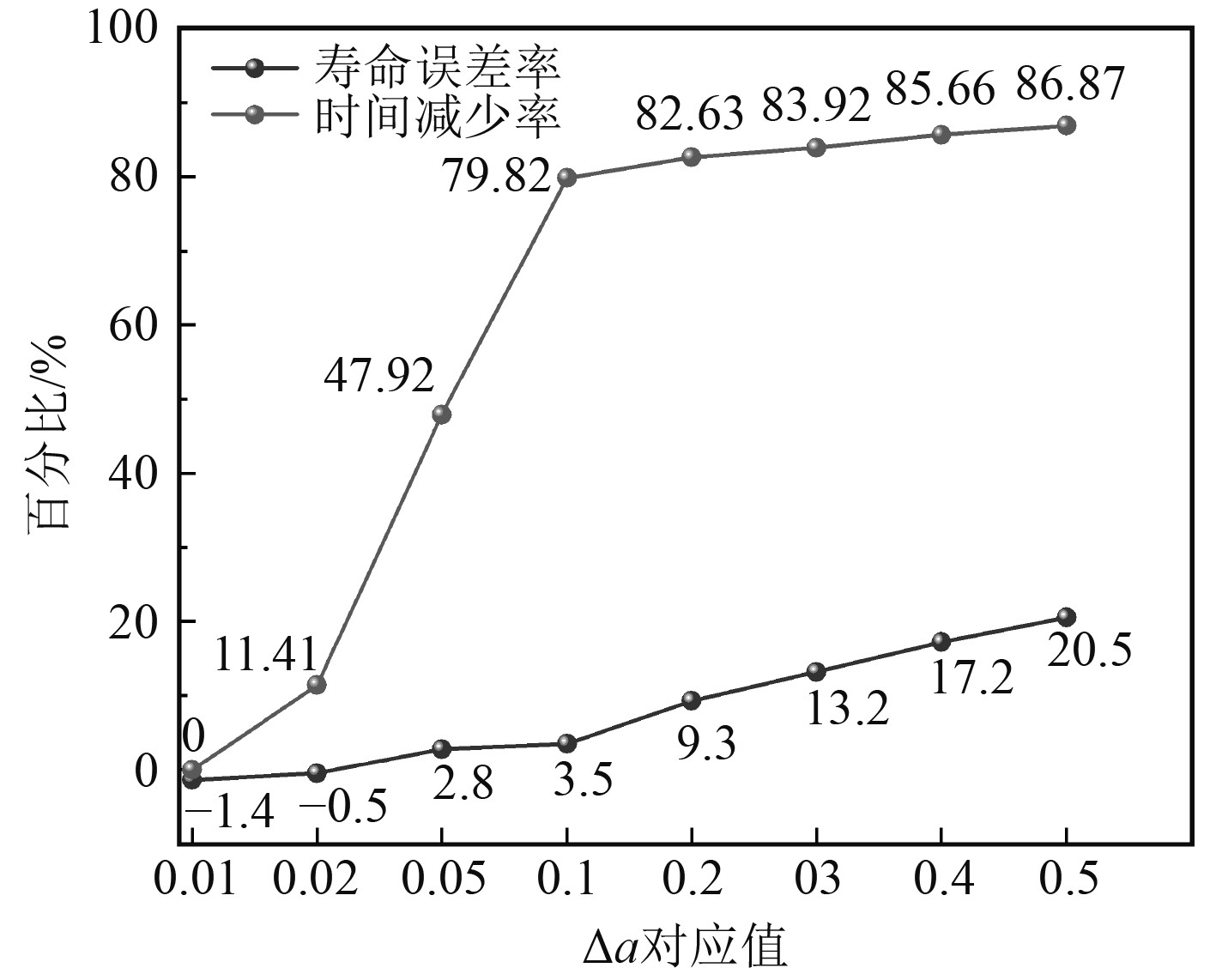
|
图 6 计算精度误差和耗时减少曲线 Fig. 6 Comparison of calculation error and time |
在预报裂纹扩展寿命时,不同裂纹形状比(a/c)会影响计算出的应力强度因子,故同尺寸但不同形状比下的疲劳寿命不同。基于da法求解不同初始尺寸裂纹及形状比下的裂纹扩展寿命,裂纹尺寸增加量Δa取0.1 mm,初始尺寸裂纹尺寸取5~20 mm,形状比a/c取1~5,计算结果如图7所示。由结果可知,裂纹形状比(a/c)对疲劳扩展寿命的影响与初始裂纹尺寸有关,在初始裂纹较小时(a0≤3 mm),不同裂纹形状比计算出的疲劳扩展寿命误差极小。但随着初始裂纹尺寸的增加,裂纹形状比(a/c)越大,则疲劳扩展寿命越大。此外,初始裂纹深度a0越大,距离临界裂纹深度ac越近,疲劳扩展寿命自然越小,图7结果也能够很好体现此规律。但从结果也能发现当裂纹尺寸超过15 mm之后,寿命下降趋势明显平缓,寿命平均变化率为4.4%/ mm,而在裂纹尺寸小于15 mm时,寿命平均变化率则达到10.4%/ mm。
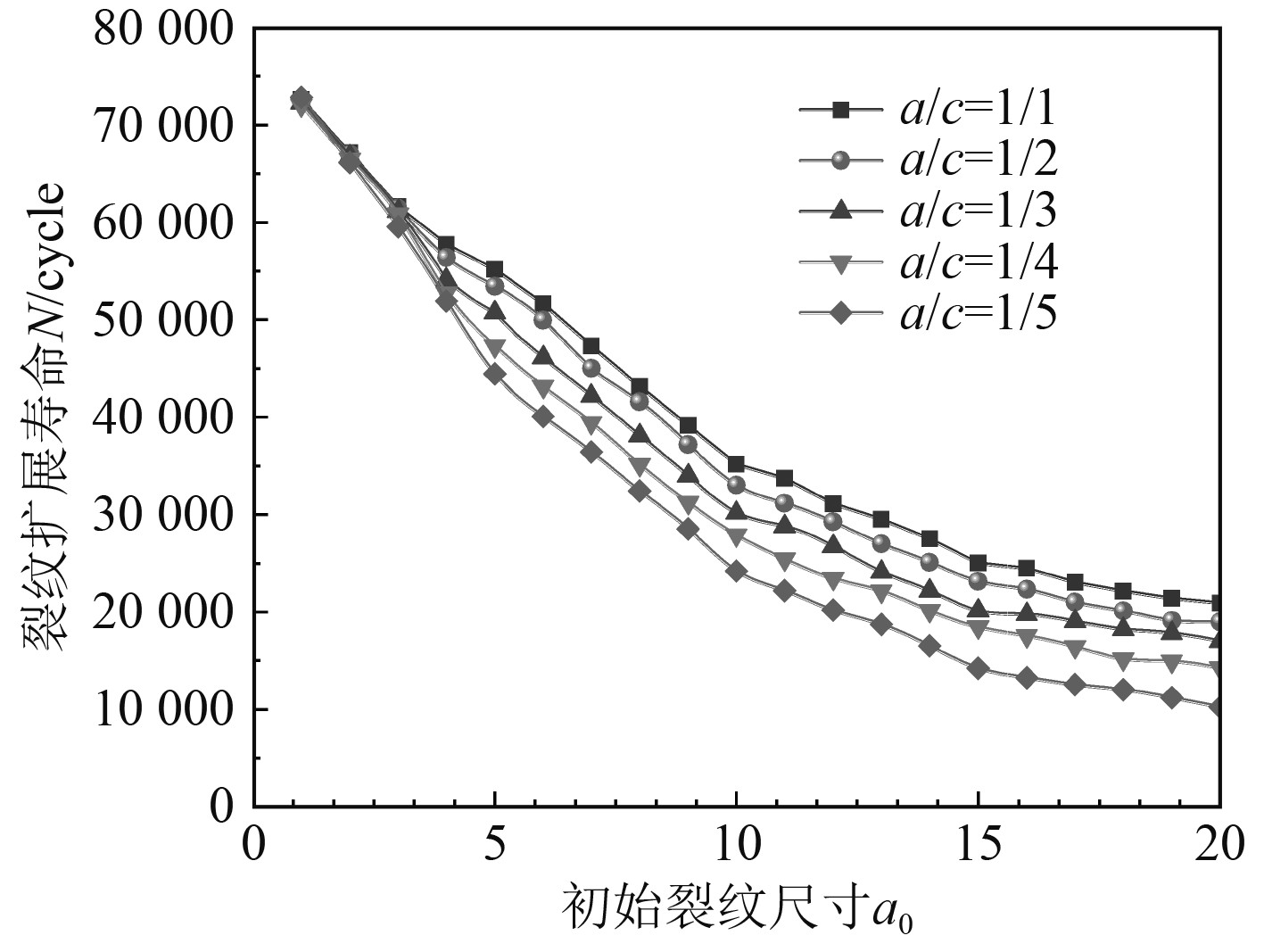
|
图 7 不同裂纹形状比(a/c)下的寿命预报 Fig. 7 Life of different crack shape ratio |
本文利用有限元法和1/4节点位移法计算出管道的裂纹应力强度因子K,基于Pairs公式的da法预报出海底管道的疲劳扩展寿命并分析数值预报中的关键参数,得到如下结论:
1)当裂纹尺寸增量Δa设置合理时, 数值方法预报的管道疲劳剩余寿命与试验值相接近,证明本文海底管道疲劳裂纹扩展寿命数值预报方法具备一定准确性。与试验值存在误差的主要原因为数值计算将裂纹扩展模式全部当成了I型裂纹扩展模式,忽略掉疲劳裂纹扩展的最后快速阶段。
2)裂纹尺寸增量Δa对海底管道裂纹扩展寿命预报影响很大,实际工程中可先通过裂纹扩展离散度Vk选择一个合适的Δa取值范围,再从计算精度和耗时成本角度出发,选择一个最优解。
3)海底管道裂纹形状比a/c对疲劳裂纹扩展寿命的影响程度与初始裂纹大小存在关联。当海底管道裂纹较小时,疲劳扩展寿命数值预报可忽略裂纹形状比a/c的影响。当管道裂纹尺寸扩展达到一定值时,此时裂纹继续增大,疲劳扩展寿命变化却相对平缓。
| [1] |
WORMSEN A, FJELDSTAD A, KIRKEMO F, et al. Fatigue analysis of low alloy steel forgings used in the subsea industry[J]. International Journal of Fatigue, 2016, 96(3): 43-66. |
| [2] |
赵雪健, 王茂廷, 王莲. 海底管道的疲劳寿命估算[J]. 机械设计与制造, 2008(5): 27-29. DOI:10.3969/j.issn.1001-3997.2008.05.012 |
| [3] |
黄如旭, 万正权. 三维裂纹扩展数值预报方法研究[J]. 中国造船, 2019, 60(1): 11-21. DOI:10.3969/j.issn.1000-4882.2019.01.002 |
| [4] |
余建星, 李修波, 谭玉娜, 等. 管道表面蚀坑-裂纹的应力强度因子分析[J]. 天津大学学报(自然科学与工程技术版), 2019, 52(5): 522-528. |
| [5] |
李修波, 余建星, 谭玉娜, 等. 基于EIFS和P-M的海底管道腐蚀疲劳寿命预测[J]. 海洋工程, 2019, 37(1): 84-92. DOI:10.16483/j.issn.1005-9865.2019.01.010 |
| [6] |
IRWIN G R. Analysis of stresses and strains near end of a crack traversing a plate[J]. Journal of Applied Mechanics, 1956, 24(24): 361-364. |
| [7] |
NEWMAN J C, RAJU I S. Prediction of fatigue crack-growth patterns and lives in three-dimensional cracked bodies[J]. Fracture, 1986.
|
| [8] |
陈景杰, 黄一, 刘刚. 基于奇异元计算分析裂纹尖端应力强度因子[J]. 中国造船, 2010, 51(3): 56-64. DOI:10.3969/j.issn.1000-4882.2010.03.007 |
| [9] |
ERGODAN F, SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Fluids Engineering 1963, 85(4): 519-525.
|
| [10] |
高旭东, 邵永波, 谢丽媛, 等. X56海底管道在腐蚀环境下疲劳裂纹扩展过程预测[J]. 材料导报, 2020, 34(2): 2123-2130. DOI:10.11896/cldb.18120135 |
| [11] |
魏周豆. 潜器锥柱结构断裂疲劳特性数值仿真研究[D]. 大连: 大连理工大学, 2019.
|
 2024, Vol. 46
2024, Vol. 46
