多水下机器人编队系统相较于单个机器人,具有鲁棒性强、任务执行效率高等特点,在一些实际工程如海底测绘[1 − 2]、海底管道检测[3 − 4]以及资源探测[5]等中有广阔的应用前景。
在多水下机器人协同控制所包含的众多研究中,编队控制是其中重要的研究内容,其关键问题是如何利用相邻个体的信息来设计编队控制器,使得编队中所有的AUV均能形成期望的编队队形,一些经典的编队控制算法,包括领航者-跟随法、基于行为法、虚拟结构法以及一系列智能算法在以往的研究中取得了很多成果。一致性问题是多智能体系统分布式协同控制的基础,被广泛应用于协同控制、聚集以及传感器网络设计等领域[6]。随着一致性理论的不断发展,越来越多的研究人员开始利用一致性理论解决多机器人的编队控制问题。Ren等[7]证明了领航者-跟随法、基于行为法、虚拟结构法这3种编队策略均可视为基于一致性算法的特殊情况。Lu等[8]提出了有向拓扑条件下,二阶多智能体系统实现时变编队跟踪的充分条件。Dong等[9]提出了具有多个领航者的多智能体系统实现时变编队跟踪控制的充要条件。Han等[10]给出了切换拓扑和时变时延条件下,二阶多智能系统实现时变编队控制的充分条件。在编队避障研究方面,Cao等[11]在一致性算法框架下解决了多智能体系统的编队控制和协同避障问题。Dong等[12]使用一致性算法解决了二阶多无人机系统的编队-包含控制。Xiong等[13]提出一种基于一致性的编队控制律来实现和维持多无人机系统期望的时变编队。Lin等[14]采用容错一致控制策略解决了异构通信拓扑条件下,无领航者的多AUV系统编队控制问题。Yan等[15]在对AUV模型进行反馈线性化处理的基础上,构建了不同拓扑结构和时变时延条件下多AUV系统的编队控制器。为了更真实地模拟多AUV系统的通信模式,Hu等[16]将脉冲控制信号引入到了一致性算法中,解决多AUV系统在间断通信条件下的编队控制问题。
相较于文献[15]中多AUV之间通信拓扑采用无向图结构,本文开展有向图条件下多AUV系统的编队跟踪控制。AUV进行集群作业时,受限于水声通信的带宽问题,通信资源紧张,若集群中个体的通信拓扑为无向图结构,即采用双向通信模式,会占用更多的带宽,不利于大规模集群化的应用。本文所采用的基于一致性的编队跟踪控制算法,其优势在于AUV仅需与邻近个体进行有向的信息交互便能够完成编队,节约了通信资源。针对多AUV系统在执行海洋勘测任务时的特点,将编队中的AUV个体简化为二阶积分器模型。利用局部邻近个体的信息,构建了基于一致性理论的编队跟踪控制协议,并提出了多AUV系统实现编队跟踪控制的充分条件。通过求解黎卡提方程,给出了控制协议增益矩阵的取值。最后,通过数值仿真验证所提算法的有效性。
1 基础理论称
假设1 AUV之间的交互拓扑图存在一个生成树。
引理1
对于矩阵L,存在一个非奇异矩阵
引理2 对于矩阵
| $ {\boldsymbol{A}} \otimes {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}B}&{{a_{12}}B}& \cdots &{{a_{1n}}B} \\ {{a_{21}}B}&{{a_{22}}B}& \cdots &{{a_{2n}}B} \\ \vdots & \vdots & \ddots & \vdots \\ {{a_{m1}}B}&{{a_{m2}}B}& \cdots &{{a_{mn}}B} \end{array}} \right] \in {R^{mp \times nq}} \text{。}$ |
同时含有以下性质:
1)
2)
引理3 考虑系统
考虑一个包含有N个AUV的编队群体,AUV之间的信息交互拓扑可使用一个有向图G来表示。群体中的每个AUV均可由有向图G中的一个节点表示,节点之间的连接权重代表了AUV之间的信息交互强度。在编队控制层面,群体中的每个AUV均可简化为以下二阶积分器模型。
| $ \left\{ {\begin{array}{*{20}{c}} {{{\dot \xi }_i}(t) = {\varsigma _i}(t)} ,\\ {{{\dot \varsigma }_i}(t) = {\tau _i}(t)},\end{array}} \right. i = 1,2,...,N 。$ | (1) |
其中:
AUV在运动过程中,由于轨迹跟踪控制周期远大于姿态调节的控制周期,因此可将AUV的动力学分解为轨迹动力学和姿态动力学。图1为AUV编队的双环控制示意图。其中,内环(姿态控制环)控制器用于驱动AUV实现期望的姿态,外环控制器(轨迹控制环)用于驱动AUV驶向期望的位置。在大规模的AUV编队中,编队的空间尺度远大于单个AUV的特征尺度,可将AUV视为编队中的一个质点。因此,在本文的编队跟踪控制研究中,可将AUV的轨迹动力学模型简化为二阶积分器模型。

|
图 1 多AUV系统双环编队控制示意图 Fig. 1 Two-loop formation control scheme for the multi-AUV systems |
AUV在执行海底测绘、海底管道检测等任务时,通常在固定深度作业。本研究开展的假定作业场景如图2所示,编队中的AUV均在固定深度层运动,AUV在深度方向的协同不予考虑。

|
图 2 作业场景 Fig. 2 Operation scene |
记
| $ {\dot {\boldsymbol{z}}_i}(t) = {\boldsymbol{A}}{{\boldsymbol{z}}_i}(t) + {\boldsymbol{B}}{{\boldsymbol{\tau}} _i}(t)。$ | (2) |
其中:
多AUV系统的期望编队定义为向量
给出多AUV系统实现编队跟踪控制的一致性协议,并给出在该一致性协议下多AUV系统实现编队控制的充分条件,最后给出了求解一致性协议中增益矩阵的方法。
针对多AUV系统(2)考虑如下控制协议:
| $ \begin{split} & {{\boldsymbol{\tau}} _i}(t) = {{\boldsymbol{K}}_1}{{\boldsymbol{z}}_i}(t) + c{{\boldsymbol{K}}_2}\sum\limits_{j \in {N_i}} {[({{\boldsymbol{z}}_i}(t) - {{\boldsymbol{h}}_i}(t)) - ({{\boldsymbol{z}}_j}(t) - {{\boldsymbol{h}}_j}(t))]} ,\\ & i \in N 。\\[-1pt] \end{split} $ | (3) |
其中,c为一个常数值,
定义
| $ \dot {\boldsymbol{z}}(t) = [{{\boldsymbol{I}}_N} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{K_1}) + cL \otimes {\boldsymbol{B}}{{\boldsymbol{K}}_2}]z(t) - (c{\boldsymbol{L}} \otimes {\boldsymbol{B}}{{\boldsymbol{K}}_2})h(t)。$ | (4) |
以下定理给出了多AUV系统(4)实现编队跟踪控制的充分条件。
定理1 在控制协议(3)的作用下,当如下2个条件满足时,多AUV系统(4)实现编队跟踪控制。
1)对于任意的
| $ \mathop {\lim }\limits_{t \to \infty } ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1})({{\boldsymbol{h}}_i}(t) - {{\boldsymbol{h}}_j}(t)) - ({\dot {\boldsymbol{h}}_i}(t) - {\dot {\boldsymbol{h}}_j}(t)) = 0。$ |
2)对于任意的
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{12}} + c{Re} ({\lambda _i}){k_{22}} < 0},\\ {({k_{12}} + c{Re} ({\lambda _i}){k_{22}}){\psi _i} + {c^2}{\rm{Im}} {{({\lambda _i})}^2}k_{21}^2 < 0},\end{array}} \right. $ |
其中,
证明 此处证明参考文献[10]。
令
| $ \begin{split} \dot {\bar {\boldsymbol{z}}}(t) =\,& ({{\boldsymbol{I}}_N} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1}) + c{\boldsymbol{L}} \otimes {\boldsymbol{B}}{{\boldsymbol{K}}_2})\bar {\boldsymbol{z}}(t)+ \\ & ({{\boldsymbol{I}}_N} \otimes ({\boldsymbol{A}} + {\boldsymbol{}}B{{\boldsymbol{K}}_1}))h(t) -({{\boldsymbol{I}}_N} \otimes {{\boldsymbol{I}}_4})\dot h(t) ,\end{split} $ | (5) |
令
| $ \begin{split} \dot {\boldsymbol{\eta}} (t) =\,& ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1}){\boldsymbol{\eta}} (t) +\\ & ({{\tilde {\boldsymbol{u}}}_1} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1})){\boldsymbol{h}}(t) - ({{\tilde {\boldsymbol{u}}}_1} \otimes {{\boldsymbol{I}}_4}){\boldsymbol{h}}(t) ,\end{split} $ | (6) |
| $ \begin{split} \dot {\boldsymbol{\gamma}} (t) =\,& ({{\boldsymbol{I}}_{N - 1}} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1}) + c\bar {\boldsymbol{}}J \otimes {\boldsymbol{B}}{{\boldsymbol{K}}_2}){\boldsymbol{\gamma}} (t) +\\ & (\tilde {\boldsymbol{U}} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1})){\boldsymbol{h}}(t)- (\tilde {\boldsymbol{U}} \otimes {{\boldsymbol{I}}_4})\dot {\boldsymbol{h}}(t) 。\end{split} $ | (7) |
若满足条件(1),则有:
| $ \mathop {\lim }\limits_{t \to \infty } [{\boldsymbol{L}} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1}){\boldsymbol{h}}(t) - ({\boldsymbol{L}} \otimes {\boldsymbol{I}})\dot {\boldsymbol{h}}(t)] = 0。$ | (8) |
将
| $ \mathop {\lim }\limits_{t \to \infty } (\bar {\boldsymbol{J}}\tilde {\boldsymbol{U}} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1})){\boldsymbol{h}}(t) - (\bar {\boldsymbol{J}}\tilde {\boldsymbol{U}} \otimes {I_4})\dot {\boldsymbol{h}}(t) = 0 。$ | (9) |
由于G中含有生成树,由引理1和J的结构可知,
| $ \mathop {\lim }\limits_{t \to \infty } [\tilde {\boldsymbol{U}} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1}){\boldsymbol{h}}(t) - (\tilde {\boldsymbol{U}} \otimes {{\boldsymbol{I}}_4})\dot {\boldsymbol{h}}(t)] = 0。$ | (10) |
考虑如下含有N-1个个体的子系统:
| $ {\dot {\bar {\boldsymbol{\gamma}}} _i}(t) = ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1} + c{{\boldsymbol{\lambda}} _i}{\boldsymbol{B}}{{\boldsymbol{K}}_2}){\bar {\boldsymbol{\gamma}} _i}(t),$ | (11) |
其中,
| $ {\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1} + c{\lambda _i}{\boldsymbol{B}}{{\boldsymbol{K}}_2} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ {{k_{11}} + c{\lambda _i}{k_{21}}}&{{k_{12}} + c{\lambda _i}{k_{22}}} \end{array}} \right],$ |
可得系统(11)的特征多项式为
| $ \dot {\tilde {\boldsymbol{\gamma}}} (t) = [{{\boldsymbol{I}}_{N - 1}} \otimes ({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1}) + c\bar {\boldsymbol{J}} \otimes {\boldsymbol{B}}{{\boldsymbol{K}}_2}]\tilde {\boldsymbol{\gamma}} (t) 。$ | (12) |
由式(7)、式(10)和式(12)可得:
| $ \mathop {\lim }\limits_{t \to \infty } {\boldsymbol{\gamma}} (t) = 0,$ | (13) |
作如下定义:
| $ {\bar {\boldsymbol{z}}_{EC}}(t) = 1 \otimes {\boldsymbol{\eta}} (t) ,$ | (14) |
| $ {\bar {\boldsymbol{z}}_{E\bar C}}(t) = \bar {\boldsymbol{z}}(t) - {\bar {\boldsymbol{z}}_{EC}}(t),$ | (15) |
则有:
| $ {\bar {\boldsymbol{z}}_{EC}}(t) = ({\boldsymbol{U}} \otimes {\boldsymbol{I}}){[{{\boldsymbol{\eta}} ^{\rm{H}}}(t),0]^{\rm{H}}}。$ | (16) |
考虑
| $ {\bar {\boldsymbol{z}}_{E\bar C}}(t) = ({\boldsymbol{U}} \otimes {\boldsymbol{I}}){[0,{{\boldsymbol{\gamma}} ^{\rm{H}}}(t)]^{\rm{H}}}。$ | (17) |
由于
| $ \mathop {\lim }\limits_{t \to \infty } (\bar z(t) - 1 \otimes {\boldsymbol{\eta}} (t)) = 0 ,$ | (18) |
即对于
| $ \mathop {\lim }\limits_{t \to \infty } ({z_i}(t) - {{\boldsymbol{h}}_i}(t) - {\boldsymbol{\eta}} (t)) = 0 。$ | (19) |
由式(19)可得,多AUV系统(4)实现了由
根据文献[21],使用局部黎卡提方程求解一致性协议(3)中增益矩阵
定理2 对于局部控制协议(3),取控制增益
| $ {{\boldsymbol{K}}_2} = - {{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{B}}^{\rm T}}{\boldsymbol{P}},$ | (20) |
| $ 0 = {({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1})^{\rm T}}{\boldsymbol{P}} + {\boldsymbol{P}}({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1}) + {\boldsymbol{Q}} - {\boldsymbol{PB}}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{B}}^{\rm T}}{\boldsymbol{P}},$ | (21) |
| $ c \geqslant \frac{1}{{2{{\min }_{i \in N - 1}}{{\mathrm{Re}}} ({\lambda _i})}}。$ | (22) |
其中,
证明 将矩阵L的特征值表示为
| $ \begin{split} & {({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1} + c{{\boldsymbol{\lambda}} _i}{\boldsymbol{B}}{{\boldsymbol{K}}_2})^{\rm{H}}}{\boldsymbol{P}} + {\boldsymbol{P}}({\boldsymbol{A}} + {\boldsymbol{B}}{{\boldsymbol{K}}_1} + c{\lambda _i}{\boldsymbol{B}}{{\boldsymbol{K}}_2})= \\ & - {\boldsymbol{Q}} - (2c{\alpha _i} - 1){{\boldsymbol{K}}_2}^{\rm T}{\boldsymbol{R}}{{\boldsymbol{K}}_2}。\end{split} $ | (23) |
由李雅普诺夫理论[22]可得,若
为验证所提出的多AUV系统实现编队跟踪控制算法的有效性,首先开展包含有3个AUV个体的编队跟踪控制仿真。本文所设计的控制协议具有规模可扩展性的特点,为此进行包含有5个个体的多AUV系统的编队跟踪控制仿真对其进行验证。
4.1 仿真试验1假定编队中有3个AUV在进行协同作业,即
| $ {{\boldsymbol{h}}_i}(t) = \left[ {\begin{array}{*{20}{c}} {10\sin (t/2 + 2{\text{π}} (i - 1)/3)} \\ {10\cos (t/2 + 2{\text{π}} (i - 1)/3)} \\ {5\cos (t/2 + 2{\text{π}} (i - 1)/3)} \\ { - 5\sin (t/2 + 2{\text{π}} (i - 1)/3)} \end{array}} \right],(i = 1,2,3)。$ |
采用定理2中的方法求解,取
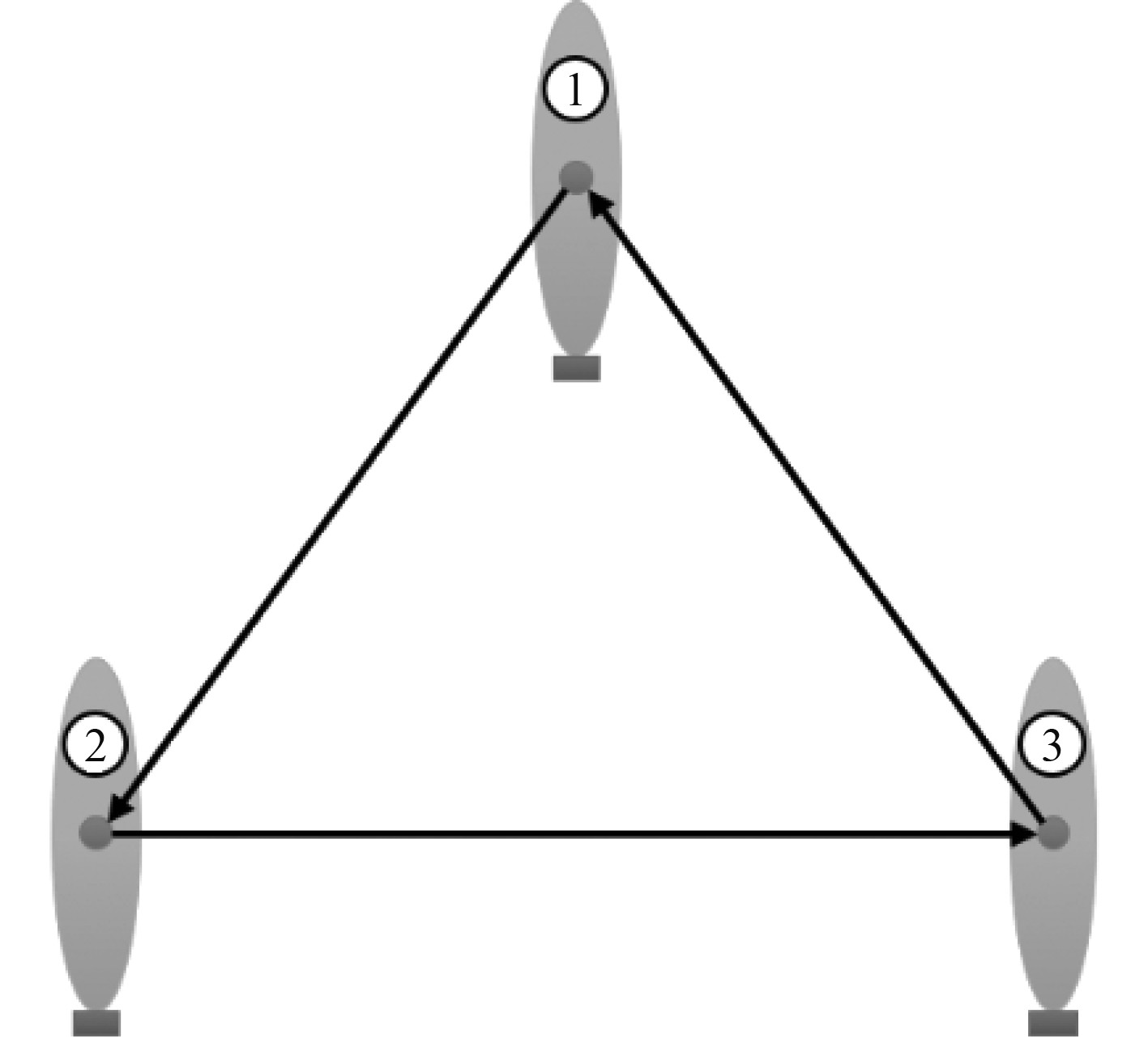
|
图 3 AUV编队通信拓扑 Fig. 3 Communication topology of the AUV formation |
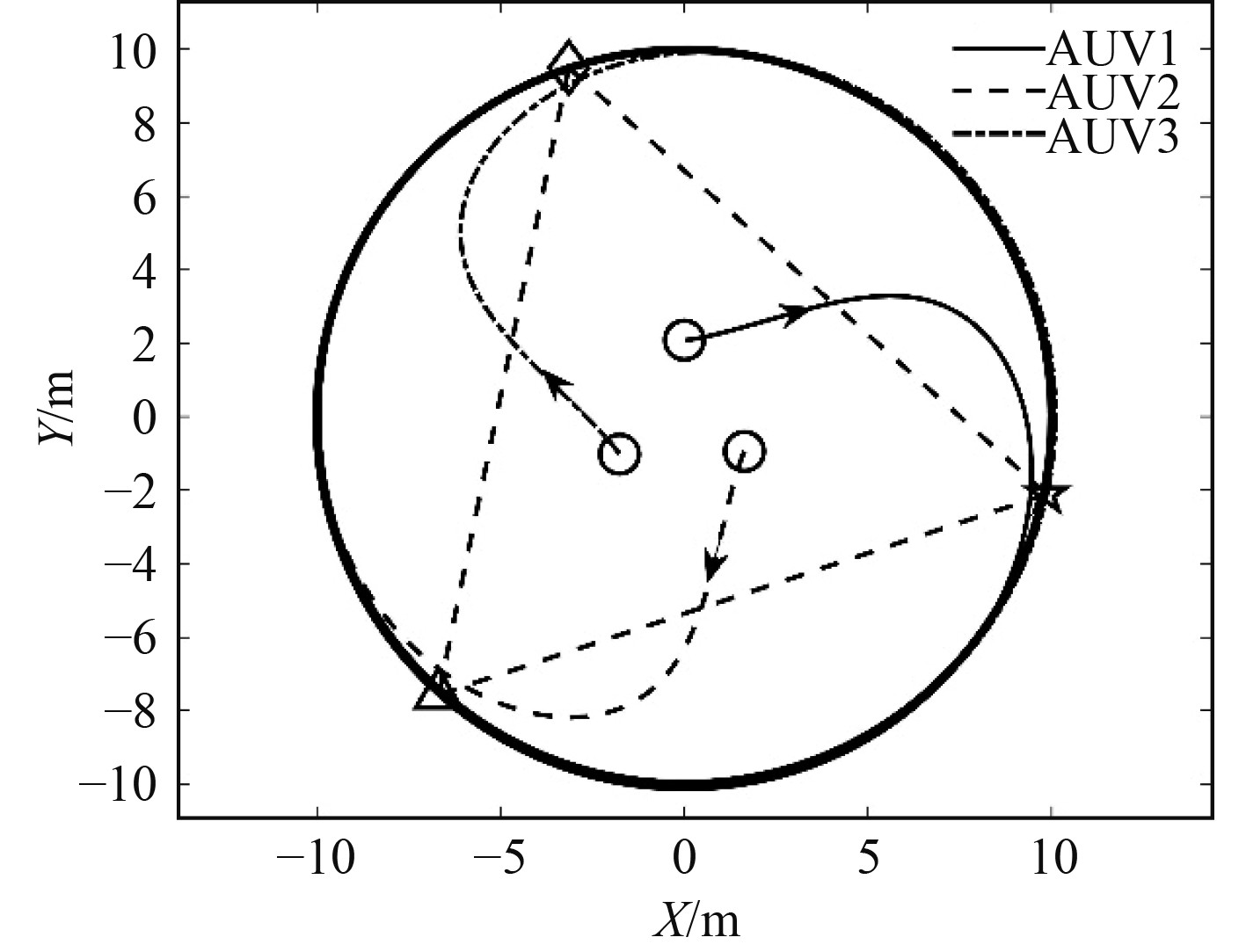
|
图 4 AUV编队路径轨迹 Fig. 4 Path trajectories of the AUV formation |

|
图 5 AUV编队速度轨迹 Fig. 5 Velocity trajectories of the AUV formation |

|
图 6 AUV编队路径跟踪误差 Fig. 6 Path tracking errors of the AUV formation |
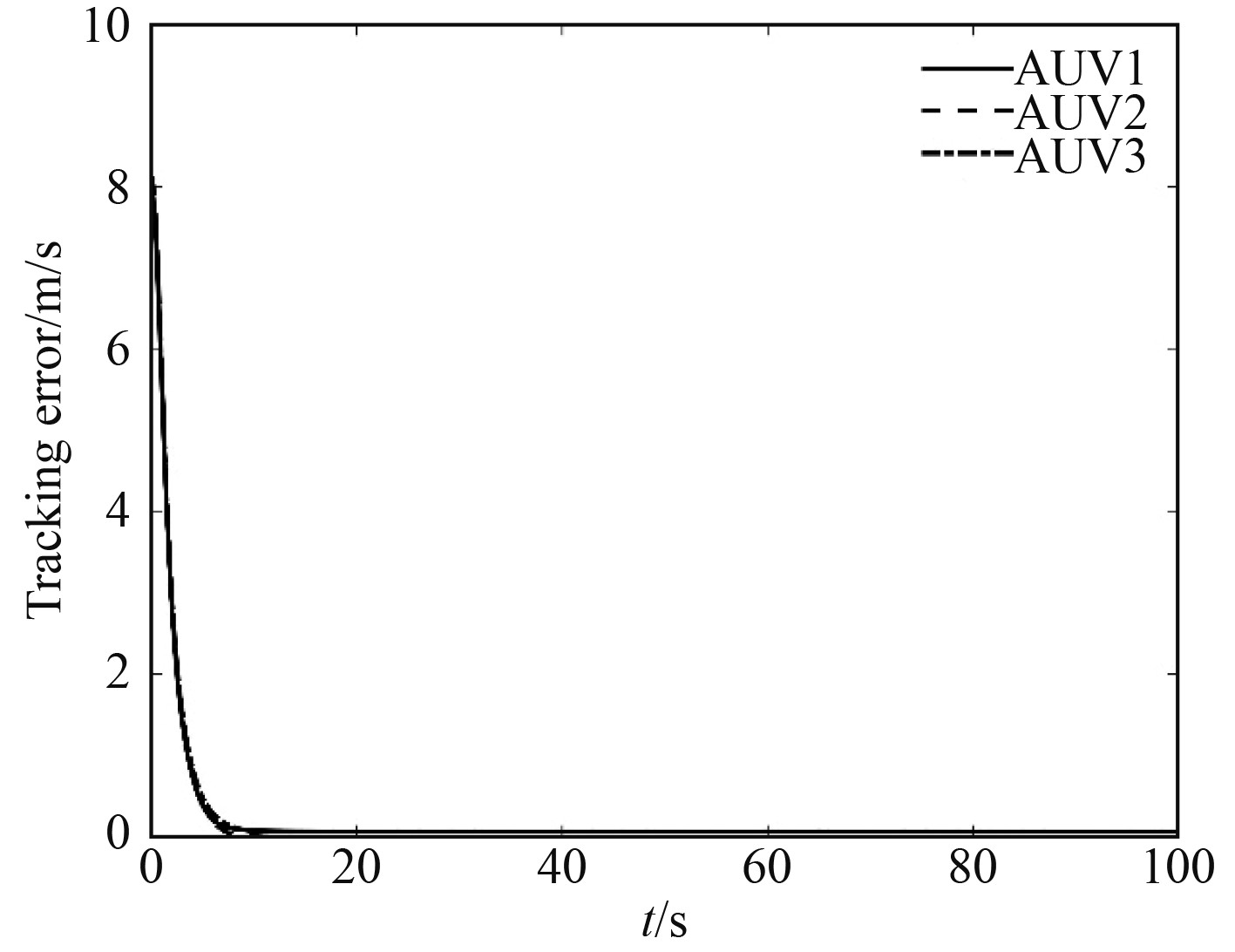
|
图 7 AUV编队速度跟踪误差 Fig. 7 Velocity tracking errors of the AUV formation |
假定有编队中5个AUV在进行协同作业,即
| $ {{\boldsymbol{h}}_i}(t) = \left[ {\begin{array}{*{20}{c}} {10\sin (t/2 + 2{\text{π}} (i - 1)/5)} \\ {10\cos (t/2 + 2{\text{π}} (i - 1)/5)} \\ {5\cos (t/2 + 2{\text{π}} (i - 1)/5)} \\ { - 5\sin (t/2 + 2{\text{π}} (i - 1)/5)} \end{array}} \right],(i = 1,2,3,4,5)。$ |
同样采用定理2所提方法求解参数,取c=3,
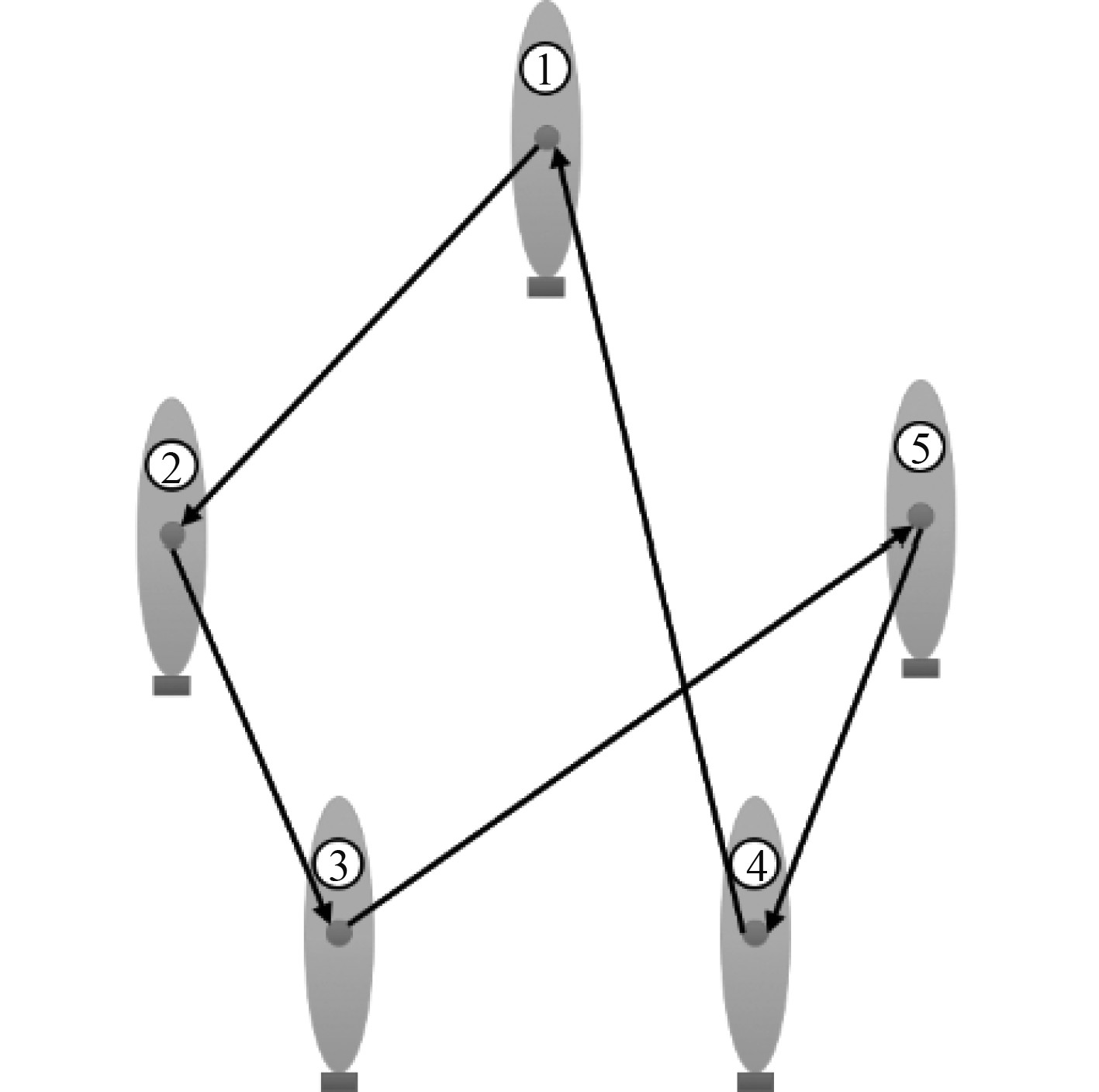
|
图 8 AUV编队通信拓扑 Fig. 8 Communication topology of the AUV formation |

|
图 9 AUV编队路径轨迹 Fig. 9 Path trajectories of the AUV formation |
|
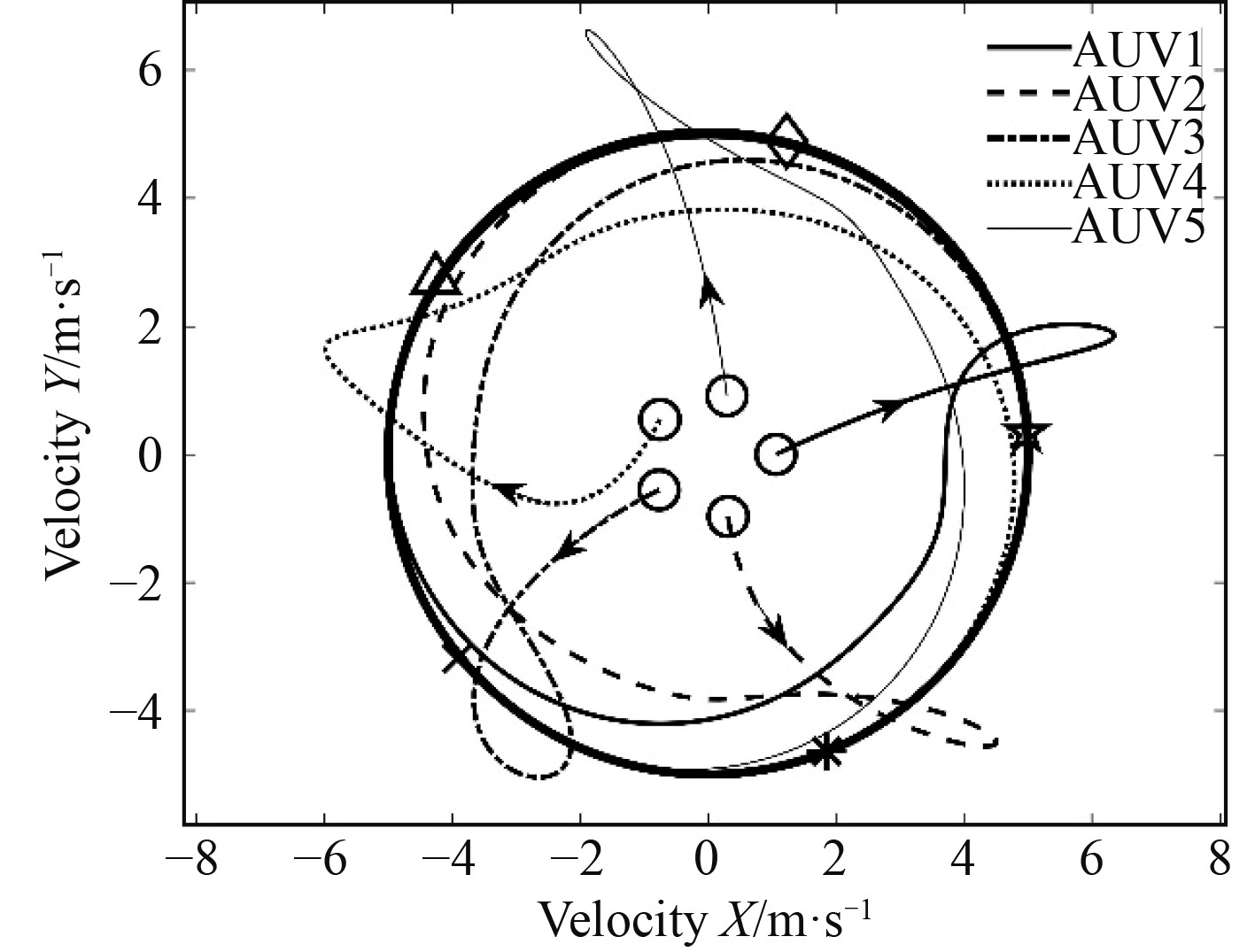
图 10 AUV编队速度轨迹 Fig. 10 Velocity trajectories of the AUV formation |
|
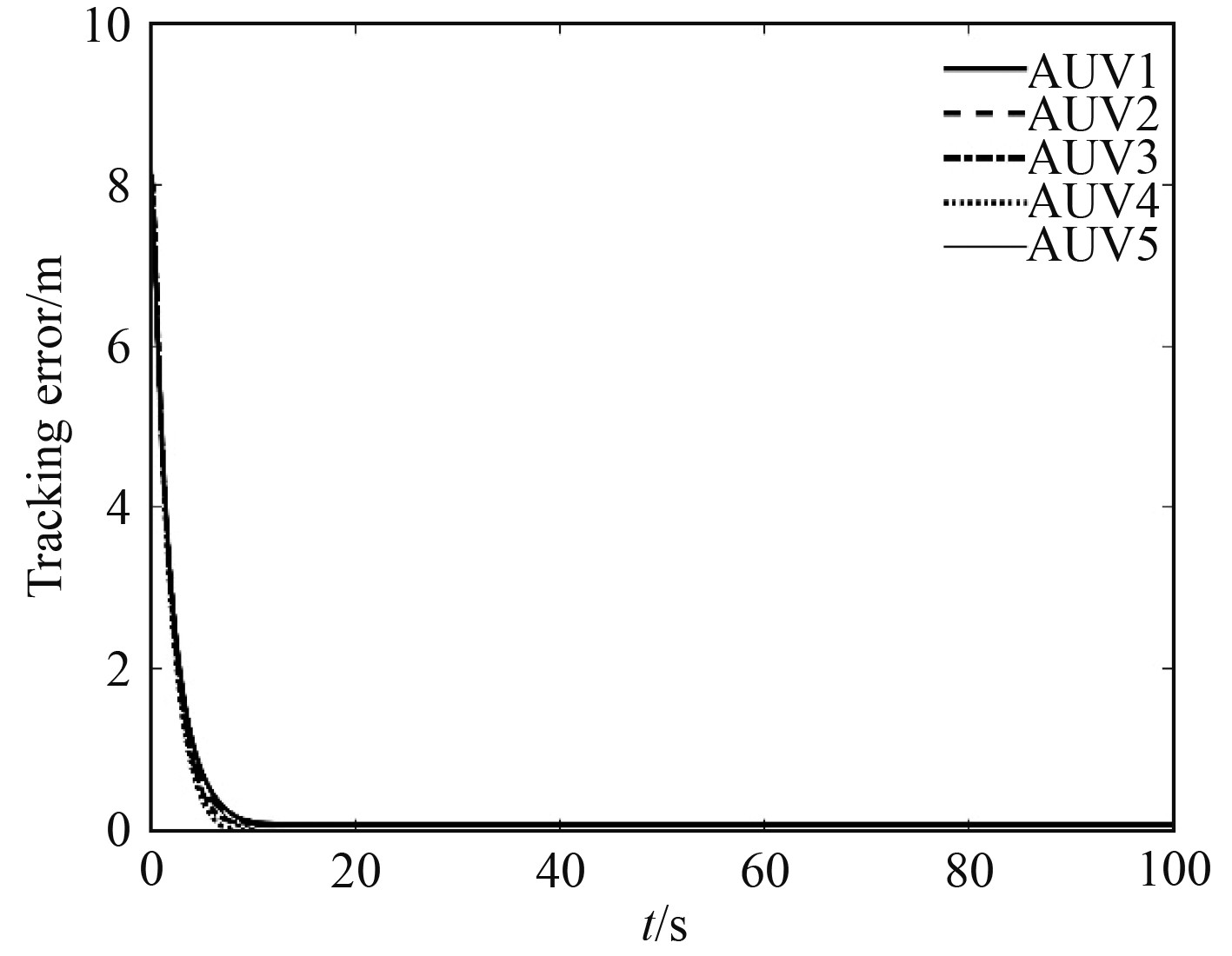
图 11 AUV编队路径跟踪误差 Fig. 11 Path tracking errors of the AUV formation |
|
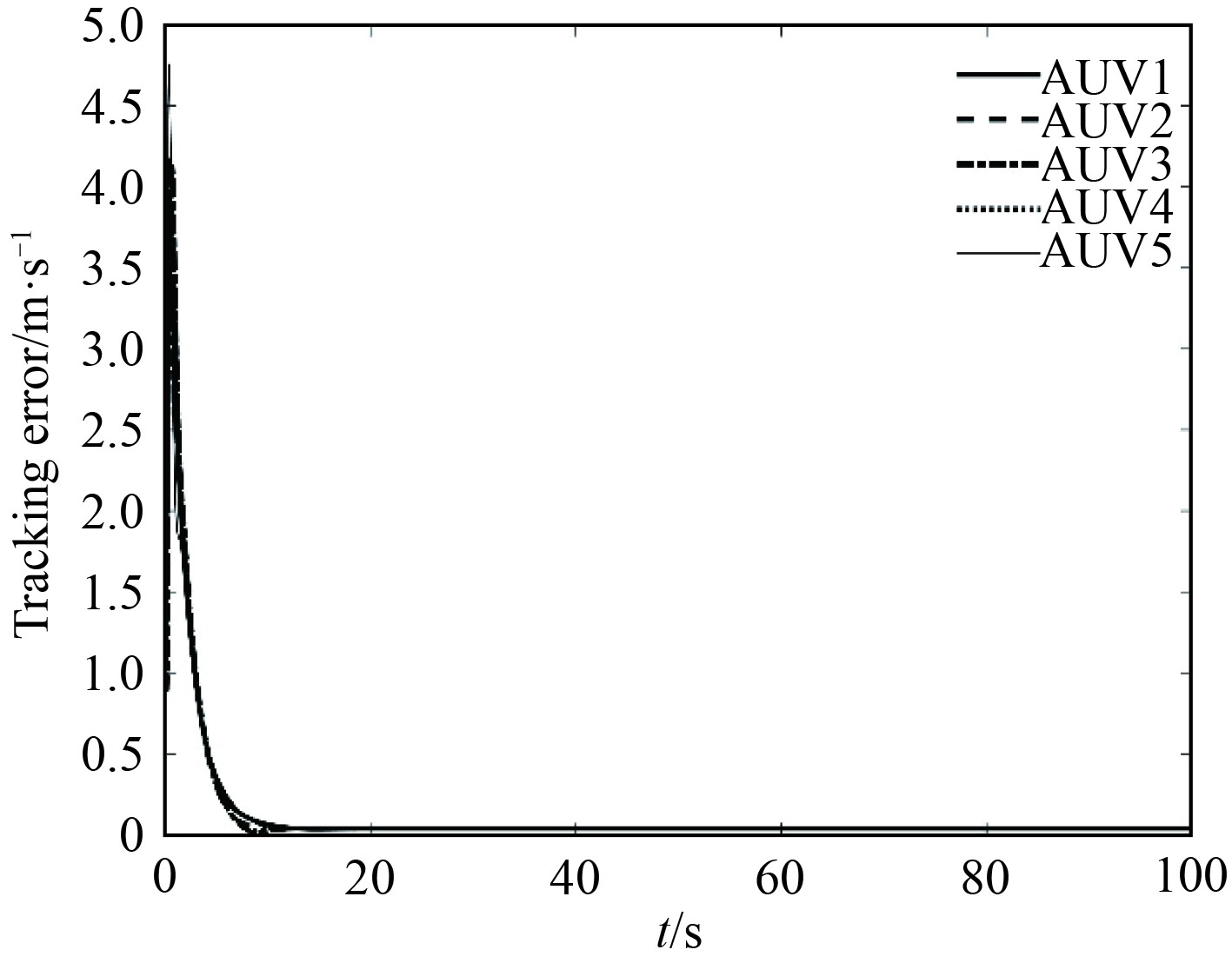
图 12 AUV编队路径跟踪误差 Fig. 12 Velocity tracking errors of the AUV formation |
本文针对面向海洋观测任务的多水下机器人编队跟踪控制问题开展研究。基于一致性理论设计了编队控制协议,提出在该控制协议的作用下,多水下机器人系统实现编队跟踪控制的充分条件,基于Lyapunov稳定性理论给出了编队控制协议增益矩阵的方法,通过数值仿真验证了本文提出方法的有效性。研究结果表明:
1)AUV仅需与邻近个体进行有向的信息交互,即可完成期望的编队跟踪;
2)若期望的编队满足所推导的充分条件,多AUV系统能够快速准确地实现编队跟踪;
3)所设计的编队控制协议,具有良好的规模可扩展性,可根据AUV的数量灵活设计队形。
| [1] |
CAMPBELL K J, KINNEAR S, THAME A. AUV technology for seabed characterization and geohazards assessment[J]. The Leading Edge, 2015, 34(2): 170-178. DOI:10.1190/tle34020170.1 |
| [2] |
PAULL L, SETO M, LI H. Design and implementation of an AUV for petroleum pipeline inspection[C]// 2015 7th International Conference on Information Technology and Electrical Engineering (ICITEE). Piscataway: IEEE, 2014: 6592−6599.
|
| [3] |
TIPSUWAN Y, HOONSUWAN P. Design and implementation of an AUV for petroleum pipeline inspection[C]// 2015 7th International Conference on Information Technology and Electrical Engineering (ICITEE). Piscataway: IEEE, 2015: 382−387.
|
| [4] |
PETILLOT Y R, REED S R, BELL J M. Real time AUV pipeline detection and tracking using side scan sonar and multi-beam echo-sounder[C]// OCEANS’02 MTS/IEEE. Piscataway: IEEE, 2002: 17−222.
|
| [5] |
OHTA Y, YOSHIDA H, ISHIBASHI S, et al. Seabed resource exploration performed by AUV Yumeiruka[C]// OCEANS 2016 MTS/IEEE Monterey. Piscataway: IEEE, 2016: 1−4.
|
| [6] |
XUE L, LIU Y, GU Z Q, et al. Joint design of clustering and in-cluster data route for heterogeneous wireless sensor networks[J]. International Journal of Automation and Computing, 2017, 14(6): 637-649. DOI:10.1007/s11633-017-1094-7 |
| [7] |
REN W. Consensus strategies for cooperative control of vehicle formations[J]. IET Control Theory & Applications, 2007, 1(2): 505-512. |
| [8] |
LU X, AYSTIN F, CHEN S. Formation control for second-order multiagent systems with time-varying delays under directed topology[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(3): 1382-1391. DOI:10.1016/j.cnsns.2011.07.029 |
| [9] |
DONG X, HU G. Time-varying formation tracking for linear multiagent systems with multiple leaders[J]. IEEE Transactions on Automatic Control, 2017, 62(7): 3658-3664. DOI:10.1109/TAC.2017.2673411 |
| [10] |
HAN L, DONG X, LI Q, et al. Formation control for time-delayed second-order multi-agent systems with switching topology[C]// 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC). Piscataway: IEEE, 2018: 1−6.
|
| [11] |
CAO J F, LING Z H, YUAN Y F, et al. Distributed formation control for a multi-agent system with dynamic and static obstacle avoidances[J]. Chinese Physics B, 2014, 23(7): 070509. DOI:10.1088/1674-1056/23/7/070509 |
| [12] |
DONG X, HUA Y, ZHOU Y, et al. Theory and experiment on formation-containment control of multiple multirotor unmanned aerial vehicle systems[J]. IEEE Transactions on Automation Science and Engineering, 2018, 16(1): 229-240. |
| [13] |
XIONG T, PU Z, YI L, et al. Consensus based formation control for multi-uav systems with time-varying delays and jointly connected topologies[C]// 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE). Piscataway: IEEE, 2018: 292−297.
|
| [14] |
LIN X, TIAN W, ZHANG W. The leaderless multi-AUV system fault-tolerant consensus strategy under heterogeneous communication topology[J]. Ocean Engineering, 2021, 237.
|
| [15] |
YAN Z P, LIU Y B, C B. Leader-following coordination of multiple UUVs formation under two independent topologies and time-varying delays[J]. Journal of Central South University, 2017, 24(2): 382-393. DOI:10.1007/s11771-017-3440-x |
| [16] |
HU Z, MA C, ZHANG L, et al. Formation control of impulsive networked autonomous underwater vehicles under fixed and switching topologies[J]. Neurocomputing, 2015, 147: 291-298. DOI:10.1016/j.neucom.2014.06.060 |
| [17] |
GODSIL C, ROYLE G F. Algebraic graph theory[M]. Berlin: Springer, 2004.
|
| [18] |
FAX J A, MURRAY R M. Information flow and cooperative control of vehicle formations[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1465-1476. DOI:10.1109/TAC.2004.834433 |
| [19] |
HORN R A, JOHNSON C R. Topics in matrix analysis[M]. Cambridge, UK: Cambridge University Press, 1991.
|
| [20] |
ZAHREDDINE Z, ELSHEHAWEY E F. On the stability of a system of differential equations with complex coefficients[J]. Indian Journal Pure Application Mathematics, 1988, 19(10): 963-972. |
| [21] |
ZHANG H, LEWIS F L, Das A. Optimal design for synchronization of cooperative systems: state feedback, observer and output feedback[J]. IEEE Transactions on Automatic Control, 56(8): 1948−1952.
|
| [22] |
CHEN CT. Linear system theory and design[M]. New York: Holt, Rinchart and Winston, 1984.
|
 2024, Vol. 46
2024, Vol. 46
