AUV协同制导方法是多个AUV通过信息交互,基于终端约束条件(如时间,终端角度与速度等)设计相应协同制导律,最终达到提高AUV突防概率与毁伤效能的目的。协同制导方法最早由In-Soo Jeon等[1]提出,是一种可应用于反舰导弹齐射的具有终端时间约束的协同制导方法,用于引导多导弹在理想时间内打击静止舰艇目标。
协同制导方法可分为开环与闭环2种,两者的区别在于在导引过程中是否存在信息交互。相较于前者,闭环协同制导方法更能体现成员之间的协同性,其根据通信拓扑结构的不同可分为集中式和分布式。张友安等[2]提出一种领弹-从弹协同制导架构,其属于典型的集中式通信结构,需要一个成员能掌握总体信息并与剩余其他成员进行通信,该方法对于通信要求较高,抗干扰能力相对较弱。而分布式结构中各成员只与相邻成员进行通信交流,降低了通信要求,并且个别成员出现通信故障时不会对整体结构产生影响,从而提高系统鲁棒性,因此也成为了相关研究的趋势。针对三维空间固定目标的分布式协同制导方法,Chen等[3]基于固定时间收敛理论与分布式滑模提出了一种多枚导弹同时攻击机动目标的三维鲁棒非线性协同制导律,LOS角的收敛时间缩短了30%左右,同时可将LOS角的脱靶量和误差降低80%以上。Dong[4]针对具有不同导引头视场约束的多枚导弹,设计了一种分布式三维非奇异协同制导律,以实现对静止目标的齐射攻击,其制导律是具有2个辅助函数的偏置比例制导方法,以保证制导律的非奇异性并满足FOV约束。针对于各成员导引律的优化研究,Zhai等[5]提出了一种基于时变的改进终端滑模的制导律,其能保持飞行控制的连续性和稳定性,并能在一定程度上消除滑模的奇异性和抖振性。Yu等[6]针对于机动目标的协同打击,设计了一种基于固定时间的非奇异终端滑模制导律,引入了饱和函数用以避免常用的符号函数引起的抖振问题。而针对通信拓扑结构切换、不持续连通以及部分节点故障情况的研究,Zhao等[7]提出了两步制导策略。第1步采用基于局部邻域信息的多枚导弹DGCG法,实现多枚导弹航程和前置角的群体一致;第2步每枚导弹在比例导航制导律下攻击目标。通过反馈线性化和收敛分析,分别给出了多枚导弹在固定定向通信拓扑和切换定向通信拓扑下实现群协同攻击的充分条件。马文卉等[8]结合牵制控制和预定时间理论,基于 M 矩阵假设的牵制分组误差和预定时间尺度函数提出拓扑切换三维预定时间协同制导律。叶鹏鹏等[9]针对于协同制导过程中的通信丢包、拓扑切变以及通信中断,基于通信采样数据设计了一种分布式线性协同制导律。王青等[10]考虑固定与切换2种情况下存在通信延迟的多导弹协同制导问题,其通信延迟采用固定值0.2 s进行计算。姜尚等[11]考虑了0~0.5 s之间的随机波动通信延迟的导弹分布式自适应协同制导方法。
协同制导方法在水下领域的研究相对较少。对水下协同制导方法而言,区别于空中的电磁通信,水声通信的延迟受传播距离的影响较大,不能简单的用固定或随机时间延迟来表示,并且水声信号发射存在一定的时间周期,而降低水声通信的频次有助于减少系统能耗并提高隐蔽性,更加满足工程应用需求。为此本文针对二维平面内的定速直航目标,建立AUV-目标相对运动模型以获得更加准确的剩余时间作为协调变量,基于比例导引法设计一种变比例系数和速度时变的多阶段协同制导律,并使用李雅普诺夫函数进行了制导律有限时间收敛的验证。制导第一个阶段针对于中远距离巡航过程,采用有向通信拓扑结构,建立了AUV的实时水声通信延迟模型,并且考虑不同的通信周期对于协同制导的影响,在一阶段结束前使各AUV剩余时间趋于一致,第一阶段也是本文分析的重点。第二阶段为断开通信连接的开环式协同制导,以最先进入末端制导范围的AUV剩余时间作为标准进行参数调节,末端制导范围大小主要取决于目标对水声通信的探测能力,最终实现同时打击目标。对以上模型进行仿真验证,结果表明该制导律具有较高精度。最后,针对不同情况下各参数的调节趋势进行了分析研究。
1 问题描述 1.1 协同制导模型假设1组n个AUV拦截定速直航目标,如图1所示。其中
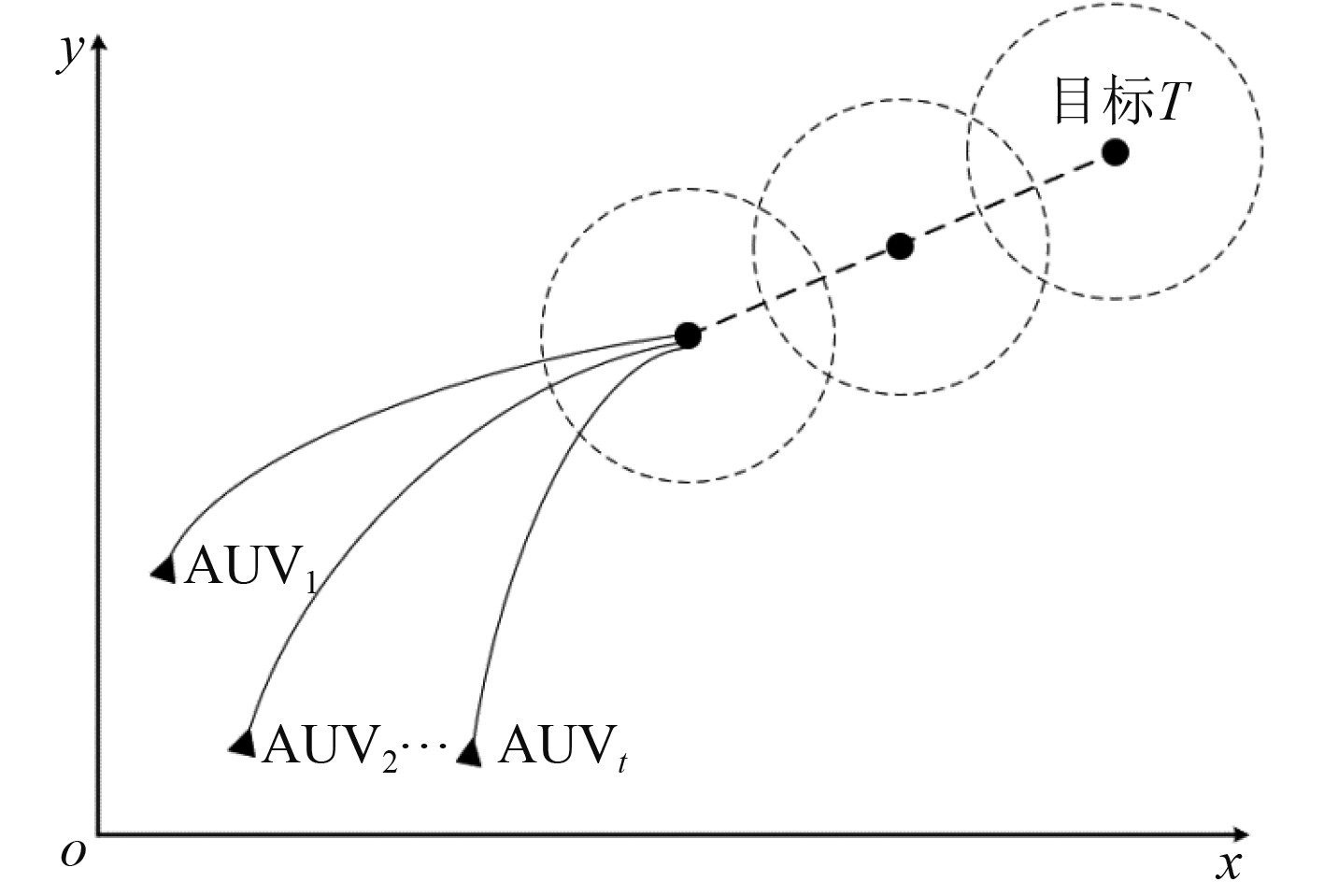
|
图 1 AUVi协同攻击示意图 Fig. 1 AUVi coordinated attack schematic |
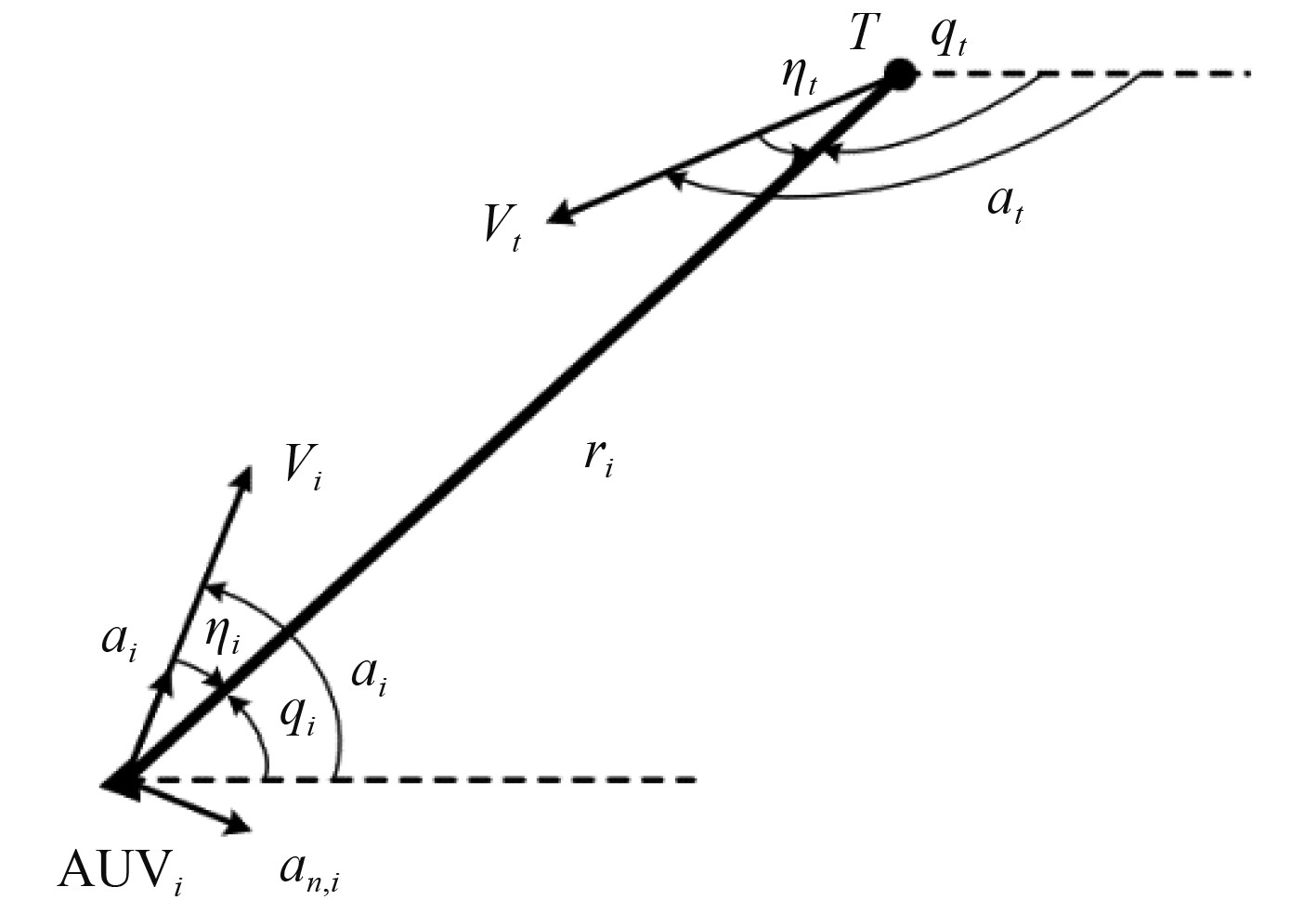
|
图 2
|
图中,
| $ \frac{{\rm{d}}{r}_{i}}{{\rm{d}}t}={v}_{t}\cdot {\rm{cos}}{\eta }_{t}-{v}_{i}\cdot {\rm{cos}}{\eta }_{i} \text{,}$ | (1) |
| $ \frac{{\rm{d}}{q}_{i}}{{\rm{d}}t}=({v}_{i}\cdot {\rm{sin}}{\eta }_{i}-{v}_{t}\cdot {\rm{sin}}{\eta }_{t})/{r}_{i}\text{,} $ | (2) |
| $ {q}_{i}={q}_{t}={\alpha }_{i}+{\eta }_{i}={\alpha }_{t}+{\eta }_{t} \text{。}$ | (3) |
| $ {a}_{i}=\frac{{\rm{d}}{v}_{i}}{{\rm{d}}t}\text{,} $ | (4) |
| $ {a}_{ni}=\frac{{\rm{d}}{\alpha }_{i}}{{\rm{d}}t}\cdot {v}_{i}\text{。} $ | (5) |
AUV之间的通信拓扑关系可用图论中的图表示。图是指若干给定的点以及连接两点的线所构成的图形,以点表示实体,用连接两点的线表示通信关系。图可表示为
AUV之间的通信拓扑图G的邻接矩阵可表示为
| $ {l}_{ii}=\sum _{j=1}^{n}{a}_{ij} \text{,}$ | (6) |
| $ {l}_{ij}=-{a}_{ij}i\ne j \text{。}$ | (7) |
针对于AUV协同制导问题,其通信图需满足存在一条通信链路能包括所有的AUV。若通信图G是无向的,则有以下引理[12]:
引理1 拉普拉斯矩阵L是半正定的对称矩阵,且仅有一个0特征值,其他特征值为正。
引理2 以下等式成立:
| $ {\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{x}=\frac{1}{2}\sum _{i=1}^{n}\sum _{j=1}^{n}{a}_{ij}{({x}_{j}-{x}_{i})}^{2} 。$ | (8) |
引理3 对于任意
| $ {\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{x}\geqslant \lambda {\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{x} \text{。}$ | (9) |
其中,
针对系统稳定性分析有以下引理[13]:
引理4 针对非线性系统
| $ \dot{V}\left(x\right)\leqslant -c{V}^{\alpha }\left(x\right),c > 0,\mathrm{ }0 < \alpha < 1 \text{,}$ | (10) |
则系统能在有限时间内稳定收敛,且收敛时间为:
| $ {T}_{x}\left({x}_{0}\right)\leqslant \frac{{V}^{1-\alpha }\left({x}_{0}\right)}{c(1-\alpha )} \text{。}$ | (11) |
采用比例导引法作为底层制导律,其制导机理为AUV速度转动速率与AUV-目标视线转动速率成比例:
| $ \frac{{\rm{d}}{\alpha }_{i}}{{\rm{d}}t}={m}_{i}\frac{{\rm{d}}{q}_{i}}{{\rm{d}}t} \text{。}$ | (12) |
将导引关系式(12)与运动学关系式(1)~式(3)相结合即为比例导引法原理。
2.1 中远距离低速巡航在第一阶段中选取剩余时间为协调变量设计分布式协同制导律,在该阶段结束前应使各AUV剩余时间趋于一致,针对固定目标制导的剩余时间
| $ t=\frac{r}{v}\left(1+\frac{{\eta }^{2}}{2\left(2m-1\right)}\right)\text{,} $ | (13) |
视目标静止,将AUV与目标的运动学模型转化为AUV-目标相对运动模型:
| $ {\overrightarrow{\mathit{v}}}_{\mathit{i}\mathit{t}}={\overrightarrow{\mathit{v}}}_{\mathit{i}}-{\overrightarrow{\mathit{v}}}_{\mathit{t}} \text{,}$ | (14) |
| $ {x}_{it}={x}_{i}-\left({x}_{t}-{x}_{t}\left(0\right)\right) \text{,}$ | (15) |
| $ {y}_{it}={y}_{i}-\left({y}_{t}-{y}_{t}\left(0\right)\right) \text{,}$ | (16) |
| $ {\alpha }_{it}={\rm{arccos}}\left({{v}_{ix}-v}_{tx}\right)/\left|\right|{\overrightarrow{\mathit{v}}}_{\mathit{i}\mathit{t}}\left(k\right)\left|\right|) \text{,}$ | (17) |
| $ {q}_{it}={\rm{arctan}}\frac{{y}_{it}-{y}_{t}\left(0\right)}{{x}_{it}-{x}_{t}\left(0\right)} \text{,}$ | (18) |
| $ {\eta }_{it}={q}_{it}-{\alpha }_{it} \text{,}$ | (19) |
| $ {m}_{it}={\rm{d}}{\alpha }_{it}/{\rm{d}}{q}_{it} \text{。}$ | (20) |
则针对定速直航机动目标的剩余时间可用下式进行估算:
| $ {t}_{i}=\frac{{r}_{it}}{{v}_{it}}\left(1+\frac{{\eta }_{it}^{2}}{2\left(2{m}_{it}-1\right)}\right)\text{。} $ | (21) |
以剩余时间为协调变量,对于无通信延迟系统,时间误差可表示为:
| $ {\delta }_{i}=\sum _{j=1}^{n}{a}_{ji}({t}_{i}-{t}_{j}) \text{。}$ | (22) |
对于存在通信延迟的系统,设s时刻
| $ \frac{\sqrt{{\left({x}_{j}\left(z\right)-{x}_{i}\left(s\right)\right)}^{2}+{\left({y}_{j}\left(z\right)-{y}_{i}\left(s\right)\right)}^{2}}}{{V}_{v}}-(z-s)=0 \text{,}$ | (23) |
则此时的实时通信延迟为:
| $ {T}_{d}=z-s\text{,} $ | (24) |
剩余时间误差为:
| $ {\delta }_{i}=\sum _{j=1}^{{n}}{a}_{ji}\left(\left({t}_{i}\right({s})-{T}_{d})-{t}_{j}\left({z}\right)\right)\text{。} $ | (25) |
根据基于相对运动模型的时间误差计算方法,设计如下协同制导率:
| $ {m{{'}}}_{it}={m}_{it}(1+{p}_{1it}\mathrm{s}\mathrm{g}\mathrm{n}({\delta }_{i}){\delta }_{i}^{s}/{t}_{i}) \text{,}$ | (26) |
| $ {a}_{it}={p}_{2i}\mathrm{s}\mathrm{g}\mathrm{n}\left({\delta }_{i}\right){\delta }_{i}^{s}{v}_{it}/{t}_{i}\text{。} $ | (27) |
其中,
| $ {a}_{nit}={m{{'}}}_{it}\cdot {v}_{it}\cdot {\dot{\alpha }}_{it} \text{。}$ | (28) |
其中,
AUV速度调节与相对速度的关系如式(14)所示,其比例系数
| $ {\alpha }_{i}={\rm{arctan}}\frac{{\overrightarrow{\mathit{v}}}_{\mathit{i}\mathit{t}}\mathrm{sin}{\alpha }_{it}-{\overrightarrow{\mathit{v}}}_{\mathit{t}}\mathrm{sin}{\alpha }_{t}}{{\overrightarrow{\mathit{v}}}_{\mathit{i}\mathit{t}}\mathrm{cos}{\alpha }_{it}-{\overrightarrow{\mathit{v}}}_{\mathit{t}}\mathrm{cos}{\alpha }_{t}} \text{,}$ | (29) |
| $ {q}_{i}={\rm{arctan}}\frac{{y}_{i}-{y}_{t}}{{x}_{i}-{x}_{t}}\text{,} $ | (30) |
| $ {m}_{i}={\rm{d}}{\alpha }_{i}/{\rm{d}}{q}_{i} \text{。}$ | (31) |
制导律中对比例系数与速度同时进行调节,两者共同作用改变法向加速度从而改变整个制导轨迹的曲率,剩余时间相对较大的AUV同时增大比例系数与速度,剩余时间较小的AUV同时减小比例系数与速度使剩余时间误差趋于0。
设
| $ {V}_{x}=\frac{1}{2}\sum _{i=1}^{n}\sum _{j=1}^{n}{{a}_{ij}({t}_{i}-{t}_{j})}^{2}=\frac{1}{2}{\boldsymbol{t}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{t} \text{,}$ | (32) |
两边同时对时间求导可得:
| $ {\dot{V}}_{x}=\frac{1}{2}{\mathrm{t}}^{\rm{T}}\boldsymbol{L}\dot{\boldsymbol{t}} \text{。}$ | (33) |
联合运动关系式与小前置角假设对剩余时间求导:
| $ \begin{split} {\dot{t}}_{i}=& \frac{{\dot{r}}_{it}{v}_{it}-{r}_{it}{\dot{v}}_{it}}{{v}_{it}^{2}}\left(1+\frac{{\eta }_{it}^{2}}{2{(2m}_{it}-1)}\right)+\frac{{r}_{i}{\eta }_{it}{\dot{\eta }}_{it}}{{v}_{it}\left(2{m}_{it}-1\right)}=\\ & \left(-{\rm{cos}}{\eta }_{it}-\frac{{r}_{it}{a}_{it}}{{v}_{it}^{2}}\right)\left(1+\frac{{\eta }_{it}^{2}}{2{(2m}_{it}-1)}\right)+ \\ & \frac{{\eta }_{i}({{m}{{{'}}}}_{it}-1){\rm{sin}}{\eta }_{it}}{2{m}_{it}-1}=-1+\frac{\left({m}_{it}-{{m}{{{'}}}}_{it}\right){\eta }_{it}^{2}}{2{m}_{it}-1} -\\ & \frac{{r}_{it}{a}_{it}}{{v}_{it}^{2}}\left(1+\frac{{\eta }_{it}^{2}}{2{(2m}_{it}-1)}\right)=-1-\frac{{p}_{1i}{\delta }_{i}^{s}{m}_{it}{\eta }_{it}^{2}}{\left(2{m}_{it}-1\right){t}_{it}} -\\ &\frac{{r}_{i}{p}_{2i}{\delta }_{i}^{s}}{{v}_{it}{t}_{it}}\left(1+\frac{{\eta }_{it}^{2}}{2{(2m}_{it}-1)}\right)\text{。} \end{split} $ | (34) |
设
| $ 96{\dot{V}}_{x}= - \sum _{i=1}^{n}\frac{{p}_{1i}{\delta }_{i}^{1+s}{m}_{it}{\eta }_{i}^{2}}{\left(2{m}_{it}-1\right){t}_{i}} - \sum _{i=1}^{n}\frac{{r}_{i}{p}_{2i}{\delta }_{i}^{1+s}}{{v}_{i}{t}_{i}}\left(1 + \frac{{\eta }_{it}^{2}}{2{(2m}_{it}-1)}\right) \text{,}$ | (35) |
假定在剩余时间误差归零前无AUV抵达目标,则存在
| $ {T}{{{'}}}\leqslant \frac{{r}_{it}}{{v}_{it}},{{\eta }{{{'}}}}_{it}\leqslant \left|{\eta }_{it}\right|,{t{{'}}}_{i}\geqslant {t}_{i} \text{,}$ | (36) |
则有:
| $ {p}_{1}=\sum _{i=1}^{n}\frac{{m}_{it}}{\left(2{m}_{it}-1\right){t{'}}_{i}}{\eta }_{it}^{2}\mathrm{m}\mathrm{i}\mathrm{n}\{{p}_{11},{p}_{12},\dots ,{p}_{1n}\} \text{,}$ | (37) |
| $ {p}_{2}=\sum _{i=1}^{n}\frac{{T}^{{{'}}}}{{t{'}}_{i}}\left(1\frac{{\eta }_{it}^{2}}{2{(2m}_{it}-1)}\right)\mathrm{m}\mathrm{i}\mathrm{n}\{{p}_{21},{p}_{22},\dots ,{p}_{2n}\} \text{,}$ | (38) |
将上式代入式(24)进行放缩可得:
| $ 105{\dot{V}}_{x}\leqslant -{p}_{1} \sum _{i=1}^{n}{\delta }_{i}^{1+s} -{p}_{2} \sum _{i=1}^{n}{\delta }_{i}^{1+s} \leqslant -({p}_{1}+{p}_{2}) \sum _{i=1}^{n}{{(\boldsymbol{\delta }}^{\mathrm{T}}\boldsymbol{\delta })}^{\tfrac{1}{2}+\tfrac{s}{2}}\text{,} $ | (39) |
因为L是半正定矩阵且
| $ {\boldsymbol{1}}^{\mathrm{T}}{\boldsymbol{L1}}={\left({{\boldsymbol{L}}}^{1/2}{\boldsymbol{1}}\right)}^{\mathrm{T}}\left({\boldsymbol{L}}^{1/2}{\boldsymbol{1}}\right)\text{,} $ | (40) |
所以有
| $ {\boldsymbol{t}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{L}\boldsymbol{t}={\boldsymbol{\delta }}^{\mathrm{T}}\boldsymbol{\delta }\geqslant \lambda {\boldsymbol{t}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{t}=2\lambda {V}_{x} \text{,}$ | (41) |
代入式(28)可得:
| $ {\dot{V}}_{x}\leqslant -({p}_{1}+{p}_{2}){\left(2\lambda \right)}^{\tfrac{1}{2}+\tfrac{s}{2}}{V}_{x}^{\tfrac{1}{2}+\tfrac{s}{2}} \text{。}$ | (42) |
由引理4可知剩余时间误差能在有限时间内稳定收敛,且收敛时间满足:
| $ {T}_{x}\left({x}_{0}\right)\leqslant \frac{{V}^{\frac{1}{2}-\frac{s}{2}}\left({x}_{0}\right)}{({p}_{1}+{p}_{2}){\left(2\lambda \right)}^{\frac{1}{2}+\frac{s}{2}}(\frac{1}{2}-\frac{s}{2})} \text{。}$ | (43) |
以上便是关于无向通信图条件下的剩余时间误差稳定性验证。对于有向通信图而言,假定任意具有信息传递的两成员之间只存在单向通信,该情况下有
因为
| $ {t}_{i}=\frac{{r}_{it}\left(1+\frac{{\eta }_{it}^{2}}{2\left(2{m}_{it}-1\right)}\right)}{\left\|{\overrightarrow{\mathit{V}}}_{\mathit{g}}\right\|-\left\|{\overrightarrow{\mathit{V}}}_{\mathit{t}}\right\|}\text{。} $ | (44) |
其他AUV均根据该剩余时间进行自身参数的调节,因此通信图需要满足以任意节点为起点都能找到一条包含全部成员的通信链路,以保证剩余时间能传递至其余各AUV。而针对于存在通信延迟的系统,假定s时刻
| $ {\delta }_{{i}}=\left({t}_{1}\left({s}\right)-(z-s)\right)-{t}_{i}\left({z}\right)\text{。} $ | (45) |
本文模拟了3个AUV对于水面定速直航目标进行拦截,假设目标点初始位置为
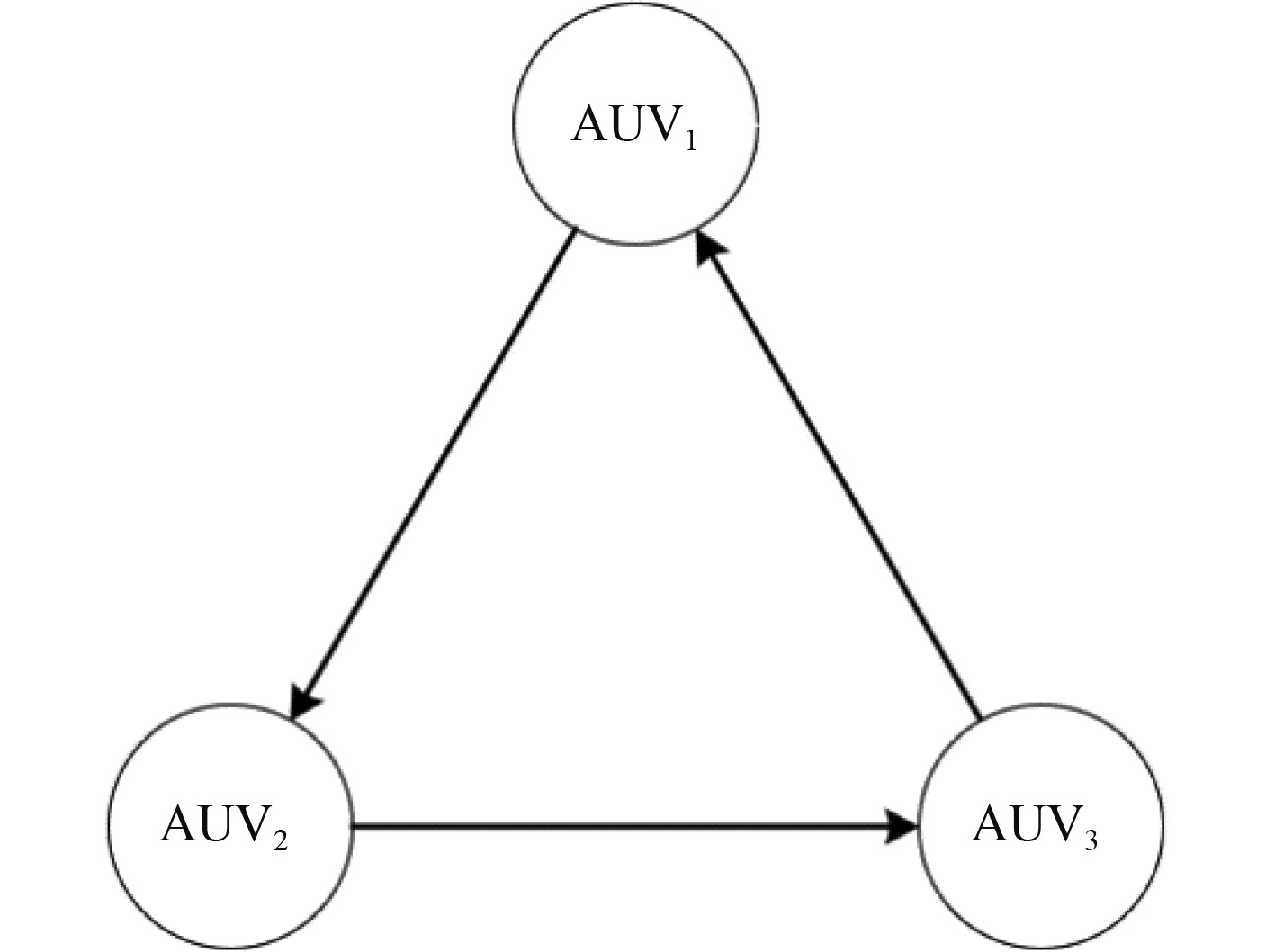
|
图 3 通信拓扑图 Fig. 3 Communication topology schematic |
邻接矩阵:
| $ {\boldsymbol{A}}=\left[{a}_{ij}\right]=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]\text{,} $ | (46) |
对应的拉普拉斯矩阵:
| $ {\boldsymbol{L}}=\left[{l}_{ij}\right]=\left[\begin{array}{ccc}1& -1& 0\\ 0& 1& -1\\ -1& 0& 1\end{array}\right]\text{。} $ | (47) |
假定
针对同时考虑通信延迟与不考虑通信延迟2种情况进行仿真,结果如图4所示。
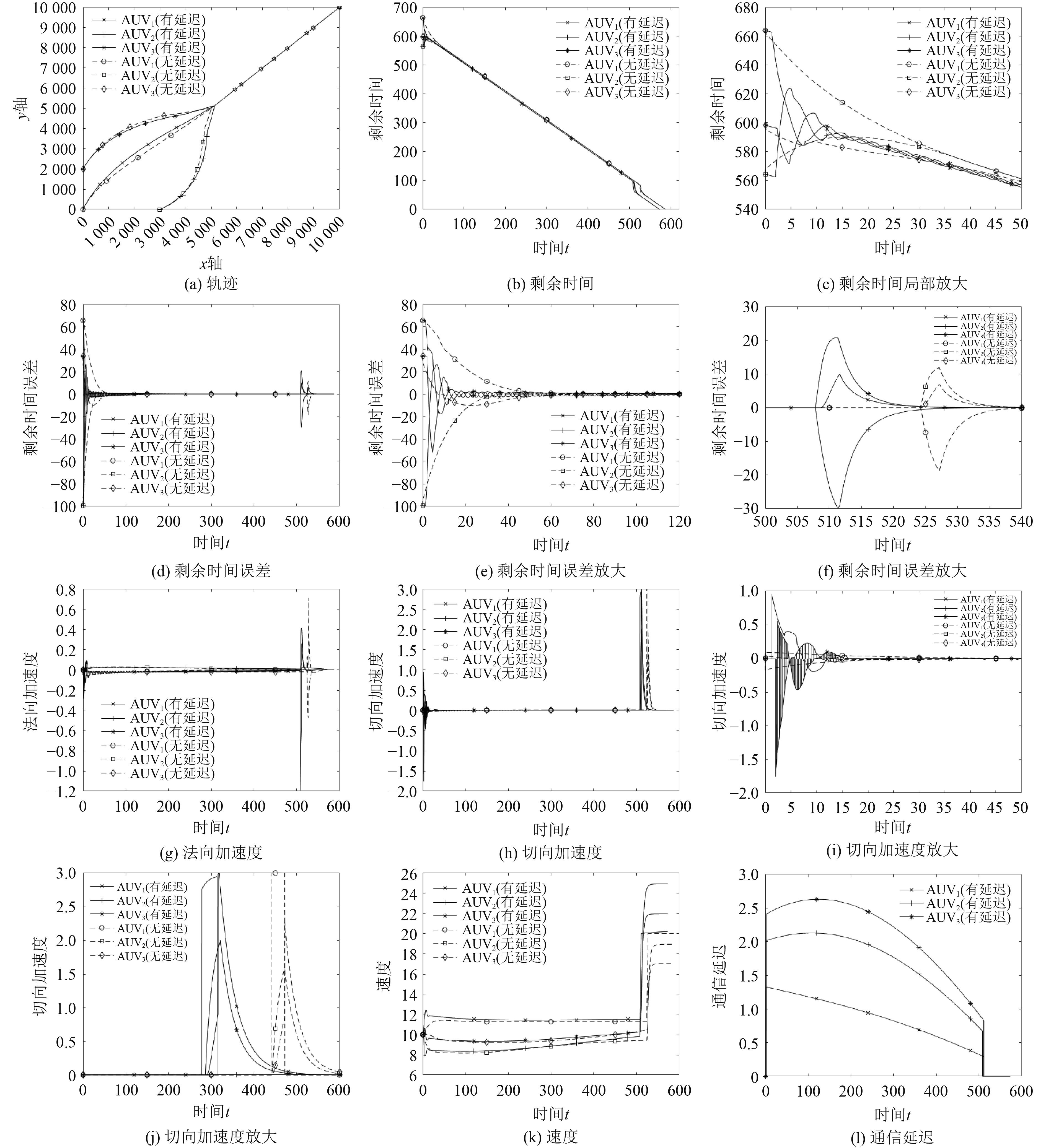
|
图 4 仿真结果图 Fig. 4 Simulation result graph |
图4(a)为2种情况下的AUV与目标的运动轨迹对比图。不难看出该制导律能满足2种情况下的协同制导,说明采用相对运动模型进行剩余时间估算具有更小的误差,可以使针对机动目标的协同制导律具有更高的制导精度。各AUV脱靶量如表1所示。
|
|
表 1 各AUV脱靶量 Tab.1 Off-target volume for AUV |
图4(b)和图4(c)为各AUV剩余时间变化曲线。因为通信延迟的存在,各AUV收到协调变量信息并调节自身参数均存在相应滞后,因此AUV剩余时间在初期存在短暂的线性变化阶段,各AUV变化滞后时间与图4中通信延迟初值保持一致。图4(e)~图4(g)为各AUV剩余时间误差变化曲线,不考虑通信延迟时,各AUV实时共享剩余时间信息并进行自身参数调节,因此其变化曲线较为平滑。而考虑通信延迟时,各AUV之间的通信延迟不相同,因此各AUV调节时所收到的剩余时间并不是来自同一时刻,这是其剩余时间误差在收敛之前存在波动的根本原因。图4(g)~图4(j)为各AUV法向与切向加速度的变化曲线,考虑通信延迟条件下的加速度变化幅度均大于不考虑的情况,图像表明考虑通信延迟条件下AUV需要更高的机动性能。该结论同样可从图4(k)速度变化曲线中得以佐证。图中有延迟情况下各AUV速度远高于无延迟情况(对应AUV高出约10 kn),这也是有延迟条件下整体制导时间反而小于无延迟情况的原因。
通过设定不同的AUV初始位置模拟不同的通信延迟,设置额外不同的2组AUV初始位置(0,0)、(4000,0)、(0,3000)与(0,0)、(5000,0)、(0,4000),其余参数设置不变。
图5为不同通信延迟所对应的剩余时间误差、切向加速度与法相加速度的变化曲线。可以看出,通信延迟增大会使各AUV的参数调节滞后时间增大,使剩余时间误差与切向加速度的波动幅度出现小范围增大,并且法向加速度的峰值也随之增大,但通信延迟相对于整体制导时间属于较小值,因此对于系统收敛速度影响较小。
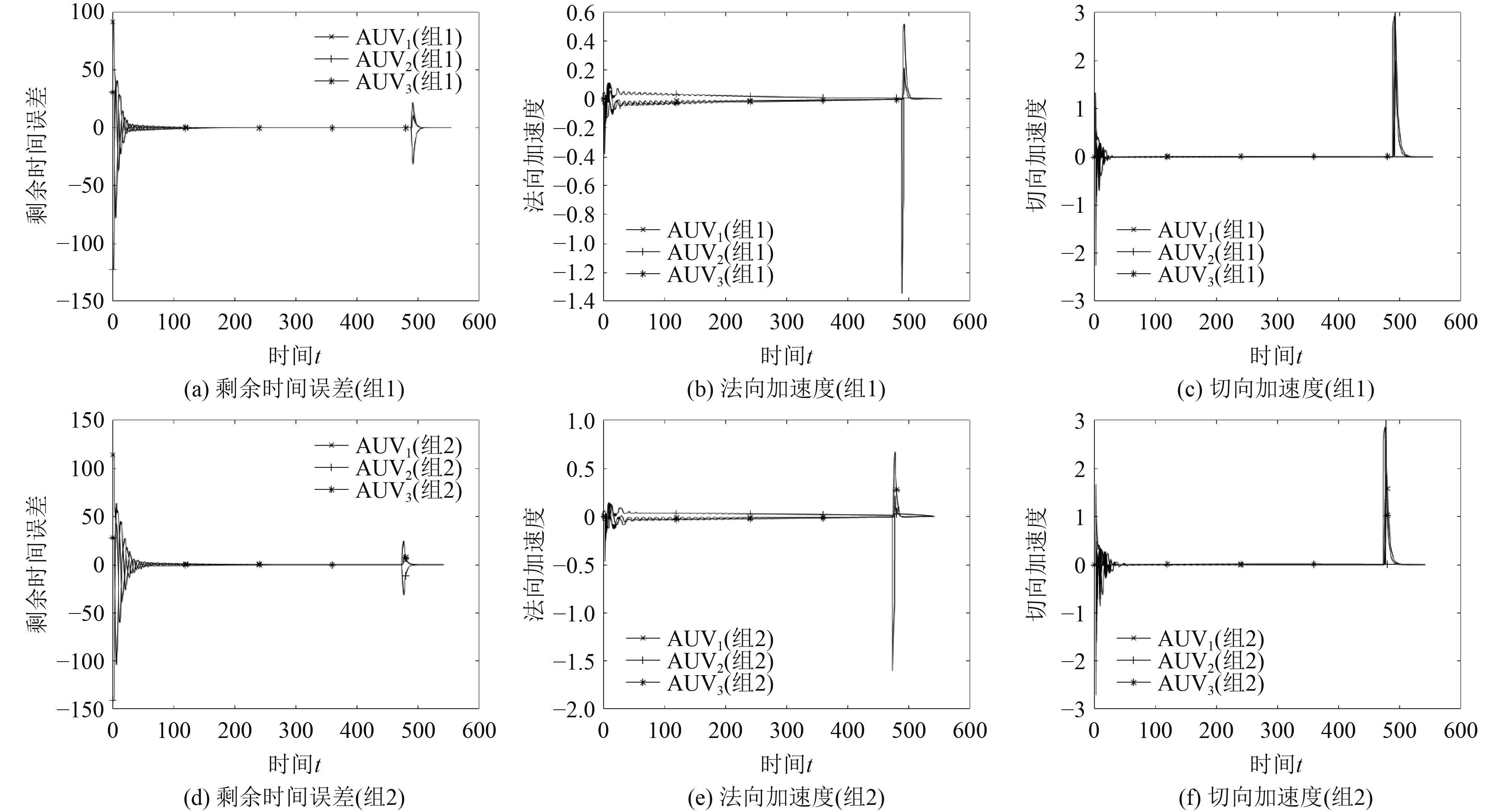
|
图 5 不同通信延迟仿真结果 Fig. 5 Simulation results with different communication delays |
对于相同的AUV参数设置,设定不同的通信周期5 s、7 s、10 s与20 s进行仿真,图6为不同通信周期所对应的剩余时间误差、切向加速度与法相加速度的变化曲线。可以看出,随着周期的不断增大,各参数调节曲线存在明显差异,对比剩余时间误差可得,随着通信周期的不断增大,剩余时间的波动周期与幅度也逐步增大,误差收敛速度明显减慢甚至于无法收敛(周期为20 s时剩余时间误差未收敛至0),并且对比有切向加速度与法向加速度可得随着周期的增大,加速度的调节幅值不断增大。综合图5和图6可知,通信延迟只在小范围内改变参数的波动大小,而通信周期则是影响参数波动幅值与误差收敛速度的主要因素,增加通信周期意味着对AUV提出更高的机动性能需求。

|
图 6 不同通信周期仿真结果 Fig. 6 Simulation results with different communication period |
本文针对水面目标的协同攻击拦截问题,考虑水声实时延迟以及通信周期对协同制导的影响,基于相对运动模型推导的剩余时间计算方法,设计了一种变比例系数与变速度的多阶段协同制导律。使用李雅普诺夫有限时间收敛原理对于协同制导律进行了数学验证,并基于有向图通信拓扑结构进行3个AUV单向通信状况下的协同制导攻击仿真,验证了使用基于相对运动模型计算的剩余时间作为协调变量能使制导律具有较高的协同制导精度。本文对比了有/无通信延迟与通信周期,以及不同的通信延迟与通信周期情况下的参数变化。结果表明,相对于无通信延迟情况,考虑通信延迟时参数变化存在明显滞后,亦是参数调节存在波动的根本原因,而随着通信周期增大,系统误差收敛速度不断降低、参数调节幅值逐步增大,AUV的机动性能要求也相应提高。研究成果为多AUV协同制导的实用提供了支撑,通信延迟与周期是不可忽视的影响因素。本文以水面定速直航机动目标为典型场景验证了方法的可行性,下一阶段将进一步在无向通信拓扑结构下以水面规则曲线机动或不规则机动目标为协同攻击对象进行研究分析。
| [1] |
JEON In-Soo, LEE Jin-Ik, TAHK Min-Jea. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2), 260–266.
|
| [2] |
张友安, 马国欣, 王兴平. 多导弹时间协同制导: 一种领弹-被领弹策略[J]. 航空学报, 2009, 30(6): 1109-1118. DOI:10.3321/j.issn:1000-6893.2009.06.023 |
| [3] |
CHEN Z, CHEN W, LIU X, et al. Three-dimensional fixed-time robust cooperative guidance law for simultaneous attack with impact angle constraint[J]. Aerospace Science and Technology, 2021, 110, 106523.
|
| [4] |
DONG W, WANG C, WANG J, et al. Three-dimensional nonsingular cooperative guidance law with different field-of-view constraints[J]. Journal of Guidance, Control, and Dynamics, 2021, 44(11): 2001-2015. DOI:10.2514/1.G005971 |
| [5] |
ZHAI S, WEI X, YANG J. Cooperative guidance law based on time-varying terminal sliding mode for maneuvering target with unknown uncertainty in simultaneous attack[J]. Journal of the Franklin Institute, 2019.
|
| [6] |
YU H, DAI K, LI H, et al. Cooperative guidance law for multiple missiles simultaneous attacks with fixed-time convergence[J]. International Journal of Control, 2022: 1−14.
|
| [7] |
ZHAO Qilun, DONG Xiwang, LIANG Zixuan. Distributed group cooperative guidance for multiple missiles with fixed and switching directed communication topologies[J]. Nonlinear Dynamics, 2017, 90(4): 2507-2523. DOI:10.1007/s11071-017-3816-3 |
| [8] |
马文卉, 符文星, 方洋旺, 等. 通信拓扑切换下的预定时间分组协同制导方法[J]. 宇航学报, 2023, 44(1): 86-98. DOI:10.3873/j.issn.1000-1328.2023.01.009 |
| [9] |
叶鹏鹏, 盛安冬, 张蛟, 等. 非持续连通通信拓扑下的多导弹协同制导[J]. 兵工学报, 2018, 39(03): 474-484. DOI:10.3969/j.issn.1000-1093.2018.03.009 |
| [10] |
王青, 后德龙, 李君. 存在时延和拓扑不确定的多弹分散化协同制导时间一致性分析[J]. 兵工学报, 2014, 35(7): 982-98. DOI:10.3969/j.issn.1000-1093.2014.07.007 |
| [11] |
姜尚, 孙东彦, 梁伟阁, 等. 考虑通信延迟的网络化弹药多约束协同策略[J/OL]. 电子学报: 1−11. [2023-08-06]
|
| [12] |
Olfati-Saber R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520–1533.
|
| [13] |
GUO J, XIONG Y, ZHOU J. A new sliding mode control design for integrated missile guidance and control system[J]. Aerospace Science and Technology, 2018, 78, 54–61.
|
| [14] |
JEON I S, LEE J I, TAHK M J. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control and Dynamics, 2010, 33(1), 275–280.
|
 2024, Vol. 46
2024, Vol. 46
