高效全局优化算法(Efficient Global Optimization, EGO)是Jones 在1998年提出[1]。它的基本思想是首先采用试验设计采样,进而构造一个初始的近似模型,EGO方法以Expected Improvement为核心加点法则进行迭代加点,用于选择下一个采样点以在全局优化问题中有效地探索设计空间,最终收敛到最优解。由于其加点法则能够智能地对目标函数进行采样,重点关注了真实最优解可能位于的区域,同时又避免了在目标函数平坦或已经被探索过的区域进行不必要的评估,从而提高了全局寻优的效率。因此,EGO方法是一种用于寻找复杂和昂贵目标函数的全局最优解机器学习优化技术。在处理黑盒函数(黑盒函数指的是数学形式未知或过于复杂而不能直接处理的函数)时特别有用。EGO目前已在飞机、汽车、风机等工程领域得到应用[2-11]。
船舶线型优化是指在设计船舶时优化其外形和线型,以达到特定的性能、经济性和环境要求。面对日益严苛的节能减排要求,船舶线型优化问题变得更加复杂,如船型设计需要满足一系列的不等或等式约束条件,如排水体积、稳性等。通常基于CFD仿真进行设计,数值模拟需要大量的计算资源和时间成本。船型几何涉及数十数百个参数定义,不单单只是阻力性能优化,还包含推进效率、载重吨、稳性高等多个冲突的目标折中优化。这些问题使得船舶线型优化难度加大。对于像水面船舶这种两相流模拟,即使采用集群或者超算进行数值计算,单个诸如150万左右网格量的静水阻力粘流算例,采用100核并行计算,也需几十分钟得到阻力值,更不要说耐波性和操纵性优化。因此,必须寻找一种适用于船舶性能多目标优化、节约计算资源、加快优化周期的优化技术。
本文对EGO优化算法应用于船型优化进行探讨,在单目标和多目标EGO算法初始样本点数的设置、加点法则、收敛条件等方面进行研究,并采用标准优化测试函数进行了验证。
1 单目标EGO算法EGO优化算法本身属于单目标优化算法,从“期望改善”(Expected Improvement,EI)函数开始剖析。
假设初始采样点的个数是n,使得
比如图1中,对于样本点
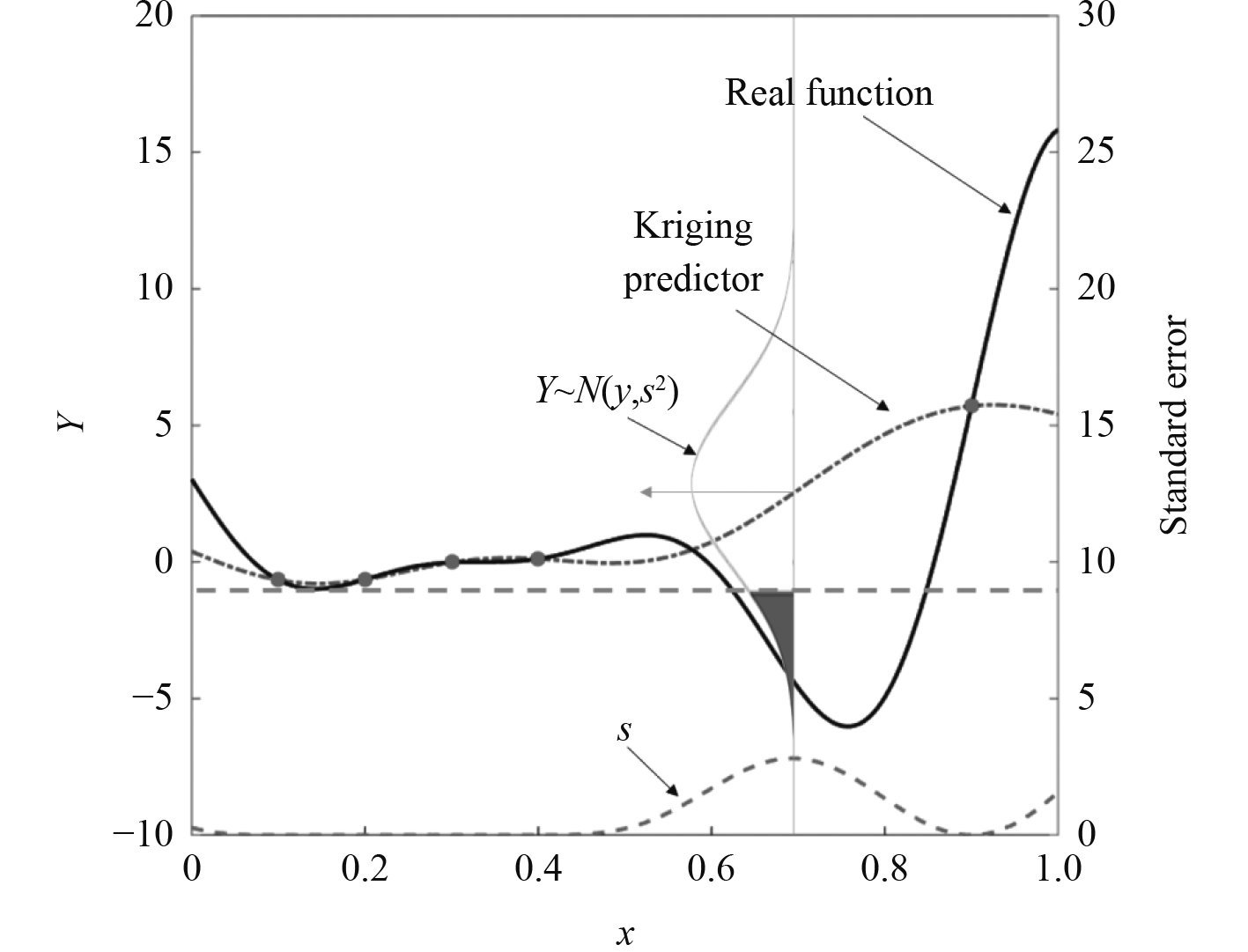
|
图 1 一维函数的近似模型和它的不确定性分析 Fig. 1 Kriging model for a function and its uncertainty |
从数学上正式定义,假设在样本点
| $ E[I({x})] \equiv E[\max({f_{\min }} - Y,0)]。$ | (1) |
其中,认为随机变量
| $ E[I({x})] = ({f_{\min }} - \hat y)\Phi \left(\frac{{{f_{\min }} - \hat y}}{s}\right) + s {\text{ϕ}}\left(\frac{{{f_{\min }} - \hat y}}{s}\right)。$ | (2) |
其中,
期望改善函数是一个多峰函数。事实上,期望改善函数在样本点处值为0,并且其他地方的值都是正数(尽管也许会很小)。这些性质使得对期望改善函数寻优较为困难,因此采用遗传算法对该函数寻优,摒弃基于梯度的优化算法寻优。根据式(3)和式(4)可知,当预测点值越小时,期望改善函数值越大,当方差较大,期望改善函数值越大。
| $ \frac{{\partial E(I)}}{{\partial \hat y}} = - \Phi \left( {\frac{{{f_{\min }} - \hat y}}{s}} \right) < 0,$ | (3) |
| $ \frac{{\partial E(I)}}{{\partial s}} = {\text{ϕ}} \left( {\frac{{{f_{\min }} - \hat y}}{s}} \right) > 0。$ | (4) |
因此提出将期望改善函数EI(
整个EGO全局优化算法主要包含试验设计、Kriging模型构建和利用EI函数寻优加点进行优化迭代三部分,具体流程如下:
1)利用优化拉丁超立方方法在设计空间采取样本点,生成设计空间的初始样本点集;
2)计算所有样本点的目标函数值;
3)根据所有样本点的设计变量值和目标函数值构建Kriging模型;
4)构建EI函数,通过单目标遗传算法求解EI函数最大值对应的设计点;
5)将该设计点添加入样本点集;
6)验证近似模型是否满足精度要求及最终停止法则(
以一个简单的一维函数为例,图2为根据期望改善函数不断添加新的样本点示意图。图中实线表示真实函数,虚线表示近似模型,阴影区域表示
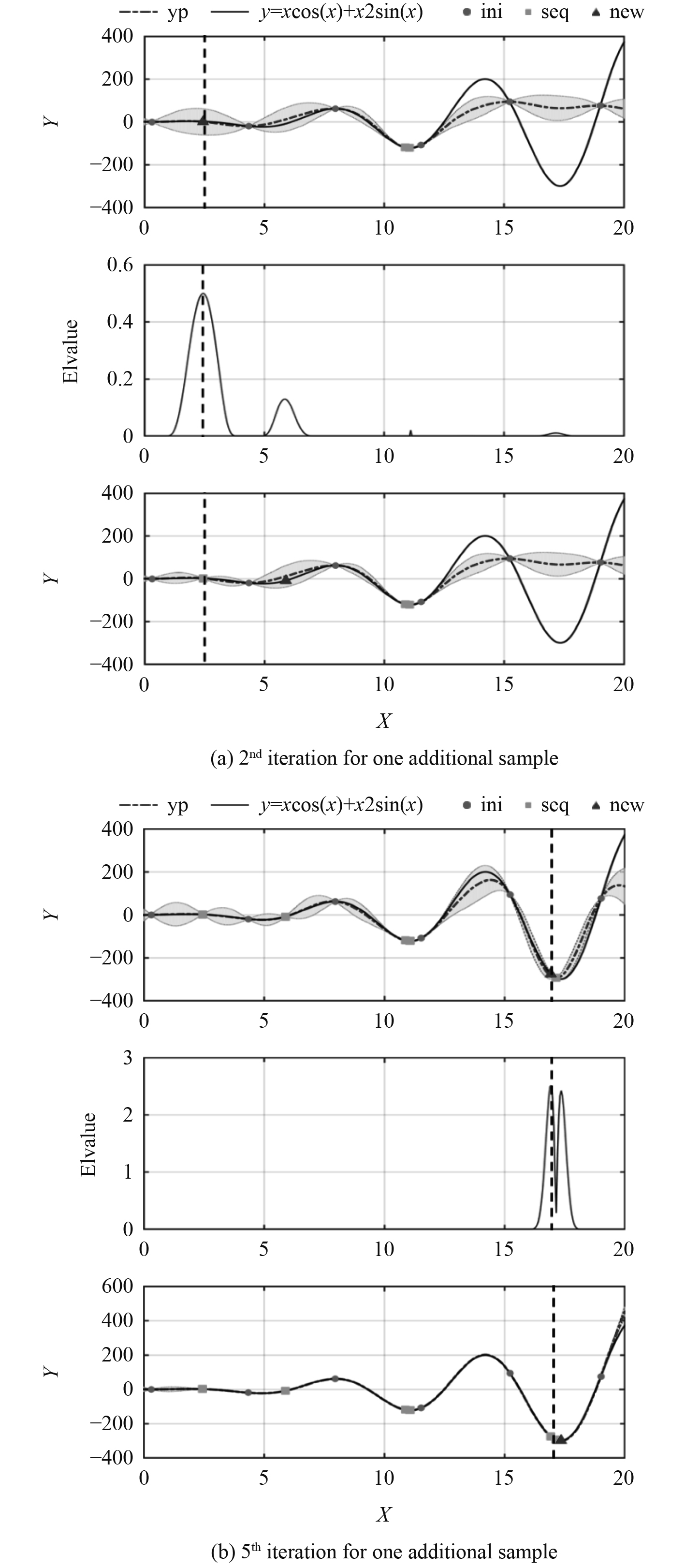
|
图 2 基于EGO方法的一维函数寻优示意图 Fig. 2 Optimization for a one-dimensional function based on EGO method |
单目标EGO算法在解决单目标优化问题上大大降低了数值模拟耗时长和计算资源耗费大的问题,而实际工程应用中存在很多的多目标优化问题,因此将EGO算法推广到多目标优化问题上具有非常重要的工程意义及价值。其实,EGO算法中最重要的是EI加点准则,而将单目标EGO算法推广到多目标EGO算法,整个算法框架和流程依旧不变,只需要提出合理的多目标EI准则,而提高函数
在多目标优化问题中,最优解并非唯一,一般由多个点组成近似Pareto前沿,这里记为:
| $ {S}{\text{ = }}\left[ \begin{gathered} f_1^1{\text{ }}f_2^1{\text{ }} \cdots {\text{ }}f_m^1 \\ f_1^2{\text{ }}f_2^2{\text{ }} \cdots {\text{ }}f_m^2 \\ {\text{ }} \vdots {\text{ }} \vdots {\text{ }} \ddots {\text{ }} \vdots \\ f_1^k{\text{ }}f_2^k{\text{ }} \cdots {\text{ }}f_m^k \\ \end{gathered} \right]。$ | (5) |
其中,S为根据当前近似模型得到的近似Pareto前沿;m为目标函数的个数;k为当前Pareto前沿上点的个数。多目标的近似Pareto前沿S将原本单目标的唯一解
| $ {\mathbf{EIM}}{\text{ = }}\left[ \begin{gathered} {{EI}}_1^1{\text{(}}{\boldsymbol{x}}{{) EI}}_2^1{\text{(}}{\boldsymbol{x}}{\text{) }} \cdots {{ EI}}_m^1{\text{(}}{\boldsymbol{x}}{\text{)}} \\ {{EI}}_1^2{\text{(}}{\boldsymbol{x}}{{) EI}}_2^2{\text{(}}{\boldsymbol{x}}{\text{) }} \cdots {{ EI}}_m^2{\text{(}}{\mathbf{x}}{\text{)}} \\ {\text{ }} \vdots {\text{ }} \vdots {\text{ }} \ddots {\text{ }} \vdots \\ {{EI}}_1^k{\text{(}}{\boldsymbol{x}}{{) EI}}_2^k{\text{(}}{\boldsymbol{x}}{\text{) }} \cdots {{ EI}}_m^k{\text{(}}{\boldsymbol{x}}{\text{)}} \end{gathered} \right]。$ | (6) |
其中的每一个元素根据式(2)可得:
| $ {{EI}}_i^j({\boldsymbol{x}}) = (f_i^j - {\hat y_i}({\boldsymbol{x}}))\Phi \left(\frac{{f_i^j - {{\hat y}_i}({\boldsymbol{x}})}}{{{s_i}({\boldsymbol{x}})}}\right) + {s_i}({\boldsymbol{x}})\phi \left(\frac{{f_i^j - {{\hat y}_i}({\boldsymbol{x}})}}{{{s_i}({\boldsymbol{x}})}}\right)。$ | (7) |
其中,
根据图3可以更加直观地理解式(6)所得的一个二维EI矩阵。矩阵中的任一元素如
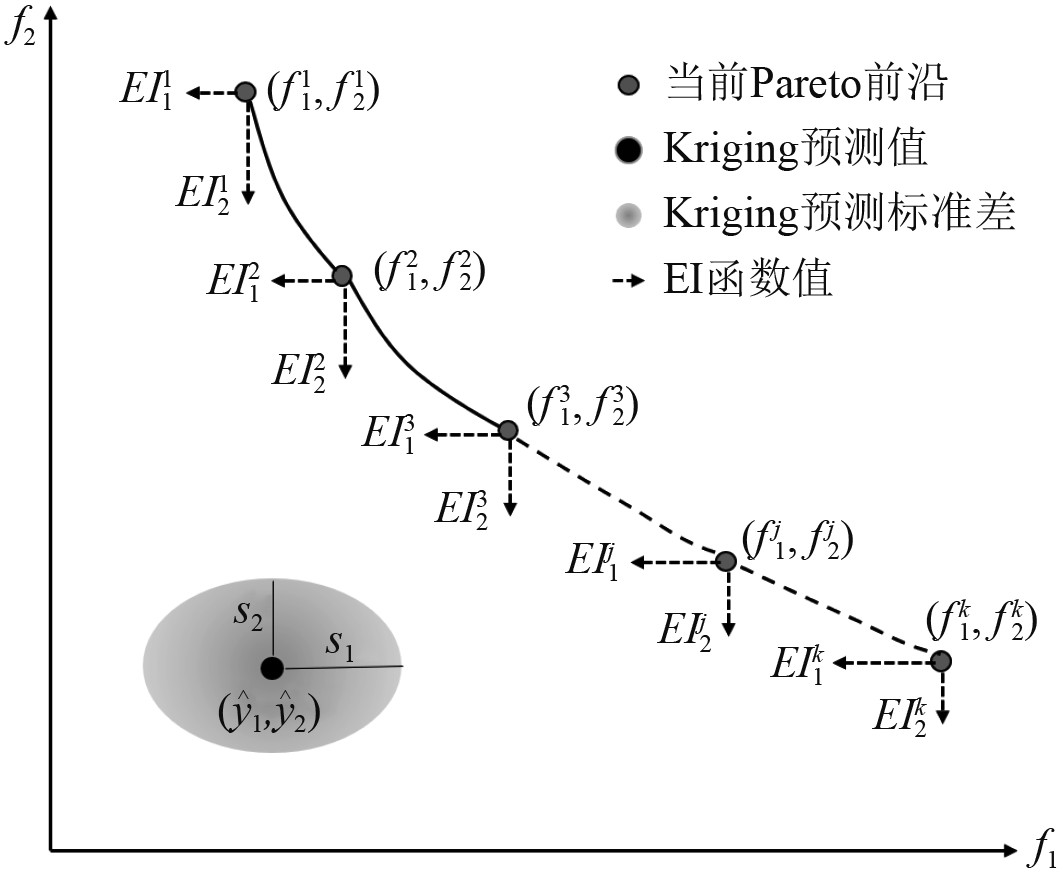
|
图 3 二维EI矩阵示意图[12] Fig. 3 2D example of the EI matrix |
本文采用欧氏距离EIM准则,表示如下:
| $ {\text{EI}}{{\text{M}}_e}({\boldsymbol{x}}) = \mathop {\min }\limits_{j = 1}^k \sqrt {\sum\limits_{i = 1}^m {{{\left( {{{EI}}_i^j\left( {\boldsymbol{x}} \right)} \right)}^2}} }。$ | (8) |
多目标EI加点的思想就是在EIM最大的点处加点,即当前近似Pareto前沿所有目标性能方向提高量最大的样本点加入样本库,更新近似模型,从而更新近似Pareto前沿,该EIM准则具有收敛性,最终会收敛到多目标优化问题的最优解。其基本流程跟单目标EGO算法流程整体相同,只是加点法则更改为EIM准则。
3 标准优化测试函数验证为了验证单目标和多目标EGO算法的可靠性,采用常用的优化测试函数进行分析验证。
1)单目标优化问题
选用标准Branin-Hoo函数测试,该函数常用来考察近似模型的精度以及EGO算法可靠性,表达式如下:
| $ f\left( {\boldsymbol{x}} \right) = a{({x_2} - bx_1^2 + c{x_1} - r)^2} + s(1 - t)\cos({x_1}) + s。$ | (9) |
其中,
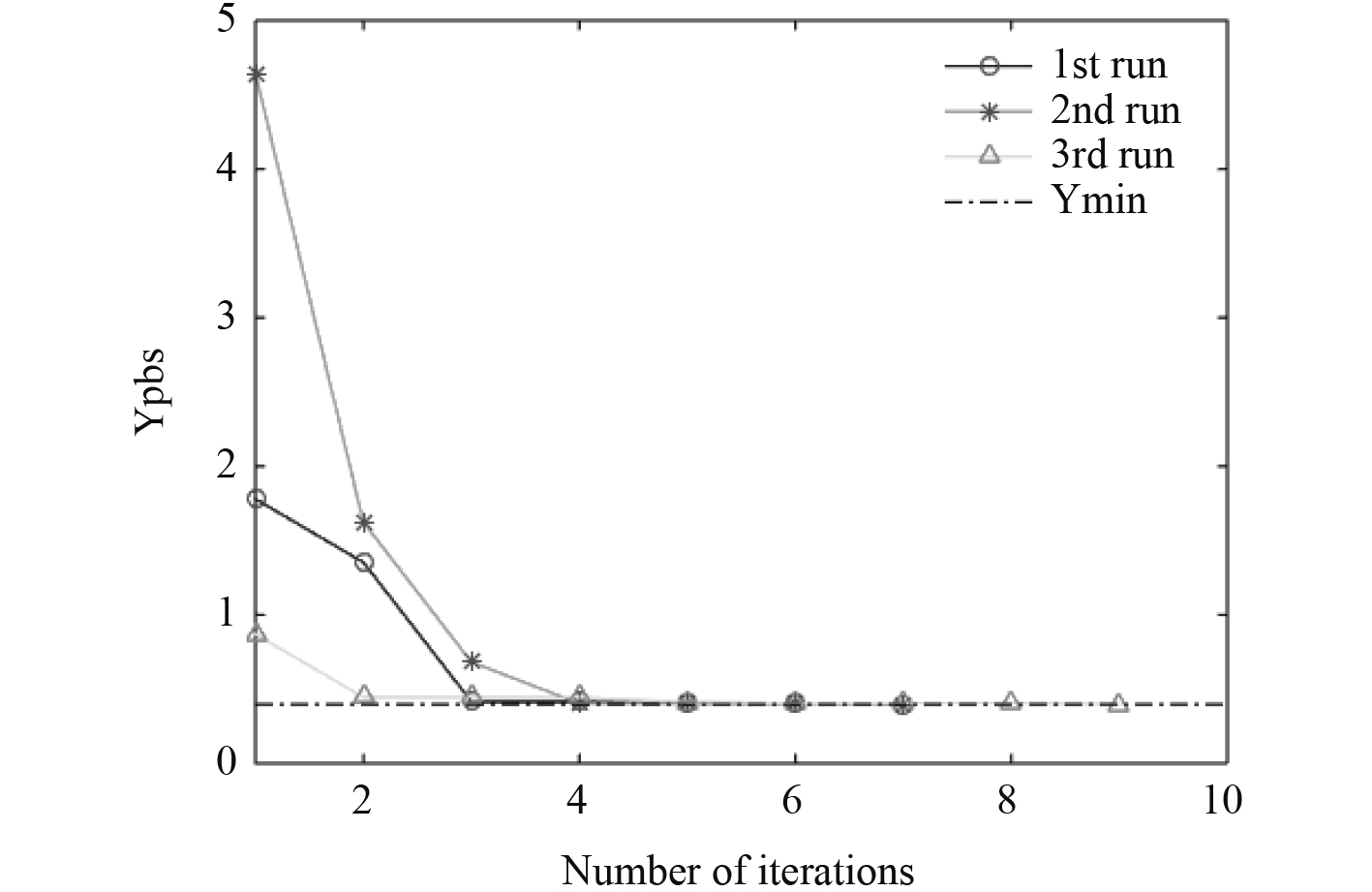
通过基于单目标EGO算法对该函数的应用,考察了两点:1)采用相同的初始样本点以及其他相同的参数配置,运行三次EGO算法(因为EI最值寻优采用遗传算法存在随机性)查看优化结果情况;2)采用不同的初始样本点,其他采用相同的配置,查看优化结果情况。图4结果显示,采用更多的初始样本点,EGO算法收敛更快,初始样本点越多。初始近似模型的精度越高,EGO算法能够更快在全局最优点附近搜索;采用较少的样本点,总体的目标函数评价次数并没有比采用较多的样本点数多。因此,也表明了EGO算法不仅依赖初始的近似模型精度,同时又不完全依赖初始的近似模型精度。图5结果显示,多次运行EGO算法整个迭代收敛过程会不同,这是由于在评价EI准则时采用了遗传算法寻优,而遗传算法具有随机性。但即便如此,对最终优化结果并未产生影响。
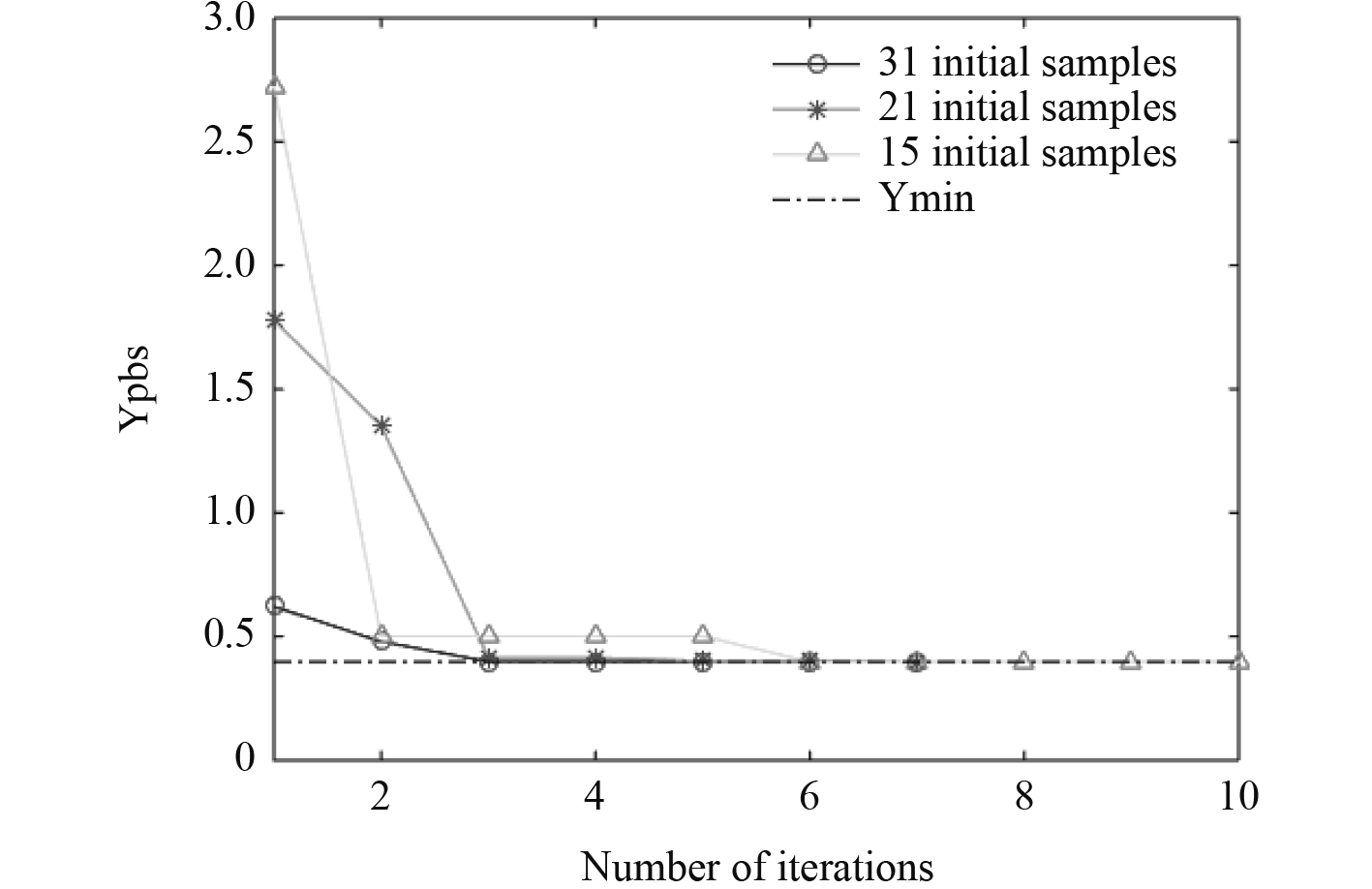
|
图 4 基于不同初始样本点数的单目标EGO算法寻优迭代结果 Fig. 4 Iteration results by single-objective EGO based on different initial numbers of samples |
|
图 5 基于相同初始样本点数的单目标EGO算法寻优三次迭代结果 Fig. 5 Three iteration results by single-objective EGO based on the same initial numbers of samples |
2)多目标优化问题
选择2个多目标优化测试函数[13],对其采用多目标EGO算法寻优,并将所得结果与文献[12]的结果进行对比分析。2个测试函数ZDT1和ZDT2分别为:
| $ \min {\text{ }}\left\{ \begin{gathered} {f_1}({{x}}) = {x_1} ,\\ {f_2}({{x}}) = g({{x}})h({f_1}({{x}}),g({{x}})),\\ g({{x}}) = 1 + \frac{9}{{29}}\sum\nolimits_{i = 2}^{30} {{x_i}} ,\\ h({f_1}({{x}}),g({{x}})) = 1 - \sqrt {\frac{{{f_1}({{x}})}}{{g({{x}})}}} 。\end{gathered} \right. $ | (10) |
其中,
| $ \min {\text{ }}\left\{ \begin{gathered} {f_1}({{x}}) = {x_1},\\ {f_2}({{x}}) = g({{x}})h({f_1}({{x}}),g({{x}})),\\ g({{x}}) = 1 + \frac{9}{{29}}\sum\nolimits_{i = 2}^{30} {{x_i}},\\ h({f_1}({{x}}),g({{x}})) = 1 - {\left( {\frac{{{f_1}({{x}})}}{{g({{x}})}}} \right)^2}。\end{gathered} \right. $ | (11) |
其中,
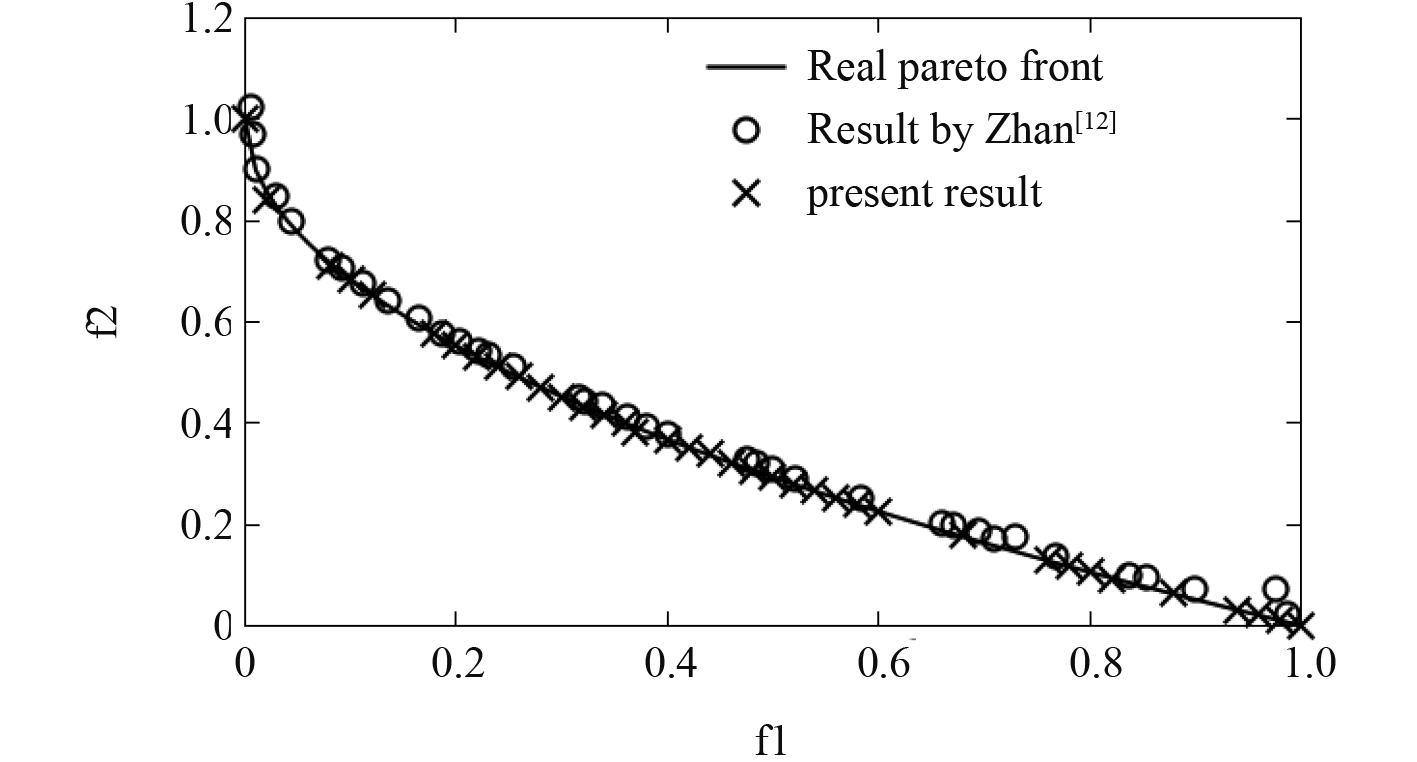
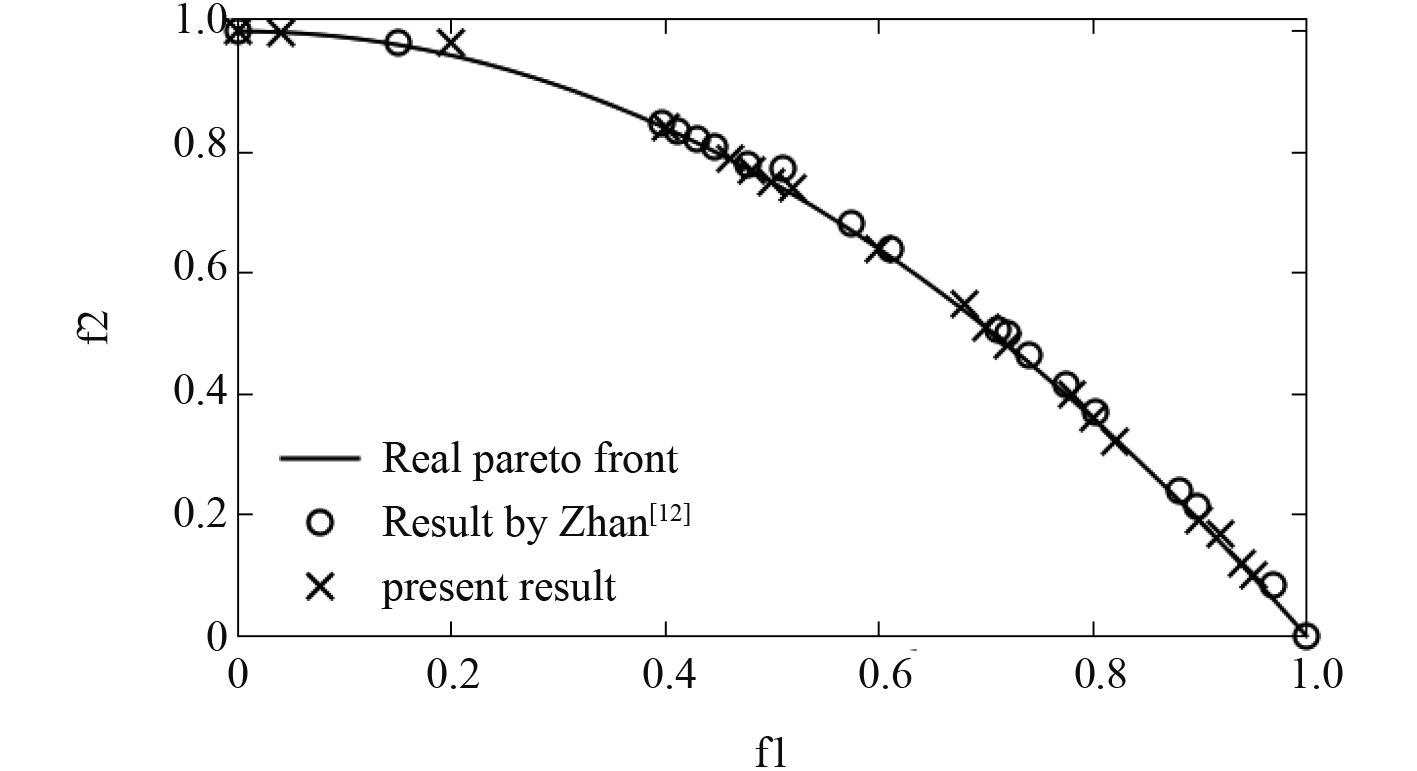
针对这2个测试函数,在寻找EIM准则最优值时采用了相同的遗传算法参数配置,EGO算法初始的样本点数为11k-1(k为设计变量个数,这里30),优化迭代次数最大50。图6和图7结果显示,本文基于多目标EGO算法成功寻找到多目标函数的最优解集,整体上得到的结果趋势也与文献[12]所得结果相差无几。ZDT1在Pareto前沿均匀获得37个,而ZDT2在Pareto前沿获得的点数为20个,虽然不是很均匀,但是也找到了相当数量的全局最优解。因此,采用多目标EGO算法非常高效,并且结果可靠。
|
图 6 ZDT1的Pareto前沿结果对比 Fig. 6 Comparison of Pareto fronts of ZDT1 |
|
图 7 ZDT2的Pareto前沿结果对比 Fig. 7 Comparison of Pareto fronts of ZDT2 |
本文提出了船型优化设计中面临的数值计算量巨大问题,针对该问题研究了高效的优化算法及优化测试函数验证。采用基于Kriging模型的高效全局优化算法(EGO)既可以快速获得全局最优解,又使得优化中从数值计算的整体计算量的角度大大缩减计算成本。在船型优化领域虽然有不少学者采用近似模型方法,可以大大加快优化求解的速度,但单纯采用近似模型首先必须考虑其精度,一般通过交叉验证方法去验证,因为后续优化求解完全依赖近似模型,如果近似模型局部预报精度较差,即目标性能的评估不可靠,则所求最优解经过CFD重新计算验证,目标性能也许并不是最优。因此,采用EGO方法为船型优化设计提供了新思路,其不完全依赖于近似模型,通过单目标或多目标EI加点准则(EIM准则)不断迭代添加新船型更新近似模型并逐代不断探寻到全局最优解。该方法兼顾近似模型的精度提升和全局最优解的探索,通过该方法可以实现单目标和多目标优化求解,未来该方法将直接应用于船型优化设计问题实例中进行进一步验证和改善。尽管针对的是船型优化设计提出的优化方法但可应用于很多工程问题,如船型几何设计、结构优化设计、船体附体优化设计、管系布置设计、舱室布置提升空气质量设计等。
| [1] |
JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global optimization, 1998, 13: 455-492. DOI:10.1023/A:1008306431147 |
| [2] |
JEONG S, OBAYASHI S. Efficient global optimization (EGO) for multi-objective problem and data mining[C]//2005 IEEE Congress on Evolutionary Computation. IEEE, 2005, 3: 2138−2145.
|
| [3] |
BARTOLI N, BOUHLEL M A, KUREK I, et al. Improvement of efficient global optimization with application to aircraft wing design[C]//17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. 2016: 4001.
|
| [4] |
HE Y , SUN J , SONG P , et al. Variable-fidelity expected improvement based efficient global optimization of expensive problems in presence of simulation failures and its parallelization[J]. Aerospace Science and Technology, 2021: 106572.
|
| [5] |
ZHANG Y, LI J, XU C, et al. Vehicle Aerodynamic Optimization: On a Combination of Adjoint Method and Efficient Global Optimization Algorithm[J]. SAE International Journal of Passenger Cars - Mechanical Systems, 2019, 12(2).
|
| [6] |
ZUHAL L R, FAZA G A, PALAR P S, et al. Multi-Objective Kriging-Based Optimization for High-Fidelity Wind Turbine Design[C]//AIAA Scitech 2019 Forum. 2019.
|
| [7] |
YE F, WANG H, LI G. Variable stiffness composite material design by using support vector regression assisted efficient global optimization method[J]. Structural and Multidisciplinary Optimization, 2017(1): 56. DOI:10.1007/s00158-017-1658-8 |
| [8] |
王普毅, 白影春, 林程, 等. 基于EGO加点策略的动力电池包多目标优化[J]. 汽车工程, 2021, 43(10): 1457-1465. |
| [9] |
毛星波, 盛冬发, 朱军. EGO算法在系杆拱桥成桥索力优化中的应用研究[J]. 河南科技, 2022(11): 041. |
| [10] |
王红涛, 竺晓程, 杜朝辉. 改进EGO算法在跨声速翼型气动优化设计中的应用[J]. 上海交通大学学报, 2009(11): 1832-1836. WANG Hong-tao, ZHU Xiao-cheng, DU Chao-hui. Application of the improved EGO algorithm in transonic airfoil aerodynamic optimization design[J]. Joural of Shanghai Jiaotong University, 2009(11): 1832-1836. |
| [11] |
王若宇. 改进的高效全局优化算法及其在车身轻量化设计中的应用研究[D]. 长沙: 湖南大学, 2023.
|
| [12] |
詹大为. 并行EGO算法研究及其应用[D]. 武汉: 华中科技大学, 2018.
|
| [13] |
ZHAN D, CHENG Y, LIU J. Expected improvement matrix-based infill criteria for expensive multiobjective optimization[J]. IEEE Transactions on Evolutionary Computation. 2017, 21(6): 956−975.
|
 2024, Vol. 46
2024, Vol. 46
