国际海事组织IMO第4次温室气体研究报告表明,航运业到2050年,碳排放量将比2018年高出50%[1] 。在国家“碳达峰”以及 “碳中和”政策的驱动下,对航行船舶做降速运营成为航运企业降低燃油消耗和减少碳排放的措施之一[2]。尽管降速航行一定程度上可以带来碳排放量和运输成本的减少,然而却也可能带来货物延期交付等问题,导致航运公司遭受损失。因此,船舶航速应该做到合理的优化,即在降速航行减少碳排放和货物及时送达之间做出折中抉择。
航速优化方面的研究很多。国内方面,李铮等[3]采用遗传算法对固定航线下,不定期船舶进行了航速优化。马征[4]则以好天气分析法对船舶期租经营中的航速和油耗索赔问题进行研究。查安平[5]通过构建小型船舶调度的目标函数和约束条件,采用遗传算法对小型船舶的调度问题进行了目标快速化选择的迭代优化。计明军等[6]以最小化航运企业运营成本为目标函数,通过构建非线性的混合整数规划模型,对支线船舶可变航速以及经济航速2种工况下的调度问题做了详细研究。马冉祺等[7]以实船监测数据为基础,采用遗传算法对固定支线的目标船舶各航段做优化,给出了每个航段的建议转速。丁坤平[8]则在油耗模型的基础上,建立了同时考虑二氧化碳排放量以及企业营运成本的多目标船舶航速优化模型和权系数计算模型,分别利用权重法与遗传算法计算了2个目标的Pareto最优解与最佳折中解。李佳欣[9]提出基于自适应遗传算法的染色体编码简化方法和基于正弦函数的自适应调整策略,研究结果表明自适应调整策略相较于经典遗传算法有效提高了算法的全局寻优能力。国外方面,WANG等[10]提出了一种考虑多种影响因素的内河船队能效优化方法,在建立船队能效优化模型的基础上采用粒子群优化算法(PSO)对所建立的能效优化模型进行求解,以获得每艘船在每个航行航段的最佳航行速度。Sun等[11]提出了一种泊位和速度的协同优化模型,以实现港口与航运线路的协调。Cheaitou等[12]建立了一个集装箱船航线和船队规模问题的整数线性规划模型,提出了一种用于速度优化的简单启发式方法用于寻找最佳的港口抵达顺序、船舶最佳的航行速度和最佳的船舶数量。Jin等[13]建立了一种结合运输时间和价格的速度优化模型,应用拉格朗日松弛算法将原问题进行分解后寻优。Wang等[14]设计了一个基于Hadoop平台架构的船舶能效管理大数据分析平台,提出了一种基于路径划分结果的发动机最优转速的简单决策方法,该方法可提高船舶能效,从而减少CO2排放。
综上所述,可看出国内外学者在船舶航速优化领域都做了不少工作,但研究数量以及细分领域是有限的,尤其以人工神经网络构建纯黑箱的油耗模型并用遗传算法以特定约束精度按历史气象数据对航线做全局优化的更是少之又少。因此非常有必要开展这方面的船舶航速优化研究。
1 常见油耗模型的构建方法油耗模型的构建是做船舶航速优化的基础,油耗模型的预测准确度会很大程度影响到航速优化的准确度。在远洋航行时,船舶的油耗量是多种影响因素共同作用的结果,风速、风向、流速、流向、波高、波周期、浪向、船舶吃水等会很大程度影响船舶的油耗。船舶即使保持相同的航速或者转速在海中稳定行驶,船舶的主机油耗在不同的风浪流工况下也会有很大区别。此外,船舶油耗的测量误差一定程度上也会影响到油耗模型的精准度。油耗预测模型可分为3类:白盒模型、黑盒模型和灰盒模型[1]。
1.1 白盒模型白盒模型的结构和参数都是已知的,船舶油耗的白盒模型基于船舶领域的相关知识,以船-机-桨间的相互作用关系为基础建立。船舶主机通过燃烧的燃油获取功率,功率在经过变速箱、主机轴系等设备的传递最终传至螺旋桨,收到传递功率的螺旋桨与水流相互作用推动船舶向前运动[1]。而风速、风向、流速、流向、波高、波周期、浪向、船舶吃水等因素会很大程度影响航行船舶的状态,尤其是顺流和逆流,迎浪和随浪等对航行的主机油耗具有巨大影响。
1.2 黑盒模型不同的是,船舶油耗黑盒模型的结构参数都是未知的。船舶油耗黑盒模型的预测精度令人满意,但却需要海量的历史运营数据训练作为基础。常见的船舶油耗黑盒模型训练算法有额外树回归算法、朴素贝叶斯算法、人工神经网络、支持向量机监督算法、线性回归学习算法、随机森林回归等。黑盒模型具有更好的预测精度以及数据拟合性能,但黑盒模型也存在不少缺点,如需依赖海量的历史运营数据作为基础,模型结构与参数也无法直接反映船舶行业的专业知识等[1]。
1.3 灰盒模型灰盒模型介于白箱模型与黑箱模型之间,其一部分物理特征数据可直接测取,另一部分难以获取的特征则通过数据训练得到。在对船舶油耗灰盒模型进行构建时,需通过数学方法将黑色的部分分割出来,再利用部分数据推测该不可观部分的数学模型,灰盒模型也是油耗模型构建的选择之一[15]。
2 目标船舶油耗模型构建虽然白盒模型的内在逻辑关系和船舶专业知识的参数结构是已知的,在构建船舶油耗模型时可视化程度也较高,但是其预测精度有限;反之,黑盒模型预测精度以及数据拟合性能令人满意,但却需要海量的历史运营数据训练作为基础,同时其参数结构均是未知。结合本文能获取实船营运监测平台海量历史监测数据的优势,综合考虑,利用BP人工神经网络对航行目标船舶的油耗模型进行黑盒构建。
BP人工神经网络包括输入层、隐含层和输出层,是一种多层前馈网络。该网络可被监督,具有信号前向传播和误差反向传播的特点。BP人工神经网络计算学习过程分为2个阶段,包括信号的前向传播以及误差的反向传播。在反向传播的过程中,隐含层到输出层的权重和偏置及输入层到隐含层的权重和偏置会被依次优化[16]。如图1所示,输入层共有

|
图 1 BP神经网络结构示意图 Fig. 1 Schematic diagram of BP neural network |
故BP神经网络信号在前向传播时,输出层输出值
| $ \begin{split} {O_k} =\;& \psi \left( {ne{t_k}} \right) = \psi \left( {\sum\limits_{i = 1}^q {{w_{ki}}} {y_i} + {\alpha _k}} \right) =\\& \psi \left( {\sum\limits_{i = 1}^q {{w_{ki}}} \phi \left( {\sum\limits_{j = 1}^M {{w_{ij}}} {x_j} + {\theta _i}} \right) + {\alpha _k}} \right)。\end{split} $ | (1) |
而神经网络误差的反向传播会对各层的权值和阈值做修正优化,预测结果的误差修正如下式:
| $ {E_p} = \frac{1}{2}\sum\limits_{k = 1}^L {{{\left( {{T_k} - {O_k}} \right)}^2}} 。$ | (2) |
修正后各节点的权值和阈值的计算式如下:
| $ \Delta {w_{ki}} = \eta \sum\limits_{p = 1}^P {\sum\limits_{k = 1}^L {\left( {T_k^p - O_k^p} \right)} } \cdot {\psi ^\prime }\left( {{\text{ne}}{{\text{t}}_k}} \right) \cdot {y_i},$ | (3) |
| $ \Delta {\alpha _k} = \eta \sum\limits_{p = 1}^P {\sum\limits_{k = 1}^L {\left( {T_k^p - O_k^p} \right)} } \cdot {\psi ^\prime }\left( {{\text{ne}}{{\text{t}}_k}} \right) ,$ | (4) |
| $ \Delta {w_{ij}} = \eta \sum\limits_{p = 1}^P {\sum\limits_{k = 1}^L {\left( {T_k^p - O_k^p} \right)} } \cdot {\psi ^\prime }\left( {{\text{ne}}{{\text{t}}_k}} \right) \cdot {w_{ki}} \cdot {\phi ^\prime }\left( {{\text{ne}}{{\text{t}}_i}} \right) \cdot {x_j} ,$ | (5) |
| $ \Delta {\theta _i} = \eta \sum\limits_{p = 1}^P {\sum\limits_{k = 1}^L {\left( {T_k^p - O_k^p} \right)} } \cdot {\psi ^\prime }\left( {{\text{ne}}{{\text{t}}_k}} \right) \cdot {w_{ki}} \cdot {\phi ^\prime }\left( {{\text{ne}}{{\text{t}}_i}} \right) 。$ | (6) |
由于黑箱模型对数据集的依赖程度较高,故本文在挑选目标船舶时,选取了油耗流量计测量数据和人工测量数据误差较小的船舶,以确保流量计采样数据的有效性。本文挑选的目标船舶上安装有若干传感器,用于采集运营船舶航行过程中遭遇的各种气象数据以及船上主机等设备运行的实时数据,其中主机油耗流量计的采样频率为1 Hz。瞬时采集的设备运营数据部分无法准确反映对主机油耗情况的影响,因此该数据采集系统会将采集的数据通过计算转化为相应的表,分别统计10 min、1 h、1 d间隔的主机燃油消耗值,取采集的数据值和,而船舶首尾吃水取10 min间隔采集的数据平均值[17]。本文最终通过实船营运监测平台获取了某大型散货船从马代拉角到湛江航线的油耗数据监测数据,该船的主要参数如表1所示。
|
|
表 1 目标船舶的主要参数 Tab.1 Main parameters of the target ship |
实船营运监测平台获取的数据集以10 min为间隔记录测量主机消耗的油耗,总计约10000条。在获取监测数据后,对该船舶营运监测数据进行清洗处理以提高数据的质量,保证油耗模型构建的训练数据满足数据质量要求,经过数据清洗后选取了6180条油耗数据。
由于建立BP人工神经网络的计算模型所用特征参数越多,计算就越复杂,因此需要选择适当的特征参数,即选取的特征参数是输入特征参数与输出量之间的相关性较为显著,同时输入特征参数间相关性较低[18]。相关系数是反映变量之间线性相关程度的统计指标,其取值范围为[−1,1],正取值表示正相关,负取值表示负相关,而取值越接近0表示其线性关系越弱。相关系数的计算式如下:
| $ r = \dfrac{{\displaystyle\sum {(x - \bar x)} (y - \bar y)}}{{\sqrt {\displaystyle\sum {{{(x - \bar x)}^2}} \displaystyle\sum {{{(y - \bar y)}^2}} } }} 。$ | (7) |
其中,
通过研究多个随机变量之间的相关系数,合并相关性较高的输入层特征参数,以减少输入层维度从而提高网络计算精度与效率。通过计算筛选,选取的模型输入参数有流向、流速、主浪向角、有义波高、有效波周期、风速、风向、首向角、船舶前后吃水以及航速。以上参数同油耗数据的相关系数绝对值如图2所示。

|
图 2 影响参数同油耗的相关系数绝对值 Fig. 2 Absolute value of correlation coefficient between influencing parameters and fuel consumption |
通过对船舶航行数据做特征参数选择、数据预处理、数据标准化之后,将数据集做随机打乱处理并按7∶3的比例分成训练集和测试集。其中,4326组数据样本作为训练集,测试集样本则有1 854组。油耗模型的训练参数如表2所示。为了后续航速优化与历史气象数据对接方便,在油耗模型训练时,把风和流分解为2组分量,其中x分量为大地坐标系下的向东分量,y分量为大地坐标系下的向北分量。输入层包括表2所示11个参数,输出层的输出为船舶的主机油耗,模型设置了5个隐含层,每个隐含层均有11个节点。
|
|
表 2 油耗模型训练输入参数 Tab.2 Training input parameters of fuel consumption model |
训练完成之后,计算训练结果的平均绝对误差,计算式为:
| $ MAE = \frac{{\displaystyle\sum\limits_{i = 1}^N {\left| {\left. {F_i^{{\mathrm{sim}}} - F_{_i}^{{\text{act}}}} \right|} \right.} }}{N}。$ | (8) |
其中,
学习训练输出数据与原始采集数据对比如图3所示。模型训练后预测平均绝对误差为2.3%,油耗模型的准确度和泛化能力基本满足工程应用要求。

|
图 3 模型预报结果与航行数据对比 Fig. 3 Comparison between model forecast results and navigation data |
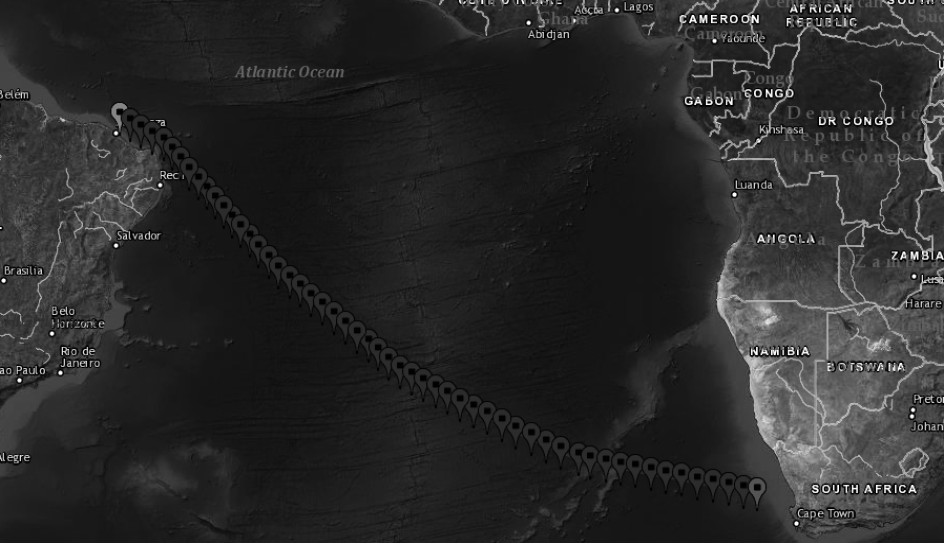
由于马代拉角到湛江的航线较长,航程前期和后期所消耗的燃油会导致船舶吃水产生一定变化,故只选取其中刚离港后一段航行距离做航速优化,起点的经纬度为(–38.26,–2.486),终点的经纬度为(15.13,–31.845),总距离为6 456 km,如图4所示。在对定航线船舶做分段航速优化时,需考虑航行船舶的航程总时间限制、相邻分段间的航速限制以及船长驾驶人意志限制等。此外,气象数据库所记录的气象数据是以1经度和1纬度作为间隔,即大约60 n mile为间隔。因此本文根据目标船舶航迹图中的气象数据和航行过程中航线的拐点对航段做聚类处理,每段按50~80 n mile将待优化的总航线分割成不同53段,确保每个航段的气象数据和航向共性较高而不同分段的共性较低,划分结果如图5所示。

|
图 4 优化航线示意图 Fig. 4 Schematic diagram of optimized routes |
|
图 5 优化航段划分示意图 Fig. 5 Schematic diagram of optimized segment division |
本文研究目的是通过对目标船舶定航线内不同航段做航速分段快速寻优,以达到航线目标函数的总油耗最低。在上述油耗模型和航段划分的基础上,构建非线性规划优化模型。
目标函数:
| $ \begin{split} &\min F =\sum\limits_{i = 1}^{53} f\left( {V_i},D{f_i},D{a_i},{H_i},W{x_i},W{y_i},W{h_i},\right.\\ & \left. W{p_i},W{d_i},C{x_i},C{y_i} \right)。\end{split} $ | (9) |
约束条件:
| $ \left\{ {\begin{array}{*{20}{l}} {\displaystyle\sum\limits_{i = 1}^{53} {{S_i}} = S} ,\\ {\displaystyle\sum\limits_{i = 1}^{53} {{{{t}}_i}} = \displaystyle\sum\limits_{i = 1}^{53} {\frac{{{S_i}}}{{{V_i}}}} \leqslant {T_{{\mathrm{total}}\exp }}},\\ {{T_0} \leqslant {T_{{\text{depart}}}}} ,\\ {{V_{\min }} \leqslant {V_i} \leqslant {V_{\max }}},\\ {\left| {\left. {\frac{{{V_{i + i}} - {V_i}}}{{{V_i}}}} \right| \leqslant 20\text% } \right.} 。\end{array}} \right. $ | (10) |
式中:
式(10)约束中,约束1表示分段航程总和要等于总航程距离;约束2表示航行时长要小于规划时长;约束3表示船舶的出发时间要早于规划时间;约束4表示航行过程船舶的航速不能大于或者小于船舶的最大或最小航速,以确保目标船舶航行过程保持良好的航行状态;约束5则为每个分段的航速变化不能超过20%,因为航段的航速变化要符合船长等操作人员的驾驶习惯,且过大的航速变化会导致主机油耗大幅度增加。
在约束优化计算中,假定每个划分航段的航速保持不变,遭遇气象数据不变,同时由于目标船舶的首向角在航段内变化不大,故在优化计算中假定航段内船舶航行的首向角不变。此外,历史气象数据库对于同一个经纬度的海流是以24 h作为间隔进行测量记录,风和浪是以6 h作为间隔进行测量记录。故当目标船舶在t时抵达第i个位置点,需获取第i+1航段气象数据时,以t时后距离t时最近的气象数据作为第i+1航段的气象数据。
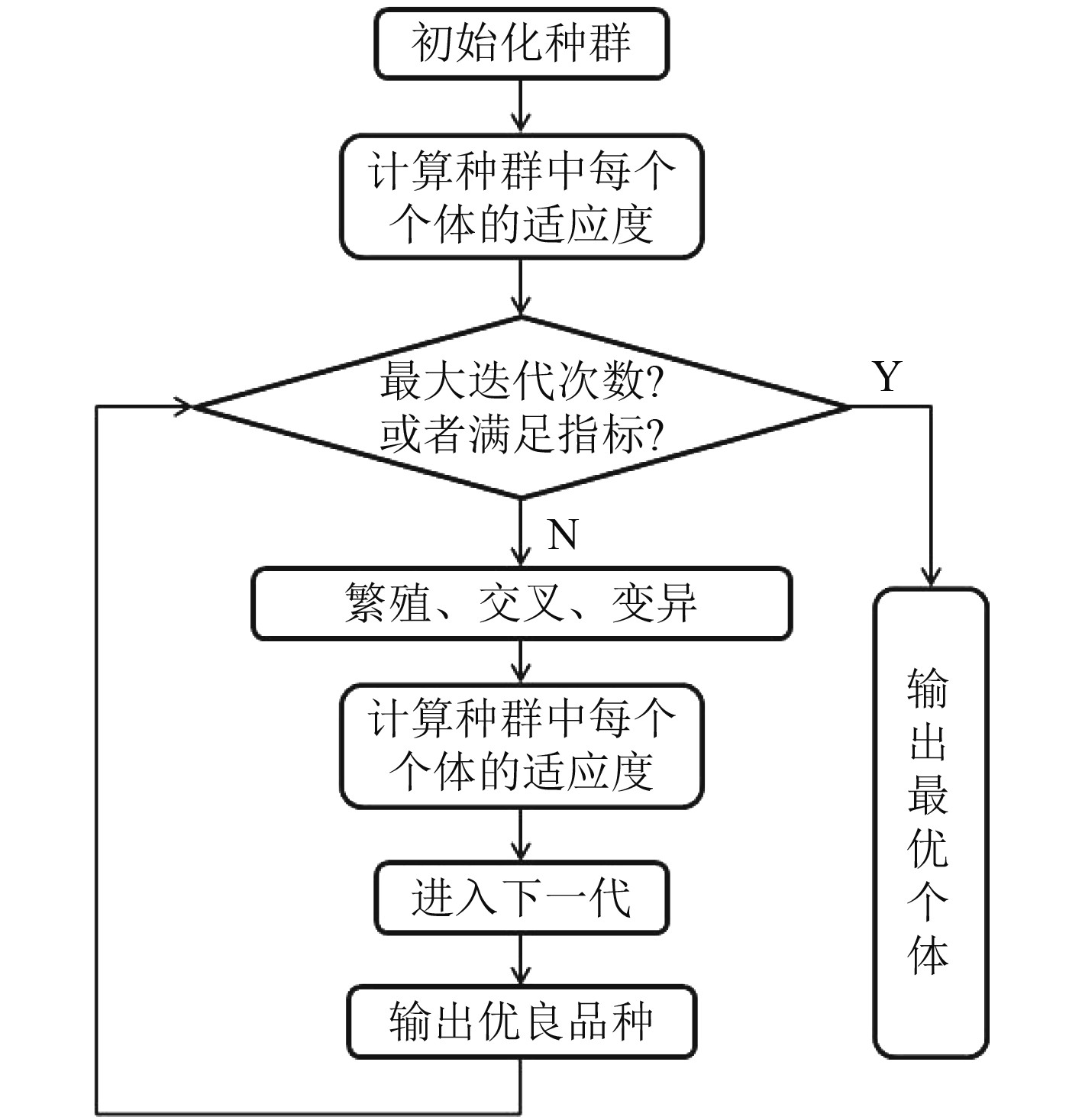
3.2 基于遗传算法的航速优化在油耗模型构建和航速优化模型构建的基础上,以遗传算法作为求解算法,对目标船舶从马代拉角到湛江航线的其中一段航行距离做航速优化。遗传算法是根据生物进化规律模拟生物进化过程中的自然选择和遗传进化而设计提出的计算模型,是一种自适应的随机搜索方法,被广泛应用于各行各业的优化计算[19]。遗传算法流程如图6所示。
|
图 6 遗传算法流程图 Fig. 6 Flow chart of genetic algorithm |
在初始化种群时,为了让算法更快搜寻到最优解,在每个划分航段航速的最大最小限制值的基础上缩小航速范围,以9~10 kn作为种群初始化的数值区间,并以种群数50,最大迭代次数1000,交叉率为0.8,变异率为0.05以及精英计数为0.05倍种群数,做全局的航速优化寻优计算。在遗传算法寻优中为克服整数模型计算误差大以及简单遗传算法精度过高导致寻优计算慢的缺点,同时考虑了实际工程的应用。在原目标函数上加入特定精度约束以小数点后1位做航线的全局寻优。更改后的目标函数如下式:
| $\begin{split} & \min F = \sum\limits_{i = 1}^{53} f( {V^{Integer}}_i,D{f_i},D{a_i},{H_i},W{x_i},W{y_i},W{h_i},\\ & W{p_i},W{d_i},C{x_i},C{y_i}) ,\end{split} $ | (11) |
| $ {V^{Integer}}_i{\text{ = }}10 \times {V_i}。$ | (12) |
其中,
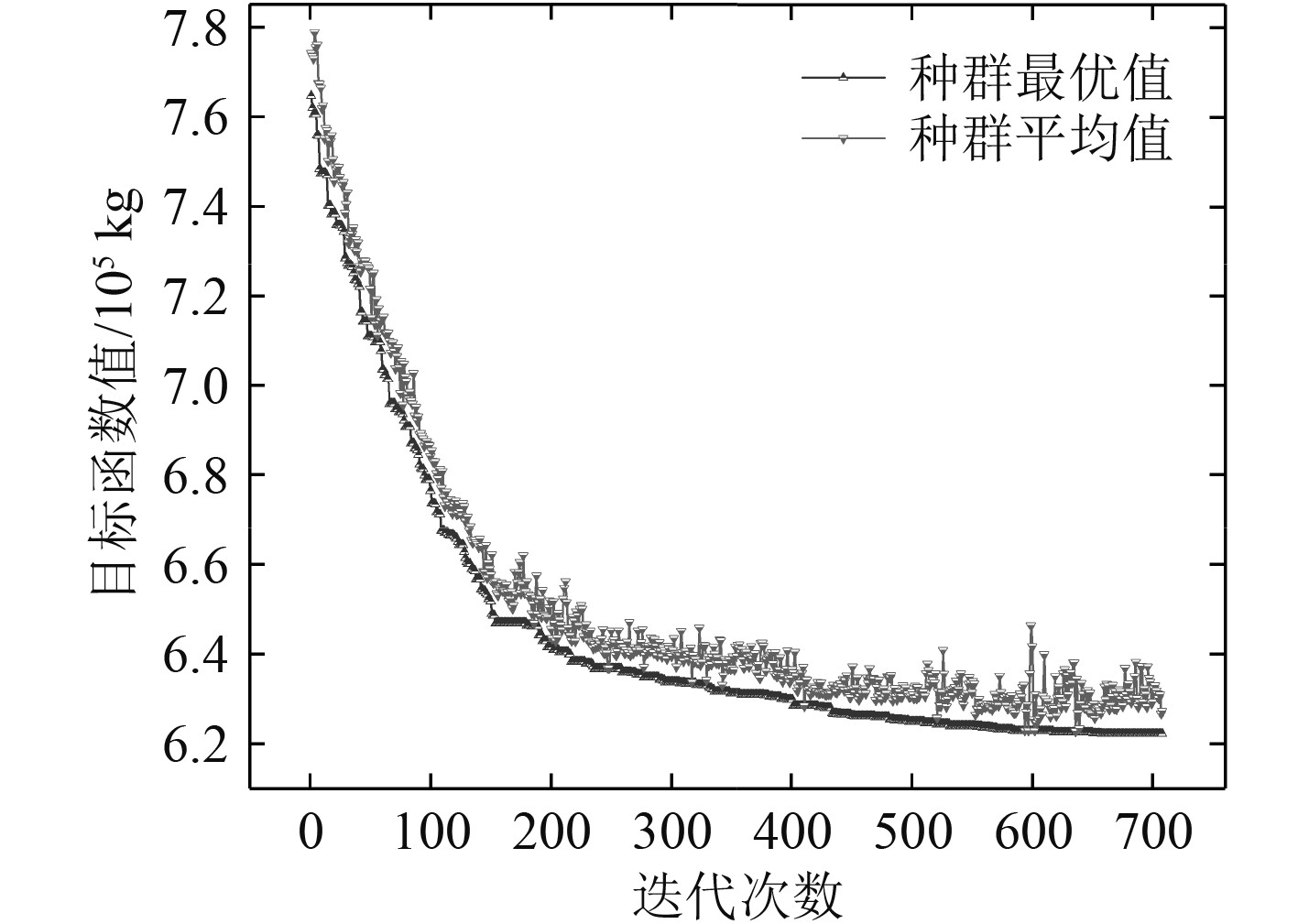
|
图 7 遗传算法航速优化迭代数据图 Fig. 7 Iterative data graph of GA speed optimization |
由表3可以看出,迭代优化后的总油耗为622.22 t,而未优化时目标船舶的实际燃油消耗为692.40 t。优化结果表明,以优化航速进行航行时,目标船舶能节省燃油70.2 t,总油耗节省10.1%。
|
|
表 3 优化前后数据对比 Tab.3 Data comparison before and after optimization |
优化前后的的航段航速数据如图8所示。可以看出,未优化时,目标船舶的航行总时长约为13.61 d,而优化后航行总时长为12.26 d,不仅可节省1.35 d的航行运输时间,还可节省燃油损耗10.1%。

|
图 8 优化前后分段航速 Fig. 8 Segmented speed before and after optimization |
本文利用BP人工神经网络建立了目标船舶的油耗模型,模型预测的平均绝对误差为2.3%,准确度和泛化能力基本满足工程应用要求。其次,构建了以航线总油耗量最低的目标函数以及定精度非线性约束的优化模型,利用遗传算法,并基于历史气象数据对目标船舶的航线做分段航速优化。计算结果表明,航速优化后目标船舶的航行时长不仅能减少1.35 d,燃油损耗还可节省10.1%,说明对航行船舶做分段航速优化是一种可行方案。
在降速节能原理基础上,如何对船舶航行中最佳节能航速进行确定,即在寻求目标函数的期望利润和期望损失之间做动态平衡抉择具有巨大的经济和环境意义。本文在定精度非线性约束下,对目标船舶的航速做了研究优化,研究结果表明对航行船舶进行分段划分并做航速优化的方法是可行的,不仅可降低碳排放还可一定程度上减少船舶航次的航行总时长。但本文的研究中也存在一些问题:首先采用的是历史气象数据对目标船舶的航速进行全局寻优,然而实际航行船舶所遭遇的气象数据是不确定的,因为目前气象数据预报精准度还有待提高;其次,远洋船舶的航行总时长一般都超过30 d,航次总时长过长导致航段后半部分的气象数据准确度大大降低,故而实际工程应用中,以气象预报作为优化基础所得出的分段航速是否是全局最优解还有待商榷。
| [1] |
袁裕鹏, 王康豫, 尹奇志, 等. 船舶航速优化综述[J]. 交通运输工程学报, 2020, 20(6): 18-34. |
| [2] |
孙超, 张均东, 刘超. 基于航速与实时能效综合目标的船舶主机转速优化[J]. 大连海事大学学报, 2020, 46(3): 60-67. |
| [3] |
李铮, 潘晓萌. 船舶航速优化算法研究[J]. 舰船科学技术, 2016, 38(12): 7−9.
|
| [4] |
马征. 船舶期租经营中的航速油耗索赔问题研究[J]. 珠江水运, 2019(19): 60-61. |
| [5] |
查安平. 航速优化下小型船舶调度目标选取优化方法分析[J]. 舰船科学技术, 2021, 43(14): 34-36. |
| [6] |
计明军, 张开放, 祝慧灵, 等. 基于可变航速的支线集装箱船舶调度优化模型与算法[J]. 运筹与管理, 2019, 28(11): 18-26. |
| [7] |
马冉祺, 黄连忠, 魏茂苏, 等. 基于实船监测数据的定航线船舶智能航速优化[J]. 大连海事大学学报, 2018, 44(1): 31-35. |
| [8] |
丁坤平. 基于权重法与遗传算法的船舶定航线多目标航速优化[D]. 哈尔滨: 哈尔滨工程大学, 2021.
|
| [9] |
李佳欣. 考虑港口拥堵的电煤航运船舶调度与航速优化研究[D]. 南京: 东南大学, 2021.
|
| [10] |
K W, J L I, L H, et al. An energy efftciency optimization methodfor inland ship fleet considering multiple influencing factors[C]//2019 5th International Conference on Transportation Information and Safety (ICTIS), IEEE, 2019: 1263−1267.
|
| [11] |
B S, B N, H X, et al. Cooperative optimization for port and shipping line with unpredictable disturbance consideration[C]//2018 14th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), 2018: 113−118.
|
| [12] |
CHEAITOU A, LARBI R, HAMDAN S. Liner shipping routing, fleet sizing and speed optimization with application to Asia-Northern Europe-trade[C]//IEEE, 2018: 1−8.
|
| [13] |
JIN Xiaochuang, QUAN Xiongwen, CHEN Qiushuang, et al. Speed optimization for a container shipping route in competitive environment[C]//Technical Committee on Control Theory, Chinese Association of Automation, 2015: 8446−8451.
|
| [14] |
WANG K, YAN X, YUAN Y, et al. Study on route division for ship energy efficiency optimization based on big environment data[C]//2017 4th International Conference on Transportation Information and Safety (ICTIS), IEEE, 2017: 111−116.
|
| [15] |
曹子涵, 明岭峰, 陈焕新, 等. 基于随机优化算法的建筑热环境灰箱模型开发与验证[J]. 制冷技术, 2021, 41(2): 24-29. |
| [16] |
张焱飞, 李荣宗, 文逸彦, 等. 基于人工神经网络的实船航行主机能耗预估自学习模型[J]. 上海船舶运输科学研究所学报, 2019, 42(2): 34-37. |
| [17] |
丁琦, 赵科. 船舶智能能效管理系统设计[J]. 舰船科学技术, 2020, 42(11): 144-147. |
| [18] |
冯亮, 董国祥, 季盛, 等. 基于航行数据的船舶航行油耗模型建立方法[J]. 上海船舶运输科学研究所学报, 2020, 43(1): 27-31. |
| [19] |
赵宏伟, 任震. 面向机组最优投入的改进遗传算法及其应用[J]. 系统工程学报, 1998(2): 92-97. |
 2024, Vol. 46
2024, Vol. 46
