2. 烟台工程职业技术学院,山东 烟台 265500;
3. 鲁东大学 蔚山船舶与海洋学院,山东 烟台 264025;
4. 鲁东大学 数学与统计科学学院,山东 烟台 264025;
5. 山东省海上航天装备技术创新中心,山东 烟台 264000;
6. 招商局海洋装备研究院,广东 深圳 518000
2. Yantai Engineering and Technology College, Yantai 265500, China;
3. Ulsan Ship and Ocean College, Ludong University, Yantai 264025, China;
4. School of Mathematics and Statistics, Ludong University, Yantai 264025, China;
5. Shandong Marine Aerospace Equipment Technological Innovation Center, Yantai 264000, China;
6. China Merchants Marine and Offshore Research Institute, Shenzhen 518000, China
随着海洋开发和利用不断向资源更加丰富的深海和远海进军,传统锚泊定位受作业水深的限制而无法满足深海和远海的定位要求。动力定位(Dynamic Positioning,DP)系统使船舶或钻井平台利用自身推进装置产生的动力来抵抗海洋环境干扰,以一定姿态保持在海面的期望位置上,具有不受水深限制和定位精度高等优点,成为深远海开发的重要支持系统,广泛应用于离岸海事作业中,如海水监测、海事搜救和石油和天然气钻探等[1]。
20世纪60年代,早期的动力定位系统采用比例-积分-微分控制器串联低通滤波器的方法以滤除位置传感器测量噪声和船舶振荡运动。由于船舶多自由度运动的耦合特性,并且低通滤波器会引起相位滞后,导致其控制精度差[2]。20世纪70年代,Balchen等[3]和Grimble等[4]将多变量线性最优控制和卡尔曼滤波器引入到动力定位系统设计中,但此方法需要将船舶运动方程在各工作点上线性化,故仅能保证系统局部稳定,且参数调节工作量大。随着非线性控制理论的发展, 船舶非线性动力定位控制方法应运而生。20世纪90年代,Fossen等分别采用解耦的观测器逆推方法[5]和矢量观测器逆推方法[6],设计仅依赖船舶位置测量值的动力定位非线性输出反馈控制律。Fossen等[7]构造了具有海浪滤波能力的无源观测器,以提供船舶低频位置和海洋低频干扰的滤波值,但要求海况的先验知识,Du等[8]利用自适应技术和动态面控制方法提出了自适应鲁棒动力定位控制律,利用带有
基于干扰观测器的控制能够有效地在线估计被控对象受到的时变扰动,逐渐被应用到船舶运动控制系统中[9]。20世纪80年代,Ohishi等[10]将线性干扰观测器应用到频率域的电机控制中。Chen等[11]提出了非线性时域干扰观测器的设计方法,将其应用到机械臂的抗干扰控制中,但该干扰观测器需要扰动模型的精确信息。Wei等[12]针对具有不确定摄动项的外部扰动模型,设计了基于模型的非线性干扰观测器,提出了复合分层抗干扰控制方法。但上述干扰观测器均要求外部谐波干扰频率信息,为了克服未知频率谐波干扰抵消问题,自适应内模控制被引入到抗干扰控制设计中。
本文针对带未知谐波干扰的船舶动力定位控制问题,通过将自适应内模观测器、指令滤波器、辅助动态系统和动态面控制方法相结合,用自适应内模原理将未知谐波干扰补偿问题转化成自适应问题。引入指令滤波器对指令控制输入进行滤波,设计辅助动态系统来降低控制输入饱和的影响,提出船舶动力定位自适应内模输出调节动态面控制策略,动态面控制方法使控制律简单易于工程实现。
1 问题描述船舶动力定位运动数学模型表示为[7]:
| $ \dot {\boldsymbol{\eta}} = {\boldsymbol{J}}(\psi )\upsilon,$ | (1) |
| $ {\boldsymbol{M}}\dot \upsilon = - D\upsilon + {\boldsymbol{\tau}} + d(t),$ | (2) |
式中:
| $ {\boldsymbol{J}}(\psi ) = \left[ {\begin{array}{*{20}{c}} {\cos (\psi )}&{ - \sin (\psi )}&0 \\ {\sin (\psi )}&{\cos (\psi )}&0 \\ 0&0&1 \end{array}} \right]。$ | (3) |
满足特性
假设1 作用在船舶上的海洋环境扰动是时变未知且有界的,并可视为一系列未知频率、相位和幅值的正弦波叠加。
海洋环境是时常变化且难以预知的,且具有有限的能量[13]。通过傅里叶分析,由海浪环境引起的扰动可分解为一系列未知频率、幅值和相位的正弦波,故假设1是合理的。
针对具有未知谐波海洋环境干扰的船舶动力定位控制问题,在假设1下,设计船舶鲁棒自适应动力定位干扰抵消控制律,迫使船舶位置
由假设1,海洋环境扰动
| $ \dot {\boldsymbol{\chi}} = {\boldsymbol{W\chi}},$ | (4) |
| $ {\boldsymbol{d}} = {\boldsymbol{V\chi}} 。$ | (5) |
式中,
引理1 海洋环境谐波扰动
| $ \dot {\boldsymbol{\varsigma}} = {\boldsymbol{G\varsigma}} + {\boldsymbol{Hd}},$ | (6) |
| $ {\boldsymbol{d}} = {{\boldsymbol{\Theta}} ^{\mathrm{T}}}{\boldsymbol{\varsigma}}。$ | (7) |
式中:
| $ {\boldsymbol{\varsigma}} = {\boldsymbol{F\chi}} 。$ | (8) |
式中,
| $ {\boldsymbol{FW}} - {\boldsymbol{GF}} = {\boldsymbol{HV}}。$ | (9) |
证明 由于
| $ \dot {\boldsymbol{\varsigma}} = {\boldsymbol{G\varsigma}} + {\boldsymbol{Hd}} 。$ | (10) |
因此,式(6)成立。进一步,由式(8)可得:
| $ {\boldsymbol{\chi }}= {{\boldsymbol{F}}^{ - 1}}{\boldsymbol{\varsigma}}。$ | (11) |
将式(11)代入式(5),可得
由引理1可知,环境扰动能够以线性回归形式表示为扰动作输入的标准线性模型的输出,回归器
构造如下内模观测器估计回归器
| $ \hat {\boldsymbol{\varsigma}} = {\boldsymbol{\rho}} + {\boldsymbol{N\upsilon}} ,$ | (12) |
| $ \dot {\boldsymbol{\rho}} = {\boldsymbol{G\rho}} + ({\boldsymbol{GN}} + {\boldsymbol{N}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{D}}){\boldsymbol{\upsilon}} - {\boldsymbol{N}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{\tau}} 。$ | (13) |
式中:
| $ {\boldsymbol{N}}{{\boldsymbol{M}}^{ - 1}} = {\boldsymbol{H}}。$ | (14) |
引理2 针对线性外部系统、标准线性模型以及构造的观测器, 作用在船舶上的海洋环境谐波扰动
| $ {\boldsymbol{d}} = {{\boldsymbol{\Theta}} ^{\mathrm{T}}}\hat {\boldsymbol{\varsigma}} + {{\boldsymbol{\varepsilon _d}}}。$ | (15) |
式中,
证明 定义估计误差向量为:
| $ \begin{split} & \tilde {\boldsymbol{\varsigma}} \in {{\boldsymbol{R}}^{2q}} ,\\ & \tilde {\boldsymbol{\varsigma}} = \hat {\boldsymbol{\varsigma}} - {\boldsymbol{\varsigma}}。\end{split} $ | (16) |
由式(16)有
根据式(2)、式(6)、式(12)、式(13)和式(14),式(16)的时间导数为:
| $ \dot {\tilde{\boldsymbol{ \varsigma}}} = \dot {\boldsymbol{\rho}} + {\boldsymbol{N}}\dot {\boldsymbol{\upsilon}} - {\boldsymbol{G\varsigma}} - {\boldsymbol{Hd}}= {\boldsymbol{G}}\tilde {\boldsymbol{\varsigma}} 。$ | (17) |
因为
由引理2可知,船舶的海洋谐波扰动的不确定性转化成式(15)参数的不确定性,船舶扰动补偿问题转化成了自适应控制问题,可用自适应控制方法设计船舶鲁棒自适应控制律。
3 基于自适应内模的动态面控制基于所构造的内模观测器、指令滤波器和辅助动态系统,利用动态面控制方法设计鲁棒自适应干扰抵消控制律,引入指令滤波器对控制信号进行滤波。
步骤1 定义位置误差面向量为:
| $ \begin{split} & {{\boldsymbol{s}}_1} \in {{\boldsymbol{R}}^3}\\ & {{\boldsymbol{s}}_1} = {\boldsymbol{\eta}} - {{\boldsymbol{\eta}} _d} 。\end{split} $ | (18) |
由式(1),式(21)的时间导数为:
| $ {\dot {\boldsymbol{s}}_1} = {\boldsymbol{J}}({\boldsymbol{\psi}} ){\boldsymbol{\upsilon}} 。$ | (19) |
式中,
设计中间控制函数向量为:
| $ \begin{split} & {{\boldsymbol{\varphi}} _1} \in {{\boldsymbol{R}}^3}\\ & {{\boldsymbol{\varphi}} _1} = - {{\boldsymbol{J}}^{\text{T}}}{\boldsymbol{(\psi}} ){{\boldsymbol{K}}_1}{{\boldsymbol{s}}_1}。\end{split} $ | (20) |
式中,
| $ {{\text{π}} }_{d}{\dot{{\boldsymbol{\beta}} }}_{d}+{{\boldsymbol{\beta}} }_{d}={{\boldsymbol{\phi}} }_{1}\text{,}{{\boldsymbol{\beta}} }_{d}(0)={\phi }_{1}(0)。$ | (21) |
式中,
微分项
步骤2 定义速度误差面向量为:
| $ \begin{split} & {{\boldsymbol{s}}_2} \in {{\boldsymbol{R}}^3} \\ & {{\boldsymbol{s}}_2} = {\boldsymbol{\upsilon}} - {{\boldsymbol{\beta}} _d}。\end{split} $ | (22) |
由式(2)、式(15)、式(22)和
| $ {\boldsymbol{M}}{\dot {\boldsymbol{s}}_2} = - {\boldsymbol{D\upsilon}} + {{\boldsymbol{\tau}} _c} + \Delta \tau + {{\boldsymbol{\Theta}} ^{\text{T}}}\hat {\boldsymbol{\varsigma}} + {{\boldsymbol{\Theta}} ^{\text{T}}}\tilde {\boldsymbol{\varsigma}} - {\boldsymbol{M}}{\dot {\boldsymbol{\beta}}_d}。$ | (23) |
式中,
引入指令滤波器:
| $ \left\{ \begin{gathered} {{\dot \lambda }_{1i}} = {\lambda _{2i}},\\ {{\dot \lambda }_{2i}} = - 2{\gamma _i}{\omega _{{\mathrm{in}}}}\left( {{\lambda _{2i}} + {\mathrm{sat}}\left( {\frac{{\omega _{{\mathrm{in}}}^2}}{{2{\gamma _i}{\omega _{{\mathrm{in}}}}}}\left( {{\lambda _{1i}} - {\mathrm{sat}}\left( {{\tau _{ci}}} \right)} \right)} \right)} \right) 。\end{gathered} \right. $ | (24) |
令
为了补偿控制输入幅值及变化率约束的影响,构造辅助动态系统:
| $ \left\{ \begin{aligned} & {{\dot \xi }_1} = - {K_1}{\xi _1} + J(\psi ){\xi _2} ,\\ & M{{\dot \xi }_2} = - {K_\xi }{\xi _2} + \Delta \tau 。\end{aligned} \right. $ | (25) |
式中,
定义辅助误差向量:
| $ {\bar s_1} = {s_1} - {\xi _1},$ | (26) |
| $ {\bar s_2} = {s_2} - {\xi _2}。$ | (27) |
设计船舶鲁棒自适应动力定位控制律:
| $ {\tau _c} = - {{\boldsymbol{J}}^{\mathrm{T}}}(\psi ){\bar s_1} - {{\boldsymbol{K}}_2}{\bar s_2} - {{\boldsymbol{K}}_\xi }{\xi _2} + {\boldsymbol{D\upsilon}} + {\boldsymbol{M}}{\dot {\boldsymbol{\beta}} _d} - {\hat {\boldsymbol{\Theta}} ^{\mathrm{T}}}\hat {\boldsymbol{\varsigma}},$ | (28) |
以及自适应律:
| $ {\dot{\widehat{\theta }}}_{i}={\varGamma }_{i}\left({\overline{s}}_{{2}_{i}}\widehat{\varsigma }-{\sigma }_{\iota }{\widehat{\theta }}_{i}\right)\text{,}i=1,2,3 。$ | (29) |
式中,
通过引入指令滤波器式(24),将所设计的指令控制信号输入到该指令滤波器,得到满足幅值及变化率约束的控制信号作为船舶实际控制向量。引入辅助动态系统式(25)在线校正控制误差和自适应律,降低输入饱和约束对频率未知谐波干扰抵消控制性能的影响。
本文的主要结果总结在定理1中。
定理1 针对具有未知时变环境扰动和控制输入饱和约束的船舶动力定位问题,在假设1下,设计基于中间控制函数向量式(20)、一阶滤波器式(21)、观测器式(12)~式(13)、指令滤波器式(24)、辅助动态系统式(25)和自适应律式(29)的鲁棒自适应控制律式(28),通过适当选取设计参数
证明 选取Lyapunov预选函数:
| $ V = \frac{1}{2}\bar s_1^{\text{T}}{\bar s_1} + \frac{1}{2}\bar s_2^{\text{T}}M{\bar s_2} + \frac{1}{2}\sum\limits_{i = 1}^3 {\tilde \theta _i^{\text{T}}\Gamma _i^{ - 1}{{\tilde \theta }_i}} + {\tilde \varsigma ^{\text{T}}}P\tilde \varsigma + \frac{1}{2}y_2^{\text{T}}{y_2}。$ | (30) |
式中,
| $ {{\boldsymbol{G}}^{\text{T}}}{\boldsymbol{P}} + {\boldsymbol{PG}} = - {\boldsymbol{\Theta}} {{\boldsymbol{\Theta}} ^{\text{T}}} 。$ | (31) |
定义紧集
| $ \begin{split} \dot V \leqslant \,&- \bar s_1^{\text{T}}\left( {{K_1} - \frac{1}{2}{I_{3 \times 3}}} \right){{\bar s}_1} - \bar s_2^{\text{T}}\left( {{K_2} - \frac{1}{2}{I_{3 \times 3}}} \right){{\bar s}_2} - \\ & \sum\limits_{i = 1}^3 {\frac{{{\sigma _i}}}{2}||{{\tilde \theta }_i}|{|^2} - \frac{1}{2}{{\tilde \varsigma }^{\text{T}}}(\Theta {\Theta ^{\text{T}}})\tilde \varsigma + \frac{1}{2}y_2^{\text{T}}{y_2}}- \\ & \left( {\frac{1}{2} + \frac{{b_M^2}}{2} + {\mu ^*}} \right)y_2^{\text{T}}{y_2} + \frac{{||b(\eta ,\upsilon ,{\eta _d})||}}{{b_m^2}}\frac{{b_m^2||{y_2}|{|^2}}}{2}+ \\ & \sum\limits_{i = 1}^3 {\frac{{{\sigma _i}}}{2}||{\theta _i}|{|^2}} + \frac{1}{2} \leqslant - 2{\alpha _1}V + {c_1} 。\end{split} $ | (32) |
式中,
式(32)两边同乘以
| $ 0 \leqslant V(t) \leqslant \frac{{{c_1}}}{{2{\alpha _1}}} + \left[ {V(0) - \frac{{{c_1}}}{{2{\alpha _1}}}} \right]{e^{ - 2{\alpha _1}t}}。$ | (33) |
由式(33)可得,
| $ ||{\bar s_1}|| \leqslant \sqrt {\frac{{{c_1}}}{{{\alpha _1}}} + 2\left[ {{V_1}(0) - \frac{{{c_1}}}{{2{\alpha _1}}}} \right]{e^{ - 2{\alpha _1}t}}}。$ | (34) |
进一步,考虑Lyapunov预选函数:
| $ {V_\xi } = \frac{1}{2}\xi _1^{\text{T}}{\xi _1} + \frac{1}{2}\xi _2^{\text{T}}M{\xi _2}。$ | (35) |
根据式(25)和式(35)的时间导数为:
| $ {{\dot V}_\xi } = \xi _1^{\text{T}}{{\dot \xi }_1} + \xi _2^{\text{T}}M{{\dot \xi }_2} \leqslant - 2{\alpha _2}{V_\xi } + \frac{1}{2}||\Delta \tau |{|^2} 。$ | (36) |
式中,
在式(36)两边同乘
| $ ||{\xi _1}|| \leqslant \sqrt {\frac{{||\Delta \tau |{|^2}}}{{2{\alpha _2}}} + 2\left[ {{V_\xi }(0) - \frac{{||\Delta \tau |{|^2}}}{{4{\alpha _2}}}} \right]{e^{ - 2{\alpha _2}t}}}。$ | (37) |
结合式(26)、式(34)和式(37),可得:
| $ \begin{split} ||{s_1}|| =\,& ||{{\bar s}_1}|| + ||{\xi _1}|| \leqslant \\ \,&\sqrt {\frac{{{c_1}}}{{{\alpha _1}}} + 2\left[ {{V_1}(0) - \frac{{{c_1}}}{{2{\alpha _1}}}} \right]{e^{ - 2{\alpha _1}t}}} + \\ \,& \sqrt {\frac{{||\Delta \tau |{|^2}}}{{2{\alpha _2}}} + 2\left[ {{V_\xi }(0) - \frac{{||\Delta \tau |{|^2}}}{{4{\alpha _2}}}} \right]{e^{ - 2{\alpha _2}t}}} 。\end{split} $ | (38) |
定位误差向量
为了验证所设计鲁棒自适应控制律的有效性,以供给船Northern Clipper[7]为例进行仿真,Northern Clipper运动数学模型的动态模型参数为:
| $ {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {5.3122 \times {{10}^6}}&0&0 \\ 0&{8.2831 \times {{10}^6}}&0 \\ 0&0&{3.7454 \times {{10}^9}} \end{array}} \right] ,$ |
| $ {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {5.0242 \times {{10}^4}}&0&0 \\ 0&{2.7229 \times {{10}^5}}&{ - 4.3933 \times {{10}^6}} \\ 0&{ - 4.3933 \times {{10}^6}}&{4.1894 \times {{10}^8}} \end{array}} \right]。$ |
作用在船舶上的谐波海洋环境干扰取为:
| $ {\boldsymbol{d}}(t) = {\kern 1pt} 500 \times {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {1.3 + 2.0\sin (0.02t) + 1.5\sin (0.1t)} \\ { - 0.9 + 2.0\sin \left( {0.02t - \dfrac{{\text{π}} }{6}} \right) + 1.5\sin (0.3t)} \\ { - 1.0\sin \left( {0.09t + \dfrac{{\text{π}} }{3}} \right) - 4\sin (0.01t)} \end{array}} \right] 。$ |
船舶动力定位的期望位置和首摇角向量取为
自适应内模观测器的设计参数取为
设计参数取为
仿真结果如图1~图4所示。由图1可知,所提出的鲁棒自适应输出调节控制律能够将船舶的位置和首摇角定位在期望值上。由图2可知,船舶实际控制信号受到饱和。由图3可见,船舶控制信号的变化率也受到饱和。图2和图3表明船舶控制信号的幅值和变化率满足船舶推进系统所能产生的能力范围内。由图4可知,自适应内模观测器(自适应律式(29)和观测器式(12)和式(13))能够提供谐波干扰
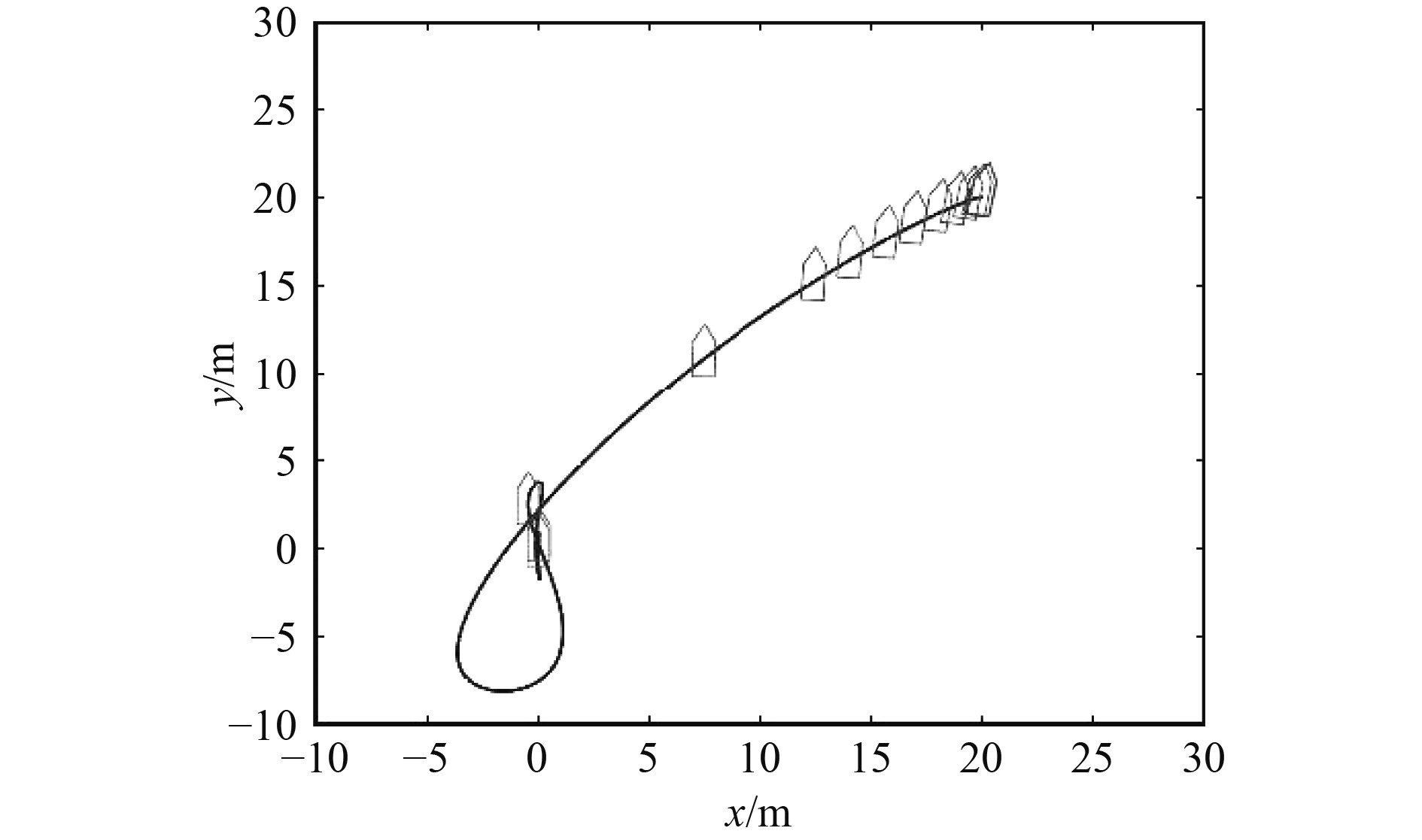
|
图 1 船舶平面轨迹 Fig. 1 Ship horizontal trajectory |
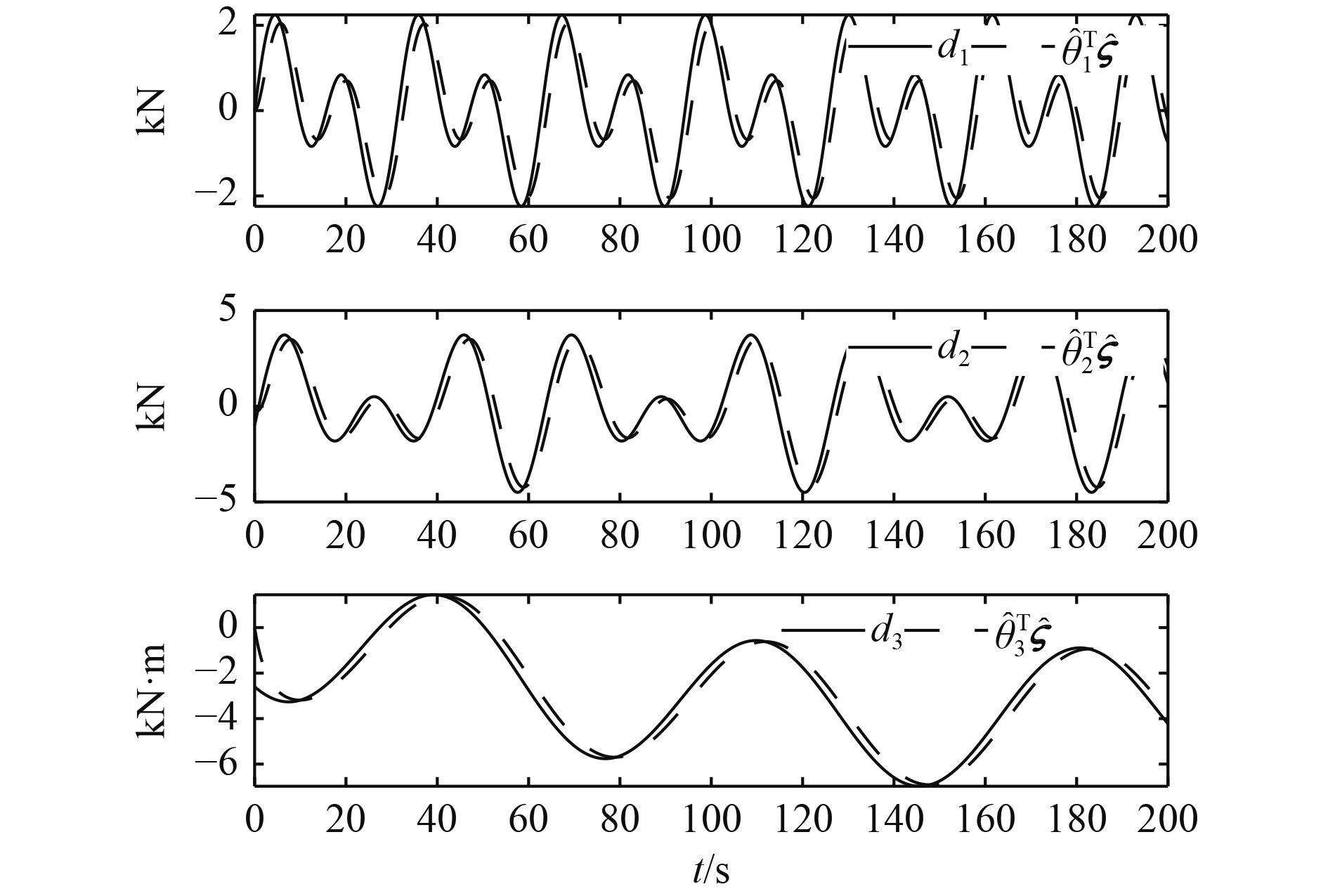
|
图 4 海洋扰动估计 Fig. 4 Ocean disturbance estimations |
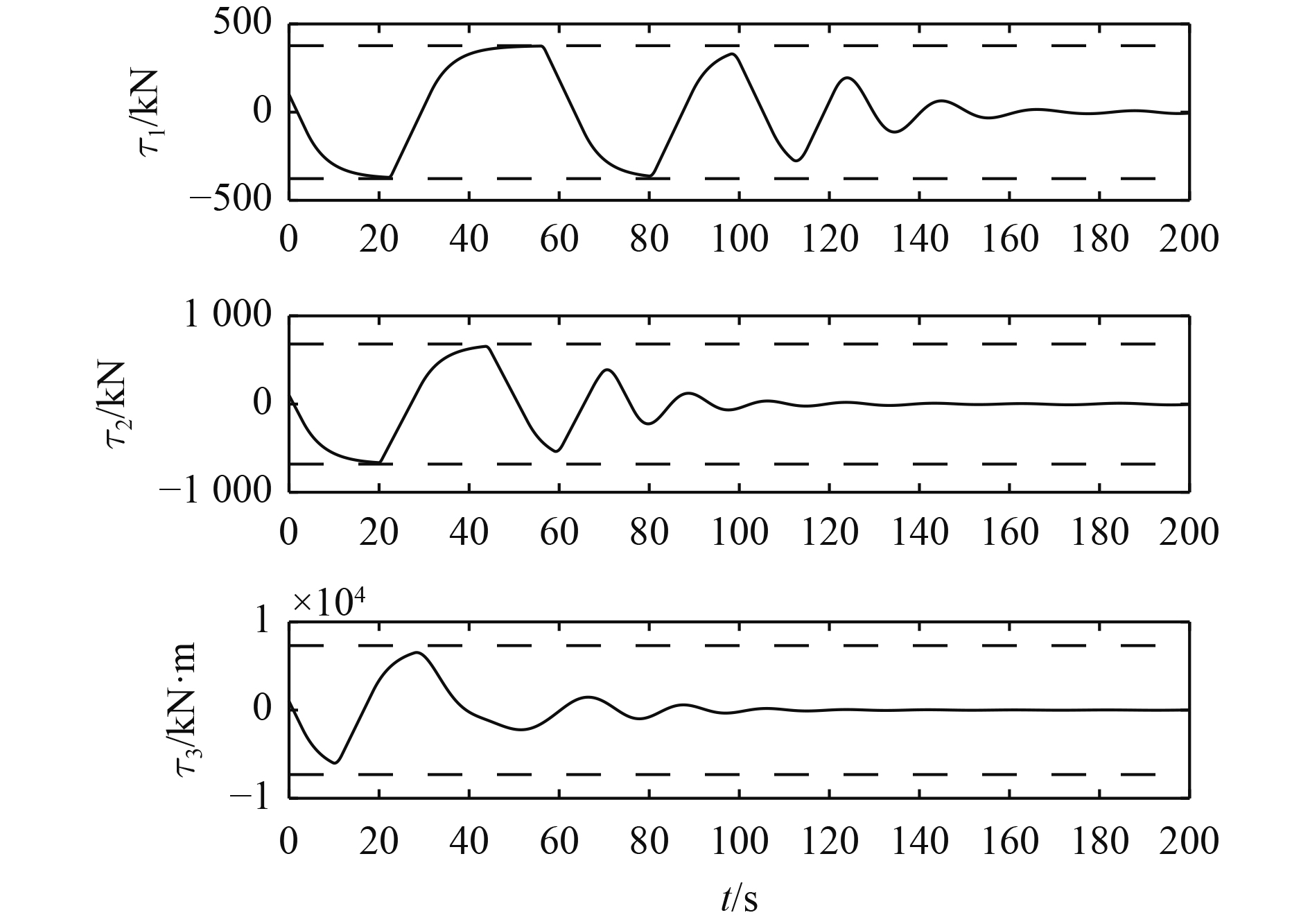
|
图 2 船舶控制信号 Fig. 2 Ship control signals |

|
图 3 控制信号变化率 Fig. 3 Rate of control signals |
本文针对具有未知谐波海洋干扰的船舶动力定位控制问题,通过将自适应内模观测器、指令滤波器、辅助动态系统和动态面控制方法相结合,提出了船舶动力定位鲁棒自适应干扰抵消控制策略,所设计的自适应干扰估计方法不要求海洋环境谐波干扰的频率信息。引入指令滤波器和辅助动态系统降低输入饱和对自适应干扰抵消控制的影响,采用动态面控制方法使控制律简单易于实现。以供给船Northern Clipper为例的仿真结果验证了有效性。
| [1] |
廖成毅, 杨颖, 吉宇人. 船舶动力定位控制策略研究综述[J]. 舰船科学技术, 2020, 42(9): 1-5. LIAO Chengyi, YANG Ying, JI Yuren. Research on ship dynamic positioning control strategies[J]. Ship Science and Technology, 2020, 42(9): 1-5. DOI:10.3404/j.issn.1672-7649.2020.09.001 |
| [2] |
FOSSEN T I, PEREZ T. Kalman filtering for positioning and heading control of ships and offshore rigs[J]. IEEE Control Systems Magazine, 2009, 29(6): 32-46. DOI:10.1109/MCS.2009.934408 |
| [3] |
BALCHEN J G, JENSSEN N A, MATHISEN E, et al. Dynamic positioning of floating vessels based on Kalman filtering and optimal control[C]//Proceedings of the 19th IEEE Conference on Decision and Control, Albuquerque, New Mexico, IEEE, 1980: 852−864.
|
| [4] |
GRIMBLE M. J, PATTON R J, WISE D A. Use of Kalman filtering techniques in dynamic ship positioning systems[J]. IEE Proceedings D-Control Theory and Applications, 1980, 127(3): 93-102. DOI:10.1049/ip-d.1980.0015 |
| [5] |
GRøVLEN Å, FOSSEN T I. Nonlinear control of dynamic positioned ships using only position feedback: an observer backstepping approach[C]//Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, IEEE, 1996: 3388–3393.
|
| [6] |
FOSSEN T I, GRøVLEN Å. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping[J]. IEEE Transactions on Control Systems Technology, 1998, 6(1): 121-128. DOI:10.1109/87.654882 |
| [7] |
FOSSEN T I, STRAND J P. Passive nonlinear observer design for ships using Lyapunov methods: full-scale experiments with a supply vessel[J]. Automatica, 1999, 35(1): 3-16. DOI:10.1016/S0005-1098(98)00121-6 |
| [8] |
杜佳璐, 杨杨, 胡鑫, 等. 基于动态面控制的船舶动力定位控制律设计[J]. 交通运输工程学报, 2014, 14(5): 36−50. DU Jialu, YANG Yang, HU Xin, et al. Control law design of dynamic positioning for ship based on dynamic surface control[J]. Journal of Traffic and Transportation Engineering, 2014, 14(5): 36−42. |
| [9] |
邹俊杰. 抗随机干扰的船舶动力系统混合控制方法[J]. 舰船科学技术, 2022, 44(22): 106-109. ZOU Junjie. Hybrid control method for ship power system against random disturbance[J]. Ship Science and Technology, 2022, 44(22): 106-109. DOI:10.3404/j.issn.1672-7649.2022.22.019 |
| [10] |
OHISHI K, NAKAO M, OHNISHI K, et al. Microprocessor controlled DC motor for load-insensitive position servo system[J]. IEEE Trans on Industrial Electronics, 1987, 34(1): 44-49. |
| [11] |
CHEN Wenhua, BALANCE D J, GAWTHROP P J. A nonlinear disturbance observer for robotic manipulators[J]. IEEE Transactions on Industrial Electronics, 2000, 47(4): 932-938. DOI:10.1109/41.857974 |
| [12] |
WEI Xin Jiang, GUO Lei. Composite disturbance-observer-based control and H-infinite control for complex continuous models[J]. International Journal of Robust and Nonlinear Control, 2010, 20(1): 106-118. DOI:10.1002/rnc.1425 |
| [13] |
图雅, 杜佳璐, 刘文吉. 船载三自由度并联稳定平台的设计及运动学分析[J]. 舰船科学技术, 2022, 44(5): 154-157. TU Ya, DU Jia-lu, LIU Wen-ji. Design and kinematics analysis of 3-DOF ship-borne parallel stabilization platform[J]. Ship Science and Technology, 2022, 44(5): 154-157. |
| [14] |
NIKIFOROV V O. Nonlinear servocompensation of unknown external disturbances[J]. Automatica, 2001, 37: 1647-1653. DOI:10.1016/S0005-1098(01)00117-0 |
 2024, Vol. 46
2024, Vol. 46
