2. 大连理工大学 船舶工程学院,辽宁 大连 116024
2. School of Naval Architecture and Ocean Engineering, Dalian University of Technology, Dalian 116024, China
海上油气开发从浅水走向深海与超深海,是大势所趋。早期的FPSO有很多性能上的局限,横摇性能差,垂荡固有周期多在波浪的能量集中区域。姚宇鑫等[1–2]提出了一种具有创新性的沙漏形浮体,借鉴圆柱形的基础,减少水线面的面积,扩大上甲板与下底面的面积,提高了FPSO的垂荡运动性能。较大的上甲板面积,使其便于布置生活和生产模块,将圆柱筒型浮体的竖直侧面变为外扩倾斜侧面设计,有利于增强新型浮体绕流的三维效应,抑制VIM和甲板上浪现象[3]。对于新概念沙漏型浮体,许多研究人员已经对其进行改进和完善,已经进行的研究有概念设计[2]、设计方法[4]、性能分析[5–6](包括外形参数、稳性设计、耐波性分析)、水池试验[7]、月池结构[5]、系泊系统设计[2]分析等。在物理模型水池试验中发现波浪对上浮体舷侧位置的砰击载荷非常大,本文主要研究运动砰击问题。
流体和结构砰击是十分复杂的流体力学问题,Wagner[8]对Von-Karman[9]的研究进行了修改,考虑了自由表面上隆起的效应,并提出一种具有创新性的平板拟合理论。Faltinsen[10]在前人理论的基础上,对入水速度和正交板底部角度对流固耦合的影响进行了系统的研究。戴仰山等[11]根据Ochi[12]在实验中总结的公式,并结合切片法,使结构在局部的砰击压力得到有效求解。在船舶与海洋工程领域中有一个基本的假设:砰击的载荷尽管很大,但是不仅作用的时间是瞬时的,而且发生在浮体局部,因此作用在结构上的冲量很小,砰击力对浮体的运动响应基本没有影响,但是会对舷侧等局部结构产生较大影响。
本文针对新概念沙漏型FPSO,结合其浮体外形和运动响应特性,对其FPSO上浮体舷侧的典型剖面砰击次数和载荷特性进行分析。首先,使用势流波浪理论模拟浮体剖面在入水时的速度,然后采用基于CFD技术的数值拟合方法,获得沙漏型FPSO剖面在砰击时所受的载荷和压力分布。两步法[13]是基于势流波浪理论和CFD理论的合理二次开发得来的,以此来形成一套可应用于工程实际的砰击强度直接计算方法。
1 沙漏型FPSO浮体在波浪中运动响应特性分析本文的研究对象是典型的新概念沙漏型FPSO浮体,该浮体的主要参数如表1和图1所示。
|
|
表 1 沙漏型FPSO主尺度表 Tab.1 Main dimension table of sandglass-type FPSO |
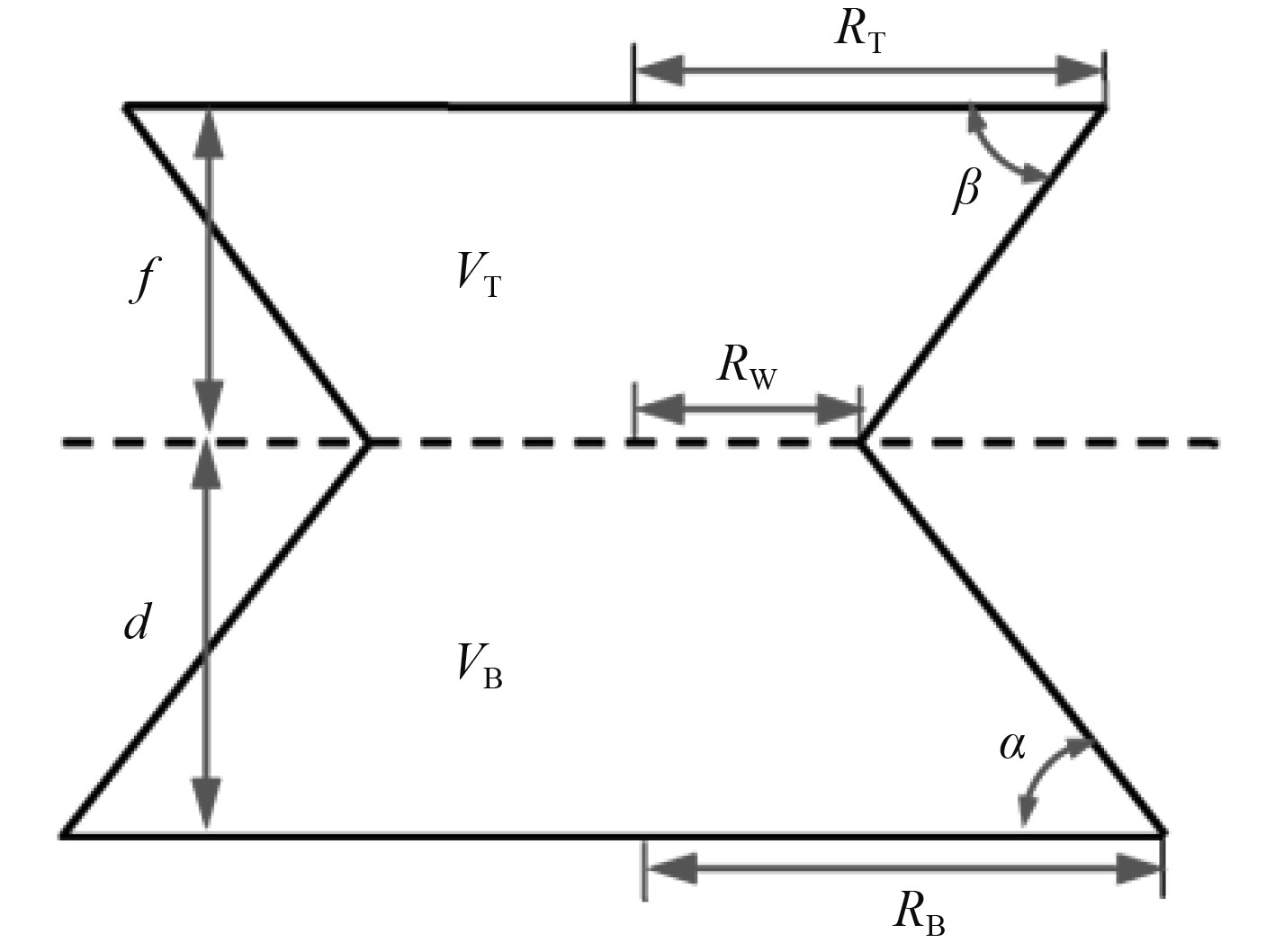
|
图 1 沙漏型FPSO主尺度表 Fig. 1 Main dimension table of sandglass-type FPSO |
为对比分析,建立圆筒形和长方形浮体2个另外模型,与沙漏型FPSO相比具有相同排水量、相同总体积和相同上甲板面积。有限元模型如图2~图4所示。

|
图 2 沙漏型FPSO有限元模型 Fig. 2 Finite element model of the sandglass-type FPSO |
|
图 3 长方形浮体的有限元模型 Fig. 3 Finite element model of a rectangular floating body |

|
图 4 圆筒形浮体的有限元模型 Fig. 4 Finite element model of a cylindrical floating body |
沙漏型FPSO在海上作业,主要的外部环境便是波浪,采用势流理论方法计算波浪与沙漏型FPSO的作用和沙漏型FPSO运动的水动力特性。
在理想的质量-弹簧-阻尼系统、线性规则波作用下浮体单自由度的垂荡运动方程如下:
| $ \left[M+{A}_{33}\left(w\right)\right]\ddot{{\mathcal{x}}_{3}}+{B}_{33}\left(w\right)\dot{{\mathcal{x}}_{3}}+{K}_{33}{\mathcal{x}}_{3}={F}_{3}\left(w\right) 。$ | (1) |
其中:M为浮体质量;
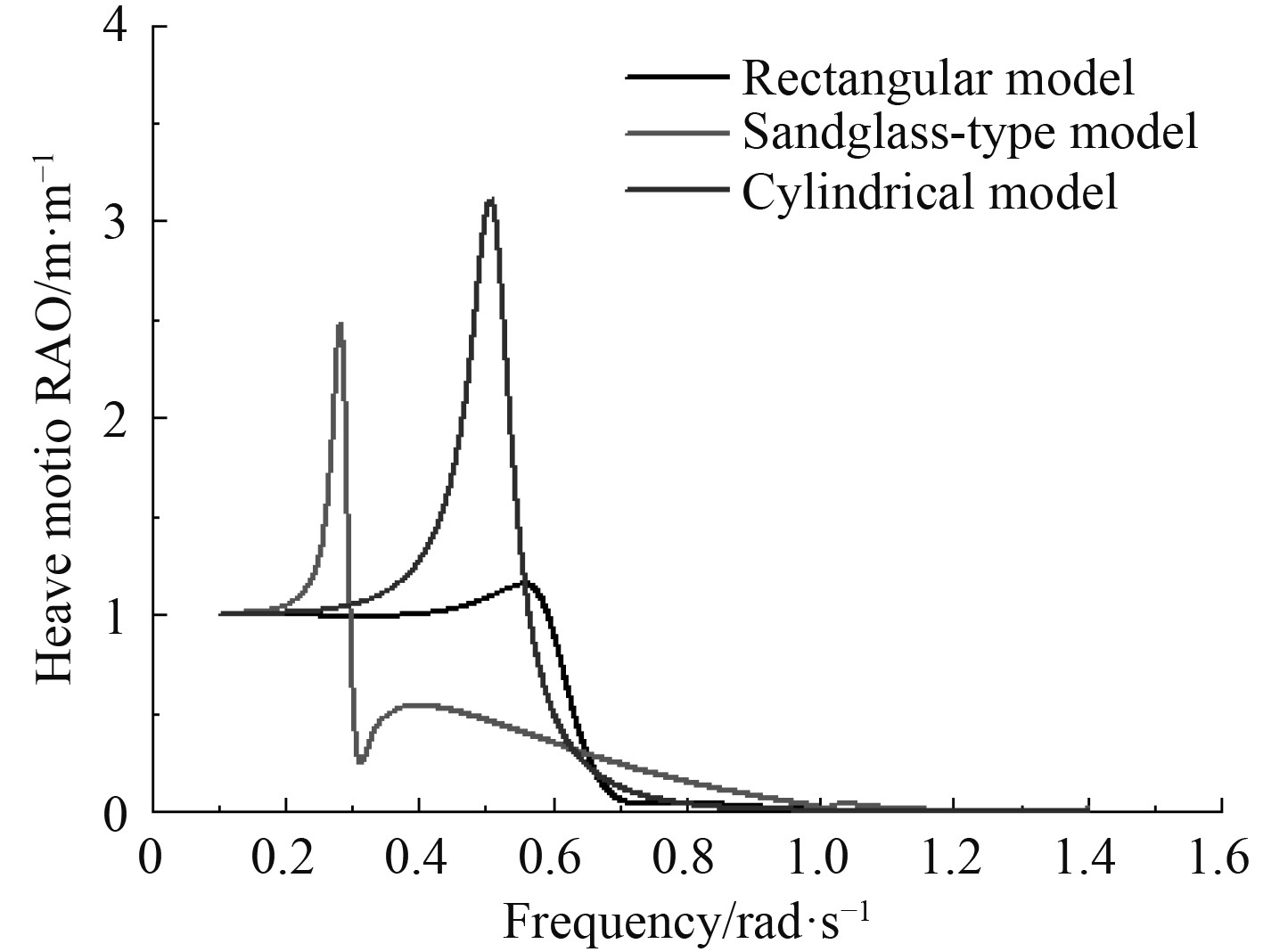
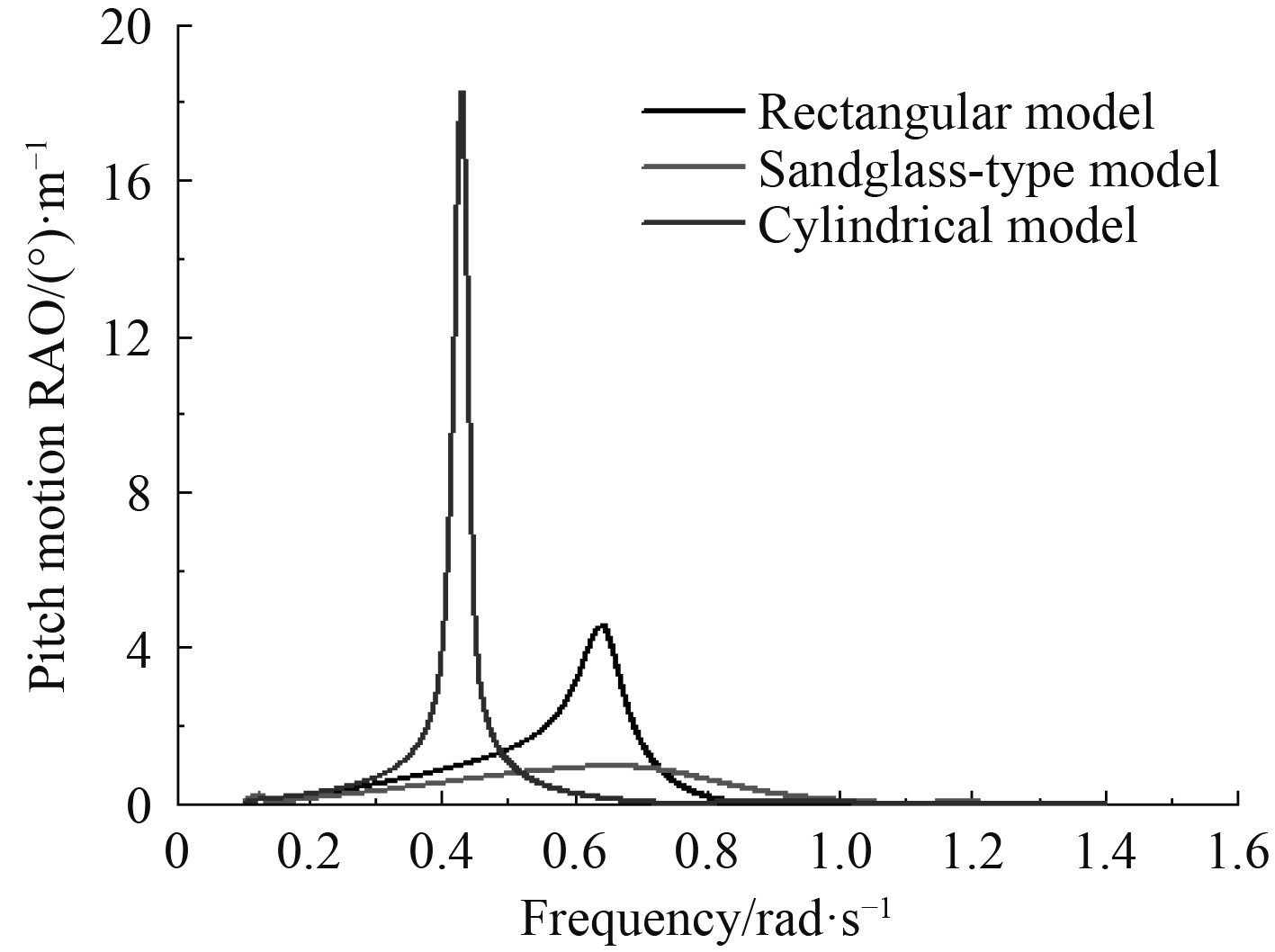
利用Aqwa-Line模块进行沙漏型FPSO的频率运动响应预报,与长方形浮体相比,沙漏型浮体和圆筒形浮体对波浪作用的方向并不敏感。沙漏型FPSO浮体的垂荡运动响应幅值算子RAO在0.2~0.3 rad/s频率段具有峰值,圆筒形浮体和长方形浮体在0.4~0.6 rad/s频率段具有峰值,沙漏型FPSO浮体的垂荡RAO峰值更加远离波浪的能量集中区域。3种浮体在180°波浪入射角下的垂荡运动RAO及纵向运动RAO分别如图5和图6所示。
|
图 5 3种浮体在180°波浪入射角下的垂荡运动RAO Fig. 5 Heave motion RAO of three kinds of floating bodies at 180° wave incidence angle |
|
图 6 3种浮体在180°波浪入射角下的纵摇运动RAO Fig. 6 Pitch motion RAO of three kinds of floating bodies at 180° wave incidence angle |
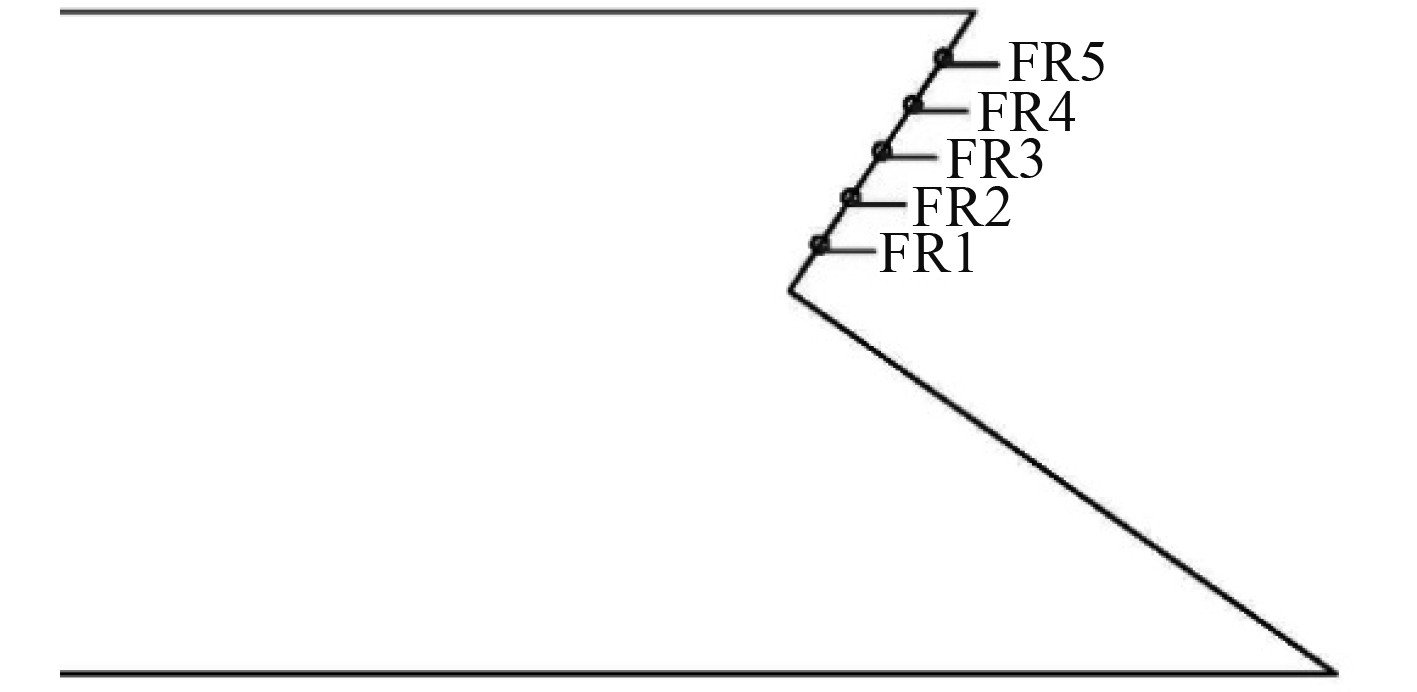
在沙漏型FPSO上浮体的舷侧位置(即浮体模型的上半圆台部分的迎浪侧边),均匀地选取5个位置点(见图7)。
|
图 7 沙漏型FPSO的典型节点位置 Fig. 7 Positions of the sandglass-type floating body |
利用Aqwa的librium与drift软件模块,针对沙漏型FPSO浮体上半圆台典型舷侧节点,进行典型位置点与波面的相对距离的运动时间历程分析。其中,按照船级社规范的规定,将波浪作用模拟的时间设定为3h (10800 s)。目标海域的波浪为中国南海百年一遇的波浪,其中有义波高Hs为13.6 m、平均周期
图8为P4节点相对波面的位移时间历程网线图。

|
图 8 P4节点相对波面的位移时间历程曲线图 Fig. 8 Displacement of the P4 relative to the wave surface |
典型节点相对波面的垂向位移响应
|
|
表 2 5个节点的砰击入水运动统计表 Tab.2 Analysis of slamming of five nodes under the wave condition |
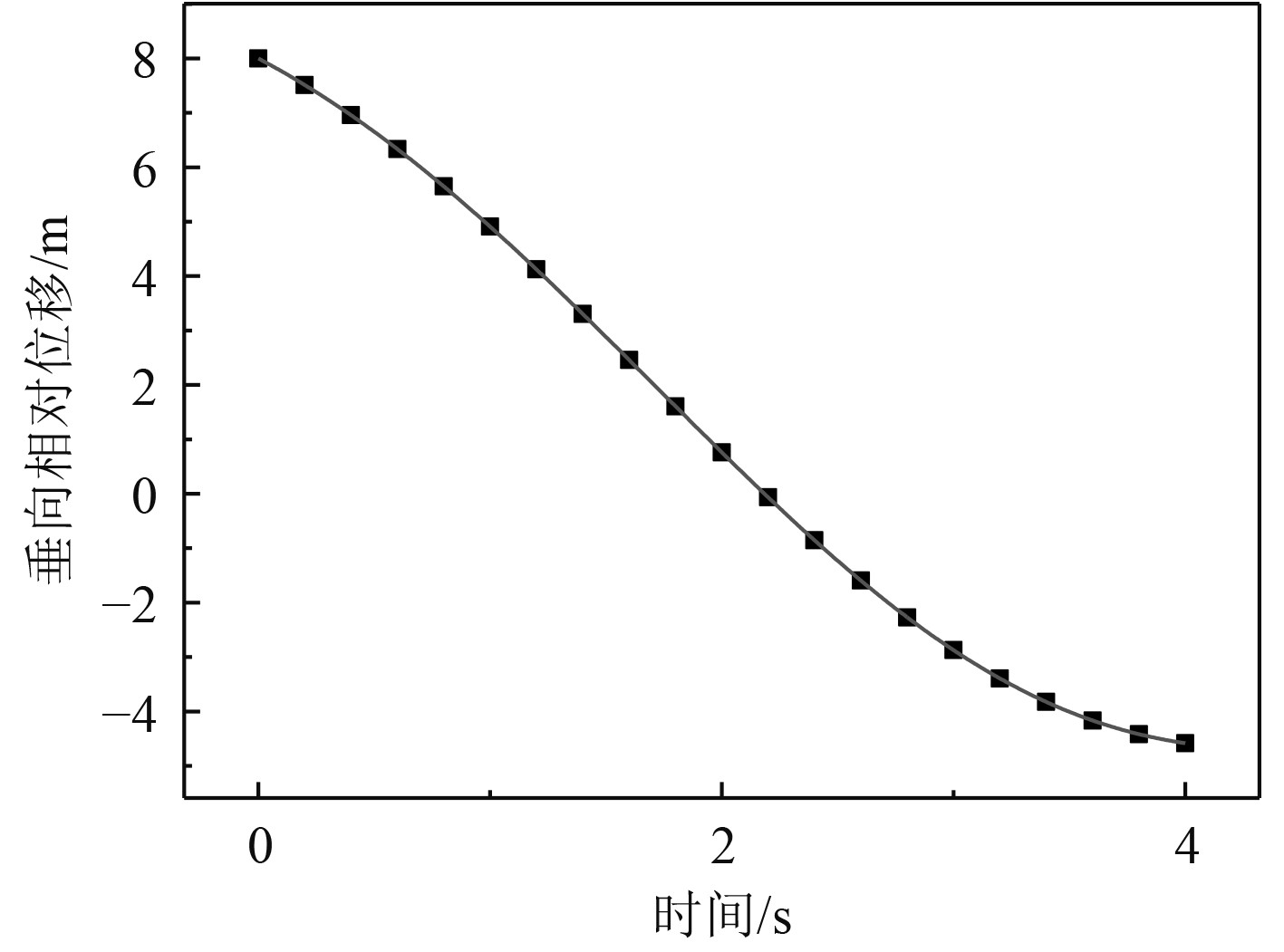
沙漏型FPSO上浮体舷侧在砰击入水过程中与水面的相对速度会随着时间的推移而变化。因此,本文选取的时间段包括最大速度入水时刻,以垂直相对位移多项式
|
图 9 P1节点相对波面垂向位移的多项式拟合 Fig. 9 Polynomial fitting of vertical displacement of the P1 |
对于横剖面入水砰击流场的流体力学问题,主要考虑3个基本方程:动量方程、能量方程和连续性方程。本文忽略流体的可压缩性和温度的变化,所以对于能量方程可以不考虑,重点关注连续性方程和动量方程。
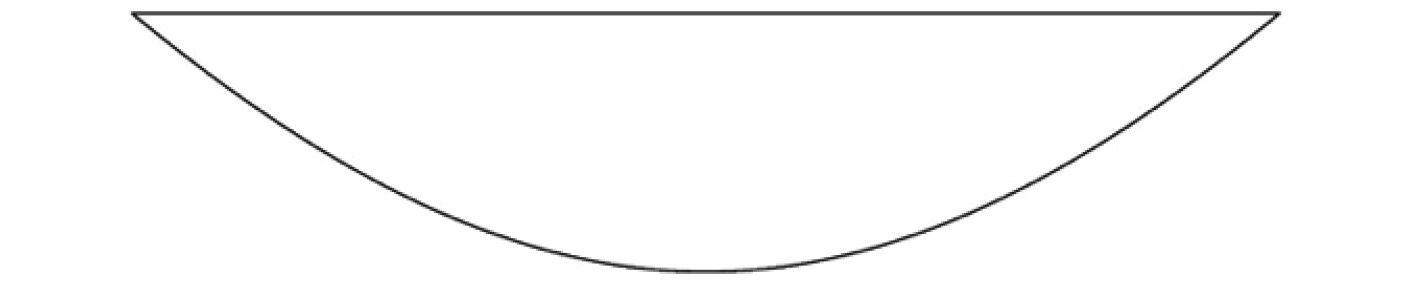
2.2 典型二维横剖面入水模型的建立以典型节点作为二维剖面最下方中心点,建立多个典型的横剖面,上半圆台舷侧的横剖面是由一条双曲线和直线围成的封闭图形,如图10所示。
|
图 10 FR1剖面图 Fig. 10 FR1 profile |
在利用Fluent进行求解的过程中采用PISO算法,这是一种压力的隐式算子分割算法,适合非结构化的动网格。在SIMPLE和SIMPLEC算法基础之上,PISO算法则增加了1个修正步,包括1个预测步和2个修正步。在完成了第1步修正并获得速度和压力变量之后,该算法寻求第2次改进值,以更好地满足动量方程和连续性方程。PISO算法通过使用预测-修正-再修正3个步骤,加快单个迭代步中的收敛速度。
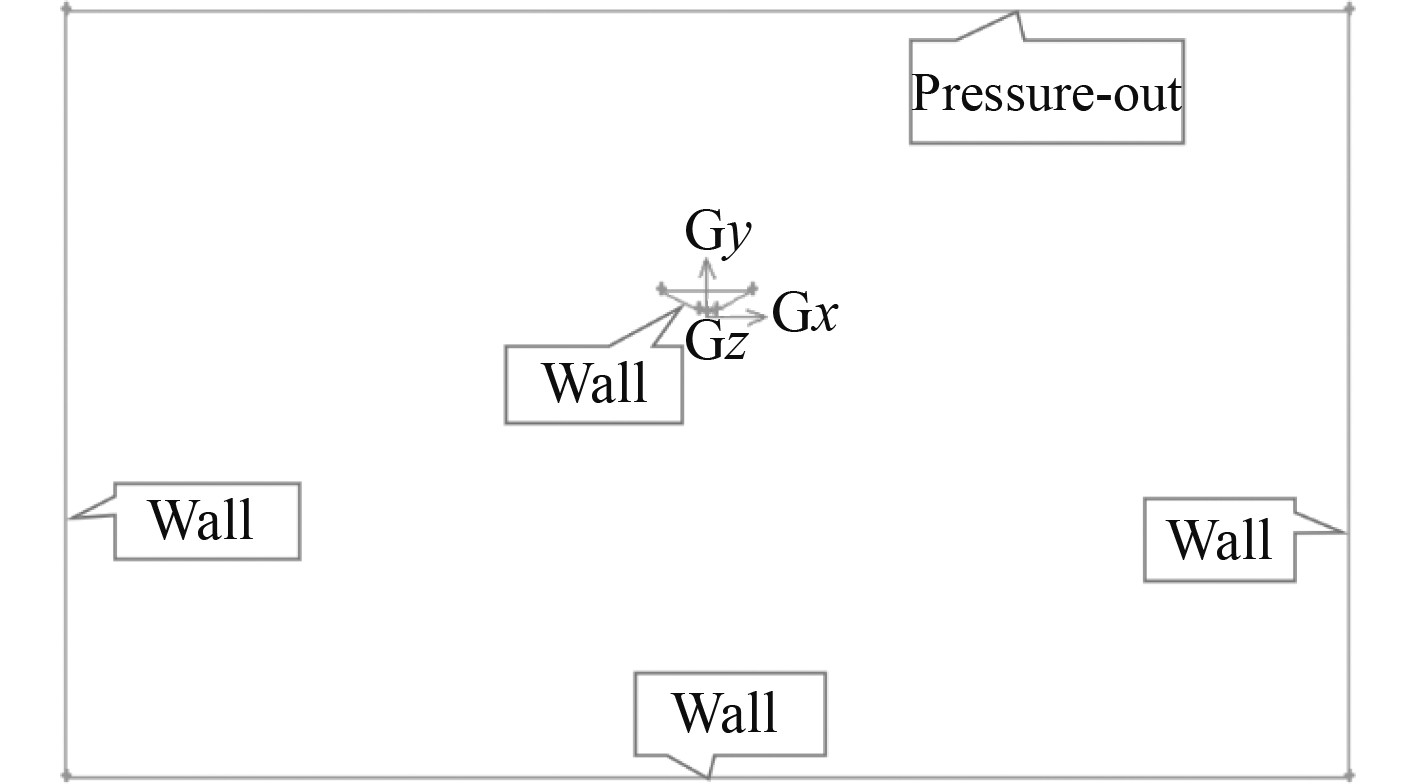
FR1剖面入水模型网格划分如图11所示,FR1的二维剖面入水模型边界条件设置如图12所示。

|
图 11 FR1剖面入水模型网格划分 Fig. 11 FR1 into the water model meshing partially |
|
图 12 FR1的二维剖面入水模型边界条件设置 Fig. 12 Boundary condition setting of FR1 |
为了观察到结构入水砰击的效果,使其更加接近现实,需要确定自由液面的位置。对于水气交界面的波动,采用VOF(Volume of Fluid)方法来追踪空气和水的自由液面。为了更准确地捕捉自由液面的变化,选择VOF模型中的几何重构方法。
对于动网格的处理,本文采用光顺法(Smoothing)与网格重构法(Remeshing)。光顺法适用于非结构区域边界位移较小的情况,网格重构法适用于二维和三维的非结构化网格。当网格边界发生运动时,局部网格会因拉伸和变形而导致网格畸变率或尺寸变化超出合理范围,从而导致计算结果误差较大。为了解决这个问题,可以对局部网格进行重新构造。如果重构后的新网格质量满足要求,则可以用新网格替换原来的网格。
定义流场计算域为刚体运动区域(Rigid body),用宏命令DEFINE_CG_MOTION编写UDF程序来控制浮体下落速度,此宏命令可以通过Fluent提供的在每一时间步的线速度和角速度,对一个特殊动态域的移动。基于立体的运动,Fluent使用这些速度更新动态域上节点的位置。
2.3 时间步长收敛性验证数值模拟时间步无关性验证,以FR5为例,在小网格条件下,选取的3个时间步的变化率
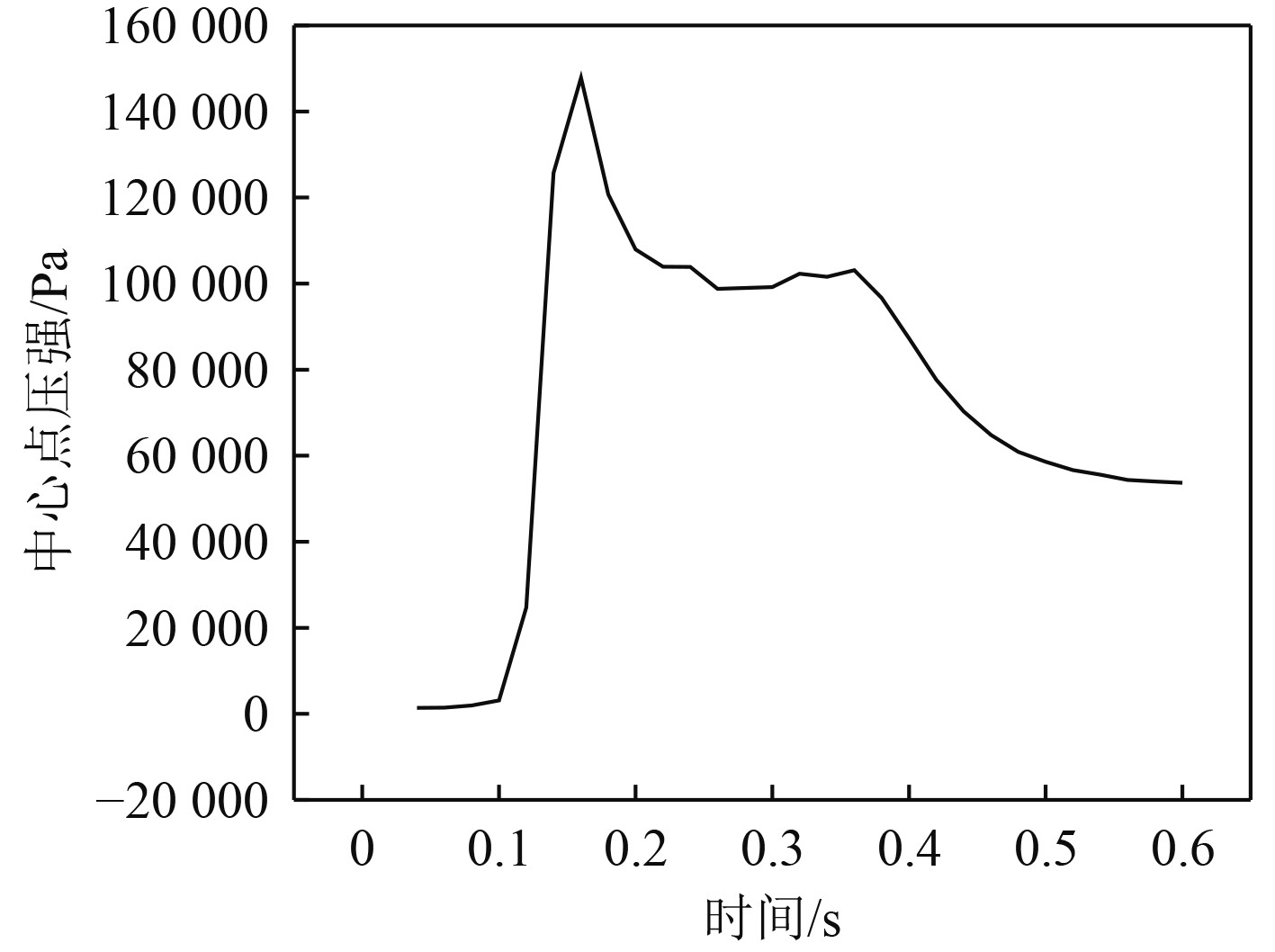
|
图 13 大步长条件下FR5剖面中心点压强时间历程曲线 Fig. 13 Time history curve of pressure at the center of FR5 profile under large step size |

|
图 14 中步长条件下FR5剖面中心点压强时间历程曲线 Fig. 14 Time history curve of pressure at the center of FR5 profile under medium step length |
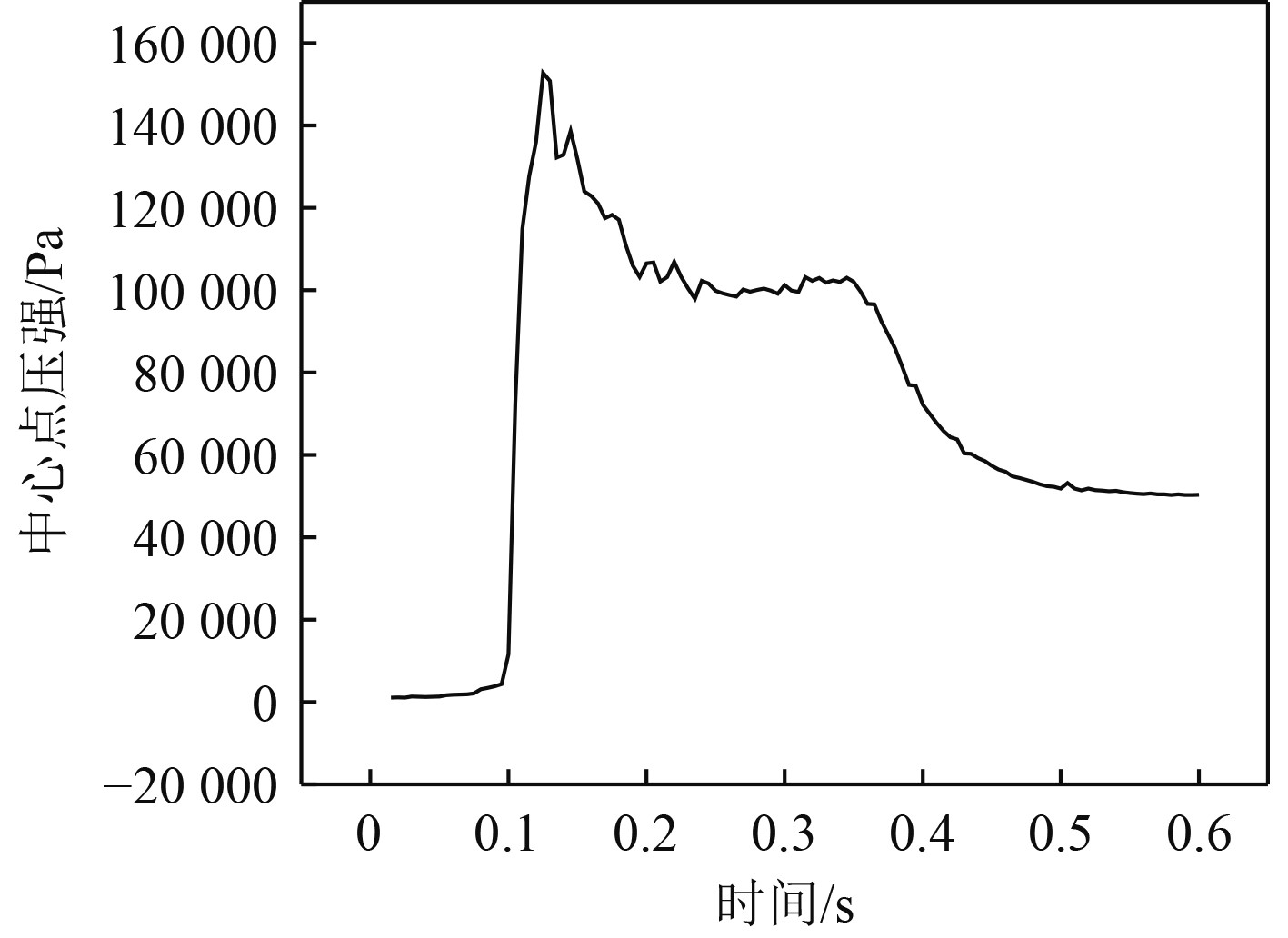
|
图 15 小步长条件下FR5剖面中心点压强时间历程曲线 Fig. 15 Time history curve of pressure at the center of FR5 profile under small step size |
可知,3种时间步长的压强时间历程曲线的变化趋势基本相同。其中,大步长的更加平缓一些。在此基础上,进一步计算大步长与中步长、以及中步长与小步长的相对差异,结果如表3所示。可以看出,随着时间步长的逐渐减小,相对差异逐渐变小。此外,综合计算精度和效率,采用中步长进行计算分析。
|
|
表 3 3种时间步长压强对比 Tab.3 Comparison of three time step pressures |
在时间步长收敛性验证之后,进一步验证模型对于网格划分的不确定度分析。同样选网格尺寸变化率为
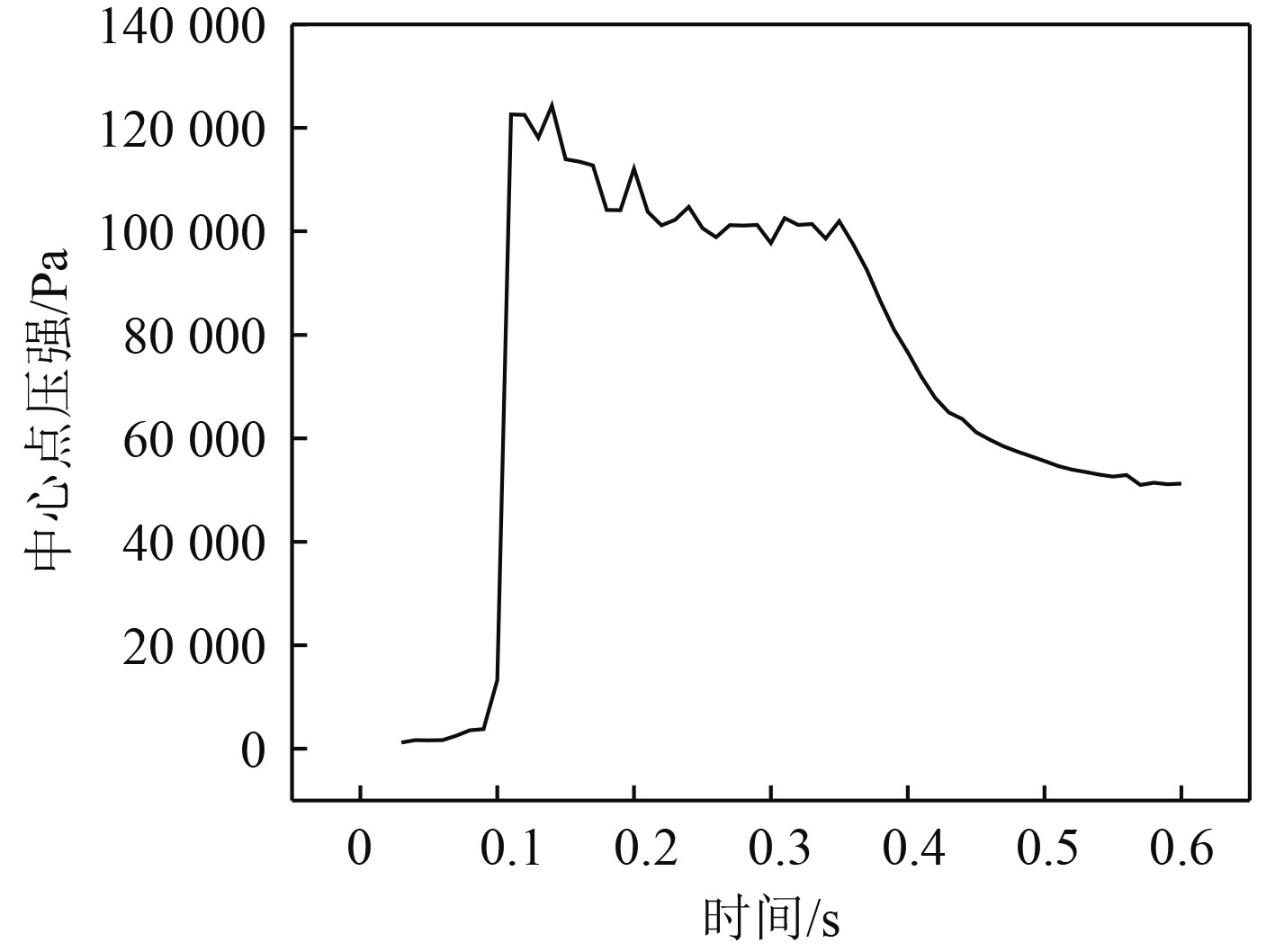
|
图 16 大网格条件FR5剖面中心点压强时间历程曲线 Fig. 16 Pressure at the center point of FR5 profile under large grid conditions |
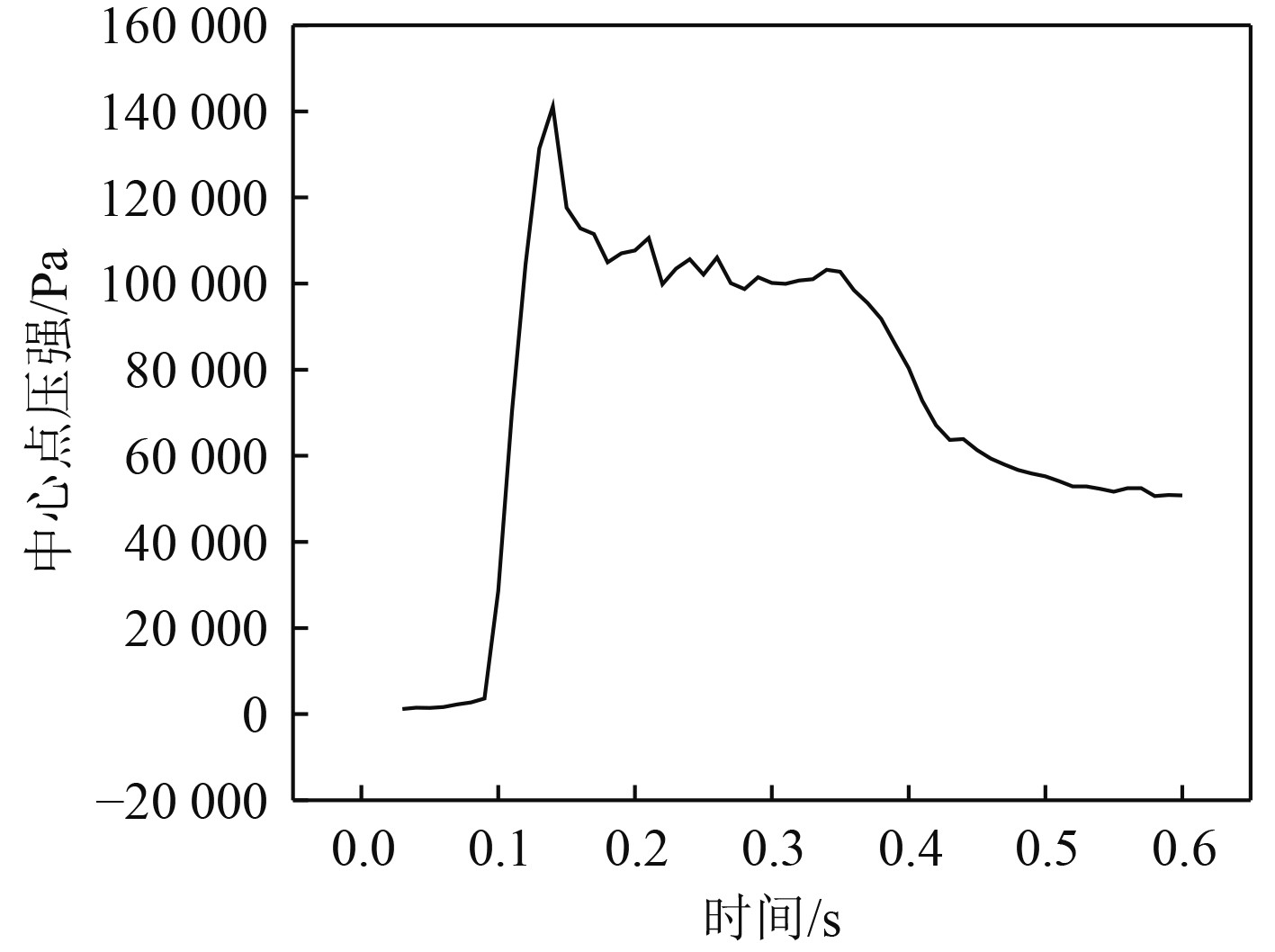
|
图 17 中网格条件FR5剖面中心点压强时间历程曲线 Fig. 17 Pressure at the center of the FR5 profile under medium grid condition |

|
图 18 小网格条件FR5剖面中心点压强时间历程曲线 Fig. 18 Pressure at the center of FR5 profile under small grid conditions |
可知,3种网格方案对应的压强时间历程曲线的变化趋势基本相同。在此基础上,进一步计算大网格与中网格、中网格与小网格的相对差异,结果如表4所示。可以看出,随着网格的逐渐减小,相对差异逐渐变小,从大网格到小网格的压强成收敛趋势。此外,综合计算精度和效率,采用中网格进行计算分析。
|
|
表 4 3种网格压强对比 Tab.4 Comparison of three grid pressures |
对于横剖面入水砰击流场的流体力学问题,CFD方法与传统的理论分析方法、实验测量方法组成研究流体流动问题的完整体系,应用Fluent软件进行砰击压强的数值模拟,利用UDF程序控制剖面的运动速度。FR1剖面中心点压强时历曲线如图19所示,FR3的入水相位图、压力云图及流量矢量图如图20~图22所示。
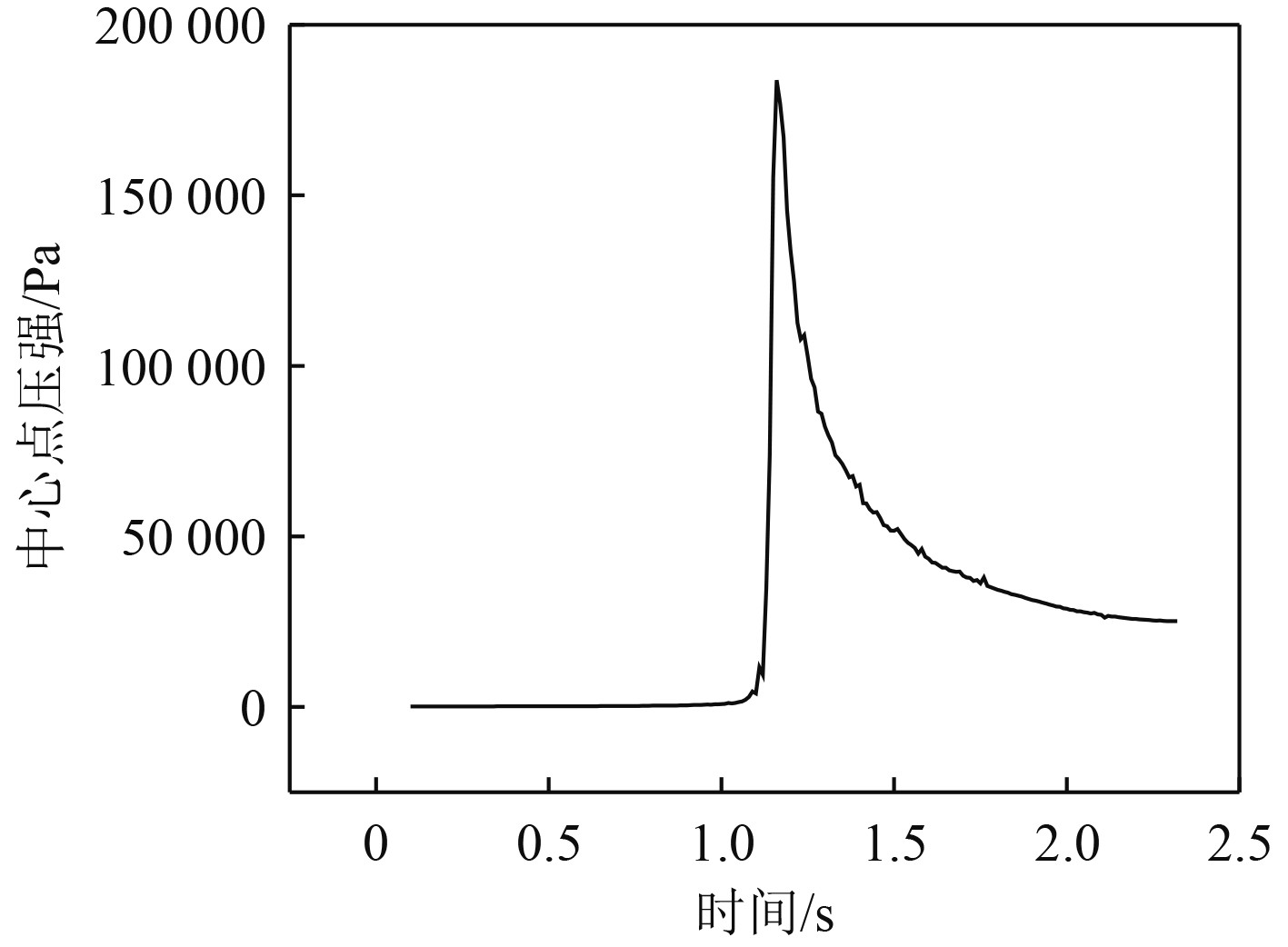
|
图 19 FR1剖面中心点压强时历曲线 Fig. 19 FR1 profile center point pressure time history curve |

|
图 20 FR3入水相位图 Fig. 20 FR3 phase diagram |

|
图 21 FR3入水压力云图 Fig. 21 FR3 pressure cloud |

|
图 22 FR3流量矢量图 Fig. 22 Flow diagram of FR3 |
砰击发生在结构刚刚接触到水面的瞬间,且这个过程极短。随后砰击的压强逐渐减小,减小的趋势则没有之前上升阶段那么剧烈。沙漏型上浮体的典型横剖面砰击入水流场随着砰击时间的推进不断发生变化,自由液面和砰击压强峰值由中间最下方向两侧扩散。在底端接近水面发生碰撞时,在砰击流场中有一个较大的压力区域出现。随着典型横剖面继续入水,自由液面随着侧边发生飞速爬升,并且砰击流场伴随有飞溅现象出现。表5为3种风格压强对比。
|
|
表 5 最大压强统计表 Tab.5 Statistics table of maximum pressure |
在底端接近水面发生碰撞时,在砰击流场中有一个较大的压力区域出现。随着典型横剖面继续入水,自由液面随着侧边发生飞速爬升,并且砰击流场伴随有飞溅现象出现。
入水速度随着距离越远而越小,但最大压强并不是越来越小。考虑到随着距离越远,剖面的越来越平缓即曲率半径越来越大。因此,不同典型横剖面在砰击过程中所受的最大砰击压强同时取决于剖面形状和砰击入水速度。
取5个不同形状的二维剖面作为研究对象,如图23~图27所示。其中FR6为带水平底面和圆角的长方形,FR7为半径为85.26 m的圆弧与直线组成的封闭图形,FR8为以半径为22.06 m的圆弧作为底面的剖面形状,FR9为半径为7.73 m的圆弧与直线组成的封闭图形,FR10为三角形形状的剖面。

|
图 23 FR6剖面外形 Fig. 23 FR6 profile |

|
图 24 FR7剖面外形 Fig. 24 FR7 profile |

|
图 25 FR8剖面外形 Fig. 25 FR8 profile |

|
图 26 FR9剖面外形 Fig. 26 FR9 profile |

|
图 27 FR10剖面外形 Fig. 27 FR10 profile |
根据剖面的平底结构形状特性,随着底部形状越平,二维剖面的砰击压强峰值越大。这几种典型剖面的砰击压强峰值作用时间较短,入水砰击具有瞬时特性。此外,随着底部形状越平或曲率半径越来越大,砰击作用时长逐渐增大。因此,首先可以从上述结论定性上验证本文使用的剖面入水砰击压强模型和算法的正确性,其次光滑、过渡的浮体线型有利于降低波浪砰击压强。各剖面压强时历曲线如图28~图32所示。
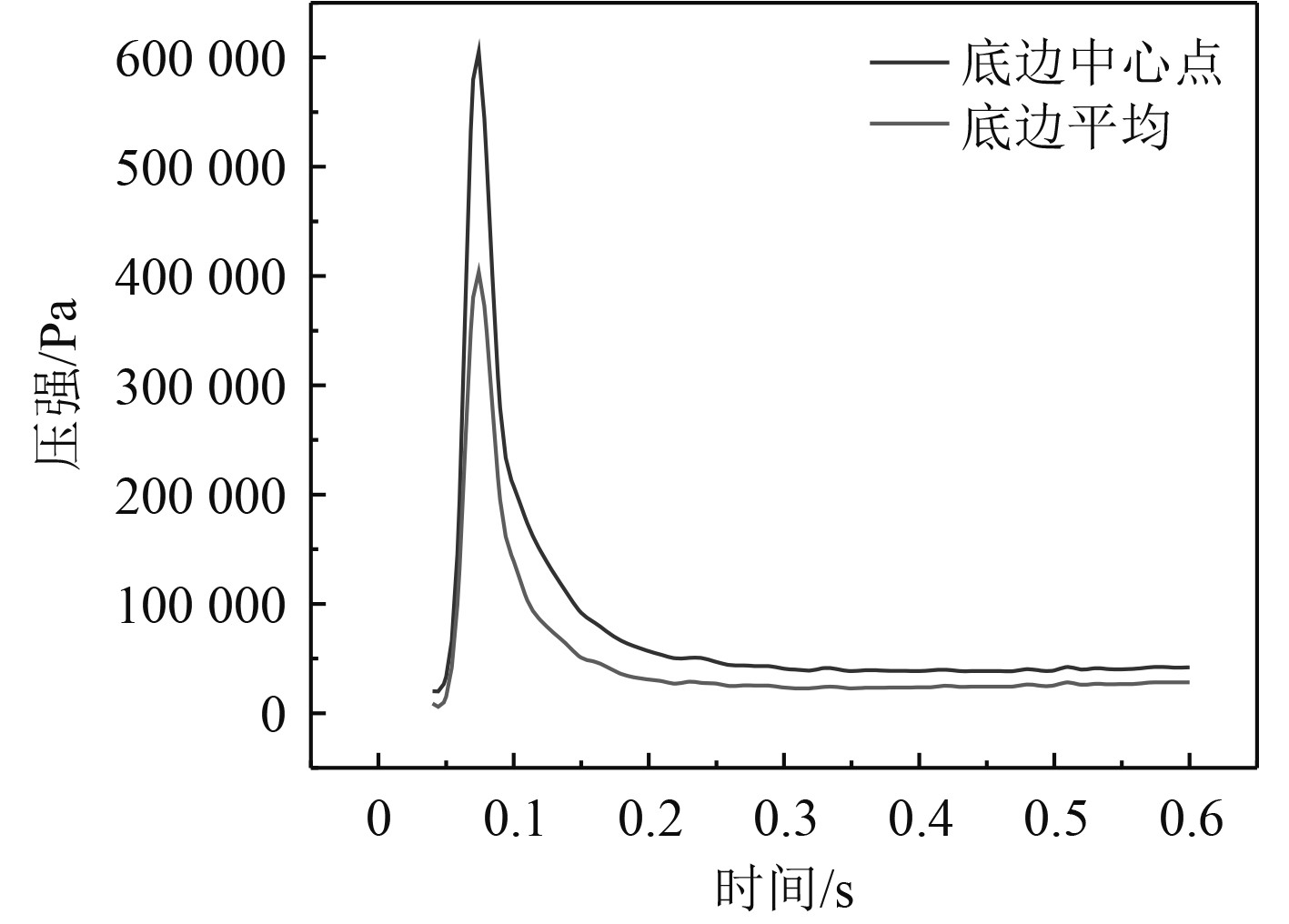
|
图 28 FR6压强时历曲线 Fig. 28 FR6 profile pressure time history curve |

|
图 29 FR7压强时历曲线 Fig. 29 FR7 profile pressure time history curve |
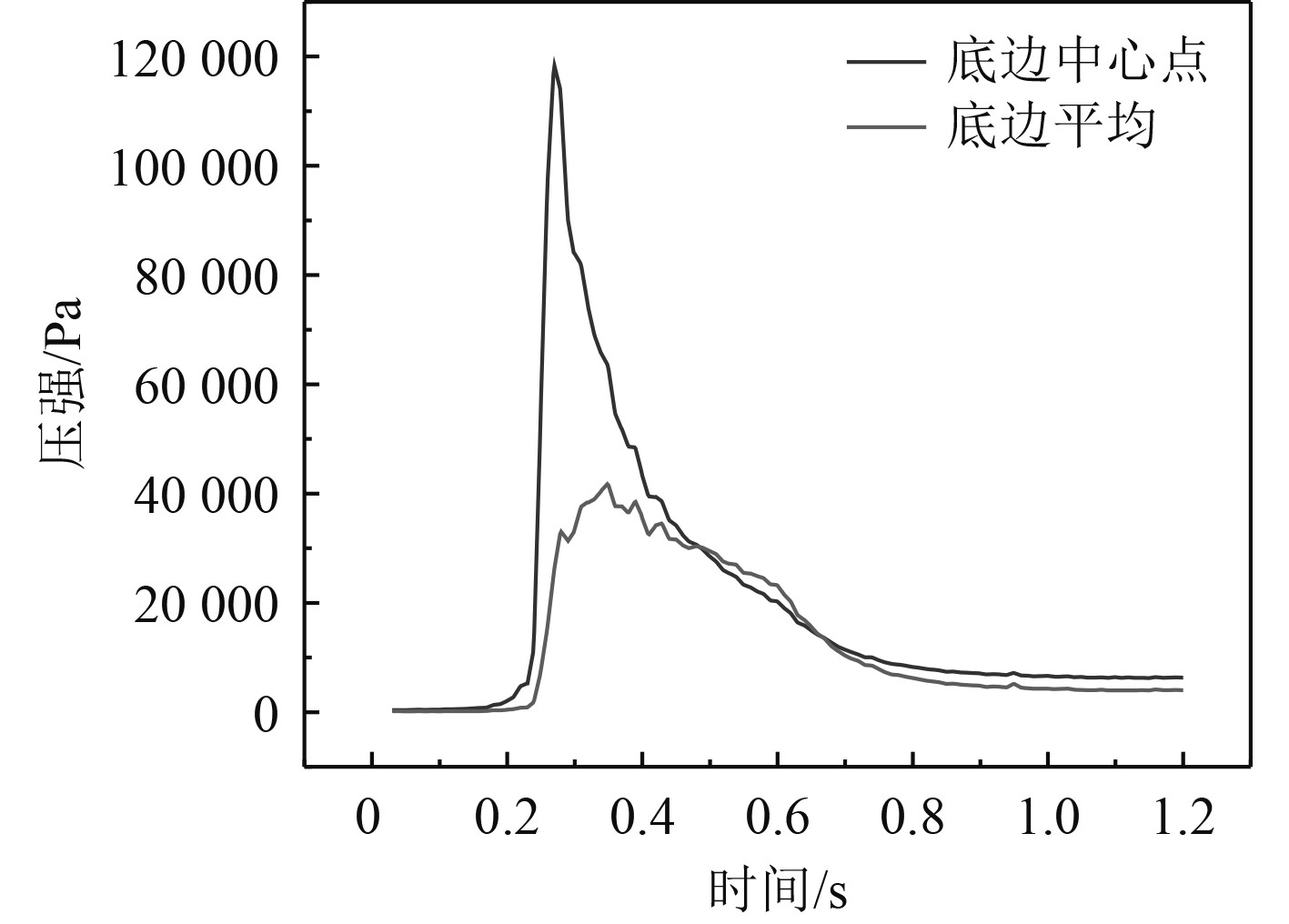
|
图 30 FR8压强时历曲线 Fig. 30 FR8 profile pressure time history curve |
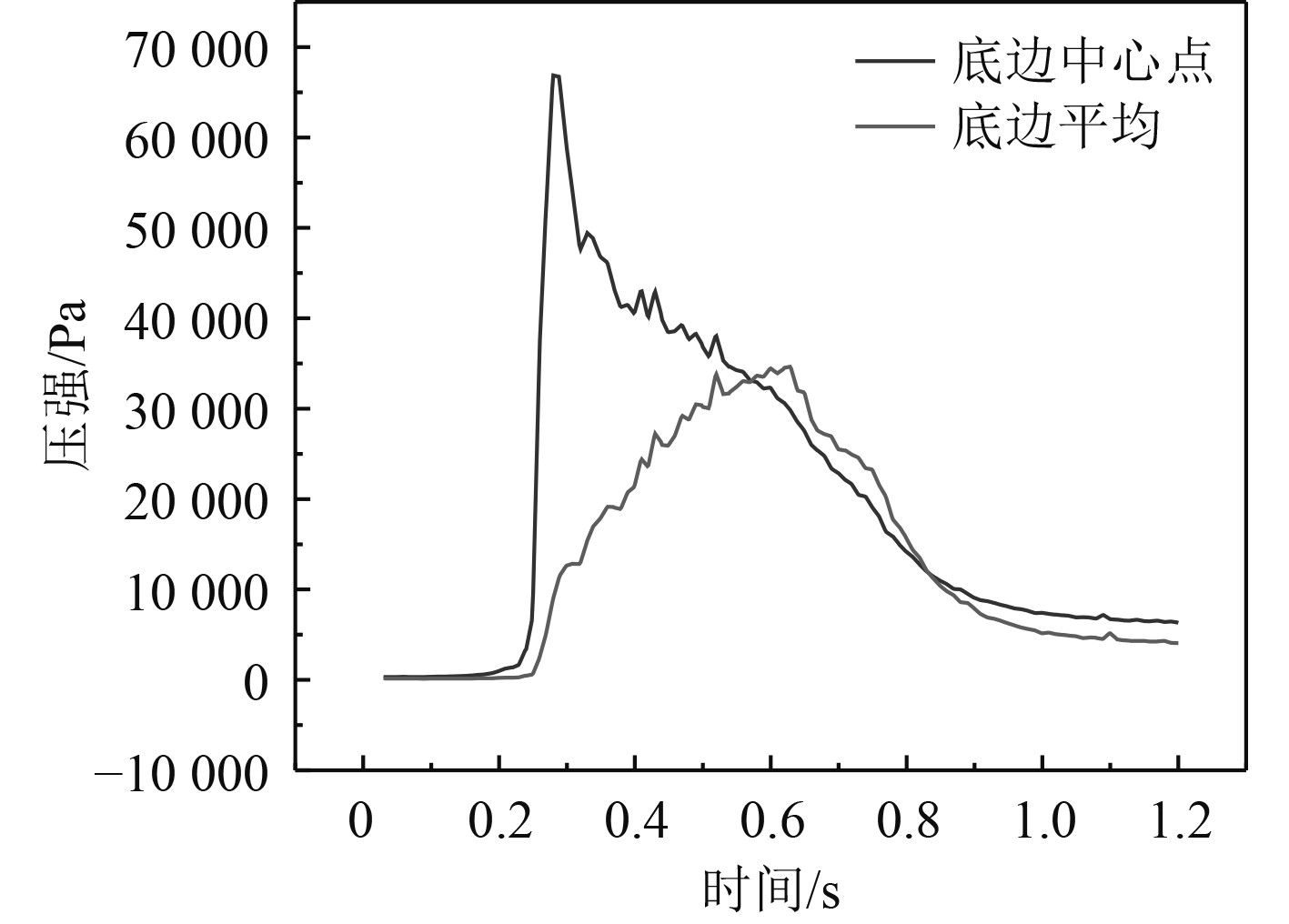
|
图 31 FR9压强时历曲线 Fig. 31 FR9 profile pressure time history curve |
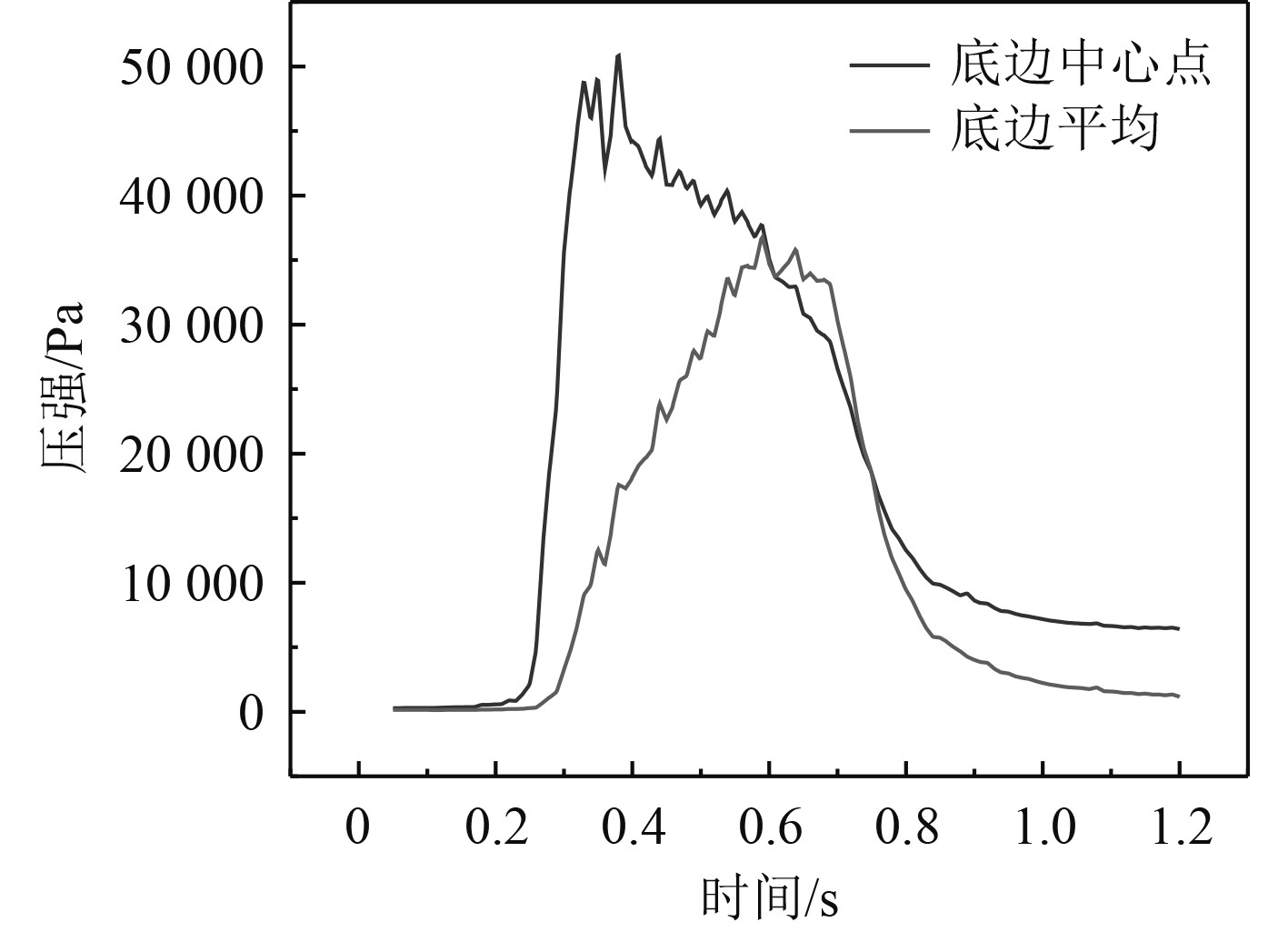
|
图 32 FR10压强时历曲线 Fig. 32 FR10 profile pressure time history curve |
本文以沙漏型FPSO上浮体在波浪中入水砰击特性作为研究对象,基于波浪势流理论和计算流体力学理论,采用Aqwa和Fluent软件平台进行合理的二次开发,建立浮体在波浪中砰击水动力载荷的数值计算方法,并且将其应用于沙漏型FPSO在波浪中的运动响应以及上浮体舷侧的典型横剖面的入水砰击问题,得到相关结论如下:
1)针对垂荡运动RAO,与长方形浮体相比,沙漏型和圆筒形浮体对波浪作用的方向并不敏感。相对沙漏型浮体,长方形浮体和圆筒型浮体的纵、横摇运动固有频率相对更接近波浪谱峰值频率段。证明了沙漏型FPSO在常规波浪海况下具有优异的水动力性能。
2)总体来说,距离水线面越近的横剖面的平均入水砰击次数和有效砰击速度越大,但是在个别海况下最大有效砰击速度会发生在距离水线面较远的位置。因此,针对沙漏型FPSO上浮体舷侧的波浪砰击问题,应该在重点关注水面附近的区域的同时,兼顾距离水面较远且波浪能够接触到的最高位置。
3)在横剖面刚刚接触到水面的瞬间,在初始中心点接触区域附近产生较大的砰击压强。砰击峰值的持续时间较短,在后续砰击入水过程中自由液面沿着横剖面两侧向上隆起,并伴随有飞溅现象发生。此外,从中心点最大砰击压强来看,需要关注的砰击入水区域依然是沙漏型FPSO上浮体舷侧的两端。
4)不同形状剖面的砰击载荷差异明显,并且剖面的曲率半径是关键影响因素。随着底部形状越平或曲率半径越来越大,二维剖面的砰击压强峰值越大,由此说明光滑、过渡的浮体线型有利于降低浮体在波浪中遭受的最大砰击压强,因此从砰击水动力角度建议采用对接圆台式沙漏型浮体外形设计。
| [1] |
姚宇鑫, 王文华, 黄一. 新型沙漏式浮式生产储油系统的概念设计分析[J]. 上海交通大学学报, 2014, 48(04): 558-564. YAO Yuxin, WANG Wenhua, HUANG Yi. Conceptual design analysis of a new type of hourglass floating production and storage system[J]. Journal of Shanghai Jiaotong University, 2014, 48(04): 558-564. DOI:10.16183/j.cnki.jsjtu.2014.04.020 |
| [2] |
姚宇鑫. 新概念沙漏型FDPSO主浮体和系泊系统设计方法研究 [D]. 大连: 大连理工大学, 2015.
|
| [3] |
WANG W-H, WANG L-L, DU Y-Z, et al. Numerical and experimental analysis on motion performance of new sandglass-type floating body in waves[J]. Marine Structures, 2016, 46: 56-77. DOI:10.1016/j.marstruc.2015.12.002 |
| [4] |
高浩. 新型沙漏式FDPSO的典型控制载荷工况分析[J]. 中国造船, 2017, 58(2): 97-107. GAO Hao. Analysis of typical control load conditions for a new type of hourglass FDPSO[J]. China Shipbuilding, 2017, 58(2): 97-107. |
| [5] |
刘兆瑞. 浅水浪流作用下沙漏型FPSO的动力响应研究 [D]: 大连: 大连理工大学, 2019.
|
| [6] |
AVALOS G O G, WANDERLEY J B V, FERNANDES A C, et al. Roll damping decay of a FPSO with bilge keel[J]. Ocean Engineering, 2014, 87: 111-120. DOI:10.1016/j.oceaneng.2014.05.008 |
| [7] |
WANG W-H, DU Y-Z, WANG L-L, et al. Experimental analysis on behaviour in waves for sandglass-type floating body[J]. Ships and Offshore Structures, 2016, 12(3): 433-441. |
| [8] |
WAGNER H. Über Stoß‐ und gleitvorgänge an der oberfläche von flüssigkeiten[J]. ZAMM ‐ Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, 1932, 12(4): 193-215. |
| [9] |
VON KARMAN T H. The impact on seaplane floats during landing [Z]. 1929.
|
| [10] |
FALTINSEN O M. Slamming on ships and marine structures[J]. Marine Systems & Ocean Technology, 2013, 8(1): 21-37. |
| [11] |
宋竞正, 任慧龙, 戴仰山. 船体非线性波浪载荷的水弹性分析[J]. 中国造船, 1995(2): 22-31. SONG Jingzheng, REN Huilong, DAI Yangshan. Hydroelastic analysis of ship hull nonlinear wave loads[J]. China Shipbuilding, 1995(2): 22-31. |
| [12] |
OCHI M K, MOTTER L E. Prediction of slamming characteristics and hull response for ship design[J]. Trans SNAME, 1973, 81: 144-76. |
| [13] |
李阔鹏. 近海风电设备安装船的耐波性研究 [D]. 大连: 大连理工大学, 2016.
|
 2024, Vol. 46
2024, Vol. 46
