敷设声学覆盖层是实现水下航行体声隐身的重要手段,一方面起到吸收入射声波降低目标强度的作用,同时也能有效抑制结构振动,减少对外辐射噪声。当水下航行体处于中高航速行驶时,表面的湍流脉动压力会激励结构振动产生水动力噪声,目前大部分学者对流激结构声辐射的研究均以弹性结构[1]或者复合夹芯结构[2]为主,很少涉及敷设声学覆盖层的结构。
流激结构振动声辐射是一个时空随机问题,所以相较于确定性激励问题求解过程更复杂。Hekmati等[3]采用Cholesky分解法研究了简支板在气动声压场激励下的声振特性;Franco等[4]研究了随机激励下的结构响应近似计算方法;Hong等[5]提出了用于补偿粗网格相关性损失的脉动压力场模型。这些方法尽管能得到精确解,却付出了很大的计算代价,因此需要提出一种快速计算流激噪声的数值方法。另外,针对声学覆盖层的声振耦合问题,学者们提出了一些近似模型。Foin等[6]利用局部反应模型将底板覆盖层结构等效为质量-弹簧单元;Berry等[7]提出更为精准的三维弹性理论来考虑覆盖层中的压缩波和剪切波的影响。
Aucejo等[8]提出了一种用于替代风洞中测量流激振动的试验方案,该方法用若干组空间随机分布的非相关平面波叠加来替代湍流脉动压力波数-频率谱。本文在此基础上,利用Matlab数值工具和Comsol振动声学有限元模块建立波数-频率域的流激噪声数值预报方法,并分析敷设声学覆盖层平板流激声辐射特性以及影响降噪的因素,为降低航行体水动力噪声提供技术支撑。
1 基本理论 1.1 湍流脉动压力非相关平面波等效理论用多组非相关平面波叠加合成湍流脉动压力,是指通过一组空间随机分布的广义平面波叠加来等效湍流脉动压力激励力,由文献[9]可知合成的湍流脉动压力表达式为:
| $ \begin{split} &{p_{inc}}({{\boldsymbol {x}}^q},\omega ) = \sum\limits_{i = 1}^{{N_x}} {\sum\limits_{j = 1}^{{N_y}} {\sqrt {{S_{{A_{xy}}{A_{xy}}}}} } } {e^{i({k_x}{x^q} + {k_y}{y^q} + {\varphi _{ij}})}}=\\ & \sum\limits_{i = 1}^{{N_x}} {\sum\limits_{j = 1}^{{N_y}} {\sqrt {\frac{{{\Phi _{pp}}({k_x},{k_y},\omega )\Delta {k_x}\Delta {k_y}}}{{4{\pi ^2}}}} } } {e^{i({k_x}{x^q} + {k_y}{y^q} + {\varphi _{ij}})}}。\end{split} $ | (1) |
其中,
式(1)中
| $ {\Phi _{PP}}({k_x},{k_y},\omega ) = {S_{pp}}(\omega ){\left(\frac{{{U_c}}}{\omega }\right)^2}{\bar \Phi _{PP}}({k_x},{k_y},\omega )。$ | (2) |
式中:
| $ {\bar \Phi _{PP}}({k_x},{k_y},\omega ) = \frac{{4{\alpha _1}{\alpha _3}}}{{\left[ {{\alpha _1}^2 + {{\left(1 - \dfrac{{{U_c}{k_x}}}{\omega }\right)}^2}} \right]\left[ {{\alpha _3}^2 + {{\left(\frac{{{U_c}{k_y}}}{\omega }\right)}^2}} \right]}}。$ | (3) |
其中,
式(1)将湍流脉动压力随机激励转化为一种确定性激励,此时可以通过常规有限元声振耦合技术来计算流激振动声辐射,对应的有限元方程如下:
| $ \left[ {\begin{array}{*{20}{c}} { - {\omega ^2}{{\boldsymbol {M}}_s} + {{\boldsymbol {K}}_s}}&{ - {{\boldsymbol {H}}_{_{fs}}}} \\ { - {\omega ^2}{\rho _f}{c_f}{\boldsymbol {H}}_{fs}^{\rm T}}&{ - {\omega ^2}{{\boldsymbol {M}}_f} + {{\boldsymbol {K}}_f}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol {u}}_l}} \\ {{{\boldsymbol {p}}_l}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {p_{inc}^l} \\ 0 \end{array}} \right]。$ | (4) |
其中:
对式(4)的求解过程在商业有限元软件Comsol平台实现,得到
| $ {S_{vv}} = - {\omega ^2}E({\boldsymbol {u}}{{\boldsymbol {u}}^ * }) ,$ | (5) |
| $ {\Pi _{rad}} = \sum\limits_S E ({\boldsymbol {p}}{{\boldsymbol {v}}^ * })\Delta {\boldsymbol {x}}。$ | (6) |
式中,
图1为采用有限元法计算流激结构声辐射示意图,图2给出了利用非相关平面波叠加等效湍流脉动压力激励结构声辐射的流程图。主要包括两部分,第1部分是以湍流脉动压力经验公式为基础利用Matlab获取非相关平面波等效幅值,第2部分是将非相关平面波加载到Comsol结构网格节点上并计算其振声响应,将原来的随机激励问题转化为一组确定性问题,这样就将包含空间自谱和互谱的大维度随机激励矩阵转化为确定性激励向量,有效地减少了计算量,提高了计算效率。
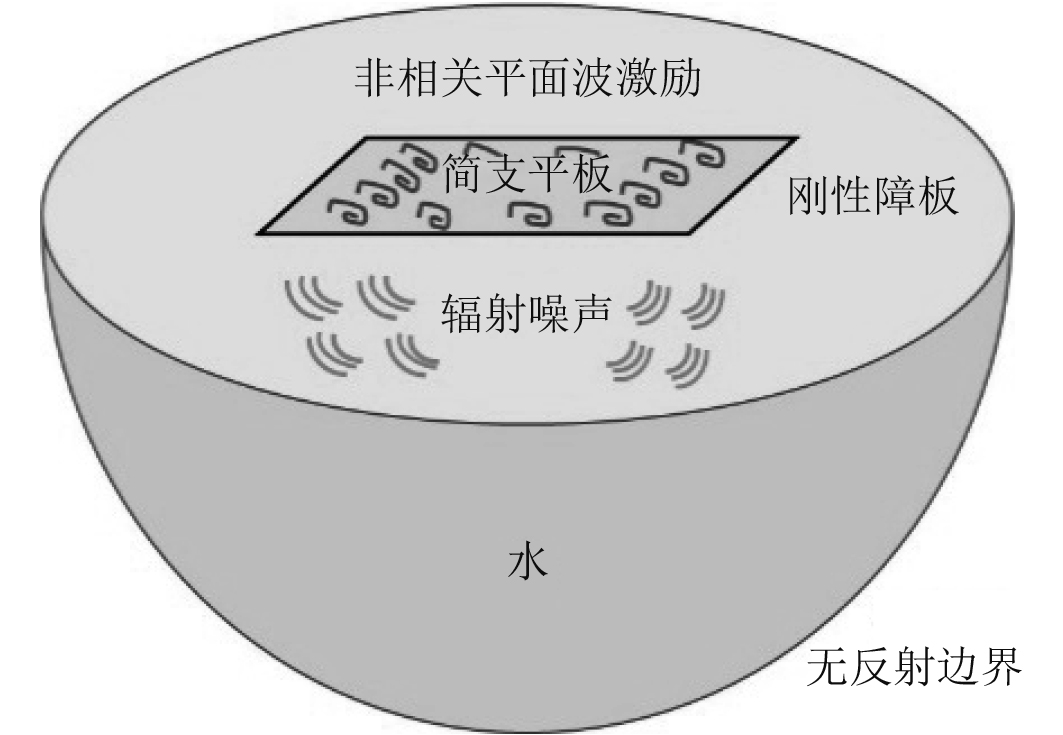
|
图 1 流激结构声辐射有限元法示意图 Fig. 1 Schematic of the flow-induced structure acoustic radiation with FEM |
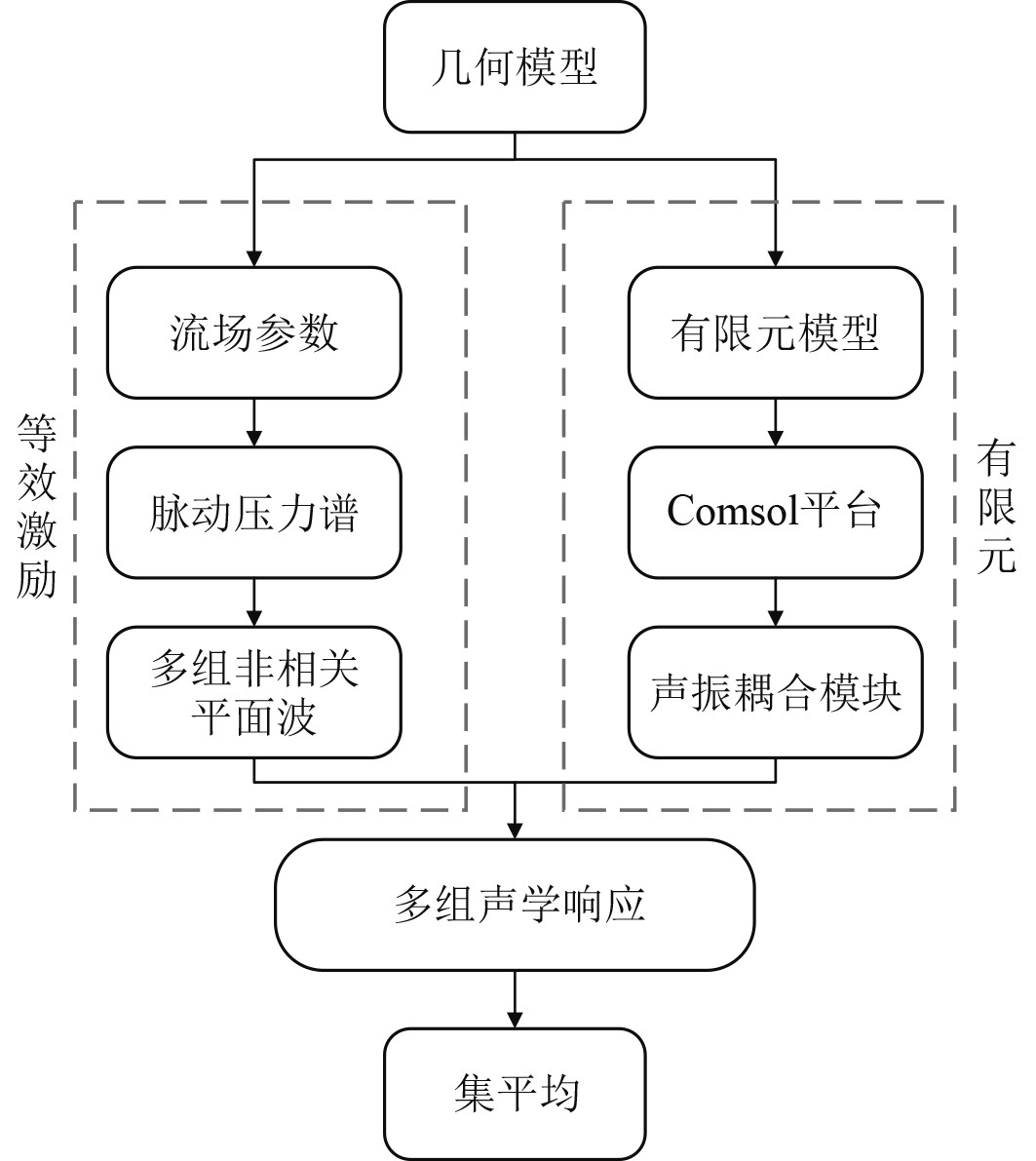
|
图 2 非相关平面波计算流激噪声流程图 Fig. 2 Flow chart of flow-induced noise with uncorrelated plane waves |
所用矩形板长为
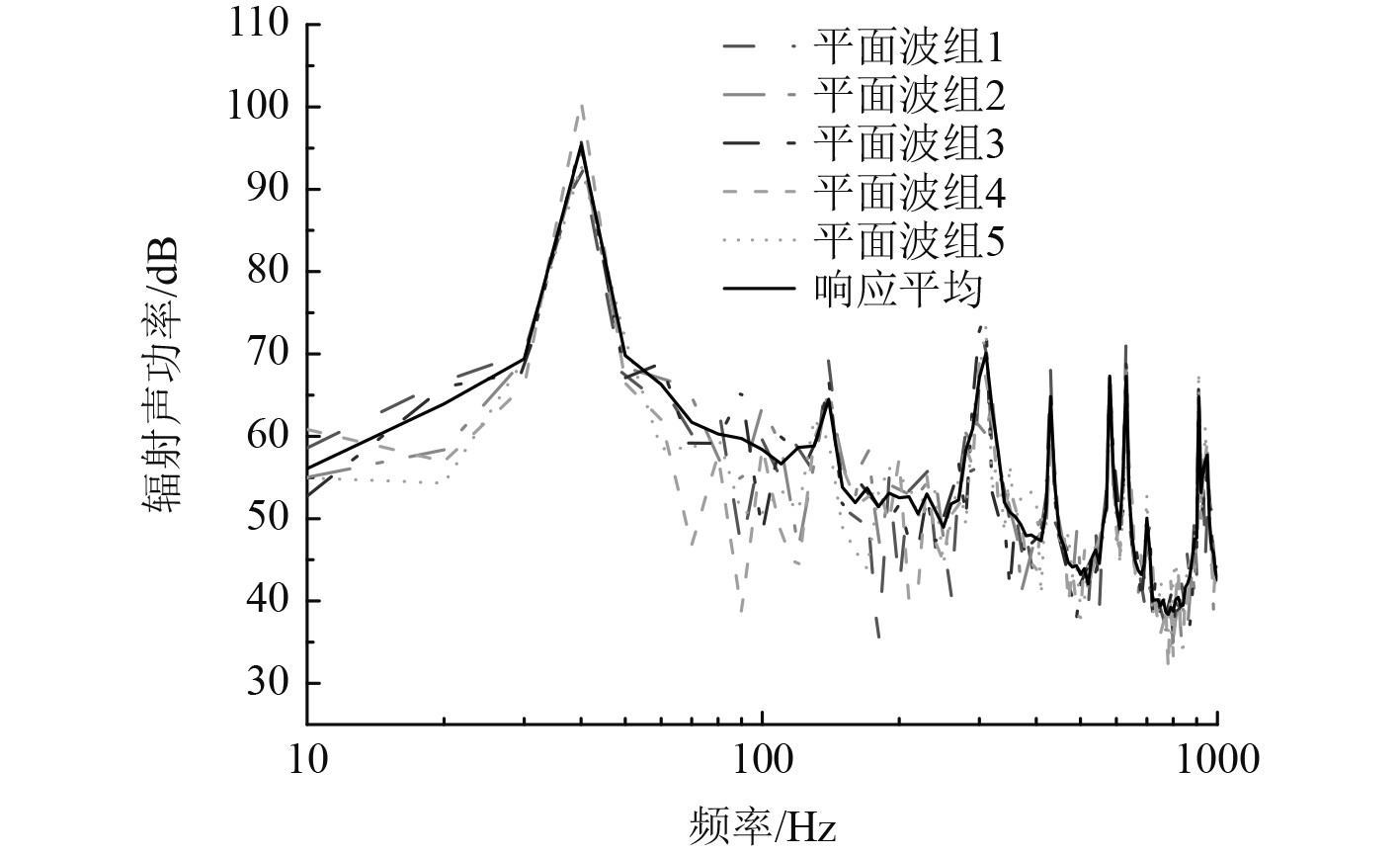
|
图 3 多组激励下的平均响应 Fig. 3 Average response with multiple excitation sets |
在采用非相关平面波叠加合成湍流脉动压力激励时,影响计算精度的参数主要包括:截断波数范围,波数分辨率,平面波组数,以及有限元网格密度。通过调试分析,在满足收敛的情况下,相应的参数设置为:截断波数
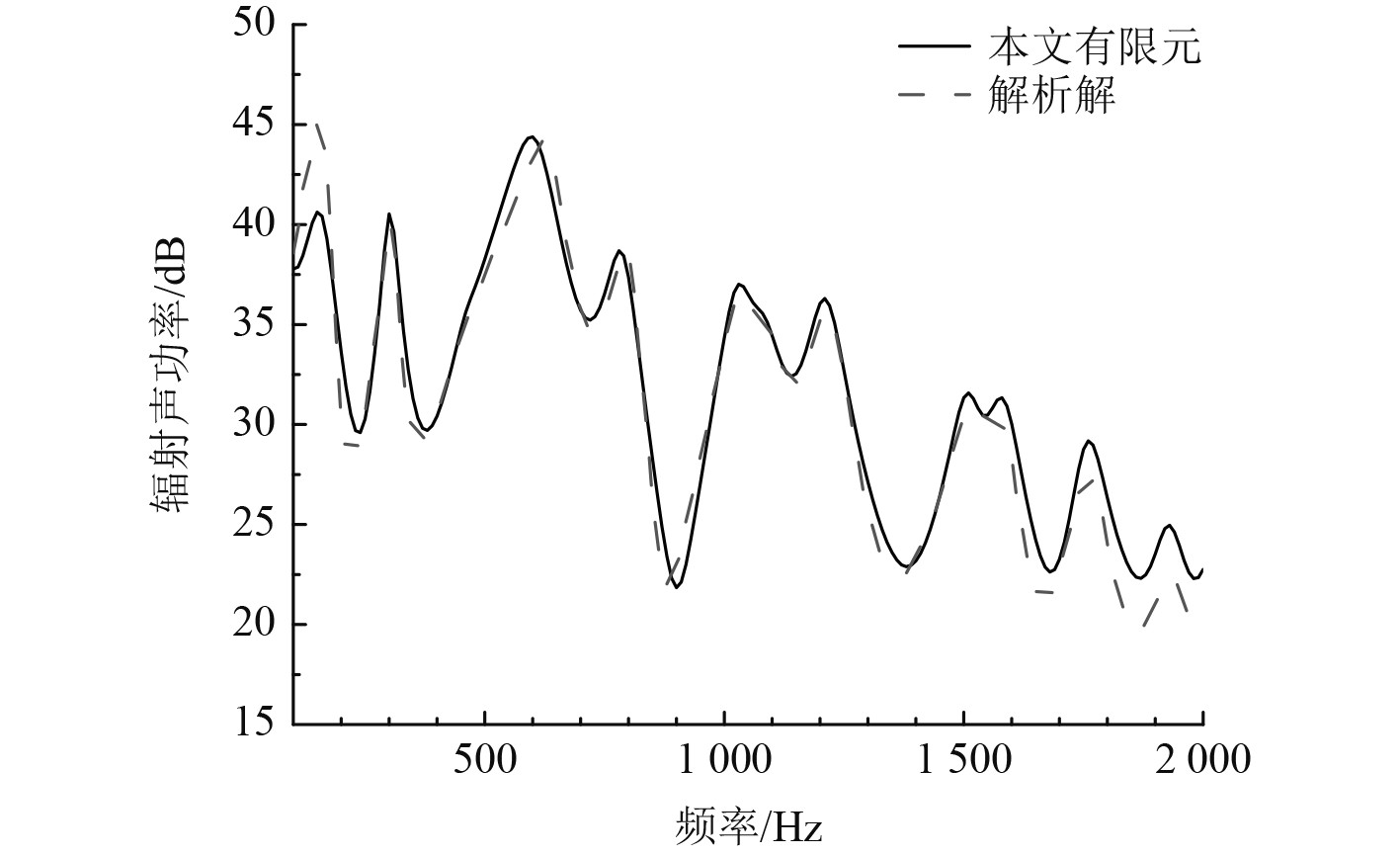
图4给出了本文算法与解析算法的计算结果对比。可看出两者有较好的一致性,说明湍流脉动压力平面波等效合成方法结合有限元计算能够准确的预报流激声辐射。图中低频时有一定的误差,可能是因为解析解假设了无限大刚性障板,而有限元法只能取有限尺寸的障板。
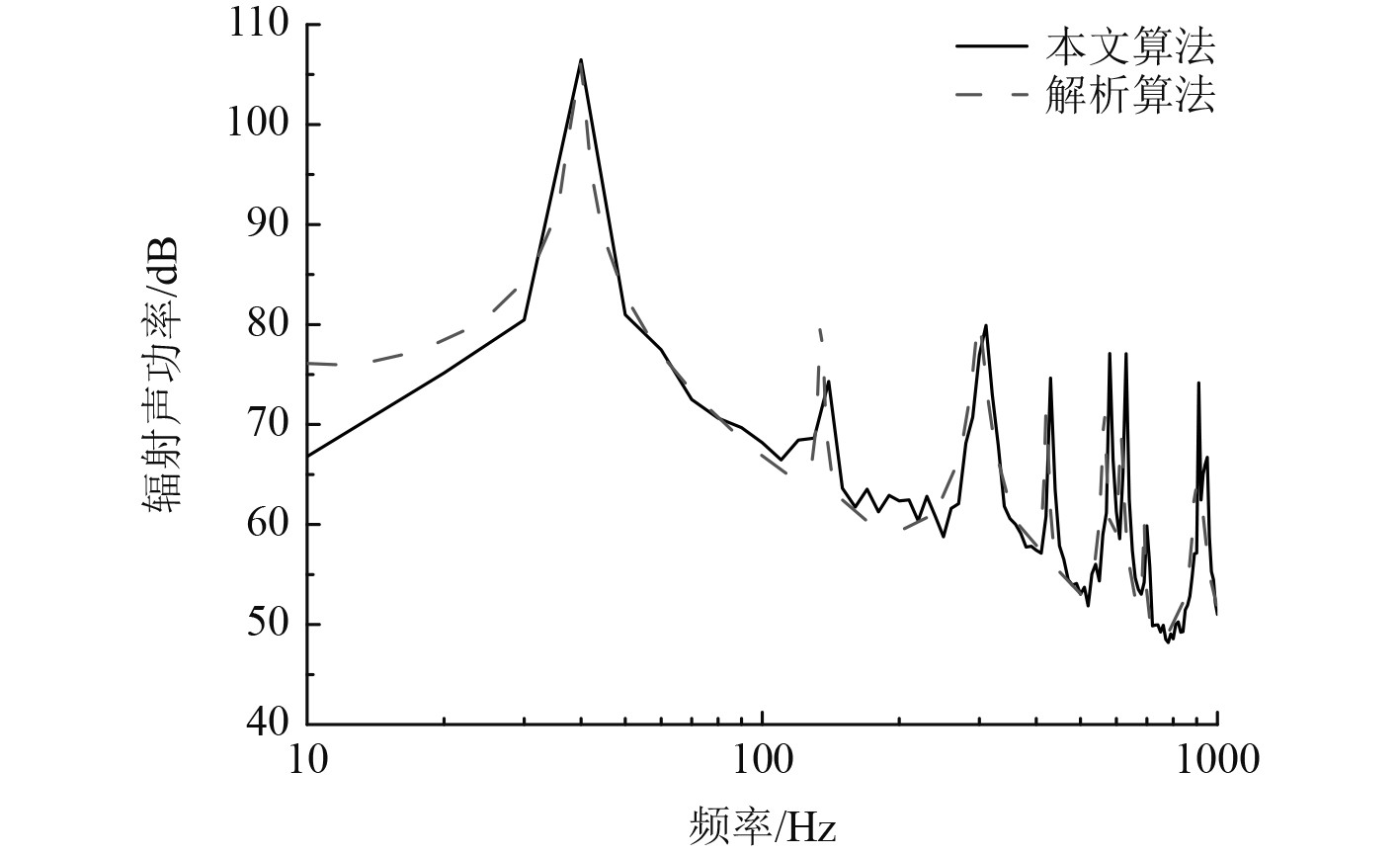
|
图 4 算法验证 Fig. 4 Algorithm validation |
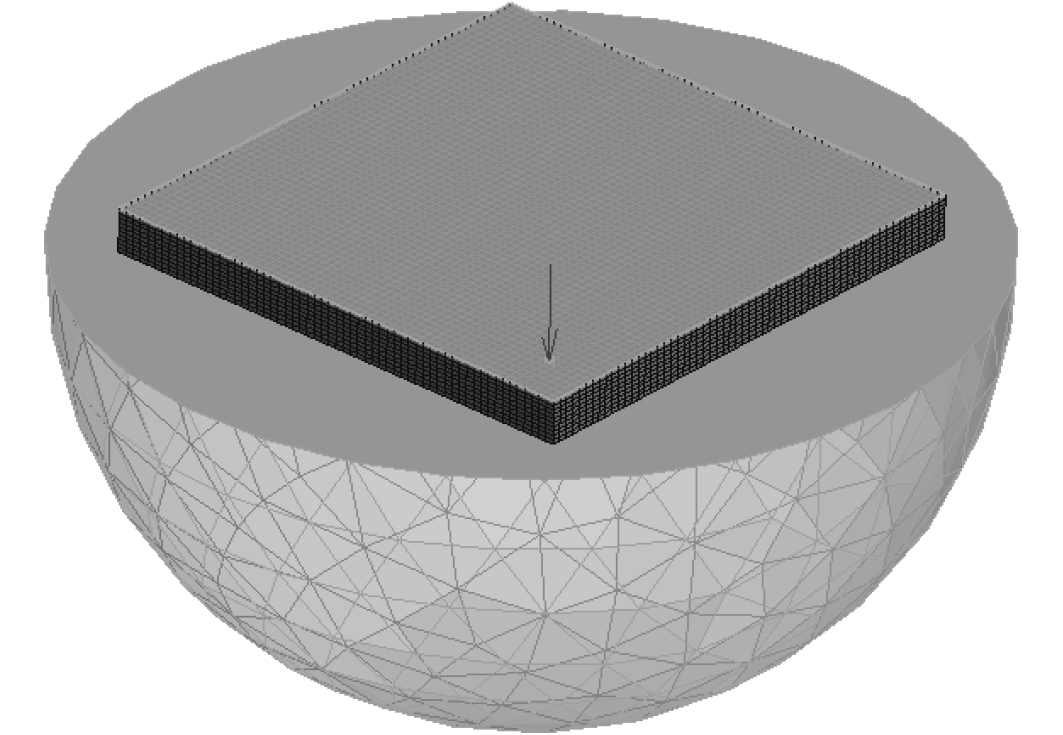
如图5所示,建立点激励下敷设声学覆盖层平板辐射噪声有限元模型,模型尺寸为
|
图 5 敷设声学覆盖层平板有限元模型 Fig. 5 Finite element model |
|
|
表 1 材料参数 Tab.1 Material parameters |
|
图 6 有限元与解析解对比 Fig. 6 Comparison of FEM with analytical solutions |
首先讨论覆盖层对流激噪声的降噪效果,从模态频率以及解耦特性方面对其降噪机理进行研究,然后分析影响流激声辐射的一些重要参数,为水动力噪声被动控制提供参考。
3.1 覆盖层降噪效果分析所分析模型长
|
|
表 2 材料参数 Tab.2 Material parameters |
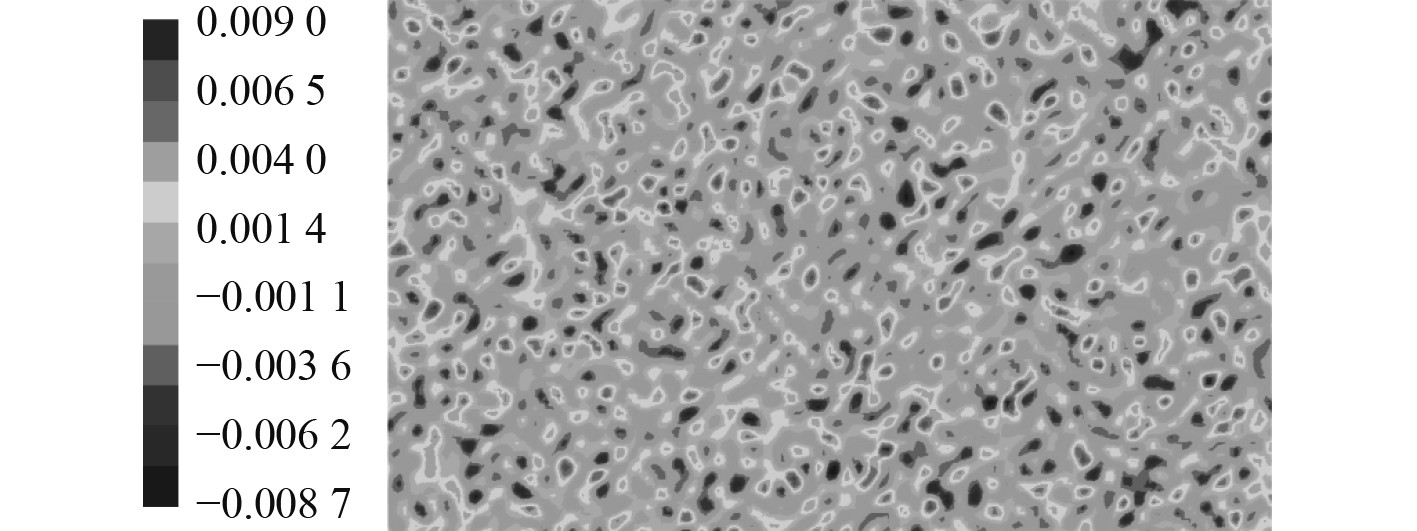
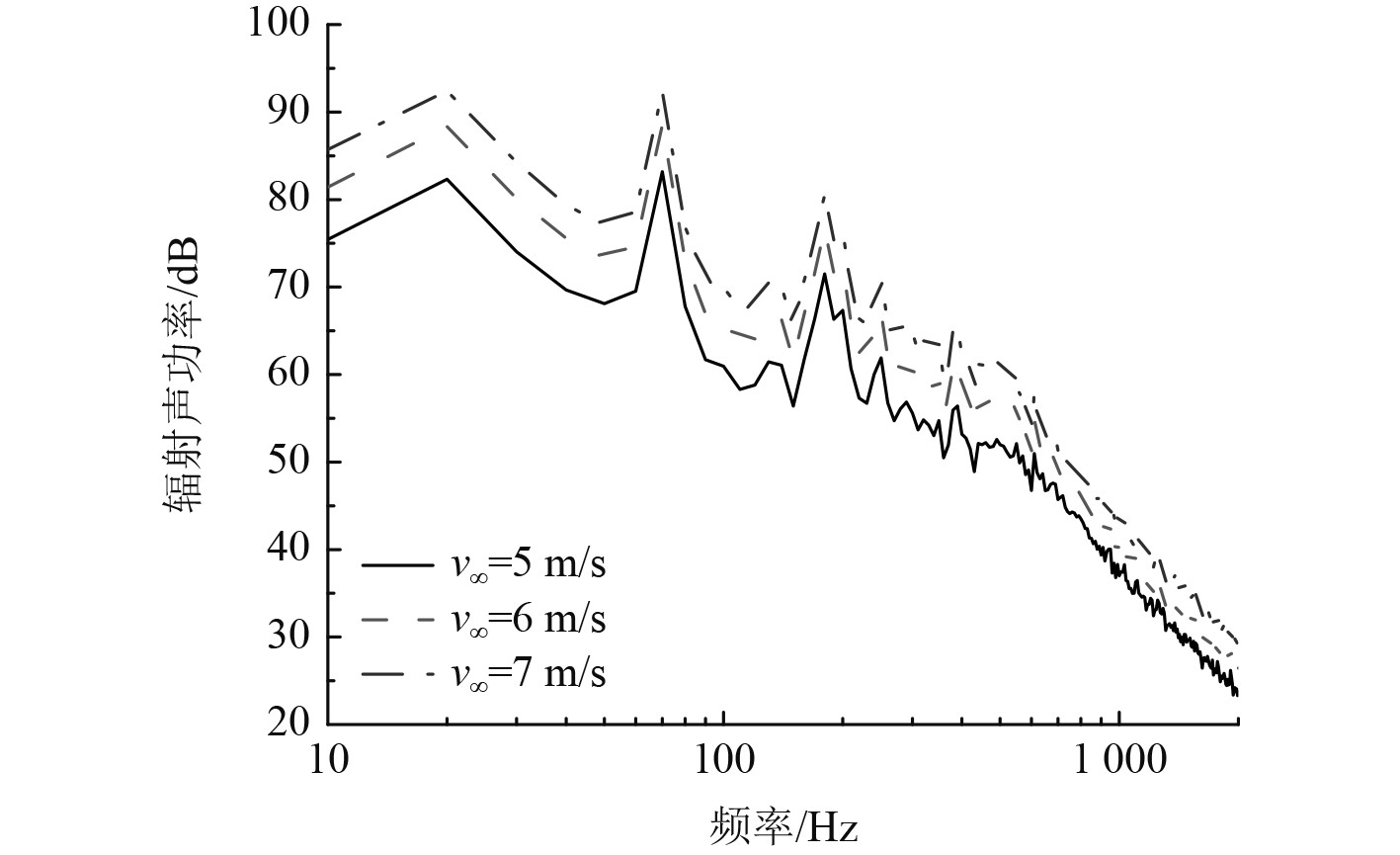
图7给出了1500 Hz时湍流脉动压力在结构表面的分布,图8给出了不同来流速度下的辐射声功率对比。可以看出,流激噪声随着流速的增加而增加,这是符合流噪声一般规律的。
|
图 7 脉动压力场云图(1500 Hz) Fig. 7 Pulsating pressure field (1500 Hz) |
|
图 8 来流速度对辐射噪声的影响 Fig. 8 Influence of incoming flow velocity |
图9为覆盖层降噪效果图。可以看出,在大于200 Hz的频率范围,声学覆盖层对流激噪声有明显的抑制作用(此时覆盖层材料的剪切损耗起到了主要作用),且敷设覆盖层后的结构模态峰值向低频偏移(因为覆盖层增加了结构的附加质量)。然而对于低阶模态峰值,覆盖层起不到降噪的作用,在某些频率辐射噪声甚至有所增加。结合表3可以看出,低阶的声辐射模态峰值主要来自有系统的低阶共振。
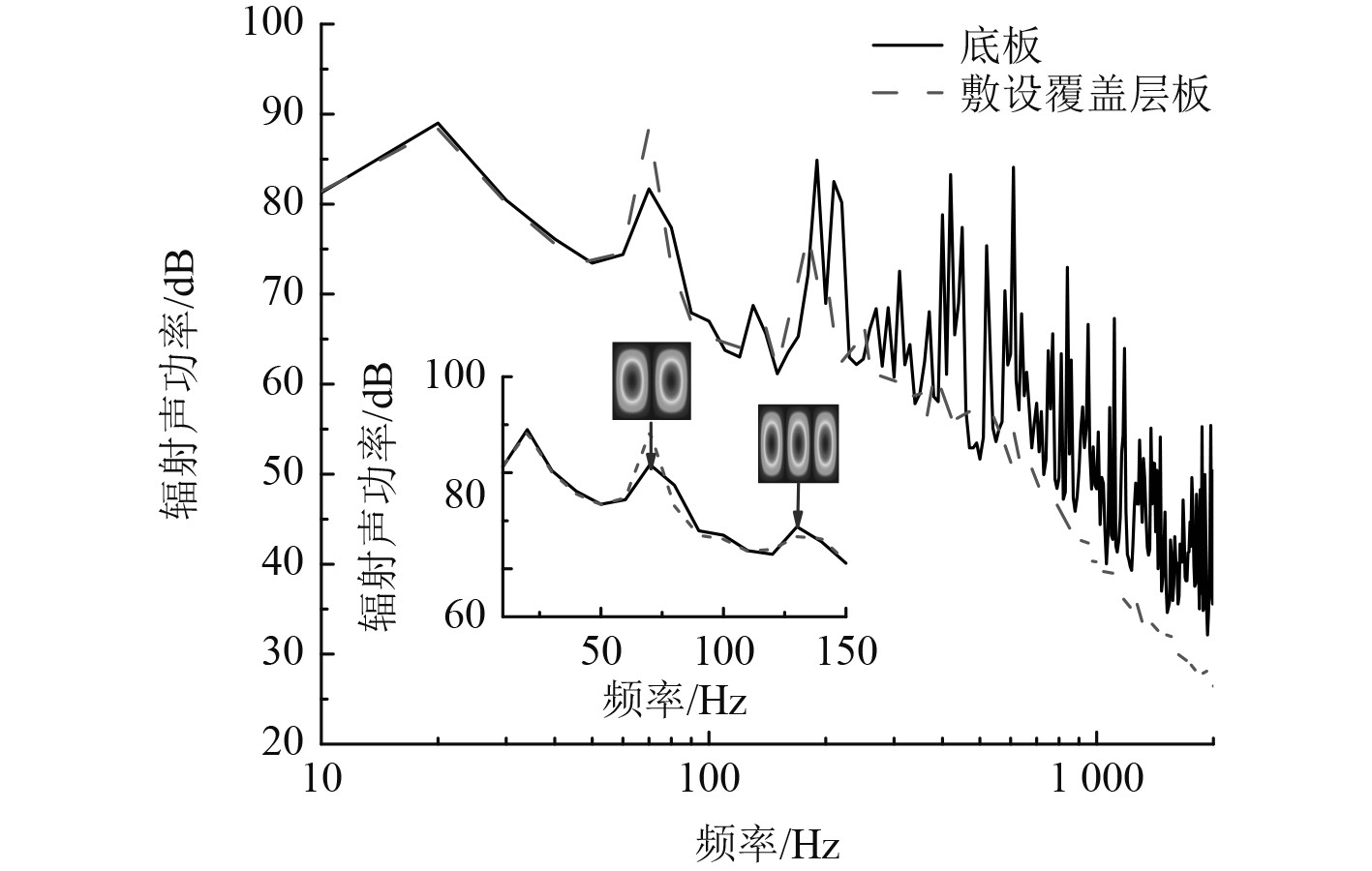
|
图 9 覆盖层降噪效果图 Fig. 9 Noise reduction effect of the coat |
|
|
表 3 前5阶模态频率 Tab.3 First 5th order modal frequency |
为了进一步阐述覆盖层的降噪机理,图10对比了敷设声学覆盖层后,底板表面与覆盖层表面的均方振速。可以看出,在中高频时覆盖层能起到较好的振动解耦作用,低频时解耦作用不明显。这是因为低频波长较长,底板和覆盖层保持相同的振动特性。当分析频率大于图10所示a点处的频率时,覆盖层对结构振动的解耦效应开始体现出来。
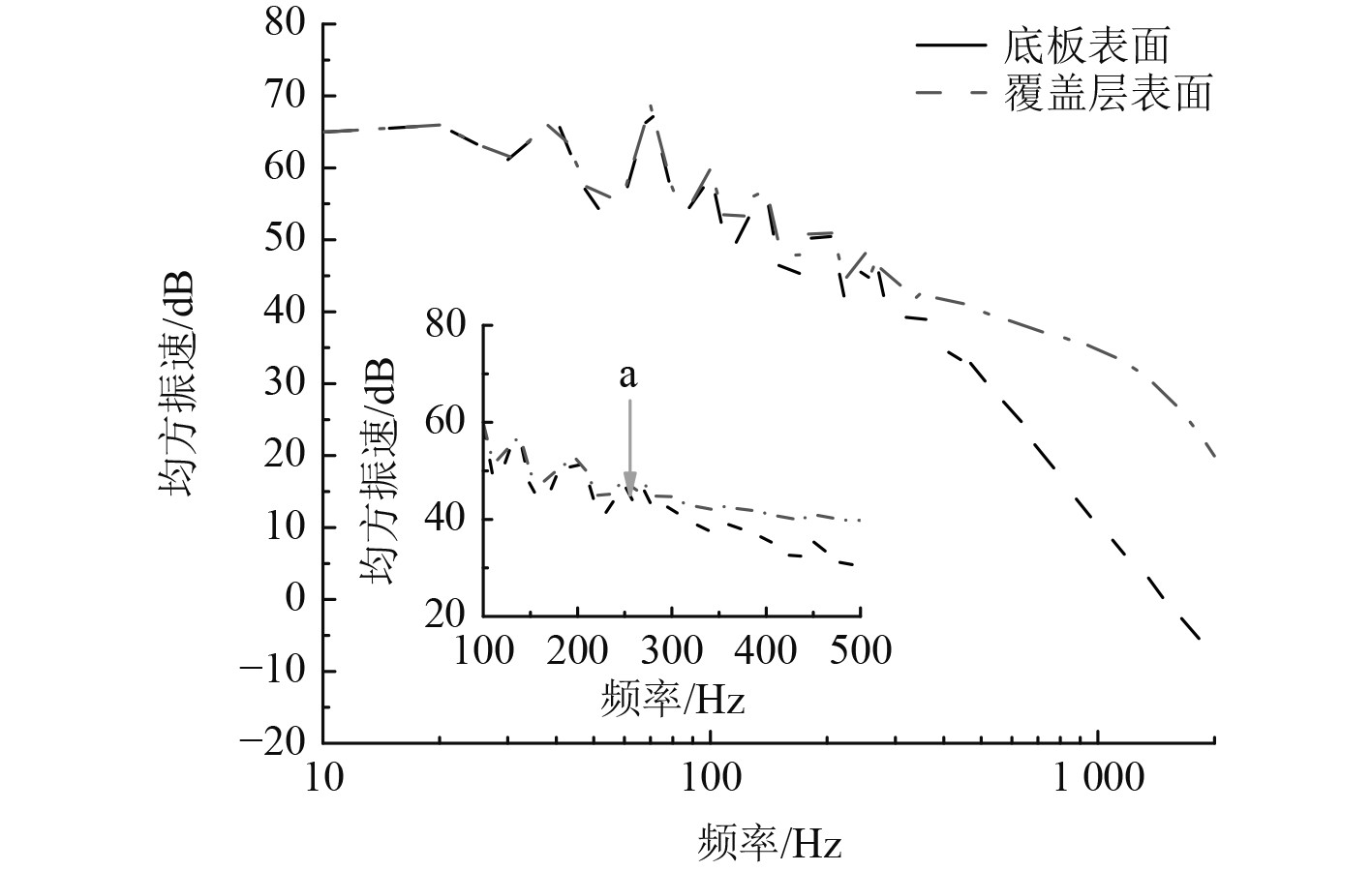
|
图 10 覆盖层振动解耦 Fig. 10 Vibration decoupling with coat |
探讨影响覆盖层降噪的一些参数,主要包括覆盖层厚度、杨氏模量、密度、损耗因子。
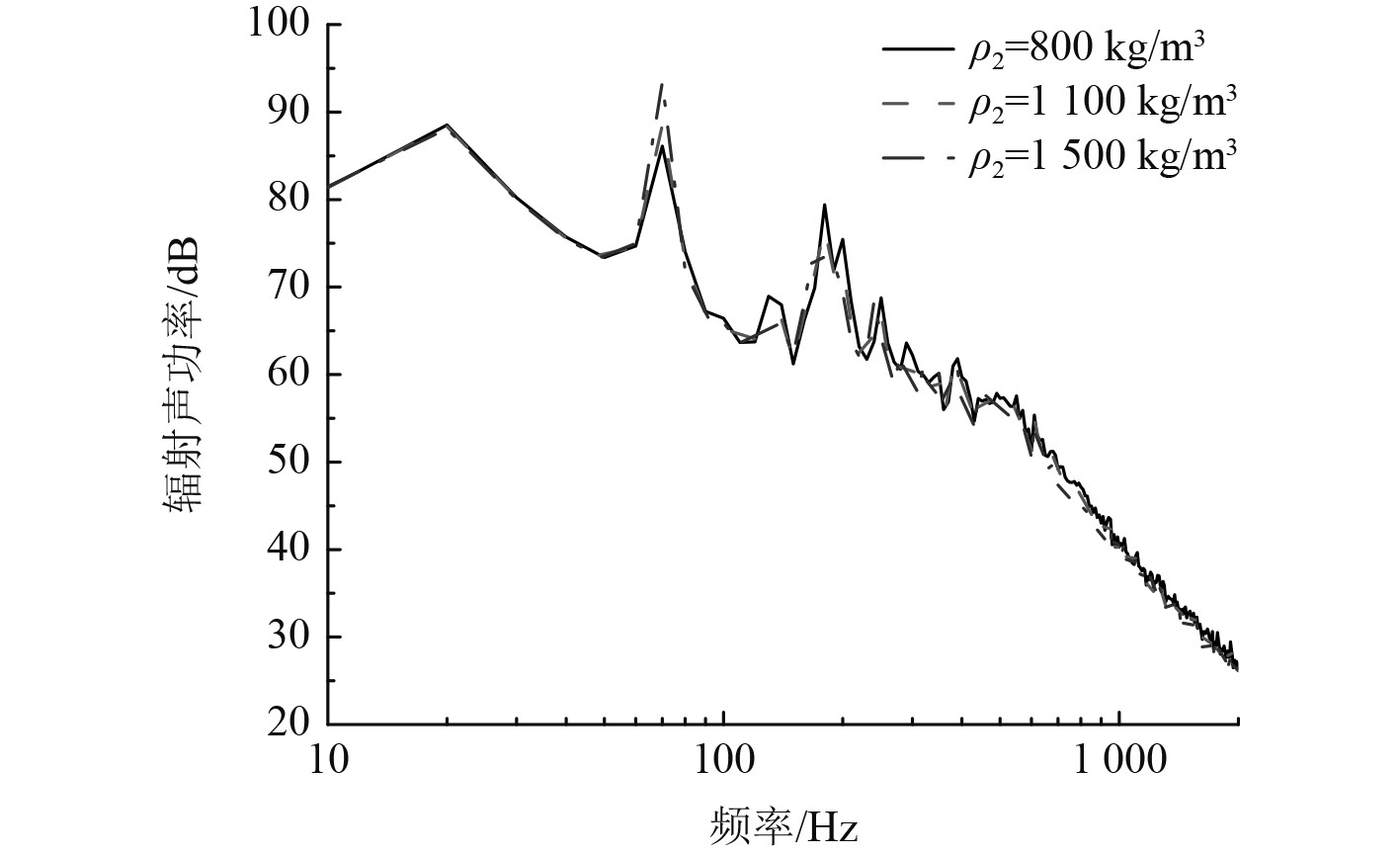
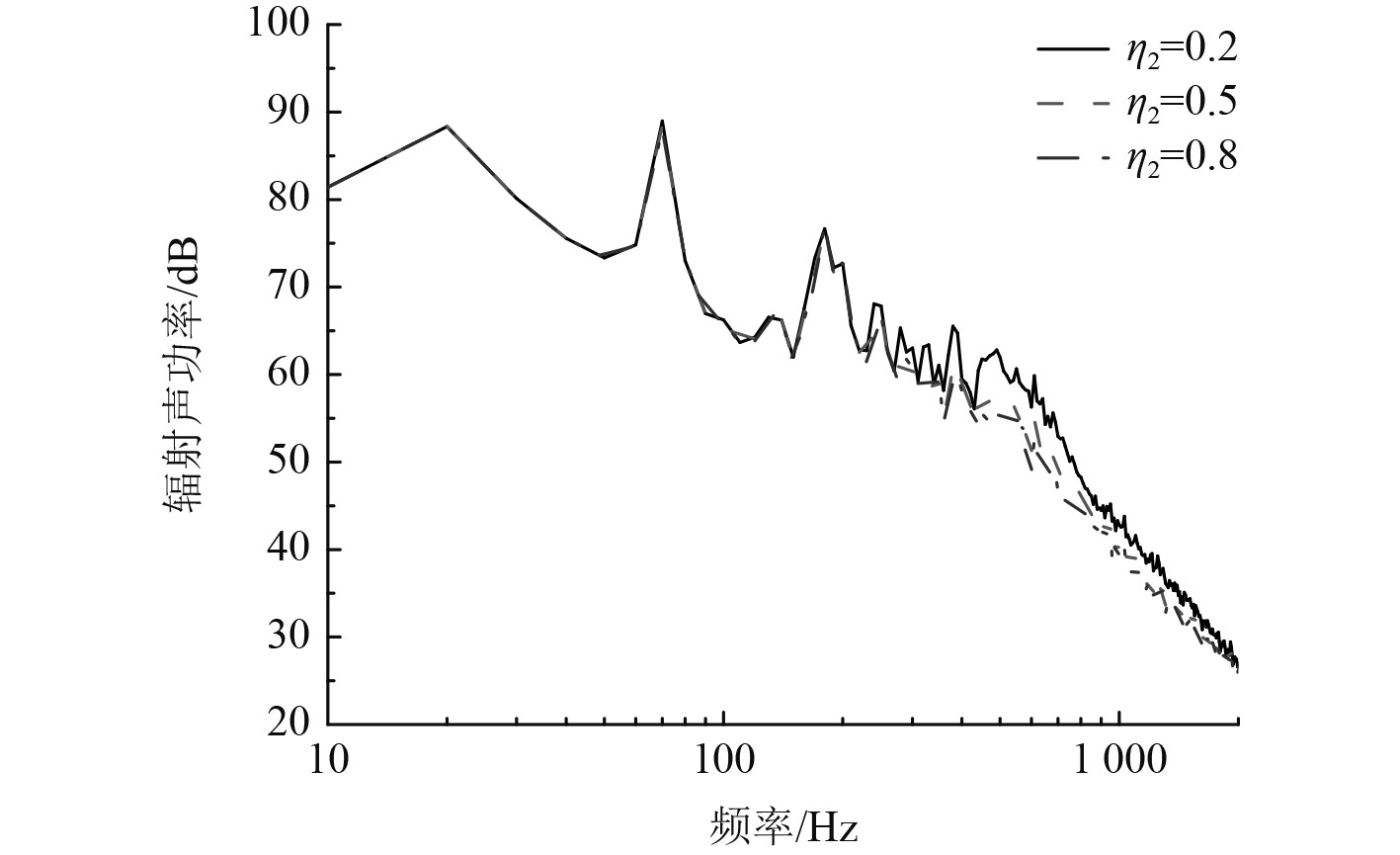
图11为覆盖层厚度的影响,就整体而言增加覆盖层厚度能有效降低流激噪声。由于改变厚度会影响系统的模态频率,因此随着厚度的改变模态峰值也出现了变化。图12为杨氏模量对流激噪声的影响,整体而言杨氏模量越大,降噪效果越好。这是因为杨氏模量对系统刚度有影响,杨氏模量越大覆盖层越难被激起振动。图13为覆盖层密度对流激噪声的影响,可以看出密度对流激噪声的影响没有其余参数大,密度主要影响覆盖层质量,因为相对于底板密度覆盖层密度较小,所以对流激噪声影响不大。图14为覆盖层损耗因子的影响,可以看出损耗因子越大高频降噪效果越好。由以上分析可知,针对具体感兴趣的频率范围,对覆盖层参数进行合理设计能起到明显降噪效果。另外,利用声学覆盖层实现水下结构流激噪声低频降噪依然是未来研究的难点。
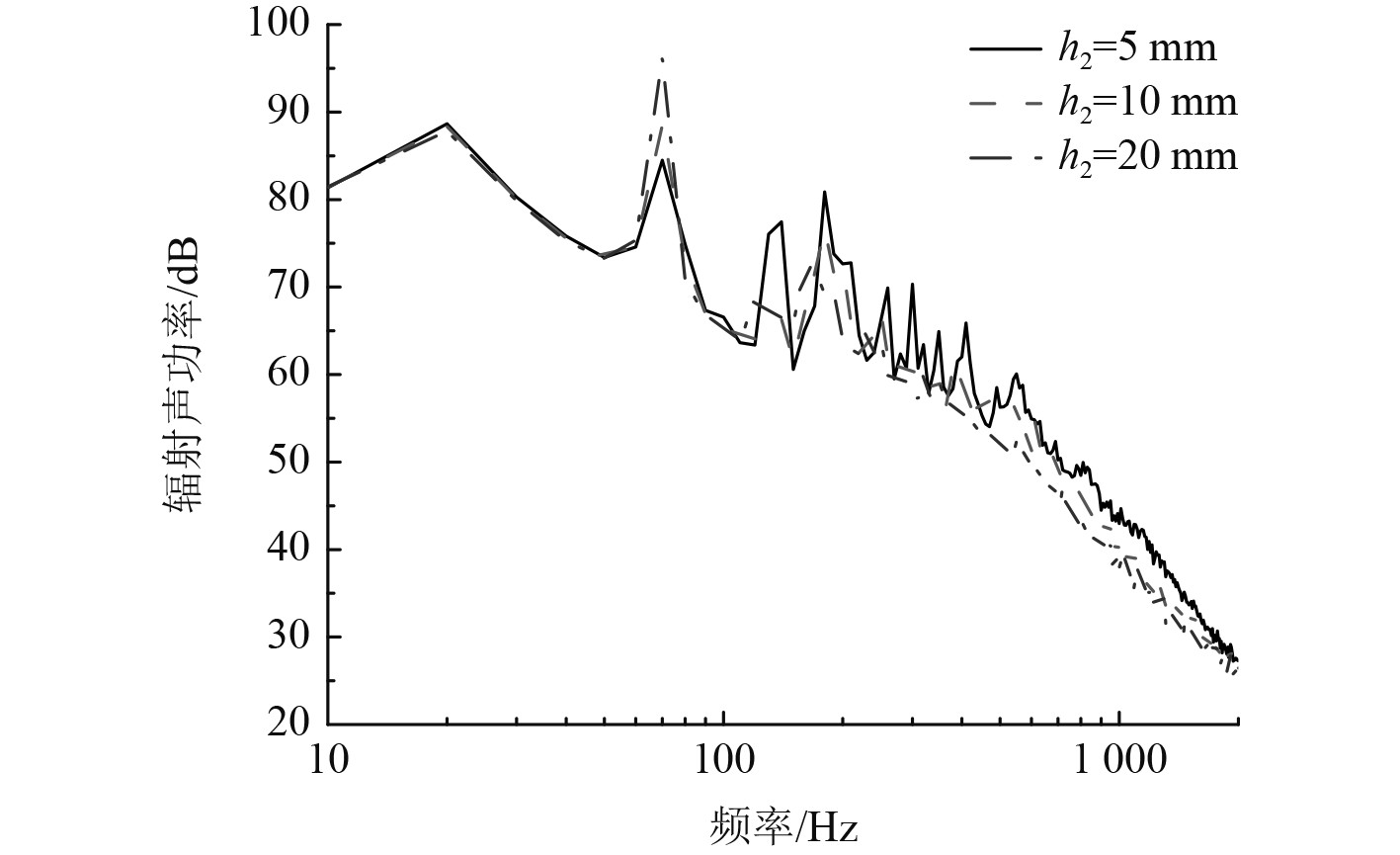
|
图 11 覆盖层厚度对流激噪声的影响 Fig. 11 Effects of coat thickness |
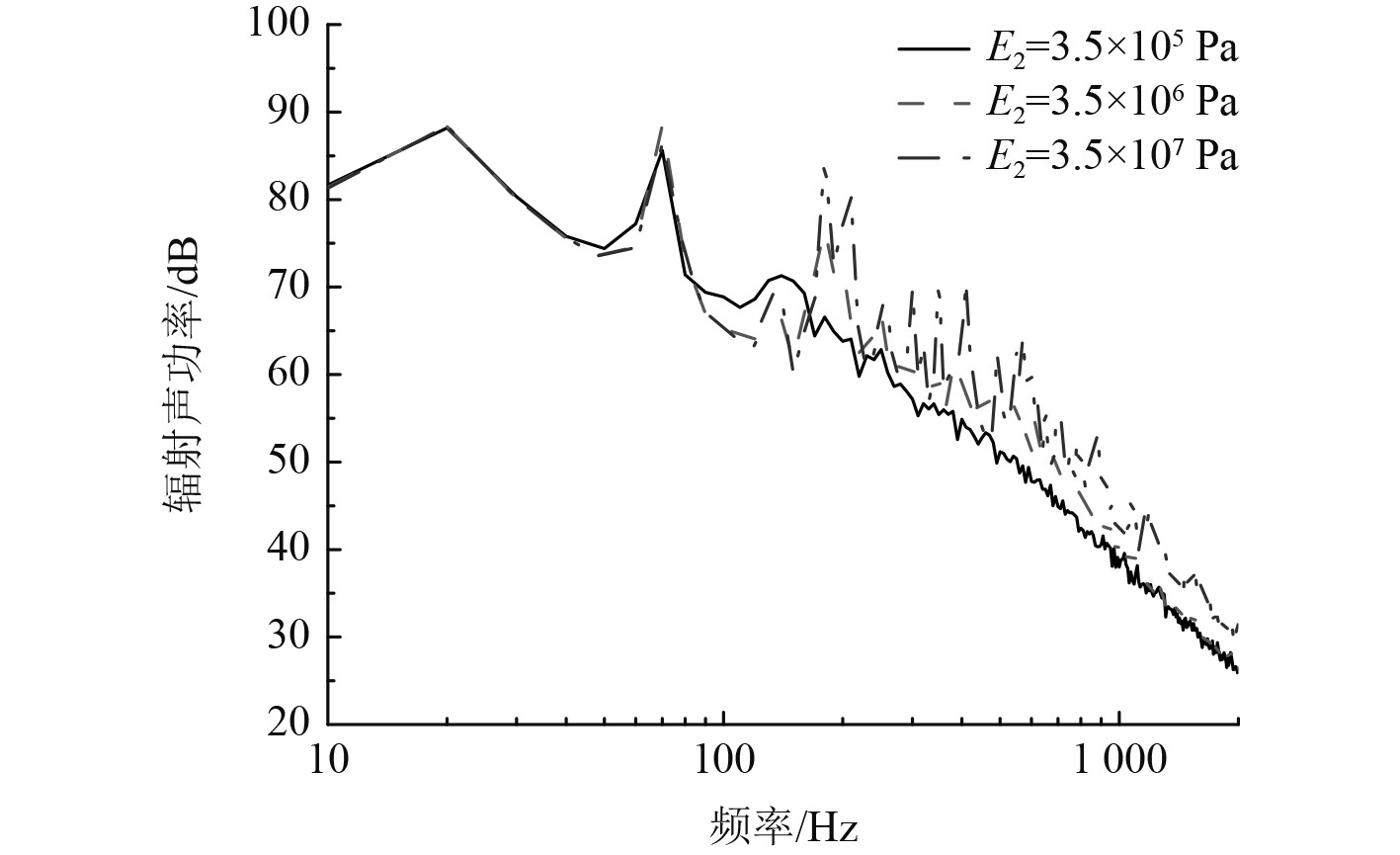
|
图 12 覆盖层杨氏模量对流激噪声的影响 Fig. 12 Effects of Young's modulus |
|
图 13 覆盖层杨氏模量对流激噪声的影响 Fig. 13 Effects of coat density |
|
图 14 覆盖层损耗因子对流激噪声的影响 Fig. 14 Effects of coat loss factor |
本文针对敷设声学覆盖层的弹性平板流激噪声问题展开研究,首先引入非相关平面波叠加理论用于合成湍流脉动压力激励力,并结合有限元模块实现了流激噪声算法建模。在算法验证的基础上,开展敷设声学覆盖层的矩形板流激噪声降噪机理研究,并分析了覆盖层参数对流激噪声的影响,得到如下结论:
1)来流速度是影响流激噪声的重要因素,敷设声学覆盖层的平板流激噪声随着来流速度增加而增加;
2)敷设声学覆盖层能有效降低结构的中高频流激噪声,但对100 Hz以下的低频噪声效果不明显,个别频率甚至辐射噪声幅值有所增加;
3)覆盖层的厚度、杨氏模量、损耗因子对降噪效果有较大影响,在感兴趣频率范围通过合理设置能够起到有效降噪。
| [1] |
吕世金, 高岩, 刘进, 等. 水下航行体表面湍流脉动压力波数-频率谱测试应用分析[J]. 中国舰船研究, 2020, 15(S1): 55-60. DOI:10.19693/j.issn.1673-3185.01581 |
| [2] |
俞孟萨, 李东升, 龚莉, 等. 声呐罩夹芯式透声窗的声学设计研究[J]. 声学学报, 2005(5): 427-434. DOI:10.3321/j.issn:0371-0025.2005.05.007 |
| [3] |
HEKMATI A, RICOT D, DRUAULT P. Numerical synthesis of aeroacoustic wall pressure fields over a flat plate: Generation, transmission and radiation analyses[J]. Journal of Sound and Vibration, 2013, 332(13): 3163-3176. DOI:10.1016/j.jsv.2013.01.019 |
| [4] |
FRANCO F, ROSA S D, CIAPPI E. Numerical approximations on the predictive responses of plates under stochastic and convective loads[J]. Journal of Fluids and Structures, 2013, 42: 296-312. DOI:10.1016/j.jfluidstructs.2013.06.006 |
| [5] |
HONG C, SHIN K K. Modeling of wall pressure fluctuations for finite element structural analysis[J]. Journal of Sound and Vibration, 2010, 329(10): 1673-1682. DOI:10.1016/j.jsv.2009.11.026 |
| [6] |
FOIN O, BERRY A. Acoustic radiation from an elastic baffled rectangular platecovered by a decoupling coating and immersed in a heavy acoustic fluid[J]. The Journal of the Acoustical Society of America, 2000, 107(5): 2501-2510. DOI:10.1121/1.428638 |
| [7] |
BERRY A, FOIN O. Three-dimensional elasticity model for a decoupling coating on a rectangular plate immersed in a heavy fluid[J]. The Journal of the Acoustical Society of America, 2001, 109(6): 2704-2714. DOI:10.1121/1.1372224 |
| [8] |
AUCEJO M, MAXIT L, GUYADER J L. Experimental simulation of turbulent boundary layer induced vibrations by using a synthetic array.[J]. Journal of Sound and Vibration, 2012, 331(16): 3824-3843. DOI:10.1016/j.jsv.2012.04.010 |
| [9] |
KARIMI M, MAXIT L, CROAKER P, et al. Analytical and numerical prediction of acoustic radiation from a panel under turbulent boundary layer excitation[J]. Journal of Sound and Vibration, 2020, 479(4): 115372. |
| [10] |
GRAHAM W R. Boundary layer induced noise in aircraft, Part 1: The flat plate model[J]. Journal of Sound and Vibration, 1996, 192(1): 101-120. DOI:10.1006/jsvi.1996.0178 |
 2024, Vol. 46
2024, Vol. 46
