2. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003
2. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China
经过长时间的发展,水下滑翔机[1 − 3]以及仿生机器蟹[4 − 5]技术日益成熟,水下滑翔机具有的驱动技术以及浮力调节技术相当成熟,通过调整水下滑翔机的浮力将其转换为前进驱动力,能大大减少能耗,提高水下滑翔机的续航性。仿生机器蟹采用仿生技术,以多足爬行作为运动方式,因其外形扁平,受浪流影响较小,可适应复杂的海底环境。
本文借鉴变形机器人变形技术,将水下滑翔机独特的驱动技术以及仿生机器蟹爬行技术融合,引进翼身融合技术,研发出一种兼备水下滑翔机低功耗与仿生机器蟹灵活性的仿生机器蟹[6 − 7]。基于粘流理论方法,建立数值仿真模型,分析仿生机器蟹滑翔状态下的受力情况,研究计及复杂附体结构的仿生机器蟹水动力特性。
1 受力分析与数值模型建立 1.1 受力分析为简化受力模型以及建立数学模型,将对仿生机器蟹作如下设定。在仿生机器蟹上建立随体坐标系(见图1),仿生机器蟹浮心为随体坐标系原点,遵循右手法则;Ox轴在仿蟹滑翔机器人的中心内,向头部为正;Oy向右翼为正;Oz轴垂直机体向下为正。仿生机器蟹工作环境为水下100~200 m,处于全沾湿状态;仿生机器蟹为刚体,其外形关于纵平面xOy对称,由于爬行足尖的存在,机体在水平面xOz不对称。

|
图 1 定常滑翔状态的运动参数及受力分析图 Fig. 1 Motion parameters and force analysis diagram of steady glide state |
仿生机器蟹上的水动力合力为F,仿生机器蟹重力为G,浮力为B,净浮力为ΔG,仿生机器蟹稳态滑翔状态时的速度为V,u为速度V在水平方向上的分量,w为速度V在垂直方向上的分量,即下潜(上浮)速度。
将仿生机器蟹所受水动力的合外力分解,阻力是机身轴线方向上的分量,设为D,升力是垂直于机身轴线并且向上的分量为升力L,回复力矩设为M,如图2所示。

|
图 2 仿生机器蟹合外力分解图 Fig. 2 Decomposition diagram of biomimetic robot crab by force |
力与力矩之间满足如下关系:
| $ G = B,$ |
| $ F = \Delta G,$ |
| $ {M_F} = \Delta G \cdot L \cdot \cos \theta = G \cdot h \cdot \sin \theta = M 。$ |
可推出姿态角
| $ \tan \theta = \frac{{\Delta G \cdot L}}{{G \cdot h}} 。$ |
水下滑翔机水动力性能主要有阻力值、升阻比等,将升阻比作为研究水动力性能的重要参数,其是升力与阻力的比值。升阻比与迎流攻角大小有关,存在最优攻角,最优攻角下获得最大升阻比,攻角过大,也可能出现失速现象,故需求取最优攻角。
1.2 计算模型选取仿生机器蟹引入航空中翼身融合布局,但是本体、机翼与足尖的连接处结构复杂,需简化模型,去除影响较小的零部件,但要保证数值结果的可靠性。
采用三维建模软件建立数值计算模型,简化后模型由主体、机翼、足尖和尾翼组成,如图3所示。简化后仿生机器蟹总长1.38 m。其中,中部为椭球体,长1 m;翼展为2.2 m;湿表面积为2.4 m2。设计航速为1.0 m/s。

|
图 3 仿生机器蟹简化模型 Fig. 3 Simplified model of bionic robotic crab |
为了确保计算结果具有参考意义,选用已有试验结果的“海鸥一号”为验证对象,将本文所使用的数值方法用于“海鸥一号”,求解直航运动下阻力值,计算航速为0.2~0.5 m/s,步长为0.1 m/s,“海鸥一号”网格划分采用全六面体非结构网格。最终对比求解结果与“海鸥一号”[8]拖曳试验结果,如图4所示。

|
图 4 阻力对比图 Fig. 4 Resistance contrast chart |
求解结果与试验结果进行比对,可见曲线基本一致,最大偏差低于3%,证明数值方法的可行性,具有一定参考意义。
2.2 网格划分依据流场的计算需求,建立数值计算域,将多计算域法与滑移网格法高效结合。
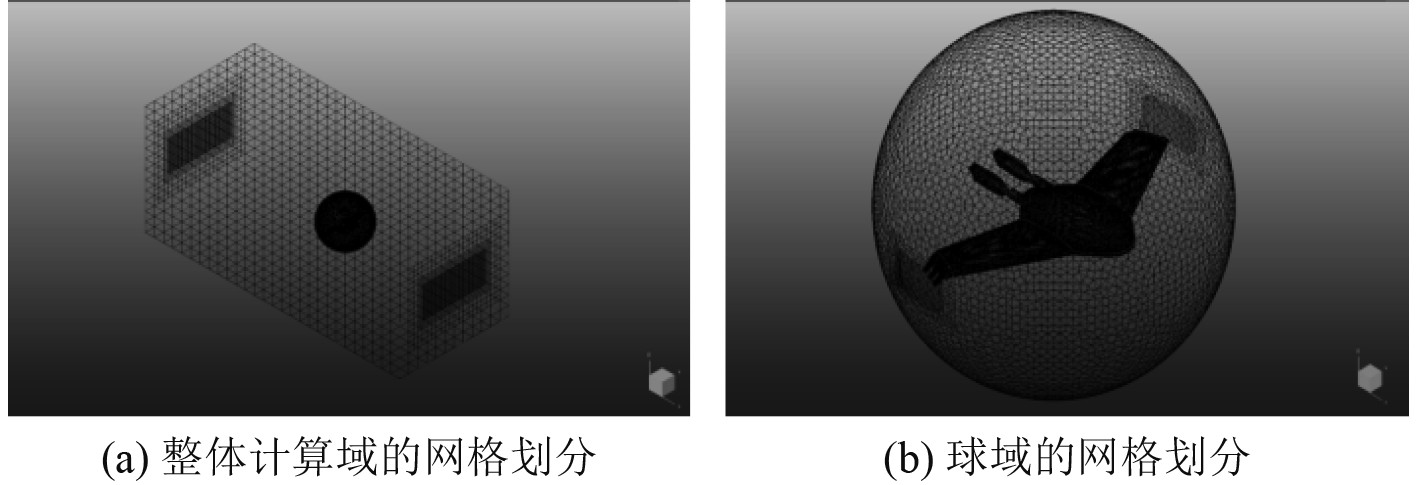
外域为 5.8L×2.4L×2.5L 的长方体(L为球域直径),外域的网格数约为 40 万。内部域为直径2.4 m的球域,网格数约为170万。图5为网格划分。
|
图 5 网格划分 Fig. 5 Division of grid |
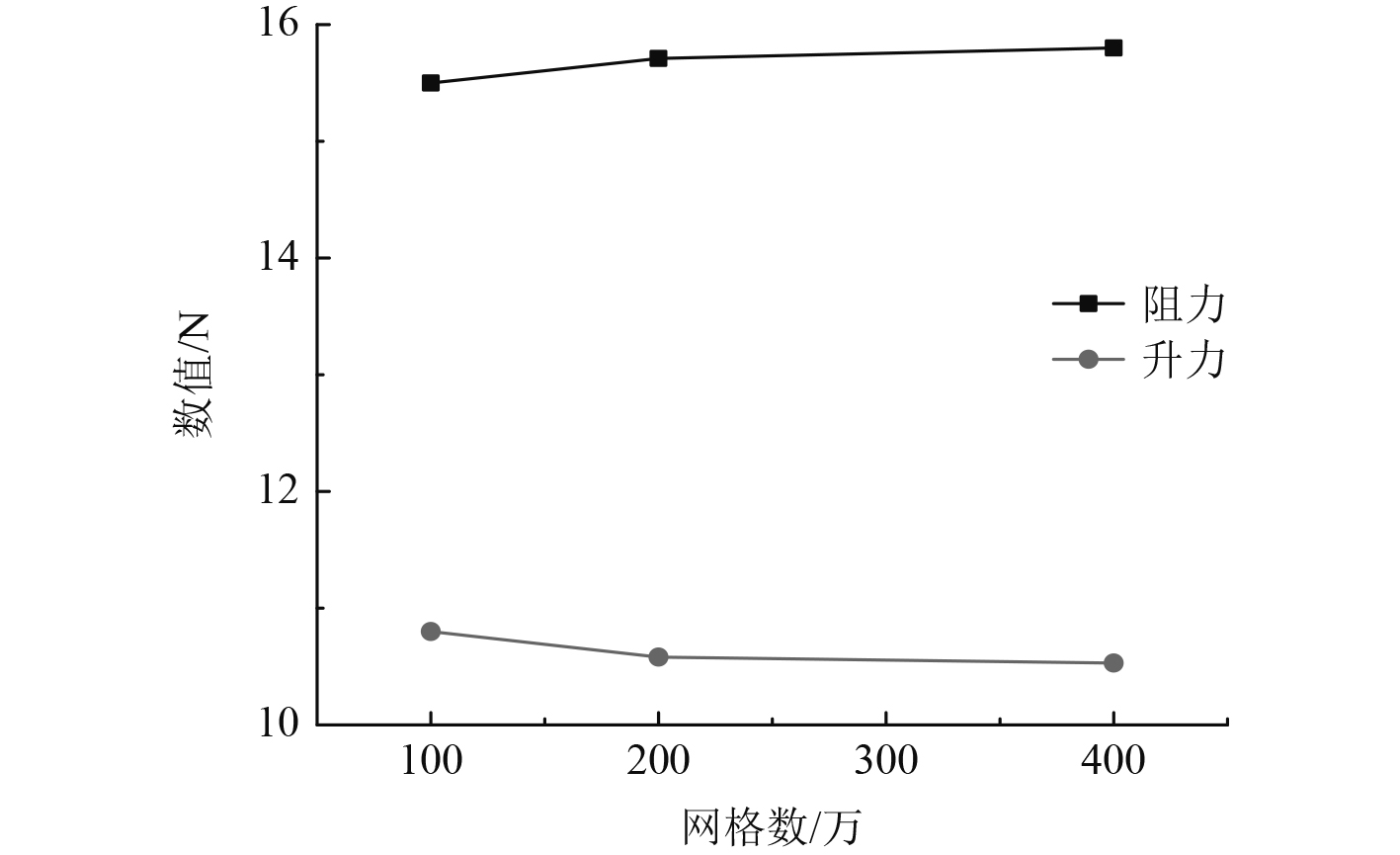
为确保数值计算结果的准确性,划分出网格数为100万、200万 和400万共3种网格,用于验证网格的收敛性。第1套网格只采用总体划分的方法。第2种网格采用与第1套网格同样方法,但对仿生机器蟹运动区域进行局部加密。第3种网格相较于第2种采用同样加密方法,加密层数增加。均设置为仿生机器蟹设计航速的直航状态下(0°攻角),结果如图6所示。
|
图 6 网格收敛性对比图 Fig. 6 Grid convergence comparison diagram |
可知,对比前2种网格,网格数量相差越大,数值误差较大。当计算域网格数量为200万,与第3种网格相比,数值结果近似,数值误差较小,计算结果已经收敛,表明采用200万网格进行数值模拟既可以保证结果的准确性,也能保证高效性。数值计算将采用第2种网格划分方法。
2.4 仿生机器蟹水动力性能 2.4.1 计算工况选取水下滑翔机存在一个最优攻角,以研究仿生机器蟹的最优航行状态为目的。计算不同速度下、不同攻角的升阻特性,分析各个参数的变化,以得到最优攻角。一般水下航行器设计攻角在为−12°~12°,间隔2°作为计算工况。
为研究边界层对水动力性能的影响,除设计航速外又选取3个不同边界层的速度作为计算航速。查阅相关文献可知,一般临界雷诺数Re为5×105,即当 Re<5×105,研究目标的外边界层均为层流,当2×106>Re>5×105,为混合边界层,当 Re>2×106时,则是湍流边界层或者湍流流动占主要的混合边界层,计算速度如表1所示。
|
|
表 1 计算速度 Tab.1 Speed of calculation |
因仿生机器蟹的不对称性,需对仿生机器蟹的上深、下潜进行数值模拟,根据计算结果,为确定最优攻角,加算±9°和±11°攻角值。
2.4.2 求解设置与边界条件在本文的数值模拟计算中,在计算航速下求解仿生机器蟹,得到仿生机器蟹的水动力性能。
基于粘性流体理论,仿蟹滑翔机器人计算方法参数设置如下:流体参数设定为15℃海水,密度为1 026 kg/m3,动力粘性系数取0.000 9 Pa·s;计算物理模型选用非稳态时间布局模型;选用
不同攻角下,速度越大阻力越大,速度与阻力呈函数关系。因仿生机器蟹航行过程中攻角在不断改变,从而使仿生机器蟹机体表面的边界层分离,此时流体流动脱离力仿生机器蟹表面,在主体前后的压强差上升,首尾产生的压力差越来越大,使得压差阻力变大。由于仿生机器蟹采用翼身融合设计,具有良好的流线型,故机体所受的粘性阻力随航速增大而增大,受攻角影响变化较小,因此攻角增大而粘性阻力变化较小。
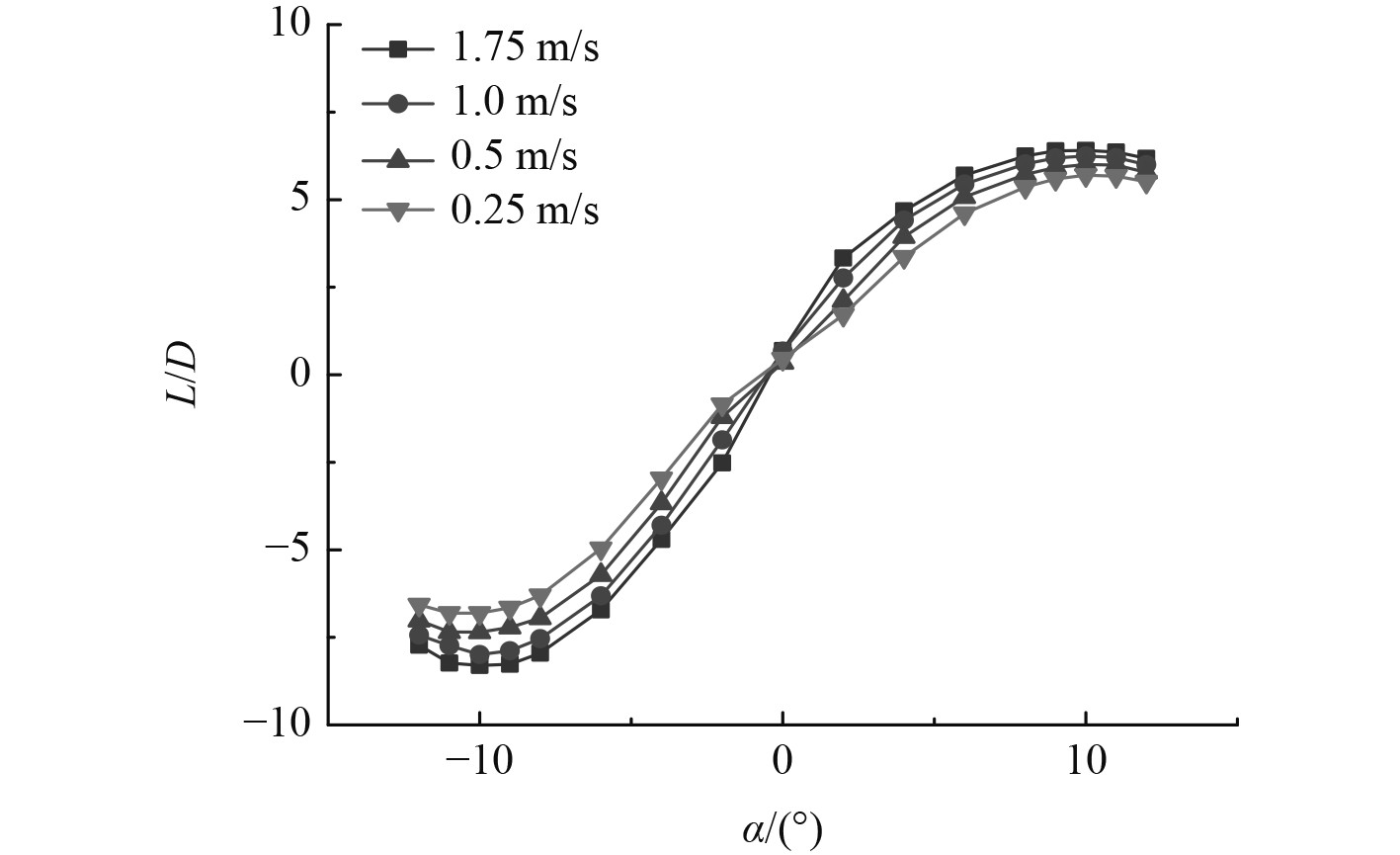
3.1 不同攻角下的升阻比变化特性将各个计算工况数值模拟结果通过运算,汇总可得仿生机器蟹滑翔状态下升阻比变化情况,如图7所示。
|
图 7 升阻比曲线 Fig. 7 Lift-drag ratio curve |
仿生机器蟹滑翔状态下攻角的不断改变导致其升阻比有相应的变化。当仿生机器蟹的升阻比达到最大时,此时攻角为最优攻角,因仿生机器蟹并不完全对称,上升和下潜状态下应各存在一个最优攻角。上升状态下,从直航状态(攻角为0°)开始,仿生机器蟹的升阻比先增大后减小,下潜状态相同,由图可知,上升和下潜状态下最优攻角均为10°。
3.2 水动力参数在研究水下滑翔机水动力性能中,为便于在不同条件下易于分析对比,通常将升阻力无量纲化。所得到的升力系数与阻力系数在仿生机器蟹的设计中起着及其重要的作用。汇总数值模拟结果如表2 所示。其中,各系数定义如下:
|
|
表 2 各系数计算结果 Tab.2 Calculation results of each coefficient |
| $ {升力系数}{C_L} = \dfrac{L}{{\dfrac{1}{2}\rho {V^2}S}},$ | (1) |
| $ {阻力系数}{C_D} = \dfrac{D}{{\dfrac{1}{2}\rho {V^2}S}},$ | (2) |
| $ {压差阻力系数}{C_f} = \dfrac{{{R_f}}}{{\dfrac{1}{2}\rho {V^2}S}} ,$ | (3) |
| ${ 粘性阻力系数}{C_p} = \dfrac{{{R_p}}}{{\dfrac{1}{2}\rho {V^2}S}} ,$ | (4) |
| $ {俯仰力矩系数} {C_m} = \dfrac{{{M_y}}}{{\dfrac{1}{2}\rho {V^2}Sl}} 。$ | (5) |
式中:
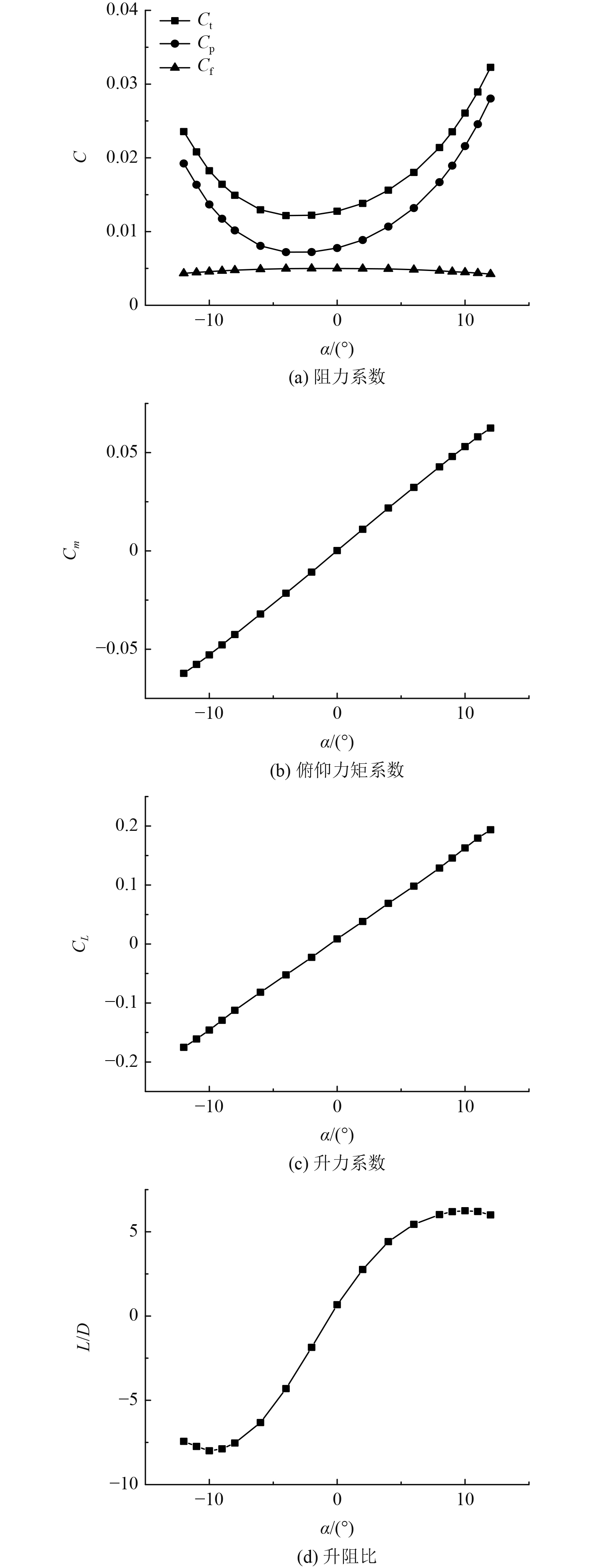
将表中数据绘制成曲线图,如图8所示。图中X坐标均为攻角,可知:
|
图 8 各系数曲线图 Fig. 8 Graph of each coefficient |
1)阻力系数与攻角呈二次函数关系,升力系数和俯仰力矩系数与攻角呈一次函数关系。三者随攻角变化影响较大。
2)阻力随攻角增加而增加,其中攻角对仿生机器蟹压差阻力影响较大,对粘性阻力攻角影响较小,证明仿生机器蟹初始外形较好。
3)将上升和下潜状态分开研究,均与攻角呈二次函数关系,因上升和下潜状态下均存最优攻角,使仿生机器蟹升阻比达到最大。升阻比会先增加后减小。通常水下滑翔机会选取最优攻角以确保其有良好的滑翔性能。由图可知,仿生机器蟹最优攻角为±10°。
4)存在一个临界攻角,在速度相同情况下,在未达到临界攻角前,回复力矩随攻角增加二增加,其滑翔较为稳定。在攻角相同情况下,升力与回复力矩随速度增加而增加,但速度对升阻比影响较小。
小攻角情况下,升力和俯仰力矩与攻角之间近似为线性关系、阻力与攻角之间近似为二次函数关系,存在以下关系:
| $ D = {C_D}\frac{1}{2}\rho {V^2}S \approx \left( {{K_{D0}} + {K_D}{\alpha ^2}} \right){V^2},$ |
| $ L = {C_L}\frac{1}{2}\rho {V^2}S \approx \left( {{K_{L0}} + {K_L}\alpha } \right){V^2},$ |
| $ M = {C_M}\frac{1}{2}\rho {V^2}S \approx \left( {{K_{M0}} + {K_M}\alpha } \right){V^2} 。$ |
式中:V为滑翔机的速度;
通过数值模拟仿真,可分别得到仿生机器蟹在x轴、y轴受到的力以及绕y轴的力矩。根据力的矢量分解,将仿生机器蟹受到x轴和y轴的力分解,可得到仿生机器蟹受到的阻力和升力。利用最小二乘法拟合可得水动力参数,如表3所示。
|
|
表 3 水动力参数 Tab.3 Hydrodynamic parameters |
为得到其压力中心点位置,通过分析仿生机器蟹压力场,了解其压力分布情况,为进一步外形优化设计做准备。由于计算工况较多,分析直航状态下( 0°攻角),不同速度的压力场,如图9 所示。

|
图 9 仿生机器蟹压力云图 Fig. 9 Pressure cloud image of bionic robotic crab |
仿生机器蟹机翼与尾翼采用NACA对称翼型,故仿生机器蟹的粘性阻力较小。
因仿生机器蟹是直航运动(攻角为0°),首部直接受力,仿生机器蟹主体与足尖的前部为高压区,压力随着航速的增加而增加。
仿生机器蟹压力从首至尾逐步减小,因直航运动,故首部为高压区,尾部为低压区,从而产生压差阻力。速度增加,首尾部的压强差上升,首尾部压力差距将会进一步增加,压差阻力增加。
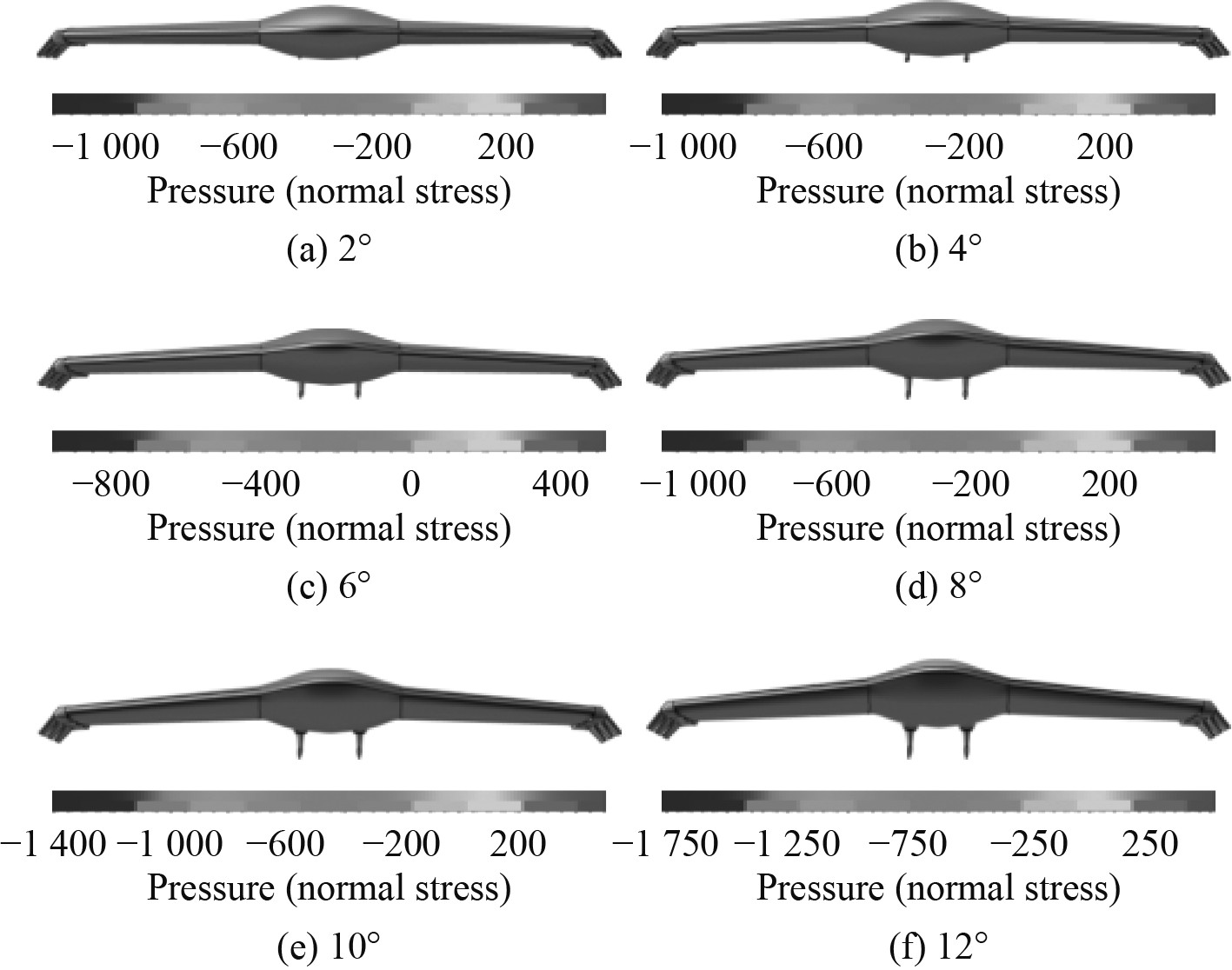
为了解不同攻角下压力场规律,分析仿生机器蟹在设计航速下,上浮状态2°~12°、间隔2°攻角下的压力云图,如图10所示。
|
图 10 仿生机器蟹不同攻角下的压力云图 Fig. 10 Pressure cloud image of bionic robotic crab at different angles of attack |
以仿生机器蟹的上浮工作为例,设计航速下,随着攻角的增加,仿生机器蟹高压区开始下移。由于上下面的压力差距变大,仿生机器蟹的升力在不断增大。
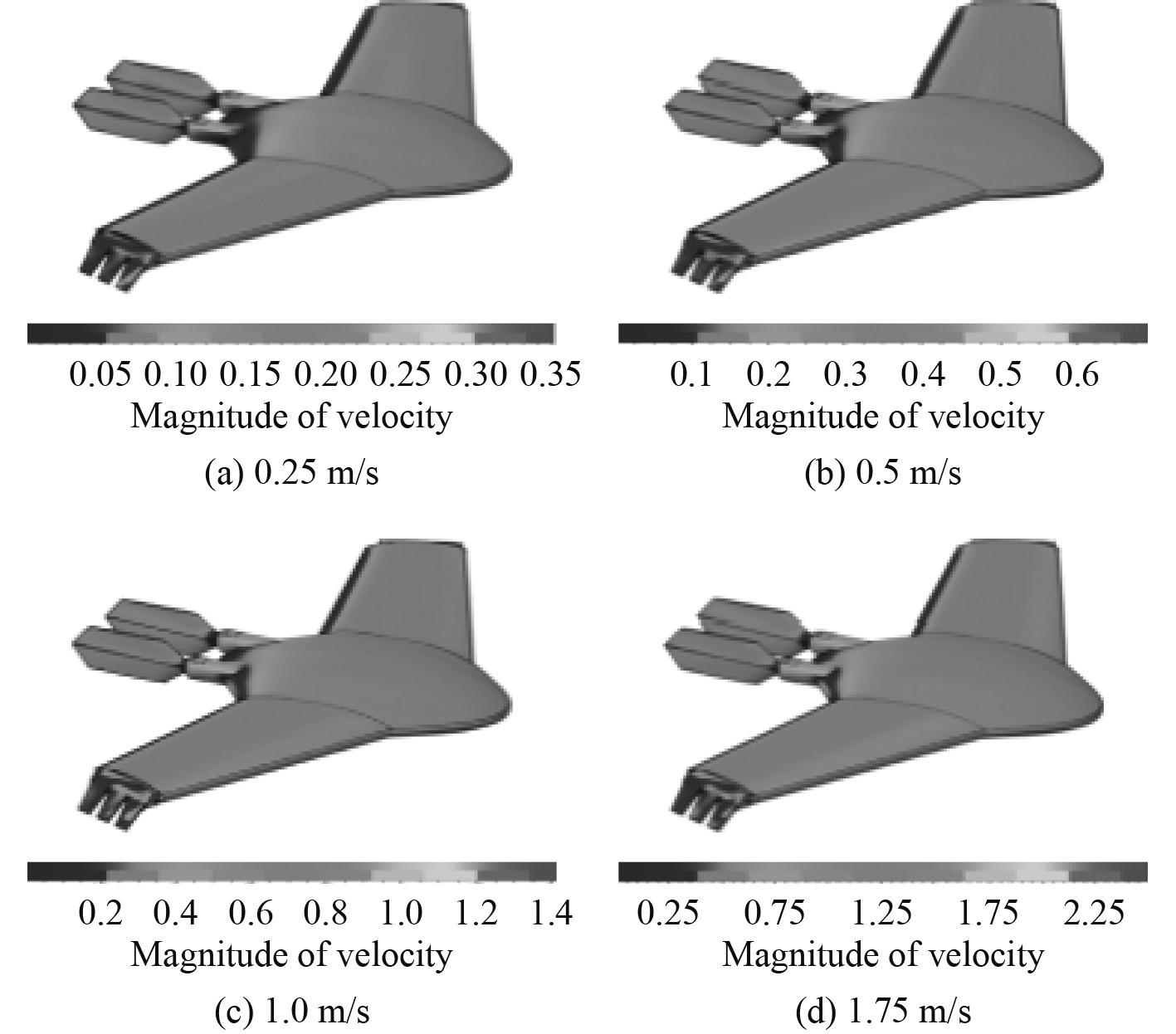
3.4 速度场分布与分析通过观察仿生机器蟹的速度场,直观了解其表面流线的分布情况以及表面流体流动情况。计算工况多,故只分析仿生机器蟹在直航状态(0°攻角)各速度下的速度场。图11和图12分别为各速度下的速度云图以及足尖截面处的速度流线图。
|
图 11 速度云图 Fig. 11 Velocity cloud map |

|
图 12 足尖速度流线图 Fig. 12 Tip velocity flow diagram |
由图12可知,在直航状态下,在仿生机器蟹首部为高速区,尾部为低速区,因首尾部压力不同,导致流速不同。
从速度流线图可得,因足尖处为复杂附体结构,其首部处压力较大,导致足尖处也形成高流速区。
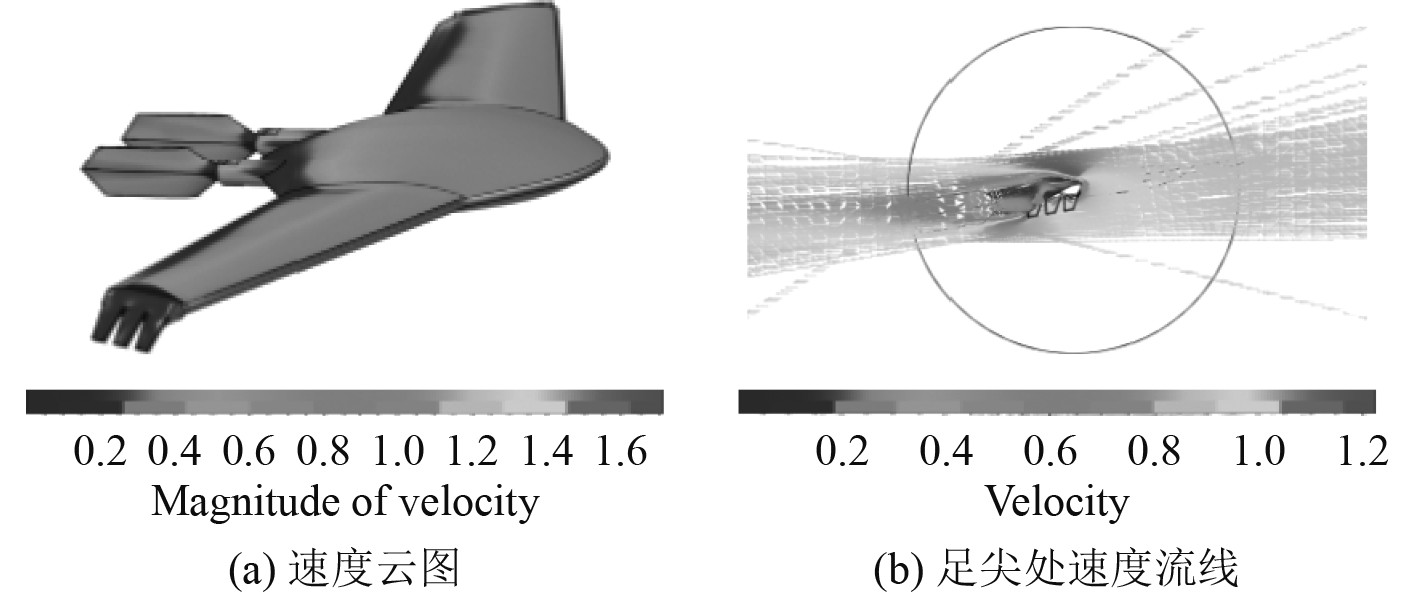
分析在设计航速下,上浮工作状态仿生机器蟹10°攻角下的速度场(见图13)。
|
图 13 10°攻角速度场 Fig. 13 10° angular velocity field of attack |
设计航速下,对比10°攻角与0°攻角足尖处速度流线可得,足尖区域的流速随攻角增加在变化,高流速区前移,低流速区面积增加。足尖形状的存在影响了流线,足尖处后出现较乱的流线。可知复杂附体对仿生机器蟹水动力性能影响很大。
设计航速下,对比10°攻角与0°攻角足尖处速度云图可得,通过增加攻角的大小,会使仿生机器蟹前部高速区面积不断扩大,且尾部低流速区逐渐前移。
3.5 涡量场分布与分析为了解涡量场的分布情况对仿生机器蟹阻力的影响,需找出主要的扰流区所处位置。为后续优化提供基础,如图14所示。

|
图 14 仿生机器蟹涡量场 Fig. 14 Bionic robotic crab vortex field |
选取设计航速下仿生机器蟹涡量场,通过观察最优攻角下仿生机器蟹表面涡的分布情况,分析仿生机器蟹涡量图。从图14可看出,仿生机器蟹主体采用NACA对称翼型,因此仿生机器蟹表面没有明显漩涡,具有良好的水动力性能。但因为足尖的不规则性,使得仿生机器蟹足尖处有较大的漩涡,导致其成为高压区、高流速区,导致仿生机器蟹的阻力较大。
4 结 语基于粘流理论开展计及复杂附体结构的仿生机器蟹的水动力特性研究,对复杂附体结构水动力性能进行分析。首先对仿生机器蟹滑翔状态进行受力分析,得到各个参数之间的关系。通过对比“海鸥一号”数值结果与试验结果,进行数值方法标定。分析仿生机器蟹水下的运动状态,建立数值仿真模型,确定仿生机器蟹计算方案。通过计算仿生机器蟹在不同航速及攻角的水动力性能,对比不同攻角下的升阻比,得出仿生机器蟹在上浮与下潜状态的最优滑翔攻角均为10°;计算不同攻角下仿生机器蟹水动力性能,分析不同攻角下压力场、速度场和涡量场,其中足尖等复杂附体对仿生机器蟹水动力性能影响较大,但机身和尾翼配合NACA翼型水动力性能较好,为进一步翼身融合外形参数化建模和低阻力外形优化提供参考。
| [1] |
刘雁集, 杨勇, 张桂臣. 水下滑翔机及其应用技术发展[J]. 船舶工程, 2021, 43(9): 14-21. |
| [2] |
李永成, 马峥, 王小庆. 水下滑翔机高效滑翔水动力性能研究[J]. 中国造船, 2020, 61(4): 52−59. LI Yong-xing, MA Zheng, WANG Xiao-qing. Hydrodynamic performance of autonomous underwater glider with high efficiency[J]. Shipbuilding of China, 2020,6 1(4): 52−59. |
| [3] |
李志伟, 崔维成. 水下滑翔机水动力外形研究综述[J]. 船舶力学, 2012, 16(7): 829−837. LI Zhi-wei, CUI Weicheng. Overview on the hydrodynamic performance of underwater gliders[J]. Journal of Ship Mechanics, 2012, 16(7): 829−837. |
| [4] |
王刚, 张立勋, 王立权. 八足仿蟹机器人步态规划方法[J]. 哈尔滨工程大学学报, 2011, 32(4): 486-491. DOI:10.3969/j.issn.1006-7043.2011.04.016 |
| [5] |
王立权, 王海龙, 陈曦, 等. 八足仿蟹机器人行走稳定性分析[J]. 中南大学学报(自然科学版), 2014, 45(10): 3416-3422. |
| [6] |
孔维翔, 凌宏杰, 王志东, 等. 仿蟹滑翔机器人水动力外形优化设计[J]. 船舶工程, 2021, 43(1): 131−137. KONG Wei-xiang, LING Hong-jie, WANG Zhi-dong, et al. Hydrodynamics and Shape Optimization Design of Crab-Like Glider Robot[J]. Ship Engineering, 2021, 43(1): 131−137. |
| [7] |
张士鹤. 水下滑翔机航向控制研究[D]. 天津: 天津大学, 2020.
|
| [8] |
陈晖. 温差能水下滑翔机试验系统研究与滑翔机外形设计[D]. 上海: 上海交通大学, 2012.
|
 2024, Vol. 46
2024, Vol. 46
