0 引　言

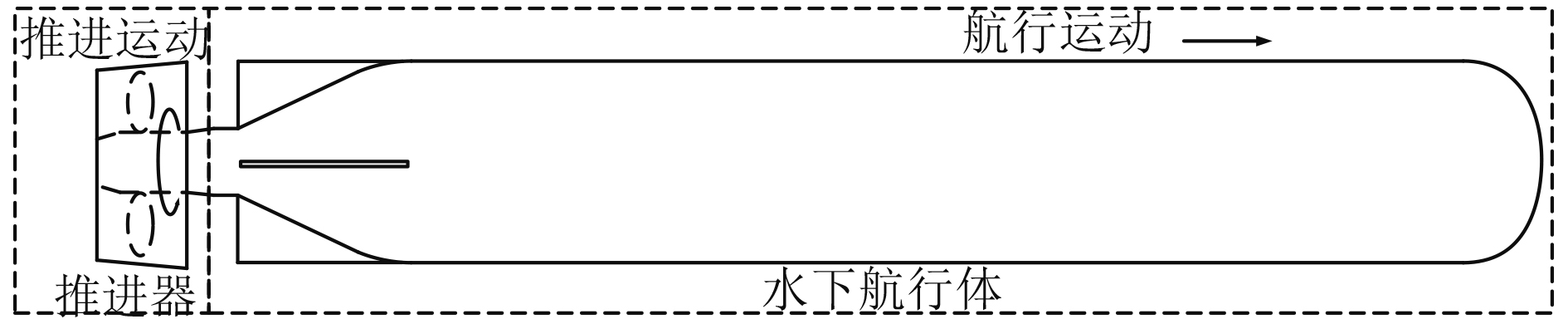
水下航行推进系统是指同时执行航行运动和推进运动的水下有人/无人系统，用于执行水下搜索、运载、探测等任务，一般包括水下航行体和推进器两部分，水下航行体的航行过程和推进器螺旋桨的旋转过程之间存在耦合作用，如图1所示。水动力是水下航行推进系统总体设计过程的重要参数，目前针对水下系统的水动力特性研究主要有试验方法、面源法、计算流体力学方法等，国内学者围绕水下航行体的水动力特性以及推进器的推力特性开展了诸多研究工作。郭魁俊^[1]采用$ k - \varepsilon $模型针对美国“曼塔”水下航行器不同运动状态下的水动力系数进行了数值仿真。吴志聪^[2]研究了推进器相对于航行器主体的不同装配位置对流体动力干扰的作用。高婷等^[3]提出了一种空间拘束运动模拟方法，提升了求取水下航行器的水动力系数的效率。李阳等^[4]基于Standard $ k - \varepsilon $湍流模型分析了仿生翼水下航行器直航运动时水动力性能。顾欣星^[5]采用动网格和滑移网格方法对全向直翼推进器在不同进速系数下的水动力性能进行了数值模拟。王培生^[6]通过编写Fortran程序建立了全回转推进器定常和非定常水动力性能的数值模型。鹿麟^[7]基于MRF模型研究了泵喷推进器的推进效能。

水下航行推进系统在执行任务的过程中，其各部分绕流流场相互干扰，而现有研究普遍是将水下航行体和推进器的水动力分开计算，将其当作一个相互耦合系统的研究较少。为此，针对单独推进器和水下航行推进系统，分别建立水动力计算的流场数学模型，对4组不同转速下的推力、扭矩进行数值计算，并进一步分析了水下航行体对推进器推进效能的影响，获取了推力减额分数。

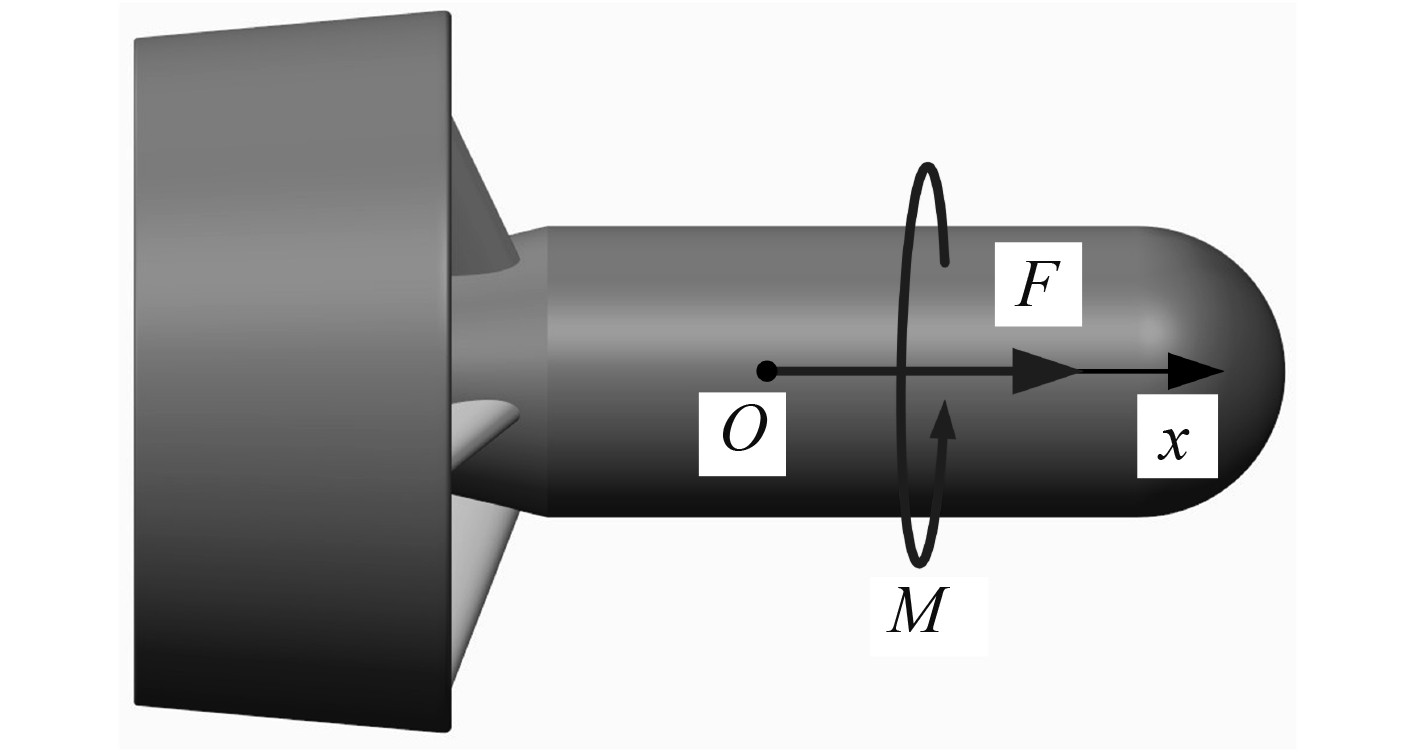
1 流场数学模型 1.1 水动力性能参数定义

为准确描述水下航行推进系统的水动力性能，以推进器的浮心为原点建立了参考坐标系$ Ox $，$ Ox $轴指向水下航行推进系统前方，如图2所示。

通常地，水下航行推进系统的水动力性能参数包括推力系数、扭矩系数及推进效率。当水下航行推进系统以固定航速向前航行且螺旋桨以固定转速旋转时，将水下航行推进系统所受到的沿$ Ox $轴正向的流体动力定义为推力$ T $，将螺旋桨产生的绕$ Ox $轴旋转并指向$ Ox $轴正向的流体动力矩定义为扭矩$ Q $，分别对推力和扭矩无量纲化，即可得到推力系数$ {K_T} $、扭矩系数$ {K_Q} $以及推进效率$ \eta $的表达式^{[7 − 9]}：

$ {K_T} = \frac{T}{{\rho {n^2}{D^4}}} \text{，}$

(1)

$ {K_Q} = \frac{Q}{{\rho {n^2}{D^5}}} \text{，}$

(2)

$ \eta = \frac{J}{{2{\text{π}} }}\frac{{{K_T}}}{{\left| {{K_Q}} \right|}} \text{。}$

(3)

式中：$ n $为螺旋桨转速，r/s；$ D $为螺旋桨直径，m；$ \rho $为流体介质密度；$ J $为进速比，$ J = {v_\infty }/nD $；$ {v_\infty } $为水下航行推进系统的航速，m/s。

1.2 控制方程

水下航行推进系统所处的流体环境为恒温下的不可压缩流体，遵循质量守恒、动量守恒定律，采用连续方程和动量守恒方程（Navier-Stokes方程，NS方程）其流域内的湍流流动进行控制。

质量守恒方程：

$ {\mathrm{div}}({\boldsymbol{U}}) = 0\text{，} $

(4)

动量守恒方程：

$ \left\{ \begin{gathered} \frac{{\partial (u)}}{{\partial t}} + {\mathrm{div}}(u{\boldsymbol{U}}) = \frac{\mu }{\rho }{\mathrm{div}}({\mathrm{grad}}(u)) - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + {f_x} \text{，} \\ \frac{{\partial (v)}}{{\partial t}} + {\mathrm{div}}(v{\boldsymbol{U}}) = \frac{\mu }{\rho }{\mathrm{div}}({\mathrm{grad}}(v)) - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + {f_y}\text{，} \\ \frac{{\partial (w)}}{{\partial t}} + {\mathrm{div}}(w{\boldsymbol{U}}) = \frac{\mu }{\rho }{\mathrm{div}}({\mathrm{grad}}(w)) - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + {f_z}\text{。} \\ \end{gathered} \right. $

(5)

式中：$ {\mathrm{div}}() = \partial {()_x}/\partial x + \partial {()_y}/\partial y + \partial {()_z}/\partial z $；$ {\mathrm{grad}}() = \partial ()/ \partial x + \partial ()/\partial y + \partial ()/\partial z $；$ {\boldsymbol{U}} $为速度矢量，$ u $、$ v $、$ w $分别为$ {\boldsymbol{U}} $在$ x $、$ y $、$ z $方向的分量；$ \rho $为流体密度；$ t $为时间；$ \mu $为流体动力粘度；$ p $为流体微元体上的应力；$ {f_x} $、$ {f_y} $、$ {f_z} $为微元体上的体力。

1.3 湍流方程

湍流模型选用SST $ k - \omega $模型，该模型兼具了$ k - \omega $模型和$ k - \varepsilon $模型的优点，既能适用于近壁面和远场的计算，而且考虑了湍流剪切应力输运方程，具有较强的适用性。

湍流强度$ k $方程为：

$ \frac{{\partial (\rho k)}}{{\partial t}} + \nabla \cdot (\rho {\boldsymbol{U}}k) = \nabla \cdot \left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}\nabla k} \right)} \right] + {P_k} - \beta '\rho k\omega \text{，}$

(6)

湍流频率$ \omega $方程为：

$ \frac{{\partial (\rho \omega )}}{{\partial t}} + \nabla \cdot (\rho {\boldsymbol{U}}\omega ) = \nabla \cdot \left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\omega }}}\nabla \omega } \right)} \right] + \alpha \frac{\omega }{k}{P_k} - \beta \rho {\omega ^2} \text{。}$

(7)

式中：$ {P_k} = {\mu _t}\left\{ 2\left[ {{{\left( {\dfrac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\dfrac{{\partial u}}{{\partial y}}} \right)}^2} + {{\left( {\dfrac{{\partial u}}{{\partial z}}} \right)}^2}} \right] + {{\left( {\dfrac{{\partial u}}{{\partial y}} + \dfrac{{\partial v}}{{\partial x}}} \right)}^2} + \left( \dfrac{{\partial u}}{{\partial z}} + \dfrac{{\partial w}}{{\partial x}} \right)^2 + {{\left( {\dfrac{{\partial v}}{{\partial z}} + \dfrac{{\partial w}}{{\partial y}}} \right)}^2} \right\} $；$ {\mu _t} $为$ k $和$ \omega $的函数，$ {\mu _t} = \rho k/\omega $；$ {\sigma _k} = 2.0 $，$ {\sigma _\omega } = 2.0 $，$ \alpha = 5/9 $，$ \beta = 0.075 $，$ \beta ' = 0.09 $。

1.4 推进器流场数学模型

水下航行推进系统中采用的推进器为导管螺旋桨构型，有3个螺旋桨叶片和5个支撑架，螺旋桨外侧有导流罩。采用计算流体力学方法对推进器流体动力性能进行仿真，建立推进器的流场仿真数学模型。推进器工作时转子部分做高速旋转运动，定子部分（导管、支撑架等非旋转部分）处于静止状态。滑移网格具有较快的计算效率和不错的精度，适用于模拟转动问题，为了精确模拟工作条件下转/定子流场相互干扰问题，采用滑移网格方法模拟推进器转子的旋转。为此，基于多域网格方法将整个计算域划分为两部分：转子域和外流域，转子域和外流域的外边界均为圆柱体，如图3所示。其中，转子域为旋转域，外流域属于静止域。转子域由螺旋桨叶片和转子轮毂组成，其余部分则构成外流域。

设定入口处的边界条件为速度入口，推进器定子表面处的边界条件为无滑移壁面，推进器转子表面处的边界条件为滑移壁面，圆柱形外流域的边界条件为剪切应力壁面，出口处的边界条件为压力出口，圆柱形转子域边界条件为交界面（interface面）。

对上述推进器流场计算域进行结构网格划分，推进器表面的网格如图4所示。为提升网格质量并减低网格数量，对推进器不同的组件设置的网格尺寸，在细小特征尺寸处进行网格加密，同时在推进器壁面附近划分边界层网格，从而可以更精确地捕获推进器壁面附近流体的流动特征。

采用Fluent软件进行数值求解，为了提高计算准确度，求解器采用双精度模式；动量方程、湍动能和耗散率采用二阶迎风格式进行离散；压力离散格式采用Standard格式；湍流模型使用SST $ k - \omega $；压力与速度耦合的求解方法采用SIMPLEC算法；残差收敛标准设置为10⁻⁶；流体介质设置为20℃的不可压缩海水，其密度为1024 kg/m³，动力粘性系数0.0010797 kg/(ms)，航行速度为3 kn（1.542 m/s），仿真计算不同螺旋桨转速下推进器的推力和扭矩。

1.5 水下航行推进系统流场数学模型

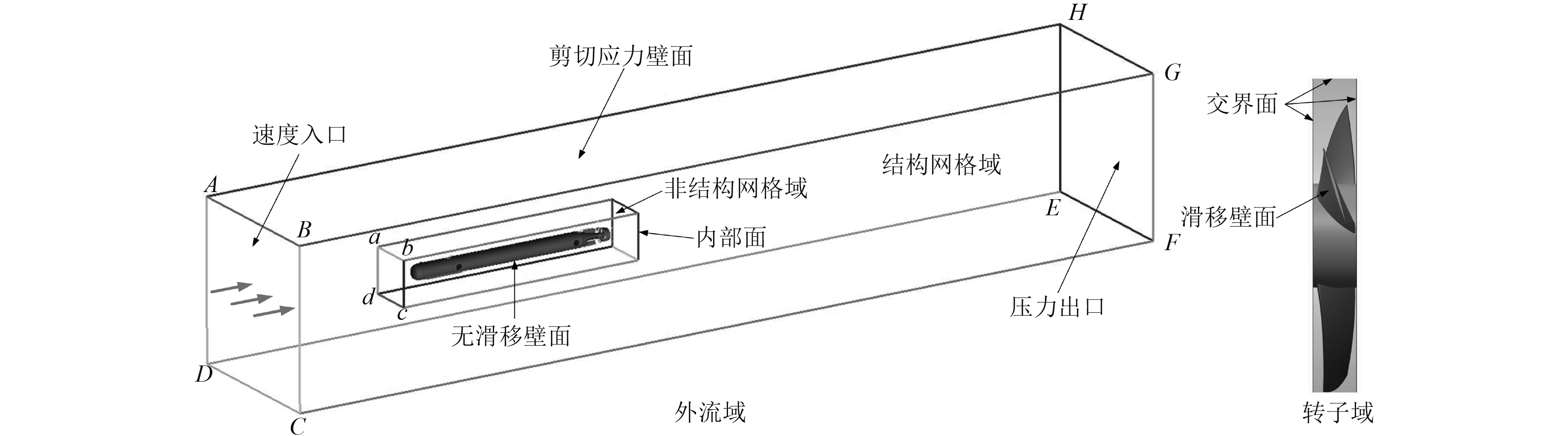
和推进器的流场数学模型类似，采用多域网格方法将水下航行推进系统的流场计算域划分为两部分：转子域和外流域，转子域为旋转域，外流域属于静止域，并进一步采用滑移网格方法模拟转子域的转动。转子域由螺旋桨叶片和转子轮毂组成，其余部分则构成外流域。转子域的外边界为圆柱体，外流域的外边界为长方体，内流域和外流域之间通过交界面（interface面）进行流场数据交互。为了减小网格数量，提高计算效率，采用混合网格技术进一步地将外流域划分为结构网格域和非结构网格域，在水下航行体周围取一小长方体形计算域，在该流域内划分非结构网格，在小长方体计算域和大长方体计算域之间划分结构网格，并使结构网格和非结构网格连接处的网格节点对齐，使用内部面（interior面）进行混合网格边界处的流场数据交互，如图5所示。

设定入口面ABCD处的边界条件为速度入口，水下航行推进系统表面处的边界条件为无滑移壁面，外流域面ABGH、BCFG、CDEF、ADEH的边界条件为剪切应力壁面，出口面EFGH处的边界条件为压力出口，小长方体6个面的边界条件为内部面，转子域表面为交界面。对航行器不同的组件设置的网格尺寸，在水下航行推进系统细小特征壁面处进行网格加密，同时在壁面附近划分边界层网格，最终所划分的网格如图6所示。求解方法与推进器流场数学模型的一致，分别仿真计算航行速度为3 kn（1.542 m/s），不同螺旋桨转速下水下航行推进系统的推力和扭矩。

2 水动力性能仿真分析 2.1 推进器水动力性能

基于所建立的推进器流场数学模型，对3 kn来流速度、不同转子转速下推进器的推力和扭矩开展数值计算，图7为推进器的螺旋桨推力面和吸力面的压力分布云图，图8为纵平面内推进器周围流场的速度分布云图。

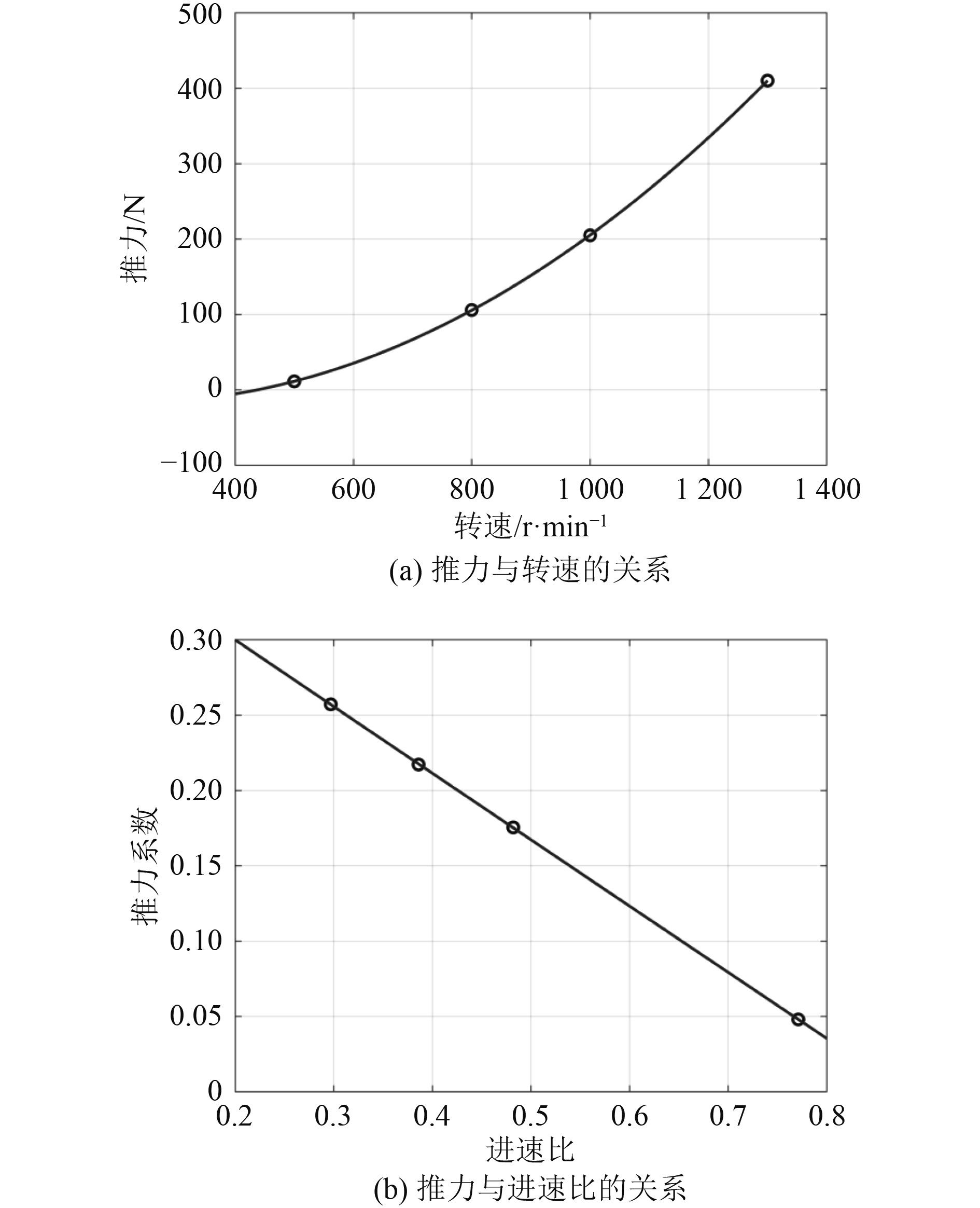
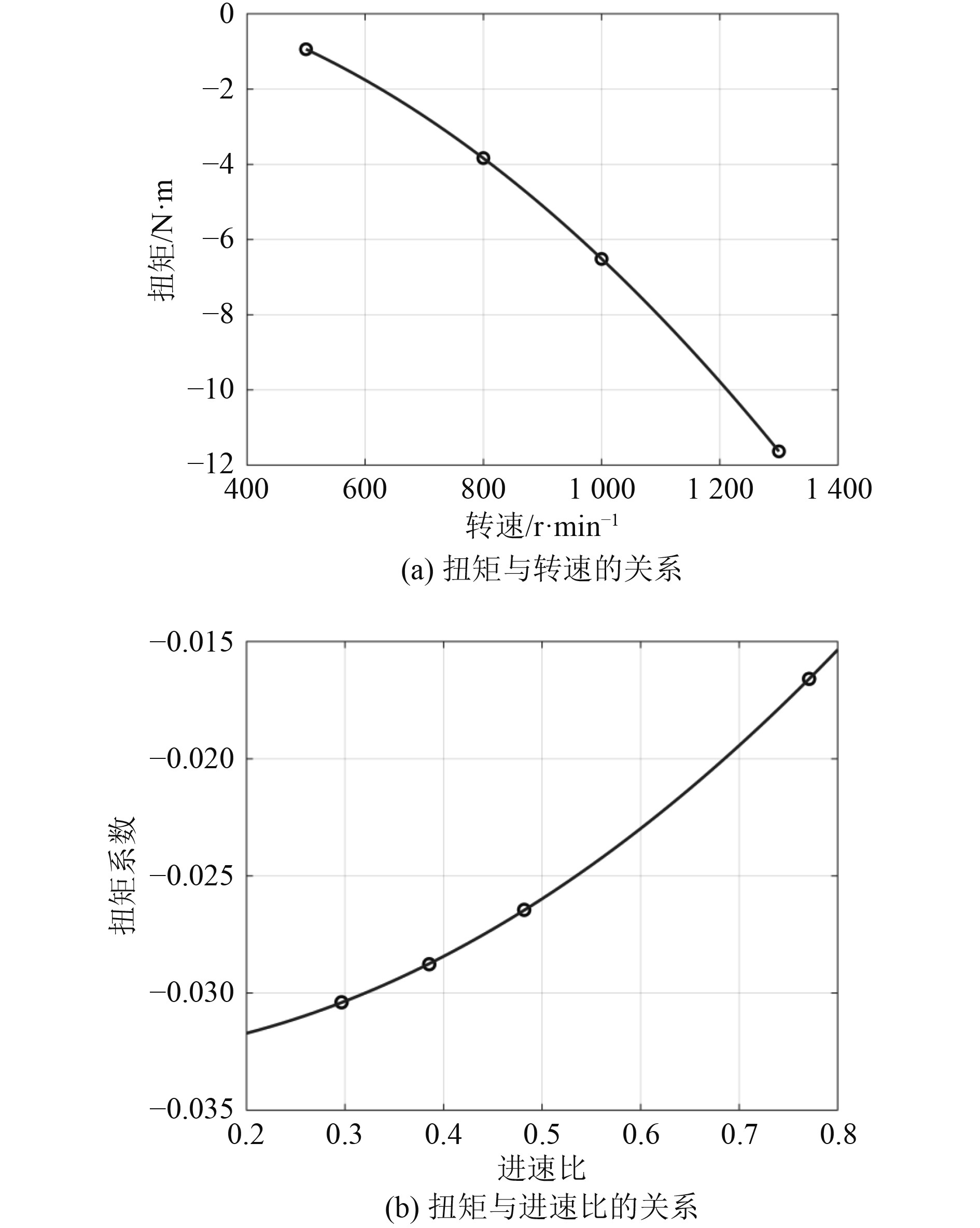
根据推进器水动力数值计算结果，可得3 kn航速下推进器推力的变化曲线，如图9所示。推进器扭矩的变化曲线如图10所示。通过数据拟合，可以得到3 kn航速下推进器水动力性能和转子转速之间的表达式：

$ T = 3.7 \times {10^{ - 4}}{n^2} - 0.16n + 1.7 \text{，} $

(8)

$ {K_T} = 4.2 \times {10^{ - 3}}{J^2} - 0.45J + 0.39\text{，} $

(9)

$ Q = - 7.4 \times {10^{ - 6}}{n^2} - 3.1 \times {10^{ - 5}}n + 0.93\text{，} $

(10)

$ {K_Q} = 0.027{J^2} + 8.8 \times {10^{ - 5}}J - 0.033 \text{。}$

(11)

由图9可知，在3 kn航速下，当推进器转子的转速约为437 r/min（进速比为0.88）时，推进器所受到的推力为0，这表明在此转速下转子产生的推动力与来流产生的流体阻力平衡，推进器能够匀速航行。

由图10可知，在3 kn航速下，当推进器转子的转速约为352 r/min（进速比为1.10）时，推进器所受到的扭矩为0，这表明在此转速下转子产生的扭矩与来流产生的流体动力矩平衡，推进器能够平稳航行。

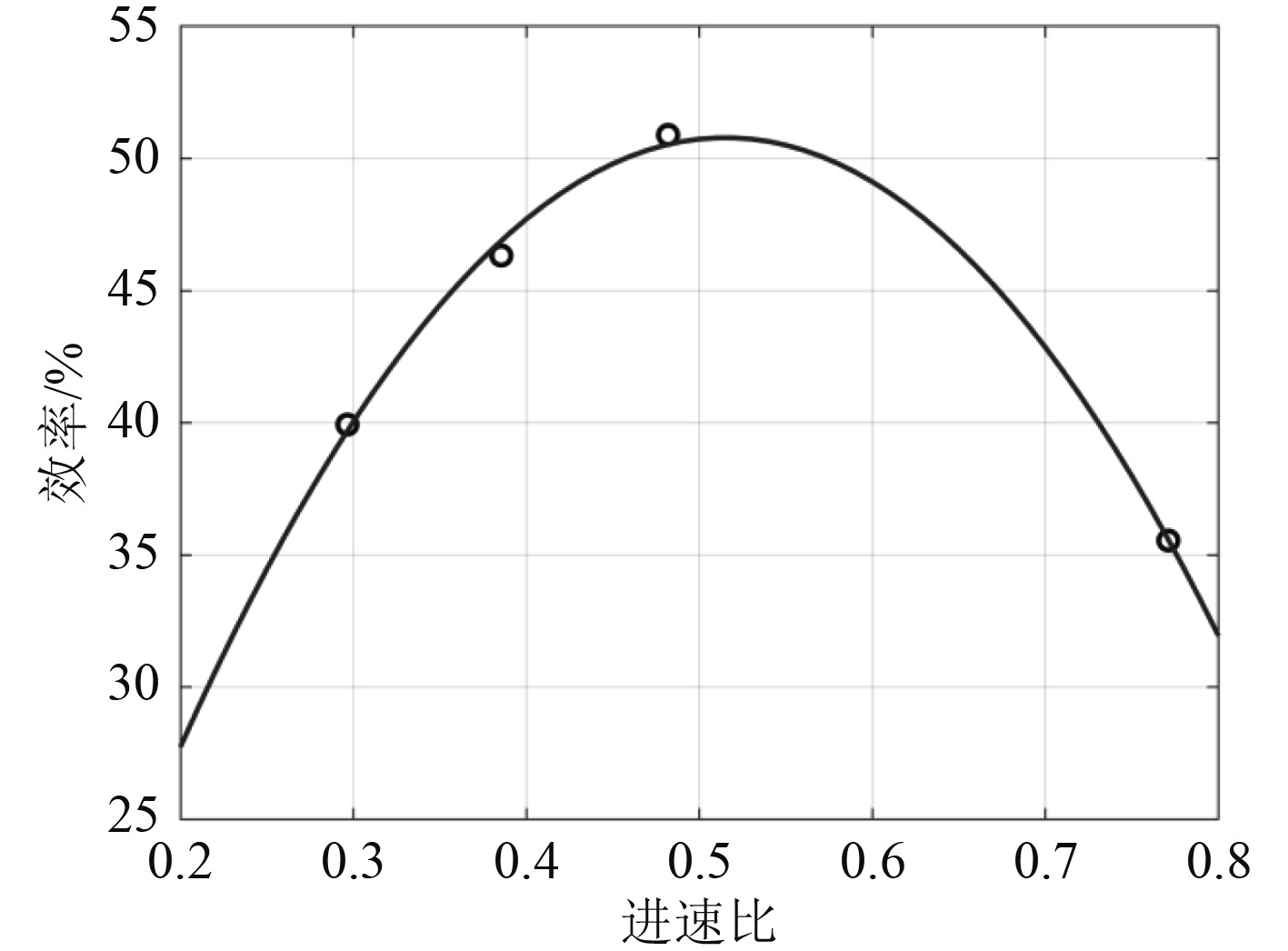
根据式（3）、式（9）和式 （11），可以得到3 kn航速下推进器的推进效率和进速比之间的关系，如图11所示。推进效率随着进速比的增大先增大后减小，当进速比为0.515（转速为749 r/min）时，推进效率最大，为50.79%。

2.2 水下航行推进系统水动力性能

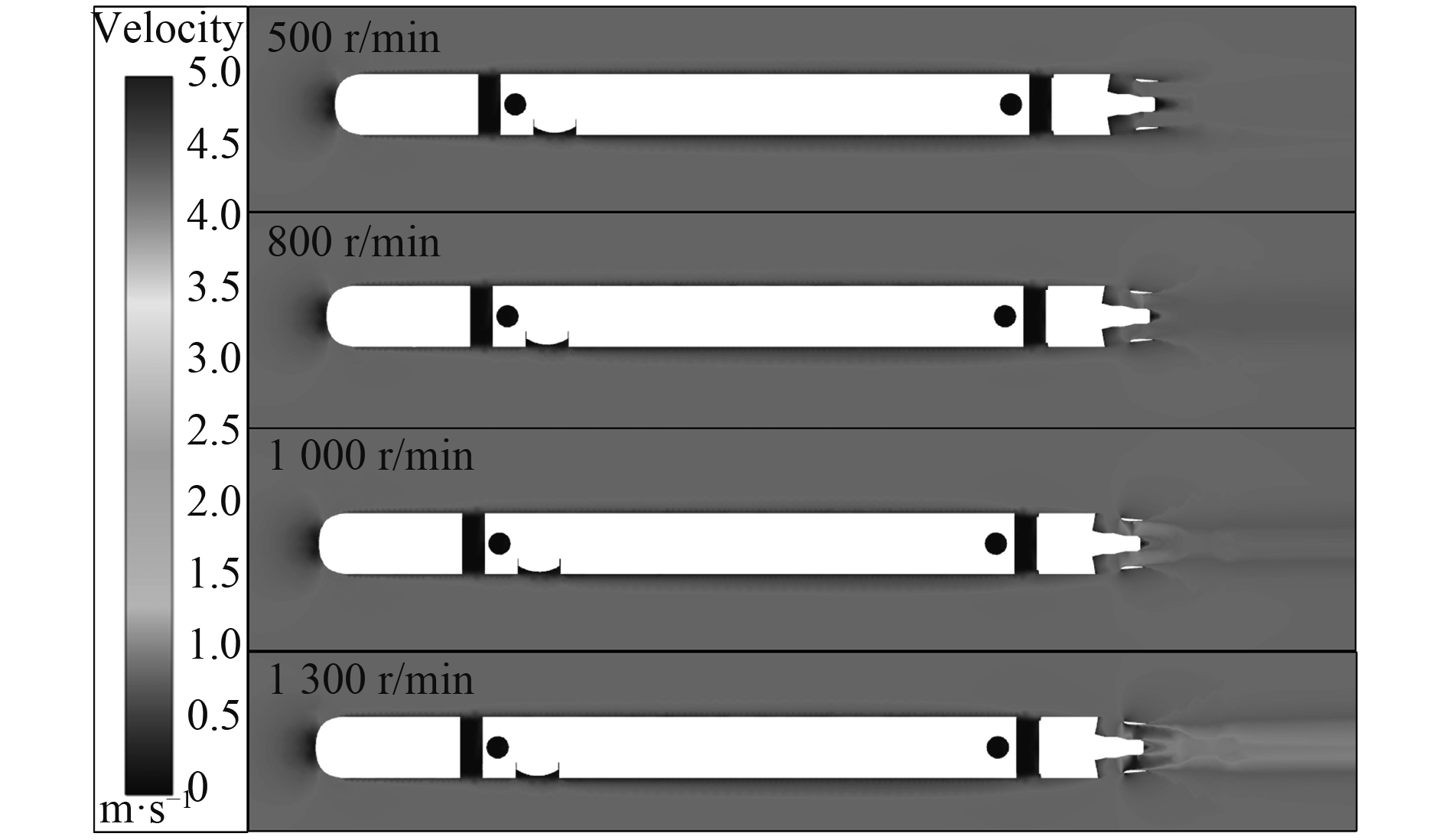
基于所建立的水下航行推进系统流场数学模型，对3 kn来流速度、不同转子转速下考虑水下航行推进系统的推力和扭矩开展数值计算，图12给出了纵平面内水下航行推进系统周围流场的速度分布云图。

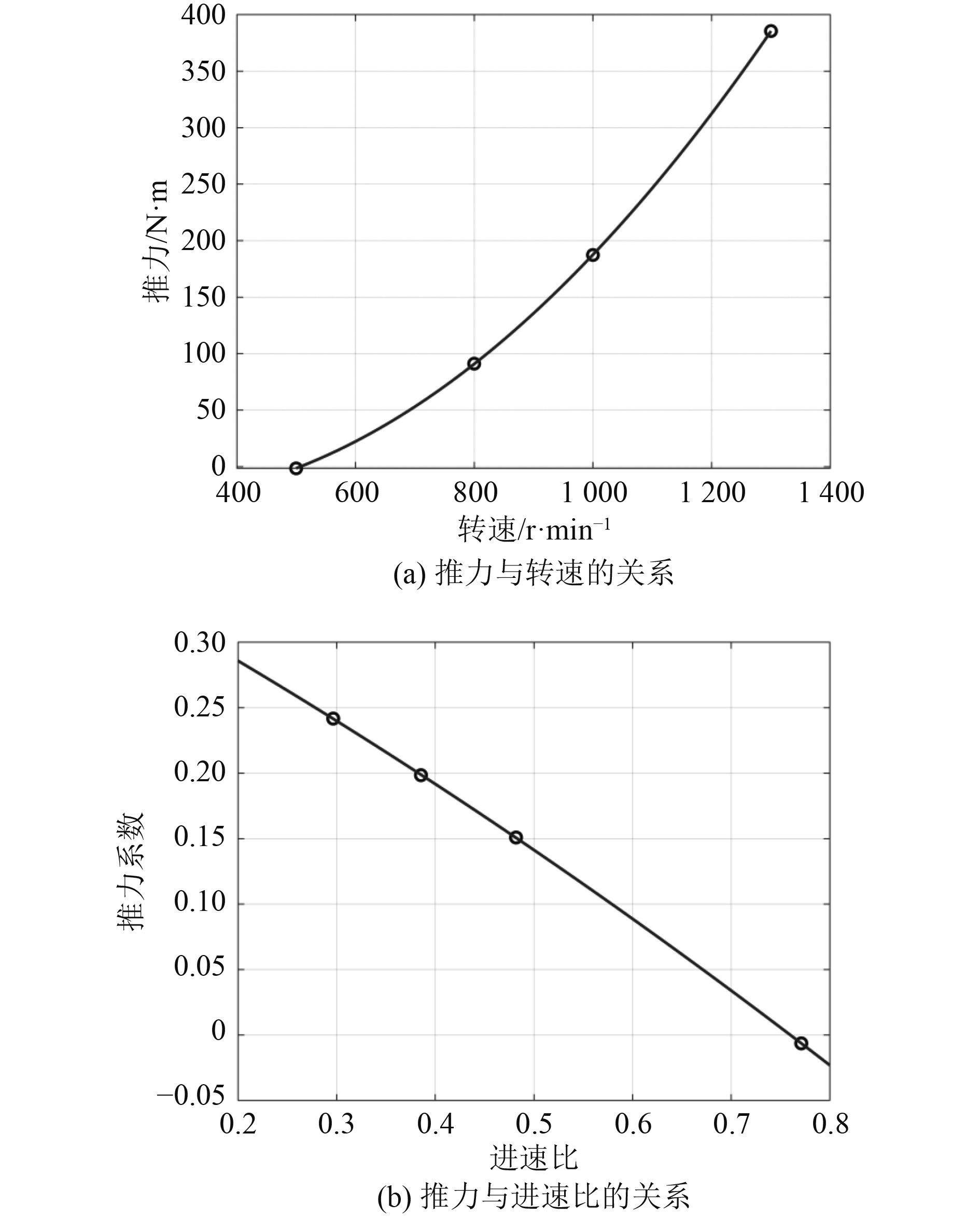
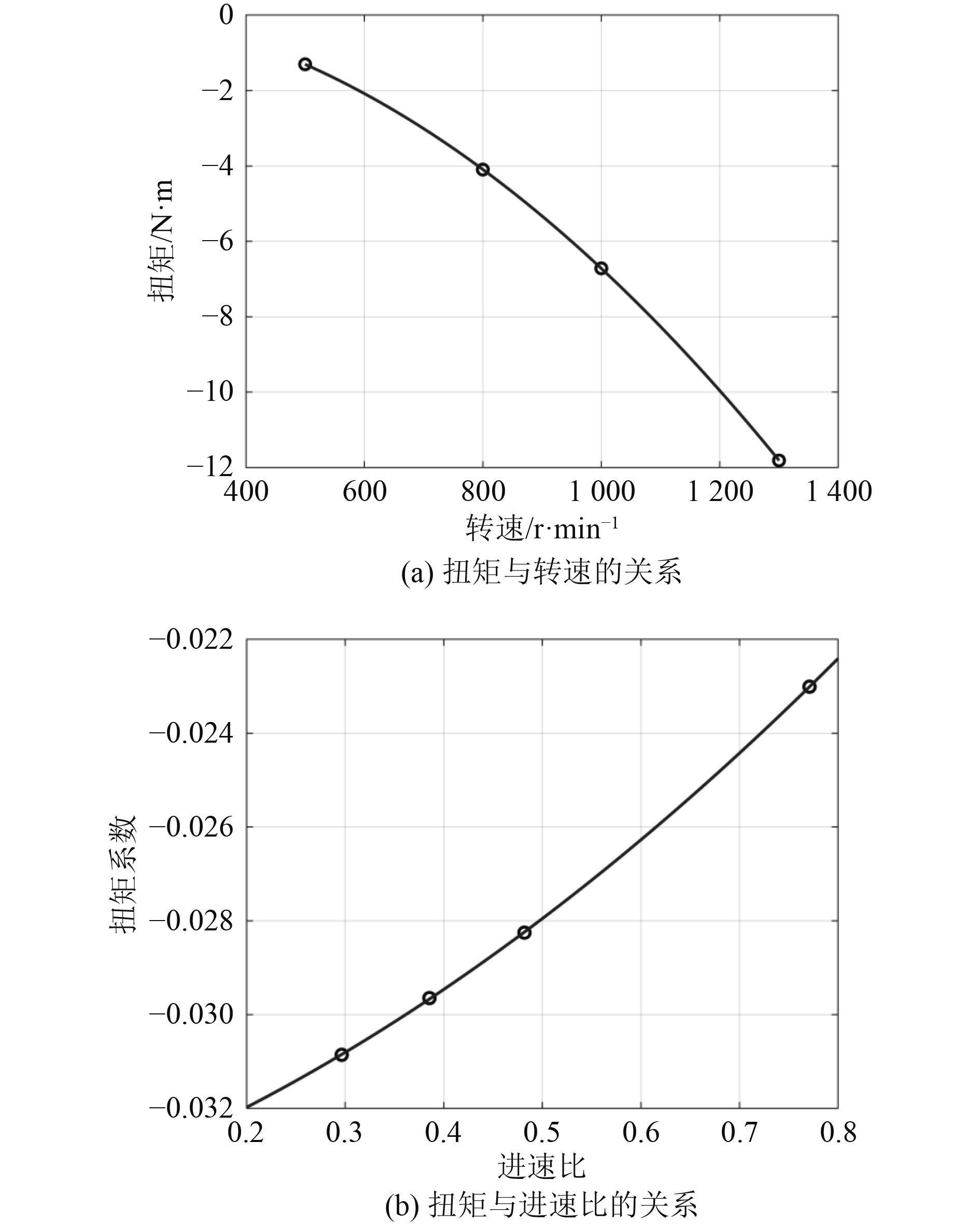
根据水下航行推进系统水动力数值计算结果，可以得到3 kn航速下推进器推力变化曲线如图13所示。水下航行推进系统扭矩变化曲线如图14所示。通过数据拟合，可以得到3 kn航速下水下航行推进系统的水动力性能和转子转速之间的表达式：

$ T = 3.5 \times {10^{ - 4}}{n^2} - 0.149n - 14.52\text{，} $

(12)

$ {K_T} = - 0.11{J^2} - 0.404J + 0.371\text{，} $

(13)

$ Q = - 7.7 \times {10^{ - 6}}{n^2} + 6.9 \times {10^{ - 4}}n + 0.27\text{，} $

(14)

$ {K_Q} = 8.4 \times {10^{ - 3}}{J^2} + 7.5 \times {10^{ - 3}}J - 0.034\text{。} $

(15)

由图13可知，在3 kn航速下，当推进器转子的转速约为507 r/min（进速比为0.76）时，水下航行推进系统所受到的推力为0，表明在此转速下转子产生的推动力与来流产生的流体阻力平衡，推进器能够匀速航行。

由图14可知，在3 kn航速下，当推进器转子的转速约为238 r/min（进速比为1.62）时，水下航行推进系统所受到的扭矩为0，表明在此转速下转子产生的扭矩与来流产生的流体动力矩平衡，推进器能够平稳航行。

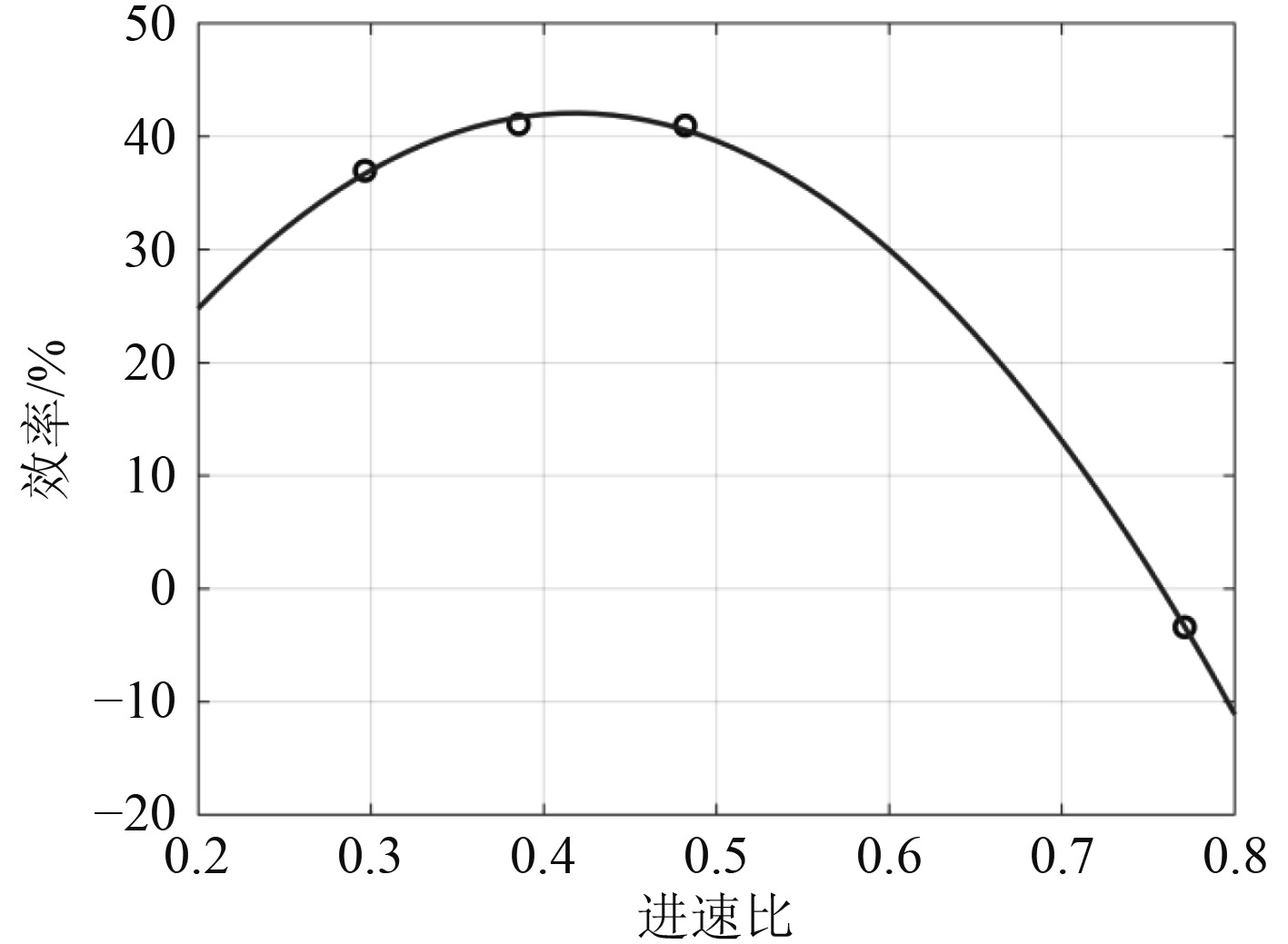
根据式（3）、式（13）和式（15），可以得到水下航行推进系统的推进效率和进速比之间的关系，如图15所示。可知，当进速比为0.418时，推进效率最大，为42.0%，此时对应的转速为922 r/min。

3 水下航行体对推进器水动力的影响 3.1 推力减小量

将水下航行推进系统整体分为航行与推进两大模块，推进模块包含推进器定子和转子，而将除推进器之外的水下航行体外壳、尾鳍、探测设备等其余部分统称为航行模块。通常情况下，推进模块的水动力特征用推力来表征，航行模块的水动力特征用阻力来表征。

当推进器安装在水下航行体上时，由于水下航行体的受到流体阻力的缘故，水下航行推进系统的推力将较单推进器时有所减小。将分析不同航速和转子转速下推进器推力的减小量，为定量分析推力的减小值，定义推力减小系数：

$ {C_{\Delta T}} = \frac{{2\Delta T}}{{\rho {v^2}S}} \text{。}$

(16)

式中：$ \Delta T $为推力减小值；$ v $为水下航行体的航速，m/s；$ \rho $为流体密度；$ S $为水下航行体的特征面积。

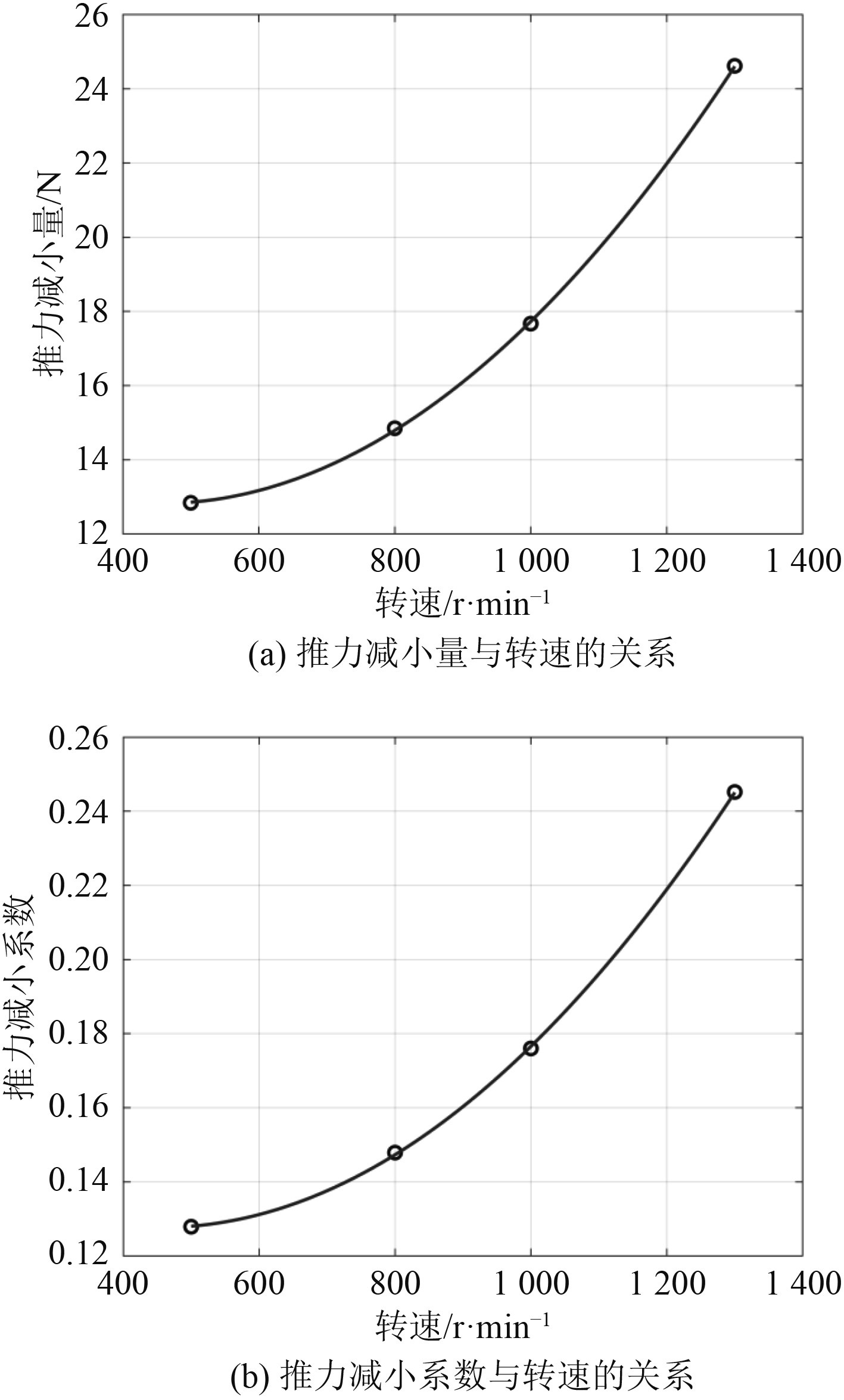
图16给出了3 kn航速时推进器的推力减小量及减小系数和转速的关系。可知，在500~1 300 r/min转速范围内，推力减小量及其推力减小系数均随着转子转速的增大而增大。

通过数据拟合，可以得到考虑航行器的推进器的水动力性能和转子转速之间的表达式如下：

$ \Delta T = 1.6 \times {10^{ - 5}}{n^2} - 0.015n{\text{ + }}16 \text{，}$

(17)

$ {C_{\Delta T}} = 1.6 \times {10^{ - 7}}{n^2} - 1.5e - 4n + 0.16 \text{。}$

(18)

3.2 推力减额分析

在相同的航行速度下，推进器螺旋桨转动时水下航行体的尾部流场与螺旋桨静止时相比明显不同，反映在流体动力上即是螺旋桨转动将使推进模块产生向前的推力，并且对航行模块的阻力产生一定的影响。因此，可用推进器螺旋桨转动前后航行模块的阻力变化来反映推进模块的推进性能变化，即水下航行体对推进器水动力性能的影响。

另外，在3 kn航速下，当推进器转速为0时，航行模块的阻力约为32.35 N，而当推进器转速为507 r/min时，航行模块的阻力约为39.09 N，阻力增大了6.74 N，阻力增大分数为20.84%，这表明如需使水下航行体继续保持3 kn稳定航速，需要推进器模块分额外提供6.74 N的推力来平衡航行模块的阻力增大量，而由于在一定转速下推进器提供的推力是确定的，这意味着推进器的实际可用推力将会减少6.74 N，即推力减额分数为20.84%。

通常情况下，推进器厂家所提供的推力是单指推进器本身的推力，而推进器的推力减额分数则意味着，在实际航行过程中，由于水下航行体的存在，推进器需要提供的推力要比只考虑推进器本身时的推力增大约20.84%，因此在推进器选型时需要考虑至少20.84%的推力裕量。

4 结　语

基于多域网格、滑移网格和混合网格技术，对不同转速时单独推进器和水下航行推进系统的推力、扭矩等水动力参数进行数值计算，得到了以下结论：

1）在3 kn航速情况下，推进器的推力与阻力平衡时螺旋桨转速约为437 r/min，而水下航行推进系统推力与阻力平衡时螺旋桨转速约为507 r/min，增加了80 r/min。推进器扭矩为0时的螺旋桨转速约为352 r/min，而水下航行推进系统扭矩为0时螺旋桨转速约为238 r/min。推进器的最大推进效率为50.79%，而水下航行推进系统的最大推进效率为42%。

2）水下航行推进系统的推力性能与单独推进器的推力性能相比，在3 kn航速情况下、500~1300 r/min转速范围内，其推力减小量及其推力减小系数均随着螺旋桨转速的增大而增大。

3）在水下航行推进系统系统中，由于水下航行体的耦合作用，推进器需要较无水下航行体时额外多提供20.84%的推力，在进行推进器选型时需要考虑这部分推力裕量。