2. 陆军军事交通学院 军事交通运输研究所,天津 300161
2. Institute of Military Transportation, Army Military Transportation University, Tianjin 300161, China
船舶破损会造成舱内大量进水,对船体造成较大危害,从而导致船舶丧失不沉性而发生倾覆沉没。对船体破损处进行及时封堵是提高船舶生命力的主要措施之一,在封堵船体破口过程中,破口水流出流的形态、距离和产生的冲击压强是堵漏作业的重要参考因素。目前,堵漏作业所面临的水流出流特性缺少相关数据支撑,对于船体破损后的水流出流特性研究显得尤为重要。
在国外,Hamid等[1]利用CFD技术模拟了0航速下受损客船在静水和波浪下的运动响应。Zhang等[2]采用改进的运动粒子半隐式方法(MPS)对自由漂浮二维破损船段的泛洪过程进行数值模拟。Josip[3]以船体底部有大破口的油船模型为研究对象,通过仿真和实验的方法研究船体破损时的阻力,研究结果表明由于破口周围的水流改变,总阻力平均显著增加27%。Siddiqui等[4]通过实验利用一个侧部开有矩形口的破船模型研究其在模拟工况中的运动。Hirotada等[5]通过损伤部件的半隐式运动粒子 (Moving Particle Simulation, MPS) 模拟和完好部件的势流理论估算流体的运动方程。通过模型试验和数值模拟的比较,表明所开发的模拟方法能够较好地再现与水淹相关的船舶瞬态行为。Kim等[6]提出一种在时域内对受损船体进行中间浸水和下沉模拟的方法,证实了船体可以根据受损位置保持平衡或下沉,估计了达到平衡的时间或下沉的时间。Cao等[7]采用SPH法对空气影响三维船舶破舱的进水特性进行研究。Lee等[8]在平静的水中进行了完整和破损船舶的自由横摇衰减试验,并测量了完整船舶在规则波中的六自由度运动响应。通过自由横摇衰减试验,研究了浸水对船舶横摇衰减运动的影响,并建立了完整船舶六自由度运动响应数据库,为船舶破损后的运动响应提供了数据支撑。Ruponen等[9]通过理论分析和在退役军舰上进行实船试验的方式研究了破损船舱舱内空气对进水过程的影响,得出了受损船舶破损舱内的空气压缩可以显著延迟浸水过程的结论。
在国内,郑宇等[10]、李月萌等[11]利用CFD技术对客船和箱型舱室的进水过程进行了模拟。卢俊尹[12]基于CFD技术模拟了潜艇破损舱室的进水过程,研究了压强、破口面积对进水速度、进水量的影响。陈振等[13]采用CFD方法研究了在考虑空气可压缩性影响情况下船舶破损舱室进水的动力学问题。孙智超[14]对各种破损舱室进水各个阶段对应的进水速率通过公式进行了理论分析,通过对计算中所选的破损舱室进水过程进行模拟仿真,根据破损后浮态结果和浮态要求计算出最佳的抗沉决策措施。
总体看来,国内外学者的研究主要集中在船体破损进水的流量、速度、进水过程、进水后船体的运动响应和船舶抗沉性方面。相关研究很少考虑破口具体类型对破口水流出流特性的影响,本文结合冲击船用钢板仿真所产生的破口形式,将破口形式与水动力学计算模型进行耦合,分析破口类型对水流出流特点的影响,为应急堵漏作业提供精准的数据支撑。
1 破口类型构建 1.1 材料失效分析及有限元模型建立船体破口形状采用冲击仿真的方式获得,在不影响冲击效果和运动轨迹的前提下,将冲击物整体形状进行相应简化。通过设置不同板厚、冲击物直径和冲击速度等进行计算分析。选取 Johnson-Cook本构模型表达船钢本构关系。引入材料失效参数与单元删除技术,建立冲击物侵彻船体钢板的三维数值模型,研究冲击物对船用钢板结构的破坏机理及损伤模式,准确有效地获得船用钢板受到冲击后的破口形式等信息。Johnson-Cook模型表达式为:
| $ \overline \sigma = \left[ {A + B\varepsilon _{}^n} \right]\left[ {1 + C\ln {\varepsilon ^*}} \right]\left[ {1 - {{\left( {\frac{{T - {T_0}}}{{{T_m} - {T_0}}}} \right)}^m}} \right]。$ | (1) |
式中:A为参考应变率和参考温度下的初始屈服应力,MPa;B为材料应变硬化模量,MPa;n为硬化指数;C为材料应变率强化参数;m为材料热软化指数;T为当前温度;T0为室温;Tm为材料熔点;
船用钢性能有别于其他普通钢,北京理工大学爆炸科学与技术国家重点实验室通过SHPB实验,确定了船钢的Johnson-Cook本构模型参数[15](见表1)。
|
|
表 1 船钢的Johnson-Cook本构模型参数 Tab.1 Johnson-Cook constitutive model parameters of shipboard steel |
可得:
| $ \overline \sigma {\text{ = }}\left[ {660 + 539\varepsilon _{}^{0.44}} \right]\left[ {1 + 0.009\ln {\varepsilon ^*}} \right]\left[ {1 - {{\left( {\frac{{T - 20}}{{853 - 20}}} \right)}^{1.06}}} \right]。$ | (2) |
Johnson-Cook断裂准则适用于金属材料在高应变、高应变率和高温度状态下发生的材料失效,综合考虑了应变硬化效应、应变率效应和温度敏感性。失效模型中引入了失效参数
失效参数
| $ \omega {\text{ = }}\sum\limits_{}^{} {\frac{{\Delta \overline {{\varepsilon ^{pl}}} }}{{\Delta \overline {{\varepsilon _{cr}}^{pl}} }}}。$ | (3) |
式中:
Johnson-Cook失效模型,其表达式如下:
| $ \varepsilon _{}^f{\text{ = }}\left[ {{D_1} + {D_2}\exp {D_3}\sigma _{}^*} \right]\left[ {1 + {D_4}\ln {\varepsilon ^*}} \right]\left[ {1 + {D_5}{{\left( {\frac{{T - {T_0}}}{{{T_{\text{m}}} - {T_0}}}} \right)}^{}}} \right]。$ | (4) |
式中:D1~D5为材料失效参数,一般通过实验计算得到。
Johnson-Cook耦合断裂准则考虑了材料损伤的累积效应,认为在材料完全失效之前,金属成型过程分为两步:1)材料经过塑性变形达到损伤初始点;2)材料经过损伤演化,刚度逐渐降低,直至材料完全失效,期间通过引入损伤变量D来表征材料损伤的程度。根据冲击物冲击钢板数值模拟研究,确定了Johnson-Cook损伤参数(见表2)。
|
|
表 2 船钢的Johnson-Cook损伤本构模型参数 Tab.2 Parameters of Johnson-Cook damage constitutive model for ship steel |
| $\begin{split} \varepsilon _{}^f =& \left[ { - 0.8 + 2.1\exp ( - 0.5\sigma _{}^*)} \right]\\& \left[ {1 + 0.002\ln {\varepsilon ^*}} \right]\left[ {1 + 0.61\left( {\frac{{T - 20}}{{853 - 20}}} \right)} \right]。\end{split}$ | (5) |
在冲击仿真过程中,冲击物与船用钢板的接触关系较为复杂,在冲击物主体冲击船用钢板过程中存在失效单元删除和内部单元接触问题。为有效地改善单元接触状态,采用对接触面类型限制较少的通用接触算法,所属实体的面都定义上自接触,确保冲击过程中攻击物与船用钢板的正确接触。冲击船钢数值模型边界条件设置及网格划分如图1所示。
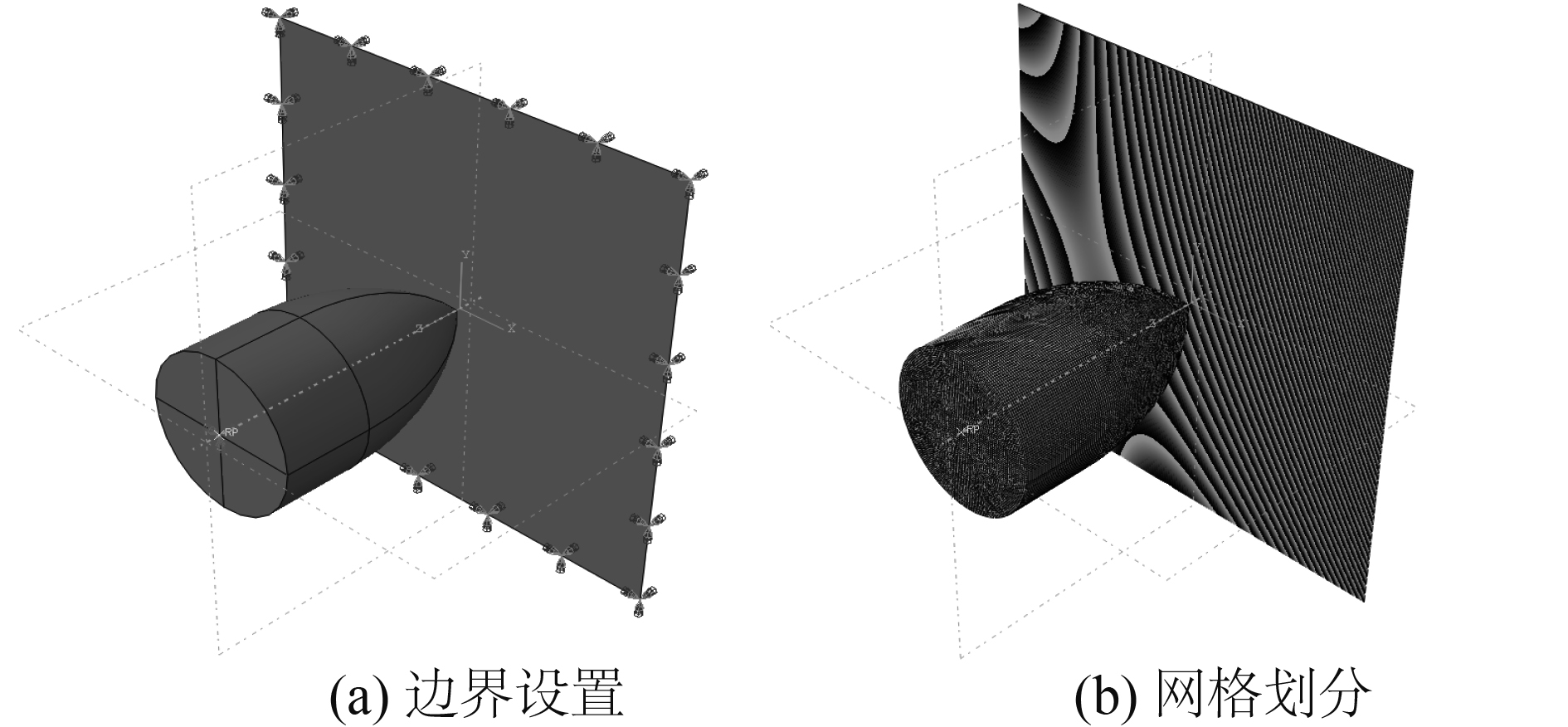
|
图 1 冲击船钢数值模型边界条件设置及网格划分 Fig. 1 Boundary condition setting and meshing of numerical model of percussive ship steel |
综合考虑目前破口分类方法和平战时某型号船艇破口形状和尺寸的可能性。确定6个工况进行冲击仿真,具体工况见表3。
|
|
表 3 船钢破口产生仿真工况表 Tab.3 Simulation working conditions of ship steel crack generation |
研究结果表明,冲击物轰击钢板是一个不断扩孔的过程中,钢体材料径向开裂而形成花瓣型破坏,由于所选冲击物在轰击钢板时产生的是穿刺破坏,将钢板的材料挤向头部的两侧,导致钢板材料只能向四周挤压,产生的瓣型破口翻边。由于金属钢板材料并不是绝对的各向同性,通常金属钢板的破坏是以混合的破坏模式出现,混合的破坏模式中,有一种破坏模式占据了主导的地位。结合实际情况,并按照上述条件通过多次仿真模拟,发现破口形成花瓣形破口或类似花瓣形破口的模式占据主导地位。冲击物冲击6 mm、8 mm这2种厚度的船用钢板,产生的破口特性相差不大。
图2为模拟冲击物冲击船板产生的“花瓣”型破口云图。根据仿真结果,攻击物冲击船用钢产生的“花瓣”型破口可大致分为2型:一种是翻边撕裂较深,花瓣状较明显;另一种是每瓣之间的金属被冲击掉,花瓣状不明显。

|
图 2 数值模拟船体破口结果云图 Fig. 2 Contours of numerical simulation hull damage result |
船体破口水流出流的水动力学模拟仿真主要研究破口的出流特性和水流流经破口壁面的出流形态,本质是涉及气、液多相流流动的流体动力学问题。本文采用VOF方法对破口水流出流的两相流动进行数值模拟,选择
其输运方程为
| $ \frac{{\partial k}}{{\partial t}} + {u_i}\frac{{\partial k}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {(v + {\sigma _k}{v_t})\frac{{\partial k}}{{\partial {x_j}}}} \right] + {\tilde P_k} - {\beta ^ * }k\omega + {S_k},$ | (6) |
| $\begin{split} {u_i}\frac{{\partial k}}{{\partial {x_i}}} = & \frac{\partial }{{\partial {x_j}}}\left[ {(v + {\sigma _k}{v_t})\frac{{\partial k}}{{\partial {x_j}}}} \right] + a{S^2} - \beta {\omega ^2} +\\ & 2(1 \sim {F_{_1}}){\sigma _{\omega 2}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}} + {S_\omega } 。\end{split}$ | (7) |
式中:
| $\begin{split} & {\varPhi _1} = \min \left[ {\max \left(\frac{{\sqrt k }}{{{\beta ^ * }\omega y}},\frac{{500v}}{{{y^2}\omega }}\right),\frac{{4\rho {\sigma _{\omega 2}}k}}{{C{D_{k\omega }}{y^2}}}} \right],\\ & {\varPhi _2} = \max \left[ {\left(\frac{{2\sqrt k }}{{{\beta ^ * }\omega y}},\frac{{500v}}{{{y^2}\omega }}\right)} \right],\\ & C{D_{k\omega }} = \max \left[ {2\rho {\sigma _{\omega 2}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}},{{10}^{ - 10}}} \right],\\ & {\tilde P_k} = \min \left[ {{v_t}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_j}}}\right),10{\beta ^ * }\rho k\omega } \right]。\end{split}$ |
将冲击仿真得到的破口形式与流域分析模型进行耦合,提取结果云图中的形状特征点信息,重建破口外形曲线,如图3所示。可以看出,冲击物冲击产生的Ⅰ型破口形状近似圆形,Ⅱ型破口形状近似矩形。两类破口翻边的形状不同,Ⅰ型破口的翻边轮廓更加平缓,Ⅱ型破口的翻边轮廓更加尖锐。破口翻边的高度为所形成破口直径的50%~60%。每瓣的形状近似相等。利用获得的外形数据建立流域模型,完成两者的耦合。
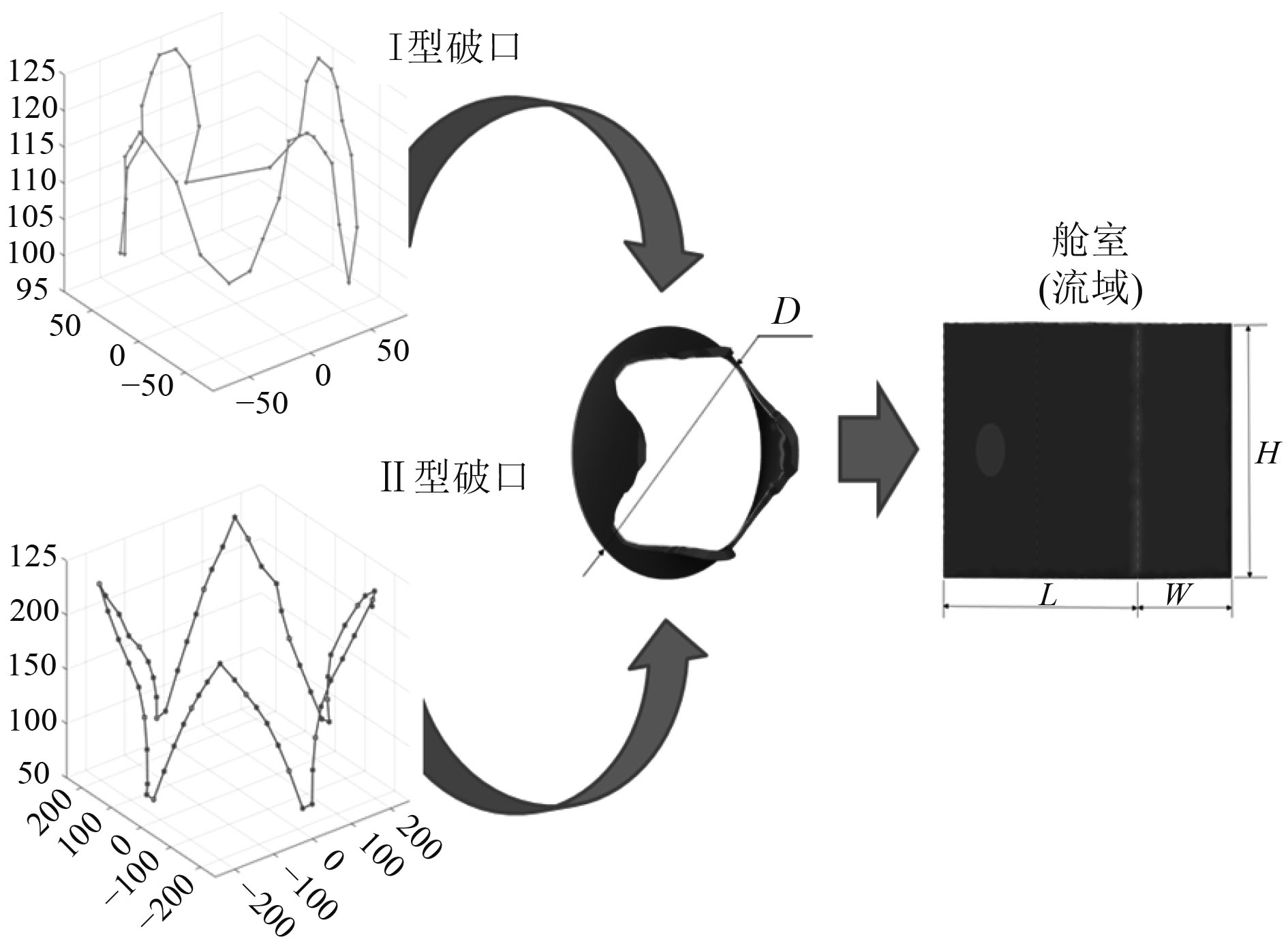
|
图 3 破口与舱室耦合过程 Fig. 3 Numerical simulation of hull crack shape diagram |
为确定合适的计算网格,本文进行了网格无关性检验,发现网格类型和数量未对产生计算结果产生影响,模型网格划分选用非结构化网格,网格质量在0.3以上。破口形状复杂,为保证破口附近流域计算精度,对破口处的网格进行分区域划分(见图4),共划分破口外表面、破口内表面和破口边刃3个面域,以Ⅱ型破口分析模型为例,破口外表面网格划分的最大尺寸约为30 mm,破口内表面网格划分的最大尺寸约为20 mm,破口边刃网格划分的最大尺寸约为5 mm,模型网格总数为1497413个。

|
图 4 破口表面和附近流域网格划分 Fig. 4 Meshing around the crevasses surface and the watershed |
为验证仿真结果的可靠性,将数值仿真中破口面临外部水流压强及其产生的流经破口进水水流速度结果与文献[17]的破口水压载荷理论解析解进行对比。外部水域环境按照069型和067型登陆艇堵漏作业时实际面临的情况确定水深为1.5 m,水流速度为10 kn。在进水压强仿真结果与解析解对比中,大部分工况误差在4%以内,最大误差为5.2%。在0.1 s时,水流刚喷涌至破口,还未形成完整的水柱,压强不稳,造成此时的误差较大。流经破口的进水水流速度的仿真结果与解析解对比,工况误差在5%以内。两类仿真的数据结果与对应的解析解吻合较好(见图5),说明仿真结果可靠,也验证了模型的正确性。

|
图 5 进水压强和进水水流速度结果对比 Fig. 5 Comparison of inlet pressure and inlet flow velocity results |
069型和067型登陆艇,满载吃水均在1.6 m以内,最高航速不超过12 kn。理论上应该按最高航速确定船艇堵漏时的最大适应流速,但实际中为了安全起见,当船艇堵漏时一般要求慢速航行,可确定外部水流适应流速为10 kn[17]。
仿真分析时,按照实际堵漏作业设置外界水流环境,分析不同破口类型的出流特性。为更好对比不同因素对破口出流的影响,在进行模拟仿真时,采用控制变量的思想,对比单一因素的影响,其他条件保持一致。
4.1 不同形状破口对破口出流特性的影响保持破口尺寸和翻边方向一致,图6为在X-Y平面内不同形状破口出流形态云图。可以看出,Ⅱ型破口各翻边之间的撕裂程度要大于Ⅰ型破口,在同样破口直径下,水流流经Ⅱ型破口形成的水柱要比流经Ⅰ型破口形成的水柱在出流距离上更近,液相在0.95以上的区域更小。两型破口水流出流形态呈类似规律:柱状水流喷涌

|
图 6 不同形状破口出流形态云图 Fig. 6 Contours of outflow shape of different shapes of crevasses |
保持破口尺寸和形状一致,图7为在X-Y平面内不同翻边方向的破口出流形态云图。可以看出,内翻边破口的出流规律为:柱状水流喷涌
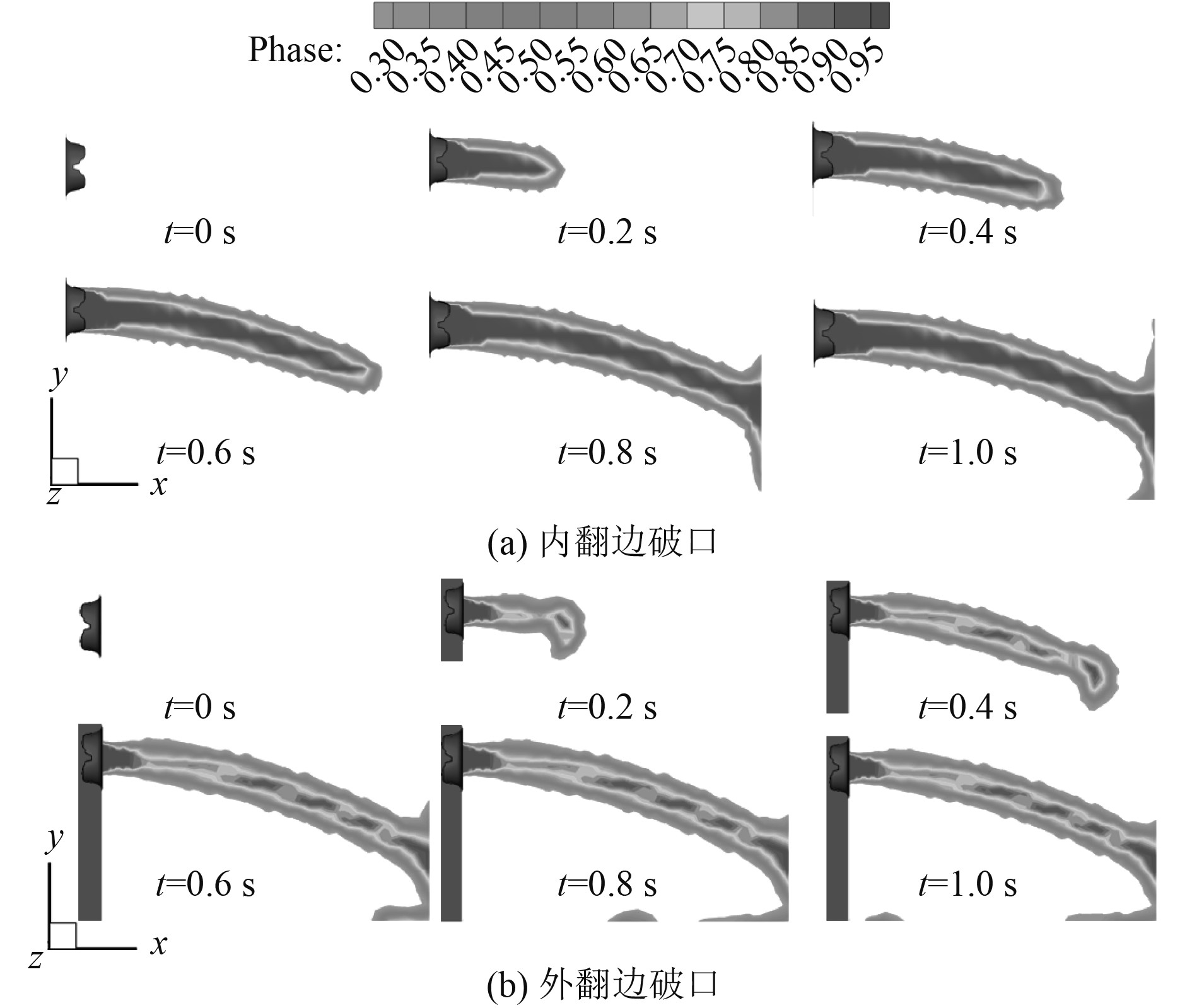
|
图 7 不同翻边破口出流形态云图 Fig. 7 Contours of outflow shape of different flanging crevasses |
控制破口形状和翻边一致,研究破口尺寸对破口出流特性的影响。按照中大型、中型和小型破口的分类标准,选择200 mm破口、300 mm破口和400 mm破口为研究对象。图8为在X-Y平面内不同尺寸破口的出流形态云图。可以看出,200 mm破口与300 mm破口、400 mm破口相比,未形成完整水柱。破口直径越小,同一时刻下喷涌出来的水流量也越少,在开始喷涌时,直径越小的破口,形成水柱越不明显,随着时间的增加喷涌出的水柱会进行收缩,形成较为稳定喷涌状态。破口的大小对破口水流的出流规律无明显影响,只影响喷涌水柱的粗细。Ⅰ型破口和Ⅱ型破口都满足这一规律。

|
图 8 不同尺寸破口出流形态云图 Fig. 8 Contours of outflow shape of different sizes of crevasses |
图9(a)为多种类型破口的水流出流距离随时间的变化。在外界水深1.5 m、水流流速10 kn条件下,I型破口在0.59 s时,水流出流距离为3 000 mm,并触碰舱壁,而II型破口达到这种状态的时间为0.61 s。Ⅰ型破口的出水速度略快于Ⅱ型破口,水流出流的距离也更长。0.27 s前,内翻边破口的出流距离要大于外翻破口。0.27 s后,外翻破口的出流距离远大于内翻边破口的出流距离。0.42 s时,外翻边破口的出流距离达到3 000 mm,并触碰到舱壁。此时内翻边破口的出流距离仅为2 380 mm,外翻破口的出流速度明显快于内翻边破口。400 mm破口、300 mm破口和200 mm破口水流出流距离达到3 000 mm的时间分别为0.59 s、0.62 s和0.66 s。在相同的出流距离下,破口尺寸越大,所需时间越短,出水流量越大。

|
图 9 水流出流距离和最大冲击压强随时间变化 Fig. 9 Variation of outlet distance with time and maximum impact pressure with time |
图9(b)为多种类型水流出流产生的最大冲击压力随时间的变化。在外界水深1.5 m、水流流速10 kn条件下,研究结果表明,I型和II型破口的最大冲击压力在0.7 s达到稳定,I型破口稳定后的最大冲击压强约为34 700 Pa,Ⅱ型破口约为33 900 Pa。封堵I型破口时施加的力大于II型破口。内翻破口的最大冲击压强稳定时间比外翻破口的最大冲击压强稳定时间晚0.20 s,稳定前的波动幅度更大。200 mm破口与300 mm破口和400 mm破口相比没有形成完整的水柱,最大冲击压强的稳定时间要早于其他2种尺寸。增加破口尺寸将产生更大的最大冲击压强。200 mm破口为33 400 Pa,400 mm破口约为34 700 Pa。破口尺寸越大,在封堵时克服水流冲击所需的力就越大。
5 结 语本文结合冲击动力学仿真和水动力学仿真,将得出的破口耦合进两相流计算模型中,采用控制外界水流环境相同的方法,研究不同破口类型、对水流出流形态、距离和最大冲击压强的影响,得出以下结论:
1)在水深1.5 m、水流流速10 kn的外界水流环境下,Ⅰ型破口在同时刻下的出流距离要比翻边撕裂更深的Ⅱ型破口远,在0.50 s时相差最大,为97 mm,最大冲击压强的稳定值大800 Pa。
2)外翻边破口在0.27 s后的水流出流距离大于内翻边破口,在0.42 s时,约为内翻边破口的1.26倍,最大冲击压强的稳定值大800 Pa,但水流出流量较少,出流形态也不同。
3)400 mm、300 mm和200 mm破口同时刻下的出流距离相差较小,出流距离为3000 mm时,所用时间分别为0.59 s、0.62s和0.66 s,最大冲击压强的稳定值相差较大,400 mm破口为34 700 Pa,比300 mm破口大1300 Pa,比200 mm破口大5700 Pa。破口尺寸越小,不易形成完整的水柱,造成水流出流时的距离和最大冲击压强等指标较小。
| [1] |
HAMID S H, KIM D H, PABLO M, et al. URANS simulations for a flooded ship in calm water and regular beam waves[J]. Ocean Engineering, 2016(120): 318-330. |
| [2] |
ZHANG G Y, WUA J X, SUN Z, et al. Numerically simulated flooding of a freely-floating two-dimensional damaged ship section using an improved MPS method[J]. Applied Ocean Research, 2020(101): 207-225. |
| [3] |
JOSIP B, NASTIA D, ROKO D. Total resistance prediction ofan intact and damaged tanker with flooded tanks in calm water[J]. Ocean Engineering, 2017(130): 83-91. |
| [4] |
SIDDIQUI M A, GRECO M, LUGNI C, et al. Experimental studies of a damaged ship section in forced heave motion[J]. Applied Ocean Research, 2019(88): 254-274. |
| [5] |
HIROTADA H, KOUKI K, MAKOTO. A numerical simulation method for transient behavior of damaged ships associated with flooding[J]. Ocean Engineering, 2017(143): 282-294. |
| [6] |
KIM J S, ROH M, HAM S H. A method for intermediate flooding and sinking simulation of a damaged floater in time domain[J]. Journal of Computational Design and Engineering, 2017(4): 1-13. |
| [7] |
CAO X Y, MING F R, ZHANG A M, et al. Multi-phase SPH modelling of air effect on the dynamic flooding of a damaged cabin[J]. Computers and Fluids, 2018(163): 7-19. |
| [8] |
LEE S K, YOU J M, LEE H H, et al. Preliminary tests of a damaged ship for CFD validation[J]. International Journal of Naval Architecture and Ocean Engineering, 2012, 4(2): 172-181. DOI:10.2478/IJNAOE-2013-0088 |
| [9] |
RUPONEN P, KURVINEN P, SAISTO I, et al. Air compression in a flooded tank of a damaged ship[J]. Ocean Engineering, 2013(57): 64-71. |
| [10] |
郑宇, 马宁, 顾解忡. 基于CFD的船舶破舱进水时域模拟[J]. 舰船科学与技术, 2017, 39(10): 29-33. ZHENG Y, MA N, GU X C. Time-domain simulation of the flooding of a damaged roro ship based on CFD[J]. Ship Science and Technology, 2017, 39(10): 29-33. |
| [11] |
李月萌, 段文洋, 金允龙, 等. 基于CFD模拟的船舶破舱进水过程研究[J]. 中国造船, 2016, 57(2): 149-163. LI Y M, D W Y, JIN Y L, et al. Flooding process of damaged ship based on CFD simulation[J]. Shipbuilding of China, 2016, 57(2): 149-163. DOI:10.3969/j.issn.1000-4882.2016.02.017 |
| [12] |
卢俊尹. 基于CFD的舱室破损进水数值研究 [D]. 武汉: 华中科技大学, 2013.
|
| [13] |
陈振, 高志亮, 刘 虎. 空气可压缩性对船舶破舱进水的影响[J]. 船舶工程, 2019, 41(5): 15-19. CHEN Z, GAO Z L, LIU H. Influence of air compressibility on ship damaged flooding[J]. Ship Engineering, 2019, 41(5): 15-19. |
| [14] |
孙智超. 舰船多舱室破损进水仿真及抗沉决策研究 [D]. 大连: 大连海事大学, 2018.
|
| [15] |
董永香, 宋卿, 葛超, 等. 10CrNi3MoCu船钢的动态力学性能研究 [C]// 北京力学会第20届学术年会论文集, 北京, 中国 , 2014: 147−148. DONG Y X, SONG Q, GE C, et al. Study on dynamic mechanical properties of 10CrNi3MoCu ship steel [C]//Proceedings of the 20th Annual Conference of Beijing Mechanics Society, Beijing, China, 2014: 147−148. |
| [16] |
雷丽, 黄楠燕. T型小通道气液两相流动特性的数值研究[J]. 山东化工, 2020, 49(15): 223-225,228. LEI L, HUANG N Y. Numerical simulation of gas-liquid two-phase flow characteristics in t-junction mini channels[J]. Shan Dong Chemical Industry, 2020, 49(15): 223-225,228. DOI:10.3969/j.issn.1008-021X.2020.15.099 |
| [17] |
李敏堂, 隋博, 孙栋, 等. 船艇堵漏器材水压环境与载荷分析[J]. 军事交通学院学报, 2017, 19(10): 91-95. LI M T, SUI B, SUN D, et al. Hydraulic pressure environment and load of leak stopper for boats[J]. Journal of Military Transportation University, 2017, 19(10): 91-95. DOI:10.16807/j.cnki.12-1372/e.2017.10.021 |
 2024, Vol. 46
2024, Vol. 46
