现代舰艇多使用高强度材料,并且在结构上使用双层壳体等防护措施,传统的水中兵器难以产生有效杀伤。常规水中兵器已很难满足现代海洋战争的需要。聚能战斗部、复合战斗部、定向爆破战斗部等高效高能毁伤武器应运而生,如美国的MK-50鱼雷、MK-90鱼雷、法国的“海鳝”鱼雷以及英国的“鳐鱼”鱼雷等[1]。
在水下聚能接触爆炸的整个过程中,金属射流、冲击波和气泡载荷作用于双层壳结构,使其产生局部穿透性裂纹、大面积塑性损伤,甚至断裂失稳。X射线被用于观测聚能射流的形成[2]。由于爆炸实验通常难以测量,并且存在危险性,通常使用数值方法来研究水下聚能爆炸的问题。聚能炸药通常是轴对称的,一般使用一维理论[3]或二维轴对称模型[1,12]来研究聚能爆炸问题。聚能炸药水下爆炸还涉及到固液两相物质的相互作用,一般采用耦合欧拉-拉格朗日方法构建计算模型[4,5]。聚能射流的形成受多种因素的影响,比如炸药类型和形状[6,13]、药型罩材料[8]和形状[11]以及是否存在隔板等辅助结构[10]。对于聚能射流穿透靶板的过程,不同的药型罩形状会影响侵彻效果[10-11],而聚能射流的拉伸断裂与材料强度、冲击速度有关[7,9]
本文基于耦合欧拉-拉格朗日方法模拟了聚能射流的形成及其对靶板的侵彻。首先,在简要讨论CEL方法之后,研究了聚能射流载荷的影响因素,掌握了聚能射流形成和发展的规律。然后,选择60°、90°、120°这3种锥形药型罩的锥角,发现了锥形药型罩锥角变化对射流侵彻能力的影响机理。最后,设计不同的药型罩形状,得到3种聚能侵彻体,研究了不同侵彻体的形成条件,得到不同侵彻体对靶板的损伤特性。
1 数值理论和验证 1.1 耦合欧拉-拉格朗日方法根据不同介质的变形特点,固体采用拉格朗日网格,流体等大变形物理采用欧拉网格。二者的结合可以很好地解决流固耦合问题。拉格朗日方法的控制方程[14]如下:
1)质量守恒方程
| $ \frac{{{\mathrm{D}}\rho }}{{{\mathrm{D}}t}} = 0 ,$ | (1) |
2)动量守恒方程
| $ \rho \frac{{\mathrm{D}}u}{{\mathrm{D}}t}=\nabla \cdot\sigma,$ | (2) |
3)能量守恒方程
| $ \rho \frac{{{\mathrm{D}}e}}{{{\mathrm{D}}t}} = \sigma :\nabla \otimes v。$ | (3) |
式中:
材料可在欧拉网格运输,即穿过网格边缘进入另一个欧拉网格。材料在欧拉网格中的运动用欧拉体积分数来表示。当体积分数为1时,视为材料占据欧拉网格,当体积分数小于1,则视为空单元。一个欧拉网格内可以有不同的材料,以拉格朗日网格单元的状态变量映射到空间网格中,其控制方程[16]为:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho u) = 0,$ | (4) |
| $ \frac{{\partial (\rho u)}}{{\partial t}} + \nabla \cdot (\rho uu) = \rho f + \nabla \cdot \sigma ,$ | (5) |
| $ \frac{{\partial (\rho e)}}{{\partial t}} + \rho u \cdot \nabla e = \sigma :\nabla \otimes u 。$ | (6) |
式中:
2种网格的耦合通过罚函数法[17]实现:
| $ {F_p} = kd 。$ | (7) |
式中:
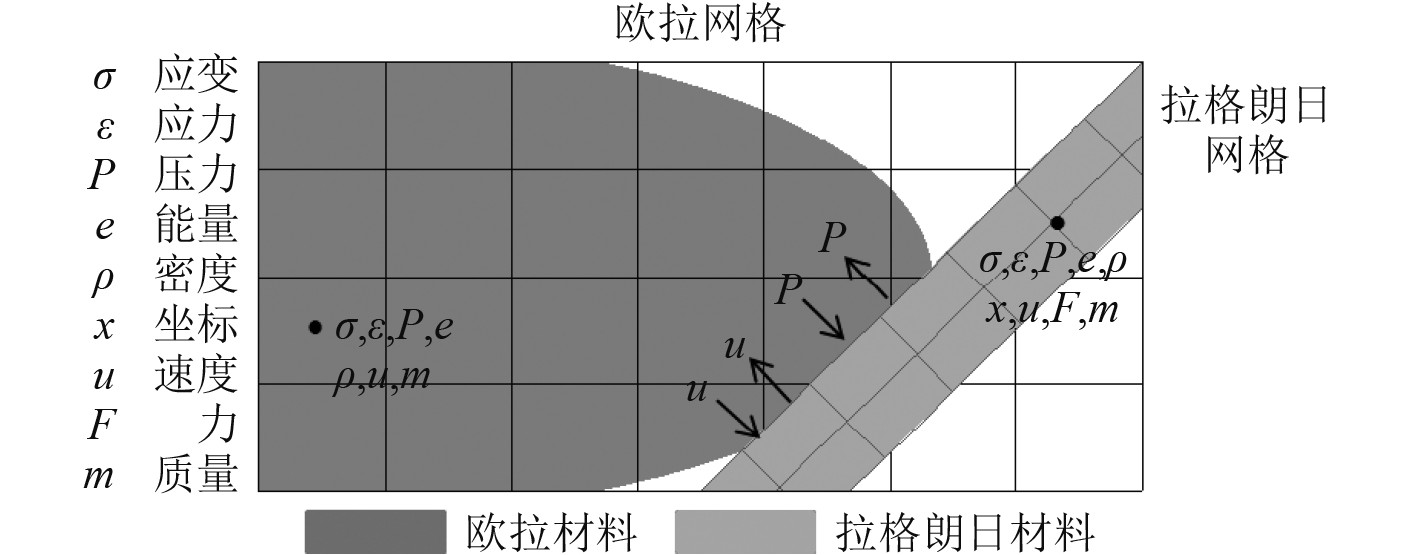
在CEL算法中,2种类型的网格无需共节点。欧拉网格的物理量,如速度和压力等,通过2种网格的接触面对拉格朗日结构施加作用,拉格朗日结构为欧拉结构提供边界条件,如图1所示[17]。
|
图 1 拉格朗日网格和欧拉网格耦合界面信息传递[17] Fig. 1 Information transfer between Lagrangian grid and Euler grid coupling interface[17] |
选取文献[19]中聚能战斗部侵彻双层目标的实验进行仿真验证。实验炸药为JWL-8,装药直径为50 mm,装药高度为100 mm,起爆距离为90 mm。药型罩由铜制成,锥角为46°,厚为1 mm。3层靶板的材料为A3钢,厚度为4 mm。上层PVC管介质为水,下层为空气。在实验过程中测量了射流穿透靶板的时间,并在2个时刻拍摄了射流图像。根据实验,建立二维轴对称数值模型,如图2所示。靶板采用拉格朗日模型[18],其余结构采用欧拉模型,边界条件设置为Flow-Out。将网格大小设置为0.5 mm×0.5 mm。在介质和靶板两侧每隔10 mm设置一个测量点。

|
图 2 仿真模型示意图 Fig. 2 Schematic diagram of simulation model |
炸药的Jones-Wilkins-Lee状态方程计算公式[19]如下:
| $ P = A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){e^{ - {R_1}V}} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){e^{ - {R_2}V}} + \frac{{\omega E}}{V} 。$ | (8) |
式中:
|
|
表 1 爆轰产物JWL状态方程参数 Tab.1 JWL equation of state parameters for detonation products |
|
|
表 2 铜的材料参数 Tab.2 Material parameters of copper |
|
|
表 3 钢的状态方程和强度模型参数 Tab.3 State equation and strength model parameters of steel |
计算后得到31 μs和39 μs时刻的仿真计算图像,并与实验结果[19]进行对比,如图3所示。

|
图 3 仿真计算与实验数据对比 Fig. 3 Comparison between simulation calculation and experimental data |
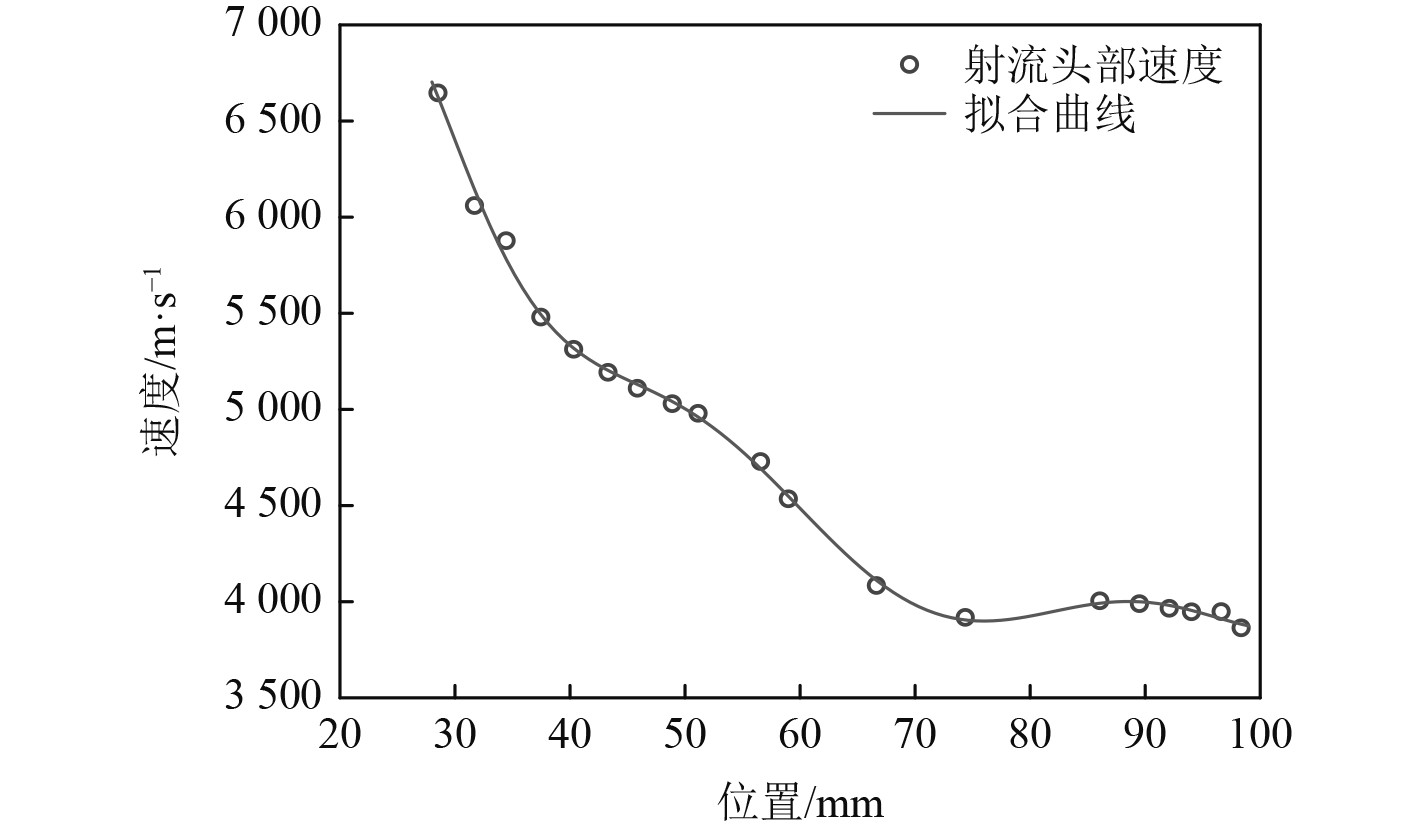
对比2个时刻的图像可看出,模拟的射流图像已经断裂,而测试中捕获的射流图像连续,这是由于网格精度的限制。实验图像与数值模拟图像基本一致,初步判断仿真结果有效。根据设定的测点可得到金属射流头速度,变化曲线如图4所示。
|
图 4 射流头速度随时间的变化曲线 Fig. 4 Variation curve of jet head velocity with time |
通过数值模拟测量计算各时间段射流头部平均速度,与实验结果[19]进行对比,如表4所示。
|
|
表 4 侵彻水层时射流头部平均速度对比 Tab.4 Comparison of jet head average velocity in penetrating water layer |
数值模拟结果与实验结果之间的相对误差均在6%以内,验证了数值方法的准确性和有效性。
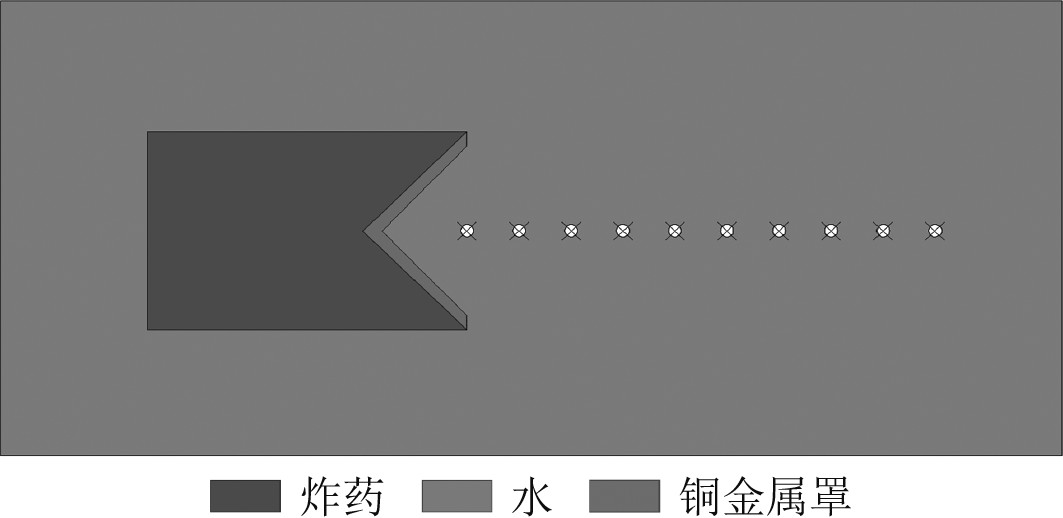
1.3 收敛性分析对于数值模拟而言,为了在保证计算结果精度的同时,尽量缩短计算时间,收敛性分析是必要的。设置一个简单的水下聚能炸药模型(见图5),并且在水域中,沿聚能战斗部的轴对称线每隔10 mm设置一个测点,测量爆炸产生射流的头部速度。

|
图 5 收敛性分析的计算模型 Fig. 5 Computational model for convergence analysis |
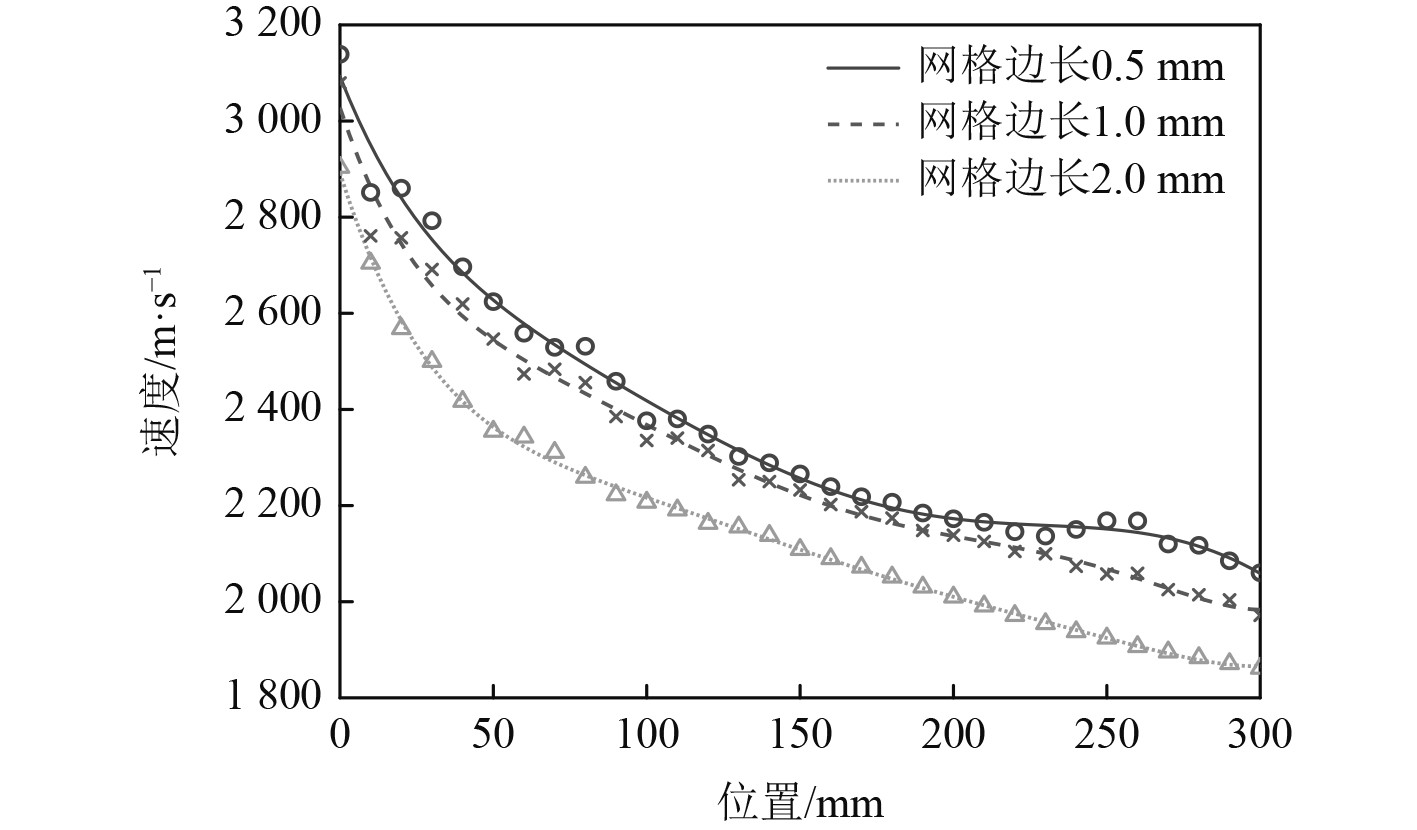
设置不同的网格大小,分别为0.5 mm×0.5 mm、1 mm×1 mm以及2 mm×2 mm。计算不同网格大小下射流头部经过相同位置时的速度,如图6所示。
|
图 6 测点处的射流头速度 Fig. 6 Jet head velocity at measuring point |
可知,考虑同一位置的速度大小和整体的速度变化,边长为1 mm网格模型的计算结果与0.5 mm网格模型的计算结果相近。可看出,在150 mm和200 mm之间,3种大小网格的速度变化未出现较大波动,此区间上的数值计算结果可靠度较高。为了更好地展示3种网格计算结果之间的差距,取150 mm和200 mm之间的5组数据,以0.5 mm网格模型的计算结果为基准,计算另外2种模型与0.5 mm网格模型的平均误差,结果如表5所示。
|
|
表 5 2种模型的平均误差 Tab.5 The average error of the two models |
可看出,网格从2 mm缩小一半时,平均误差由6.98%降低为1.55%。在此基础上网格大小再缩小一半,计算所得数据的精度变化相对并不明显,然而计算时间却增加了5倍以上。综合考虑计算的精度和耗时,可以认为1 mm×1 mm网格大小的模型最为适宜。
2 水下聚能金属射流载荷特性分别选取锥角为60°、90°和120°的三角形金属罩结构进行研究,聚能战斗部的尺寸均为200 mm×100 mm(长×宽),为中心轴对称结构。保持金属罩的厚度统一,3种锥角下金属罩的内外表面平行,保持每个位置的厚度均为4 mm。起爆点均设置在炸药远离金属罩的一侧,并且均设置在对称轴上,起爆方式为点起爆。锥角为90°时三角形金属罩聚能战斗部工况设置如图7所示,计算域的大小为600 mm×200 mm,欧拉网格大小为1 mm×1 mm,网格总数为120000个。其中聚能战斗部周围的环境为水环境,炸药采用PBX-9502型炸药,金属罩的截面形状为三角形,材料为铜。
|
图 7 锥角为90°金属罩的工况 Fig. 7 Cone angle of 90° metal hood working condition |
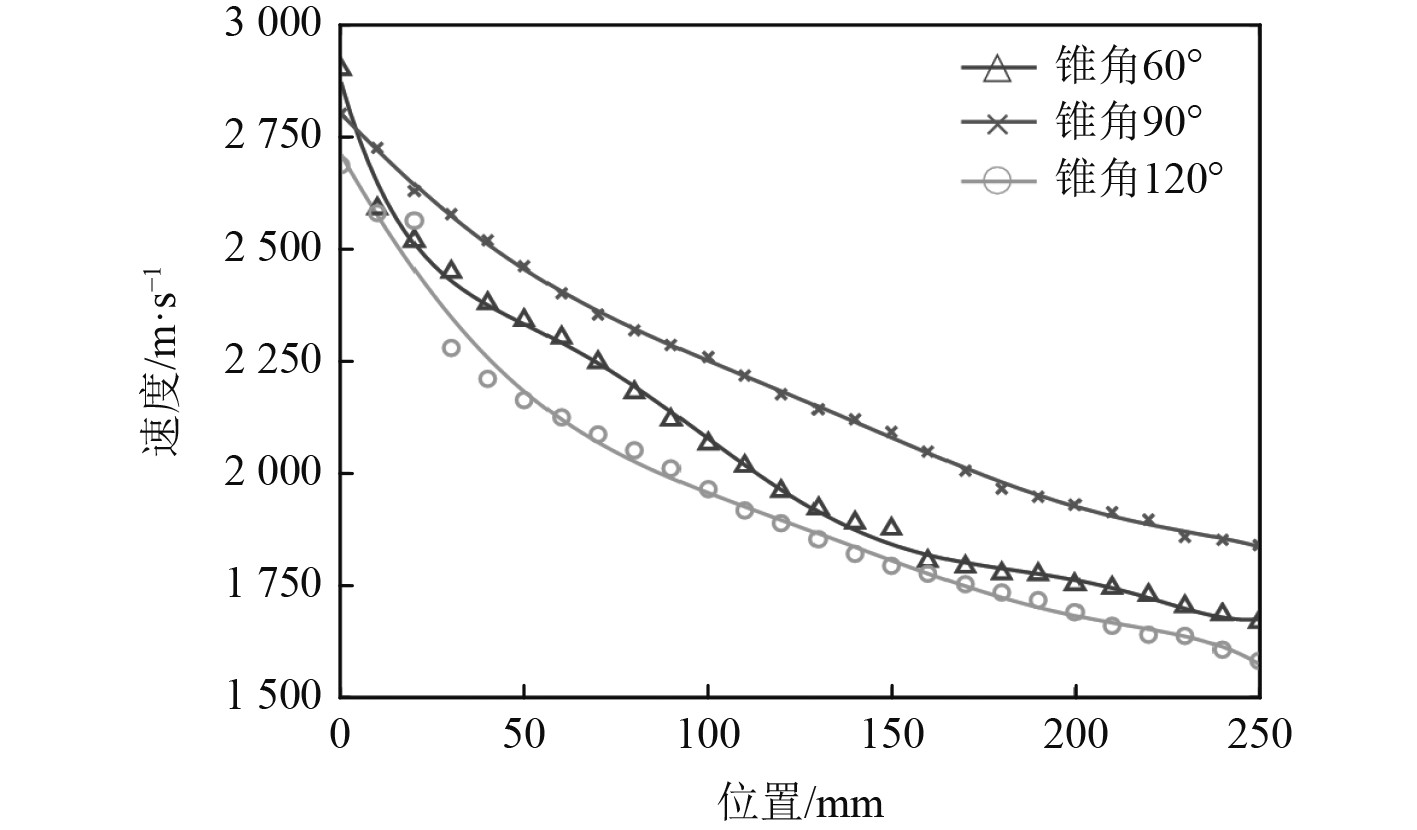
根据在聚能战斗部前方设置的10个测点测得的聚能射流速度的数据,测点处在整个模拟过程最大的速度即为聚能射流头部的速度,对比3种几何结构的金属罩形成聚能射流在水环境中运动速度的变化,如图8所示。
|
图 8 测点处射流头部速度变化 Fig. 8 Velocity variation of jet head at measuring point |
可知,3种角度的金属罩产生射流的最大速度均形成于x=0 mm附近,这是由于金属罩在未脱离聚能战斗部时,不断受到爆轰波产生的压力作用,而速度不断变大。在这之后,爆轰波对金属罩的作用迅速衰减直至消失,此时聚能射流受到周围水环境的阻力,速度不断减小。虽然锥角越小的金属罩形成的射流初速度越大,但是射流在穿过水中同等距离后,锥角为90°的金属罩形成的射流速度衰减最小,在同样位置的速度大于另外2种射流。可认为在水下爆炸中,锥角大小与射流速度之间并无线性关系,而是存在一个最合适的角度使射流速度最大。在设置的工况中,最合适的角度为90°。
3 聚能金属射流对靶板的毁伤特性根据作用形式和毁伤元素划分,聚能战斗部的装药形式一般分为射流(JET)装药、射弹(EFP)装药和高速杆式弹丸(JPC)装药。这几种装药形式的主要差别在于药型罩形成杵体和射流的质量分配及速度差距。
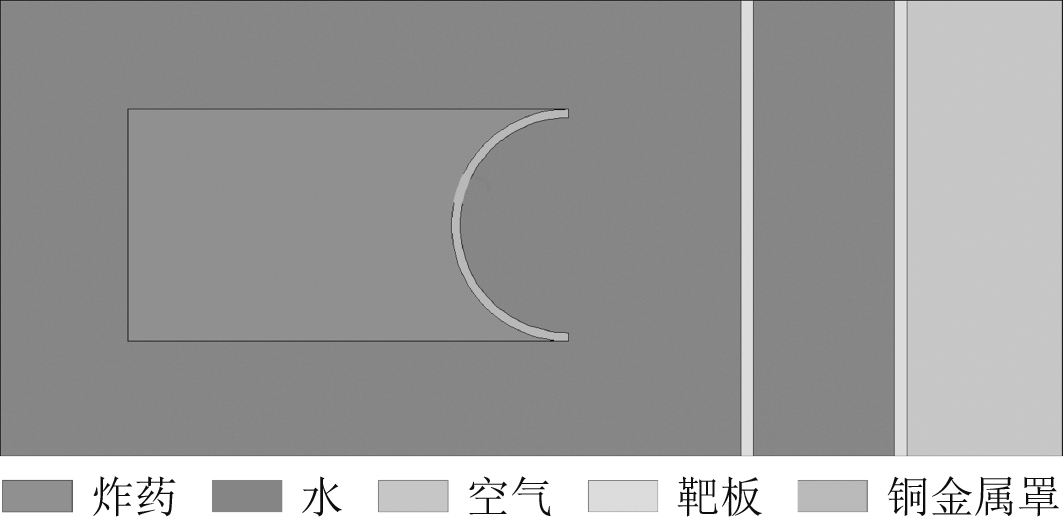
设置3种不同几何形状的装药形式,分别为锥角为90°的锥形装药、锥角为120°的锥形装药以及半球形装药,聚能战斗部的尺寸均为200 mm×100 mm,为中心轴对称结构。保持金属罩的厚度统一,3种锥角下金属罩的内外表面平行,保持每个位置的厚度均为4 mm。起爆点均设置在炸药远离金属罩的一侧,并且均设置在对称轴上,起爆方式为点起爆。计算域的大小为600 mm×200 mm,欧拉网格大小为1 mm×1 mm,网格总数为120000个。聚能战斗部周围水环境,炸药采用PBX-9502型炸药,金属罩的材料为铜。观察这些聚能战斗部形成的射流形状并判断其属于何种聚能侵彻体。2层钢制靶板的距离为50 mm,距离聚能炸药100 mm,用以研究不同工况下聚能侵彻体的毁伤效果。图9为半球形装药工况沿对称轴的剖面图,在聚能战斗部的轴线上每隔10 mm设置一个测点,并在靶板前后设置测点,用来监测聚能侵彻体在空间上的速度变化情况,其余2种工况的设置类似。
|
图 9 半球形药型罩工况 Fig. 9 Hemispherical charge cover condition |
通过仿真模拟计算,观察在各种工况下射流完全成型后的形状,如图10所示。

|
图 10 各类聚能侵彻体 Fig. 10 Various types of shaped charge penetrators |
可知,图10(a)的质量主要集中在杵体部分,符合聚能射流的特征,图10(b)的质量在杵体和头部之间近似均匀分布,符合聚能杆式侵彻体的特征,而图10(c)的质量完全集中在头部,符合爆炸成型弹丸的特征。
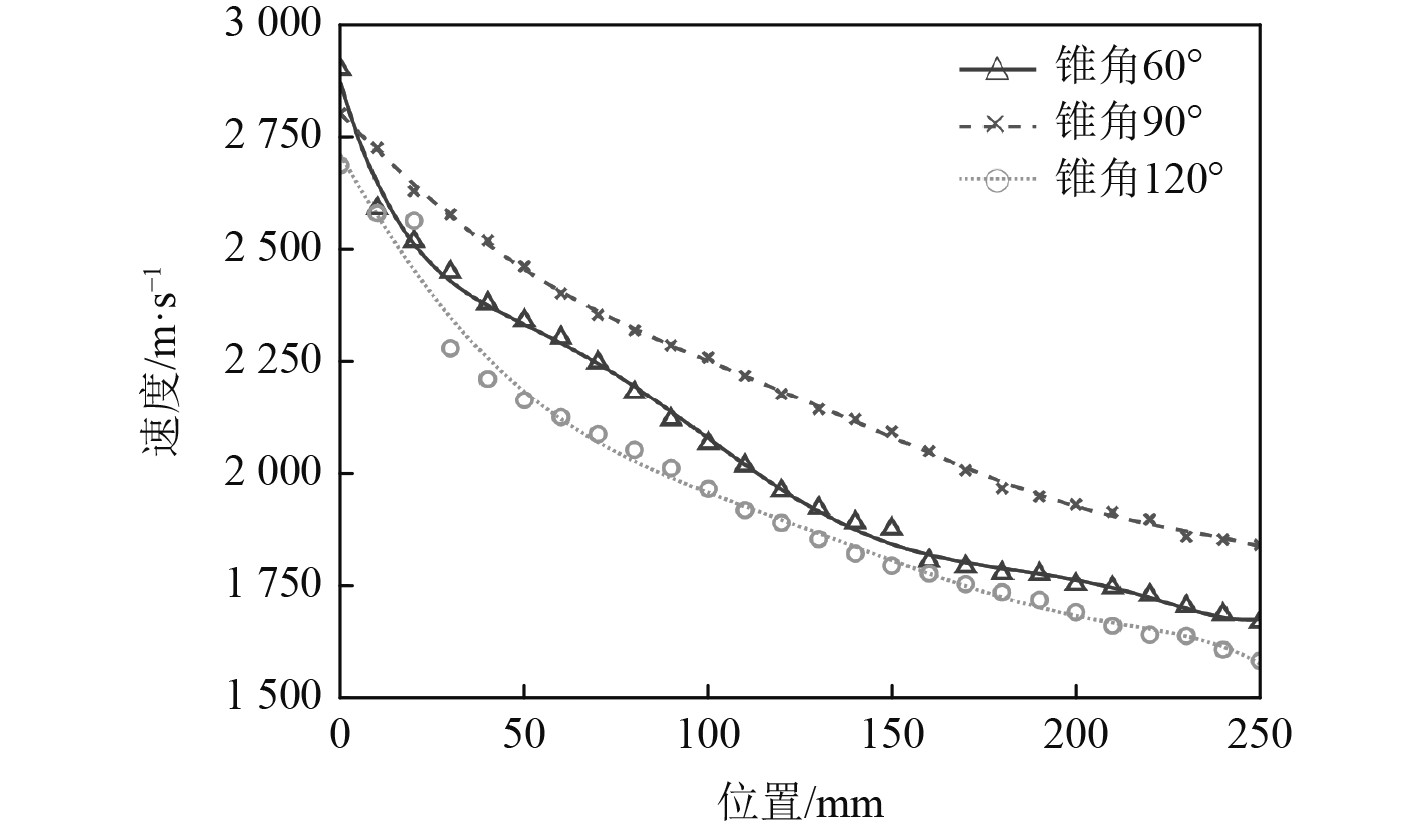
读取3种工况下测点处的射流头部速度数据,速度变化如图11所示。
|
图 11 测点处射流头部速度变化 Fig. 11 Velocity variation of jet head at measuring point |
可知,侵彻体速度由大到小依次是聚能射流、聚能杆式侵彻体、爆炸成型弹丸。初速度的大小主要与药型罩的形状有关。射流头部直径越大,其在水中收到的阻力也就越大,故聚能射流的速度梯度最小,而爆炸成型弹丸的速度梯度最大。可以看出,在x=150 mm处,3条曲线均出现了明显的下降,此处为靶板的作用所致。
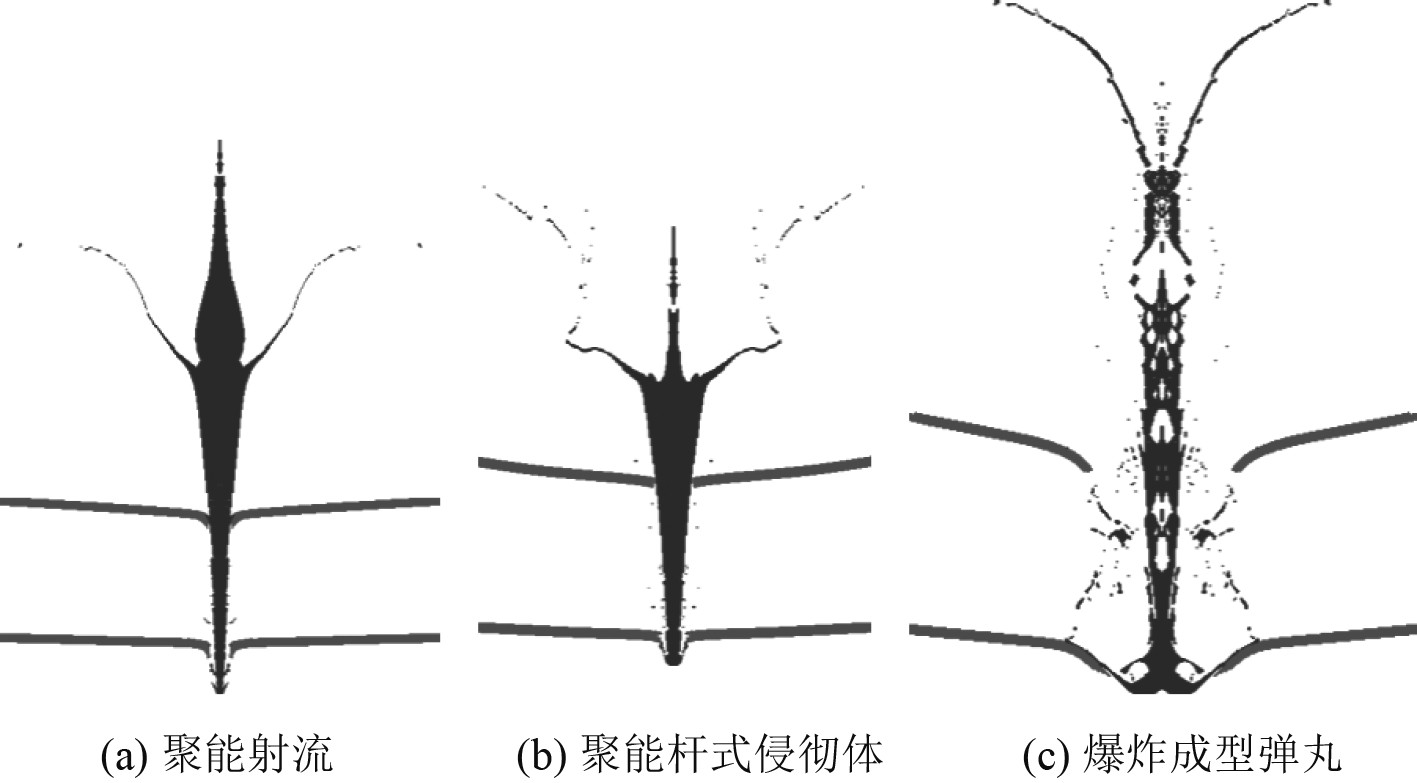
在得到各种聚能侵彻体的类型后,观察不同聚能侵彻体对同种靶板的侵彻效果,如图12所示。
|
图 12 侵彻体穿透双层靶板的形态 Fig. 12 The morphology of the penetrating body through the double layer target plate |
可知,在穿过2层靶板及其层间水后,聚能射流和聚能杆式侵彻体仍然能够保持完整的形状,并未出现断裂或散射。而爆炸成型弹丸已经完全失去应有的形状,多处位置出现空腔,甚至断裂。根据计算结果,测量得到各种工况下靶板的破孔半径,如表6所示。
|
|
表 6 不同类型侵彻体的毁伤效果 Tab.6 The damage effect of different types of penetrating body |
可知,聚能射流的破孔直径最小,这是因为其射流头部质量占比最小、直径也最小。而破孔直径和射流头部直径正相关。由于射流接触靶板时,靶板会挤压射流,使其速度降低,直径增大,所以会出现破孔直径大于射流头部直径的情况。
综合上述分析,发现3种聚能侵彻体有不同的作用特性,可满足多种破坏要求。如在打击距离较近且较脆弱的装甲时,可使用爆炸成型弹丸造成更大的破坏面积;而对于远距离的厚装甲,需要更好的穿透效果,则优先考虑聚能射流或聚能杆式侵彻体。
4 结 语基于流固耦合理论和有限元分析,研究了水下聚能爆炸的聚能射流载荷特性和对双层靶板的毁伤效果。发现在水环境中,同等药型罩厚度的情况下,锥角为90°的药型罩形成的聚能射流速度最大且不易衰减,侵彻能力强于其他锥角的药型罩;不同的药型罩可产生不同类型的聚能侵彻体,其中锥角为90°的圆锥形药型罩可形成聚能射流,聚能射流具有较高的速度,有良好的侵彻效果,半球形药型罩可形成爆炸成型弹丸,其头部直径大,破孔效果好,锥角为120°的三角形药型罩可形成聚能杆式侵彻体,其既具有速度较大的特征,也具有较大的药型罩利用率。
| [1] |
MOLINARI J F. Finite element simulation of shaped charges[J]. Finite Elements in Analysis and Design, 2002, 38(10): 921−921.
|
| [2] |
GREEN J RE. First x-ray diffraction photograph of a shaped charge jet[J]. Review of Scientific Instruments, 1975, 46: 1257-1261. DOI:10.1063/1.1134456 |
| [3] |
CHOU Pei-chi. The stability of shaped-charge jets[J]. Journal of Applied Physics, 1977, 48(10): 4187-4195. DOI:10.1063/1.323456 |
| [4] |
CORNISH R, MILLS J T, CURTIS J P. Degradation mechanisms in shaped charge jet penetration[J]. International Journal of Impact Engineering, 2001, 26(1): 105−114.
|
| [5] |
HUANG Junqing, MA Yalong, HUANG Kelei, et al. Analysis of aperture shape changing trend base on the shaped charge jet penetration through the steel target[J]. AsiaSim, 2012: 7−12.
|
| [6] |
QU Hong fei, HAN Feng, CHEN Fang. The numerical simulation of shaped charge jet under the influence of charge structure[J]. Applied Mechanics and Materials, 2013, 444-445+996-1000.
|
| [7] |
CORNISH R, MILLS J T, CURTIS J P, et al. Degradation mechanisms in shaped charge jet penetration[J]. International Journal of Impact Engineering, 2001, 26(1): 105−114.
|
| [8] |
MOLINARI J F. Finite element simulation of shaped charges. [J]. Finite Elements in Analysis and Design, 2002, 38(10): 921−921.
|
| [9] |
FOMIN V M, ZVEGINTSEV V I, BRAGUNTSOV E Y. Specific features of stretching and breaking of shaped-charge jets[J]. Journal of Applied Mechanics and Technical Physics, 2020, 61(2): 171-180. DOI:10.1134/S0021894420020030 |
| [10] |
FU Jianping, CHEN Zhigang, HOU Xiucheng, et al. Simulation and experimental investigation of jetting penetrator charge at large stand-off distance[J]. Defence Technology, 2013, 9(2): 117-124. |
| [11] |
ZHANG Z, MING F, ZHANG A. Damage characteristics of coated cylindrical shells subjected to underwater contact explosion[J]. Shock and Vibration, 2014, 18: 1−12.
|
| [12] |
CHEN Q, LIU K. A high-resolution Eulerian method for numerical simulation of shaped charge jet including solid–fluid coexistence and interaction[J]. Computers & Fluids, 2012, 56: 92-101. |
| [13] |
HUANG C, LIU M, WANG B, et al. Underwater explosion of slender explosives: directional effects of shock waves and structure responses[J]. International Journal of Impact Engineering, 2019, 130: 266-280. DOI:10.1016/j.ijimpeng.2019.04.018 |
| [14] |
ZHANG A M, YANG W S, HUANG C, et al. Numerical simulation of column charge underwater explosion based on SPH and BEM combination[J]. Computers & Fluids, 2013, 71: 169-178. |
| [15] |
张之凡. 聚能装药水下爆炸载荷及其对结构的毁伤特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [16] |
杨刚, 韩旭, 龙述尧. 应用 SPH 方法模拟近水面爆炸[J]. 工程力学, 2008, 25(4): 204-208. YANG Gang, HAN Xu, LONG Shuyao. Simulation of near-surface explosion by SPH method[J]. Engineering Mechanics, 2008, 25(4): 204-208. |
| [17] |
BENSON D J, OKAZAWA S. Contact in a multi-material Eulerian finite element formulation[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(39): 4277-4298. |
| [18] |
2013 Inc A. Ansys Autodyn User's Manual, Release 15.0[R
|
| [19] |
史进伟, 罗兴柏, 张玉令, 等. 基于正交优化法的抗射流侵彻水夹层间隔靶结构优化[J]. 军械工程学院学报, 2016, 28(2): 24-28. SHI Jinwei, LUO Xingbai, ZHANG Yuling, et al. Structure optimization of water-interlayer spacer target against jet penetration based on orthogonal optimization method[J]. Journal of Ordnance Engineering College, 2016, 28(2): 24-28. |
| [20] |
JOHNSON G R. A constitutive model and data for materials subjected to large strains, high strain rates, and high temperatures[J]. Proceedings of 7th Intemational Symposium on, 1983: 541−547.
|
 2024, Vol. 46
2024, Vol. 46
