2. 河南省水下智能装备重点实验室,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligence Equipment, Zhengzhou 450015, China
入水问题是涉及固、液、气三者相互耦合作用的复杂物理过程,广泛存在于自然界及工程实际中,如水上飞机的降落、船首的入水砰击、宇宙器件的水上着落、空投鱼雷的入水、海上救生艇抛落等问题[1]。近年来,国内外学者在入水冲击、入水初期流场、入水航行体道等方面做了大量的试验和数值仿真研究,Park等[2]假设流体不可压缩并忽略流体的粘性,用平板法推导了数学模型,解决高速入水冲击力问题,施红辉等[3]对钝头体垂直落水过程水中压力进行测量,试验得到了水域内部声波和压力随钝头体运动过程的变化规律。王占莹等[4]针对回转体垂直入水流体动力问题,基于 RANS 方程、VOF 多相流模型和动网格技术进行数值模拟分析,研究回转体不同入水速度对流体动力分布特性的影响。姚保太等[5]对航行体水弹道进行了数值仿真得到航行体水中段的弹道特性,但对于出水以及重新入水过程的弹道求解难度非常大,建议采用试验方法进行获取。高速物体的出入水过程中一般都带有空泡,这样就存在空泡自由面和水面自由面的相互作用,结构物入水运动的同时还伴随航行体高频弹性振动,尤其是穿越自由液面时,涉及到三相介质的相互作用问题,入水的力学过程十分复杂,很难准确模拟其运动姿态及砰击载荷。
为减小跌落时的俯仰角,航行体尾部安装有偏置舵板。在跌落过程中,舵板受到的重力与水阻力方向相反,舵板张合具有随机性和较宽的角度变化范围,这给航行体水弹道预测造成了很大困难。
航行体从平台发射后再次入水可能会砸平台,出于安全性考虑,不宜采用原模型进行发射试验研究。可开展缩比试验件进行跌落研究,通过试验获得下沉数据,分析运动规律,为航行体安全发射提供支撑。
1 试验方案航行体发射后冲出水面,其在空中的运动可看作是质心的平动和绕质心的转动。航行体到达最高点时,垂向速度为0,水平速度极小,存在一定俯仰角及俯仰角速度,随后航行体在重力作用下下落。下落过程中俯仰角持续变小,最终以一定的姿态落于水面上,然后持续下沉。下沉过程中俯仰角持续变大,到达最深处后,依靠浮力上浮,最终漂浮于水面上。
影响到最终跌落深度的主要有出水最大高度、此刻的俯仰角及俯仰角速度。最大高度直接影响到初始的动能,高度越大理论上落水后跌落入水越深。俯仰角则直接影响到阻尼系数,俯仰角越大则入水的阻尼系数越小,跌落后最大深度越大。俯仰角速度则比较复杂,一方面角速度值越大,则入水时俯仰角越小,阻尼系数越大,入水深度越小;另一方面角速度越大,初始能量越大,入水深度越大,因而综合分析得俯仰角速度可能对跌落深度影响较小。
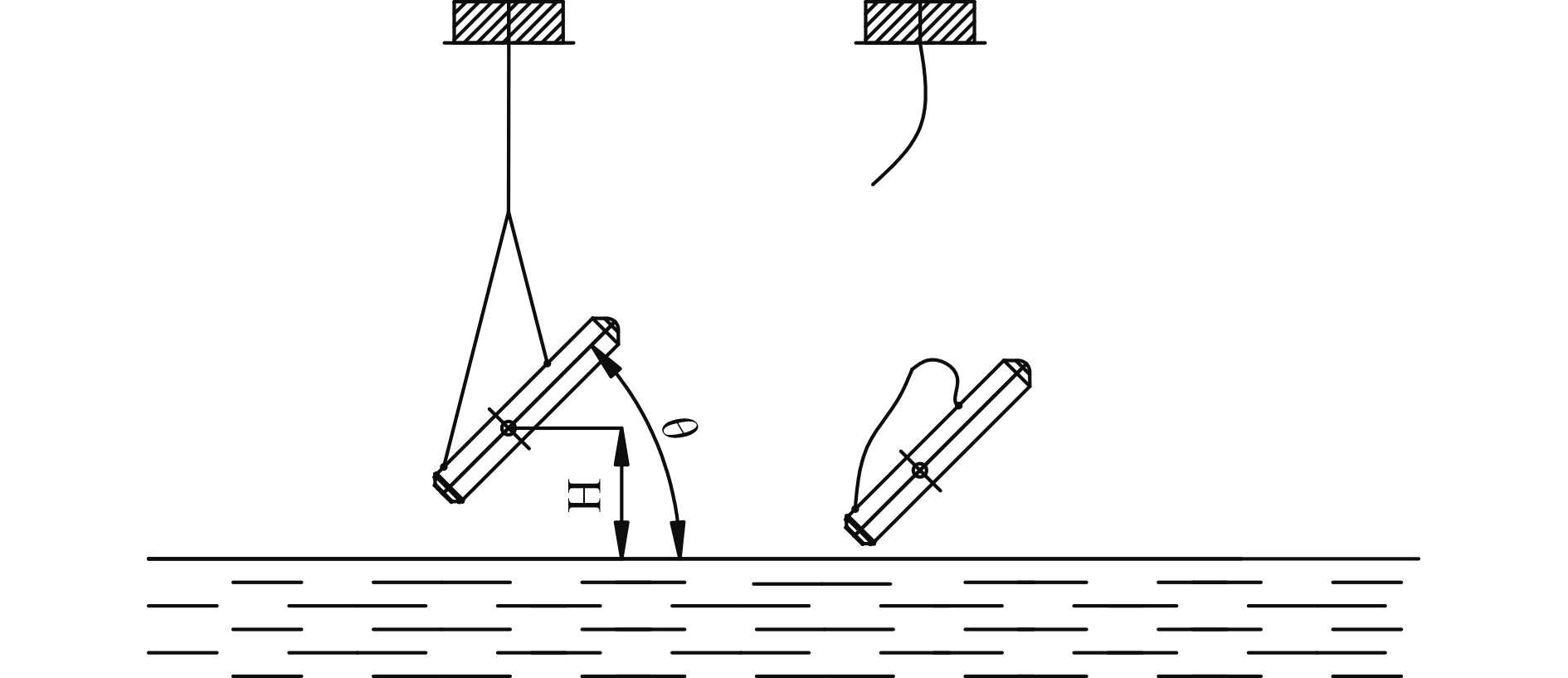
试验时主要考虑出水最大高度以及此刻的俯仰角作为试验的初始条件。拟采用三绳两点进行跌落试验,如图1所示。
|
图 1 模拟高度、俯仰角跌落试验方案 Fig. 1 Simulation height and pitch angle drop test |
通过调整航行体上前后点吊绳的长度来调整初始俯仰角,通过中绳的位置来调整初始高度,达到试验条件后剪断中绳进行跌落试验,通过航行体尾部压力传感器的数值判定入水深度。
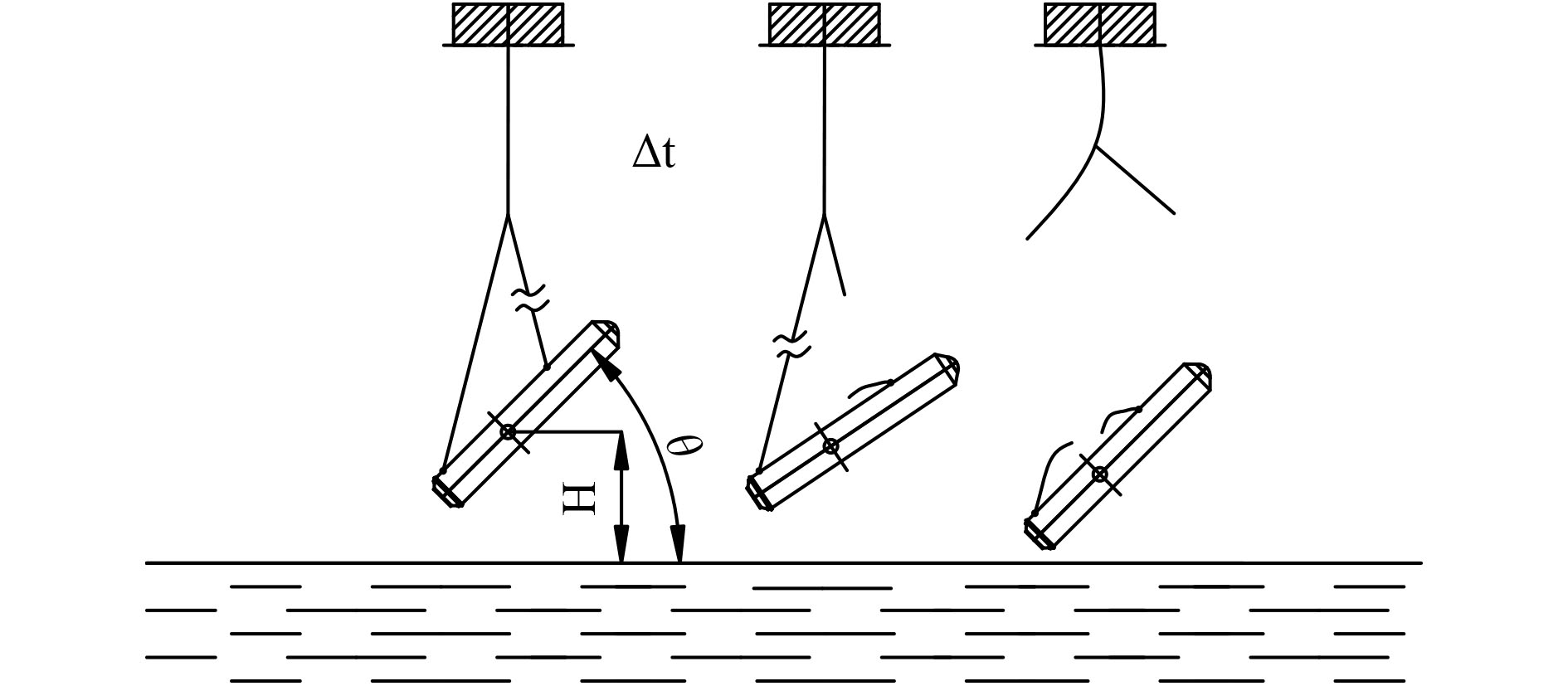
为模拟俯仰角速度,通过时序程序控制航行体头、尾吊点的释放时间。首先释放头部吊点,航行体在重力作用下,围绕后吊点旋转,其角速度达到规定值后,尾部释放,航行体以“自由下落+旋转”落入水中,如图2所示。
|
图 2 模拟高度、俯仰角、角速度跌落试验方案 Fig. 2 Simulation height, pitch Angle, angular velcocity drop test |
初始的高度及角度可事先在水槽中调节,通过调整上下吊绳的长度实现在设定高度位置的俯仰角。
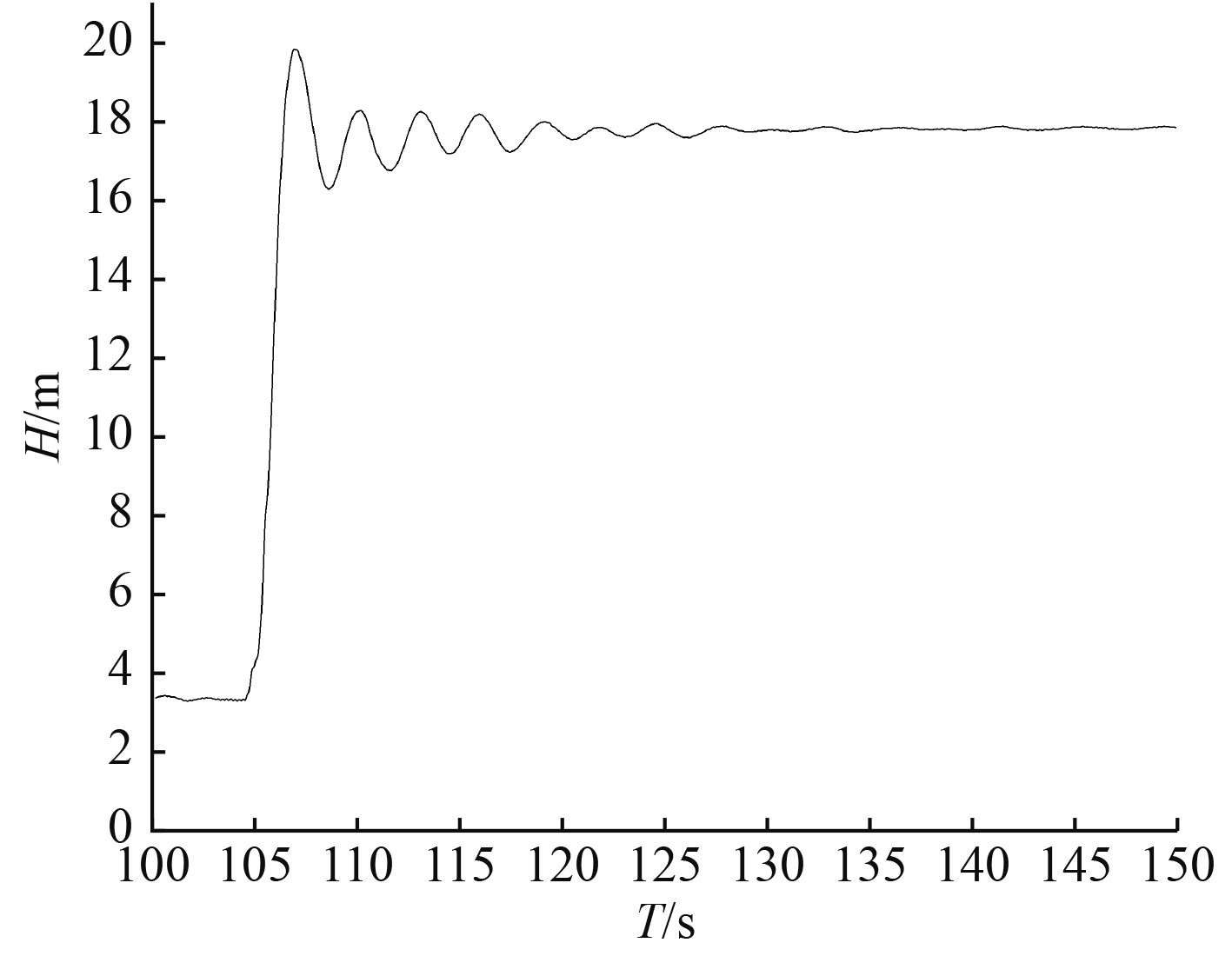
航行体跌落试验的重复性非常好,典型的测试结果如图3所示。航行体跌落过程中,迅速下沉到最大深度。航行体第一次上浮后自身在水中较大幅度的上下跌宕并逐步衰减,约20 s后稳定在水面,同时受水池波浪影响小幅波动。
|
图 3 典型下沉深度测量图 Fig. 3 Typical sinking deptch survey chart |

|
图 4 第1点爆破 Fig. 4 The first point blast |

|
图 5 第2爆点爆破 Fig. 5 The second point blast |
针对出水最大高度、俯仰角及俯仰角速度等变化进行大量的试验,测试结果见表1所示。
|
|
表 1 测试结果 Tab.1 Test results |
通过分析数据可初步得到以下结论:
1) 相同角度的状态下,随着初始高度变大,下沉深度越深;
2) 对于不同的角度,该下沉深度的变化量不一样;
3) 对于小角度(小于40°),包括小的负角度均是初始位置高度的增加量大于跌落深度的变化量,如0°时高度从1 m增加到4.5 m,尾部最大下沉深度从21.34 m仅增加到22.24 m;
4) 对于大角度(大于59.6°),初始位置高度的增加量不及跌落最深的变化量,如90°时高度从0 m增加到3.53 m,尾部最大下沉深度从32.52 m增加到44.06 m。
3.2 相同高度不同角度结果分析通过分析数据可初步得到以下结论:
1) 对于大高度如3.53 m、4.5 m跌落,水平跌落下沉深度最浅;
2) 对于小高度如1 m、2.3 m跌落,0°比小角度(40°以内)跌落下沉深度更大;
3) 相同高度如3.53 m跌落,角度从−12.5°到32.3°范围内,跌落最大下沉深度变化仅有0.60 m;
4) 角度超过59.6°后,跌落最大下沉深度迅速变大,特别是90°跌落时,即使是质心位于水面跌落,下沉深度也高达32.52 m。
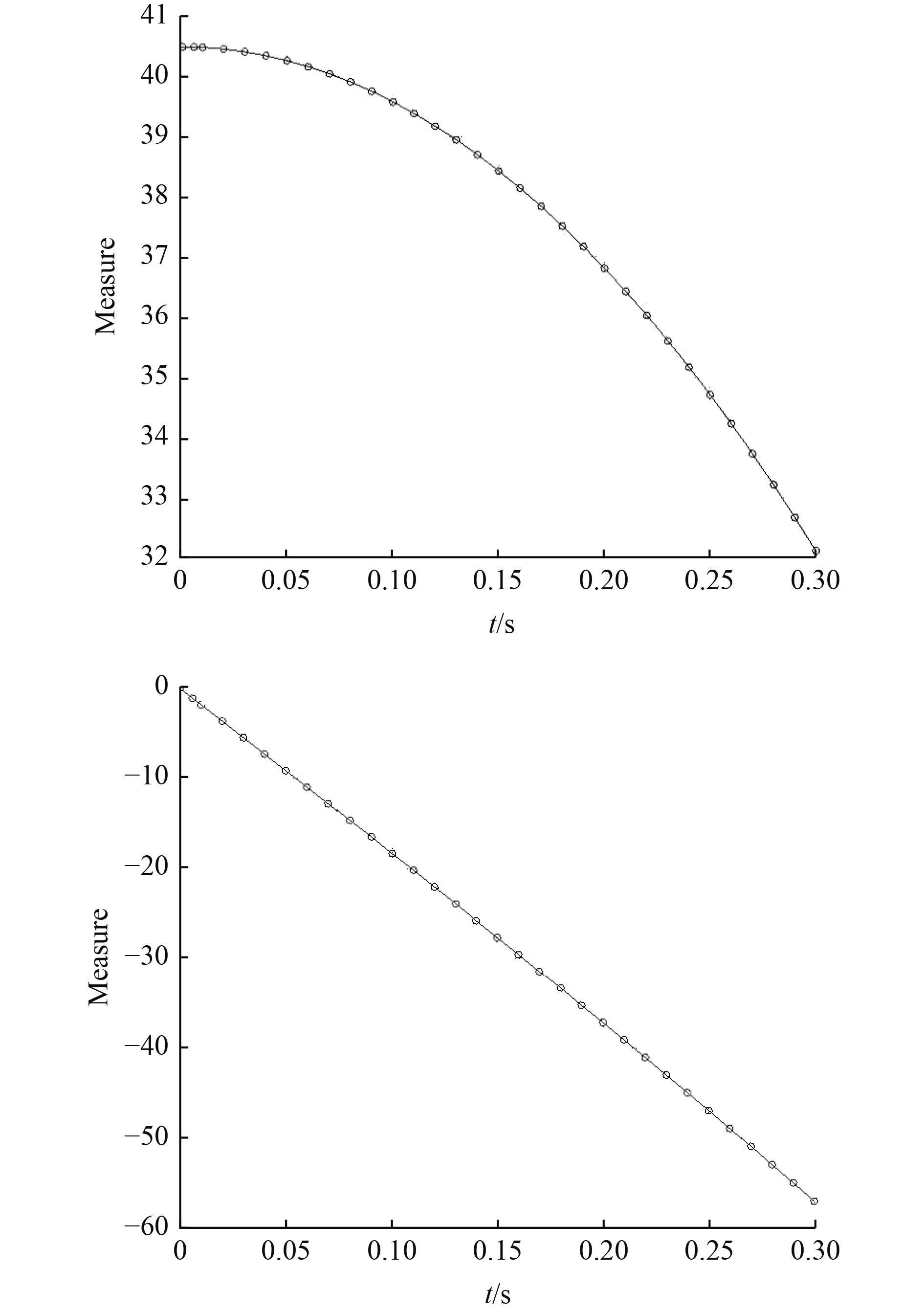
3.3 角速度的影响分析针对初始高度2.3 m,角度32.3°,通过机构动力学仿真,计算出分步起爆的间隔时间为0.288 s,及初始位置为2.5 m,俯仰角为40.5°,如图6~图8所示。
|
图 6 航行体机构动力学仿真结果 Fig. 6 Simulation results of vehicle mechanism dynamics |
进行爆破试验,实测第二次爆破时,角速度为54.45°/s,俯仰角为32.5°,下降高度为0.2 m,最大深度为19.50 m。
经分析可知,角度不大于40°时,最大跌落深度随角度的变化很小,由此可以跟32.3°剪绳状态进行比较,高度2.3 m时,最大跌落深度为19.83 m。
对比可知带角速度的落水深度略浅,相差仅1.7%,因而可以采用剪绳跌落试验替代复杂的时序爆破试验。
3.4 原模型实测比对分析俯仰角为32.3°、高度为0.41 m跌落状态对应某次原模型试验状态。试验压力传感器测量的深度为20.04 m,航行体水池缩比跌落还原到原模型的下沉深度为19.74 m。参考俯角为32.5°、高度为2.3 m的跌落试验,带角速度的落水深度变浅0.33 m,可推断相同状态带角速度的水池跌落试验的下沉深度约为20.07 m,两者相差仅仅0.2%。
由此可初步判定,常压水池做航行体跌落试验在满足傅汝德数Fr相等的前提下,可反推原模型的下沉深度。
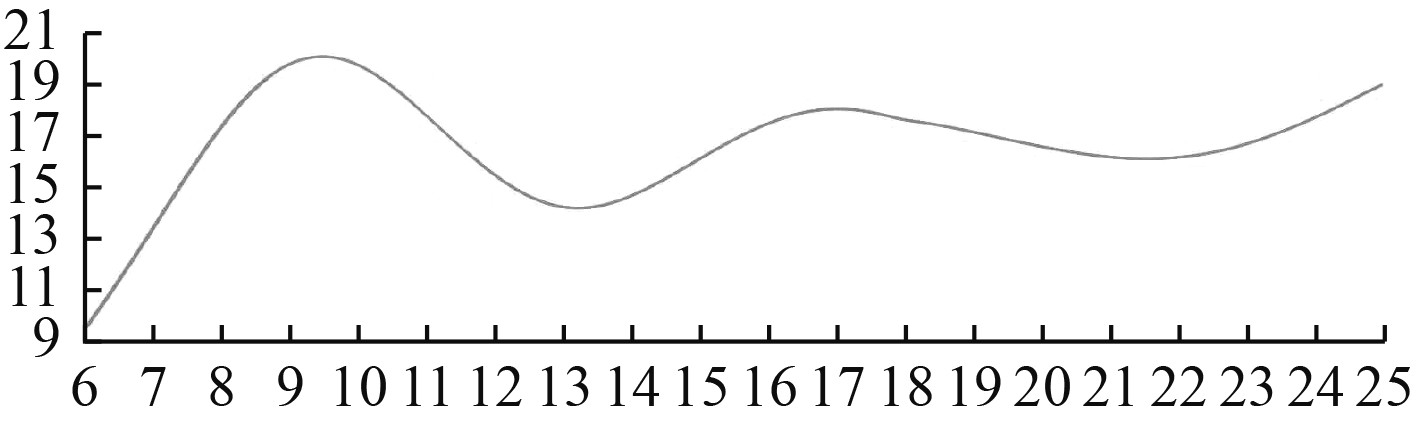
|
图 7 原模型试验测试下沉深度 Fig. 7 The original model test thesinking depth |
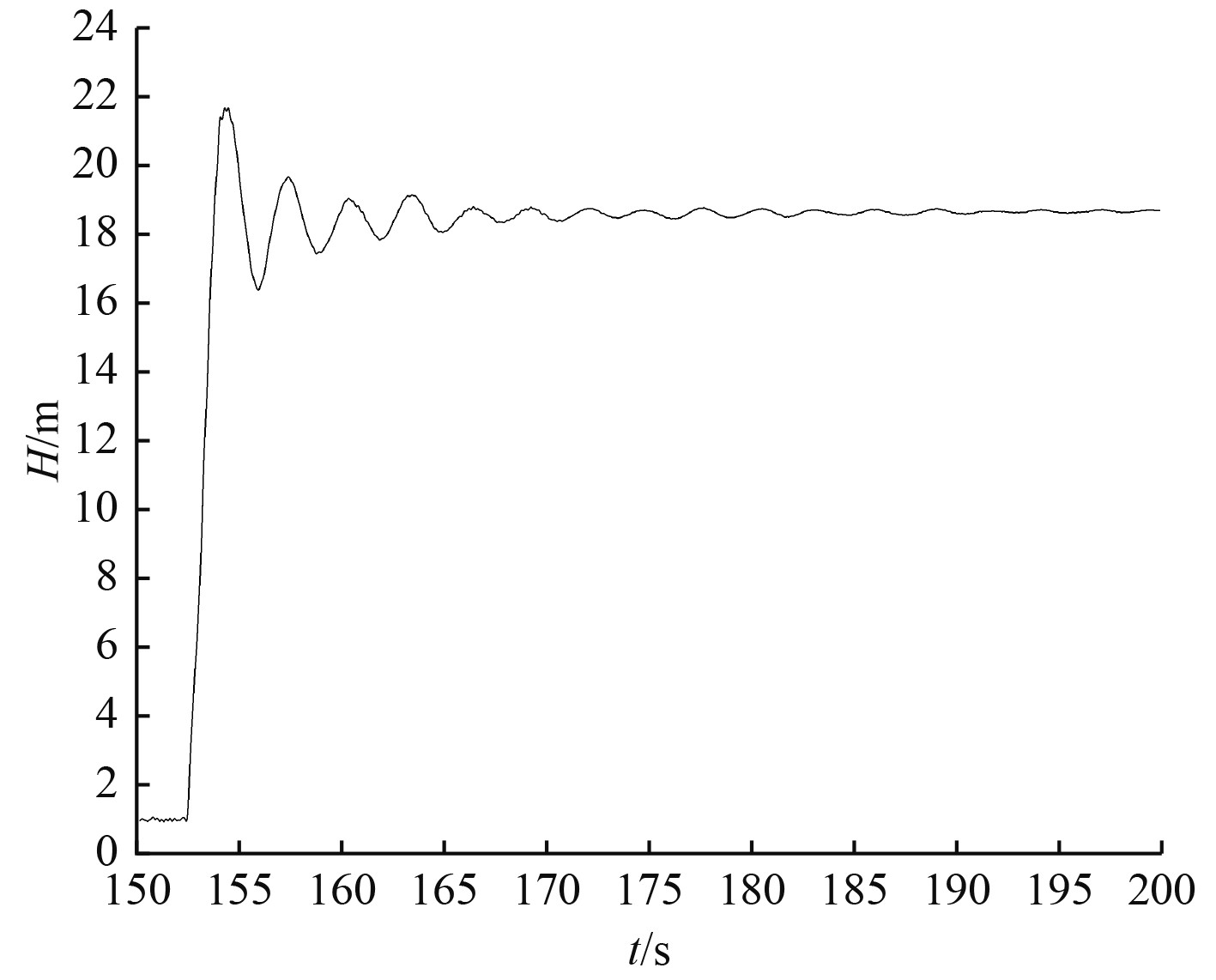
|
图 8 缩比试验转换原模型下沉深度 Fig. 8 The shrinkage test converted the original model'sinking depth |
本文介绍2种跌落试验方案,分析试验数据,得到了采用剪绳跌落试验替代复杂的时序爆破试验的合理可行性。研究了跌落高度、俯仰角及俯仰角速度的变化对最终跌落深度的影响规律,为航行体的安全发射范围提供支撑。
| [1] |
秦洪德, 赵林岳, 申静. 入水冲击问题综述[J]. 哈尔滨工业大学学报, 2011, S1: 158−163. QIN H D. ZHAO L Y, SHEN J. Overview of water impact issues[J]. Journal of Harbin Institute of Technology, 2011, S1:158−163. |
| [2] |
PARK M, JUNG Y, PARK W. Numerical study of the impact force and ricochet behaviour of high speed water entrybodies[J]. Computers and Fluids, 2003, 32: 939-951. DOI:10.1016/S0045-7930(02)00087-7 |
| [3] |
施红辉, 陈波, 王昀. 钝体超空泡倾斜穿过自由面出水实验及数值模拟[J]. 实验流体力学, 2016, 30(5): 30−34. SHI H H, CHEN B, WANG J. Experimental and numerical simulation of blunt body supercavity tilting through free surface water outlet[J]. Experimental Fluid Mechanics, 2016, 30(5):30−34. |
| [4] |
王占莹, 王冠军. 回转体垂直入水过程数值模拟[J]. 导弹与航天运载技术, 2014, 335(5): 22−25. WANG Z Y, WANG G J. Numerical simulation of vertical inflow process of a rotating body into water[J]. Missiles and Space Vehicles, 2014, 335(5):22−25. |
| [5] |
姚保太, 都军民. 一种航行体水弹道的数值仿真与试验研究[J]. 舰船科学技术, 2015, 37(7): 104−107. YAO B T, DU J M. Numerical simulation and experimental research on water trajectory of a navigation body[J]. Ship Science and Technology, 2015, 37(7):104−107. |
 2023, Vol. 45
2023, Vol. 45
