潜载导弹武器装备在国家军事力量重点建设领域中占据突出地位。其中,发射技术作为潜载导弹武器装备研制中的关键,代表着国家核心战略打击能力的强大程度。
在潜载导弹武器系统发展初期,发射导弹时潜艇需浮出水面继而进行发射作业,发射装置直接影响着发射状态,故而各国都十分关注发射装置的研制。
发射装置的主要技术包括鱼雷管发射、冷发射、自力式发射(热发射)和运载器发射[1]等。其中,冷发射由于没有热发射所需的燃气排导系统,具有发射筒结构简单、重量轻、易安装、可靠性高的特点。燃气-蒸汽式弹射技术具有能量利用充分,压力变化平稳,内弹道参数较理想,能量可调,较容易实现变深度发射等特点。
燃气-蒸汽水下发射系统地面试验装置规模大、试验投入成本高且系统的非定常性使得试验参数不易获得,关于此类发射系统的试验研究见诸报道的并不多。赵世平等[2]对比了燃气-蒸汽发射形式和纯燃气发射方式并进行了相关试验研究。结果显示,燃气-蒸汽水下发射系统需要更大的燃气发生器装药量,而且对热防护设计的需求要小得多。吕翔等[3]针对燃气-蒸汽水下发射系统搭建了缩比试验台并进行了试验研究,得出导弹出筒时运动摩擦系数和发射速度的关系,建立了运动方程求解方法。由于零维内弹道模型能提供的流场信息有限,试验周期长、耗费大且获取试验参数困难。计算流体力学(CFD)研究方法的出现给研究者提供了一种更加便捷且低成本的了解内流场特性的方法。肖虎斌[4]采用CFD方法初步模拟了燃气-蒸汽水下发射动力系统内流场的情况。采用粒子追踪方法计算高温燃气中液滴的运动规律,TAB模型模拟液滴二次破碎现象。计算结果准确模拟了发射动力系统内液滴的运动蒸发情况。芮守祯等[5]基于欧拉坐标的有限体积方法计算气态流场,采用拉格朗日方法追踪液滴相的运动规律,子模型描述液滴的蒸发行为。计算结果表明,喷注的初始液滴直径越小则穿透深度越低,蒸发时液滴寿命越小。液滴温度越高则越容易蒸发。
目前学者们大多对于发射系统内弹道特性进行研究,而对发射系统内流场的特征及演变规律研究较少。本文以燃气-蒸汽水下发射系统内流场试验装置为背景,通过数值模拟研究了燃气-蒸汽发射系统中内流场的总压、静温和液滴蒸发率,明确了燃气经过各部件后的压力损失和静温变化情况,探讨了冷却水喷入对发射动力系统内流场的影响。
1 数学模型 1.1 物理模型及网格划分计算所针对的燃气-蒸汽发射动力系统结构如图1所示。系统工作时,燃气发生器产生的高温高压燃气经由喷管加速至声速,燃气在经由喷管流入冷却器后经历一个突扩结构而进一步加速,通过设计冷却器直径,使得燃气在经历突扩后马赫数在一定数值范围内。在冷却器中,冷却水经由水室横向射流进入高温高压超声速燃气内对燃气进行降温。冷却水采用可控压力的高压氮气进行挤压加注。掺混后的工质经过观察窗后进入弯管。冷却水与燃气所形成的混合工质进入弯管,弯管前端设计有一锥管,此种设计是防止整个气动系统的气流堵塞。经过弯管的锥管段后,燃气-蒸汽混合工质在圆弧段内转弯并排出到发射筒或通过排气管路排放至室外。
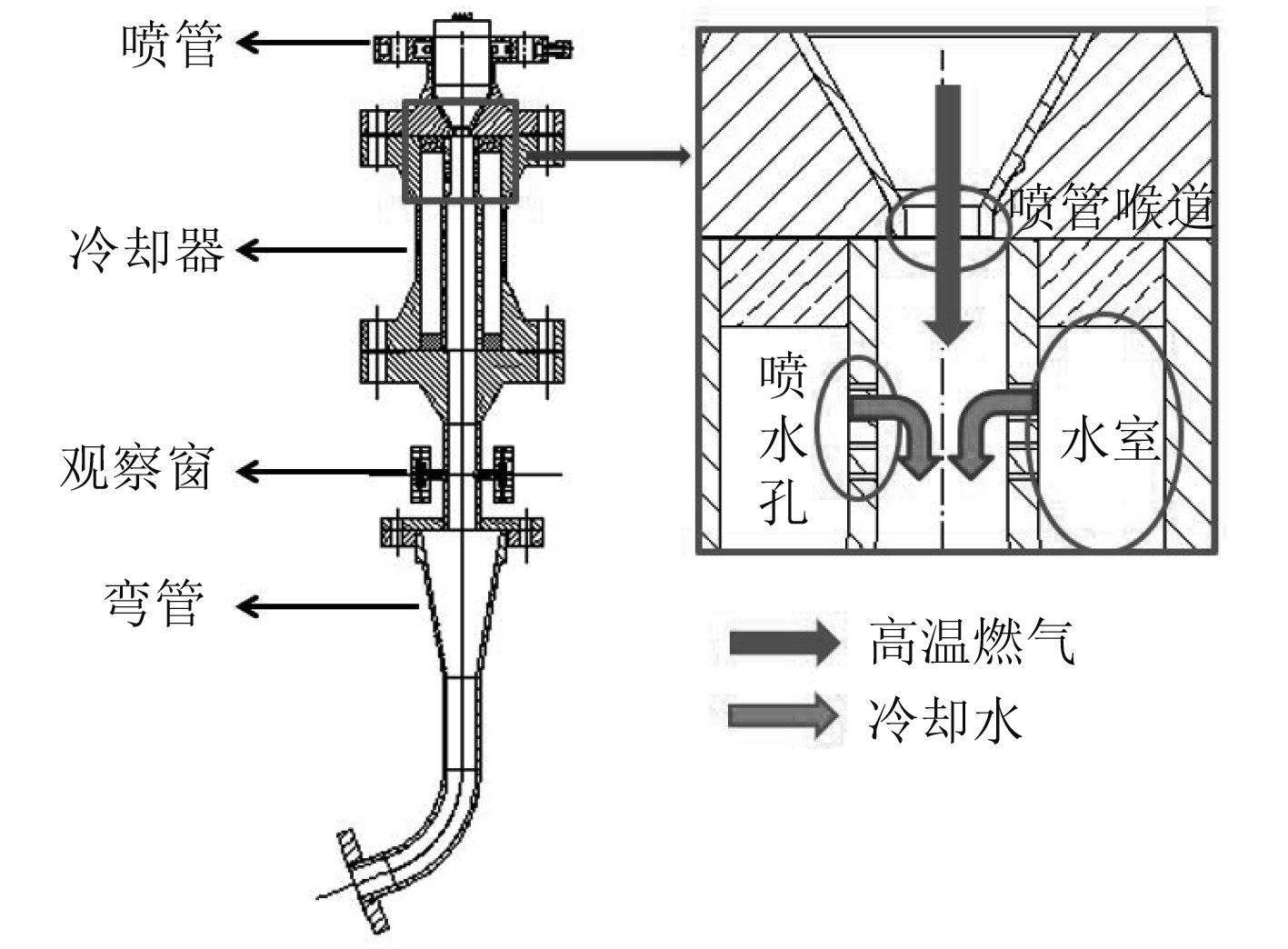
|
图 1 发射动力系统结构图 Fig. 1 Launch power system structure diagram |
所用仿真几何模型如图2所示。喷管内气流流速较低且经过喷管进入冷却器后燃气流为超声速状态,气流状态不剧烈变化时对喷管内气体不会产生影响,故在计算几何模型中减少了喷管收敛段长度。水室内冷却水用高压氮气定压加注与超声速燃气进行掺混降温,故将水室省略。在进行计算时,冷却水以粒子形式横向射流进入燃气流中。

|
图 2 发射动力系统计算几何模型图 Fig. 2 Computational geometric model of launch power system |
燃气-蒸汽水下发射系统工作过程中涉及的物理现象复杂。在进行数值计算时,对高温高压燃气进行如下假设:
1)燃气为冻结流,即不考虑高温燃气各组分之间的化学反应;
2)燃气视为理想气体;
3)不考虑流场中除液滴外少量的其他固体粒子。
在粒子追踪方法中,气相流场采用欧拉方法进行求解。可压缩的雷诺时均(RANS)Navier-Stokes方程被用于描述气相的超声速/跨声速流动过程:
1)质量守恒方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}(\rho {u_j}) = {S_m}。$ | (1) |
式中,
2)动量守恒方程
| $ \frac{{\partial (\rho {u_i})}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial P}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} + {F_i} 。$ | (2) |
3)能量守恒方程
| $ \frac{\partial }{{\partial t}}(\rho H) + \frac{\partial }{{\partial {x_j}}} (\rho {u_j}H) =- \frac{{\partial ({u_k}{\tau _{kj}})}}{{\partial {x_j}}} + \frac{{\partial {q_j}}}{{\partial {x_j}}} + {S_H}。$ | (3) |
在液体高速射流情况下的破碎问题中,液滴破碎的同时受气动力引起的Kelvin-Helmholtz波和由于液滴自身加速而产生的Rayleigh-Taylor波的影响。在KHRT模型中,模型同时考虑了2种波在液滴破碎中的作用。破碎产生的子液滴的半径计算式为:
| $ r = {B_0}{\Lambda _{{{KH}}}} 。$ | (4) |
式中:
| $ \frac{{{\Lambda _{{{KH}}}}}}{a} = 9.02\frac{{\left( {1 + 0.45{Z^{0.5}}} \right)\left( {1 + 0.4{T^{0.7}}} \right)}}{{{{\left( {1 + 0.87We_g^{1.67}} \right)}^{0.6}}}}。$ | (5) |
式中:
在液滴破碎过程中,父液滴破碎产生的质量剥离导致液滴直径的减少,父液滴半径的减小速度可由以下半径减少率方程计算:
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}t}} = - \left( {a - r} \right)/{\tau _{{\text{KH}}}},$ | (6) |
式中:
| $ {\varOmega _{KH}}\left[ {\frac{{{\rho _l}{a^3}}}{\sigma }} \right] = \frac{{0.34 + 0.38We_g^{1.5}}}{{\left( {1 + Z} \right)\left( {1 + 1.4{T^{0.6}}} \right)}} ,$ | (7) |
在RT破碎模式下,RT波的生长同样代表了液滴什么时间和如何破碎,增长最迅速的波长
| $ {\Lambda _{RT}} = 2 {\text{π}} {C_1}\sqrt {\frac{{3\sigma }}{{{a_p}\left( {{\rho _l} - {\rho _g}} \right)}}}。$ | (8) |
式中,
| ${\tau _{RT}} = \sqrt {\frac{{{\sigma ^{0.5}}\left( {{\rho _l} + {\rho _g}} \right)}}{2}{{\left( {\frac{3}{{{a_p}\left( {{\rho _l} - {\rho _g}} \right)}}} \right)}^{1.5}}} 。$ | (9) |
当液滴在气流中,满足破碎时间的条件时,液滴即发生破碎现象,新生成液滴的半径为:
| $ r = 0.5{\Lambda _{RT}}。$ | (10) |
在进行液滴破碎的计算时,父液滴的质量减少同样在计算中给予考虑,父液滴的质量减少3%时,引入一个新液滴集合代表新生成的液滴,否则破碎现象只在同一液滴集合中进行模拟。
高速气流中液滴的随流蒸发现象传热传质特征由对流和扩散一同控制。其中,液滴与气体相对运动引起的对流传输效应由薄膜理论考虑,液滴蒸发分为预热和稳定蒸发2个阶段,质量变化率分别为:
| $ {\dot m_k} = {\text{π}} {d_k}{D_g}{\rho _g}Sh\ln (1 + B) ,$ | (11) |
| $ {\dot m_k} = {\text{π}} {d_k}\frac{\lambda }{{{c_p}}}Nu\ln (1 + B) 。$ | (12) |
式中:
| $ Sh = 2 + 0.6{{Re} _k}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}S{c^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}},$ | (13) |
| $ Nu = 2 + 0.6{{Re} _k}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}{Pr ^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}},$ | (14) |
| $ {{Re} _k} = \frac{{\rho {d_k}\left| {v - {v_k}} \right|}}{\mu }。$ | (15) |
在刘易斯数
| $ \frac{{{\rm{d}}(d_k^2)}}{{{\rm{d}}t}} = - \frac{{4Nu{\lambda _r}}}{{{\rho _k}{c_{pr}}}}\ln (1 + B) 。$ | (16) |
其中,B为质量传输数。
在预热蒸发阶段:
| $ B = {{{Y_{ls}}} \mathord{\left/ {\vphantom {{{Y_{ls}}} {(1 - {Y_{ls}})}}} \right. } {(1 - {Y_{ls}})}} ,$ | (17) |
在稳定蒸发段:
| $ B = {{{c_{pr}}(T - {T_k})} \mathord{\left/ {\vphantom {{{c_{pr}}(T - {T_k})} L}} \right. } L},$ | (18) |
| $ {Y_{ls}} = {\left[ {1 + \left( {\frac{p}{{{p_{ls}}}} - 1} \right)\frac{{{M_g}}}{{{M_l}}}} \right]^{ - 1}} 。$ | (19) |
式中:
| $ {p_{ls}} = 133.322\exp \left( {18.3036 - \frac{{3816.44}}{{{T_k} - 46.13}}} \right) 。$ | (20) |
L为液滴汽化潜热,有
| $ L = 2257.1 \times {10^3}{\left( {\frac{{647.3 - {T_k}}}{{647.3 - 373.15}}} \right)^{0.31}} 。$ | (21) |
考虑流体与颗粒由于变质量产生的能量源,忽略辐射热,得到液滴颗粒在预热阶段的温度变化方程:
| $\frac{{d{T_k}}}{{dt}} = \frac{{\left[ {{Q_k} - {Q_h} - {{\dot m}_k}({c_p}T - {c_k}{T_k})} \right]}}{{({m_k}{c_k})}} 。$ | (22) |
其中,
| $ {Q_k} = {\text{π}} {d_k}Nu\lambda ({T_k} - T)\frac{{\ln (1 + B)}}{B} 。$ | (23) |
| $ {Q_h} = {\dot m_k}L 。$ | (24) |
当液滴达到平衡温度后进入稳定蒸发阶段,液滴温度保持不变。
1.3 数值方法本文基于欧拉-拉格朗日的粒子追踪方法进行系统的数值仿真,采用欧拉网格的非稳态雷诺时均方程(URANS)来模拟高温高压高速燃气的流动,适用旋流流动的
发射系统的燃气发生器产生的高温高压燃气总压为10 MPa,总温为2 000 K,流量为8 kg/s。冷却水与燃气流量之比为1。产生的燃气组分如表1所示。
|
|
表 1 燃气组分组成表 Tab.1 Gas composition table |
采用33万、66万和128万共3种网格数量的计算网格针对纯燃气流动情况下系统的流场进行网格无关性检验。网格无关性的对比计算结果为发射动力系统中心轴线上沿程总压变化规律,对比结果如图3所示。结果证明,66万网格和128万网格所获得的计算结果与网格数量无关,故本文采用66万的计算网格。

|
图 3 燃气-蒸汽发射动力系统计算网格无关性检验结果 Fig. 3 Independence test results of calculation grid for gas-steam launch power system |
Barata等[14]研究了横向气流中的液滴蒸发特性。其工况中气流速度为10 m/s,气流温度为800 K,液滴初始直径为0.23 mm。本文计算粒径结果如下:0 s时为0.23 mm,0.01 s时0.218 mm,0.02 s时0.199 mm,0.03 s时0.189 mm和0.04 s下0.173 mm。对应时刻的文献中结果分别0.23 mm、0.223 mm、0.206 mm、0.193mm和0.178 8 mm。对比可知本文液滴蒸发计算结果与文献中结果基本一致。
Lin[15]采用水为工质进行了超声速条件下,液体横向射流雾化的试验研究。观测了射流液体的穿透深度和液滴索泰尔平均直径(SMD)情况,获得射流穿透深度与气液动量比之间的经验关系式。试验条件如表2所示。
|
|
表 2 Lin等进行试验的试验状态表 Tab.2 The test status table of Lin et al.'s test |
如图4所示,本文数值计算模型可以很好地模拟超声速条件下液体横流雾化情况。在喷口附近,数值模型获得的射流深度稍高于经验公式的结果。在随后的随流过程中,数值模型所计算求得的液滴包络边界与经验公式所求的结果一致性良好,在绝对数值上也有着很好的契合性,求得的液滴雾化场全局SMD值为10.8 μm,对比实验值所获得的15.3 μm,未产生重大偏离。这表明数值模型有较好的仿真性。
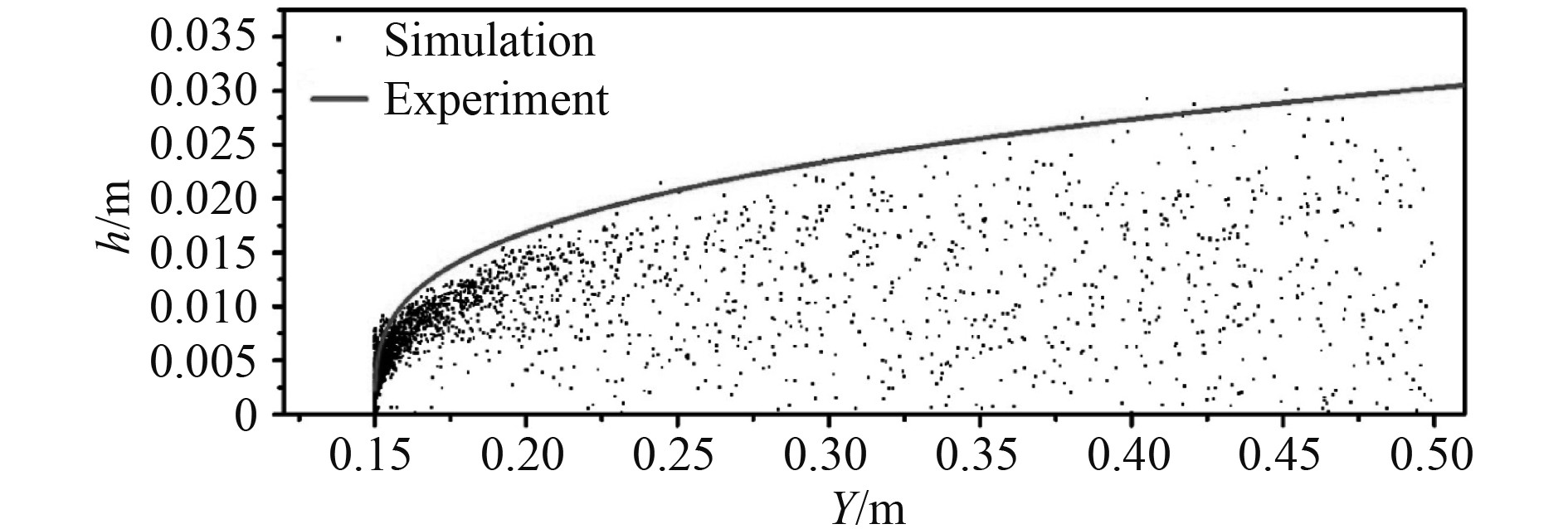
|
图 4 穿透深度计算值与实验值对比 Fig. 4 Comparison of penetration depth calculation value and experimental value |
为避免高温燃气进入发射筒后损坏潜射导弹的弹体结构和弹载设备,通常会将冷却水注入高温燃气中,既可以保证弹射工质气体不会损坏潜射导弹又可以通过对喷水量的调节实现变深度发射的目的。
在冷却水雾化及蒸发后,发射系统内从纯燃气工况下变为燃气-液滴-蒸汽下的多相流动工况,其流场进一步复杂化。图5为发射系统内纯燃气工况及燃气-蒸汽工况下,沿流动方向各截面的质量加权平均总压的分布情况,其中区域I表示喷管(包含突扩结构)区域,区域II表示冷却器区域,区域III表示长直管段区域,区域IV表示锥管段区域,区域V表示弯管段区域。由图可知,冷却水注入高温燃气后形成水蒸气,使得系统出口处总压值明显高于纯燃气工况下的总压值。在喷管喉道出口处总压的急剧下降是由于喷管喉道出口与冷却器入口之间形成的突扩结构造成的。之后气流经过冷却器后半部分的渐扩结构,导致了燃气流总压的进一步损失。相较纯燃气工况下,冷却器中的总压变化情况,燃气-蒸汽工况下冷却器中的气流总压明显低于纯燃气工况下的总压。这是由于在燃气-蒸汽工况下,冷却器内冷却水横向射流进入高温燃气中,射流液柱对高温燃气的流动有很强的阻碍作用,致使气流总压明显下降。在长直管段后半程中燃气-蒸汽工况下的气流总压值逐渐上升,在长直管段出口处燃气-蒸汽工况工质气流总压高于纯燃气工况。这是因为随着冷却水的蒸发,气体质量流量剧烈上升,最终使得在长直管段出口处燃气-蒸汽工况下的气流总压超过了纯燃气状态。在弯管的锥管段中,2种工况下气体的总压均大幅降低。在弯管转弯段中,燃气-蒸汽工况下,工质气体总压变化趋势与纯燃气工况下工质气体总压变化趋势相同。对比图7中的冷却水沿程蒸发率变化情况可知,此段中冷却水已蒸发完毕,导致了此段2种工况下气体总压变化趋势相同,冷却水蒸发导致的系统内质量流量增加则提高了系统出口处的总压。
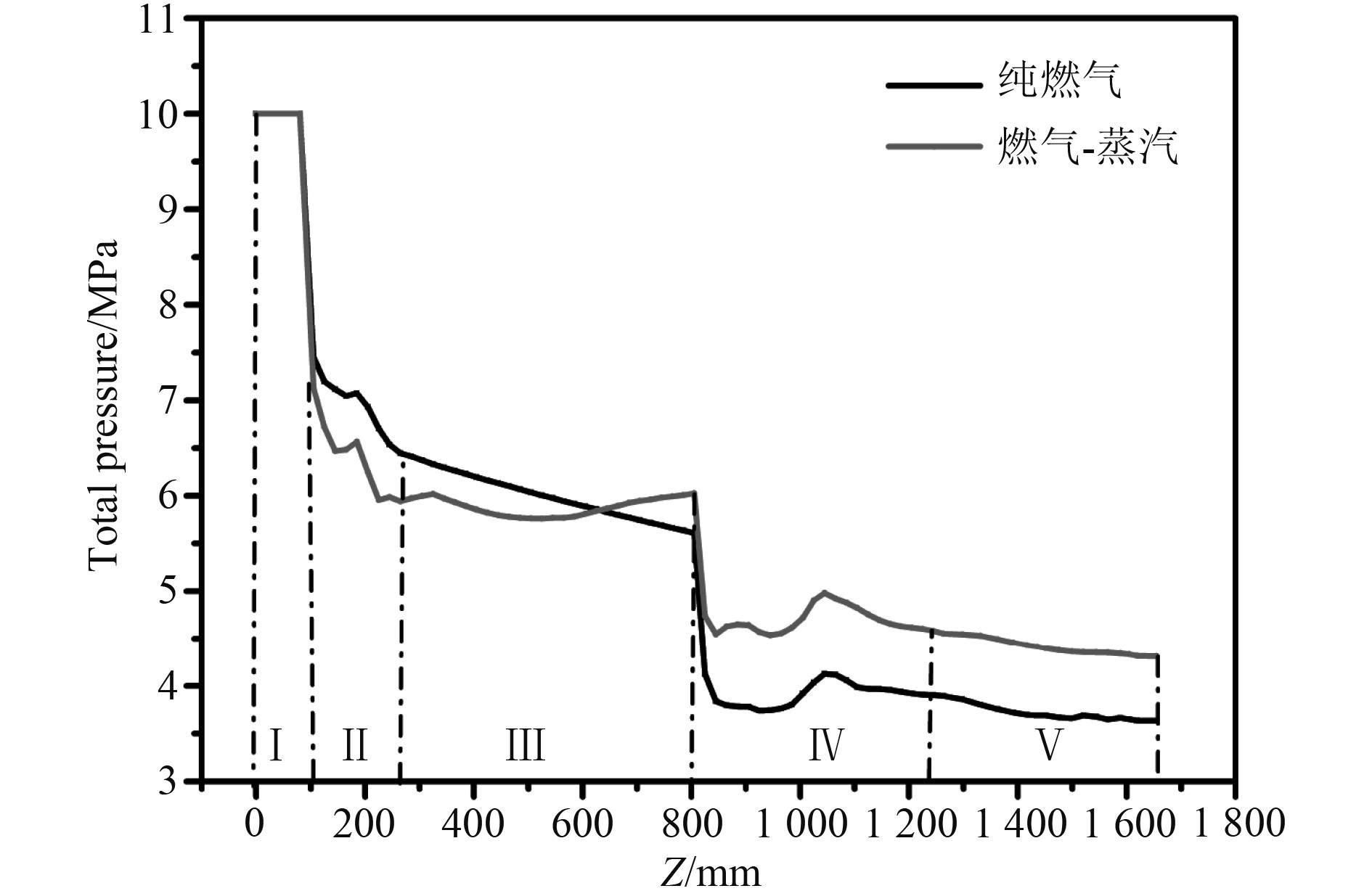
|
图 5 发射动力系统纯燃气工况及燃气-蒸汽工况质量加权平均总压分布情况 Fig. 5 The distribution of mass-weighted average total pressure of the launch power system under pure gas conditions and gas-steam conditions |
在动力系统中,冷却水注入系统高温燃气后的气体温度是发射动力系统能否正常工作的重要指标。图6为发射动力系统在燃气-蒸汽工况和纯燃气工况下的沿程各截面静温变化情况。可知,在燃气-蒸汽工况下,气体静温明显低于纯燃气工况。可见冷却水的注入对于降低系统工质的静温有重要作用。在喷管段中,2种工况下气体静温差异不大,气体静温的降低主要是由于喷管对气流的加速导致。冷却器中的静温变化剧烈,结合图7可知,冷却器中冷却水蒸发超过了50%,故而静温大幅下降。在之后的长直管段中,气体静温变化相对稳定,相较于纯燃气状态,燃气-蒸汽工况下气体的静温在长直管段中有略微下降的趋势,这同样是由于冷却水雾化形成的液滴在长直管段中蒸发的结果。只是在长直管段中液滴蒸发率变化稳定,这也导致了静温的变化缓慢。气体流经锥管段和弯管段时,静温先略微上升后便保持稳定。这是因为在弯管中超声速气流马赫数先下降导致了静温的上升,同时又由于液滴的蒸发使得燃气-蒸汽工况下,气体静温上升的幅度较纯燃气工况下小。
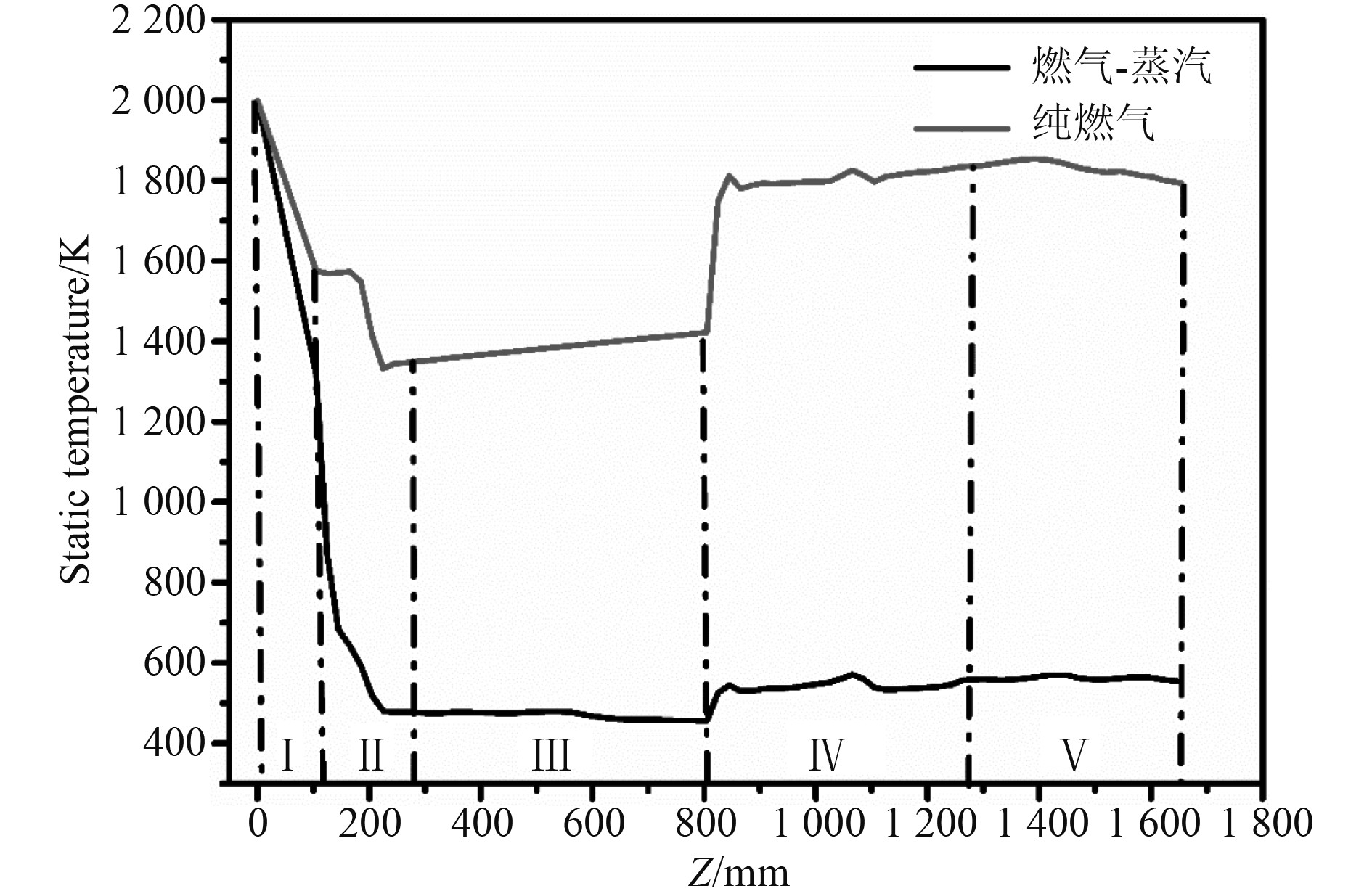
|
图 6 发射动力系统纯燃气工况及燃气-蒸汽工况静温分布情况 Fig. 6 The static temperature distribution of the pure gas and gas-steam operating conditions of the launch power system |
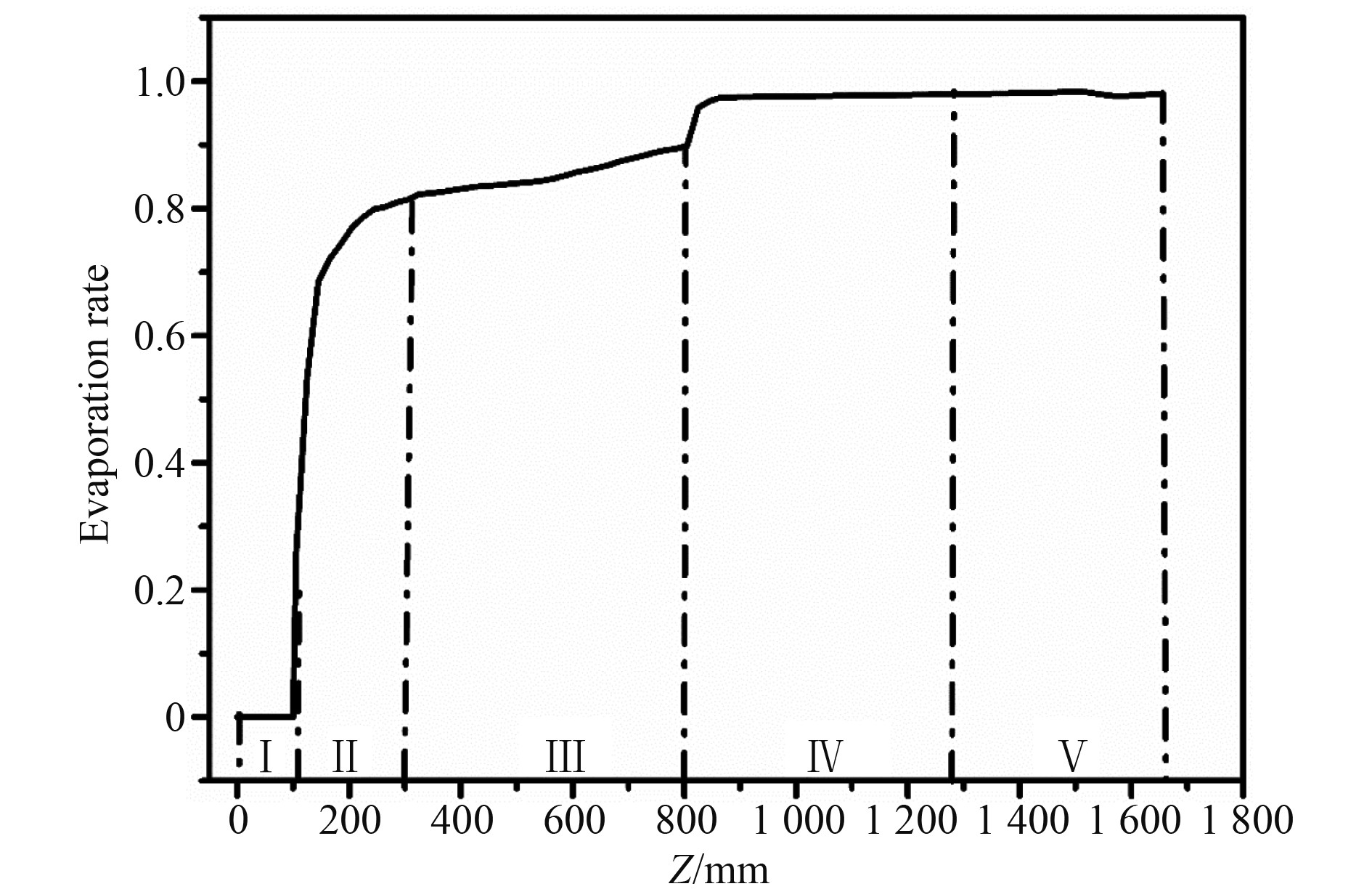
|
图 7 燃气-蒸汽工况下发射动力系统内冷却水蒸发情况 Fig. 7 Evaporation of cooling water in the launch power system under gas-steam conditions |
为保证发射筒底的压力稳定,希望冷却水在工质气体进入发射筒底前完全蒸发。图7为发射动力系统在燃气-冷却水流量比为1∶1工况下的冷却水沿程蒸发情况。可知,系统中冷却水在气体流出出口时已基本蒸发完全,发射系统全局蒸发率约为98%,基本所有冷却水在发射动力系统内就已完全蒸发。在喷管段中,无冷却水的加入,故蒸发率为0。在冷却器中,冷却水蒸发率剧烈上升。这是因为燃气-冷却水间较大的相对速度差使得冷却水雾化液滴表面换热强烈,导致冷却水的剧烈蒸发。在随后的长直管段中,未蒸发的残存液滴与燃气流的相对速度差较冷却器中小,故而液滴蒸发率的增加较为平稳。之后的弯管和锥管段中,气体的速度变化和静温上升,液滴由于惯性的作用使得气-液两相间的速度差又一次变大。这也导致了液滴蒸发率变化趋势的又一次陡峭。经历这一次液滴蒸发率的变化后,冷却水雾化形成的液滴基本在发射动力系统内蒸发完全。
3 结 语本文建立了燃气-蒸汽水下发射系统内高温高压燃气流动、冷却水横向喷注后雾化及蒸发的数值模型,并计算研究了混合工质的流动传热现象。发现:
1)纯燃气工况及燃气-蒸汽工况下,发射动力系统内突扩结构及渐扩结构对气流总压损失有着决定性作用;2)弯管结构并没有对发射动力系统总压产生太大损失;3)冷却水的注入对于气流总压有着明显耗散损失作用;4)冷却水注入后发射动力系统出口静温大幅下降;5)在冷却水注入高温燃气后,在毫秒量级内发射动力系统又回归稳定工作状态;6)冷却水注入发射动力系统后,在发射动力系统内几乎全部蒸发。
| [1] |
PAUL C, GLEN C. Submarine missile launch system[P]. United States Patent, 3857321, December, 31.
|
| [2] |
赵世平, 李江, 何国强, 等. 固体燃气发生器动力模拟水下发射试验研究[J]. 固体火箭技术, 2006, 29(1): 5-8. DOI:10.3969/j.issn.1006-2793.2006.01.002 |
| [3] |
吕翔, 李江, 陈剑, 等. 变深度水下发射系统内弹道实验研究[J]. 固体火箭技术, 2012, 35(1): 24-28. DOI:10.3969/j.issn.1006-2793.2012.01.005 |
| [4] |
肖虎斌, 赵世平. 燃气蒸汽式发射动力装置复杂内流场数值模拟[J]. 固体火箭技术, 2009(4): 392-395. DOI:10.3969/j.issn.1006-2793.2009.04.009 |
| [5] |
芮守祯, 邢玉明. 导弹弹射装置冷却器中液滴轨迹及特性的数值模拟[J]. 舰船科学技术, 2010, 32(4): 113-116. DOI:10.3404/j.issn.1672-7649.2010.04.028 |
| [6] |
YANG S, LE JIALING, WEI H E, et al. Fuel atomization and droplet breakup models for numerical simulation of spray combustion in a scramjet combustor[C]//AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2013.
|
| [7] |
BHANDARKAR A, MANNA P, CHAKRABORTY D. Assessment of droplet breakup models in high-speed cross-flow[J]. Atomization & Sprays, 2017: 61–79.
|
| [8] |
阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006.
|
| [9] |
胡晓磊, 乐贵高, 马大为, 等. 喷水对冷却器流场影响数值研究[J]. 计算机仿真, 2015, 32(1): 117-121. |
| [10] |
杨琦, 郭佳肄, 胡晓磊. 喷水对燃气-蒸汽弹射内弹道影响数值研究[J]. 赤峰学院学报(自然科学版), 2016, 32(14): 191-192. DOI:10.13398/j.cnki.issn1673-260x.2016.14.081 |
| [11] |
李仁凤, 乐贵高, 马大为, 等. 结构参数对燃气-蒸汽弹射载荷和弹道影响[J]. 上海交通大学学报, 2016(11): 1789-1793. DOI:10.16183/j.cnki.jsjtu.2016.11.022 |
| [12] |
李仁凤, 乐贵高, 马大为, 等. 进气角与注水规律对燃气-蒸汽弹射的影响[J]. 航空动力学报, 2017(4): 961-969. DOI:10.13224/j.cnki.jasp.2017.04.023 |
| [13] |
胡晓磊, 孙船斌, 李仁凤, 等. 喷水孔数量对燃气-蒸汽弹射内弹道的影响[J]. 弹道学报, 2018(2): 37-41. DOI:10.12115/j.issn.1004-499X(2018)02-07 |
| [14] |
BARATA J M M, MATOS H M M, SILVA A R R. Numerical simulation of an array of evaporating droplets through a crossflow[C]//43 rd AIAA Aerospace Sciences Meeting and Exhibit. 2005: 2005.
|
| [15] |
LIN K C, KENNEDY P, JACKSON T. Structures of water jets in a mach 1.94 supersonic crossflow[C]// AIAA Aerospace Sciences Meeting and Exhibit, 2004.
|
 2023, Vol. 45
2023, Vol. 45
