2. 江苏海事职业技术学院,江苏 南京 211170
2. Jiangsu Maritime Institute, Nanjing 211170, China
为了加强物流运输港口中的船舶航行管理,减少因天气、交通流量大、航道条件差等因素导致的船舶碰撞,需要对船舶港口避撞路径进行跟踪控制[1],及时调整航行计划和避让措施,确保船舶在安全、高效的路径下航行,减少灾害损失和货物损失[2]。黄国良等[3]通过改进的蚁群算法与人工势场法结合的方式完成船舶港口避撞路径跟踪控制。首先通过动力学特性对船舶建模,制定避撞策略,通过改进的蚁群算法寻找一条最优避障路径。但是该方法收敛速度慢,实时性较差。杨琪森等[4]利用海图和海上避撞规则,构建了马尔可夫模型,并采用深度学习技术设计了一种航行势能引导机制,以实现船舶避撞。然而,这种方法在面对复杂的海上环境时,其安全避障的时间可能会相应延长。
本文提出一种基于鱼群算法的物流运输船舶港口避撞路径跟踪控制方法。
1 物流运输船舶港口避撞路径跟踪控制 1.1 船舶会遇情形分析保证船舶安全航行的水域定义为船舶区域,驾驶员只需把海上其余目标排除在该区域外,即可保证航行的安全。避撞路径的基础条件需满足其余目标航行在本船船舶区域外。
正面会遇表示目标船舶和本船在相反航线上碰面的情形,与本船舶船首两舷呈0~10°的冲突侧面会遇表示两船舶的航向在空间上侧面相撞。追尾会遇表示两船舶的航向相同,发生首尾相撞。
1.2 避撞路径跟踪控制目标函数将发生会遇情形并采取相应避撞措施到本船舶恢复原始航线的距离看做避撞路径跟踪控制目标函数。并采用鱼群算法对自适应最短避撞路径的目标函数进行求解,获取最佳的最短避撞路径参数,得到最佳最短避撞路径。
设定对方船舶的航向和速度分别设为
| $ J = \min \left\{ {{d_s} + {d_r}} \right\}。$ | (1) |
式中,
| $ {d_s} = {T_a}{V_o}{\text{,}} $ | (2) |
| $ {d_r} = {T_a}{V_o}\sin C_o'/\left| {\sin C_b'} \right|{\text{。}} $ | (3) |
式中:
该模型需满足:
| $ \left\{ \begin{gathered} {30^{\circ }} \leqslant C_o' \leqslant {90^{^\circ }} {\text{,}} \\ - {60^{\circ }} \leqslant {C_b} \leqslant - {30^{\circ }} {\text{,}} \\ {T_{CPA1}} \leqslant {T_a} \leqslant 60 {\text{,}} \\ \left( {{d_{CPA1}} \leqslant {d_G}} \right){\text{and}}\left( {{d_{CPA2}} \geqslant {d_G}} \right) {\text{。}} \\ \end{gathered} \right. $ | (4) |
式中:正负分别表示船舶避撞转向向右和向左;
船舶避撞转向后新的
| $ {d_{CPA1}} = d\sin \theta{\text{。}} $ | (5) |
船舶避撞转向后新的
| $ {T_{CPA1}} = d\cos \theta /V_R' {\text{。}} $ | (6) |
式中:
| $ C_{OT}' = C_o' - {C_T} {\text{,}} $ | (7) |
| $ V_R' = \sqrt {{V^2} + V_o^2 - 2{V_T}{V_o}\cos C_{OT}'}{\text{。}} $ | (8) |
式中:
建模是为了将船舶在港口物流运输时的环境转变成数学模型,同时区分运输过程中的障碍。栅格法将船舶运输过程中的立体环境按照船舶尺寸、空间障碍物排布情况按一定比例转换到平面坐标系中。该方法建立过程中需注意伞型结构阻挡物和栅格的大小确定应以实际船舶行驶速度和阻挡物分布情况确定。船舶在港口运输过程中的栅格模型如图1所示。空白区域为可航行区域,栅格属性记为1;黑色为阻挡物区域,栅格属性记为−1。
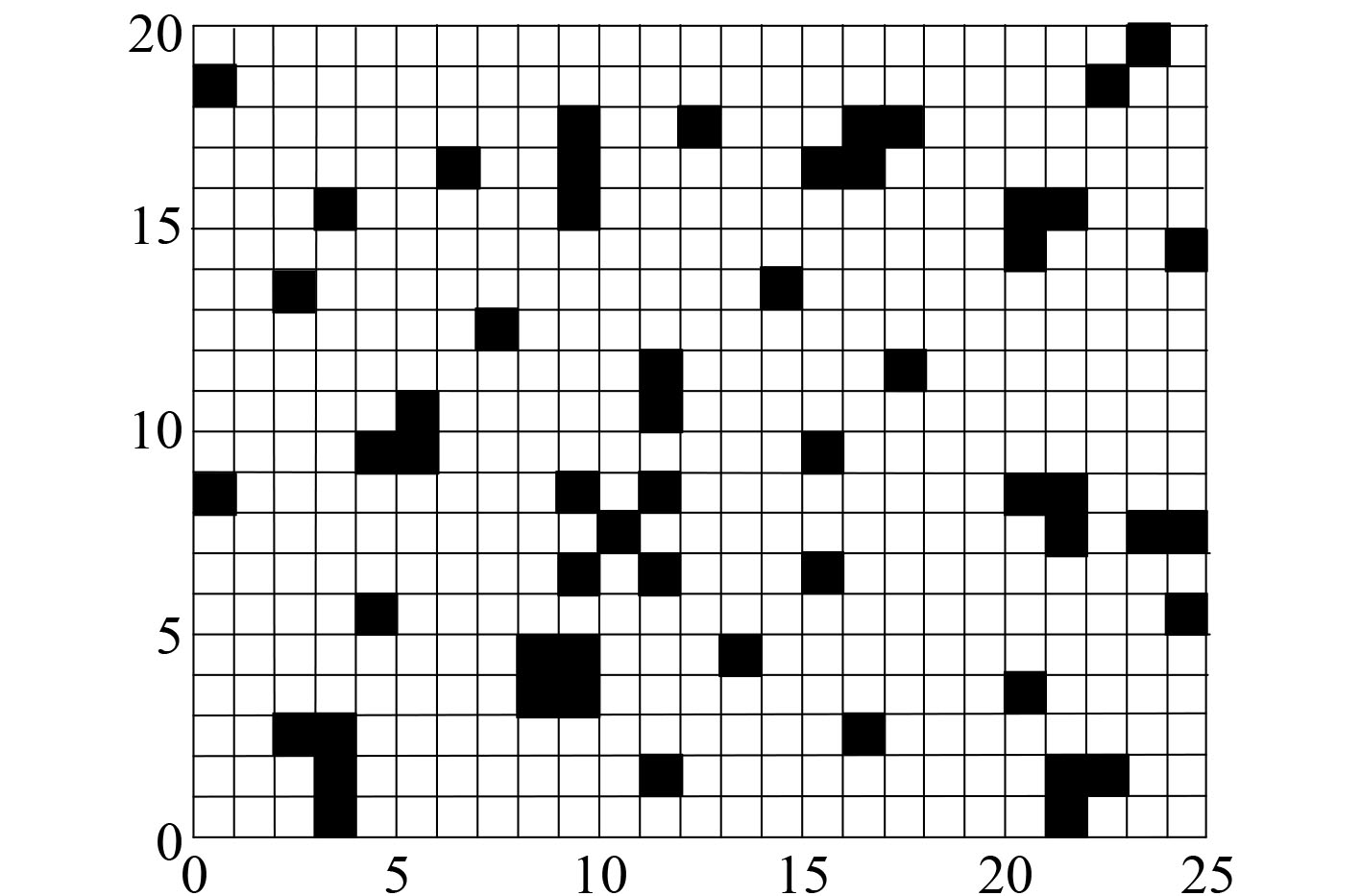
|
图 1 船舶运输栅格模型 Fig. 1 Grid model of ship transportation |
鱼群算法基本原理为利用人工鱼在栅格环境中进行节点寻优选择,将鱼群中的每条鱼均视为一个物流运输船舶避撞路径跟踪控制结果的可行解,通过鱼群的觅食、聚群和追尾行为寻找船舶最优的避撞路径跟踪控制结果。
在栅格内设鱼群的当前位置和食物浓度分别为
| $ h = \sqrt {{{\left( {{x_f} - {x_g}} \right)}^2} + {{\left( {{y_f} - {y_g}} \right)}^2}} {\text{,}} $ | (9) |
式中,
本文选用的鱼群算法策略如下:
以鱼群中一条鱼的最佳船舶避撞路径跟踪控制结果寻优为例,栅格中该鱼此刻位置为
聚群行为:该鱼此刻在栅格中的位置为
| $ {g_c} = F\left( {P\left( {{x_f},{y_f}} \right)} \right)\left( {\sum\limits_{j = 1}^{{N_f}} {{g_j}} } \right)/{N_f}{\text{。}} $ | (10) |
式中,
下一刻该鱼的位置
| $ {g}_{n}=\left\{\begin{array}{l} {g}_{c},{h}_{gc}\cdot {N}_{f}\leqslant I\cdot {h}_{{g}_{i}}{\text{,}}{g}_{c}\in {g}_{i}{\text{,}} \\ {\mathrm{arg}}\;\mathrm{min}\left\{d\left(g,{g}_{c}\right)\right\},{h}_{gc}\cdot {N}_{f}\leqslant I\cdot {h}_{{g}_{i}}{\text{,}}{g\in {g}_{i}}{\text{,}} \\ -\infty ,{h}_{gc}\cdot {N}_{f} > I\cdot {h}_{gi}{\text{。}} \end{array} \right.$ | (11) |
追尾行为:设在此刻栅格
| $ {g}_{n}=\left\{\begin{array}{l}{g}_{j},{h}_{gi}\cdot{N}_{f}\leqslant I\cdot{h}_{gi}{\text{,}}{g}_{j}\in {g}_{i}{\text{,}} \\ {\mathrm{arg}}\;\mathrm{min}\left\{d\left(g,{g}_{j}\right)\right\},{h}_{gi}\cdot{N}_{f}\leqslant I\cdot{h}_{gi}{\text{,}}{g\in {g}_{i}}{\text{,}}\\ {g}_{j}\notin {g}_{i}{\text{,}} \\ -\infty \text{,}{h}_{gj}\cdot{N}_{f} > I\cdot{h}_{gi}{\text{。}} \end{array}\right. $ | (12) |
通过上述的觅食、聚群和追尾行为搜索最佳船舶避撞路径跟踪控制结果。
2 实验分析S港船舶交通流密集且航道窄小,具有多个分支航道,这些航道交叉分布,使得船舶在交汇处会遇频繁且易发生碰撞事故。本文以S港的交汇水域为研究对象,验证本文方法的船舶港口避撞路径跟踪控制效果。为了验证鱼群算法的自适应性和收敛速率,采用图1所示的栅格,随机产生100个障碍,设船舶从栅格的A点出发,到达目标点B,鱼群规模为20,迭代30次,拥挤度因子为0.8。
为了验证改进的鱼群算法的有效性,分别使用传统鱼群算法和改进后的鱼群算法对栅格进行避撞路径跟踪控制实验,实验结果如图2所示。
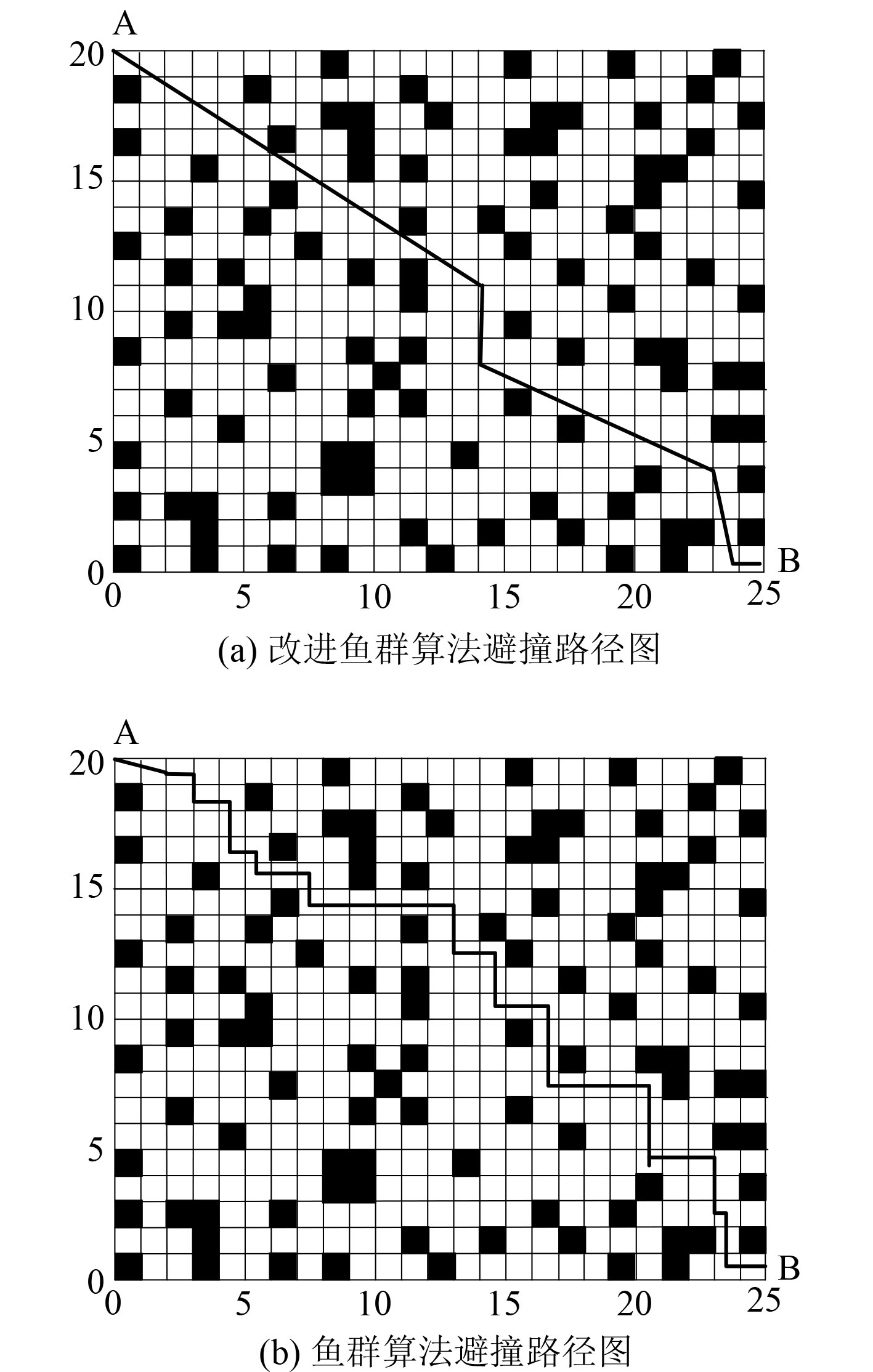
|
图 2 船舶避撞路径图 Fig. 2 Collision avoidance path diagram of ship |
可以看出,改进后的鱼群算法的获取避撞路径要比传统鱼群算法避撞路径更短。
为了验证本文算法对动态障碍的避撞效果,在上述无动态栅格中,以三角形C(三角形障碍物)和圆形D(圆形障碍物)2个动态障碍物模拟动态碰撞过程。船舶从A点出发沿图2(a)路径前进,动态碰撞实验结果如图3所示。
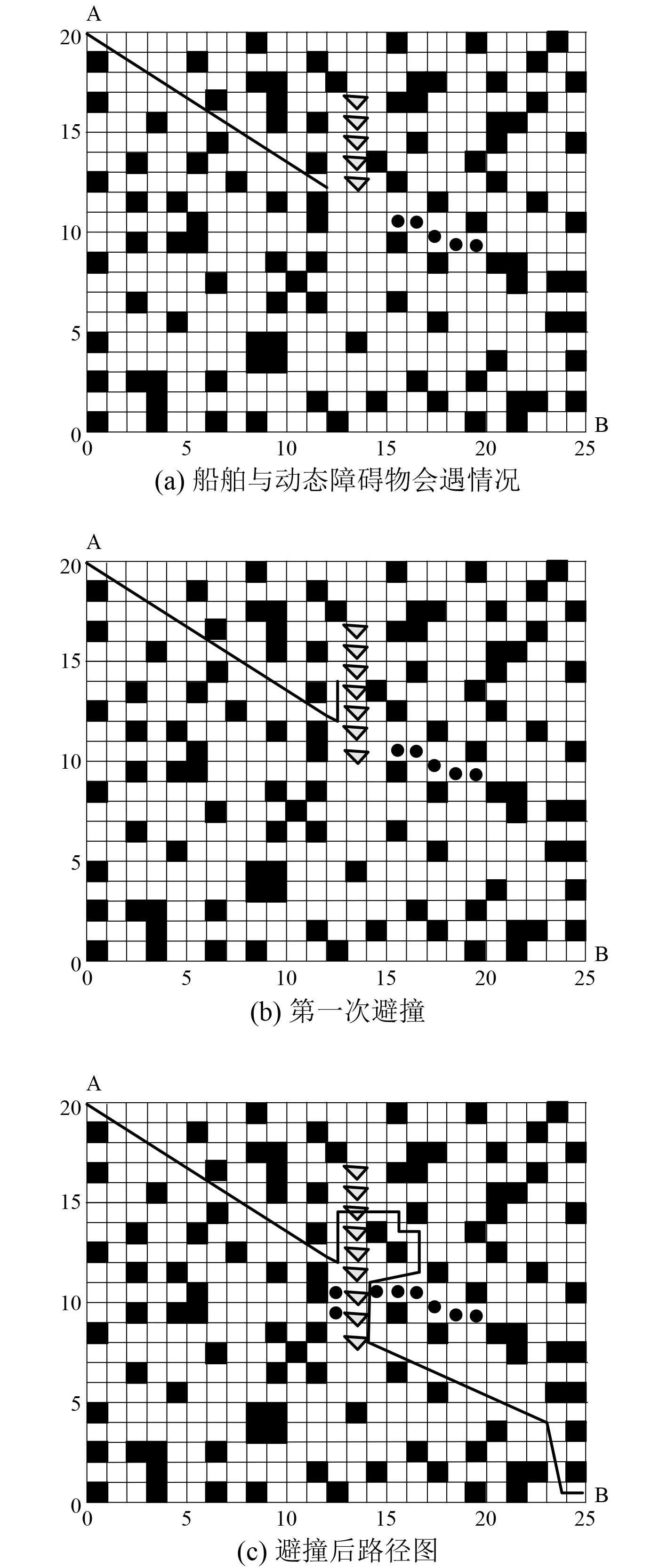
|
图 3 动态障碍碰撞过程 Fig. 3 Dynamic obstacle collision process |
可知,当本船舶与两动态障碍物会遇时,避撞决策被触发,本船舶能够及时更改原始航线,成功避开动态障碍物,并以最短路径航行到原来的航线。
设本船舶速度为12 kn,初始航向为0°,不出现意外不会更改原始航道,对方船舶速度设为14 kn。3个不同时刻下的路径跟踪实验结果如表1所示。
|
|
表 1 鱼群算法下优化避撞路径跟踪控制参数 Tab.1 Optimization control parameters of collision avoidance path tracking under fish swarm algorithm |
可知,本文方法不仅能够对物流运输船舶港口的避撞路径实施有效的跟踪控制,更能在保证安全的前提下,提供最经济、最合理的避撞路径,提升了船舶港口的安全运营和效率。
3 结 语为确保物流运输港口中船舶与货物的安全,并提高物流运输效率,研究了鱼群算法下的船舶避撞路径跟踪控制。实验结果表明,本文方法能够精准测定船舶实时航行中的会遇情形,并且能够提供最佳最短的避撞路径,全面实现运输船舶港口航行的跟踪控制。
| [1] |
谢新连, 刘超, 魏照坤. 海洋气象环境影响下的复杂水域船舶路径规划[J]. 重庆交通大学学报(自然科学版), 2021, 40(2): 1-7+20. XIE Xinlian, LIU Chao, WEI Zhaokun. Ship path planning in complex waters under the influence of Marine meteorological environment[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2021, 40(2): 1-7+20. |
| [2] |
童帮裕, 胡坚堃. 基于改进蚁群算法的船舶冰区航行路径规划[J]. 中国航海, 2019, 43(1): 24-28. TONG Bangyu, HU Jiankun. Ship navigation path planning in ice area based on improved ant colony algorithm[J]. Navigation of China, 2019, 43(1): 24-28. |
| [3] |
黄国良, 周毅, 郑坤, 等. 基于改进蚁群算法的全局船舶路径规划方法[J]. 船海工程, 2019, 52(2): 97-101+136. HUANG Guoliang, ZHOU Yi, ZHENG Kun, et al. Global ship path planning method based on improved ant colony algorithm[J]. Ship and Ocean Engineering, 2019, 52(2): 97-101+136. |
| [4] |
杨琪森, 王慎执, 桑金楠, 等. 复杂开放水域下智能船舶路径规划与避障方法[J]. 计算机集成制造系统, 2022, 28(7): 2030-2040. YANG Qisen, WANG Shenzhi, SANG Jinnan, et al. Path planning and obstacle avoidance method for intelligent ships in complex open waters[J]. Computer Integrate Manufacturing Systems, 2022, 28(7): 2030-2040. DOI:10.13196/j.cims.2022.07.009 |
 2023, Vol. 45
2023, Vol. 45
