2. 海军工程大学 舰船与海洋学院,湖北 武汉 430033;
3. 中国人民解放军 91007部队,浙江 舟山 316000
2. College of Naval Architecture and Ocean Engineering, Naval University of Engineering, Wuhan 430033, China;
3. No. 91007 Unit of PLA Liberation Army, Zhoushan 316000, China
近场声全息技术(Nearfield Acoustic Holography, NAH)由Maynard等在20世纪80年代提出[1-2],是声学研究中一种具有高分辨率重建精度的噪声源定位和声场可视化方法,在声场重构以及振动噪声控制等领域有着广泛应用。近场声全息通过多个传感器组成的测量面在被测声源物体表面的近场区域获取全息测量数据,建立重建面与测量面之间的空间变换关系,进而重建三维空间的声压场、声强场、质点振速场或者预测远场指向性,从而为声源识别定位、有效控制结构振动噪声提供技术参考[3]。
在声场逆向重构过程中,位于高波数区的倏逝波成分将与噪声误差一起被逆传递因子按指数规律放大,导致重建结果产生很大误差,严重影响声场重建的准确性[4]。针对这一问题,在重建过程中,必须对高波数区噪声误差进行滤波处理,以确保重建精度,为此国内外学者进行了广泛研究。Veronesi等[5]提出一种在波数域加低通滤波窗的方法来抑制高波数成分波对噪声的放大效应,该方法采取指数滤波器对波数域噪声信号进行处理,其算法简单,可操作性强,但该方法没有考虑声波频率、信噪比以及测量面与源面间距离等因素的影响,使用中常会出现因截止波数取值不当以致滤波效果不理想的情况。赵晨等[6]对指数滤波器中窗函数参数的合理设置进行分析,针对截止波数和窗函数陡度系数2个关键参数,总结了在不同声源频率下取得最优重建效果的截止波数和陡度系数的最优取值,对窗函数的设计优化具有重要意义。张德俊[7]在系统存在噪声情况下,对指数滤波器的截止波数进行修正,同时还考虑到指数滤波器仅在测量有限距离时有效,随着测量距离增大,滤波窗收效甚微,提出一种带约束条件的最小二乘法滤波函数。罗禹贡等[8]总结了倏逝波随距离变化的规律并设计了相应的空间频域滤波器。由于指数滤波器仅对被逆传递函数按指数规律放大的噪声误差有效,对其他区域噪声误差过滤效果不佳,何其伟等[9]提出一种波数域循环加窗逼近法,通过循环加窗筛选最接近理论声压幅值的数据作为重建数据,从而确保声场重构的准确性。莫登沅等[10-12]将空间域滤波和波数域滤波相结合,提出一种空间域即波数域联合迭代滤波窗,该滤波窗可对重建面边缘误差进行有效消除,并且经过多次迭代,明显提高了声场重建精度。在指数滤波器实际使用中发现,窗函数陡度系数的取值变化决定着窗函数的衰减速率,陡度系数取值越小,指数窗函数衰减越快,相较于截止波数的取值变化,陡度系数取值变化对反演效果影响较小,故其对指数滤波器衰减程度的调整也有限。此外,指数滤波器的陡度系数会同时影响通带内和高频带内滤波曲线的衰减速度,且不能时时兼顾两者之间的平衡,甚至会导致有价值的倏逝波被剔除,影响滤波效果,进而影响声场重建精度。
本文针对上述问题,选取2个脉动球源作为研究对象,采用巴特沃斯数字滤波器(Butterworth filter)作为滤波函数,对脉动球源声场反演过程进行数值仿真研究。基于重构误差最小原则,得到了使声场重建误差最小的巴特沃斯滤波器最优参数,并比较了该参数条件下,巴特沃斯滤波器与常用指数滤波器的效果。
1 基于Fourier空间声场变换的近场声全息在均匀理想流体介质中,小振幅声波的三维波动方程为:
| $ {\nabla ^2}p(x,y,z;t) = \frac{1}{{{c^2}}}\frac{{{\partial ^2}p(x,y,z;t)}}{{\partial {t^2}}} 。$ | (1) |
式中:
| $ {\kern 1pt} {\nabla ^2}p(x,y,z) + {k^2}p(x,y,z) = 0 。$ | (2) |
式中:
| $ \begin{aligned} & \;{\kern 1pt} p\left( {{x_H},{y_H},{z_H}} \right) = \iint_S p\left( {{x_S},{y_S},{z_S}} \right){g_D}。\\ & \left( {{x_H} - {x_S},{y_H} - {y_S},{z_H} - {z_S}} \right){\rm{d}}{x_S}{\rm{d}}{y_S}。\end{aligned}$ | (3) |
式中:S为用于积分的无穷大平面;
| $ {g_D}(x,y,z) = \frac{{z(1 - {{i}}kR){{{e}}^{{{i}}kR}}}}{{2{\text{π}} {R^3}}} 。$ | (4) |
式中,
对式(3)两边取空间二维Fourier变换,将空域卷积转化为波数域乘积可得:
| $ P( {{k_x},{k_y},{z_H}} ) = P( {{k_x},{k_y},{z_S}} ){G_D}( {{k_x},{k_y},{z_H} - {z_S}} ) 。$ | (5) |
式中:
| $ {G_D}( {{k_x},{k_y},{z_H} - {z_S}} ) = {{{e}}^{{{i}}\left( {{z_H} - {z_S}} \right){k_z}}}。$ | (6) |
式中:
当
| $ {k_z} = \sqrt {\left( {k_x^2 + k_y^2} \right) - {k^2}}。$ | (7) |
当
| $ {k_z} = \pm i\sqrt {\left( {k_x^2 + k_y^2} \right) - {k^2}}。$ | (8) |
当
当已知测量面上声压分布
| $ p\left( {{x_s},{y_s},{z_s}} \right) = {{\rm{F}}^{ - 1}}\left[ {P\left( {{k_x},{k_y},{z_H}} \right)G_D^{ - 1}\left( {{k_x},{k_y},{z_H} - {z_S}} \right)} \right]。$ | (9) |
式中,
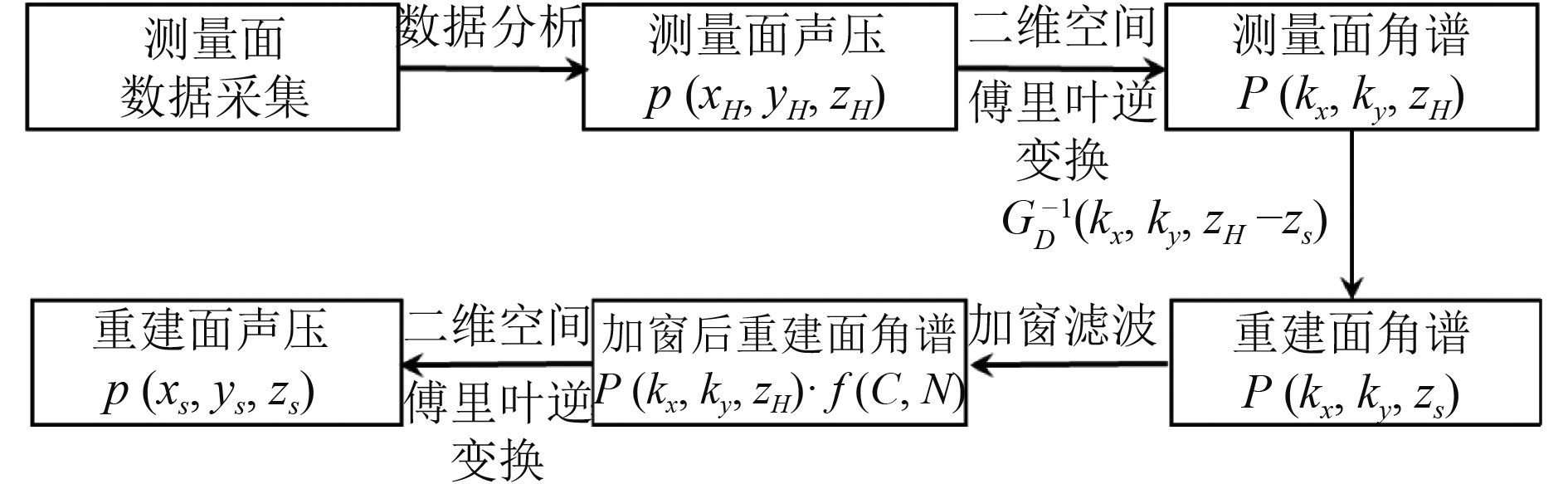
基于空间声场变换的平面近场声全息逆向重构流程,如图1所示。
|
图 1 基于空间声场变换的平面近场声全息逆向重构流程图 Fig. 1 Reverse reconstruction flow chart of planar near-field acoustical holograph based on spatial sound field transformation |
在实际声场反演过程中,位于高波数区的倏逝波成分将与噪声误差一起被逆传递函数按指数规律放大,若不对噪声信号进行低通滤波,将导致重建结果产生很大误差,严重影响声场重建的准确性,因此必须在声场逆向重构过程中进行滤波处理。
2.1 指数滤波器指数滤波器是声场重构过程中常用的滤波方法,其算法简单、可操作性强、应用广泛。截止波数和陡度系数是该方法的2个关键系数,截止波数对参与声场重构过程的测量面声压角谱范围做出了限定,其取值受声波频率、信噪比以及测量面与源面间距离等因素的影响。截止波数取值过大,则达不到滤波效果,重建误差大;截止波数取值偏小,将导致过滤波,影响重建精度。陡度系数决定着窗函数的衰减速率,其取值越小,窗函数在截止波数处截止得越陡峭,且陡度系数会同时影响通带和高频带内滤波曲线的衰减速度,有时无法兼顾两者之间的平衡,甚至会导致有价值的倏逝波被剔除,影响滤波效果,进而影响声场重建准确性。
指数滤波器计算公式为:
| $ W\left( {{k_x},{k_y}} \right) = \left\{ {\begin{split} &{1 - \frac{1}{2}\exp \left[ {\left( {{k_r}/{k_c} - 1} \right)/\alpha } \right],{k_r} \leqslant {k_c}} ,\\ & {\dfrac{1}{2}\exp \left[ {\left( {1 - {k_r}/{k_c}} \right)/\alpha } \right],{k_r} > {k_c}} 。\end{split}} \right. $ | (10) |
式中:
巴特沃斯滤波器被称为最大平坦滤波器,其在通带的频率响应曲线符合最大限度平坦特性,是连续衰减的滤波器,该滤波器能够保持增益的平坦特性,尤为适合设计低通滤波器进行滤波处理,消除高频噪声干扰。巴特沃斯滤波器过渡带的陡峭程度与阶次成正比,随着阶次的增加,幅频特性曲线越陡峭,巴特沃斯滤波器更接近于理想低通状态,抑制噪声的能力变强。随着截止频率增加,系统响应速度变快,但系统稳定性也随之下降[14]。
巴特沃斯滤波器计算公式为:
| $ f({\text{C}},N) = \frac{1}{{1 + {{{C}}^2}{{\left( {\dfrac{{{k_r}}}{k}} \right)}^{2N}}}}。$ | (11) |
式中:
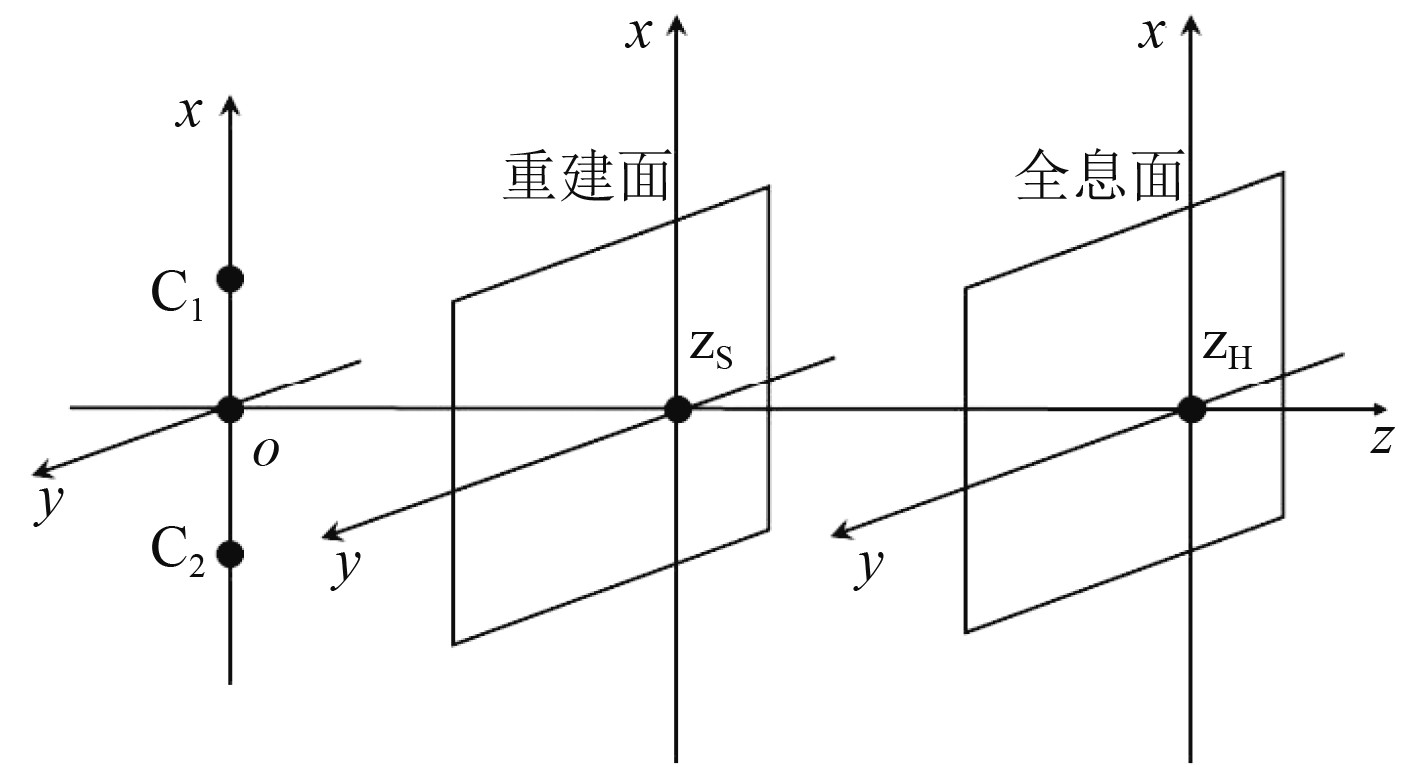
如图2所示,两脉动球源的中心坐标分别为
|
图 2 声场模型 Fig. 2 Sound field model |
脉动球源辐射声压表达式:
| $ {{p}} = \frac{A}{r}{e^{ikr}} 。$ | (12) |
式中:r为单个声源到测点距离;
| $ {{A}} = - {{i}}\frac{{k\cdot \rho \cdot{c_0}}}{{4 {\text{π}} }}{\kern 1pt} {Q_0}。$ | (13) |
式中:
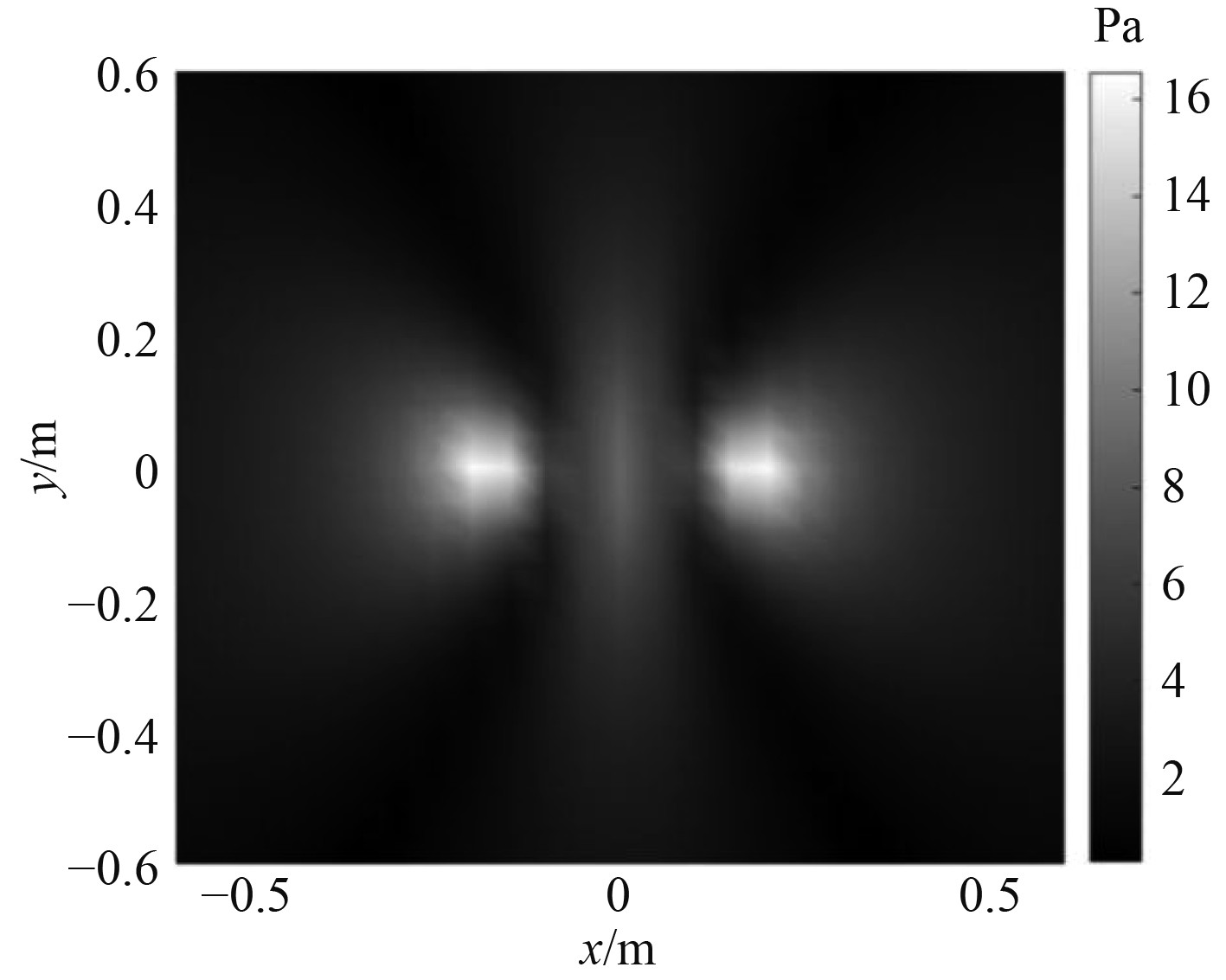
在频率为1 000 Hz时,测量面测得声压分布图如图3所示。在理论计算的基础上,添加高斯白噪声,模拟信噪比为20 dB时,测量面测得声压如图4所示。
|
图 3 测量面声压分布图 Fig. 3 Sound pressure distribution on the measuring surface |

|
图 4 加噪后测量面声压分布图 Fig. 4 Sound pressure distribution image with noise on the measuring surface |
为了能够定量描述滤波器滤波效果,定义重建误差为:
| $ {\kern 1pt} E = \frac{{\sqrt {{{\left| {{p_s} - p_s^{the{\text{ }}}} \right|}^2}} }}{{\sqrt {{{\left| {p_s^{the{\text{ }}}} \right|}^2}} }} \times 100 \text% 。$ | (14) |
式中:
声源频率为1000 Hz时,指数滤波器误差曲线如图5所示。可知,随着截止波数的增加,重建面误差急剧下降,而在该阶段相较于截止波数的取值变化,陡度系数取值变化对重建误差影响较小。当指数滤波器截止波数到达

|
图 5 指数滤波器误差曲线图 Fig. 5 Error curve of exponential filter |
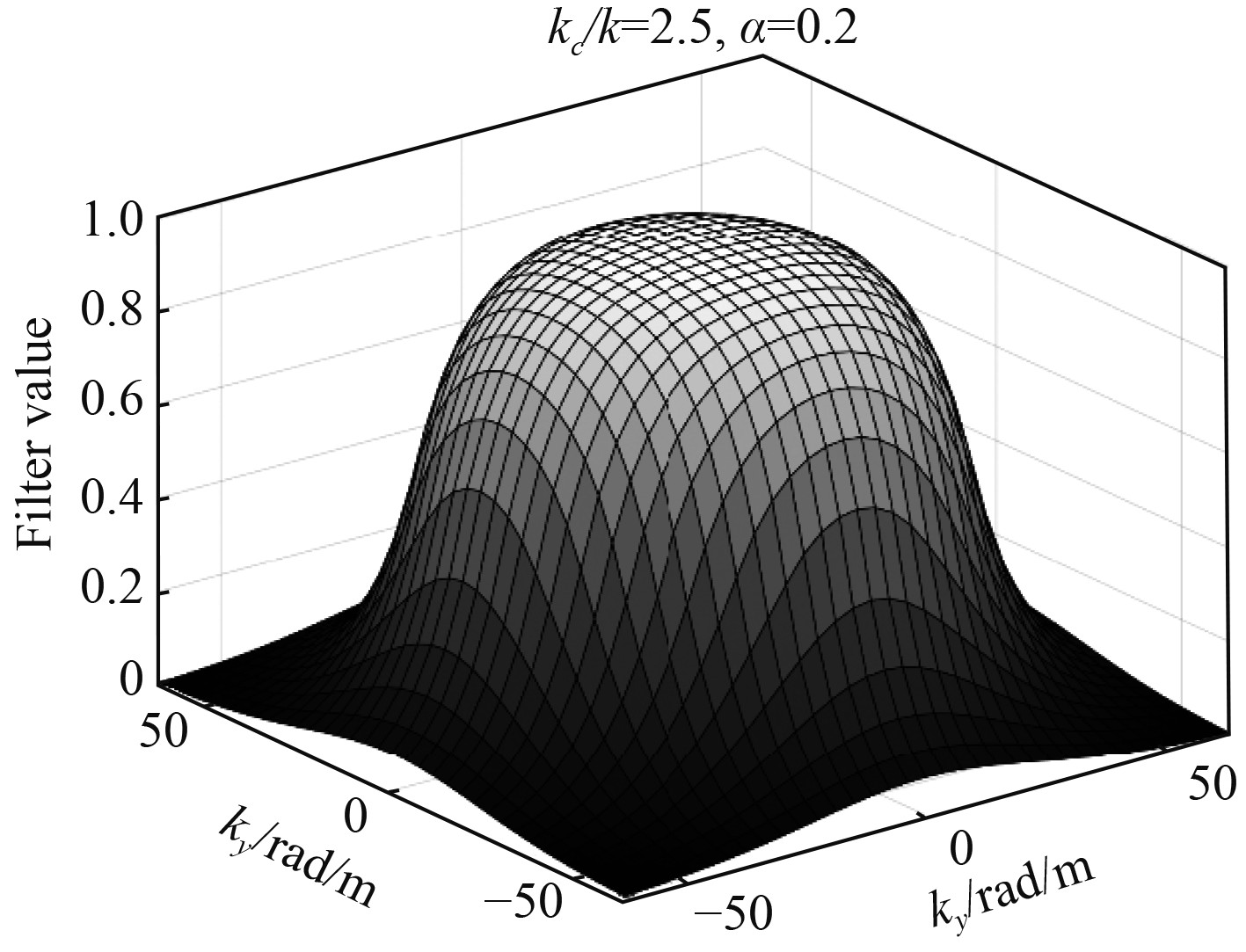
|
图 6 最优参数下指数窗函数示意图 Fig. 6 Diagram of exponential window function with optimal parameters |
声源频率为1000 Hz时,巴特沃斯滤波器误差曲线如图7所示。可以看出,在阶次

|
图 7 巴特沃斯滤波器误差曲线图 Fig. 7 Error curve of Butterworth filter |

|
图 8 最优参数下巴特沃斯窗函数示意图 Fig. 8 Diagram of Butterworth window function with optimal parameters |
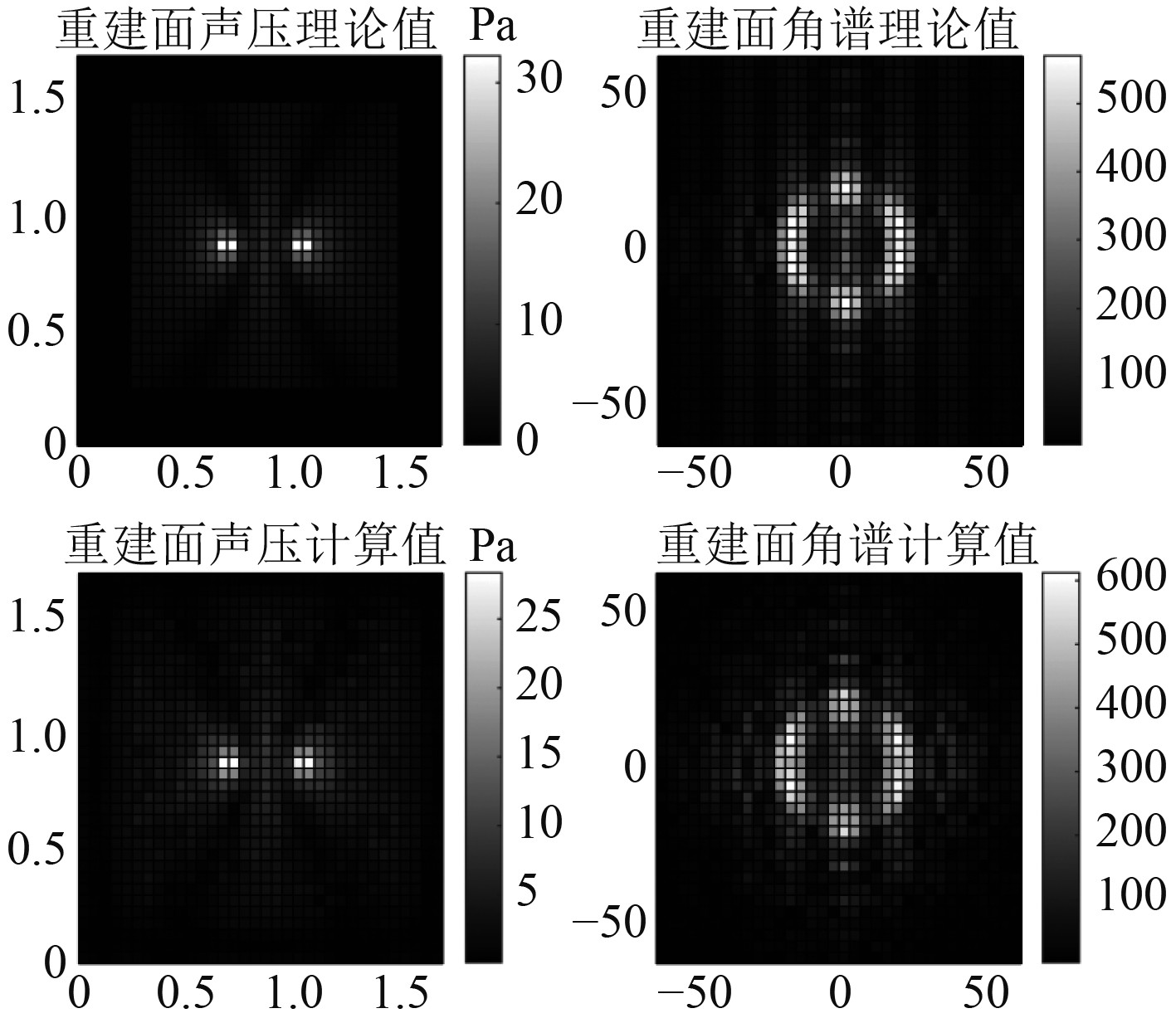
当声源频率为1000 Hz时,分析图5指数滤波器误差曲线可知,指数滤波器选择最优参数:截止波数
|
图 9 指数窗函数滤波后重建结果 Fig. 9 Reconstructed result filtered by exponential window function |
|
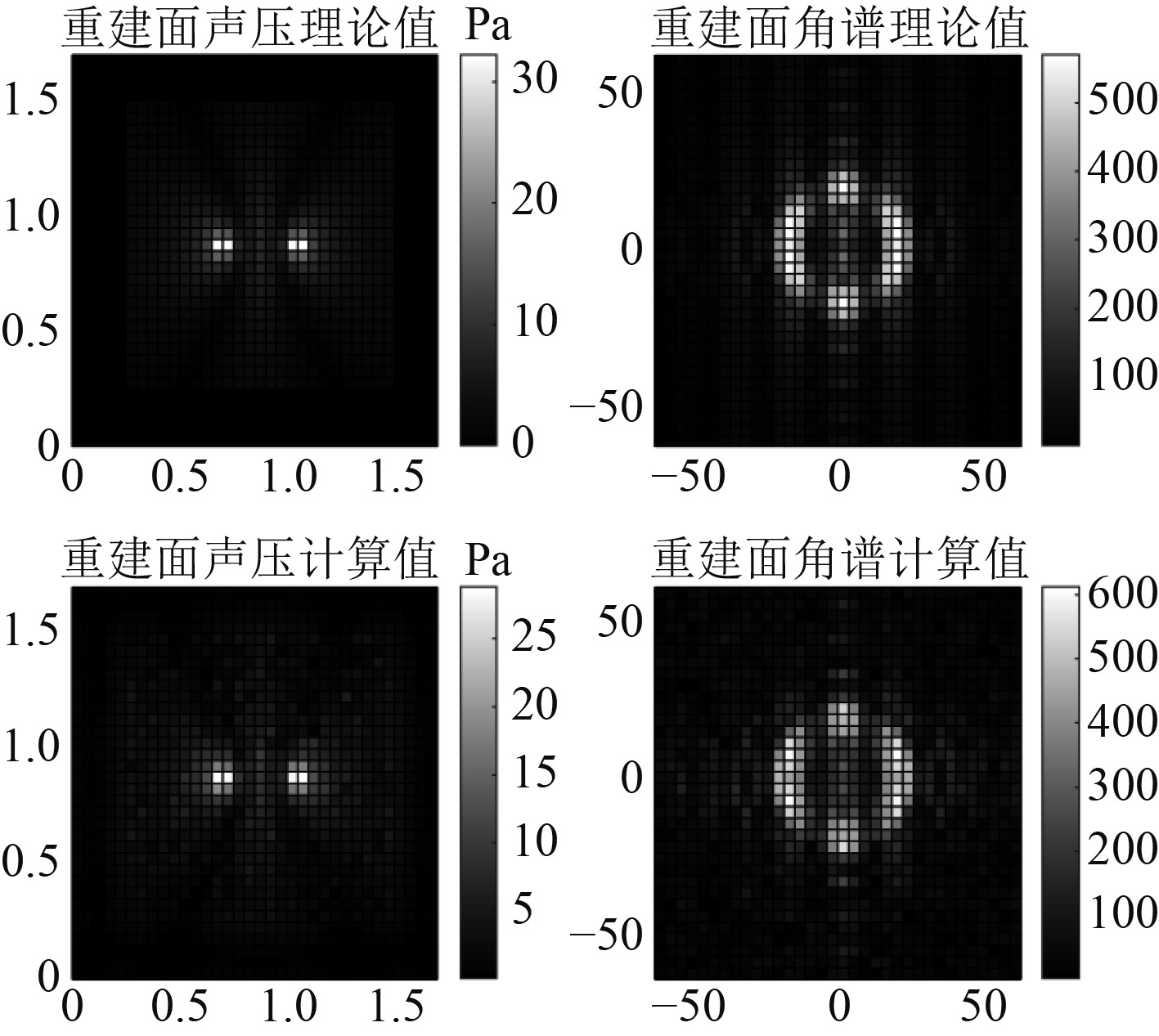
图 10 巴特沃斯窗函数滤波后重建结果 Fig. 10 The reconstructed result filtered by Butterworth window function |
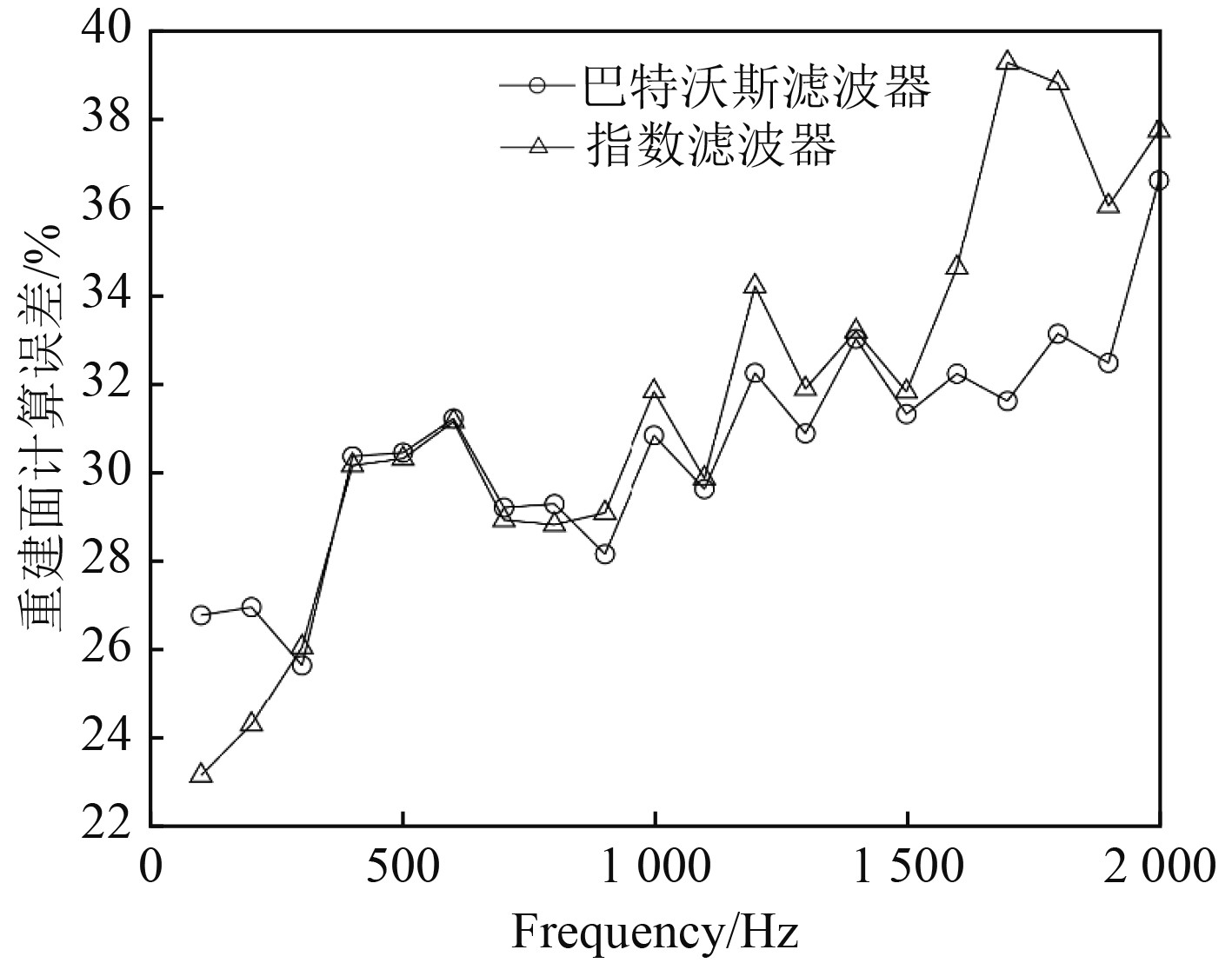
不同频率条件下,巴特沃斯滤波器与指数滤波器误差曲线如图11所示。重建距离为0.04 m时,巴特沃斯滤波器全频段平均误差为14.3%,指数滤波器为14.5%,全频段滤波效果相当。从图中可看出,在高频段,巴特沃斯滤波器重建误差明显小于指数滤波器重建误差,滤波效果更好。这是由于指数滤波器的陡度系数会同时影响通带内和高频带内滤波曲线的衰减率,且不能兼顾两者之间的平衡,导致有价值的倏逝波被滤出,从而影响滤波精度。后移测量面至

|
图 11 重建距离0.04 m时,巴特沃斯滤波器与指数滤波器误差曲线 Fig. 11 The comparison of error curves of Butterworth filter and exponential filter with reconstruction distance 0.04 m |
|
图 12 重建距离0.09 m时,巴特沃斯滤波器与指数滤波器误差曲线 Fig. 12 The comparison of error curves of Butterworth filter and exponential filter with reconstruction distance 0.09 m |
针对指数滤波器无法兼顾通带衰减率和高频带的衰减率,可能导致有价值的倏逝波被剔除,影响声场重建精度问题,本文提出采用巴特沃斯数字滤波器作为滤波函数的近场声全息滤波方法,选取2个同向振动的脉动球源作为研究对象,对两脉动球源声场反演过程进行数值仿真。通过仿真分析得到了使声场重建误差最小的巴特沃斯数字滤波器最优参数,并使用最优参数下该滤波器与最优参数下指数滤波器的滤波效果进行了对比。结果表明,巴特沃斯滤波器可替代指数滤波器在声场重构过程中,进行滤波处理,且在高频段巴特沃斯滤波器重建误差明显小于指数滤波器重建误差,滤波效果更好,重建精度更高。
| [1] |
MAYNARD J D, WILLIAMS E G, LEE Y. Nearfield acoustic holography: I. Theory of generalized holography and the development of NAH[J]. The Journal of the Acoustical Society of America, 1985, 78(4): 1395-413. DOI:10.1121/1.392911 |
| [2] |
WILLIAMS E G, MAYNARD J D, SKUDRZYK E. Sound source reconstructions using a microphone array[J]. The Journal of the Acoustical Society of America, 1980, 68(1): 340-344. DOI:10.1121/1.384602 |
| [3] |
WILLIAMS E G, FOURIER A. Sound radiation and nearfield acoustical holography[J]. Academic Press, 1999: 590.
|
| [4] |
于飞, 陈剑, 周广林, 等. 噪声源识别的近场声全息方法和数值仿真分析[J]. 振动工程学报, 2003, 16(3): 39-343. YU F, CHEN J, ZHOU G L, et al. A study on noise sources identification using near field acoustic holography method and its numerical simulation analysis[J]. Journal of Vibration Engineering, 2003, 16(3): 39−343. |
| [5] |
VERONESI W A, MAYNARD J D. Near-field acoustic holography (NAH) II. holographic reconstruction algorithms and computer implementation[J]. The Journal of the Acoustical Society of America, 1987, 81(5): ;1307-22. DOI:10.1121/1.394536 |
| [6] |
赵晨, 冯丹平, 杨明明, 等. 平面近场声全息中指数滤波器窗函数设计优化[J]. 声学技术, 2021, 40(6): 723-727. ZHAO C, FENG D P, YANG M M, et al. Optimization of window function design of exponential filter in planar near-field acoustic holography[J]. Technical Acoustics, 2021, 40(6): 723-727. DOI:10.16300/j.cnki.1000-3630.2021.05.020 |
| [7] |
张德俊. 近场声全息对振动体及其辐射场的成像[J]. 物理学进展, 1996, 16(3/4): 614-623. ZHANG D J. Imaging for vibrating mode and radiation field of vibrating object using NAN[J]. Progress in Physics, 1996, 16(3/4): 614-623. DOI:10.3321/j.issn:1000-0542.1996.04.032 |
| [8] |
罗禹贡, 郑四发, 杨殿阁, 等. 基于倏逝波衰减特性的空间频域滤波器研究[J]. 声学技术, 2004(1): 54-56+66. LUO Y G, ZHENG S F, YANG D G, et al. K-space filter based on decaying characteristics of evanescent waves[J]. Technical Acoustics, 2004(1): 54−56+66. |
| [9] |
何其伟, 许国良, 陈志敏, 等. 波数域循环加窗逼近法滤波方法研究[J]. 现代电子技术, 2015, 38(3): 64-67. HE Q W, XU G L, CHEN Z M, et al. K-space filtering by cyclically windowing approximation method[J]. Modern Electronics Technique, 2015, 38(3): 64-67. DOI:10.3969/j.issn.1004-373X.2015.05.019 |
| [10] |
莫登沅, 周其斗, 谷高全, 等. 声全息重构中的滤波窗优化设计[J]. 海军工程大学报, 2017, 29(3): 109-112. MO D Y, ZHOU Q D, GU G Q, et al. Design of filtering window for acoustical holography[J]. Journal of Naval University of Engineering, 2017, 29(3): 109-112. |
| [11] |
黄波. 巴特沃斯数字滤波器的设计与仿真实现[J]. 河南科技, 2021, 40(36): 10-12. HUANG B. Design and simulation of butterworth digital filter[J]. Henan Science and Technology, 2021, 40(36): 10-12. DOI:10.3969/j.issn.1003-5168.2021.36.008 |
| [12] |
肖锦龙. 巴特沃斯低通滤波器在图像增强中的应用研究[J]. 智能计算机与应用, 2021, 11(5): 179-182. XIAO J L. Application of Butterworth low pass filter in image enhancement[J]. Intelligent Computer and Application, 2021, 11(5): 179-182. DOI:10.3969/j.issn.2095-2163.2021.05.035 |
| [13] |
陈心昭, 毕传兴, 等. 近场声全息技术及其应用[M]. 北京: 科学出版社, 2013.
|
| [14] |
刘凯悦. 复杂系统的解耦内模与事件触发故障补偿控制[D]. 北京: 北京化工大学2021.
|
 2023, Vol. 45
2023, Vol. 45
