高频地波雷达(High Frequency Surface Wave Radar,HFSWR)对海上目标探测时,存在检测概率低、信噪比低、探测精度低、虚警率高的特点[1-2],海上目标类型繁多,仅使用目标运动学参数进行跟踪难以得到连续的目标航迹。除运动学参数外,目标自身特征及其所处环境相关的先验知识可以用来提高目标跟踪性能。利用知识辅助提高雷达目标跟踪能力的方法主要分为基于环境辅助方法与基于目标特征辅助方法。基于环境辅助的跟踪方法主要利用海上航道的方向改进目标的运动模型和根据不同杂波区域采用不同航迹管理策略的跟踪方法[3-5]。基于目标特征辅助的跟踪方法将目标的幅度、雷达散射截面积(Radar Cross Section,RCS)等参数作为特征修正目标量测和航迹的关联概率计算公式,提高了数据关联的准确性[6-9] 。
目前,广泛应用的机动目标跟踪方法分为基于变维滤波器与交互多模型的方法两大类。其中,基于变维滤波器的跟踪方法通过设置机动检测因子检测目标机动情况,实时切换状态预测模型实现对机动目标的跟踪。交互多模型算法使用多个运动模型组合估计目标状态,并根据各模型的概率加权计算目标状态值,提高了对机动目标的跟踪性能。但交互多模型算法通常会设置模型数量较多的模型集合,导致模型之间出现竞争,降低了目标状态估计精度与跟踪连续性。
考虑到船舶在海上按照特定的航道行驶[10-11],目标在航道上的位置可以为交互多模型算法中运动模型集合的设置提供决策。为了降低模型集合中与目标运动状态不匹配的模型对状态估计带来的不利影响,本文提出一种基于航道辅助的地波雷达机动目标跟踪方法,根据目标在航道区域的位置自适应调整运动模型集合,提高状态估计的准确性。
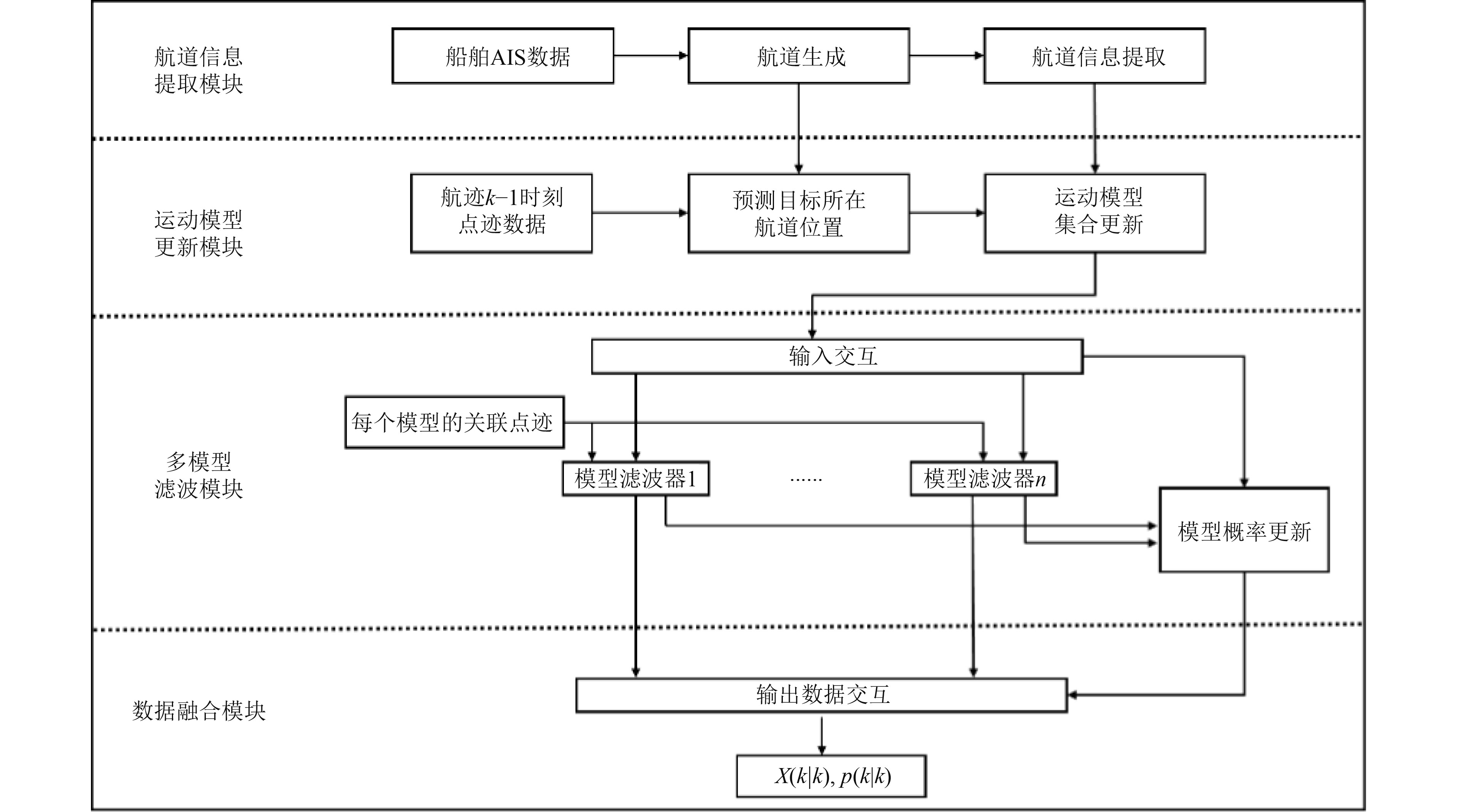
1 基于航道辅助的交互多模型机动目标跟踪方法IMM基于固定的运动模型集合进行状态估计,当目标机动时,不匹配模型与匹配模型之间的竞争降低了目标状态估计的精度,造成航迹断裂与丢失。对此,本文提出一种基于航道辅助的运动模型集合自适应调整IMM方法,如图1所示。该方法由航道信息提取、运动模型集合更新、多模型滤波、数据融合4部分模块组成,其中基于航道辅助运动模型集合更新是该方法的核心环节,承担着抑制模型竞争,提高目标状态估计准确性的任务[12-15]。
|
图 1 基于航道辅助IMM方法流程 Fig. 1 Flow of the channel-assisted IMM-based method |
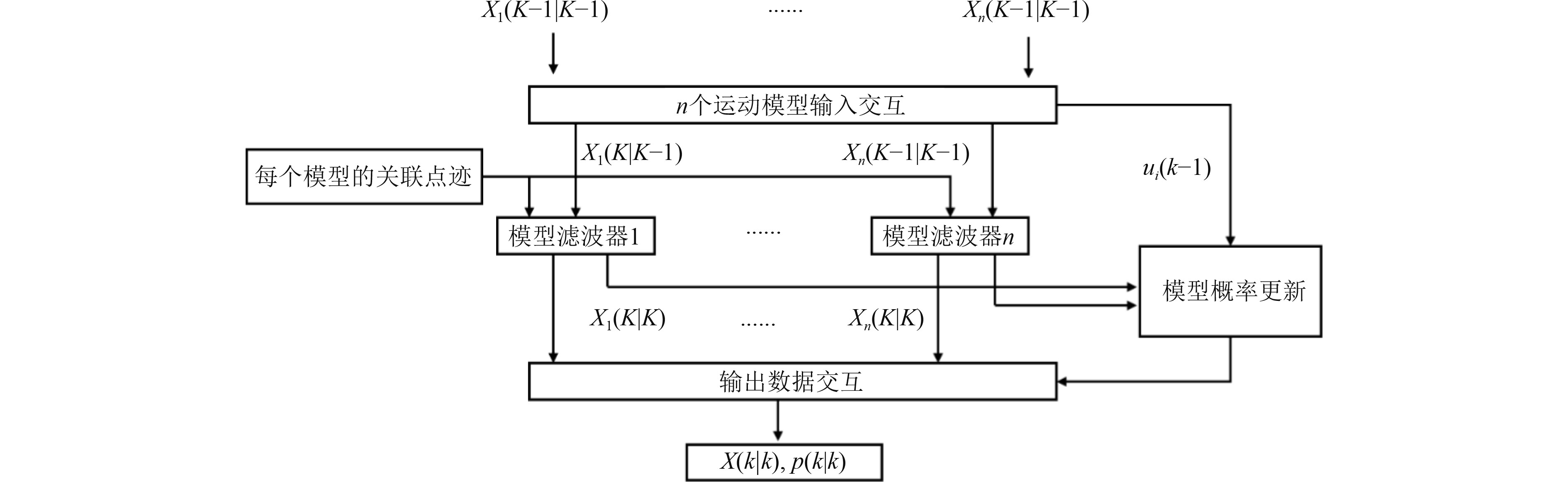
如图2所示,IMM方法由输入交互、状态滤波、模型概率更新、状态融合4部分组成。其中,输入交互模块计算各模型的初始化目标状态值;滤波模块利用卡尔曼滤波算法计算目标状态预测值与状态估计值;模型概率更新模块通过计算各模型似然函数值赋予模型不同的权重对模型的概率进行更新;状态融合模块根据各模型的权重与状态估计值输出融合状态估计值。
|
图 2 IMM方法流程图 Fig. 2 Flow chart of IMM algorithm |
1)输入交互
在
| $ \begin{split} {X^{0j}}(k - {\text{1}}|k - {\text{1}}) =\;& \sum\limits_{i = 1}^r {X^j}(k - {\text{1}}|k - {\text{1}}){u_{ij}}(k - {\text{1}}|k - {\text{1}}), \\&j = {\text{1}}, {\text{2}}, \ldots, r,\end{split} $ | (1) |
| $ \begin{split} {p^{0j}} (k - {\text{1}}|k - {\text{1}}) =\;&\sum\limits_{i = 1}^r {{u_{ij}}(k - {\text{1}}|k - {\text{1}})\{ {p^j}(k - {\text{1}}|k - {\text{1}}) + } \\ &[{x^j}(k - {\text{1}}|k - {\text{1}}) - {x^{0j}}(k - {\text{1}}|k - {\text{1}})]\cdot \\& [{x^j}(k - {\text{1}}|k - {\text{1}}) - {x^{0j}}(k - {\text{1}}|k - {\text{1}})]^{\rm T}\},\\& j = 1,2,\ldots, r 。\end{split} $ | (2) |
其中:
| $ {u_{ij}}(k - {\text{1}}|k - {\text{1}}) = \frac{{{p_{ij}}{u_i}(k - {\text{1}})}}{{{c_j}}} ,$ | (3) |
| $ {c_j} = \sum\limits_{i = 1}^r {{p_{ij}}{u_i}(k - {\text{1}})}。$ | (4) |
式中:
2)滤波器滤波
滤波模块利用各模型初始状态估计与协方差估计预测目标下一时刻的状态,计算方法如下式(5)所示。
| $ \begin{split} &{X^{0j}}(k) = {{\boldsymbol{F}}_j}{X_j}(k - {\text{1}}) + {W_k}, \\ &{p^{0j}}(k|k - {\text{1}}) = {{\boldsymbol{F}}_j}{p^{0j}}(k - {\text{1}}|k - {\text{1}}){{\boldsymbol{F}}_j}^{\rm T} + {Q_j},\;\;j = {\text{1}},{\text{2}},...,r ,\end{split} $ | (5) |
| $ {K_j}(k) = {p_j}(k|k - {\text{1}}){{\boldsymbol{H}}^{\rm T}}{[H{p_j}(k|k - {\text{1}}){{\boldsymbol{H}}^{\rm T}} + {R_j}]^{ - 1}} 。$ | (6) |
| $ \begin{split} & {X^j}(k|k) = {X^j}(k|k - {\text{1}}) + {K_j}(k)[Z(k) - H{X^j}(k|k - {\text{1}})] ,\\ & {p^i}(k|k) = [{\text{I}} - {K_j}(k){\boldsymbol{H}}]{p^j}(k|k - {\text{1}})。\\ \end{split} $ | (7) |
其中:观测矩阵
3)模型概率更新
IMM方法通过极大似然函数法计算模型和目标当前运动状态的匹配度给出各模型的权重。
在
| $ {\varLambda _j}(k) = \frac{1}{{\sqrt {2{\text{π}} \left| {{S_{ j}}(k)} \right|} }}\exp \left\{ - \frac{1}{2}d_j^{\rm T}(k)S_{ j}^{ - 1}{d_j}(k)\right\} 。$ | (8) |
其中:
| $ {u_j}(k) = \frac{1}{c}{\varLambda _j}(k)\sum\limits_{i = 1}^r {{p_{ij}}{u_i}(k - {\text{1}})} 。$ | (9) |
4)状态融合
状态融合根据每个模型计算的状态估计值与模型权重给出
| $ X(k|k) = \sum\limits_{i = 1}^r {{X_i}{u_i}(k)} 。$ | (10) |
式中:
| $ \begin{split} p(k|k) = \;&\sum\limits_{i = 1}^r {{u_i}(k|k)\{ {p_i}(k|k) + [{x_i}(k|k) - x(k|k)} ] \cdot \\ &{[{x_i}(k|k) - x(k|k)]^{\rm T}}\} 。\end{split} $ | (11) |
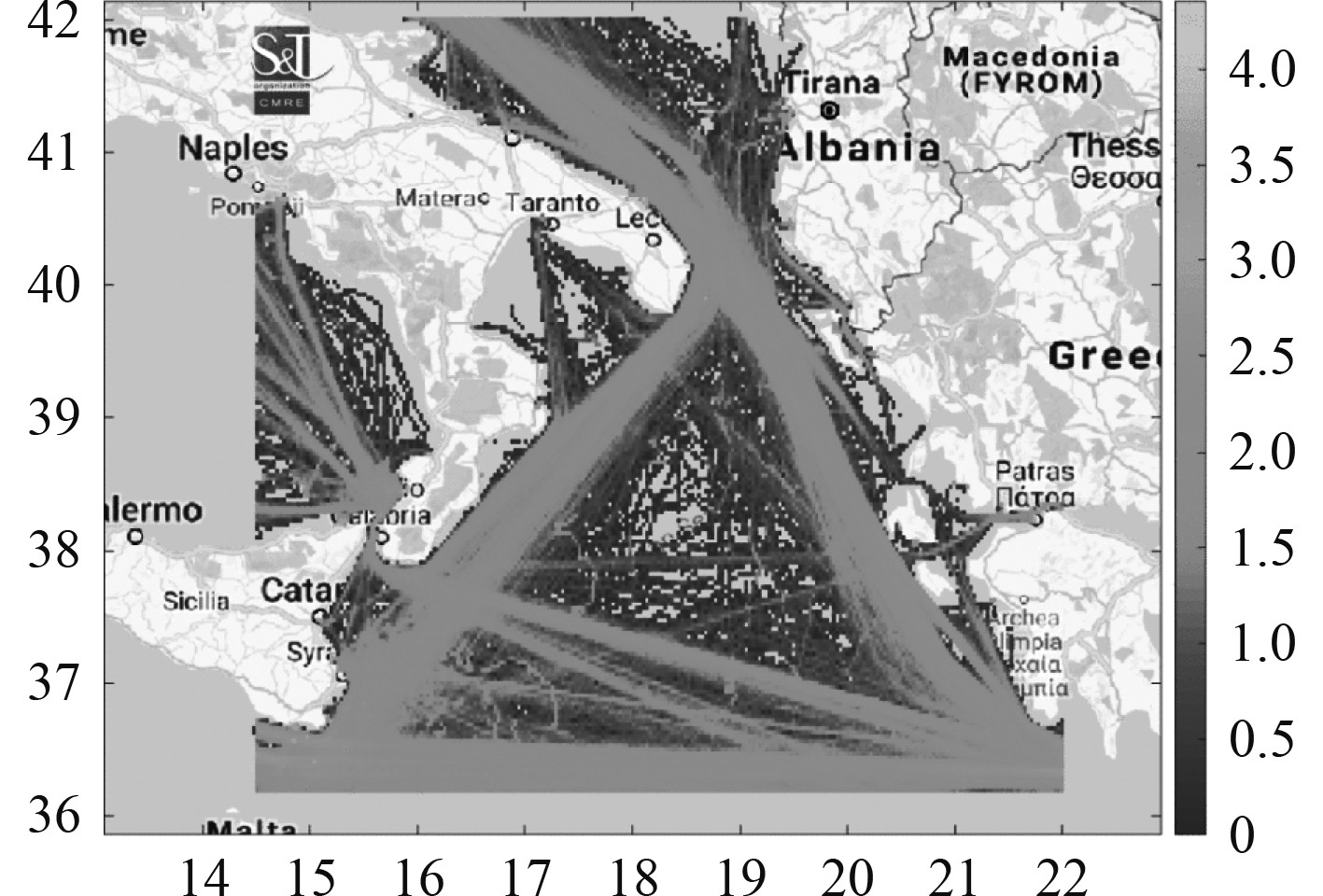
船舶航行以直线行驶为主,仅个别时间段内发生机动,考虑到在不同的区域,IMM跟踪方法可以采用不同的模型集合进行状态估计,能够缓解由非匹配模型引起的状态估计精度下降的不足。因此,动态模型集合调整方法的关键在于如何实时的确定符合目标运动状态的运动模型集合。图3给出了2018年6~8月Ionian Sea的船舶历史AIS航迹叠加结果,通过观察可以得到以下结论:
1)船舶航迹分布呈现出沿航道行驶的特征;
2)船舶航行时机动性较低,主要以直线行驶为主;
3)船舶机动的位置分布集中。
船舶AIS航迹呈现受航道约束的特征,船舶机动位置集中在固定区域,因此,通过提取航道的机动区域确定船舶发生机动概率较高的区域,当目标行驶至航道机动区域时,采用机动运动模型集合跟踪目标;在直线航道区域,使用直线运动模型集合跟踪目标,基于此思想,能够根据目标所在的航道区域调整IMM方法运动模型集合,抑制模型竞争。
1.2.1 海上航道提取及表示方法目前航道提取方法可分为交通路径异常检测(Traffic Route Extraction for Anomaly Detection,TREAD)法与船舶轨迹聚类法。其中,TREAD法以船舶航速作为目标机动特征,认定航速波动较大时船舶发生机动,该方法具有运行速度快,能够准确提取船舶机动区域的优点。因此,选用TREAD算法作为航道提取方法,该方法通过一系列航道航路点及其之间连接的航段组成的有向图模型表示航道,航道航路点

|
图 4 海上航道示意图 Fig. 4 Schematic diagram of the maritime channel |
TREAD航道提取方法认定船舶行驶至航道航路点处发生机动,在航段上行驶的船舶为匀速直线行驶,在不同航路点的船舶机动特性由航路点所对应的交通属性给出。如图4所示,航路点
|
|
表 1 航路点和航段交通属性与不同航道区域船舶运动模型 Tab.1 Traffic attributes of waypoints and segments in different channel areas ship movement model |
通过对船舶在不同航道区域的运动特性建模,IMM方法能够根据船舶所在的航道区域设置运动模型集合。如图5所示,运动模型集合调整是通过判断目标状态预测点所在航道区域位置反馈模型集合更新的过程,算法步骤如下:

|
图 5 运动模型集合调整过程 Fig. 5 Motion model set adjustment process |
步骤1 状态预测
根据上一时刻确定的模型集合预测目标下一时刻位置。
步骤2 确定目标所在航道位置
根据目标预测位置判断目标所在航道位置。
步骤3 模型集合更新
根据目标所在的航道区域使用该区域所对应的船舶运动模型更新运动模型集合。
由于TREAD算法不能获取航道的宽度信息,因此在步骤2中无法通过判断目标是否在航道内确定目标所在航道位置,对此,此处给出了判断目标所在航道位置方法,其过程如下:
1)预测目标位置是否位于航道航路点区域
以目标
| $ {\left[ \begin{split} {x_j} - \hat x(k|k - {\text{1}}) \\ {y_j} - \hat y(k|k - {\text{1}}) \\ \end{split} \right]'}{\boldsymbol{P}}_{pos}^{ - 1}(k|k - {\text{1}})\left[ \begin{split} {x_j} - \hat x(k|k - {\text{1}}) \\ {y_j} - \hat y(k|k - {\text{1}}) \\ \end{split} \right] \leqslant \alpha 。$ | (12) |
其中:
| $ {{\boldsymbol{P}}_{pos}}(k|k - {\text{1}}) = \left[ {\begin{array}{*{20}{c}} \begin{split} {p_{xx}}(k|k - {\text{1}}) \\ {p_{xy}}(k|k - {\text{1}}) \\ \end{split} &\begin{split} {p_{xy}}(k|k - {\text{1}}) \\ {p_{yy}}(k|k - {\text{1}}) \\ \end{split} \end{array}} \right] 。$ | (13) |
式中:
2)预测目标位置是否位于航道航段区域
以目标
| $ {\left[ \begin{split} x - \hat x(k|k - 1) \\ y - \hat y(k|k - 1) \\ \end{split} \right]'}P_{pos}^{ - 1}(k|k - 1)\left[ \begin{split} x - \hat x(k|k - 1) \\ y - \hat y(k|k - 1) \\ \end{split} \right] \leqslant \beta 。$ | (14) |
其中:
交互多模型方法使用多个运动模型组合进行状态估计,当模型集合中至少存在一个运动模型的状态预测值满足上述2种情况之一时,则根据其目标状态预测位置所在航道的区域,自动的添加/删除该区域所对应的模型集合,实现运动模型集合的最优组合,根据确定的模型集合进行IMM方法多模型滤波处理,实现准确地目标状态估计。
1.2.4 转移概率矩阵调整方法IMM算法根据先验知识或人为选择转移概率矩阵,当采用动态模型集合调整IMM方法时,运动模型集合的数量与种类会发生变化,不匹配模型转化为匹配模型的概率应增加,保持现有模型的概率需要减小,固定的转移概率矩阵不能提高匹配模型概率,导致目标状态估计精度下降。为此提出一种转移概率矩阵动态调整方法,使用新息构造修正因子更新转移概率矩阵,该方法步骤如下:
步骤1 构建模型似然函数
根据新息构建的目标运动模型似然函数为:
| $ {\varLambda _j}(k) = \frac{1}{{\sqrt {2{\text{π}} \left| {{S_{ j}}(k)} \right|} }}\exp \left\{ - \frac{1}{2}d_j^{\rm T}(k)S_{ j}^{ - 1}{d_j}(k)\right\}。$ | (15) |
步骤2 计算修正因子
定义模型转移概率矩阵修正因子为:
| $ {k_i}_j = \frac{{{\text{π}} _k^{ji} \times \varLambda _k^j}}{{{\text{π}} _k^{ij} \times \varLambda _k^i}} 。$ | (16) |
其中,
步骤3 更新转移概率矩阵
修正的转移概率矩阵为:
| $ {\text{π}} _{ij}' = {({k_{{i_j}}})^\alpha }{{\text{π}} _{ij}},\;\;\alpha \in [{\text{0}},{\text{1}}],$ | (17) |
式中:
| $ {\text{π}} _{ii}' = 1 - {({k_{i1}})^\alpha }{{\text{π}} _{i1}} - \ldots - 1 - {({k_{iN}})^\alpha }{{\text{π}} _{iN}}。$ | (18) |
考虑到主对角线元素占优原则,设置一个阈值
| $ {\text{π}} _{ii}' = \varphi,$ | (19) |
| $ {\text{π}} _{ij}' = ({\text{1}} - \varphi )\frac{{{{\text{π}} _{ij}}}}{{{\text{1}} - {{\text{π}} _{ii}}}}。$ | (20) |
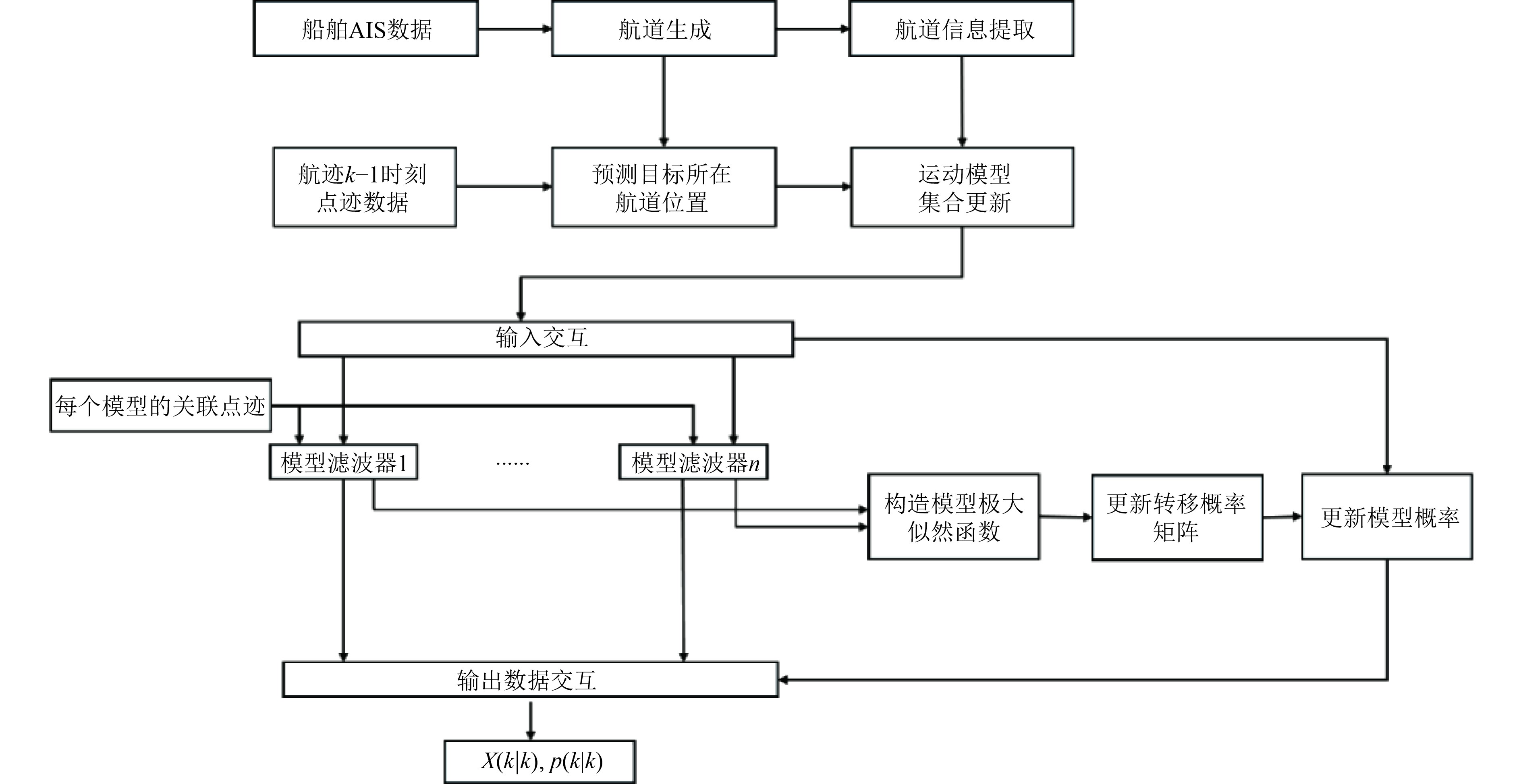
综上所述,基于航道辅助IMM目标跟踪方法流程如图6所示。
|
图 6 基于航道辅助IMM目标跟踪方法流程 Fig. 6 Flow of channel-assisted IMM target tracking based method |
为了验证本文提出方法的性能,分别使用交互多模型方法及本文方法开展海上机动目标跟踪实验。利用跟踪时长、方法运行速度、运动模型概率等指标对跟踪结果进行评价。
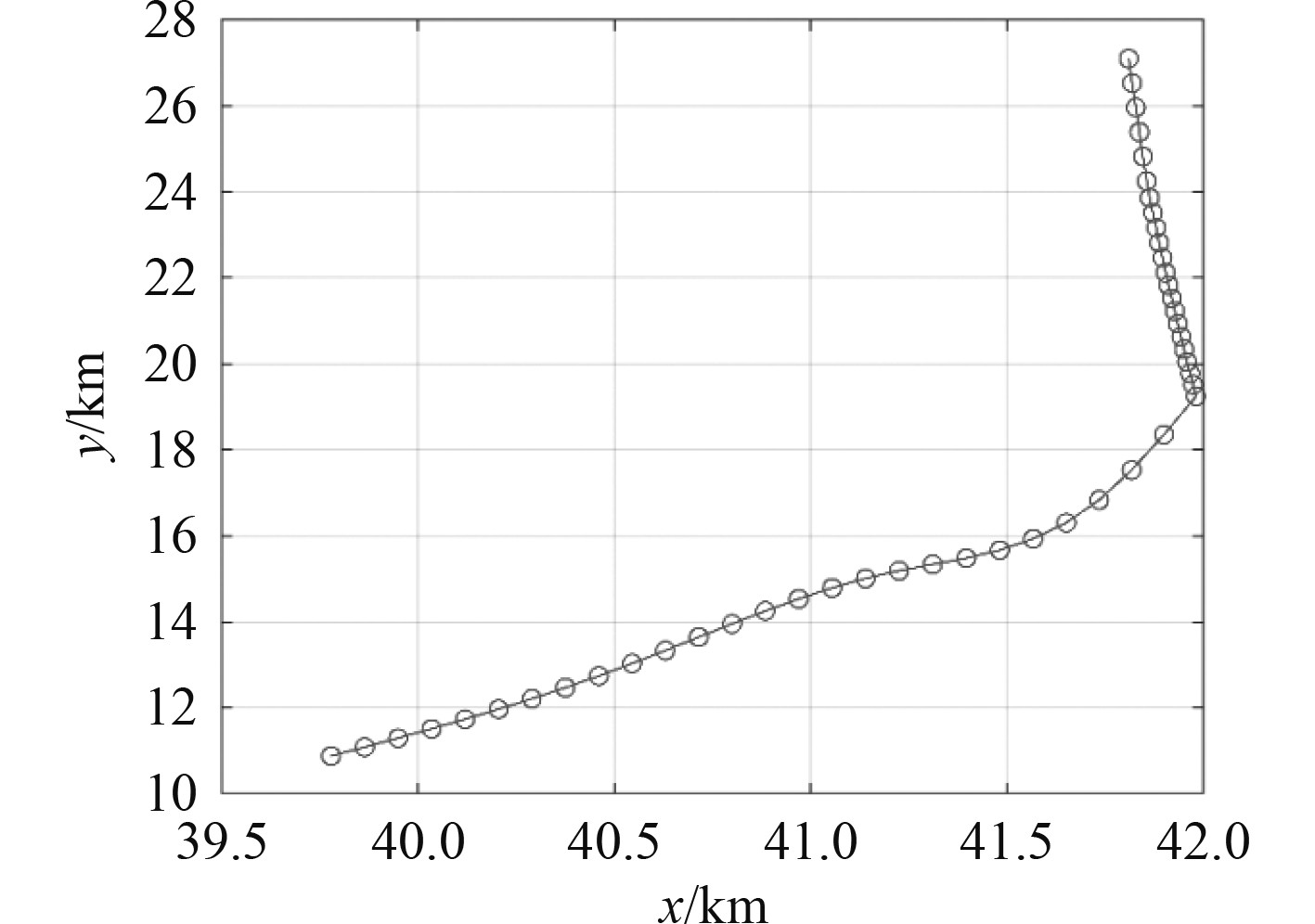
2.1 雷达实验数据本次实验数据采用AIS数据网站提供的AIS航迹数据作为数据输入,按照雷达站与AIS点迹位置的对应关系,将AIS数据中的经纬度、航速、航向转换为雷达系统下的距离、径向速度、方位角数据。目标航迹如图7所示。
|
图 7 雷达坐标系下仿真航迹 Fig. 7 Simulated trajectory in radar coordinate system |
分别采用本文方法与IMM方法开展目标跟踪实验,利用TREAD海上航道提取方法提取海上船舶航道,结果如图8所示。不同航道区域船舶运动模型如表2所示。
|
图 8 潍坊港-连云港港航道 Fig. 8 Weifang Port - Lianyungang Port Channel |
|
|
表 2 航路点和航段交通属性与不同航道区域船舶运动模型 Tab.2 Traffic attributes of waypoints and segments in different channel areas ship movement model |
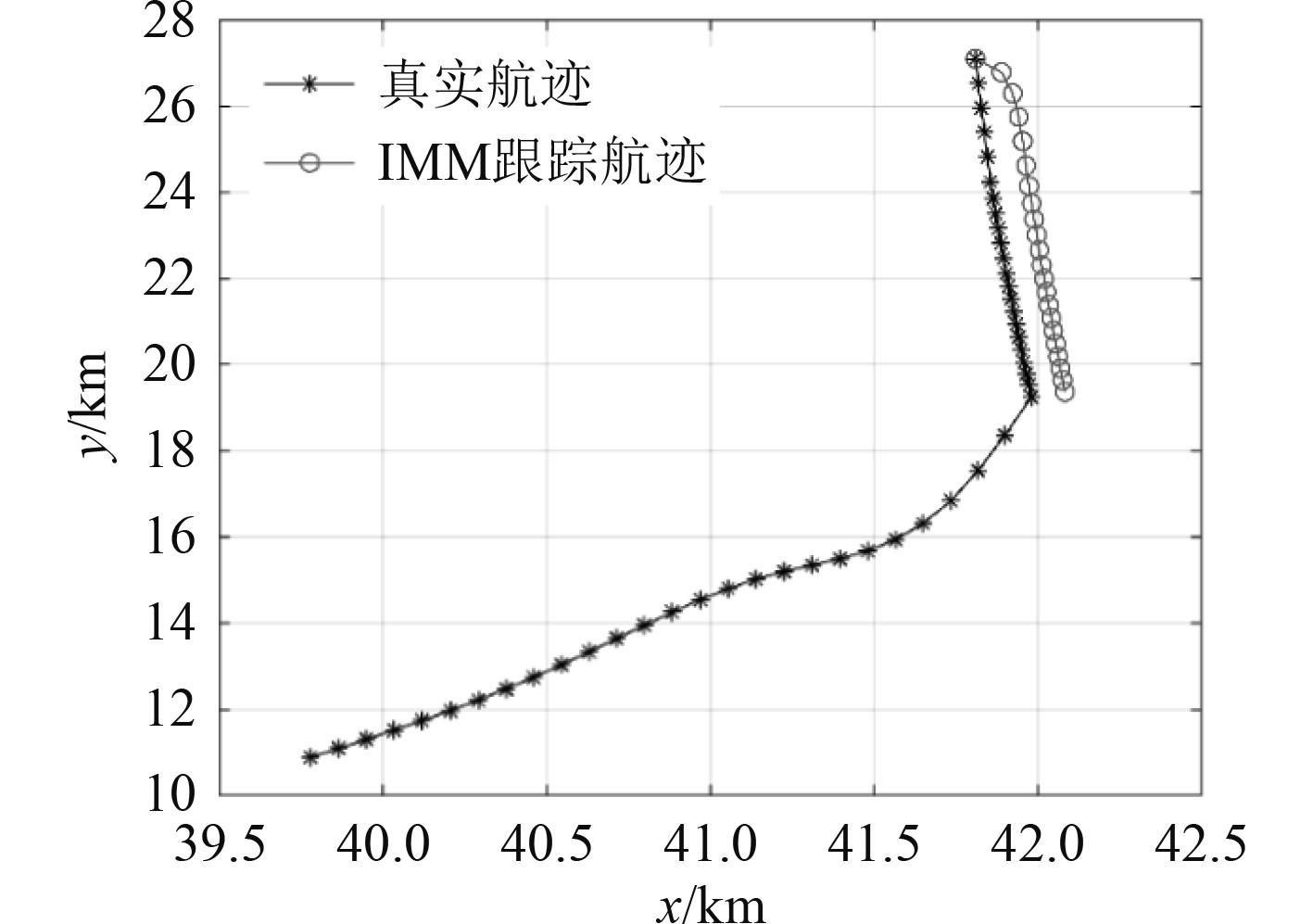
分别采用IMM方法与动态模型集合调整方法开展海上目标跟踪实验,跟踪结果如图9与图10所示。
|
图 9 标准IMM算法目标跟踪结果 Fig. 9 Target tracking results of standard IMM algorithm |

|
图 10 基于航道辅助的IMM方法跟踪结果 Fig. 10 Tracking results of IMM method based on channel assistance |
表3与表4为2种方法的航迹维持时间、100次蒙特卡罗实验运行时间和不同时间段内模型集合数量与类型。
|
|
表 3 2种算法的实验对比结果 Tab.3 Experimental comparison results of the two methods |
|
|
表 4 目标跟踪过程中的各时间段模型集合 Tab.4 Model sets of each time period in the target tracking process |
由表3可知,相比于标准IMM算法的目标跟踪结果,本文方法的航迹维持时间提高了54.2%。这是由于在跟踪过程的第23 min时刻,当目标发生机动时,IMM算法对目标的速度预测值为
由表3可知,基于航道辅助的IMM算法的运行速度提高了30%。由表4可知,基于航道辅助IMM方法通过模型集自适应调整,删除了非匹配运动模型,缓解了模型竞争,降低了输入交互、模型滤波、输出融合的时间,提高了算法的运行速度。
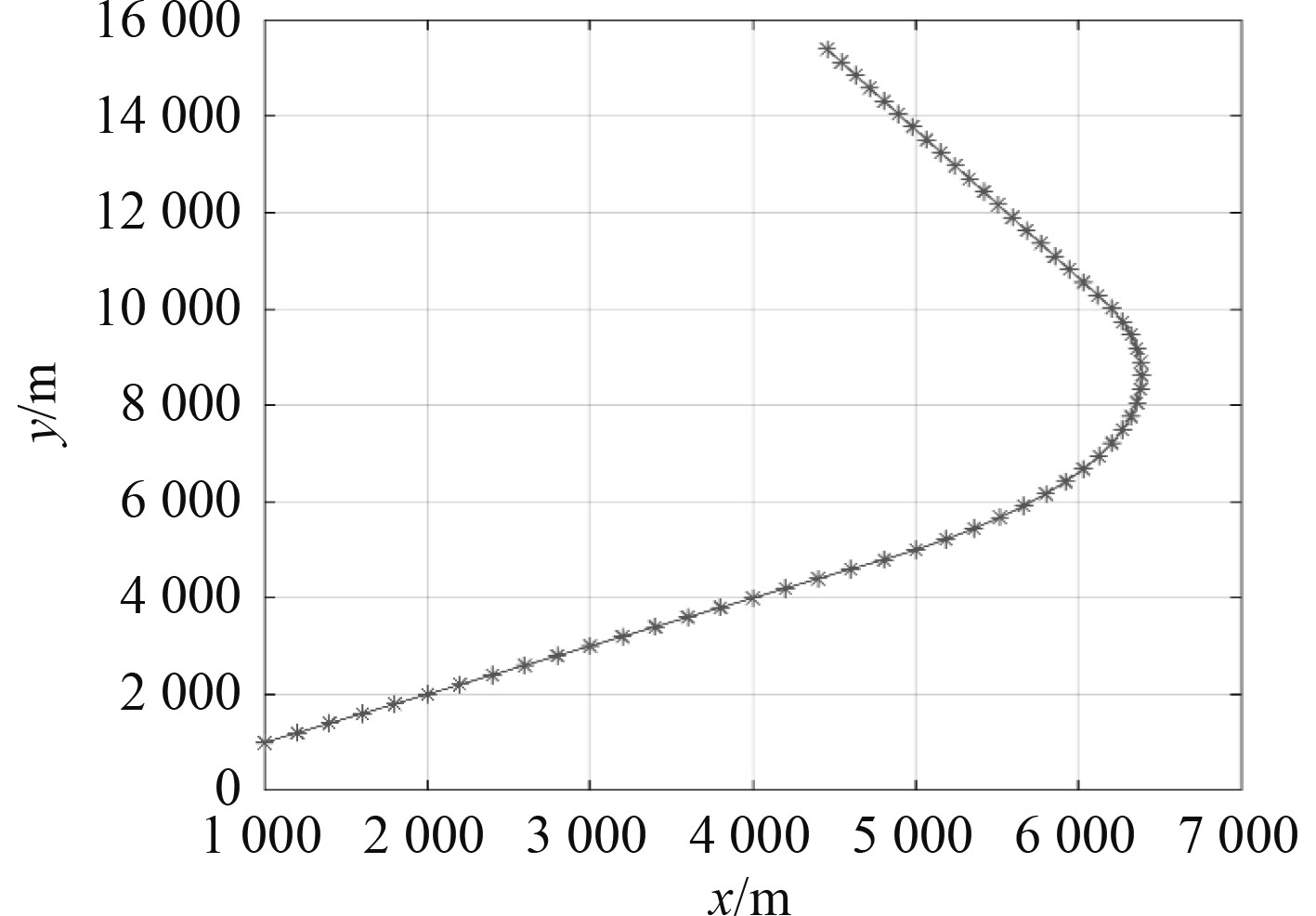
2.2.2 模型概率验证实验为了验证转移概率矩阵动态调整方法的性能进行了目标仿真实验,目标在0~20 min与40~60 min时间段内做匀速直线运动;在20~40 min时间段内做匀速转弯运动。目标轨迹如图11所示。
|
图 11 仿真目标航迹 Fig. 11 Simulation target track |
分别使用标准IMM算法与转移概率矩阵动态调整方法对目标进行跟踪,2种方法在不同时刻的模型概率如图12与图13所示。图14为2种方法在跟踪过程中与目标运动状态所匹配模型的概率。
|
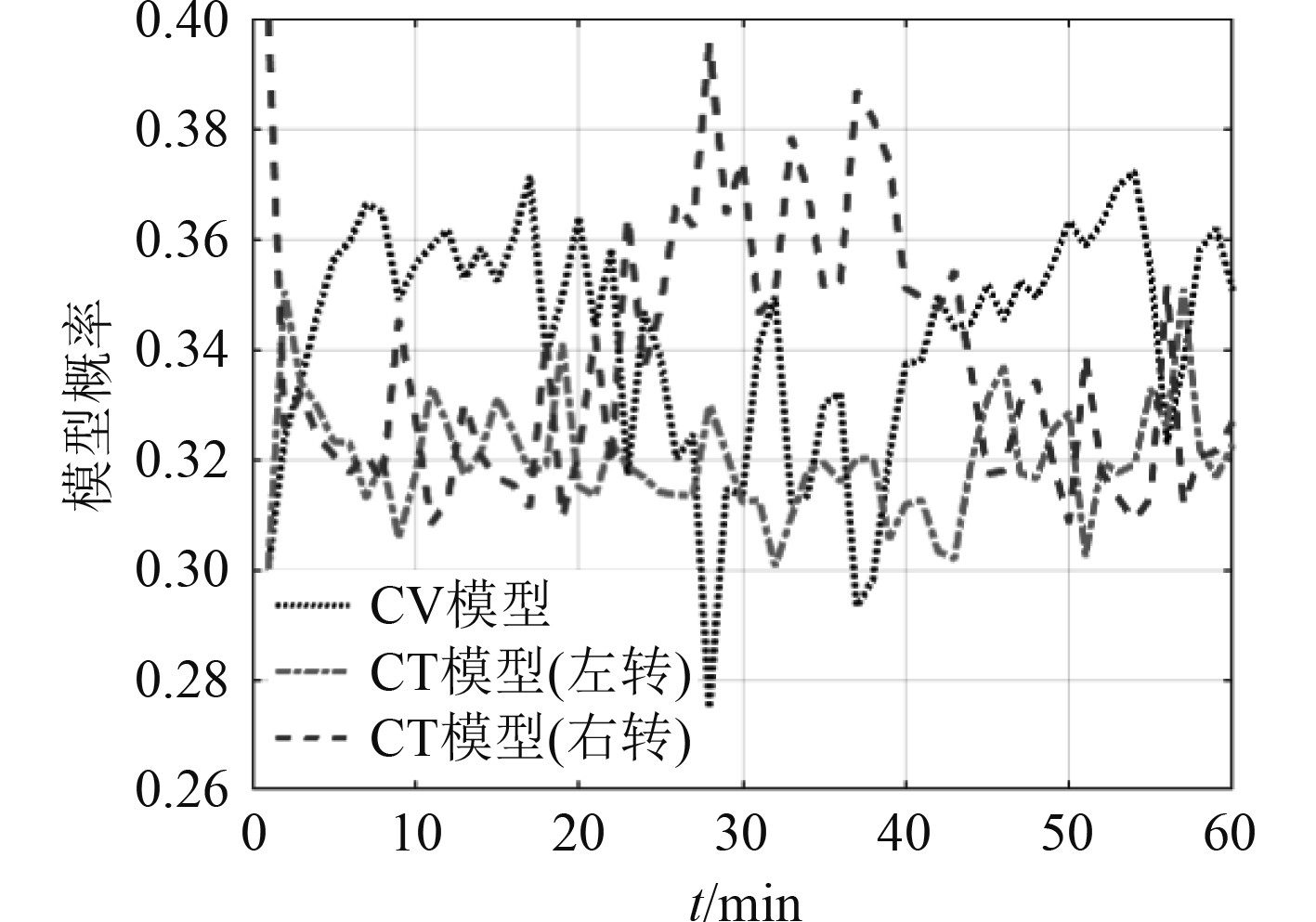
图 12 标准IMM算法各时刻模型概率 Fig. 12 Model probability at each moment of the standard IMM algorithm |
|
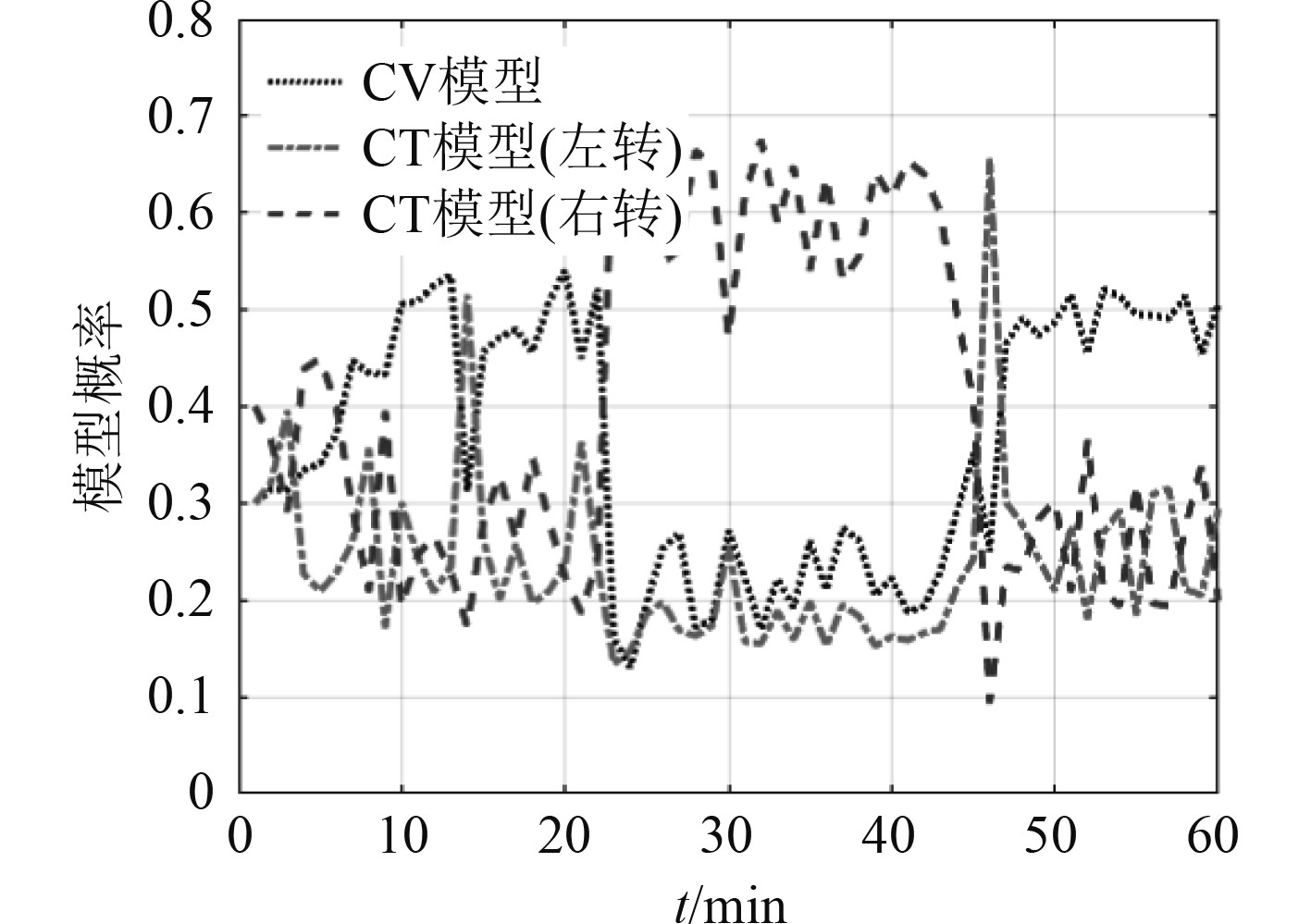
图 13 改进IMM算法各时刻模型概率 Fig. 13 Model probability at each moment of the improved IMM algorithm |
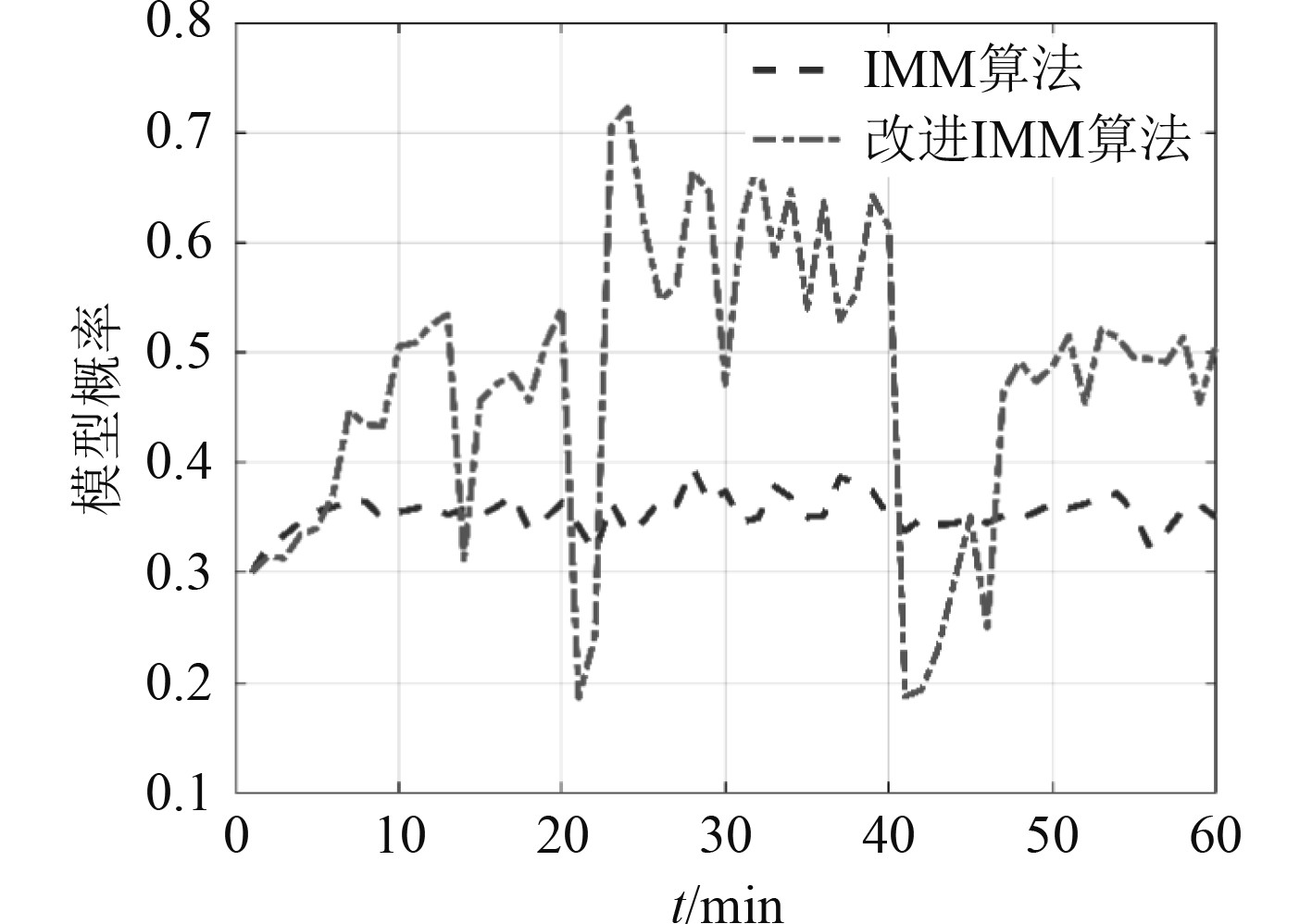
|
图 14 2种方法每时刻与目标状态所匹配模型概率 Fig. 14 Probability of the model matched by the two algorithms at each time and the target state |
通过图12~图14的实验结果可见,在跟踪过程中的第20 min与40 min目标运动状态切换时刻,改进的IMM方法的模型切换速度与模型概率明显优于标准IMM算法。IMM算法与目标真实运动状态匹配模型的模型平均概率为34.3%,改进IMM算法与目标运动状态所匹配模型的平均概率为48.4%,有效提高了模型的切换速度和与目标运动状态匹配的运动模型概率。
3 结 语为了提高紧凑型地波雷达对机动目标的跟踪性能,本文提出一种基于航道辅助的IMM机动目标跟踪方法,利用航道提取方法给出目标在不同航道区域的最优运动模型集合,并根据目标在航道的位置动态调整IMM方法的模型集合,抑制IMM方法存在的模型竞争问题。实验结果表明,该方法可以有效提高模型概率,减少航迹断裂,提高航迹维持时间,减小算法的运算复杂度。
| [1] |
纪永刚, 张杰, 王祎鸣, 等. 紧凑型高频地波雷达目标探测研究进展[J]. 中国海洋大学学报(自然科学版), 2017, 47(2): 1-7. JI Y G, ZHANG J, WANG Y M, et al. An overview of target monitoring with Compact HFSWR[J]. Periodical of Ocean University of China, 2017, 47(2): 1-7. |
| [2] |
YE L, WANG Y, YANG Q, et al. High frequency surface wave radar detector base on log-determinant divergence and symmetrized log-determinant divergence[J]. Journal of Electronics & Information Technology, 2019, 41(8): 1931-1938. |
| [3] |
VIVONE G, BRACA P, HORSTMANN J. Knowledge-based multitarget ship tracking for HF surface wave radar systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(7): 3931-3949. DOI:10.1109/TGRS.2014.2388355 |
| [4] |
BENAVOLI A, L CHISCI, A FARINA S, et al. Knowledge-based system for multi-target tracking in a littoral environment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 1100-1119. DOI:10.1109/TAES.2006.248193 |
| [5] |
SUN M, MA Z, Li Y. Maneuvering target tracking using IMM kalman filter aided by elman neural network[C]//2015 7th International Conference on Intelligent Human-Machine Systems and Cybernetics, 2015, 44–148.
|
| [6] |
GUO J P. An improved IMM algorithm based on maneuvering-adaptive model set[C]//2016 CIE International Conference on Radar (RADAR), 2016, 1–5.
|
| [7] |
HAN B, HUANG H, LEI L, et al. An improved IMM algorithm based on STSRCKF for maneuvering target tracking[J]. IEEE Access, 2019, 7: 57795-57804. DOI:10.1109/ACCESS.2019.2912983 |
| [8] |
CLOUTIER J R, LIN C-F, YANG C.. Enhanced variable dimension filter for maneuvering target tracking[J]. Aerospace & Electronic Systems IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(3): 786-797. |
| [9] |
XIE G, SUN L, WEN T, et al. Adaptive Transition Probability Matrix-Based Parallel IMM Algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2021, 51(5): 2980-2989. DOI:10.1109/TSMC.2019.2922305 |
| [10] |
FORTI N, MILLEFIORIL BRACA. M, P. Unsupervised extraction of maritime patterns of life from Automatic Identification System data[C]//OCEANS 2019 - Marseille, 2019, 1–5.
|
| [11] |
MA J, GUO X. Combination of IMM algorithm and ASTRWCKF for maneuvering target tracking[J]. IEEE Access, 2020, 8: 143095-143103. DOI:10.1109/ACCESS.2020.3013561 |
| [12] |
HWANG I, SEAH C E. A Study on stability of the interacting multiple model algorithm[J]. IEEE Transactions on Automatic Control, 2017, 62(2): 901-906. DOI:10.1109/TAC.2016.2558156 |
| [13] |
夏楠, 王珏, 李博. 基于粒子滤波和交互多模型的移动定位方法[J]. 电子学报, 2019, 47(1): 197: 203. XIA N, WANG J, LI B. A Mobile localization method based on particle filter and interacting multiple models[J]. Acta Electponica Sinica, 2019, 47(1): 197: 203. |
| [14] |
戴定成, 姚敏立, 蔡宗平, 等. 改进的马尔可夫参数自适应IMM算法[J]. 电子学报, 2017, 45(5): 1198-1205. DAI D C, YAO M L, CAI Z P, et al. Improved adaptive markov IMM algorithm[J]. Acta Electponica Sinica, 2017, 45(5): 1198-1205. |
| [15] |
王平波, 刘杨. 基于改进自适应IMM-UKF算法的水下目标跟踪[J]. 电子与信息学报, 2022, 44(6): 1999–2005. WANG P B, LIU Y Underwater Target Tracking algorithm based on improved adaptive IMM-UKF[J]. journal of electronics & information technology, 2022, 44(6): 1999–2005. |
 2023, Vol. 45
2023, Vol. 45