2. 上海交通大学 三亚崖州湾深海科技研究院,海南 三亚 572024
2. SJTU Yazhou Bay Institute of Deepsea Technology, Sanya 572024, China
作为水声对抗重要装备,声诱饵在现代海战中发挥着重要作用,可以显著提升舰艇的生存率。根据工作方式,声诱饵可分为被动式和主动式两类,其中主动式声诱饵是对抗末制导阶段鱼雷的重要装备,又可分为存储转发和边收边发2种模式。随着鱼雷主动声制导技术的发展,存储转发模式逐渐被边收边发模式取代,后者已成为现代化声诱饵的标志性技术。
发射-接收声串漏是主动式声诱饵技术面临的严峻挑战,增加声诱饵长度与声障板面积是提高声隔离度的主要措施。为了提高机动性,声诱饵长度与声障板面积不断缩减,结构形式也从悬浮式逐渐向一体化式过渡,而声串漏问题愈加凸显。公开资料表明,国外海军已装备了一体化式声诱饵装备[1]。为了迅速发展我军一体化式声诱饵装备,探索全新的、有效的声隔离度措施迫在眉睫。
一体式主动声诱饵外部结构表现为电子舱[2],为耐压壳体结构,可作为圆柱发射换能器、圆柱接收换能器和信号处理装置、滤波器以及配套电源、连接线的支撑体和储藏体。
向大威等[3]率先提出借助自适应滤波器来消除由发射端-接收端引起的直达声串漏。吴培荣[4]提出利用发射和接收换能器的指向性和自适应噪声抵消技术这2种方式来抑制声串漏。何陈[5]采用基于系统辨识理论的主动干扰抑制技术对串漏通路系统建模,由辨识结果对干扰抵消滤波器进行设计,以达到干扰抑制的目的。上述几种方法均未考虑电子舱对声串漏的影响以及边收边发模式下,系统反馈导致串漏信号加剧的问题。
在已有研究基础上,本文引入一个可有效消除声串漏的滤波器,与转发增益以及发射-接收传递函数有关,并利用发射、接收带限白噪声及最小二乘方法获取发射-接收传递函数,为提高一体式主动声诱饵声隔离度提供了新思路。
1 理论基础 1.1 2种工作模式的对比一体式主动声诱饵工作过程有2种,一种是存储转发模式,一种是边收边发模式。存储转发指的是接收完敌方探测信号之后关闭接收端,接收信号经过信号处理装置处理再转发出去,如图1(a)所示。边收模式指接收换能器持续接收信号,发射换能器持续发射诱骗信号,对敌方主动声呐探测信号进行实时处理转发的模式,如图1(b)所示。

|
图 1 主动声诱饵工作模式框图 Fig. 1 Active sound decoy working mode block diagram |
图中:
存储转发模式下,转发诱骗信号
| $ {{{K}}_1}(\omega ) = {Y_1}(\omega )\cdot {H_s}\cdot{e^{ - j\omega {t_0}}} 。$ | (1) |
边收边发模式下,接收信号经过处理后通过发射换能器发射,发射信号串漏到接收换能器,不断循环,接收信号和发射信号形成闭环反馈系统[7]。声诱饵转发诱骗信号
| $ {K_2}\left( \omega \right) = {Y_1}\left( \omega \right) \cdot {H_{d1}}\left( \omega \right) 。$ | (2) |
由线性系统的性质可得到系统传递函数
| $ {H_{d1}}\left( \omega \right) = ({H_s}\left( \omega \right))/(1 - {H_s}\left( \omega \right) \cdot {H_j}\left( \omega \right)) 。$ | (3) |
存储转发模式将接收到的信号不失真转发,但整个过程产生较长时延,且无法应对敌方鱼雷发射的复杂编码和诱骗脉冲,如图2(c)所示。相比存储转发模式,边收边发模式没有较大的时延问题,但存在声串漏现象,转发诱骗信号相比接收主动声呐信号发生严重畸变,信号幅度差距较大且毫无规律性,如图2(d)所示。

|
图 2 主动式声诱饵转发诱骗仿真分析图 Fig. 2 Active acoustic decoy forwarding deception simulation analysis diagram |
设敌方主动声呐探测信号
在信号处理领域,通常通过计算互相关系数来分析2个信号的相关程度[8],相关系数公式为:
| $ \rho (X,Y) = \frac{{C{\text{ov(X,}}Y{\text{)}}}}{{\sqrt {Var[X]Var[Y]} }} 。$ | (4) |
式中,
为了解决边收边发模式下的声串漏现象,增大系统声隔离度,本文提出在电子舱壳体内部配置滤波器改善系统传递函数,工作流程如图3所示。
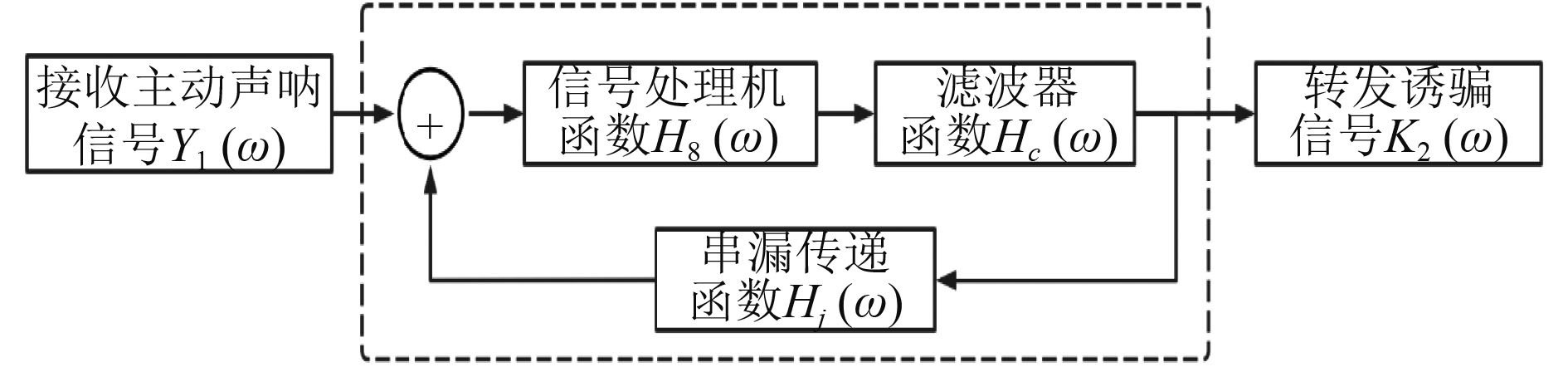
|
图 3 声串漏消除流程框图 Fig. 3 Block diagram of acoustic cross leakage cancellation |
图中,
| $ {K_2}\left( \omega \right) = {Y_1}\left( \omega \right) \cdot {H_{d2}}\left( \omega \right)。$ | (5) |
由线性系统的性质可得到系统传递函数
| $ {H_{d2}}\left( \omega \right) = ({H_s}\left( \omega \right){H_c}(\omega ))/(1 - {H_s}\left( \omega \right) \cdot{H_j}\left( \omega \right)\cdot {H_c}(\omega ))。$ | (6) |
为了让系统实现实时增益转发,设置滤波器传递函数
| $ {H_c}\left( \omega \right) = 1/(1 + {H_j}\left( \omega \right)\cdot{H_s}(\omega )) 。$ | (7) |
将式(7)代入式(6),可得:
| $ {H_{d2}}\left( \omega \right) = {H_s}\left( \omega \right)。$ | (8) |
由式(2)得到:
| $ {K_2}\left( \omega \right) = {Y_1}\left( \omega \right) \cdot {H_s}\left( \omega \right)。$ | (9) |
通过添加滤波器,使得边收边发模式转发诱骗信号在没有时延的条件下,无失真转发。对式(7)进行分析,串漏传递函数
电子舱壳体使用高声速金属材料,发射信号带限白噪声如图4(a)所示,信号长度为0.2 s,频率为5~25 kHz,幅度为1 V,接收信号如图4(b)所示。
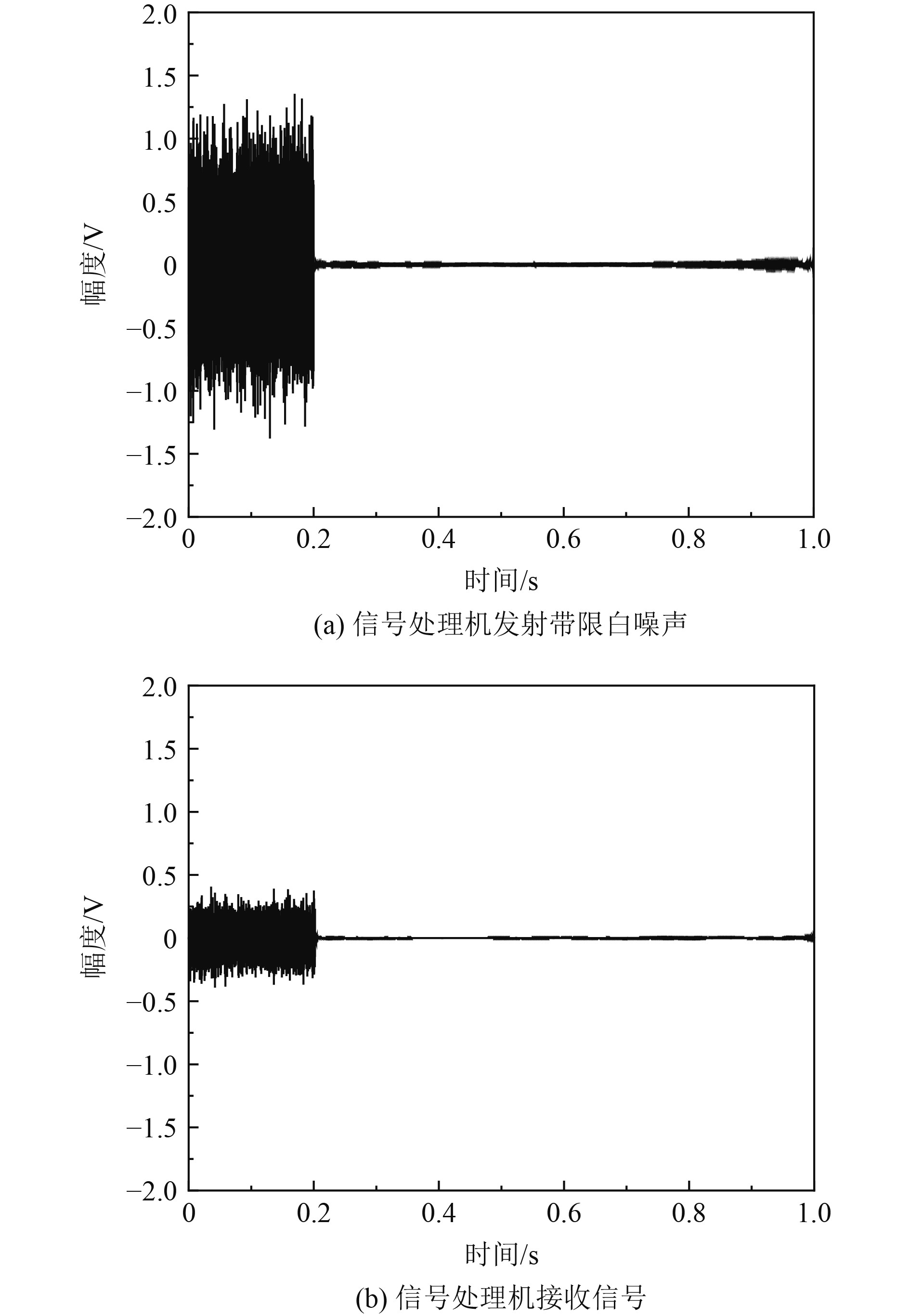
|
图 4 串漏传递函数仿真信号 Fig. 4 Simulation signal of cross-leakage transfer function |
自适应滤波处理模型是基于一体式主动声诱饵工作过程,对应于自适应算法基本工作原理得到的,是经典单输入信号单输出信号的自适应滤波器[9]。滤波器工作原理如图5所示。
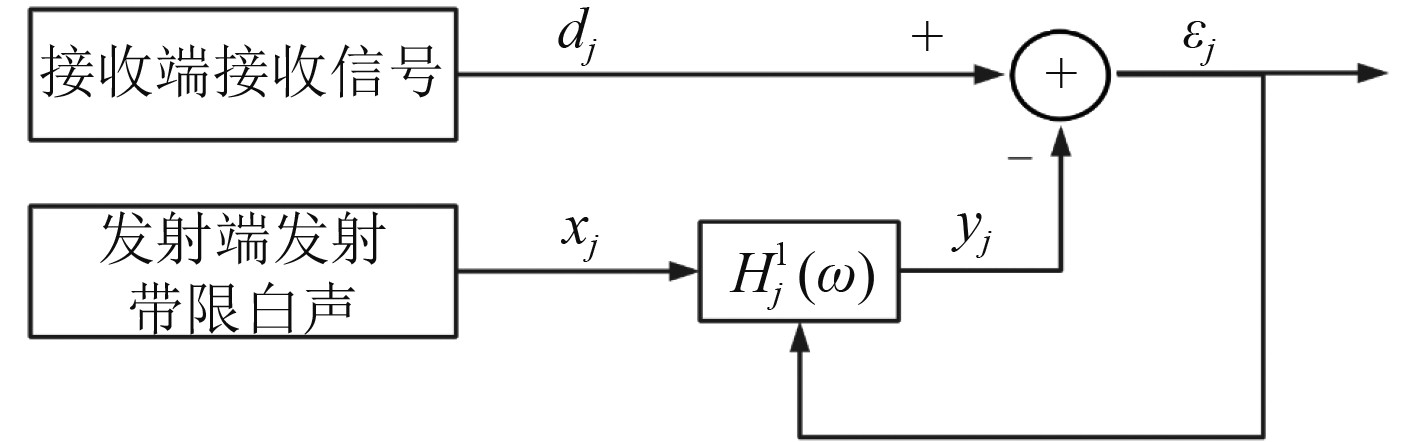
|
图 5 自适应滤波器工作原理图 Fig. 5 Adaptive filter working principle diagram |
图中,
假设自适应计算过程已收敛误差信号
| $ {H_j}^1(\omega ) = {H_j}(\omega )。$ | (10) |
式中,
最小二乘算法目的是让期望信号与模型滤波器输出信号之差的平方和达到最小,使用递归求解最小二乘问题,可得到递归最小二乘(Recursive least-square,RLS)算法。RLS算法的目标是选择新的滤波系数值来保证输出信号基于最小二乘运算上尽可能接近所需信号,在输入信号的相关矩阵特征值扩展较大的情况下,能保证快速收敛并且跟踪能力为自适应算法中最好[10]。因此,选择RLS算法仿真串漏传递函数
COMSOL Multiphysics是一款具有多物理场直接耦合功能的有限元分析软件[11]。常见的声诱饵电子舱是圆柱形轴对称结构,可直接简化为二维轴对称的几何模型[12]。声诱饵电子舱数值模型如图6所示,包含电子舱外壳、计算水域和吸声的完美匹配层,在流体和固体之间设置声-结构多物理场耦合边界,基于一体式主动声诱饵模型进行接收总声场仿真。壳体材料见表1。
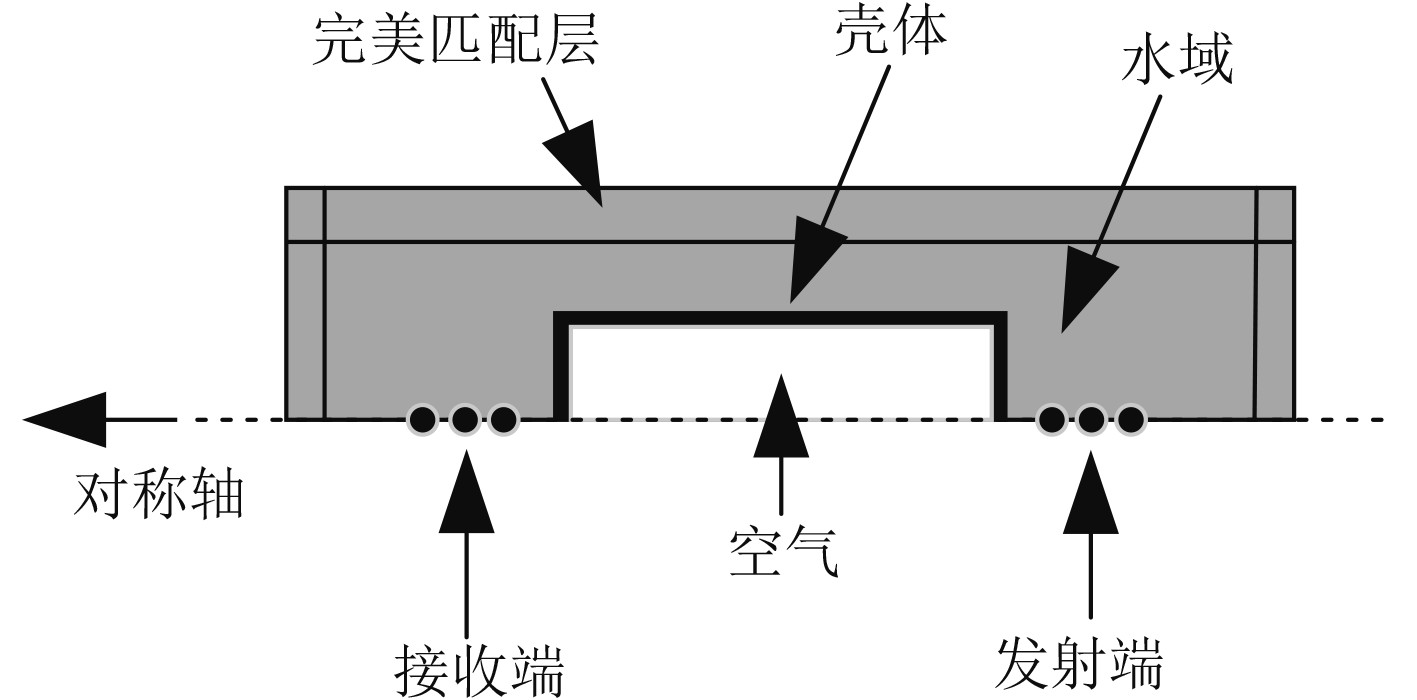
|
图 6 电子舱数值计算模型 Fig. 6 Electronic cabin numerical calculation model |
电子舱长度为1 m,半径为0.3 m,壳体厚度为0.02 m。设置声诱饵发射阵和接收阵均为三元点源阵列,间距为0.01 m,利用3个点源代替体积源,在点源间距小于波长时适用。发射阵总发送电压响应为120 dB,接收阵总接收灵敏度为–120 dB,发射阵阵元中心在电子舱壳体的正上方0.5 m处,接收阵阵元中心在电子舱壳体正下方1.5 m,二者指向性相同。计算频率为5~25 kHz,计算完成后,计算提取传递函数,得到接收总声场[13]。将包含目标的声信道看作线性系统,接收总声场即为系统对发射信号的响应。发射信号为单位脉冲响应,通过频域间接法获得有电子舱时的串漏传递函数
|
|
表 1 壳体材料参数表 Tab.1 Shell material parameter table |
电子舱壳体为高声速金属材料和低声速PMMA材料时,得到接收端接收总声场,如图7所示。
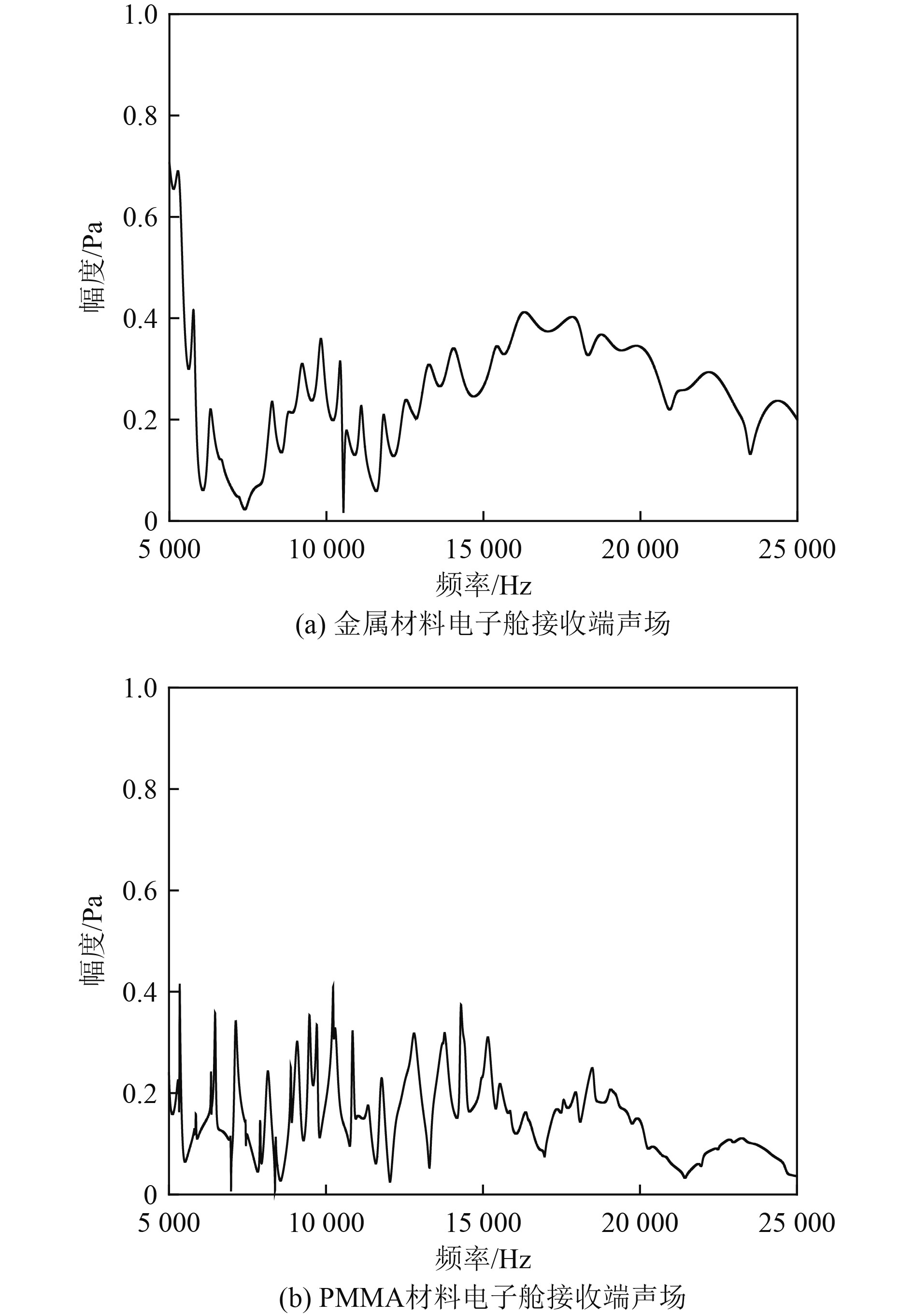
|
图 7 接收端声场图 Fig. 7 Receiver sound field diagram |
分析可知,可看到低声速PMMA材料比高声速金属材料声场更加复杂。因为低声速PMMA材料波长更短,所以有限长度内,共振现象更加严重,共振峰更多,导致接收总声场尖刺更多,串漏传递函数更加复杂。
当电子舱壳体存在时,声波通过壳体传播,对于不同材料的电子舱壳体,由于介质的弹性模量和密度不同,弹性波的传播速度也不同。相速度频散曲线如图8所示。

|
图 8 相速度频散曲线 Fig. 8 Phase velocity dispersion curve |
对相速度频散曲线进行分析,金属材料纵波速度
自适应滤波器可用许多不同的结构来实现,结构的选取会影响计算处理的复杂度,还会对达到期望性能标准所需的迭代次数产生影响[16]。
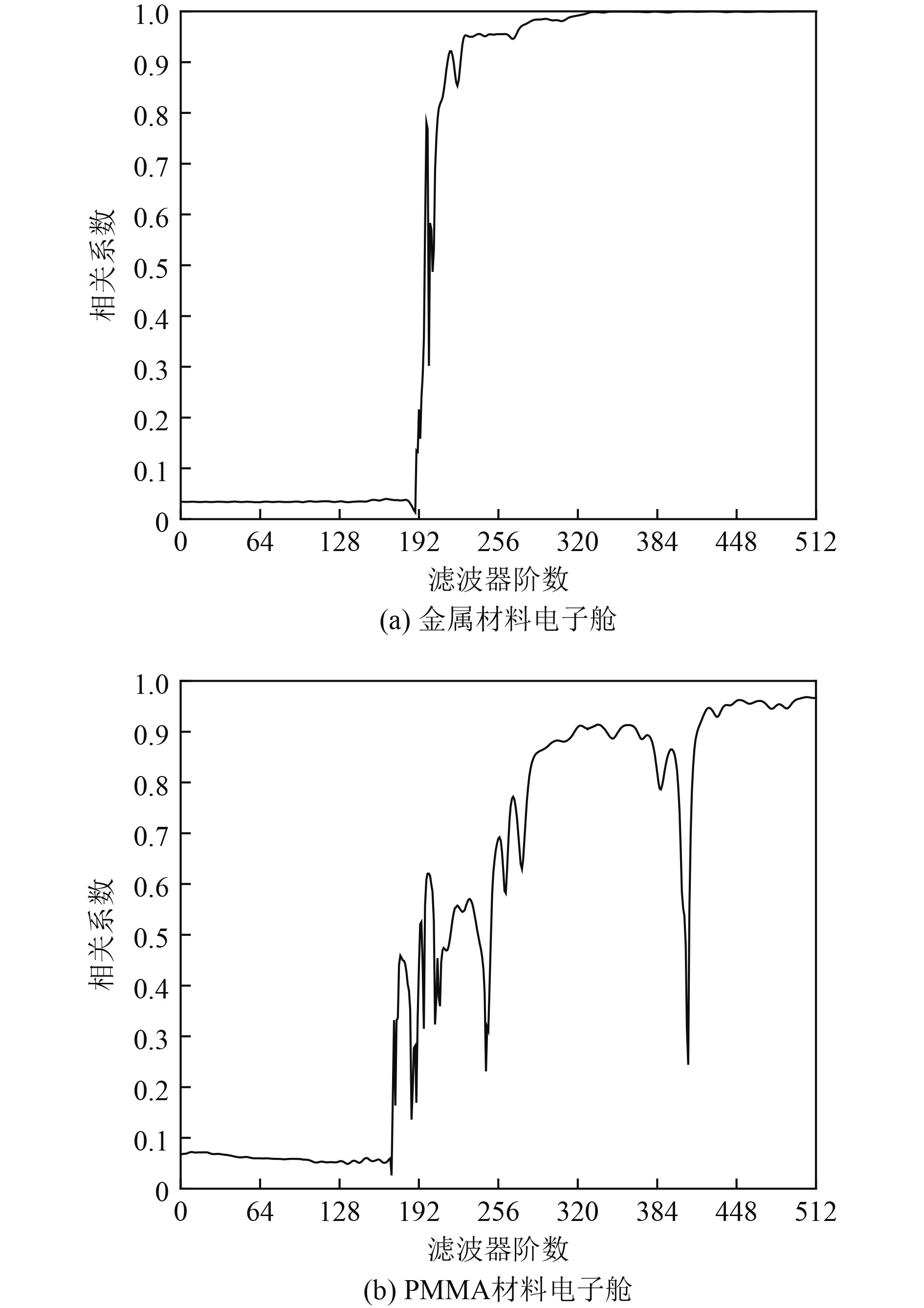
|
图 9 相关系数随自适应滤波器阶数变化图 Fig. 9 Correlation coefficient changes with adaptive filter order |
可知,针对不同壳体材料,共性为随着滤波器阶数增大,相关系数逐渐变大。如图9(a)所示,对于高声速金属材料,滤波阶数为192阶时,相关系数低于0.1无相关性。随着滤波器阶数上升,在192-256阶相关系数会有一个较大的上升,当滤波器阶数为256阶时,相关系数达到0.9552,具有高相关性且稳定性较高,声隔离度效果较好。当滤波器阶数超过256阶时,相关系数逐渐向1靠近且更加稳定。此时,用自适应算法处理的转发诱骗信号代替理想转发诱骗信号效果较好。如图9(b)所示,对于低声速PMMA材料,由于共振现象严重,因此串漏传递函数更加复杂,对滤波器阶数要求更高。当滤波器阶数低于170阶时,相关系数低于0.1且具有无相关性。随着滤波器阶数上升,当滤波器阶数在170~512阶时,相关系数整体呈上升趋势,但是稳定性较低,波动性较大,且当滤波器阶数为246和409阶时,出现低峰值,相关系数0.3,且具有低相关性。当滤波器阶数超过448阶时,仿真处理的诱骗信号与理想转发诱骗信号相关性较高并达到0.96。
当滤波器阶数为256和512阶时,针对高声速金属壳体材料和低声速PMMA材料,得到仿真串漏传递函数,并将其配置到信号处理机中得到图10和图11。

|
图 10 256阶自适应滤波器转发诱骗信号图 Fig. 10 256-order adaptive filter forwarding decoy signal diagram |

|
图 11 512阶自适应滤波器转发诱骗信号图 Fig. 11 512-order adaptive filter forwarding decoy signal diagram |
当滤波器阶数为256阶时,对高声速材料,自适应处理后的转发诱骗信号变好,相关系数达到0.95;对低声速PMMA材料,处理后的信号效果较差,相关系数只有0.4216且稳定性较差。当滤波器阶数为512阶时,如图11所示,对高/低声速材料整体转发诱骗信号较好;对高声速金属材料,经过自适应滤波器处理后的转发诱骗信号与理想转发诱骗信号的相关系数达到0.998,远超过未经处理声串漏下相关系数为0.0328的情况,而且幅度畸变和时延混叠现象都被过滤掉;对于低声速PMMA材料,相关系数达到0.9764,整体仿真效果较好。利用最小二乘法仿真串漏传递函数
针对一体式主动声诱饵边收边发工作模式存在的声串漏现象,提出增加滤波器改变系统传递函数增大声隔离度。以带限白噪声作为激励,利用自适应最小二乘法仿真串漏传递函数,通过改变自适应滤波器阶数,对高声速金属材料和低声速PMMA材料电子舱壳体进行声隔离验证。分别利用有限元、频域间接法方法获得了系统串漏传递函数、串漏信号时域波形。证明最小二乘法是一种获得一体式主动声诱饵串漏传递函数的有效方法,最小二乘法可用来增大一体式主动声诱饵边收边发系统的声隔离度。通过仿真对比得到如下结论:
1) 边收边发模式下,由于发射接收较近导致声串漏,电子舱壳体存在使得接收声场发生严重畸变;低声速壳体材料比高声速材料波长短,共振现象导致串漏传递函数更加复杂。
2) 对于边收边发模式,使用最小二乘法仿真不同壳体材料电子舱串漏传递函数,高声速金属电子舱自适应处理后与理想转发诱骗信号相关系数随滤波器阶数增大上升且稳定性较高,滤波器阶数超过256阶时,保持0.95以上。
3) 低声速PMMA电子舱串漏传递函数更加复杂,对滤波器阶数要求更高。当滤波器阶数在128~448阶时,相关系数整体上升但稳定性较差,滤波器阶数超过448阶时,保持0.96以上。
| [1] |
高新生, 付为工. 试论新时代海防观及现代海防建设[J]. 南海学刊, 2019, 5(1): 11-19. GAO Xinsheng, FU Weigong. On the concept of coastal defense in the new era and the construction of modern coastal defense[J]. South China Sea Journal, 2019, 5(1): 11-19. |
| [2] |
王新华, 高洪林, 穆连运, 等. 舰艇反鱼雷技术[J]. 舰船科学技术, 2011, 33(9): 86-90. WANG Xinhua, GAO Honglin, MU Lianyun, et al. Ship anti-torpedo technology[J]. Ship Science and Technology, 2011, 33(9): 86-90. DOI:10.3404/j.issn.1672-7649.2011.09.020 |
| [3] |
向大威, 顾亚平, 李秀红. 声泄漏的自适应抵消[J]. 声学技术, 1993, 12(4): 1-3. XIANG Dawei, GU Yaping, LI Xiuhong. Adaptive cancellation of acoustic leakage[J]. Acoustic Technology, 1993, 12(4): 1-3. |
| [4] |
吴培荣. 基于边收边发技术的声隔离度研究[J]. 声学技术, 2013, 32(4): 281-285. WU Peirong. Research on acoustic isolation based on transmitting while receiving technology[J]. Acoustic Technology, 2013, 32(4): 281-285. |
| [5] |
何陈. 声呐目标模拟器的主动干扰抑制研究[D]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [6] |
戴雅丽. 自动控制原理与系统[M]. 北京: 北京希望电子出版社, 2006.
|
| [7] |
唐丽媛, 王琦. 声诱饵电子舱散射声场对接收信号影响研究[J]. 舰船科学技术, 2021, 43(7): 163-166. TANG Liyuan, WANG Qi. Research on the effect of scattering sound field of acoustic decoy electronic cabin on received signal[J]. Ship Science and Technology, 2021, 43(7): 163-166. |
| [8] |
江征风. 测试技术基础 [M]. 北京: 北京大学出版社, 2007.
|
| [9] |
B WIDROW et al. Adaptive noise cancelling: principles and applications[J]. In Proceedings of the IEEE, 1975, 63(12): 1692−1716.
|
| [10] |
ELEFTHERIOU E, FALCONER D, Steady-state behavior of RLS adaptive algorithms, ICASSP '85[C]// IEEE International Conference on Acoustics, Speech, and Signal Processing, 1985: 1145-1148.
|
| [11] |
COMSOL Multiphysics® v. 6.0. cn. comsol. com[R]. COMSOL AB, Stockholm, Sweden.
|
| [12] |
卢笛. 基于有限元原理的弹性目标声散射计算[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [13] |
何祚镛, 赵玉芳同. 声学理论基础[M]. 北京: 国防工业出版社, 1981.
|
| [14] |
汤渭霖, 范军, 马忠成. 水中目标声散射 [M]. 北京: 科学出版社, 2018.
|
| [15] |
汤渭霖, 范军, 赵开琦等. 水中结构振动与声辐射 [M]. 北京: 科学出版社, 2022.
|
| [16] |
DINIZ P S R. Adaptive filtering: algorithms and practical implementation[BK]. Bibtex Nuhag, 2008.
|
 2023, Vol. 45
2023, Vol. 45
