海洋上某一点自动泊位在实际操作中存在很多问题,这些问题包括水深不同对船舶动力系统的力矩要求不同,风浪、洋流也对船舶动力定位形成了很多的扰动,特别是在高海况下,这些扰动会影响船舶的首向和位置以及船舶定位精度,从而提升了海上资源开采的成本。
船舶动力定位控制系统包括推进器系统、控制系统以及传感测量系统。传感测量系统包括位置系统和水深系统等一系列综合传感系统,位置系统能够获取船舶当前的位置,其主要通过差分全球定位系统来实现,水深系统主要获取当前船舶位置的水深情况。控制系统是船舶动力定位控制系统的核心,将神经网络控制技术、模糊控制等应用到船舶定位控制中,能够不断适应外界的环境变化,通过传感测量系统反馈来不断调整船舶定位精度。推进器系统是为船舶提供动力或者力矩,现代船舶大部分是通过液压马达来实现船舶推进。在高海况下,普通的船舶定位锚泊技术难以实现定位精度,且不能适应不同海洋地区的水深,无法适应复杂的洋流环境。因而国内外学者将大部分的精力用于非线性控制理论以及模型构建方向。骆寒冰等[1]将专家PID与SQP算法综合应用到船舶动力定位控制系统中,取得了不错的定位效果。贺广健等[2]研究了有限时间控制和超螺旋滑模控制在船舶动力定位系统中的应用;郑大明等[3]研究了Backstepping方法在自适应动力定位系统中的应用。这些研究结果表明,将不同的算法应用到船舶动力定位系统中可以取得不错的效果,但是对于高海况而言,应用一种控制算法很难达到较好的定位效果,因而本文针对高海况下船舶定位面临的问题,提出一种船舶动力定位混合控制器,将改进PID算法、模糊控制等算法综合应用到船舶动力定位控制中,并通过仿真实验来验证混合控制器的控制效果。
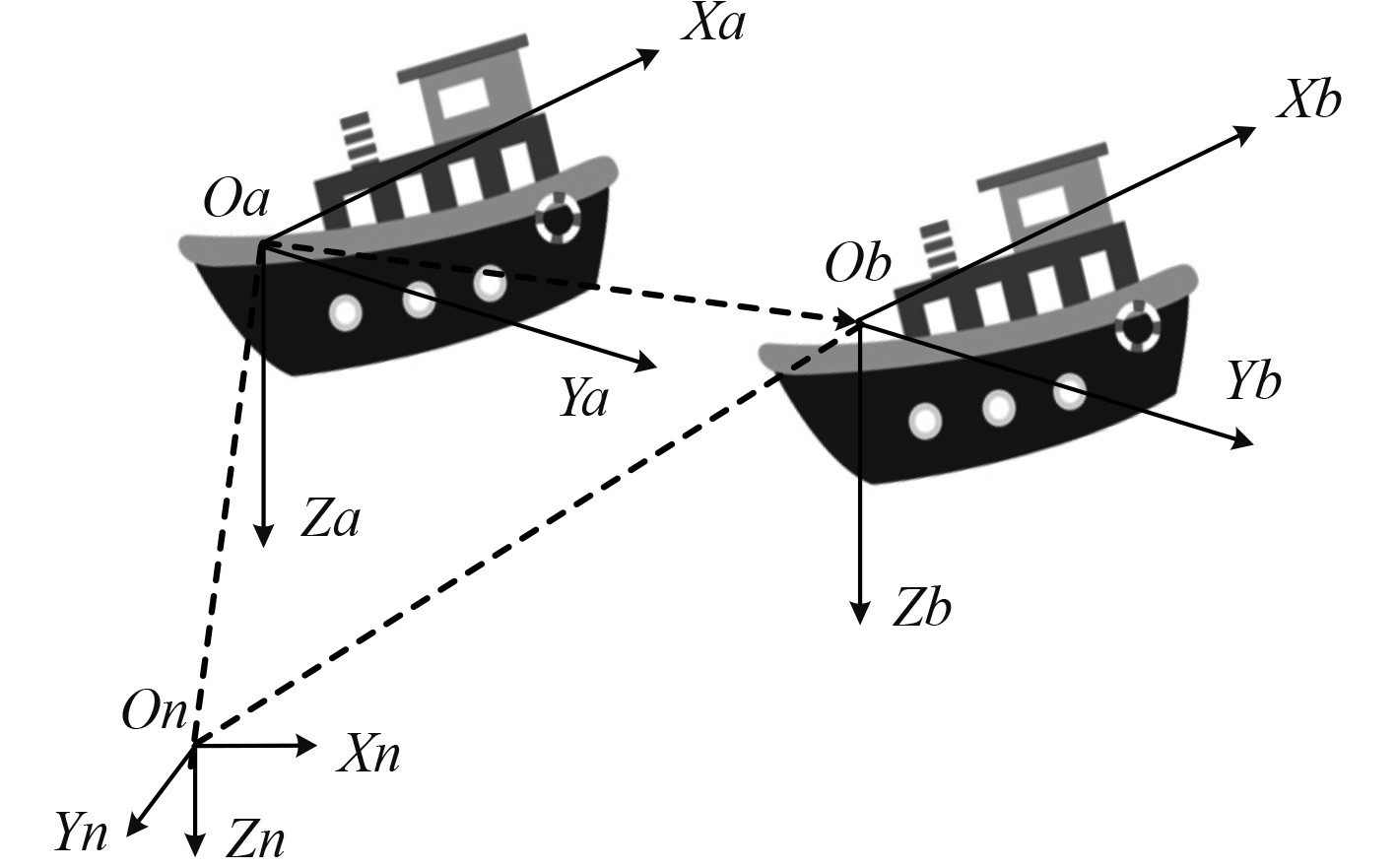
1 高海况下船舶动力学模型分析 1.1 船舶耐波坐标系分析高海况下船舶的动力定位,需要建立高海况下船舶的动力学模型,而动力学模型的建立和分析需要依托坐标系,传统的固定坐标系或者船体坐标系无法完全将高海况下的海浪、洋流等作用表现出来,因而本文使用耐波坐标系[4],如图1所示。
|
图 1 船舶耐波坐标系 Fig. 1 Ship seakeeping coordinate system |
在耐波坐标系中,Oa-XaYaZa坐标系为原始船舶坐标系,Ob-XbYbZb为虚拟船舶坐标系,两者X轴的船舶首向在一条直线上,在存在波浪的情况下,则Ya轴指向虚拟船舶方向运动,若不存在波浪的情况下两坐标系重合。
1.2 动力学模型分析在高海况下船舶的运动具有6个自由度,分别是纵摇、横荡、纵荡、垂荡、首摇及横摇,定义船舶的速度向量为V=[u,v,w,p,q,r],船舶力矩向量Q=[α,β,γ,δ,ε,ζ],其中w1~w6为船舶在6个自由度内的运动系数,则建立的动力学模型满足以下条件[5]:
| $\begin{split} \alpha =& {\omega _1}[u + wq - vr] - {X_{a}}\left( {{{q}^2} + {{r}^2}} \right) + {Y_{a}}(pq - r) + \\ &{Z_a}(pr + q)\beta = {\omega _2}[v + wp - ur] - {Y_{a}}\left( {{p^2} + {{\rm{r}}^2}} \right) + \\ &{Z_{a}}(qr - p) + {X_a}(qp + r)r = {\omega _3}[w + vp - uq] - \\ &{Z_{a}}\left( {{{p}^2} + {{q}^2}} \right) + {X_{a}}(rp - q) + {Y_a}(rq + p)\delta = \\ &{\omega _4}(w + vp - uq) + {I_{xy}}(pr - q) + \left( {{r^2} - {q^2}} \right){I_{yz}} - \\ &(r + pq){I_{xz}}\varepsilon = {\omega _5}[u + wq - vr] + {I_{yz}}(qp - r) + \\ &\left( {{p^2} - {r^2}} \right){I_{xz}} - (p + qr){I_{xy}}\xi = {\omega _6}[v + ur - wp] + \\ &{I_{xz}}(qr - p) + \left( {{q^2} - {p^2}} \right){I_{xy}} - (q + rp){I_{xz}}。\end{split}$ | (1) |
在船舶动力定位控制器设计中,对船舶的运动情况进行基本分析非常重要,它能够分析船舶在首向一定的情况下面对不规则的洋流、海浪的运动情况。同时为了简化分析,此时船舶的运动速度为恒定速度,可利用耐波坐标系中的虚拟船舶来模拟分析船舶在海浪、洋流作用下的运动情况[6]。
2 船舶动力定位混合控制器开发 2.1 动力定位混合控制器结构设计船舶动力定位混合控制器是动力定位系统的核心,但是其功能实现不仅需要核心控制算法的设计,同时还需要传感测量系统和动力系统的紧密配合。混合控制器结合现有先进控制理论,对船舶在高海况下所面临的波浪、洋流等恶劣情况自行进行预判,并将这些预判结果输出控制量到动力系统,同时不断通过传感测量系统来获取定位控制效果,实现船舶动力定位的全闭环控制。根据此控制思想,设计的船舶动力定位混合控制器结构如图2所示。

|
图 2 动力定位混合控制器结构 Fig. 2 Dynamic positioning hybrid controller structure |
动力定位混合控制器的控制目标是船舶位置以及船舶首向,目标船舶在洋流、海风以及海浪的影响下极难达到控制目标,主要实现手段是通过将改进PID算法、神经网络算法以及模糊控制算法等应用到控制器中,并将算法控制器中运算所获得的结果输出到液压马达,从而控制多个液压马达动力的分配,同时传感测量反馈负责将当前的船舶首向、速度以及位置反馈到算法控制器,将当前船舶的相关数据和目标数据求取差值,进一步确定控制参数。
2.2 算法控制器设计本文设计的算法控制器主要使用改进PID算法、神经网络算法以及模糊控制算法等。
1)改进PID算法控制器
传统PID算法通过在控制中调整比例(P)参数、微分(I)参数、积分(D)参数来提升控制效果,但在高海况下对船舶的扰动较多,传统PID算法在进行调整时动态性能较差,扰动较多时P、I、D参数对环境很敏感,同时当外界条件发生变化时需要不断地调整P、I、D参数,对环境的适应性较差。高海况意味着外界的条件可能存在较大的跳变情况,而传统PID则无法应对这种情况,其基本输出具有一定的惯性,因而本文在传统PID控制算法的基础上进行改进,具体方法为对不同时刻的数据赋予不同的权值,越接近当前时刻的数据权值越大,将历史数据值加权后求平均值作为当前的信号滤波控制参数,控制信号将有效去除信号扰动。
图3(a)为传统PID控制时存在扰动情况下,无法在短时间内将这些扰动清除掉,回到正常情况。图3(b)为改进PID的控制效果,可以发现,改进PID算法消除了扰动信号。

|
图 3 改进PID算法控制器仿真效果 Fig. 3 Improve the simulation effect of PID algorithm controller |
2)神经网络控制器
神经网络算法是目前应用较多的算法之一,在船舶动力定位混合控制器中,由于改进后的PID依然缺乏预测能力,因而在高海况下对船舶的控制仍然存在一定的滞后性。定义控制器的输出为y,则误差△y为:
| $ \Delta y= {y} - y_d \text{。} $ |
假设y为一非线性系统,则有:
| $ y = f(x) + bu \text{。} $ |
式中:b为未知常量,f(x)为高海况下非线性干扰。利用李雅普诺夫函数
| $ \dot{V}=\text{sgn}({{b}})e(\frac{f(x)-{f}_{d}({x}_{d})}{b}+u) 。$ |
其中
使用Matlab对神经网络控制器进行仿真(见图4),输入一个标准信号用于模拟高海况下的干扰信号,此时就需要对这个干扰信号进行估计,并在后续的控制中对这个干扰信号加以处理,改进后的PID算法显然无法对该信号进行预测和跟随,但神经网络控制器在初期判断出该干扰信号的变化方向后就可以很快跟随该信号,在船舶动力定位系统中就可以对该干扰信号作出预测,从而解决在此干扰信号存在的情况下,提前发出控制信号,保证船舶首向和位置的稳定性。

|
图 4 神经网络控制器仿真结果 Fig. 4 Neural network controller simulation results |
3)模糊控制器
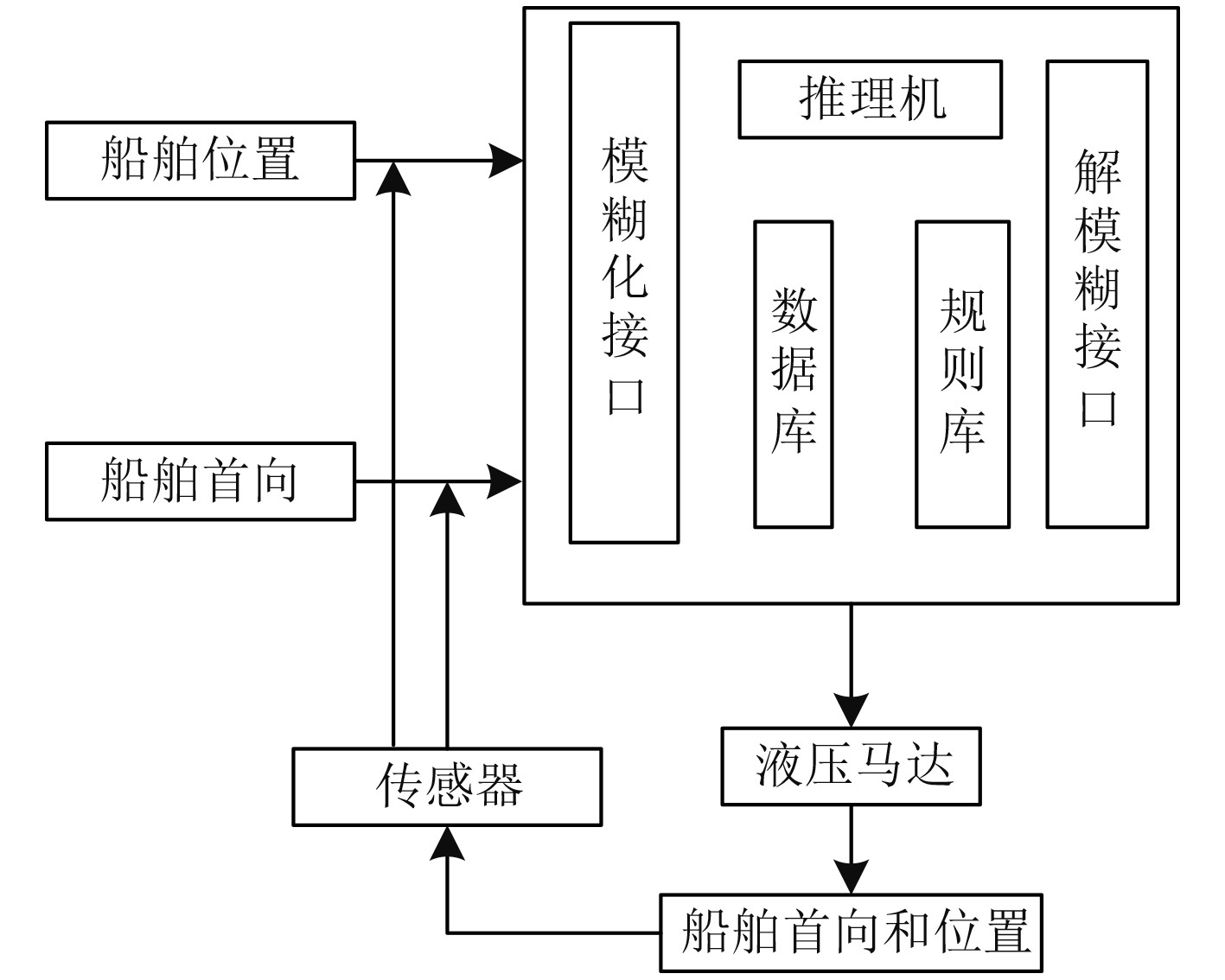
本文建立的模糊控制器是改进PID控制器以及神经网络控制器的有效补充,改进PID控制器主要针对高海况下的线性变化,神经网络控制器主要针对有规律的非线性变化,并对这些干扰进行预测。模糊控制器通过模糊语言和模糊逻辑来对船舶首向和位置进行控制,其控制基本过程如图5所示。模糊控制器实现的核心是通过将船舶位置和船舶首向模糊化后,作为模糊控制器的输入,在模糊控制器中设定有推理机,同时还包含数据库和规则库,数据库和规则库是专家经验以及所有模糊规则的集合,推理机依靠数据库和规则库提供的数据求解模糊关系方程,从而获得液压马达的控制量,实现对船舶动力定位的目的。
|
图 5 模糊控制器结构 Fig. 5 structure of fuzzy controller |
以船舶首向控制为例,仿真结果如图6所示。设定首向角度为5°,在将控制目标模糊化并建立模糊规则后,模糊控制器快速向目标首向运动,并且出现了少量的超调,超调量为0.3°。在0.8 s左右完成首向控制调整,达到控制目标,且在后续的控制中几乎没有出现波动,这是改进PID算法和神经网络控制难以达到的。

|
图 6 模糊控制仿真结果 Fig. 6 Fuzzy controller simulation results |
综上可以发现,在高海况下本文设计的改进PID算法控制器、神经网络控制器和模糊控制器对清除干扰、干扰信号预测和跟踪、快速响应控制等方面均具有一定效果,在实际应用中将多种控制器混合使用能够有效应对高海况下的船舶动力定位问题。
3 结 语在高海况下船舶的动力定位精度受到洋流、海风以及海浪等多种因素影响,这对船舶动力定位控制系统提出了更高的要求。本文提出一种基于改进PID算法、神经网络算法、模糊控制算法的船舶动力定位混合控制器,得到如下结论:
1)设计船舶动力定位混合控制器需要建立高海况下的船舶耐波坐标系以及动力学模型;
2)本文设计的船舶动力定位混合控制器能够实现对干扰信号的预测和跟随,且能够适应快速响应控制,因而具有较大的实用性。
| [1] |
骆寒冰, 李元芳, 谢芃, 等. 专家PID与SQP算法在动力定位船模试验中的应用[J]. 中国海洋平台, 2021, 36(5): 18-22. LUO Han-bing, LI Yuan-fang, XIE Peng, et al. Application of expert PID and SQP algorithm in dynamic positioning ship model test[J]. China Offshore Platforms, 2021, 36(5): 18-22. |
| [2] |
贺广健, 刘海波, 宫勋, 等. 基于有限时间超螺旋滑模控制的船舶动力定位控制律设计[J]. 长春理工大学学报(自然科学版), 2022, 45(6): 1-9. HE Guang-jian, LIU Hai-bo, GONG Xun, et al. Design of ship dynamic positioning control law based on finite time superspiral sliding mode control[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2022, 45(6): 1-9. |
| [3] |
郑大明, 方诚. 考虑未知死区输入的船舶鲁棒自适应动力定位控制[J]. 中国航海, 2021, 44(2): 21-26. ZHENG Da-ming, FANG Cheng. Ship robust adaptive dynamic positioning control considering unknown dead zone input[J]. Navigation of China, 2021, 44(2): 21-26. |
| [4] |
于子文, 魏新江. 船舶动力定位系统的复合抗干扰控制[J]. 鲁东大学学报(自然科学版), 2023, 39(1): 42-49. YU Zi-wen, WEI Xin-jiang. Compound anti-interference control of Ship dynamic positioning System[J]. Journal of Ludong University (Natural Science Edition), 2023, 39(1): 42-49. |
| [5] |
孟一平. 带有广义噪声的船舶动力定位系统控制器设计[D]. 大连:大连海事大学, 2022.
|
| [6] |
杨锡明. 模糊系统的容错控制及船舶动力定位应用[D]. 大连:大连海事大学, 2022.
|
 2023, Vol. 45
2023, Vol. 45
