0 引　言

燃气轮机作为一种应用广泛的复杂设备，其良好的性能状态对工业生产活动及航行运输尤为重要。因其结构复杂、运行工况多变、环境恶劣，高温部件易发生退化或故障，从而造成经济损失。异常检测作为燃气轮机健康管理的一项关键技术，可根据燃机运行的可测量参数，对燃气轮机进行实时监测与诊断，识别早期的异常状态或退化，从而减少计划外维护，提高设备的安全性和可用性。

燃气轮机异常检测的方法可分为基于模型的方法和数据驱动的方法。基于模型的方法^[1-2]主要依赖于精确的数学物理模型，由于燃气轮机机理的复杂性导致难以建立精确的数学模型在实际中应用；数据驱动的异常检测方法大多是基于机器学习的，其中利用已标注的数据训练机器学习^[3-6]分类模型，在燃气轮机故障检测与诊断中被广泛应用，基于卷积神经网络的深度学习方法^[7]也被用于识别燃气轮机气路故障，以上方法依赖于足够的已标注数据，但燃气轮机监测数据极不平衡，正常数据远大于异常数据，甚至没有异常数据。另外，从有限个燃气轮机得到的异常样本不能包括所有可能的异常行为，所以需要标注异常方法在燃机排温异常检测中的应用受限。

无需标注异常的方法在故障缺失场景中具有独特优势。Tan等^[8]提出了隔离森林用于评估燃气轮机系统退化状态的方法。Yan^[9]使用深度自编码器对排温传感数据进行提取特征，然后利用学习到的特征进行异常检测。白明亮等^[10]采用深度自编码器的重构误差作为异常指标，并结合支持向量机描述算法进行燃气轮机高温部件异常检测。Fu等^[11]设计了重新优化的深度自编码器用于燃气轮机的无监督异常检测。深度自编码器可将高维传感数据的信息保存在隐藏特征和重构误差中，少量研究同时考虑了两者包含的全面信息。同时，隔离森林在无监督异常检测中取得了优异的成效，尚未用于燃气轮机排气温度的异常检测问题。

刘娇^[12]研究表明，当燃气轮机部件发生积垢、磨损、打伤等故障时，低压涡轮排气温度的周向分布会发生改变。以船用三轴燃气轮机为例，在低压涡轮出口有16个测量温度的热电偶，考虑了一定的气流旋转角度的影响，可间接反映环管型燃烧室燃烧情况，因此可通过排气温度分布对燃气轮机健康状态进行监测^[13]。本文针对异常样本稀缺场景下的燃气轮机高温部件故障检测问题，提出深度自编码器和隔离森林融合的异常检测方法，同时考虑了DAE模型的隐藏特征和重构误差，大幅度提升燃气轮机高温部件的异常检测精度。

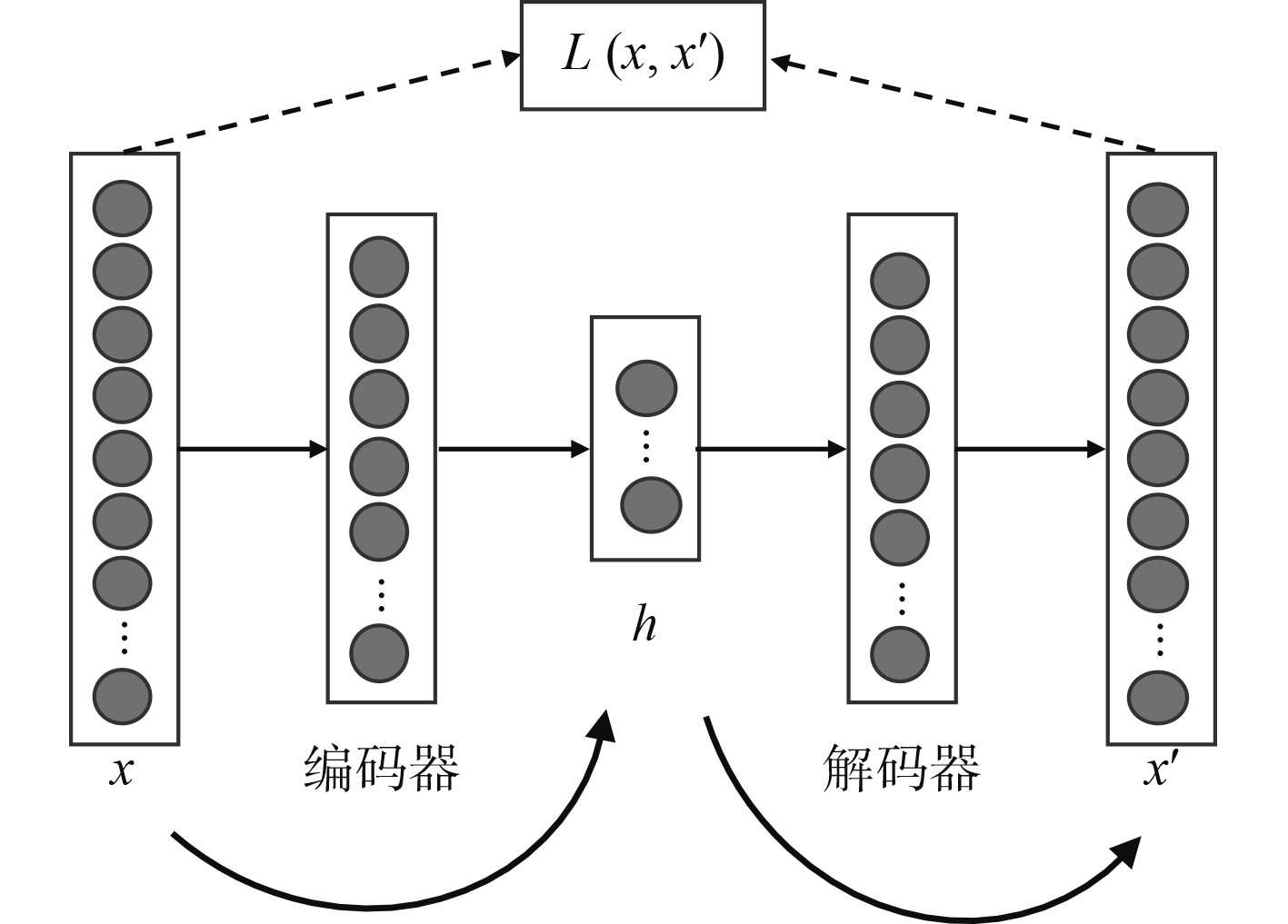
1 模型与方法 1.1 深度自编码器

深度自编码器是一种深层网络结构，属于无监督学习的方法，可使具有噪声的数据更具有鲁棒性，这对使用噪声传感器测量的数据进行异常检测应用十分重要。深度自编码器（DAE）网络的基本形式包括：编码器和解码器，使用2个DAE层的结构如图1所示。

输入向量$x \in {R^p}$通过编码器映射至隐变量$h \in {R^m}$，隐变量$h$通过解码器映射得到输入向量x的重构，输出$x' \in {R^p}$。该过程可表示如下：

$ h = {f_\theta }(x) = s({\boldsymbol{W}}x + b)，$

(1)

$ x' = {g_\theta }(h) = s({\boldsymbol{W}}'h + b') 。$

(2)

其中，${\boldsymbol{W}}$和${\boldsymbol{W}}'$分别为$m \times p$和$p \times m$网络权重矩阵，$b$和$b'$为隐含层偏差，$s( \cdot )$为非线性激活函数。

DAE将训练集D上的重构误差作为目标函数，通过利用反向传播算法中的目标函数进行优化来确定网络参数$\theta = \{ {\boldsymbol{W}},{\boldsymbol{W}}',b,b'\} $。

$ {J_{AE}}(\theta ) = \frac{1}{{{N_D}}}\sum\limits_{x \in D} {L(x,g(f(x)))}。$

(3)

采用平方误差重构误差函数：

$ L = \sum\nolimits_{i = 1}^{{d_x}} {{{({x_i} - {{x'}_i})}^2}}。$

(4)

1.2 隔离森林算法

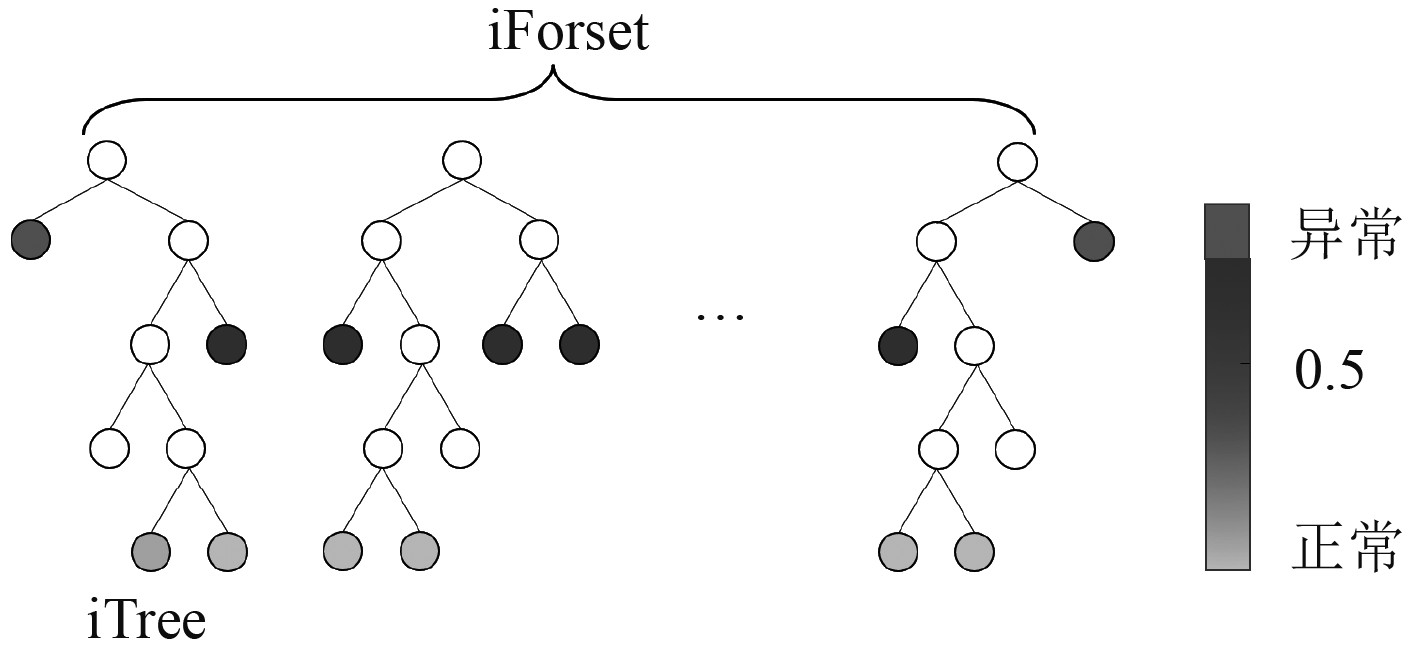
隔离森林（isolated Forset，iForset）算法由Liu等^[14]提出，其相关研究奠定了iForset算法的理论基石。其结构示意图如图2所示。隔离森林是隔离树的集合，隔离树由矩阵样本$X \in {R^{n \times p}}$构建，构建每一棵iTree的细节如下：

1）在p维属性中随机选择一个属性x_i；

2）在x_i最大值与最小值之间随机选择一个分隔值p；

3）分别根据X中每个样本的x_i属性大于或小于p将X划分为X_l和X_r。

4）将X_l和X_r作为新的X重复以上步骤构造一棵iTree，直到子节点只有一个实例，或者数据集X中的所有数据具有相同值，或者iTree达到了限制高度。

隔离森林由许多隔离树定义：

$ IF = \{ {t_1},...,{t_T}\}。$

(5)

对于每棵隔离树t，都可计算隔离样本的迭代次数，也叫路径长度h_t(x)，在隔离森林中的平均路径长度为：

$ h(x) = \frac{1}{T}\sum\limits_{t \in IF} {{h_t}(x)} 。$

(6)

该算法的思想为仅需几个步骤来隔离异常，隔离观察样本x所需的步数受训练样本数n的影响，需采用标准化异常分数$s(x,n)$来说明：

$ s(x,n) = {2^{ - \frac{{h(x)}}{{c(n)}}}} 。$

(7)

c(n)为规范h(x)的标准化因子，是将一个样本与其他n个样本隔离所需的平均步骤数，用作给定n个样本的平均路径长度基准，定义为：

$ c(n) = \left\{ {\begin{array}{*{20}{l}} {2H(n - 1) - 2(n - 1)/n{\text{ }},n > 2}，\\ {1{\text{ }},n = 2}，\\ {0{\text{ }},{\rm{otherwise}}} 。\end{array}} \right. $

(8)

其中，$H(i) = \ln n + \varepsilon $，为调和数，$\varepsilon $为欧拉常数，其近似为0.5772156649。

当$h(x) \to c(n)$时，$s(x,n) \to 0.5$，即测试实例x没有明显异常；当$h(x) \to 0$时，$s(x,n) \to 1$，即测试实例x可视为异常；当$h(x) \to n - 1$时，$s(x,n) \to 0$，即异常分数接近0时，测试实例x很大可能为正常值。

1.3 基于DAE-iForset的异常检测流程

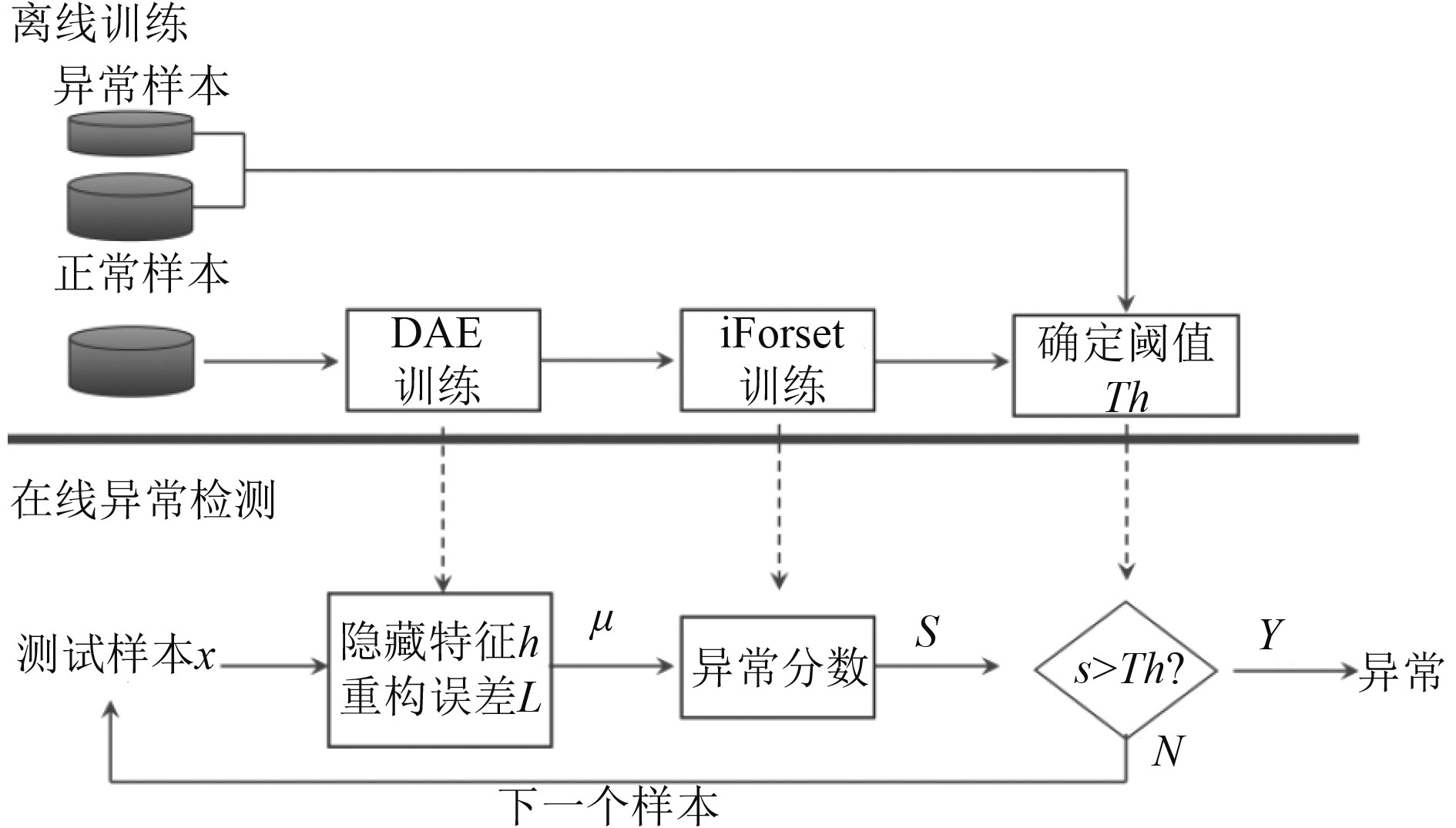
本文提出深度自编码器和隔离森林相结合的DAE-iForset燃气轮机排气温度分布的异常检测算法。DAE-iForset异常检测算法流程如图3所示，该算法有2个独立阶段，即离线训练阶段和在线检测阶段。其详细步骤如下：

1）数据的预处理。首先，将正常数据划分为训练集、验证集和测试集，然后将数据进行均值归一化处理。

2）训练DAE。用训练集${X_{train}}$对训练集进行训练，在训练过程中，通过验证集来调整DAE的超参数。训练好的深度自编码器可将输入样本的关键信息保存在一个低维空间中，包括提取的隐藏特征和导致样本重建错误的特征。其次，DAE可将正常数据的重构误差降至最低，这使得异常数据的重构误差较大，所以DAE更适合于无监督异常检测。

3）训练iForset。通过DAE计算得到每个样本的隐藏特征h和重构误差L，然后将其合并为最终特征$\mu = [h,L]$来训练隔离森林算法，得到正常样本的异常分数，根据异常分数确定阈值。

4）测试和异常检测。将测试实例x输入到DAE模型中计算得到隐藏特征h和重构误差L，合并为最终特征$\mu = [h,L]$，将$\mu $输入至iForset模型，得到异常分数，然后与异常分数阈值Th进行比较，若大于Th则为异常样本，反之则为正常样本。

2 实例验证 2.1 数据描述

本文采用某船用三轴燃气轮机的实际运行数据进行燃气轮机排气温度的异常检测研究。在该燃气轮机的低压涡轮出口处周向均匀布置了16个热电偶温度传感器，用来测量低压涡轮的排气温度。采集的数据包括2630个正常数据和200个异常数据，并将其中70%正常数据作为训练集，15%正常数据作为训练DAE模型的验证集，其余15%正常数据作为测试集，与异常数据合并用来测试所提出算法的性能。其中，本文采集的数据平均排气温度的变化范围为507℃~575℃ 。其中，部分正常数据和某一故障数据的分布如图4所示。

2.2 实验设置与评价指标

使用RTX2060显卡在Pytorch和Sklearn机器学习框架上，进行DAE-iForset模型的搭建。iForset的模型超参数有隔离树数目T=300和子采样规模S=256，这些超参数通过在不同的T∈[100,200,…,500]和S∈[2⁴, 2⁵,…, 2⁹]中，采用网格搜索和交叉验证的方法，根据训练集上的准确率来确定，并将提出的模型与单分类支持向量机(one-class SVM, ocSVM)进行比较。为了确保模型的鲁棒性，在训练集上采用五折交叉验证进行模型的训练与验证。

在异常检测任务中，通常采用混淆矩阵对结果进行分析。混淆矩阵是一种特殊的矩阵，用来呈现监督学习或非监督学习的可视化效果。其每一列代表预测值，每一行代表实际的类别。分类常用的核心指标有准确率、精度、召回率和F₁值，具体如下：

$ {\text{ Accuracy }} = \frac{{TP + TN}}{{TP + FP + TN + FN}} ，$

(9)

$ {\text{Precision }} = \frac{{TP}}{{TP + FP}} ，$

(10)

$ {\text{Recall }} = \frac{{TP}}{{TP + FN}} ，$

(11)

$ F_1 - {\text{score }} = \frac{{2 \times {\text{ Precision }} \times {\text{ Recall }}}}{{{\text{ Precision }} + {\text{ Recall }}}} 。$

(12)

式中：TP为将故障数据正确预测的数量；TN为将正常数据正确预测的数量；FP为将正常数据预测为故障数据的数量；FN为将故障数据预测为正常数据的数目。

另外，受试者工作特性 （Receiver Operating Characteristic，ROC）曲线及相关曲线下面积（Area-Under-Curve，AUC）是二分类任务常用的性能度量，ROC曲线是由真正例率TPR为纵轴，以假正例率FPR为横轴，根据异常分数在不同的阈值下获得的。本文采用以上指标进行比较研究，在排气温度异常检测任务中，正常数据在总测试样本中的比例要多于故障数据，所以需着重关注召回率的指标。

2.3 实验结果对比与分析

通过采用正常数据对DAE模型训练之后，将测试集和故障的排温分布数据输入到DAE中，得到隐藏特征和重构误差。其中，正常数据集和故障数据集的均方根误差如表1所示。可以看出，DAE在故障数据上的均方根误差大于正常数据，因此DAE模型的重构误差可作为用于异常检测的特征。

利用训练好的DAE计算得到训练集的重构误差L和隐藏特征h，合并为最终特征$\mu $用于iForest的训练。通过网格搜索和交叉验证对模型参数及阈值进行优化，选择测试集上准确率最高模型作为最终模型，使用测试集和故障数据对DAE-iForest检测模型评估，得到的混淆矩阵如图5所示。为了验证模型的有效性，将本文方法与ocSVM方法分别在原始数据和DAE提取的特征数据上进行对比，2种方法均采用正常数据的训练集训练，无需标注异常数据，其性能指标如表2所示。根据数据集的异常分数，选择不同阈值，得到多个模型的ROC曲线如图6所示。

燃气轮机排气温度数据为高维时间序列数据，由图4可知，其正常数据存在固有的分布，而非相当均匀分布，这是由于其受装配误差或维修等因素的影响；当发生故障时，某一或几个热电偶测点的温度会发生改变，导致温度分布的改变。在本文研究中，如表2可知，无论是原始传感数据还是DAE提取的最终特征，iForest的评价指标均优于ocSVM，尤其在召回率上更为明显，表明iForest更能在高维的排温分布数据中识别出异常；DAE-iForest和DAE-ocSVM的指标均高于采用原始数据训练的iForest和ocSVM，表明经DAE模型提取的特征用于异常检测，能够大幅提高异常检测算法识别故障的性能。结合图6可知，对于不同的模型，当选择合适的阈值时，DAE-iForest具有最佳的性能，即更高的精度和更低的误报率。

3 结　语

针对故障样本缺失场景下的燃气轮机高温部件异常检测问题，提出了基于深度自编码器和隔离森林的排气温度异常检测算法，以实现对燃气轮机高温部件的健康监测。该方法通过深度自编码器得到原始传感数据的深层特征和重构误差，单分类模型隔离森林用于学习深层特征和重构误差，并在确定异常分数的阈值后进行异常检测。本文所提出方法在异常检测指标评估中，均优于单分类支持向量机和采用原始传感数据训练的隔离森林算法，可实现对燃气轮机高温部件有效和灵敏的状态监测，有助于提高燃气轮机高温部件运行的安全性和可靠性。