异步电机是舰船的主要电力拖动设备,数量庞大,地位重要,但对电机的状态检测一直缺乏有效且可靠的手段,使得维修工作比较盲目。异步电机故障包括轴承故障、定子绕组匝间短路故障、转子故障和气隙偏心等,其中轴承故障占比约40%~60%[1],因此,对电机轴承故障进行诊断尤为重要。
本文基于振动信号分析的轴承故障诊断方法,采用振动加速度峭度系数、振动速度有效值2个时域指标,以及振动加速度共振解调频谱分析,作为轴承外圈故障依据,并以1台Y100L-2型异步电动机,进行不同严重程度的外圈故障,以实验结果验证该方法的有效性。
1 轴承故障机理、对振动的影响及诊断方法 1.1 异步电机轴承机理电机的构成部件中,轴承起到固定、支撑等作用,对电机长期稳定运转起重要作用。异步电机轴承主要结构如图1所示,包括外圈、内圈、滚动体和保持架[2]。轴承外圈与电机壳体紧密配合,内圈随电机转轴同步旋转,在内圈旋转时,保持架能够维持滚动体之间保持距离,避免其相互间发生碰撞,同时防止滚动体因高速旋转而脱出滑轨。在电机运行过程中,轴承需要承受来自轴向和径向的双重压力,长时间运转过程中不可避免的摩擦会产生大量热量,因长期承受高强压力、高温,加之其他可能的外部因素,会导致轴承出现不同种类、不同程度的损伤,常见的故障形式包括表面磨损、裂痕、点蚀、断裂、压痕等。外圈故障和保持架故障是滚动轴承的多发故障。

|
图 1 轴承示意图和结构图 Fig. 1 Structure and illustration of rolling bearing |
异步电机轴承故障的诱因大致可分为内因和外因。内因包括滚动轴承制造材料、制造安装工艺等,即滚动轴承本身所蕴含的部分风险因素;外因包括电机其他部件对轴承施加的外力、润滑不充分以及温度、湿度等环境因素。2种因素均有可能引发轴承故障。
1.2 轴承故障对振动的影响轴承引起的振动可分为确定性振动和随机振动[3],异步电机正常工作时,轴承外圈与电机外壳紧密结合保持固定不动,轴承内圈与电机定子保持同步旋转,此时滚动体由保持架固定在内外圈之间的轨道内转动,此时周期性振动信号较弱而随机性振动信号较强,当轴承表面出现磨损、点蚀等故障时,滚动体每次经过不平整表面时,会因刚性连接引起的碰撞而产生冲击振动,此时随机振动中的周期性成分加强,并且随着故障程度的加剧,冲击振动将越来越强。当故障位置不同时,产生的冲击振动与电机固有振动相互叠加,在振动信号频谱上体现出不同的故障特征频率,同时电机轴承尺寸、电机转速等因素也会影响其特征频率。
轴承不同类型的故障将引起轴承系统不同频率的特征振动,并在振动信号中体现为某些特征频率下的分量。以外圈故障、保持架故障为例,二者对应的特征频率分别为[4]:
| $ f_{\text {ouler }}=\frac{n}{2} f_{{r}}\left(1-\frac{B_{{d}}}{P_{{d}}} \cos \varPhi\right) ,$ | (1) |
| $ f_{\mathrm{cag}}=\frac{1}{2} f_{{r}}\left(1-\frac{B_{{d}}}{P_{{d}}} \cos \varPhi\right) 。$ | (2) |
其中:n为滚动体的数目;fr为转频,即转子转速(以r/min为单位)/60;Bd为滚动体的直径;Pd为滚动轴承的节径;
通过监测振动信号的时域指标以及分析振动信号的频谱来进行轴承故障诊断,是广为采用的方法。
振动加速度信号的峭度系数与振动速度信号的有效值兼具灵敏性(对于故障敏感)、稳定性(对于工况变化鲁棒),因此这2个时域指标广泛应用于轴承故障诊断。
对于离散的轴承振动加速度信号xi,其峭度系数Ku定义为:
| $ {K_{{u}}} = \frac{{N\displaystyle\sum\limits_{i = 1}^N {{{({x_{\text{i}}} - \bar x)}^4}} }}{{\displaystyle\sum\limits_{i = 1}^N {{{({x_{\text{i}}} - \bar x)}^2}} }},\;\;\bar x = \frac{1}{N}\sum\limits_{i = 1}^N {{x_{\text{i}}}}。$ |
式中:N为离散序列xi的长度;
对于正常轴承,其振动加速度信号服从正态分布,此时的Ku≈3。在工程实际中,一般将Ku=4作为轴承故障的诊断阈值。
对于离散的轴承振动速度信号vi,其有效值V为:
| $ V = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{v_{{i}}}^2} }。$ |
表1为ISO根据振动速度信号有效值所制订,用于小型电机(<15 kW)的评定标准(ISO 2372标准)。
|
|
表 1 小型电机的评定标准 Tab.1 Evaluation criteria for smallmachines |
时域参数监测简单、有效,但仅能诊断轴承整体故障与否,无法进一步诊断轴承故障类型。为此,需进行振动加速度频谱分析,通过考察其包含的特征频率分量而诊断轴承故障类型。
轴承故障特征信号一般是低于1 kHz的低频振动信号,而在工程实际中存在大量机械松动、装配不当等原因造成的。同样是低频的结构性振动信号,因而将严重污染轴承故障特征信号。
可见,振动加速度峭度系数、振动速度有效值监测,以及振动加速度共振解调频谱分析,是具有代表性的基于振动信号分析轴承故障诊断方法。本文将以某型舰船装备的Y100L-2为例,以实验方式验证其对轴承外圈故障诊断的有效性。
2 实验设备与方法 2.1 实验设备主要实验设备包括电机、控制箱(控制电机启停)、测功机和电阻箱(作为电机的可调负载)、以及振动及电流信号采集装置。其中,电机型号分别Y100L-2,表2为额定值与配套的轴承型号,表3为轴承的结构参数。
|
|
表 2 实验电机的额定值与轴承型号 Tab.2 Rated values and bearing typeoftested motors |
|
|
表 3 轴承的结构参数 Tab.3 Structural parameters of tested bearings |
振动传感器为Lance LC0104T压电加速度传感器,在实验中安装于轴承座正下方以测取垂直方向的振动加速度信号,其主要技术指标如表4所示。
|
|
表 4 压电式振动加速度传感器的技术参数 Tab.4 Specifications of used piezoelectric accelerometer |
为进行轴承外圈故障诊断测试,使用线切割机在外圈加工出不同宽度的凹槽以模拟外圈故障。如图2所示,2只故障轴承的外圈上分别有1 mm宽、3 mm宽的凹槽(深度均为1.5 mm),其故障程度分别代表为“轻度”、“重度”。

|
图 2 外圈故障轴承(6206) Fig. 2 Faulty bearingswith outer race defects(6206) |
分别针对轴承正常、外圈故障进行实验,并将电机的负载状况近似设定为满载、半载、空载,对振动加速度瞬时信号进行采样、分析,并进行轴承故障诊断。
3 实验结果图3为Y100L-2型电机在近似满载,轴承(6206型)正常、外圈轻度故障、外圈重度故障3种情况下振动加速度信号的瞬时波形,图4为对应的共振解调频谱。此时,转速约为2 909.4 r/min,转频约为48.49 Hz,根据式(1)可计算出振动特征频率为fouter≈173.02 Hz。表5为该实验对应的振动加速度峭度系数、振动速度有效值、振动特征分量的频率fouter及幅值。
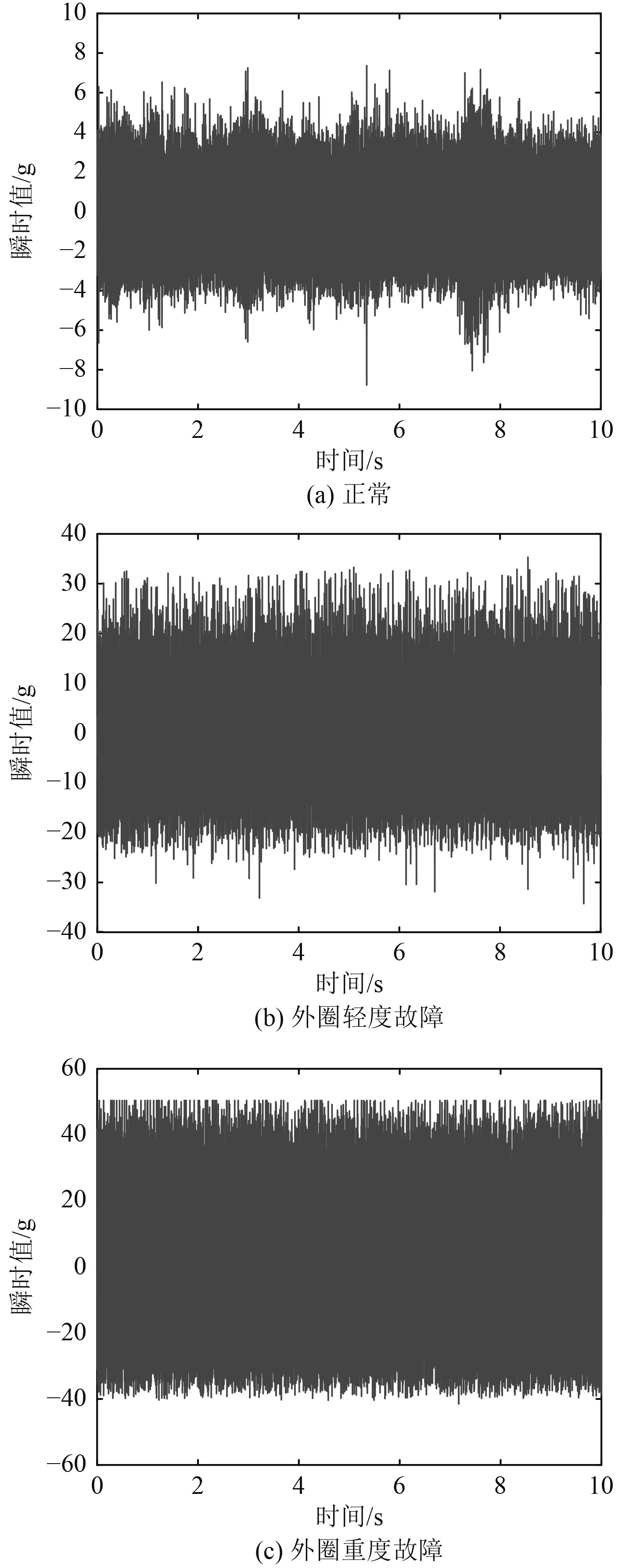
|
图 3 Y100L-2型电机满载时振动加速度的瞬时波形 Fig. 3 Waveformsof vibration acceleration signal of Y100L-2 motor with full load |
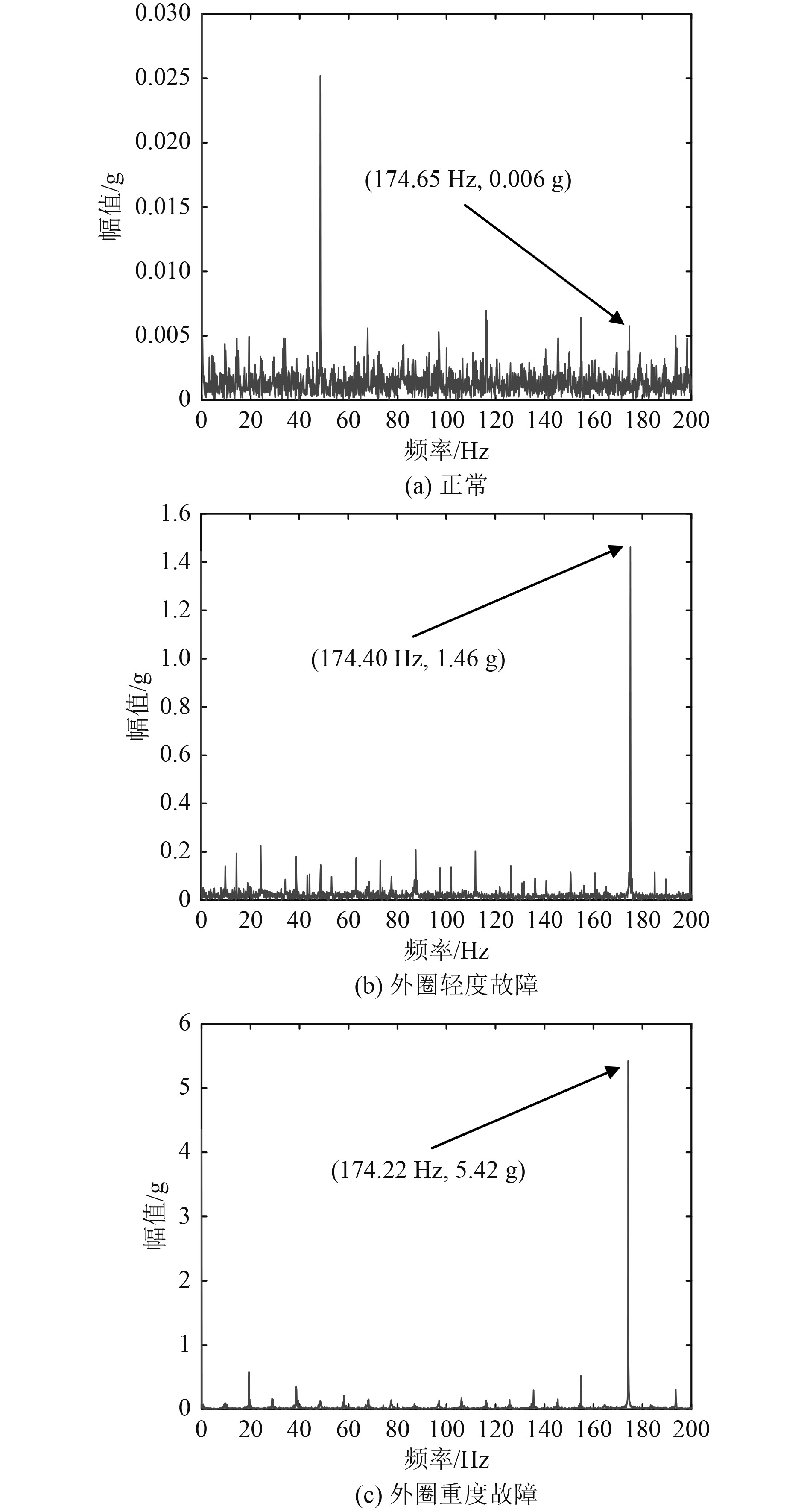
|
图 4 Y100L-2型电机满载时振动加速度的共振解调频谱 Fig. 4 Resonant demodulated spectra of vibration acceleration signal of Y100L-2 motor with full load |
|
|
表 5 Y100L-2型电机满载时轴承外圈故障的诊断结果 Tab.5 Bearing outer race defect diagnosis results of Y100L-2 motor with full load |
另外,针对近似半载、空载状态,进行类似实验。近似半载状态下,转速约为2 951.4 r/min,转频约为49.19 Hz,振动特征频率为fouter≈175.49 Hz。空载状态下,转速约为2 982.0 r/min,转频约为49.70 Hz,振动特征频率为fouter≈177.32 Hz。表6和表7分别为对应的振动加速度峭度系数、振动速度有效值、振动特征分量的频率fouter及幅值。
|
|
表 6 Y100L-2型电机半载时轴承外圈故障的诊断结果 Tab.6 Bearing outer race defect diagnosis results of Y100L-2 motor with half load |
|
|
表 7 Y100L-2型电机空载时轴承外圈故障的诊断结果 Tab.7 Bearing outer race defect diagnosis results of Y100L-2 motor with no load |
根据Y100L-2型电机的实验结果,由图4可知,对应于外圈正常、轻度故障、重度故障3种状态,振动加速度的时域振幅呈显著递增趋势。同时,由图4可知,对应于外圈正常、轻度故障、重度故障3种状态,振动加速度的外圈故障特征分量的频域幅值呈显著递增趋势,具体参数见表5~表7。这就表明,基于振动信号分析的轴承故障诊断方法是有效的。
另外,表5~表7的振动加速度峭度系数、振动速度有效值,对应于外圈正常、轻度故障、重度故障3种状态,均呈现出显著递增趋势,并且具体数值与ISO 2372关于轴承状态“可”、“不可”的评定标准相吻合。
振动加速度峭度系数、振动速度有效值以及振动加速度共振解调频谱分析,是工程实际中广泛应用的电机轴承故障诊断方法。本文针对一台Y100L-2型异步电动机,进行了不同程度的外圈故障,并以实验数据分析上述电机轴承故障诊断方法的性能。实验结果证明,该方法可提高电机轴承故障诊断的性能。
| [1] |
OLAV VAAG T, MAGNUS D. A survey of faults on induction motors in offshore oil industry, petrochemical industry, gas terminals, and oil refineries[J]. IEEE Transactions on Industry Applications, 1995, 31(5): 1186-1196. DOI:10.1109/28.464536 |
| [2] |
CERRADA M, SÁNCHEZ R V, LI C, et al. A review on data-driven fault severity assessment in rolling bearings[J]. Mechanical Systems and Signal Processing, 2018, 99: 169-196. DOI:10.1016/j.ymssp.2017.06.012 |
| [3] |
韩睿. 基于振动信号的电机轴承故障诊断方法研究[D]. 合肥: 合肥工业大学, 2020.
|
| [4] |
梅宏斌. 滚动轴承振动监测与诊断——理论·方法·系统[M]. 北京: 机械工业出版社, 1996.
|
 2023, Vol. 45
2023, Vol. 45
