2. 国家能源深水油气工程技术研发中心, 北京 100028;
3. 中国海洋大学 工程学院 山东 青岛 266100
2. National Energy Deepwater Oil and Gas, Beijing 100028, China;
3. College of Engineering, Ocean University of China, Qingdao 266100, China
随着我国油气开发逐渐由浅海走向深水海域,浮式生产储卸油船(FPSO)已经成为南海油气资源开发的重要海洋工程装备[1],极端波浪条件下FPSO作业时可能面临甲板上浪的风险,虽然事件发生的概率较低,但是一旦发生将会对设备造成严重的破坏,因此甲板上浪是FPSO设计时面临的一个重要问题。
甲板上浪高度是FPSO总体设计时重点关注的问题之一,不同海域海洋环境差异较大,对于规则波作用下的甲板上浪问题已经被众多学者所关注[2−3],韩国、美国、挪威等国家也都依据本国海洋环境特征对船体上浪开展了研究[4],并且多以规则波研究为主,畸形波由于波陡较大,携带的能量较高,对海洋工程结构带来的损害更大[5]。中国南海海域水深面宽,海浪波陡高,畸形波频发,FPSO面临的上浪风险更大[6−7],因此需要根据中国南海实测海洋环境数据,对畸形波作用下FPSO甲板上浪问题开展研究。
在以往的波浪-浮体水动力响应分析中,多采用简化计算过程的势流理论[8]。随着FPSO建造体积越来越大,波浪经过大型浮式结构时的绕射和辐射效应越来越明显,基于无旋假设的势流理论在计算波浪荷载作用下大型浮式结构的运动响应时结果失真严重[9],同时在波浪荷载计算过程中缺少考虑波浪动能。极端波浪荷载条件下,波浪与结构之间具有相对较高速度的运动,与船体作用区域发生变形及爬升破碎等强非线性现象,随着计算机性能的高速发展,CFD在波浪结构非线性相互作用模拟中得到快速应用,很多学者基于网格法对船体的甲板上浪进行研究[10],但网格法在模拟波浪破碎时会出现网格畸变及流体质量不守恒的问题。由于光滑粒子法将计算域离散为带有物理属性的粒子,在模拟计算中不依赖网格,能够更为准确地处理流固耦合问题[11]。
本文基于粘性流理论,充分考虑波浪结构相互作用过程中的波浪能耗散,探究中国南海环境条件下极端波浪对船体的砰击及运动响应。基于光滑粒子法建立非线性波浪-结构全耦合数值模型,通过推板造波法模拟畸形波及规则波的生成过程,分析不同波浪条件下船体的上浪、运动响应及砰击荷载分布,研究结果为船体的总体设计提供参考。
1 数值方程 1.1 光滑粒子法基本方程为了解决流固耦合界面容易发生网格畸变的问题,采用光滑粒子法将整个计算域离散为带有物理属性的粒子,通过对计算域中任意点x处进行积分,得到积分表达式:
| $ F(r)=\int F(r')w(r-r',h) {\rm{d}}r' 。$ | (1) |
对于计算域内任意粒子i及其邻近粒子j,利用核函数替换狄拉克函数,通过对核函数影响域内的点求和得到连续逼近表达式:
| $ F(r_i)\approx\sum_j F(r_j)\cdot \omega\left(r_i-r_j,h\right)\frac{m_j}{\rho_j}。$ | (2) |
式中:
| $ \omega \left( {{r_i} - {r_j},h} \right) = {\alpha _D}{\left( {1 - \frac{q}{2}} \right)^4}\left( {{2}q + {1}} \right) 。$ | (3) |
其中,三维模型中
| $ \frac{{{\rm{d}}\nu }}{{{\rm{d}}t}}{\text{ = }} - \frac{1}{\rho }\nabla P + g + \varGamma ,$ | (4) |
| $ \frac{{{\rm{d}}{\rho _i}}}{{{\rm{d}}t}}{\text{ = }}\sum\limits_j {{m_i}} {\nu _{ij}} \cdot \nabla {W_{ij}} 。$ | (5) |
利用水体密度表达流体压力的状态方程表达式为:
| $ P{\text{ = }}\frac{{{c_0}^2{\rho _0}}}{\gamma }\left[ {{{\left( {\frac{\rho }{{{\rho _0}}}} \right)}^\gamma } - 1} \right] 。$ | (6) |
通过将多个具有不同振幅、波数和初始相位的余弦波进行叠加构成随机波,波面方程可以表示为:
| $ \eta {\text{ = }}\left( {x,t} \right) = \sum\limits_{i = 1}^N {{\alpha _i}\cos \left( {{k_i}x - {\omega _i}t + {\varepsilon _i}} \right)} 。$ | (7) |
式中:N为叠加波的数量,
| $ \begin{array}{l}\eta \text=\left(x,t\right)={\displaystyle \sum _{i=1}^{N}\sqrt{2PS\left({\omega }_{i}\right)\Delta \omega }\mathrm{cos}\left({k}_{i}\left(x-{x}_{f}\right)-{\omega }_{i}\left(t-{t}_{f}\right)\right)}+\\ {\displaystyle \sum _{i=1}^{M}\sqrt{2(1-P)S\left({\omega }_{i}\right)\Delta \omega }\mathrm{cos}\left({k}_{i}x-{\omega }_{i}t+{\epsilon }_{i}\right)}。\\[-20pt]\end{array} $ | (8) |
式中:P为聚焦波的能量比,一般取值P=0.8[12]时得到的畸形波较为理想,当P=0时,波型为随机波,当P=1时,波型为聚焦波,由于JONSWAP与实际测量结果具有良好的一致性,在海洋工程波浪模拟中得到广泛应用,波浪的频谱密度S(f)的表达式为:
| $ S\left( f \right) = {\beta _J}H_{_{1/3}}^2T_p^{ - 4}{f^{ - 5}}\exp \left[ { - 1.25{{\left( {{T_p}f} \right)}^{ - 4}}} \right]{r^{\exp \left[ {{{\left( {{T_p}f - 1} \right)}^2}/2{\sigma ^2}} \right]}}。$ | (9) |
其中:
| $ \;{\beta _J}{\text{ = }}\frac{{0.0624}}{{0.23 + 0.0336\gamma - 0.185{{\left( {1.9 + \gamma } \right)}^{ - 1}}}}\left[ {1.09 - 0.01915\ln \gamma } \right] ,$ | (10) |
| $ {T_p} \approx \bar T/\left[ {1 - 0.532\left( {\gamma + 2.5} \right) - 0.569} \right] ,$ | (11) |
| $ \sigma = \left\{ \begin{gathered} {\sigma _{\text{a}}} = 0.07,f < {f_p} ,\\ {\sigma _b} = 0.09,f \geqslant {f_p} 。\\ \end{gathered} \right. $ | (12) |
利用水力传递函数构建波面方程与推板板之间的关系,推板运动速度
| $ U\left( t \right){\text{ = }}\sum\limits_{i = 1}^M {\frac{{{\omega _i}{\eta _i}\left( {0,t} \right)}}{{T{r_i}}}} = \sum\limits_{i = 1}^M {\frac{{{\omega _i}{\alpha _i}}}{{T{r_i}}}\cos \left( {{k_i}\left( {0 - {x_f}} \right) - {\omega _i}\left( {t - {t_f}} \right)} \right)}。$ | (13) |
式中,Tr为水力传递函数[13],一个时间步长内推板的水平位移
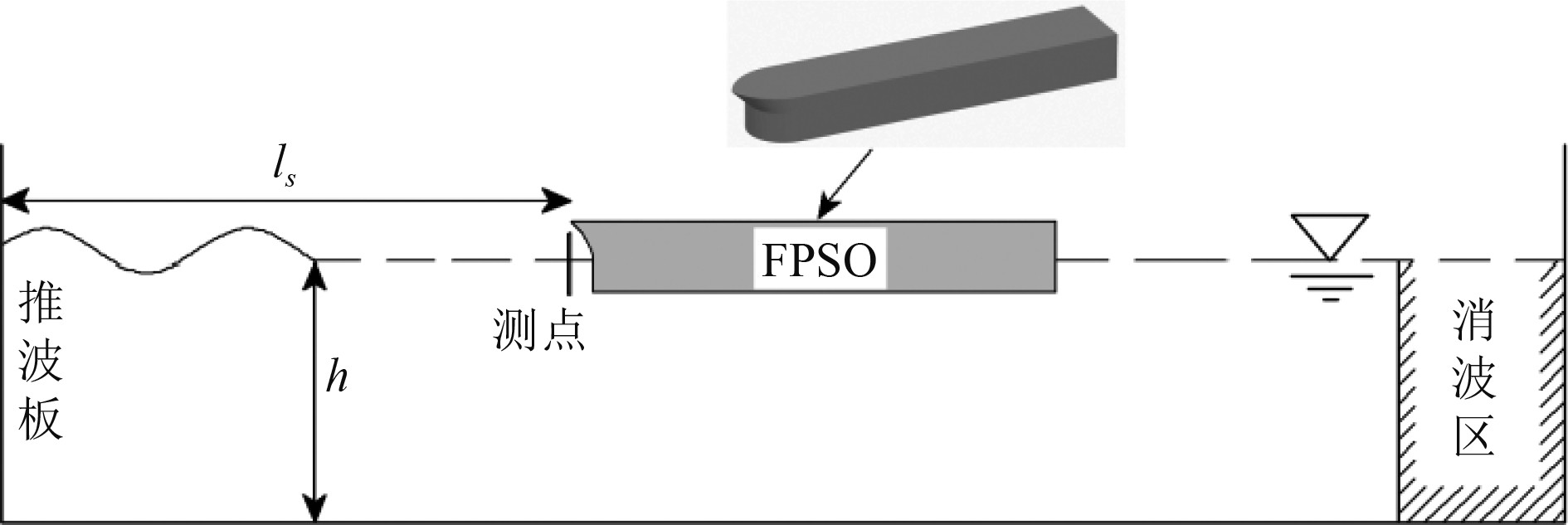
以中国南海某FPSO为研究对象,建立如图1所示的数值分析模型。在水槽左侧设立推波板,推波板在水平方向的运动轨迹根据式(13)计算得到,采用光滑粒子动力学方法开展甲板上浪过程的数值分析研究,分析极端波浪对甲板上浪及运动响应的影响,船体的主尺度如表1所示,在船首设置波高测点记录甲板上浪高度。
|
图 1 波浪荷载作用下FPSO数值模型示意图 Fig. 1 Schematic diagram of numerical model of FPSO under wave loads |
|
|
表 1 船体主要物理参数 Tab.1 Main physical parameters of the FPSO |
环境条件选取中国南海百年一遇的海洋环境数据,由于波浪砰击荷载主要与波高有关,为了提高计算效率,设定模型水深h=70 m,有效波高Hs=13.3 m,最大波高Hp=22.3 m,谱峰频率fp=0.06,fmin=0.053,fmax=0.34,谱峰因子γ=2.4,船首距离造波入口ls=150 m,畸形波的波峰聚焦位置位于船首处。利用式(8)中的双波列叠加模型,生成满足畸形波定义的的波浪序列,单独波浪作用下测点位置的波高时程曲线如图2所示。

|
图 2 数值模型测点位置的波高时程曲线 Fig. 2 Wave elevations of the numerical model at wave gauges |
可知,目标测点位置的畸形波最大波高22.5 m,峰值谱周期16.3 s,畸形波的波高大于有义波高的2倍,为规则波最大波高的1.73倍,与南海实测波浪参数基本一致。
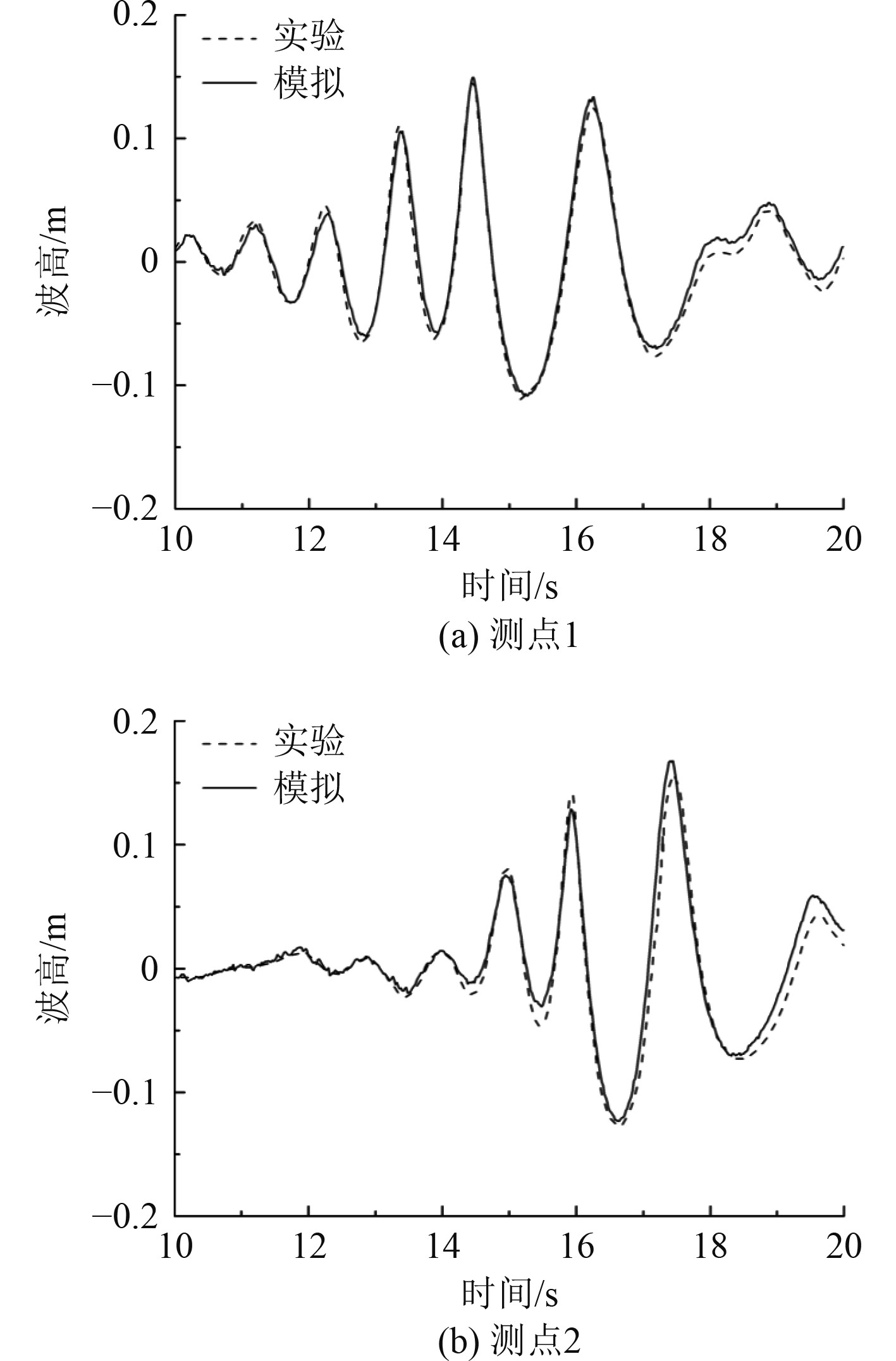
2.2 畸形波模型验证根据JONSWAP波谱生成满足畸形波定义的波高时间序列,并依据转换方程得到推板运动特征,为了验证造波方法的正确性,将数值模拟结果与实验结果[14]进行对比,实验水深0.65 m,采用推板式造波,第1个波高测点距离造波入口6.9 m,第2个测点距离造波入口9.6 m,畸形波的数值模拟结果与实验结果对比如图3所示。
|
图 3 实验结果和数值结果在测点位置的波高时间序列 Fig. 3 Wave elevations of experimental and numerical results at two wave gauges |
可以看出,数值造波结果与实验结果吻合较好,部分位置出现轻微偏差,这是由于畸形波为多波叠加,波浪与波浪之间的强非线性耦合作用导致模拟结果与实验结果出现偏差,总体来说推板式造波法能够较为准确的模拟畸形波的生成。
3 结果分析 3.1 FPSO甲板上浪及运动响应波浪与船体相互作用时会对船体产生砰击作用,当波面高程大于船首高程时形成甲板上浪,造成甲板上部设备损坏,百年一遇海况下,畸形波和规则波与FPSO相互作用的数值模拟结果如图4所示。

|
图 4 波浪作用下FPSO运动特征 Fig. 4 Motion characteristics of the FPSO under wave loads |
可知,畸形波作用下,当波谷到达船首时船体首倾,船首吃水大于船尾吃水(见图4(a)),船体发生逆时针倾斜,随后畸形波的波峰靠近船首,形成高速流动的水舌,船首前方水位抬升,对船首产生砰击作用,此时波浪产生的砰击荷载最大(见图4(b)))。规则波作用下船体的运动特征与畸形波作用下的结果类似,通过对2种波浪作用下的模拟结果对比可知,畸形波砰击时的水质点最大速度比规则波砰击时的速度大50%。
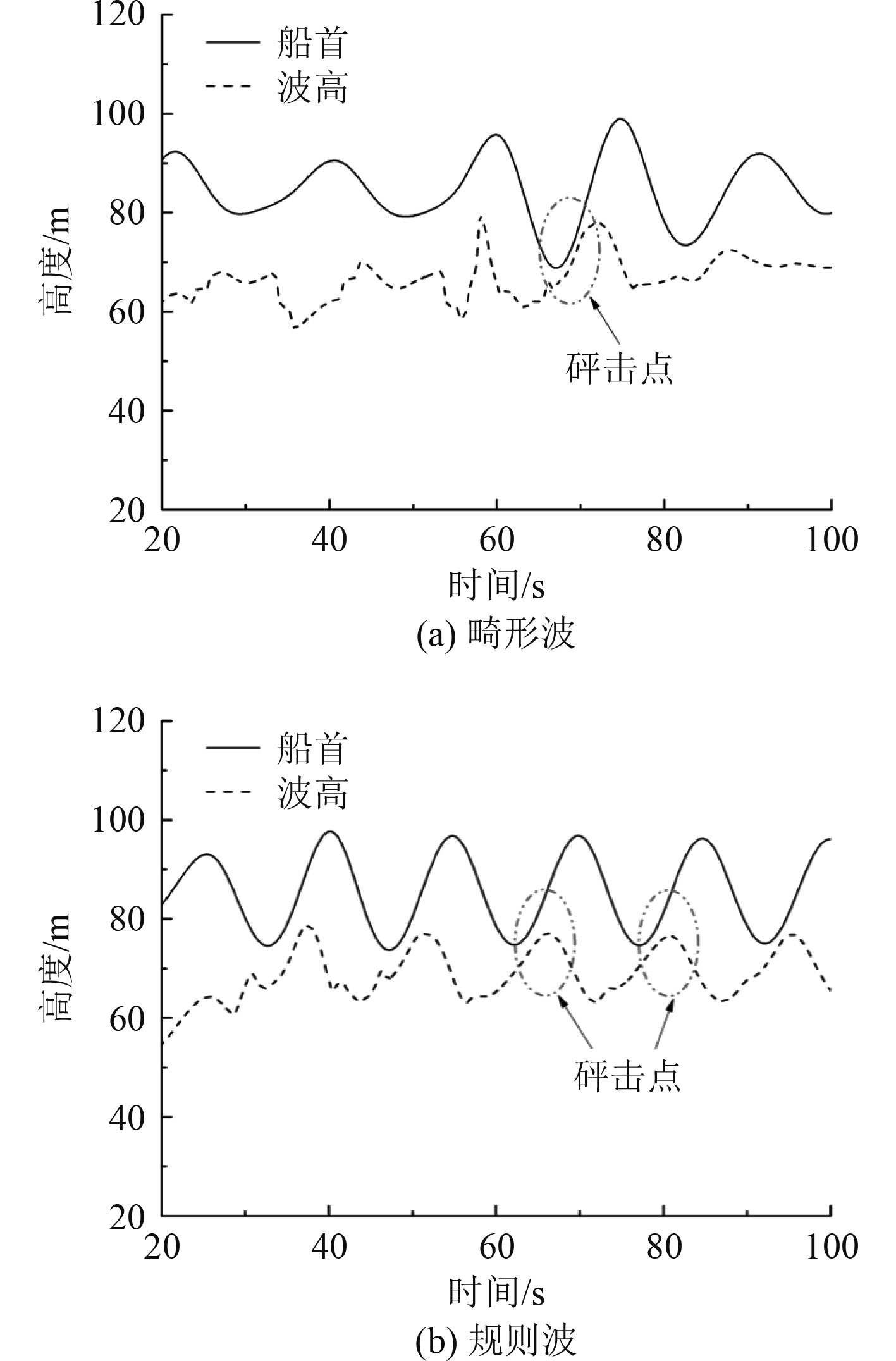
提取船首和测点位置的高度变化曲线,分析波面与甲板的相对高度变化。由图5可知,当船体的纵倾角度最大时,船首位于最低点,此时畸形波波峰与船体相互作用,形成砰击荷载,船体开始顺时针偏转,最有可能发生甲板上浪,本文选定百年一遇极端工况下波面与船首的高度差为2.7 m,未发生甲板上浪,满足船体设计要求。规则波作用下波面与船首的高度差为2.8 m,与畸形波作用下的结果相差较小,这是由于畸形波波峰的波陡较高,与楔形船首相互作用时发生波浪破碎,影响了上浪高度。纵摇对船舶造成多方面的不利影响,是甲板上浪的主要因素之一,2种波浪荷载作用下船体的纵摇变化如图6所示。
|
图 5 波浪作用下船首上浪高度 Fig. 5 The wave elevation and bow height under wave loads |
|
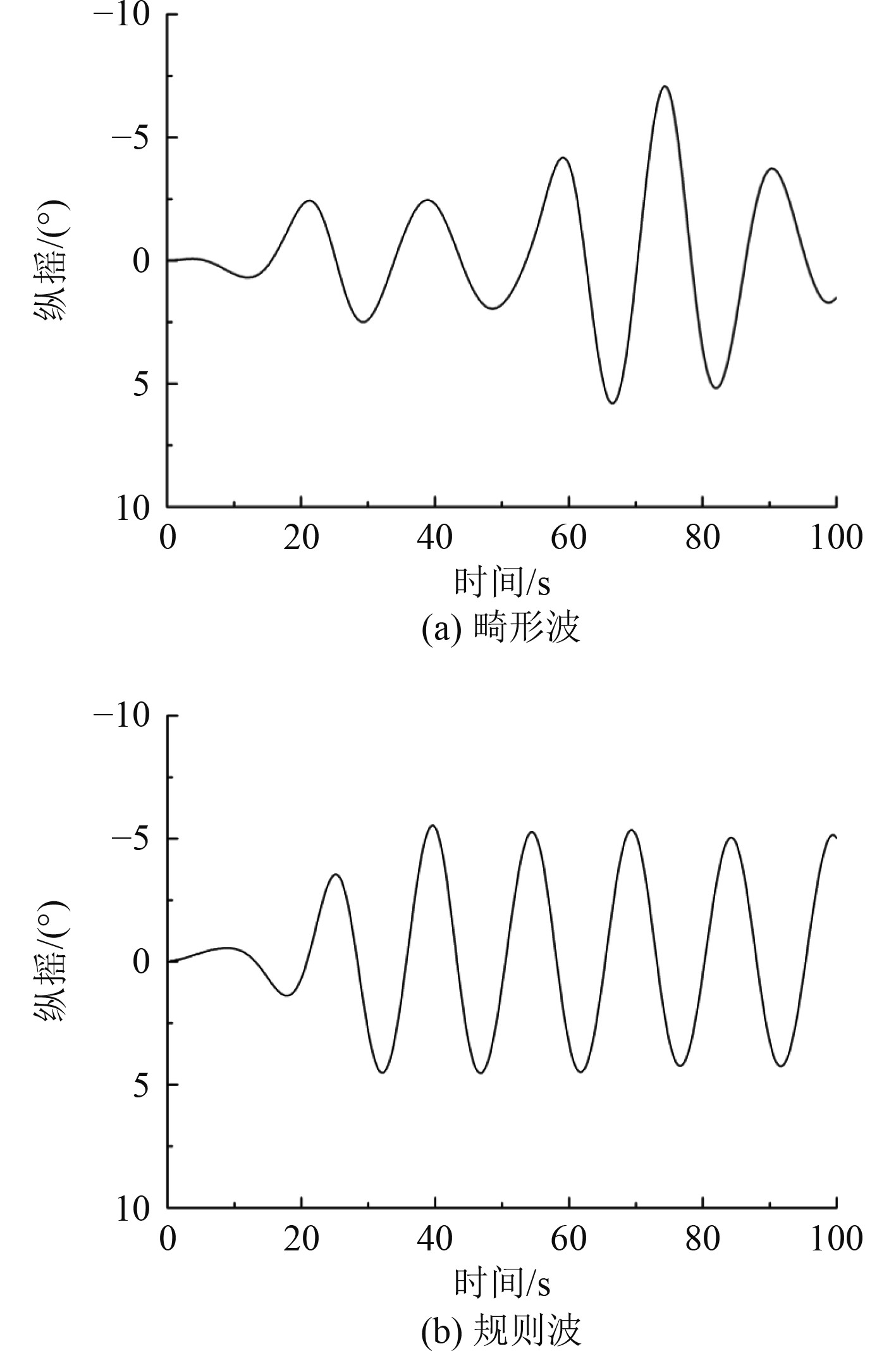
图 6 波浪荷载作用下船体纵摇变化 Fig. 6 The pitch of the ship under wave loads |
可知,畸形波作用下船体的纵摇最大值出现在波峰作用于船首时(见图6(a)),纵摇最大值出现的时间晚于波峰出现的时间,这是由于船体惯性导致纵摇最大值的出现具有一定的滞后性。规则波作用下船体的纵摇呈现周期性变化(见图6(b)),第一个波峰作用于船首时由于船体惯性纵摇周期偏小,畸形波作用下船体的纵摇幅值比规则波作用下船体纵摇幅值大30%,因此基于规则波计算船体运动的结果偏于危险。
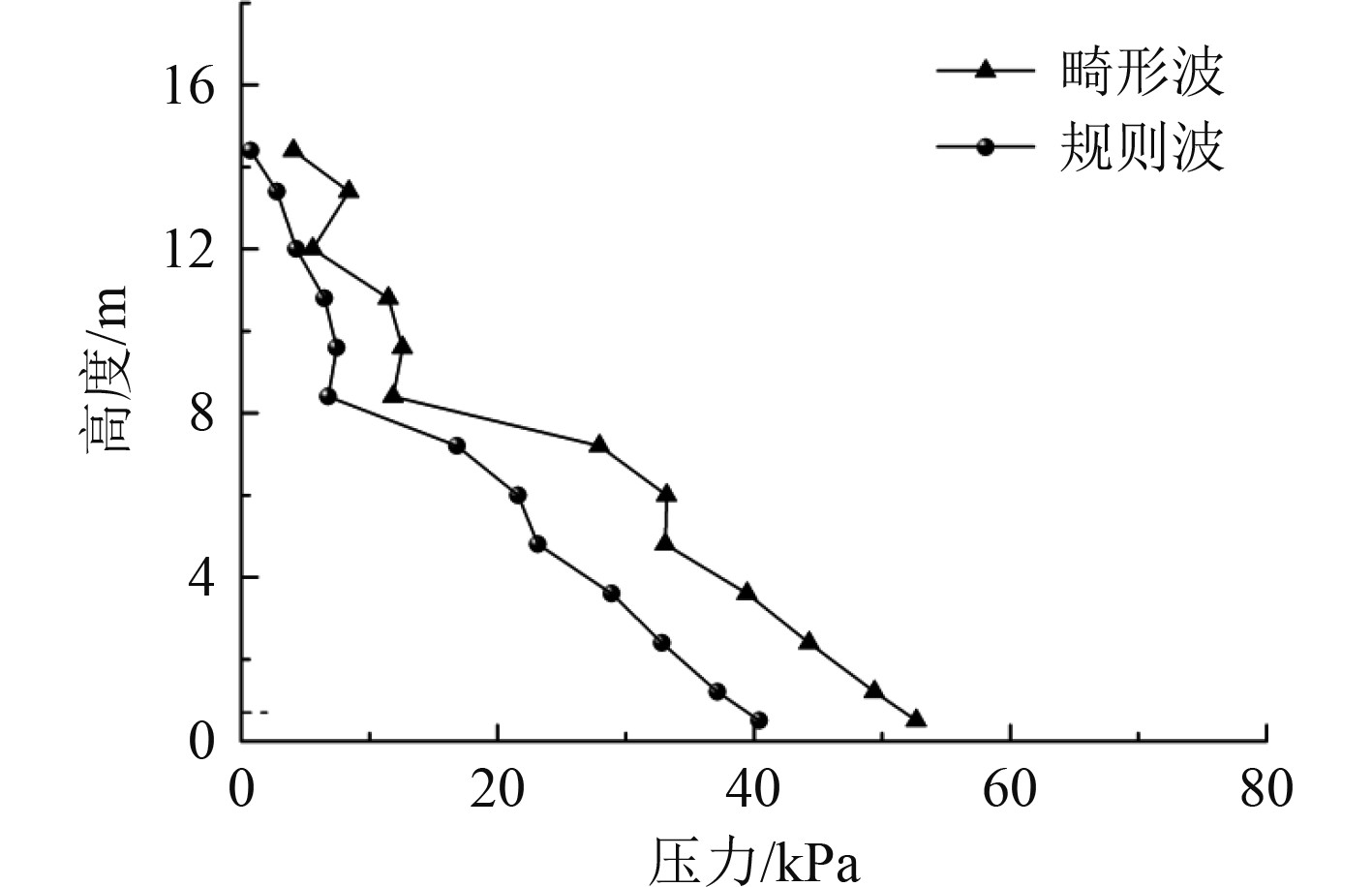
3.2 船首波浪冲击船首除了承受静水压力之外还会承受波浪冲击,因此研究船首的局部受力情况十分有必要。2种波浪荷载作用下波浪砰击的竖向荷载如图7所示。
|
图 7 不同波浪荷载作用下砰击压力竖向分布 Fig. 7 Vertical distribution of slamming loads with different wave loads |
可知,2种波浪荷载作用下砰击荷载随着距离静水面高度的增大而减小,在靠近水面区域(0~6 m),随着高度的增加,砰击荷载呈线性减小,在中间区域(6~8 m),荷载降低速率显著增大,上部区域(8~14 m)砰击荷载变化不大,这是由于上部区域砰击荷载主要是由波峰携带的动能产生,荷载值主要与水质点的流速有关,而在靠近水面区域,砰击荷载由波浪产生的动能和水压力产生的势能构成,因此距离静水面越近,砰击荷载越大。畸形波砰击荷载峰值是规则波作用下的1.25倍,这是由于畸形波波峰较大,携带的能量较高,产生的砰击荷载更大。
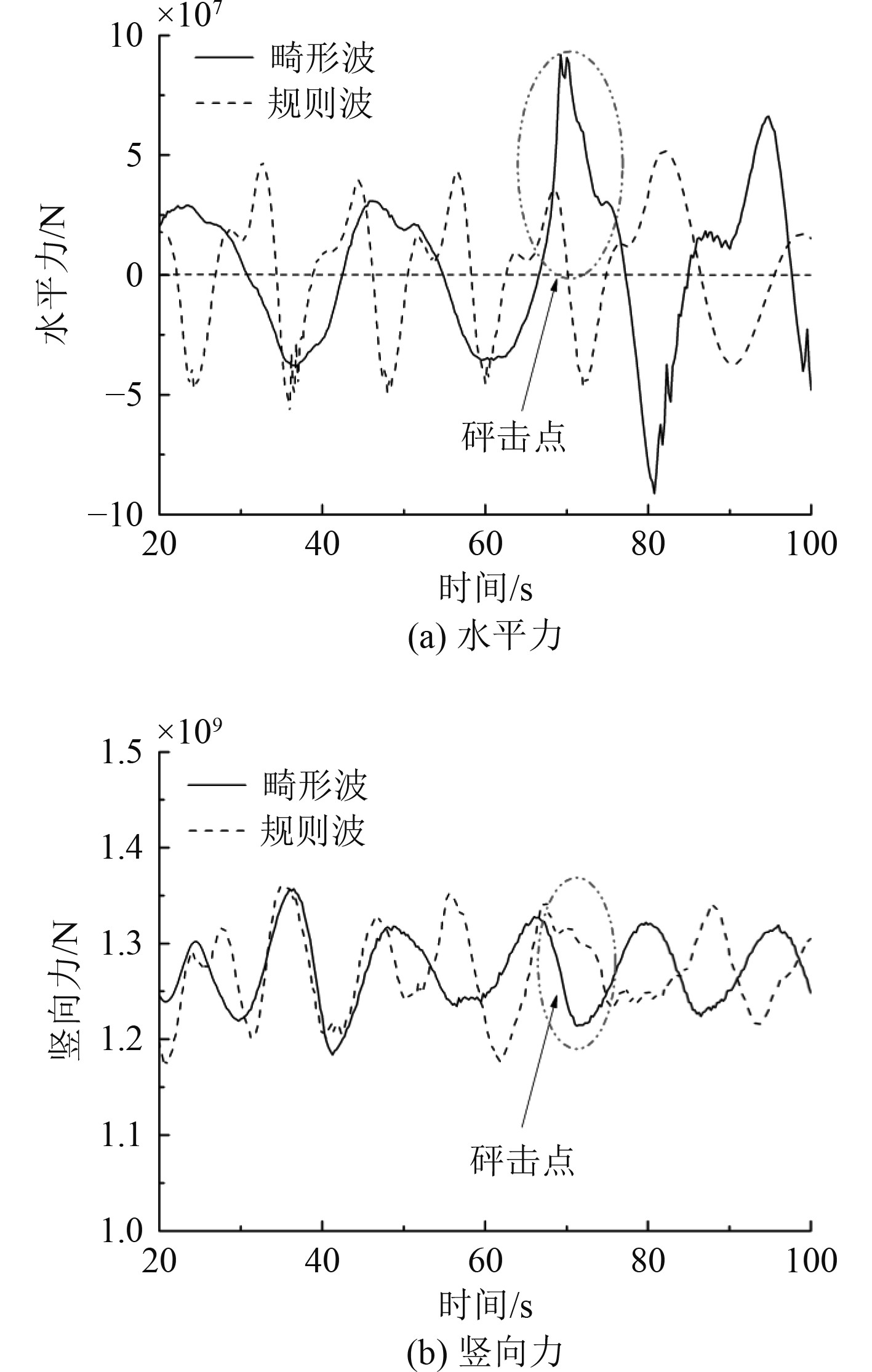
波浪作用于船体时的水动力造成船体摇荡运动,同时会将荷载传递给潜在的系泊系统,2种不同波浪荷载作用下船体受力如图8所示。可知,畸形波作用下船体受到的水平力最大值是规则波作用下的2.2倍,而竖向力与规则波作用下的结果基本相同,这是由于携带较高能量的畸形波波峰直接作用于船体正面,造成船体受到的水平力较大;船体受到的竖向力来源于船底,畸形波对较大船体底部的影响区域较小,导致2种波浪荷载作用下船体受到的竖向力基本相同。
|
图 8 不同波浪荷载作用下船体受到的波浪力 Fig. 8 Wave forces on the hull with different wave loads |
本文基于光滑粒子动力学方法建立了波浪-浮体全耦合数值模型,对中国南海环境条件下的FPSO的甲板上浪及波浪砰击荷载进行研究,并对比分析了畸形波与规则波作用下船体的运动特性及砰击荷载的分布特征。
1)基于光滑粒子法建立的数值水槽实现了对畸形波和规则波的模拟,通过与实验结果进行对比,验证了数值模型的可靠性。
2)畸形波作用下船体的纵摇幅值显著大于规则波作用下的纵摇幅值,畸形波造成的纵摇幅值比规则波大30%,本文选定工况下船体设计满足南海百年一遇条件下船体的甲板上浪要求。
3)畸形波产生的砰击荷载大于规则波产生的砰击荷载,本文选定工况下畸形波砰击荷载为规则波砰击荷载的1.25倍,船舶设计时应充分考虑极端波浪对船体砰击的影响。
| [1] |
高巍, 马林静, 董璐, 等. 南海某FPSO STP单点系泊系统的再评估[J]. 船舶工程, 2017, 39(7): 79-83. GAO W, MA L J, DONG L, et al. Re-evaluation of FPSO STP mooring system in south china sea[J]. Ship Engineering, 2017, 39(7): 79-83. |
| [2] |
RUGGERI F, WATAI RA, et al . Fundamental green water study for head, beam and quartering seas for a simplified FPSO geometry using a mixed experimental and numerical approach[J]. Mar Syst Ocean Technol, 2015, 10(2): 71–90.
|
| [3] |
ÖSTMAN A, PAKOZDI C, SILVA DFC. A fully non-linear RANS-VOF numerical wavetank applied in the analysis of green water on FPSO waves[C]//ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, USA, 2014.
|
| [4] |
WANG D X, DONG S, FANG K Z. Breaking wave impact on perforated caisson breakwaters: A numerical investigation[J]. Ocean Engineering, 2022, 249: 110919. DOI:10.1016/j.oceaneng.2022.110919 |
| [5] |
MA Y, DONG G, PERLIN M, et al. Higher-harmonic focused-wave forces on a vertical cylinder[J]. Ocean Engineering, 2009, 36(8): 595-604. DOI:10.1016/j.oceaneng.2009.02.009 |
| [6] |
付明春. 船桥碰撞下船体结构强度及动力响应分析[J]. 舰船科学技术, 2022, 44(19): 18-21+137. FU M C. Strength and dynamic response analysis of ship structure under bridge collision[J]. Ship Science and Technology, 2022, 44(19): 18-21+137. DOI:10.3404/j.issn.1672-7649.2022.19.004 |
| [7] |
王美玉. 波浪作用下船舶横向振动控制系统[J]. 舰船科学技术, 2022, 44(19): 28-31. WANG M Y. Ship transverse vibration control system under wave action[J]. Ship Science and Technology, 2022, 44(19): 28-31. DOI:10.3404/j.issn.1672-7649.2022.19.006 |
| [8] |
高巍, 石扬, 张继春. Spar基础浮式风机系泊系统全耦合分析[J]. 船舶工程, 2018, 40(1): 106-112. GAO W, SHI Y J, ZHANG J C. Unity coupling analysis of mooring system of spar type offshore floating wind turbine[J]. Ship Engineering, 2018, 40(1): 106-112. DOI:10.13788/j.cnki.cbgc.2018.01.106 |
| [9] |
ROSETTI G F, PINTO M L, DE MELLO P C, et al. CFD and experimental assessment of green water events on an FPSO hull section in beam waves[J]. Marine Structures, 2019, 65(5): 154-180. |
| [10] |
刘殿勇, 李福祯, 曲颖. 畸形波中甲板上浪船舶的运动与砰击响应研究[J]. 中国造船, 2022, 63(4): 115-123. LIU D Y, LI F ZH, QU Y. Motion and slamming response of hull to green water in freaking waves[J]. Shipbuilding of China, 2022, 63(4): 115-123. DOI:10.3969/j.issn.1000-4882.2022.04.011 |
| [11] |
林鹏智, 刘鑫. 光滑粒子水动力学在水利与海洋工程中的应用研究进展[J]. 水利水电科技进展, 2015, 35(5): 36-46. LIN P ZH, LIU X. Recent advances of application of smoothed particle hydrodynamics in hydraulic and ocean engineering[J]. Advances in Science and Technology of Water Resources, 2015, 35(5): 36-46. |
| [12] |
倪兴也, 冯卫兵, 杨斌. 基于DualSPHysics的数值波浪水槽研究[J]. 水道港口, 2014, 35(2): 7-111. NI X Y, FENG W B, YANG B. Numerical wave tank based on DualSPHysics[J]. Journal of Waterway and Harbor, 2014, 35(2): 7-111. DOI:10.3969/j.issn.1005-8443.2014.02.003 |
| [13] |
常爽, 黄维平, 魏东泽, 等. 二阶波浪力和聚焦位置对畸形波作用下张力腿平台动力响应的影响研究[J]. 振动与冲击, 2020, 39(17): 254-260. CHANG S, HUANG W P, WEI D Z et al. Effects of second-order wave force and focusing location on dynamic response of a tension leg platform under freak wave[J]. Journal of Vibration and Shock, 2020, 39(17): 254-260. DOI:10.13465/j.cnki.jvs.2020.17.033 |
| [14] |
SUN P N, LUO M, DAVID LE Touzé, et al. The suction effect during freak wave slamming on a fixed platform deck: Smoothed particle hydrodynamics simulation and experimental study[J]. Physics of Fluids, 2019, 31: 117108. DOI:10.1063/1.5124613 |
 2023, Vol. 45
2023, Vol. 45
