0 引　言

多AUV系统由于具有分布、冗余的特点，在效率、经济、可扩展等方面相较单AUV系统具有很大优势，成为了近十余年来AUV装备的研究热点之一。多种AUV系统编队控制方法被提出并得到实际应用，如基于领航者-跟随者的编队控制^[1-3]、基于虚拟结构的编队控制^[4]、基于势函数的编队控制^[5]、基于一致性的编队控制^[4,6]、基于行为的编队控制^[7]、基于路径跟随的编队控制^[7-9]等。其中，基于领航者-跟随者和基于路径跟随等2种编队控制方法由于自身优点，得到了更广泛的工程应用。

基于领航者-跟随者的编队控制方法控制结构简单、容易实现，只需设定领航者的期望路径，然后跟随者以预定的位置偏移跟随领航者即可实现编队控制。基于路径跟随的编队控制方法将编队控制任务进行时空分解，得到空间上的路径跟随任务和时间上的协调同步任务，进而实现协调编队控制。协调同步任务进行多AUV间的路径同步信息交换。该方法具有交换数据量很小，且短时通信链路故障下AUV 仍可沿预设路径航行的特点，也成为近年比较热门的AUV编队控制研究方法。

基于领航者-跟随者的编队控制方法需要解决的关键问题是如何获得领航者的位置信息、航向信息。同时，该方法十分依赖领航者AUV的性能。在领航者AUV切换航向时，跟随者AUV跟踪的目标位置迅速变化，造成跟随者跟随速度抖动。而基于路径跟随的编队控制方法需要解决的关键问题是多AUV间路径同步信息定义并据同步信息完成各AUV间的速度协调。一般情况下，可以航行距离的百分比作为同步信息，但在路径拐点为保持较好的队形各AUV所需航行路径长度不一。同时，AUV欠驱动、回转半径限制、路径点切换距离设计、路径偏差距离客观存在等因素，在航行路径为不规则的曲线，较难定义合适的同步信息以实现编队的协调同步。

针对上述2种方法在路径切换点附近的共性问题，本文采用B样条曲线对规划航路做在线的局部B样条拟合优化，对路径切换点处领航AUV的控制航向角作适度平滑处理，改善路径切换时，基于领航者-跟随者的编队控制中跟随AUV的目标跟踪位置变化速度和曲率，削弱了跟随AUV的点跟随难度。对于基于路径跟随的编队控制采用B样条基函数自变量t作为路径拐点附近协调同步参数的一部分，增加局部路径在路径同步调整的权重。最后，通过典型AUV平台水动力模型，采用2种AUV编队控制算法进行编队航行数值仿真，并对比分析2种方法的异同点及局部优化改进的效果。

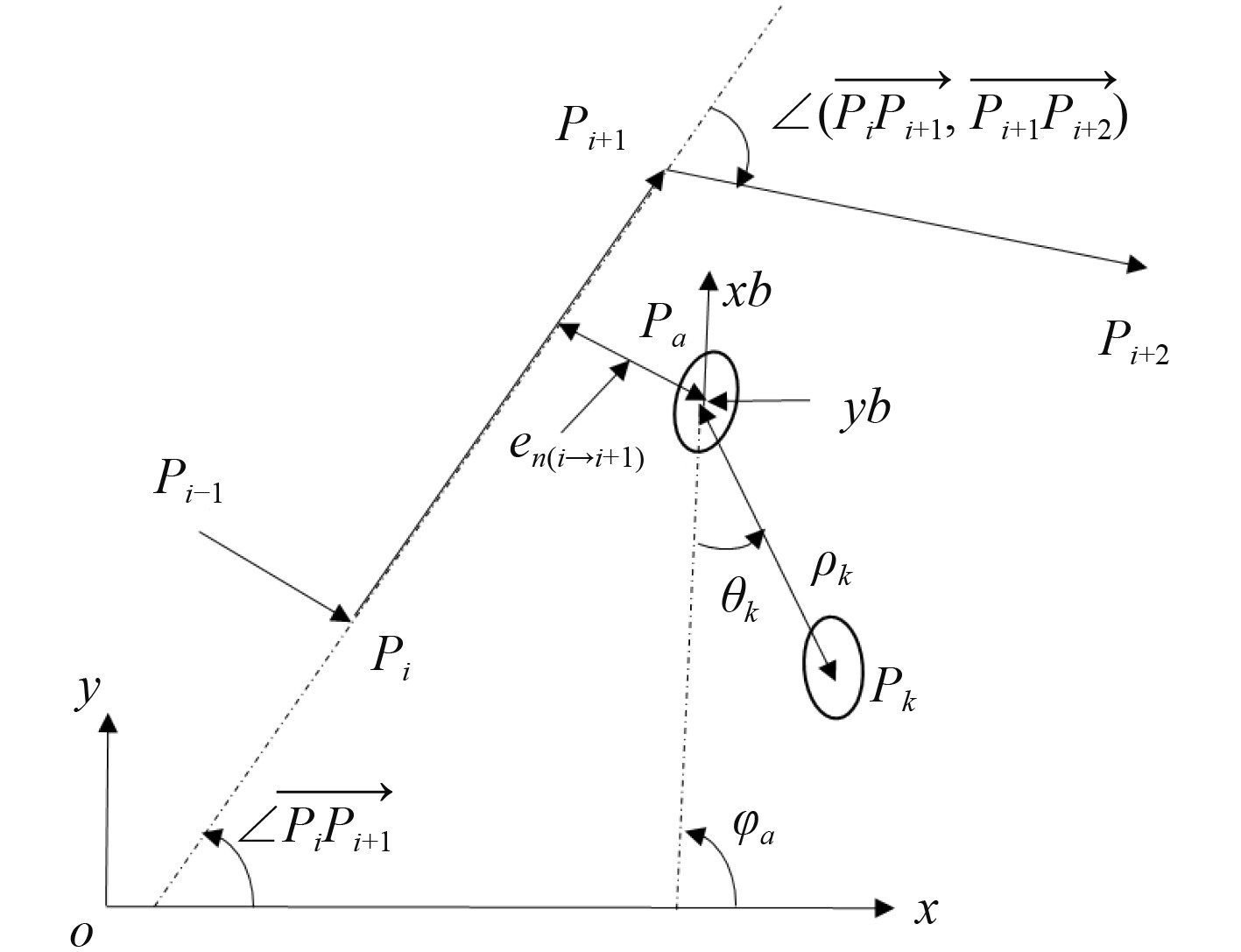
1 问题描述与局部路径优化 1.1 路径切换附近的编队队形抖动问题

基于领航者-跟随者的编队控制中，一般领航AUV执行路径跟随任务，路径跟随任务一般通过组成路径的路径点序列发送给领航者AUV。跟随者AUV通过接收领航者AUV的位置和航向，并根据队形设定计算跟踪位置点，进行点跟综，从而实现编队控制。坐标系与角度定义如图1所示。

一般将AUV编队控制限定在水平面内，路径由路径点序列P表示：

${\boldsymbol{P}} \;=\; \left[ {{P_1},{P_2}, \cdots {P_i},{P_{i + 1}},{P_{i + 2}}, \cdots {P_n}} \right],\;i = 1,2,...,n - 2$，$ \overrightarrow{{P}_{i}{P}_{i+1}}，\overrightarrow{{P}_{i+1}{P}_{i+2}}\left(i=1,2,\mathrm{..},n-2\right) $不平行。

在路径切换点$ {P_{i + 1}} $前后，路径由$ \overrightarrow {{P_i}{P_{i + 1}}} $切换至$ \overrightarrow {{P_{i + 1}}{P_{i + 2}}} $，根据领航者AUV位置P_a距路径切换点的距离$ \left\| {\overrightarrow {{P_a}{P_{i + 1}}} } \right\| $小于阈值$ d\left( {R,\angle \left( {\overrightarrow {{P_i}{P_{i + 1}}} ,\overrightarrow {{P_{i + 1}}{P_{i + 2}}} } \right)} \right) $作为路径切换判断依据。其中，R为AUV的回转半径、$ \angle \left( {\overrightarrow {{P_i}{P_{i + 1}}} ,\overrightarrow {{P_{i + 1}}{P_{i + 2}}} } \right) $为路径 $ \overrightarrow {{P_i}{P_{i + 1}}} $与$ \overrightarrow {{P_{i + 1}}{P_{i + 2}}} $的夹角，记为角$ {\alpha _{i + 1}} \in ( - \text{π} ,0) \cup (0, \text{π} ) $。跟随者AUV位置记为$ {P_f} $，其与领航者AUV的相对位置用$ \left( {\rho ,\theta } \right) $表示，领航者的航向用$ {\varphi _a} $表示。则跟随者的目标跟踪点位置$ p_f^d $为：

$ p_f^d = {p_a} + {\boldsymbol{{R}}^{bo}}\left( {{\varphi _a}} \right)\left[ \begin{gathered} \rho \cos \left( {\text{π} + \theta } \right) \\ \rho \sin \left( {\text{π} + \theta } \right) \\ \end{gathered} \right]。$

(1)

式中：${{\boldsymbol{R}}^{bo}}\left( {{\varphi _a}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _a}}&{ - sin{\varphi _a}} \\ {\sin {\varphi _a}}&{\cos {\varphi _a}} \end{array}} \right]$为领航AUV机体坐标系到大地坐标系的转换矩阵。

领航者AUV采用改进视线法^[10,11]进行路径跟随任务，在转换点前领航AUV的理想航向角为：

$\varphi _a^d\left( {\angle \overrightarrow {{P_i}{P_{i + 1}}} ,{e_{{n}\left( {i \to i + 1} \right)}}} \right) = \angle \overrightarrow {{P_i}{P_{i + 1}}} + \arctan ( - \frac{{{e_{{n}\left( {{i} \to i + 1} \right)}}}}{\Delta })。$

(2)

转换点后，领航AUV的理想航向角为：

$\begin{split} &\varphi _a^d\left( {\angle \overrightarrow {{P_{i + 1}}{P_{i + 2}}} ,{e_{{n}\left( {i + 1 \to i + 2} \right)}}} \right) = \\& \angle \overrightarrow {{P_{i + 1}}{P_{i + 2}}} + \arctan ( - \frac{{{e_{{n}\left( {{i + 1} \to {i + 2}} \right)}}}}{\Delta })。\end{split}$

(3)

其中：$ {e_{{n}\left( {i \to i + 1} \right)}} $为领航者位置P_a到直线$ \overrightarrow {{P_{i + 1}}{P_{i + 2}}} $的距离，$ \Delta $一般取3~5倍AUV的长度。

为降低分析难度，假设领航AUV路径跟随能力较强，在切换点前后领航AUV与路径的偏差距离$ {e_{{n}\left( {{i} \to {i + 1}} \right)}},{e_{{\text{n}}\left( {{\text{i + 1}} \to {\text{i + 2}}} \right)}} $均近似等于0。以跟随者在领航AUV正后方进行跟随的情况进行分析，切换前后领航AUV的理想航向角变化量为：

$ \delta (\varphi _a^d)\sim{\alpha _{i + 1}} = \angle \left( {\overrightarrow {{P_i}{P_{i + 1}}} ,\overrightarrow {{P_{i + 1}}{P_{i + 2}}} } \right) 。$

(4)

跟踪AUV理想跟踪点位置变化的二范数为：

$d \left( {\hat p_f^d - p_f^d} \right) = {\rho _k}\sqrt {2 - 2\cos {\alpha _{i + 1}}}。$

(5)

其中：$ \hat p_f^d $为路径切换后跟随者的目标跟踪点。由上式可知，路径 $ \overrightarrow {{P_i}{P_{i + 1}}} $与$ \overrightarrow {{P_{i + 1}}{P_{i + 2}}} $的夹角较小时，跟踪AUV的理想跟踪点位置变化距离较小，编队队形较好保持。在路径 $ \overrightarrow {{P_i}{P_{i + 1}}} $与$ \overrightarrow {{P_{i + 1}}{P_{i + 2}}} $的夹角较大时，除了AUV机动性不足的航向超调问题外，跟随AUV的理想跟踪点位置变化较大也是影响AUV编队队形保持的重要影响因素。

在基于路径跟随的编队控制方法中，在设定完成领航AUV的航行路径后，可根据领航AUV的路径点计算获得跟随AUV的航行路径。同时在每段路径上，采用路程百分比作为同步控制信息。在拐点附近路程百分比均接近于1，变化缓慢，此时通过路程百分比协调内外侧AUV航行速度误差较大。这恰好与在拐点附近内外侧AUV航行路径长度变化较大，需航速较准确的快速调整以保持较好的编队航行效果相矛盾。因此，基于路径跟随的编队控制方法在路径切换点附近同基于领航者-跟随者的编队控制方法一样，均表现不佳。

1.2 基于B样条曲线的局部路径重规划

考虑2种控制方法在路径切换点处的编队控制效果不佳，故采用B样条曲线在切换点附近拟合出一段平滑路径，改善AUV编队在切换点局部的控制效果。

本文采用均匀2次B样条对局部路径进行拟合平滑。以路径 $ \overrightarrow {{P_i}{P_{i + 1}}} $到$ \overrightarrow {{P_{i + 1}}{P_{i + 2}}} $的切换为例，取${P_{i + 1}} - \alpha \left( d \right) \cdot \frac{{\overrightarrow {{P_i}{P_{i + 1}}} }}{{\left\| {\overrightarrow {{P_i}{P_{i + 1}}} } \right\|}}、{P_{i + 1}}、{P_{i + 1}} + \beta \left( d \right) \cdot \frac{{\overrightarrow {{P_{i + 1}}{P_{i + 2}}} }}{{\left\| {\overrightarrow {{P_{i + 1}}{P_{i + 2}}} } \right\|}}$作为2次B样条的3个控制点，记为$P_{i + 1}^{(\alpha )}、P_{i + 1}^{(0)}、P_{i + 1}^{(\beta )}$。其中$ d $为路径切换的判别依据。则路径切换点附近的规划航迹和航迹的导数为：

$ \begin{array}{l} \vec P(t) = {B_{0,2}}(t)P_{i + 1}^{(\alpha )} + {B_{1,2}}(t)P_{i + 1}^{(0)} + {B_{2,2}}(t)P_{i + 1}^{(\beta )}，\\ \dot {\vec P}(t) = {{\dot B}_{0,2}}(t)P_{i + 1}^{(\alpha )} + {{\dot B}_{1,2}}(t)P_{i + 1}^{(0)} + {{\dot B}_{2,2}}(t)P_{i + 1}^{(\beta )}。\end{array} $

(6)

其中：

$ \left\{ \begin{gathered} {B_{0,2}}(t) = {(1 - t)^2}/2，\\ {B_{1,2}}(t) = ( - 2{t^2} + 2t + 1)/2, {{t}} \in \left[ {0,1} \right] ，\\ {B_{2,2}}(t) = {t^2}/2 。\\ \end{gathered} \right. $

(7)

$ \left\{ \begin{gathered} {{\dot B}_{0,2}}(t) = t - 1，\\ {{\dot B}_{1,2}}(t) = - 2t + 1, {{t}} \in \left[ {0,1} \right] ，\\ {{\dot B}_{2,2}}(t) = t。\\ \end{gathered} \right. $

(8)

在路径切换点，附近采用拟合路径的导数作为领航者AUV的理想航向角为：

$ \varphi _a^d\left( t \right) = \arctan \left( {\dot {\vec P}(t)} \right) 。$

(9)

AUV在路径切换点的局部路径时，参数$ t $计算式为：

$ t = \frac{{{P_a} - P_{i + 1}^{(\alpha /{\text{2}})}}}{{\left\| {{P_a} - P_{i + 1}^{(\alpha /{\text{2}})}} \right\| + \left\| {{P_a} - P_{i + 1}^{(\beta /{\text{2}})}} \right\|}}。$

(10)

其中：

$ P_{i + 1}^{(\alpha /{\text{2}})} = {P_{i + 1}} - \frac{{\alpha \left( d \right)}}{2} \cdot \frac{{\overrightarrow {{P_i}{P_{i + 1}}} }}{{\left\| {\overrightarrow {{P_i}{P_{i + 1}}} } \right\|}}, $

(11)

$P_{i + 1}^{(\beta /{\text{2}})} = {P_{i + 1}} + \frac{{\beta \left( d \right)}}{2} \cdot \frac{{\overrightarrow {{P_{i + 1}}{P_{i + 2}}} }}{{\left\| {\overrightarrow {{P_{i + 1}}{P_{i + 2}}} } \right\|}}。$

(12)

在基于路径跟随的编队控制方法中可以采用参数$ t $作为协调同步参数。

2 模型参数计算及路径参数设置 2.1 AUV模型参数

AUV水动力模型采用NPS AUV Ⅱ^[12]的水动力模型，其表达式为：

$ {\boldsymbol{M}}\dot v + {\boldsymbol{C}}\left( v \right)v + {\boldsymbol{D}}\left( v \right)v + {\boldsymbol{g}}\left( \eta \right) = {\boldsymbol{Q}} 。$

(13)

其中：$ {\boldsymbol{M}} $为系统的惯性矩阵（包含附加质量）；$ {\boldsymbol{C}}\left( v \right) $为科里奥利向心力矩阵，$ {\boldsymbol{D}}\left( v \right) $为阻尼矩阵；$ {\boldsymbol{g}}\left( \eta \right) $为重力、浮力的力和力矩向量；$ {\boldsymbol{Q}} $为外力和外力矩的合向量；具体表达见文献[12]。

航速及俯仰舵角均采用比例微分控制。

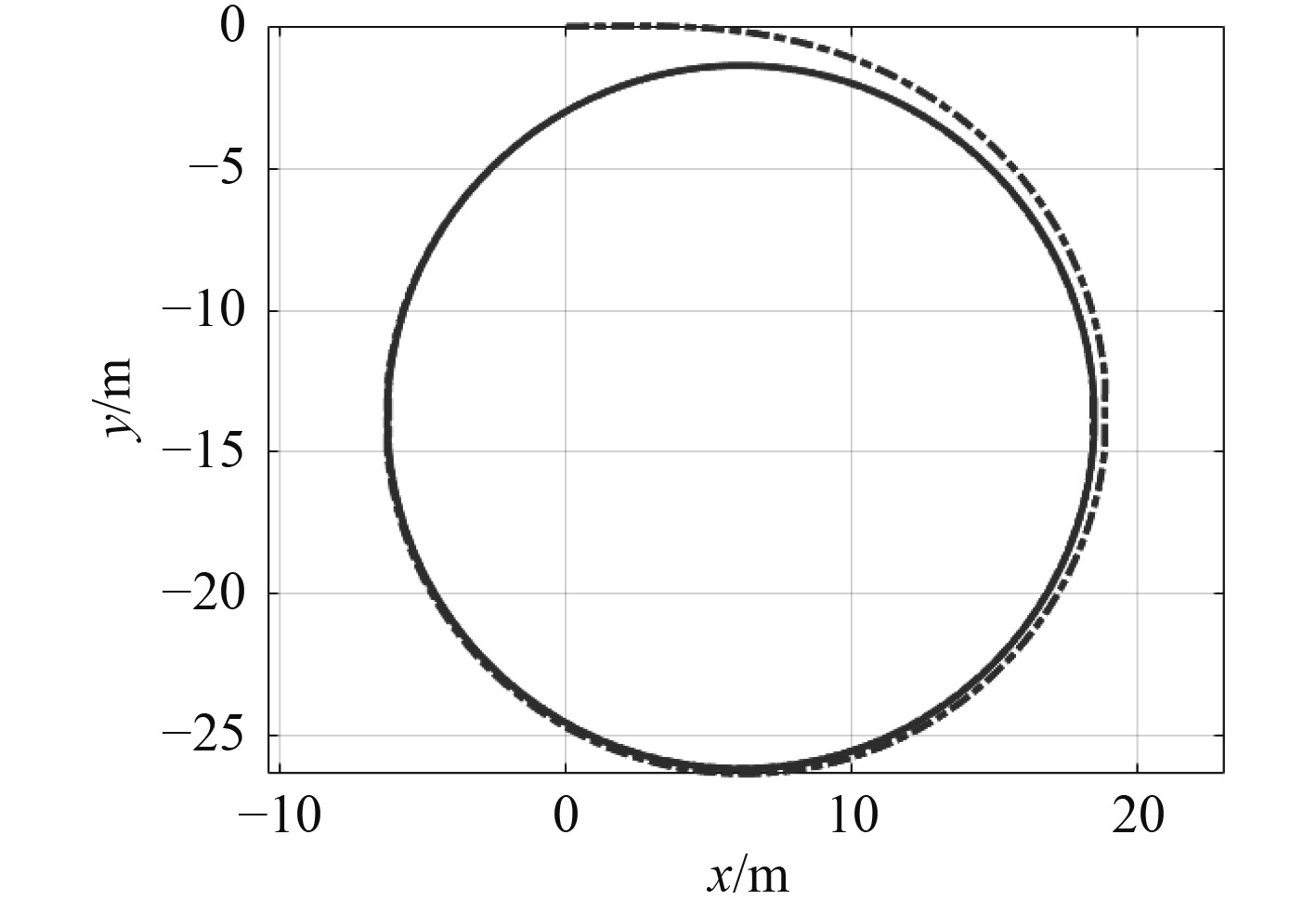
NPS AUV Ⅱ模型长度5.3 m，推进器最大转速设定为1500 r/min，最大舵角限制30°。设计编队航速2 kn，首先计算此模型的回转半径$ R $用于后面计算路径点的切换判断距离$ d $。在2 kn航速下，该模型的回转计算如图2所示，回转半径$ R = 12.66\;{\text{m}} $。

2.2 路径参数

领航者AUV的路径由路径点序列P给出，AUV在路径$ \overrightarrow {{P_i}{P_{i + 1}}} $上某点开始回转，与$ \overrightarrow {{P_{i + 1}}{P_{i + 2}}} $相切进入路径$ \overrightarrow {{P_{i + 1}}{P_{i + 2}}} $，则切换判断距离计算式为：

$ {d_{i + 1}} = \frac{R}{{{\rm{tan}}\left( {\frac{1}{2}{\alpha _{i + 1}}} \right)}},i = 1,....,n - 2 。$

(14)

考虑在实际应用中，路径设置时一般不会夹角过小，同时切换判断距离$ d $过小可能导致AUV偏离路径造成AUV切换路径点失败（$ \left\| {\overrightarrow {{P_a}{P_{i + 1}}} } \right\| > {d_{i + 1}} $一直成立）。考虑一定的机动需要一定的提前量，本文取路径切换判断距离$ d = 2R $，在进行局部路径B样条拟合时，取

$ \beta \left( d \right) = \frac{1}{3}\alpha \left( d \right) = \left\{ \begin{gathered} d/\sqrt 3 \cos {\alpha _{i + 1}} \geqslant 0.5 ，\\ d_0 \leqslant \cos {\alpha _{i + 1}} < 0.5，\\ \sqrt 3 d - 0.5 \leqslant \cos {\alpha _{i + 1}} < 0，\\ 2d \cos {\alpha _{i + 1}} \leqslant - 0.5。\\ \end{gathered} \right. $

(15)

在基于路径跟随的编队控制方法中，首先根据领航者AUV的路径点序列$ {\boldsymbol{P}} $及跟随者与领航者的相对位置用$ \left( {\rho ,\theta } \right) $计算获得跟随者AUV的路径点序列${{\boldsymbol{P}}^f} = $$\left[ {P_1^f,P_2^f, \cdots P_n^f} \right],i = 1,2,...,n$。

AUV在路径$ \overrightarrow {{P_i}{P_{i + 1}}} $上时，路径同步控制参数可取为：

$ \begin{gathered} {\lambda ^a} = \left\| {\overrightarrow {{P_a}{P_{i + 1}}} } \right\|/\left\| {\overrightarrow {{P_i}{P_{i + 1}}} } \right\|，\\ {\lambda ^f} = \left\| {\overrightarrow {{P_f}P_{i + 1}^f} } \right\|/\left\| {\overrightarrow {P_i^fP_{i + 1}^f} } \right\|。\\ \end{gathered} $

(16)

其中，$ {\lambda ^a}、{\lambda ^f} $分别为领航者与跟随的同步控制参数。当$ \left\| {\overrightarrow {{P_a}{P_{i + 1}}} } \right\| \leqslant {d_{i + 1}} $，切换路径时，路径同步参数取为：

$ \begin{gathered} {\lambda ^a} = \left\| {\overrightarrow {{P_a}{P_{i + 1}}} } \right\|/\left\| {\overrightarrow {{P_i}{P_{i + 1}}} } \right\| + {t^a} ，\\ {\lambda ^f} = \left\| {\overrightarrow {{P_f}P_{i + 1}^f} } \right\|/\left\| {\overrightarrow {P_i^fP_{i + 1}^f} } \right\| + {t^f} 。\\ \end{gathered} $

(17)

其中，$ {t_a}、{t_f} $分别为领航者和跟随者在局部B样条拟合路径上定义的同步参数，参考上文路径参数。

2.3 航速调整策略

在基于领航者跟随者的编队控制中，根据跟随者位置$ {P_f} $与目标跟踪点位置$ p_f^d $的距离调整航速：

$ \hat u = \left\{ \begin{gathered} u, \left\| {p_f^d - {P_f}} \right\| \leqslant {\delta _1}，\\ u + {{{k}}_1}\frac{{\left\| {p_f^d - {P_f}} \right\|}}{\delta }, \left\| {p_f^d - {P_f}} \right\| > {\delta _1} 。\\ \end{gathered} \right. $

(18)

在基于路径跟随的编队控制中，根据路径协调参数${\lambda ^a}、{\lambda ^f}$进行航速调整：

$ \hat u = \left\{ \begin{gathered} u, \left\| {{\lambda ^a} - {\lambda ^f}} \right\| \leqslant {\delta _2}，\\ u + {k_2}\frac{{\left\| {{\lambda ^a} - {\lambda ^f}} \right\|}}{{{\delta _2}}}, \left\| {{\lambda ^a} - {\lambda ^f}} \right\| > {\delta _2} 。\\ \end{gathered} \right. $

(19)

式中：$ u、\hat u $分别为领航者的航速与跟随者的期望航速；$ {{k}_1}、{\delta _1} $分别为航速调整系数与跟踪误差参考值；$ {{k}_2}、{\delta _2} $分别为基于路径跟随的编队控制中航速调整系数与同步参数偏差参考值。

3 数值仿真 3.1 领航AUV路径跟随优化前后对比

NPS AUV在2 kn航速下完成给定路径的跟随任务，设计航行路径为（单位：m）：

$ \begin{gathered} {P_1} = \left( {250,0} \right),{P_2} = \left( {350,0} \right),{P_3} = \left( {350,500} \right), \\ {P_4} = \left( {550,500} \right),{P_5} = \left( {550,0} \right),{P_6} = \left( {800,250} \right), \\ {P_7} = \left( {800,850} \right),{P_8} = \left( {550,600} \right),{P_9} = \left( {300,600} \right), \\ {P_{10}} = \left( {550,850} \right),{P_{11}} = \left( {300,850} \right),{P_{12}} = \left( {50,600} \right), \\ {P_{13}} = \left( { - 100,600} \right),{P_{14}} = \left( { - 100,0} \right),{P_{15}} = \left( { - 500,0} \right)。\\ \end{gathered} $

航向采用比例微分控制，控制系数取：

$ {K_p} = 0.5,{K_d} = 0.5。$

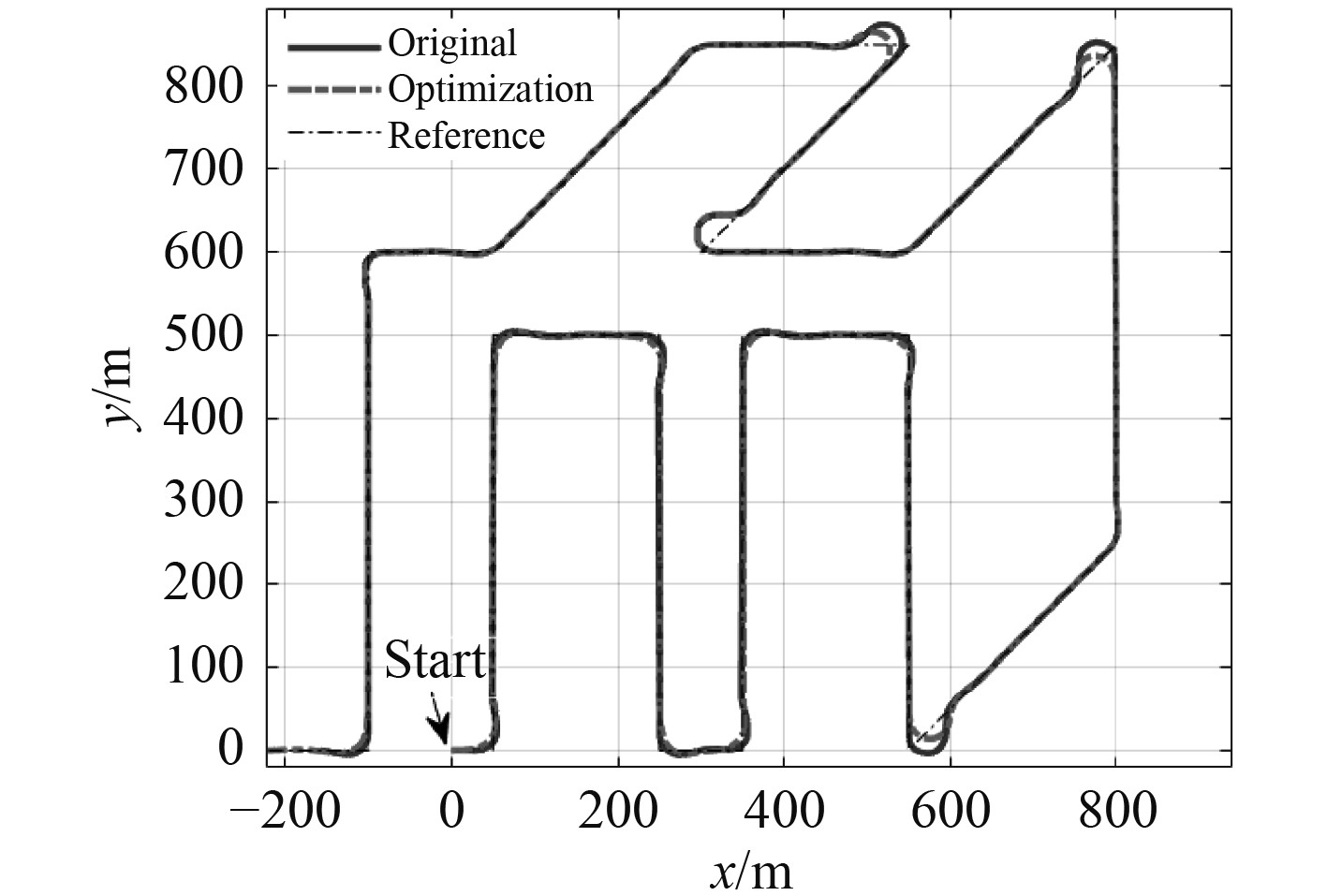
采用改进视线法进行路径跟随，仿真可得其循迹轨迹如图3所示。

在路径转换点处根据路径夹角设计局部路径的B样条曲线拟合，可以优化AUV模型循迹效果。同时AUV的航向过渡更加平滑，如图4所示。

3.2 基于领航跟随的AUV编队控制仿真

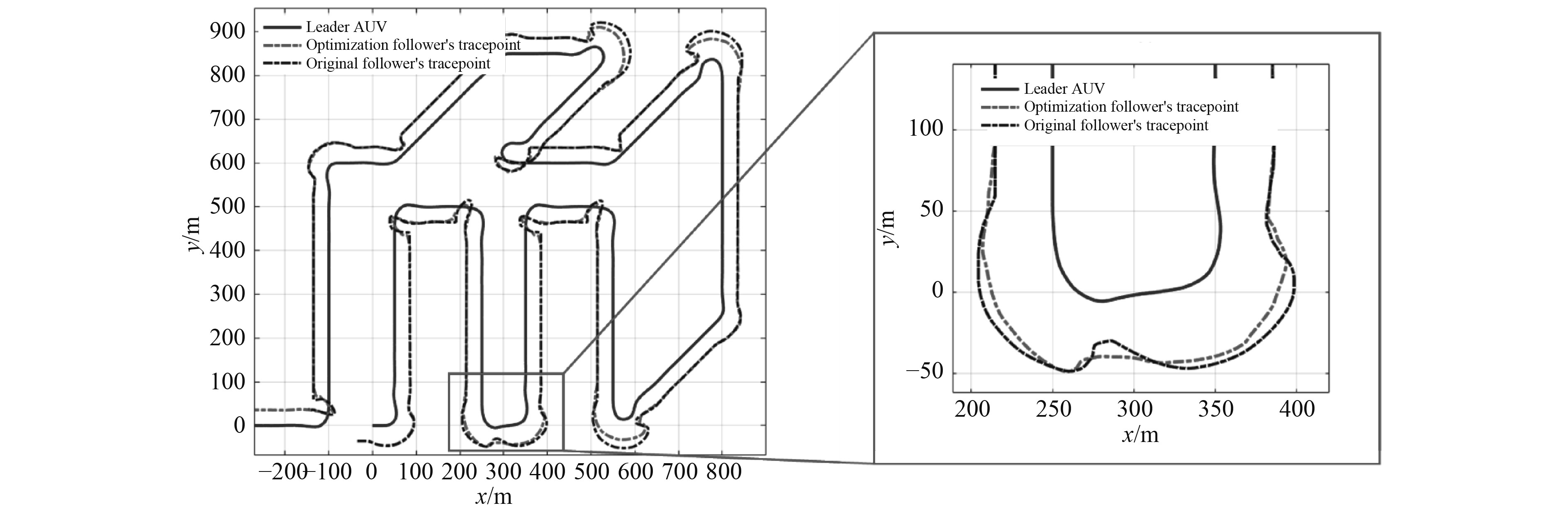
跟随AUV与领航者AUV的相对位置为：$ \left( {\rho ,\theta } \right) = $ (50,45°)，航速调整系数$ {{k}_1} = 0.1\; {\text{m/s}} $，跟踪误差参考值$ {\delta _1} = 5\;{\text{m}} $。仿真得到基于领航跟随的控制算法领航者AUV航行轨迹及跟随AUV的目标跟踪点轨迹，如图5所示。可以看出，在路径切换点前后领航AUV航向角$ \varphi _a^d $的变化都较大，导致编队队形在切换点保持效果不佳。在局部进行B样条曲线拟合后，对跟随AUV的目标跟随点局部路径上过渡曲率和速度有改善，对编队队形的保持具有积极意义。

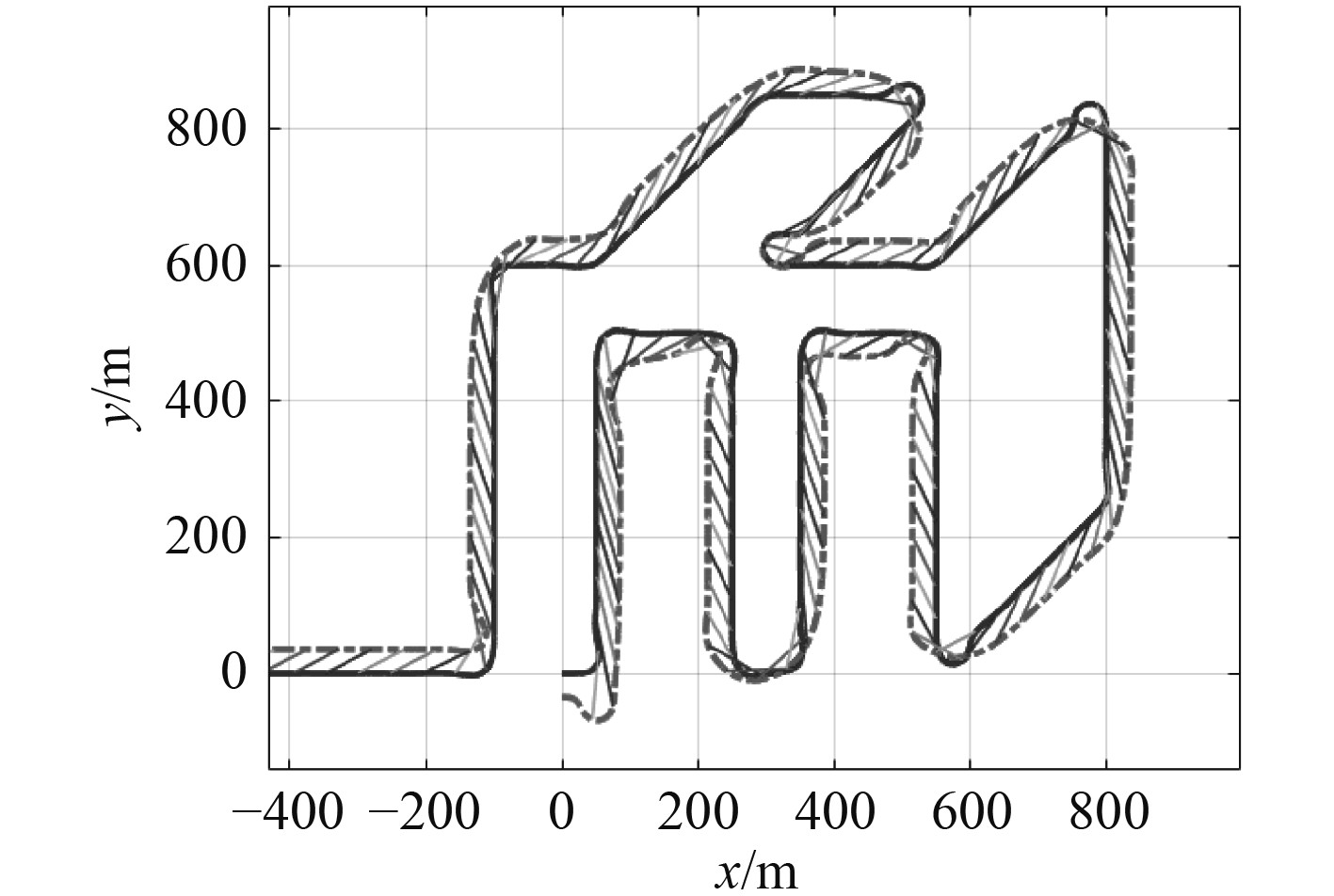
采用局部B样条优化的路径进行基于领航者跟随者的编队控制仿真，领航AUV与跟随AUV的航行轨迹如图6所示。跟随AUV与领航AUV距离时间历程如图7所示，得益与跟踪点曲率及变化速度的改善，跟踪误差有所减小。

3.3 基于路径跟随的AUV编队控制仿真

跟随AUV与领航者AUV相对位置为：$\left( {\rho ,\theta } \right) = $ (50,45°)，航速调整系数$ {{k}_2} = 0.05 $，同步参数误差参考值$ {\delta _2} = 0.1 $。仿真得到路径跟随的AUV编队控制算法的AUV编队航行轨迹，路径跟随算法领航者AUV与跟随者AUV均采用改进视线法进行路径跟随任务，跟随AUV的路径点通过领航AUV的路径点及相对偏移距离计算获得。路径切换点局部采用B样条曲线拟合，并将拟合参数$ t $作为协调同步参数的一部分，在路径切换点附近调整跟随AUV的航速。仿真结果如图8所示。

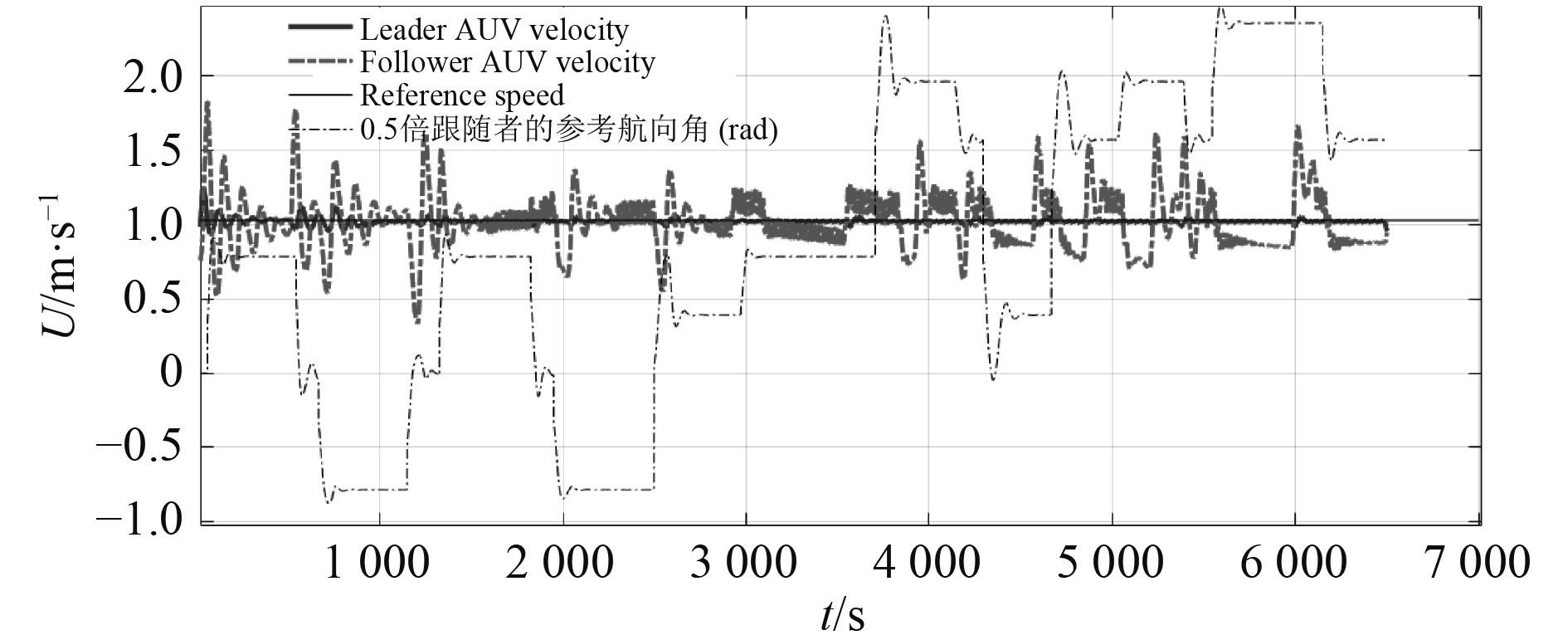
领航AUV及跟随AUV的航速如图9所示。在路径切换附近，通过局部路径的同步参数引入，航速调整更迅速。

3.4 2种编队控制方法的控制效果比较

从仿真实现的角度来说，基于领航者-跟随者的AUV编队控制结构简单，跟随者以领航AUV的位置及航向为输入，根据设定的相对方位及距离进行点跟踪，完成编队任务。整体编队队形的保持效果依赖于领航AUV位置及航向的实时获取、跟随AUV自身较高的机动性或平滑的路径设置。基于路径跟随的AUV编队控制队形保持则更加依赖合理的路径同步参数定义及AUV的速度调整性能。

4 结　语

本文通过B样条曲线进行局部路径拟合，改善了基于领航者-跟随者的编队控制方法和基于路径跟随的编队控制方法等2种常用的AUV编队控制方法，在路径切换点附近的编队控制效果。

针对基于领航者-跟随者的编队控制，通过B样条曲线在路径切换点附近根据路径变化角度、路径点切换距离确定拟合路径控制点，对局部路径平滑处理。该处理方式改善了领航AUV的路径跟随效果，削弱了领航AUV切换航向导致计算的跟随AUV跟踪目标位置变化速率，使得跟随AUV在进行点跟随时的路径更平滑。

针对基于路径跟随的编队控制，通过B样条曲线对领航AUV和跟随AUV的切换点处路径进行光滑化处理，同时利用B样条基函数自变量参数$ t $作为在切换点的局部路径协调同步参数的一部分，提高了在切换点附近编队的时间同步速度。